On the nature of the stimulus information necessary for estimating mean size of visual arrays

Abstract

This paper explores the nature of the representations used for computing mean visual size of an array of visual objects of different sizes. In Experiment 1 we found that mean size judgments are accurately made even when the individual objects (circles) upon which those judgments were based were distributed between the two eyes. Mean size judgments were impaired, however, when a subset of the constituent objects involved in the estimation of mean size were rendered invisible by interocular suppression. These findings suggest that mean size is computed from relatively refined stimulus information represented at stages of visual processing beyond those involved in binocular combination and interocular suppression. In Experiment 2 we used an attentional blink paradigm to learn whether this refined information was susceptible to the constraints of attention. Accuracy of mean size judgments was unchanged when one of the two arrays of circles was presented within a rapid serial visual presentation sequence, regardless of task requirement (single vs. dual task) and the array’s time of presentation relative to the brief appearance of a target that was the focus of attention. Evidently the refined stimulus information used for computing mean size remains available even in the absence of focused attention.

Introduction

People may claim to be poor at arithmetic, but they nonetheless behave as if their brains contained a calculator capable of executing statistical computations. For example, humans are quite good at detecting the central tendency and the variance of velocity signals within a large array of moving dots (Atchley & Andersen, 1995). People can also implicitly learn statistical regularities within the speech streams they hear (Saffran, Aslin, & Newport, 1996) and within the visual sequences they see (Chun & Jiang, 1999; Fiser & Aslin, 2002).

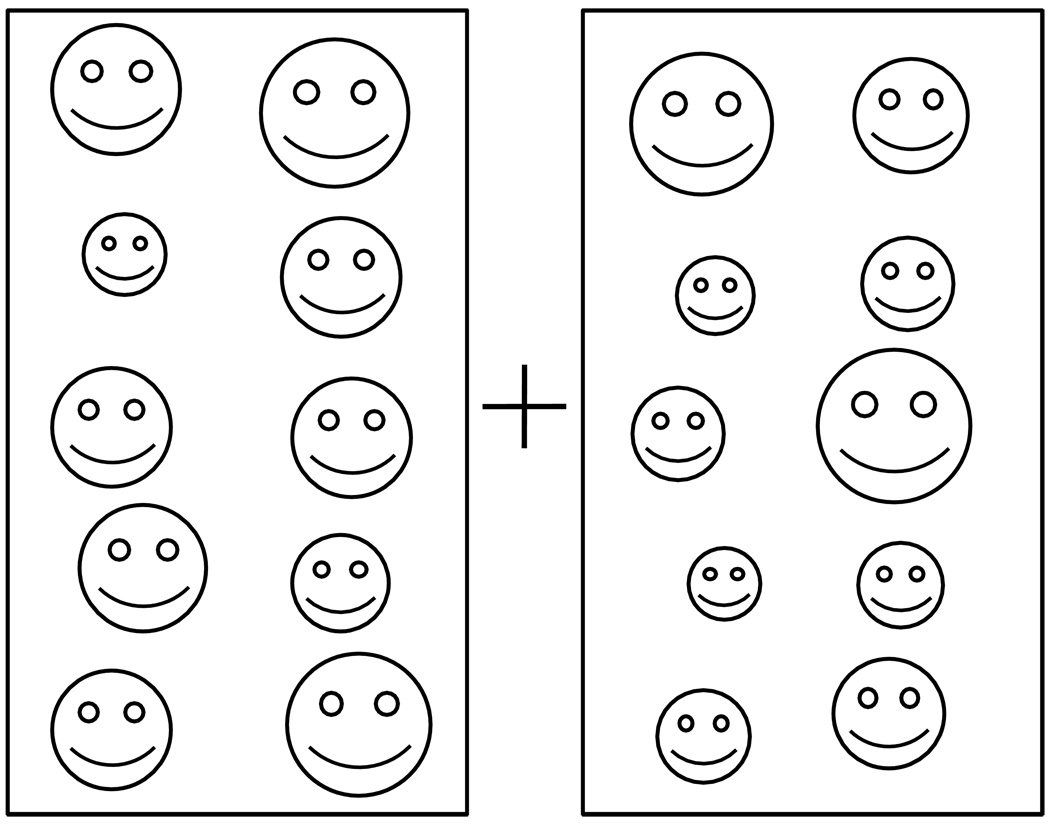
Our statistical abilities are also evidenced on a seemingly abstract visual task: judging the mean size of sets of objects within the visual scene (Ariely, 2001). Look at the two arrays of different sized faces in Figure 1. In one array, the average size of the constituent faces is 10% larger than the average size of the faces in the other array. Even when the arrays are very briefly presented, observers can accurately judge in which array the average size is larger, down to average size differences as small as 6% (Chong & Treisman, 2003). Although the required judgment seems complex and computationally demanding, performance on the task is surprisingly accurate even under challenging conditions (Chong & Treisman, 2005a, 2005b). This remarkable ability may represent one instance of our general ability to think and reason about numerical properties (Feigenson, Dehaene, & Spelke, 2004).

Figure 1.

Which array of faces, left or right, portrays an overall larger average face size? The correct answer is given in the caption to Figure 2.

In this paper, we have used converging techniques to identify the nature of the representations used for computing mean visual size. Results from the main experiments point to a central representation that is surprisingly immune to attentional constraints.

Experiment 1: Can invisible circles contribute to mean size judgments?

In our first experiment, we tested whether mean size judgments could be performed when some of the elements comprising the two arrays were perceptually invisible. The possibility that observers could perform mean size judgments under these conditions is not all that farfetched. Indeed, there is considerable evidence that visual stimuli falling outside of awareness are still processed to an extent sufficient to influence subsequent decisions or behavior. To give just a few examples, pictures masked to invisibility can still facilitate performance on a subsequent naming task (Bar & Biederman, 1998), words not explicitly perceived are still processed semantically (Shapiro, Driver, Ward, & Sorensen, 1997), and oriented texture elements erased from awareness by visual crowding still contribute to the overall impression of global texture (Parkes, Lund, Angelucci, Solomon, & Morgan, 2001).

The purpose of this first experiment is simple: to learn the extent to which stimulus information critical for estimating mean size can be utilized even when some of the elements portraying that information fall outside of visual awareness. To implement the experiment, we utilized interocular suppression produced by dissimilar stimulation of the two eyes (Kim & Blake, 2005).

Methods

Observers

Eleven participants (including two of the authors) participated in this experiment. All had normal or corrected-to-normal visual acuity and good stereopsis. All aspects of the study were carried out in accord with the regulations of Departmental Review Committee of Yonsei University.

Apparatus and stimuli

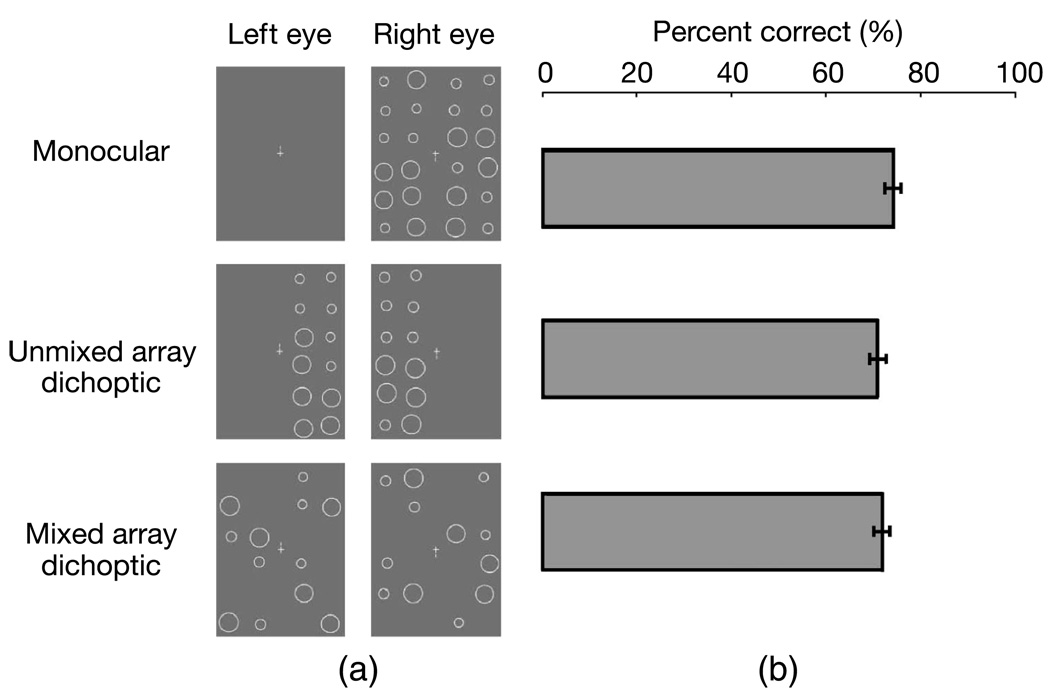
Stimuli were created using MATLAB in conjunction with the Psychophysics Toolbox (Brainard, 1997; Pelli, 1997) and were displayed on a linearized 21″ Samsung monitor the average background luminance of which was 6.65 cd/m². Figure 2 shows a schematic of the dichoptic display for one of the test conditions. Two gray rectangles (9.6° × 7.2°) were centered on the left and right halves of the video display, and they constituted the stimuli viewed by the left-eye and the right-eye, respectively (details of dichoptic stimulation are given below). Both rectangular regions were subdivided into two virtual matrices comprising 6 × 2 cells (24 cells/rectangle). Each of the 12 cells in the left-hand matrix in one rectangle contained a circle, and each of the 12 cells in the right-hand matrix in the other rectangle contained a circle; thus the together the two rectangular regions contained two arrays of 12 circles (total of 24 circles in all). All circles comprising the two arrays were blurred slightly by Gaussian filtering, with the luminance of the circles ranging from 6.86 cd/m² to 8.37 cd/m² from edge to center. Participants dichoptically viewed the left- and the right-halves of the video screen, and thus the two rectangular areas, through a conventional mirror stereoscope. A small fixation cross and nonious lines were always present at the center of the two rectangular regions to facilitate binocular alignment.

Figure 2.

The stimuli of Experiment 1. In “suppressed” condition, some sizes were suppressed by the random dot pattern, whereas suppressed sizes were physically removed in “yoked” condition. From the observer’s viewpoint, these two conditions were perceptually identical. In Figure 1, the array of faces on the left has an overall larger mean size.

In one of the arrays of 12 circles, each circle was either 0.7° or 1.2° in diameter. For different test conditions, these two sizes of circles could appear in the following proportions, expressed as small relative to large: 2:10, 4:8, 8:4, or 10:2. For the other array of 12 circles, we generated two different circle diameters, always assigned in equal proportion to the circles (6:6); these two diameter values were selected so that the mean circle size of this array always differed by 15% relative to the mean size of the other array. The absolute value of average sizes was varied over trials to prevent participants from judging mean size differences based on the actual sizes of individual circles. By using this method of size generation, we could rule out the possibility that participants used the sampling strategy of relying on the largest circles (Myczek & Simons, 2008) and, rather, forced them to make their judgments based on the mean rather than the median (Chong & Treisman, 2005b). In fact, if they made their judgment based just on the largest circles in a display, their performance would be at chance level (50%).

Next, consider the cells formed by the two 6 × 2 matrices comprising the regions within left- and right-eye arrays not occupied by circles. Presented within some of these cells was a variable number of texture patches, each consisting of a 1.6° × 1.6° random dot pattern composed of small (0.16°), equal density gray (6.65 cd/m²) and white (14.82 cd/m²) square pixels. The number of texture patches was equal for the two halves of the arrays, and the total number varied from 0 to 18 in steps of 6. Aside from one important constraint, the locations of the texture patches in one array were randomly assigned from trial to trial, independently for the two matrices of texture patches. The constraint was that the unsuppressed, visible circles had to create the same mean size difference between left and right arrays as did all of the circles, both suppressed and visible; there were no “inconsistent” trials where these two possible perceptual states might yield opposing responses and, therefore, confound error feedback following each trial. These high contrast, sharp-edged dot patterns were considerably stronger than the low contrast, blurred circles imaged on the corresponding areas of the other eye and, consequently, the texture patches very effectively dominated perception when the displays were presented dichoptically at the exposure duration used in this experiment, 200 ms—the blurred circles in rivalry with the texture patches were reliably blocked from visual awareness by interocular suppression.

Procedure

Two types of trials were randomly intermixed during a test session. On “suppression trials” a variable number of suppressors was presented to the eye not receiving the two arrays of circles, with the actual number ranging from 0 to 18 in steps of 6 (i.e., 0, 6, 12, or 18 suppressors). The suppressors were randomly distributed between the two halves of the display, with the provision that “inconsistent” trials were not permitted (see previous paragraph). On “yoking trials” a variable number of suppressors was also presented but the corresponding circles in the other eye’s view were physically removed on these trials; this latter condition provides an estimate of task performance when a reduced number of real, visible circles are available for the judgment.

The two different trial types—“suppressed” and “yoking”—together with the number of suppressors made 7 distinct trial types because the display was exactly the same for each trial types when the number of suppressors was 0. Each observer was given 48 practice trials followed by 336 experimental trials (7 distinct trial types × 48 repetitions/trial type). The order of trials was randomized for each participant.

Participants pressed the ‘1’ key when they thought the left array had the larger mean size, and they pressed ‘2’ when they thought the right array had the larger mean size. Error feedback was given following each trial, with “correct” corresponding to the mean size difference associated with all circles (suppressed or not) presented on that trial; on no trials would the visible circles produce a different correct answer than would all of the circles (i.e., potential “inconsistent” trials that would confound error feedback were never presented).

Results and discussion

For our main experiment to work, it is essential that observers be able to perform the mean size judgment task under conditions of dichoptic presentation of the two arrays of circles. To confirm that this was possible, we first performed a control experiment in which elements comprising the two arrays were divided between left and right eyes. Figure 3a shows examples of stimuli in the three different conditions tested in this control experiment. The strategy for generating sizes was similar to the main experiment. One array had varying proportions (small: large; 3:9, 5:7, 7:5, or 9:3) of two sizes (0.72° and 1.32°). The other array had the same proportion of two sizes and the two sizes were determined to generate the mean size differences, either 7% smaller or larger than the corresponding array. Figure 3b shows results for this control experiment. Overall accuracy was 72%, comparable to performance measured previously with similar arrays (Chong & Treisman, 2005b). ANOVA with display type as a factor showed no significant differences (F(2, 14) = 1.53, p = .25). Likewise, pairwise t-tests between the three conditions showed no significant differences (all ps > .05). So, observers can compute mean size regardless how the elements of the arrays are distributed between the eyes. Evidently, then, stimulus information supporting this judgment is represented and extracted at a level of processing after binocular combination, which is generally agreed to be no earlier than primary visual cortex (Hubel & Wiesel, 1968; Poggio & Fischer, 1977). This conclusion stands to reason, given that the statistical judgment requires spatial integration of size information among local elements, a form of information representation not provided in the very earliest stages of visual processing.

Figure 3.

The stimuli and the results of control experiment. (a) shows three types of stimuli. Note that these three types generated the same percept. (b) plots the performance of mean size judgments against these three conditions. The error bars are SEMs.

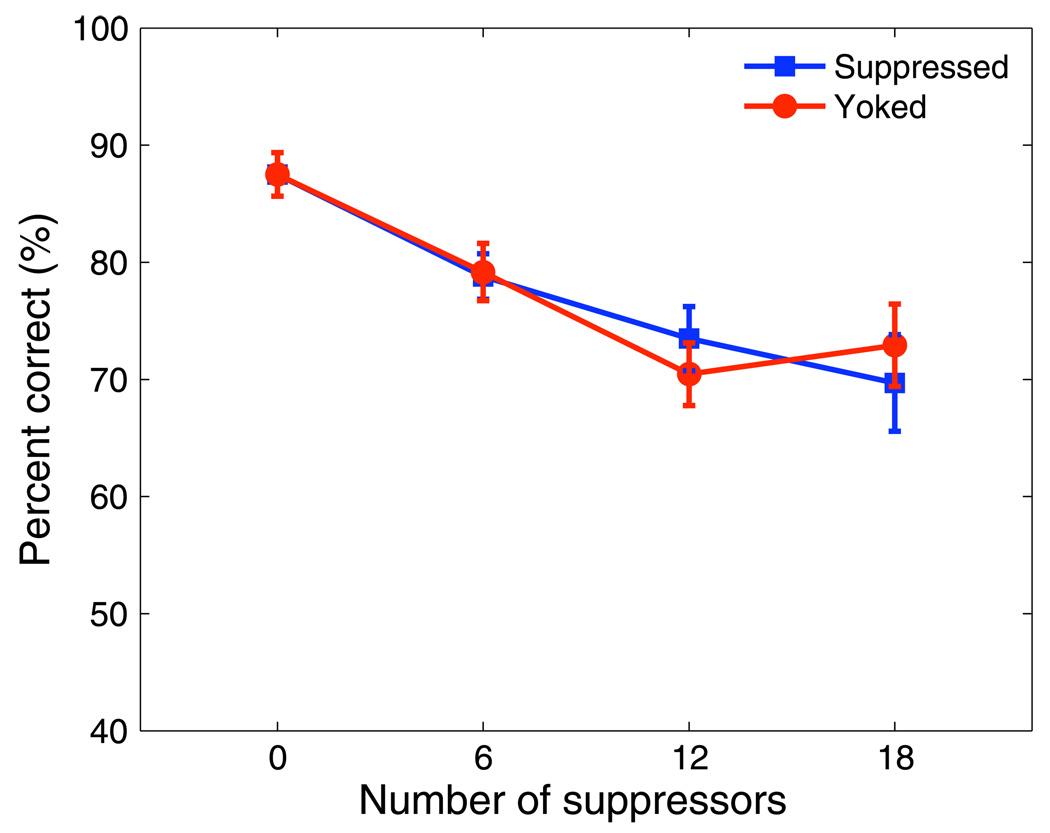
Figure 4 summarizes results from the main experiment, for the “suppressed” and “yoking” trials. Looking first at the “yoked” condition, performance deteriorated as the number of circles available for the judgment decreased; this observation, of course, is not surprising and merely confirms that the sample size influences the accuracy with which the mean can be estimated. The important finding is that performance significantly deteriorated not only for the “yoked” condition (F(3, 30) = 9.33, p < .01), in which circles were physically missing from the display, but also for the “suppressed” condition (F(3, 30) = 8.61, p < .01) in which circles were present but not visible. For statistical comparisons between the “suppressed” and the “yoked” conditions, we removed from the data set those trials on which no suppressors were presented, because for those trials there is no distinction between “suppressed” and “yoking” trials. ANOVA based on the remaining trials confirmed that performance between the two conditions did not significantly differ (F(1, 10) = 0.07, p = .80). Moreover, the interaction between the two conditions and the number of suppressors was not significant (F(2, 10) = 1.64, p = .22). Clearly, the suppressed circles lose their effectiveness as stimuli for mean size judgments. In the course of earlier, pilot work leading up to this experiment, we also tested other, related display presentation modes (e.g., presentation of suppressors to one eye only, and suppression of all circles and not just some of them). In all cases, interocular suppression effectively removed circles from the computation of mean size, as evidenced by the steady decline in task performance with number of suppressors.

Figure 4.

The results of Experiment 1. Percent correct for suppressed (squares) and yoked (circles) conditions. The error bars are standard errors of the mean (SEMs). Note that the mean size difference used in this main experiment (15%) is larger than the mean size (7%) used for the control experiment summarized in Figure 3.

The results from this experiment, and the control experiment preceding it, are consistent with the notion that statistical properties of sets are computed from relatively refined stimulus information represented at stages of visual processing beyond those involved in binocular combination and interocular suppression, processes themselves construed as arising within a hierarchy of stages (Tong, Meng, & Blake, 2006). The idea that statistical properties pertaining to object sizes is based on refined stimulus information is also consistent with recent findings implying that mean size is computed after modulation of perceived size by the Ebbinghaus illusion (Im & Chong, 2009).

These findings led us next to ask whether the refined stimulus information used for mean size judgments is susceptible to the constraints of attention, constraints that presumably compromise the resolution with which objects and events are represented? To answer this question, we performed the following experiment.

Experiment 2: Judging mean size with limited attention

To manipulate attentional resources available for making mean size judgments, we employed the attentional blink (AB) paradigm (Raymond, Shapiro, & Arnell, 1992; Chun & Potter, 1995). With this procedure, observers are required to identify two targets, T1 and T2, appearing within a sequence of rapidly presented items; detection of T2 can be significantly impaired when it follows T1 by ½ sec or less, presumably because T1 continues to occupy attentional resources for a short time after its appearance. The AB, in other words, provides an index of the susceptibility of a visual task to limited attentional resources, and it has been used in a variety of contexts including implicit learning with limited attentional capacity (Luck, Vogel, & Shapiro, 1996; Seitz, Lefebvre, Watanabe, & Jolicoeur, 2005).

Experiment 2-1: Judging mean size when the stimulus information is spatially distributed

In Experiment 2-1, T1 was a single digit and T2 constituted the pair of circle arrays used to generate estimates of mean size. We compared accuracy of mean size estimates between various lags in an AB stream and between two conditions that use identical sequences of stimuli: a dual task requiring perceptual judgments concerning T1 and T2 versus a single task requiring a perceptual report based on T2 only.

Methods

Observers

Thirty-three Yonsei University undergraduate students participated to fulfill a course requirement. Seventeen students were assigned to the dual task condition and sixteen students were assigned to the single task condition. All participants gave informed consent after reading the form approved by the Departmental Review Committee of Yonsei University. All participants reported having normal or corrected-to-normal vision. All were naive to the purpose of the experiment.

Apparatus and stimuli

The apparatus was the same as in Experiment 1. Figure 5a shows a schematic of the stimuli used in Experiment 2-1. Single digits (3 ~ 9) portrayed in Helvetica font were used as T1, and the distractors were the capital alphabet letters (excluding B, I, O, Q, S, Z) also presented in Helvetica. The average size for T1 and distractors was 1.31° × 2.09° and 1.63° × 2.09°, respectively. They appeared one at a time at the center of a square (2.95° × 2.95°) window located at the center of the video display. Low contrast (~3.8%) Gaussian random noise was added to the grayscale images of T1 and to the distractors embedded in the square. T2 comprised two arrays of circles located in the right and left halves of the display frame. Each array contained 16 circles placed randomly within a 28-cell (7 × 4) virtual matrix, each cell of which subtended 2.95° × 2.95°. The position of each circle was randomly jittered within its cell (±0.12° on average).

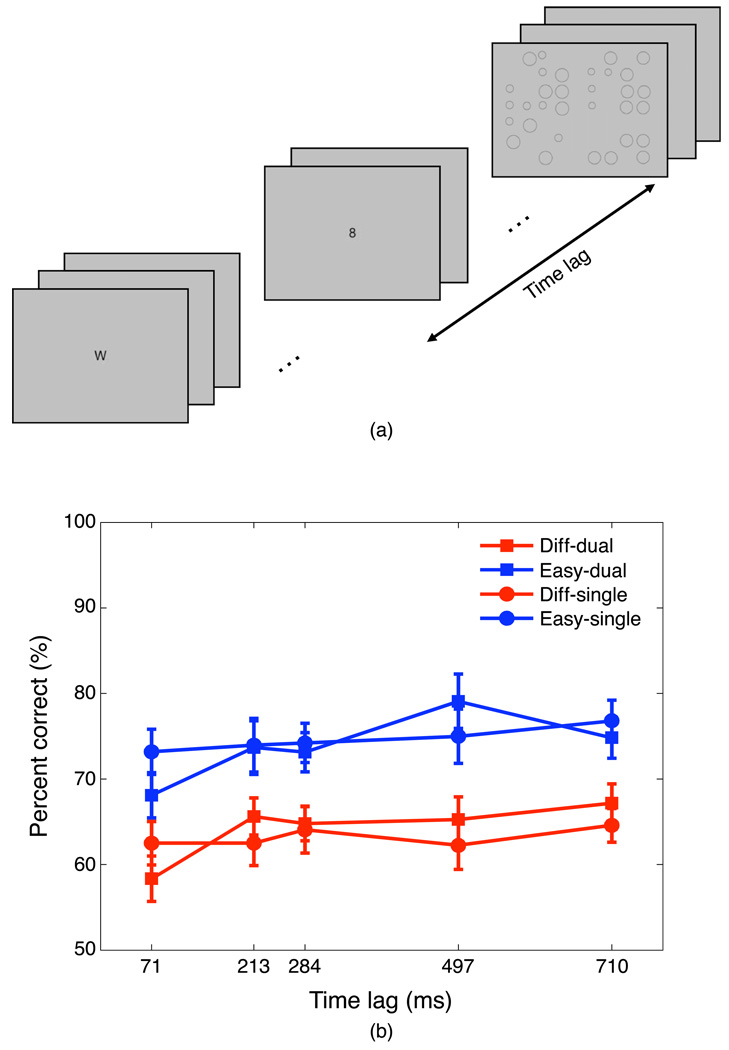
Figure 5.

(a) The timeline of Experiment 2-1. Time lag was defined by the time difference between T1 (digit) and T2 (circle arrays). Stimulus onset asynchrony (SOA) was 71 ms. (b) the percent correct of T2 given correct report of T1. Both T1 and T2 were reported in the dual task whereas only T2 was reported in the single task. The mean size difference was 8% for the difficult condition and 13% for the easy condition. The error bars are SEMs.

To generate the arrays constituting T2 we used the same method as that used in Experiment 1. Each half of the T2 display contained 16 elements. One half of the display had the two sizes (1.22° and 2.26°) and two sized circles could appear in the following proportions (small: large): 4:12, 6:10, 10:6, or 12:4. For the other half, we selected two different sizes to have the mean size difference of 8% or 13% as compared to the first half. In this half, we always kept the number circles of each size equal (8:8) and the range of the two sizes was the same as in the first half. The luminance of background was 51.34 cd/m² and the luminance of T1, distractors, and T2 was 0.72 cd/m².

Procedure

In this experiment we varied three factors: 1) level of difficulty—8% and 13% average size differences, 2) time lag between T1 and T2, which could be—1, 3, 4, 7, or 10 lags (T2 follows T1), and 3) type of task, single task (monitor T2 only) and dual task (monitor T1 and T2). The first two variables (difficulty and lag) were manipulated as within subject variables and the last (task) varied between subjects. For each task, one experimental block consisted of 10 trials (5 time lags × 2 levels of difficulty). Observers performed 40 trials as practice and 24 experimental blocks (240 trials).

Figure 5a shows the timeline for a single trial. A small, central fixation character appeared for 506 ms followed by sequential presentation of 22 display frames each presented for 59 ms with a blank ISI of 12 ms between successive displays. The position of T1 was randomly selected from the 5th to 7th positions. At the end of each stimulus sequence, observers performed their designated task (single or dual judgment, depending on the observer’s group assignment). For observers performing the dual task, they identified T1 by pressing the target digit presented (3–9) and, next, they judged whether the circle array with larger mean size appeared on the left (“press 1”) or on the right (“press 2”), guessing if necessary. For observers performing the single task, they performed just the mean size judgment on T2.

Results and discussion

Figure 5b shows the results from Experiment 2-1. As expected, performance on this task did depend on the level of difficulty of the judgment as manipulated by the difference in mean size between the two arrays (8% vs. 13%); a repeated measures ANOVA confirmed that the effect of task difficulty was statistically significant (F(1, 31) = 98.89, p < .01). Comparing single and dual task results, however, we did not find evidence for an AB effect: accuracy in the single task condition (68.9%) was not significantly different from that in the dual task condition (69.0%; F(1, 31) = .003, p = .96). Nor did performance depend on the delay between T1 and T2: separate analyses showed no significant effect of time lag for the easy (F(4, 64) = 2.07, p = .10) or for the difficult conditions (F(4, 64) = 2.44, p = .06). So, neither hallmark of an AB—T2 dependence on time delay and T2 dependence on performing T1—is evident when the T2 task involves estimating mean size. Although there was no main effects of lag, observers’ performance in lag 1 (71 ms) seemed low comparing to other lags. This was true only in difficult condition. Planned contrasts showed there was a significant difference between lag 1 and lag 3 in difficult condition (F(1, 16) = 5.82, p < .05) but not in easy condition (F(1, 16) = 1.96, p = .18). This might be due to the cost to switch between two tasks in such a short time (71 ms), but this cost was disappeared in the easy condition.

Note that T1 and T2 were different tasks in our paradigm and our results might be from the fact that observers required to use different resources for each task. However, in other studies T1 being a white letter detection task and T2 being odd-ball detection task in periphery successfully manipulated attentional resources engaged in T2 in AB streams (Braun, 1998; Joseph, Chun, & Nakayama, 1997).

The absence of evidence for an AB effect led us to wonder whether our implementation of this paradigm somehow failed to engage attentional resources to a degree sufficient to yield the AB. To test that possibility, we performed another experiment in which the T2 task, judging mean size, was replaced by another T2 task involving just two stimuli. Specifically, T2 in this new experiment consisted of two circles presented on either side of fixation. The location of each circle was randomly chosen among 28 cells of the same virtual matrix as in mean judgments. One circle was always smaller than the other by the same difference as in mean judgments, and the observer was required to indicate on which side—left or right—the larger circle appeared. In all other respects, the sequence of trial events was identical to the one used before (Figure 4a). Nine naive observers participated in a single-task condition and ten in dual-task condition, with task difficulty and T1–T2 delay varied randomly. Results were consistent for all observers: T2 performance was significantly worse under the dual-task condition (69.5%) than under the single-task condition (74.8%, F(1, 17) = 6.48, p < .05). Furthermore, a statistically significant effect of lag was found for both the easy (F(4, 36) = 3.15, p < .05) and the difficult conditions (F(4, 36) = 3.21, p < .05).

Our results suggest that attentional limitation affects single size judgments whereas mean size judgments are robust to attentional limitation. Although individual sizes in the arrays cannot be perfectly processed when attentional resources are limited, mean size computation of the arrays is less influenced by the attentional limitation. This might be contradictory because mean size computation must use the impaired individual stimulus information. However, it is consistent with the fact that the visual system computes the average orientation of Gabor patches presented in a crowding condition where the visibility of each individual patch presumably is impaired due to feature pooling (Parkes et al., 2001; Pelli, Palomares, & Majaj, 2004).

In Experiment 2-1 we did not present a visual mask following T2, which raises the possibility that visual persistence may have provided sufficient stimulus information for observers to perform the mean size judgment unimpeded by a time-limited influence of the AB. Because substitution masking can be a prominent component of the AB (Giesbrecht & Di Lollo, 1998), we felt obliged to repeat our experiment this time using a trailing mask consisting of a briefly flashed (106 ms) random-dot noise field that coincided in size and location to the entire region encompassed by the two 7 × 4 matrices containing the circular stimuli. To insure that the visual mask following T2 did not abolish visibility of T2, we increased the duration of T2 to 106 ms and, as well, we utilized a larger mean size difference between the two arrays to elevate baseline performance into the 80–85% range. Except these differences, the procedure was the same as in the main experiment. Ten observers including one of the authors participated in this experiment. Consistent with the results of the main experiment, the single-task performance (84.5%) did not differ significantly from the dual-task performance (79.7%; F(1, 9) = 3.31, p = .10). Furthermore, there was no significant effect of lag in the dual-task condition (F(4, 36) = 1.67, p = .18). The interaction between task type and lag was not significant, either (F(4, 36) = 0.65, p = .63). So, we are confident that the absence of an AB effect in our main experiment is not attributable to idiosyncrasies of our procedure. This, in turn, confirms that mean size judgments are indeed immune to the AB. At first glance, this immunity may seem somewhat surprising, since a significant AB effect (i.e., impaired T2 detection) has been documented on a feature search task that presumably involves preattentive selection (Joseph et al., 1997). There are, however, substantial differences in the set representations supporting feature search and mean size judgments, a point emphasized by others (Ariely, 2001; Chong & Treisman, 2005a). Furthermore, a recent study found that the visual system could extract the center of mass of several objects outside the focus of attention (Alvarez & Oliva, 2008).

Experiment 2-2: Judging mean size when the stimulus information is temporally distributed

In Experiment 2-1 we discovered that people can perform mean size judgments with limited attentional resources when the elements portraying mean size information are spatially distributed. Mean size judgments are not influenced by limited attentional resources, whereas single size judgments are impaired.

Another method to investigate whether observers can compute the mean sizes from an array of variable sized items despite limited attentional resources is to present individual sizes sequentially in an AB stream. We embedded individual sizes in an AB stream and measured each observer’s psychometric function using method of constant stimuli (MCS). This was a challenging task not only because observers had to accumulate each individual size information embedded in an AB stream to compute mean size, but also because they had to attend to the central letter stream to report both T1 and T2 (both were white letters).

Selective attention seems to fail during the blink due to suppression, delay, and diffusion (Vul, Nieuwenstein, & Kanwisher, 2008). It is likely that individual sizes embedded in an AB stream can also be affected by this attentional impairment. If stimulus information for mean size computation is also affected by the attentional limitation, observers should not be able to discriminate the probe size from the mean size. On the other hand, if stimulus information embedded in an AB stream is unaffected by the limited attentional resources, observers’ psychometric functions should reveal reliable discrimination ability.

We also wanted to insure that the absence of an effect of AB in Experiment 2-1 was not due to insufficient engagement of attention. If the performance of mean size judgments did not vary while the performance of T2 suffered from the AB, the null results of Experiment 2-1 could not be due to insufficient engagement of attention.

Methods

Observers

Five participants including one of the authors participated in this experiment. All had normal or corrected-to-normal vision. All aspects of the study were carried out in accord with the regulations of Departmental Review Committee of Yonsei University.

Apparatus and stimuli

The apparatus was the same as in Experiment 1. Figure 6a shows a schematic of the stimuli used in Experiment 2-2. T1, T2, and distractors were the capital alphabet letters presented in Helvetica (1.63° × 2.09° on average). The distractors were black (0.72 cd/m²) and the targets were white (102.68 cd/m²) in gray background (51.34 cd/m²). Seven sizes for mean size computation were generated between 2.51° and 3.51°. They had equal distance from each other on psychological scale (Chong & Treisman, 2003; Teghtsoonian, 1965). One of three multiplicative factors (1, 1.1, 1.2) was applied to the seven sizes in each trial to make the mean size vary. The center of the sizes was jittered by randomly selecting from the points on a circle of 0.38° radius from the center of the display. The luminance of the sizes was as same as the distractors.

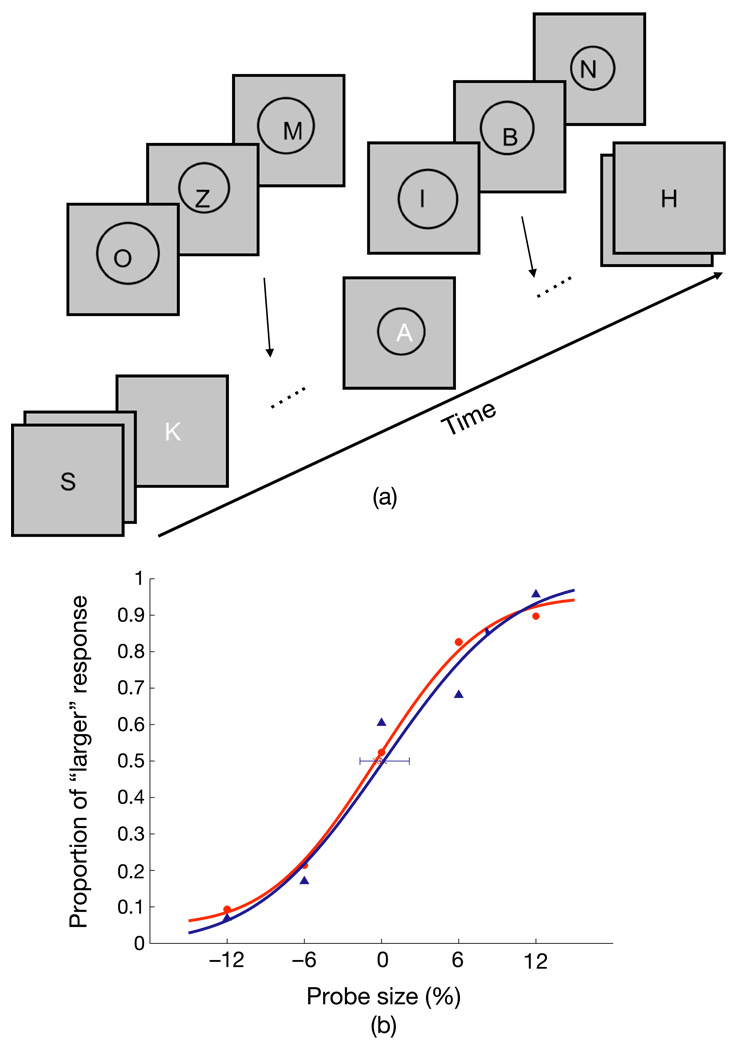
Figure 6.

(a) Timeline of Experiment 2-2. Observers reported the identity of white letters as well as the mean size of the circles. Seven circles for mean size computation were presented around T2 position. (b) Results of an observer. X-axis is the probe size and y-axis is the proportion of larger response for each probe size. Red and blue dots are responses for the AB and the NoAB conditions, respectively. Red and blue curve depicts the observer’s psychometric function for the AB and the NoAB conditions, respectively. The error bars are the 95% confidence intervals.

Probe sizes were −12%, −6%, 0%, 6%, or 12% smaller or larger than the mean size of the seven sizes. Probe sizes were presented after the AB stream together with one of the alphabet letters. The luminance of the probe sizes was the same as the seven sizes in the AB stream.

Procedure

Two conditions—lags (4; AB condition or 7; NoAB condition) and sizes of probe circle (−12%, −6%, 0%, 6%, or 12% smaller or larger than the mean size) were randomly intermixed in one experimental block. One experimental session (120 trials) consisted of 12 experimental blocks. Observers performed five experimental sessions. The first session served as a practice session and the data of the first session were discarded before data analysis.

The AB stream was the same as in Experiment 2-1 except for the followings. The duration of each lag was 83 ms (stimulus duration 71 ms + ISI 12 ms). At the end of each stimulus sequence, nine buttons with possible target-letters were presented in the center of the display. Observers used a computer mouse to report T1 and T2 by clicking the buttons. They were instructed to click T1 and T2 in order. Then, a probe size was displayed and observers clicked ‘yes’ button in the screen if the probe size was larger than the mean size and ‘no’ button otherwise.

Results and discussion

First, we analyzed the percent correct responses to T2 given correct responses for T1. A t-test (t(4) = 3.71, p < .05) confirmed that observers could detect T2 better for the NoAB condition (84.35%) than for the AB condition (66.05%), indicating that our procedure successfully limited the attentional resources engaged in T2.

Next, we compared the mean size judgments for the AB condition with those for the NoAB condition. We used a bootstrap method (Efron & Tibshirani, 1993) to fit the data to cumulative Gaussian functions and to obtain the 95% confidence intervals. Figure 6b is an example of a psychometric function of one of our observers. Again, the AB did not influence mean size judgments. The points of subjective equality (PSE) for the AB and the NoAB condition did not significantly differ (t(4) = 0.38, p = .72). Moreover, average PSE in the AB condition (−0.2%) did not significantly differ from 0 (t(4) = 0.11, p = .92) and neither did that in the NoAB condition (0.01%; t(4) = 0.04, p = .97).

These results suggest that observers can compute the mean size from the individual sizes embedded in an AB stream while they attend to the central letter stream looking for targets. Chong and Treisman (2005a) showed that people could accumulate size information for mean size computation when the individual sizes were presented sequentially in different locations without concurrent task. In the present experiment, although attention to individual size information was limited due to central AB task, observers’ ability to compute mean sizes was preserved. These results together with the results in Experiment 2-1 strongly suggest that mean size computation is indeed immune to limited attentional resource.

General discussion

The present results, together with earlier work, testify to the ability of human vision to extract properties from a set of objects not embodied in the individual objects that comprise that set. Our results also show that, within the visual hierarchy, the neural computations underlying extraction of this global property of a set transpire after the site of binocular combination. This conclusion is perhaps not surprising, but what is remarkable is the immunity of mean size judgments to depleted attentional resources. This latter finding is consistent with Ariely’s hypothesis (Ariely, 2001) that groups of objects can be represented in a manner that is not impacted by loss of resolution consequent to limited processing capacity (Neisser, 1967).

Viewed in another context, the present results could be construed to indicate that people are experts at perceiving global properties among objects in a cluttered scene. From other domains we know that expertise develops with exposure to novel objects (Gauthier, Williams, Tarr, & Tanaka, 1998) and that expertise can counteract the AB (Braun, 1998). Moreover, explicit training is unnecessary for development of expertise, for simply playing action video games can reduce the impact of the AB (Green & Bavelier, 2003). In our work, people come into the laboratory with refined ability to perform mean set size judgments, with practice being unnecessary and error feedback providing little further improvement (Chong & Treisman, 2003). Moreover, people are best at this task when it is performed under a distributed attention mode rather than with focused attention (Chong & Treisman, 2005a). This characteristic, too, is a hallmark of expert, holistic processing (Gauthier & Tarr, 2002).

What is the usefulness of being able to represent statistical properties of items comprising arrays? Ariely (2001) has speculated that people unwittingly rely on those properties for all sorts of tasks, ranging from perceiving the gist of a scene (Treisman, 2006) to remembering the overall affective connotation of a series of events comprising an episode (Kahneman, Fredrickson, Schreiber, & Redelmeier, 1993). Indeed, our facility at perceptually grasping the statistical properties of sets of objects or events may represent a basic component in everyday decision making (Peterson & Beach, 1967). It is ironic, then, that this ability to compute mean size is preserved in the face of limited attentional resources yet, at the same time, the elements entering into those computations must be available to conscious awareness.