Abstract
Background
Regulation of plasma glucose concentration for type 1 diabetic patients is challenging, and exercise is an added complication. From a metabolic prospective, the significant exercise-induced effects are increased glucose uptake rate by the working tissues, increased hepatic glucose release to maintain overall glucose homeostasis, and decreased plasma insulin concentration. During prolonged exercise, glucose levels drop significantly because of the decrease in hepatic glucose production. With the long-term goal of developing a closed-loop insulin delivery system operating under various physiological conditions, it is necessary to develop a model that is capable of predicting blood glucose concentration at rest and during physical activity.
Methods
A minimal model developed previously was extended to include the major effects of exercise on plasma glucose and insulin levels. Differential equations were developed to capture the exercise-induced dynamics of plasma insulin clearance and the elevation of glucose uptake and hepatic glucose production rates. The decreasing liver glucose output resulting from prolonged exercise was modeled using an equation depending on exercise intensity and duration.
Results
The exercise model successfully captured the glucose and insulin dynamics during short- and long-term exercise. Model predictions of glucose and insulin dynamics during the postexercise recovery period were also consistent with literature data.
Conclusion
The model successfully emulated the physiological effects of exercise on blood glucose and insulin levels. This extended model may provide a new disturbance test platform for the development of closed-loop glucose control algorithms.
Keywords: diabetes, exercise, glucose, insulin, minimal model
Introduction
Diabetes mellitus is a metabolic disease caused by either the loss of pancreatic insulin secretion (type I) or the resistance developed by the body toward the glucoregulatory action of insulin (type II). In order to prevent major health complications, it is important to maintain the plasma glucose concentration within the normoglycemic range (70–120 mg/dl).1,2 The major long-term effects of diabetes are caused by hyperglycemia, where the plasma glucose concentration exceeds 120 mg/dl.1,2 Prolonged hyperglycemia can cause complications, which may lead to kidney disease, blindness, loss of limbs, and so on.1,2 Of more immediate concern is hypoglycemia, defined by a plasma glucose concentration below 70 mg/dl. Such a condition can lead to dizziness, coma, or even death.1,2 Intensive insulin therapy involves three to four daily blood glucose measurements by finger pricking, followed by subcutaneous insulin injection; these usually correspond to meal times and bed time.3 Although this process is adequate to maintain the blood glucose level within an acceptable range, wide fluctuations persist throughout the day as a consequence of personal daily life activities (such as food intake and exercise) occurring between glucose measurements. In order to achieve tighter glucose control, there is a focus on the synthesis of an automated insulin delivery system composed of a continuous glucose measuring device, an insulin pump, and a control algorithm to govern the system.4,5 To have a reliable model-based insulin delivery system operating under various physiological conditions, a model must be developed that can predict blood glucose concentration at rest and during physical activity.
Since the 1960s, mathematical models have been used to describe glucose–insulin dynamics.6 Bergman and colleagues7 proposed a three-compartment minimal model to analyze the glucose disappearance and insulin sensitivity during an intravenous glucose tolerance test. Modifications have been made to the original minimal model to incorporate various physiological effects of glucose and insulin. Cobelli and co-workers8 developed a revised minimal model in order to separate the effects of glucose production from utilization. The overestimation of glucose effectiveness and the underestimation of insulin sensitivity by the minimal model were addressed in yet another publication by Cobelli et al.,9 where a second nonaccessible glucose compartment was added to the original model. Hovorka and co-workers10 extended the original minimal model by adding three glucose and insulin subcompartments in order to capture absorption, distribution, and disposal dynamics, respectively. While these models refine glucose–insulin descriptions for various situations or behaviors, none of these models captures the changes in glucose and insulin dynamics due to exercise. The goal of the present work is to incorporate the effects of physiological exercise into the Bergman minimal model7 in order to capture the plasma glucose and insulin dynamics during, as well as after, periods of mild-to-moderate exercise.
Methods and Materials
Bergman Minimal Model
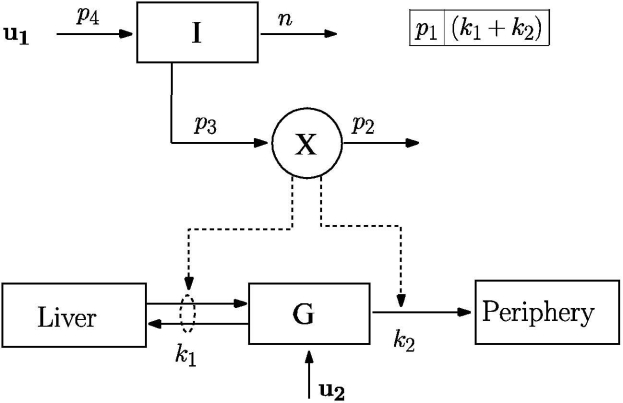
Bergman and colleagues7 successfully quantified the pancreatic responsiveness and insulin sensitivity of a diabetic patient using a three-compartmental mathematical model, as shown in Figure 1. Compartments I, X, and G represent plasma insulin (μU/ml), remote insulin (μU/ml), and plasma glucose (mg/dl) concentrations, respectively. The model as written assumes that all the necessary insulin is infused exogenously (u1), thereby modeling the insulin-dependent diabetic patient. A portion of the infused insulin enters into the remote compartment, X, from the circulatory system, I. The remote insulin (X) actively takes part in promoting the uptake of plasma glucose (G) into the hepatic and extrahepatic tissues.
Figure 1.
Bergman minimal model of insulin and glucose dynamics, adapted from Bergman and colleagues.7
The Bergman minimal model7 is given mathematically by
| (1) |
| (2) |
| (3) |
Here, Ib and Gb are the basal plasma insulin and glucose concentrations, respectively. The exogenous insulin infusion rate to maintain Ib is represented by u1b (mU/min). The rate constant n represents clearance of plasma insulin. The rates of appearance of insulin in, and disappearance of remote insulin from, the remote insulin compartment are governed by the parameters p3 and p2, respectively. Dietary absorption or external infusion of glucose is indicated by u2(t), and the glucose distribution space is indicated by VolG. Parameter p1 represents the rate at which glucose is removed from the plasma space independent of the influence of insulin. Glucose uptake under the influence of insulin is governed by the term X(t)G(t). Parameter values for the Bergman minimal model (p1, p2, and p3) were obtained from Bergman et al.7 and were fixed for the rest of the study (see Table 1).
Table 1.
Parameters of the Bergman Minimal Model
| Parameter | Value | Unit |
|---|---|---|
| p1 | 0.035 | 1/min |
| p2 | 0.05 | 1/min |
| p3 | 0.000028 | ml/μU·min2 |
| p4 | 0.098 | 1/ml |
| n | 0.142 | 1/min |
| VolG | 117.0 | dl |
| Gb | 80.0 | mg/dl |
Quantitating Exercise Intensity
The maximum rate of oxygen consumption for an individual during exercise is given by VO2max (ml/kg/min). Oxygen consumption is approximately linearly proportional to energy expenditure.11 Hence, it is possible to indirectly measure the maximum capacity of an individual for aerobic work by measuring oxygen consumption. When physical activity is expressed as a percentage of VO2max (PVO2max), exercise effects may be compared between individuals of the same sex and similar body weight at the same PVO2max. The average PVO2max for a person in the basal state is 8%.12 Ahlborg and co-workers13 demonstrated that PVO2maxincreases rapidly at the onset of exercise, reaches its ultimate value within 5–6 minutes, and remains constant for the duration of exercise. The exercise model developed in this study uses PVO2max to quantify exercise intensity. The ordinary differential equation for PVO2max is given by
| (4) |
Here, PVO2max is the exercise level as experienced by the individual, and u3(t) is the ultimate exercise intensity above the basal level—an input to the model spanning 0 to 92%. The parameter value of 0.8 (1/min) was selected to achieve a PVO2max(t) settling time of approximately 5 minutes.
Minimal Exercise Model
Physiological exercise induces several fundamental metabolic changes in the body.14 Elevated physical activity promotes a drop in plasma insulin concentration from its basal level.12 Dog studies conducted by Wasserman and colleagues15 found that an insulin clamp at its basal level disrupted the glucose homeostasis of the dogs during exercise. Similar trends have been observed in human studies.13,16
An increase in exercise intensity also amplifies glucose uptake by the working tissues.17 In order to maintain plasma glucose homeostasis, hepatic glucose release also increases with increasing work intensity.18 During a mild-to-moderate work load, the major source of increased splanchnic glucose release is contributed by elevated hepatic glycogenolysis. As the duration of exercise increases, the rate of hepatic glycogenolysis diminishes because of the limited supply of liver glycogen stores.19 Simultaneously, hepatic gluconeogenesis is stimulated.20 However, the rate of glucose produced via liver gluconeogenesis does not fully compensate for the decrease in glucose release by liver glycogenolysis (the former is a slower process), thereby resulting in a net decrease in hepatic glucose release during prolonged exercise.21 Because of this imbalance between glucose uptake and hepatic glucose release, the plasma glucose concentration declines and hypoglycemia occurs.19,20 As an added complication in glucose regulation, studies have shown that liver glycogen content declines more rapidly with increasing exercise intensity.19,22
During the recovery period after short-term exercise, both the elevated glucose uptake rate by working muscles and the rate of hepatic glucose release decline gradually to their respective basal levels. However, glucose fluxes after prolonged exercise are quite different. Because of the substantial depletion of liver glycogen stores during prolonged exercise, the rate of glycogenolysis is suppressed significantly, leading to a net decrease in the hepatic glucose release rate. During the recovery period, the elevated muscle glucose uptake rate gradually declines to the basal level; however, the already suppressed net hepatic glucose release rate is elevated significantly as a consequence of an increase in hepatic gluconeogenesis.21 In vivo studies have revealed a significant increment in hepatic lactate consumption immediately after prolonged exercise, and this lactate serves as a substrate for enhanced postexercise gluconeogenesis.23
The glucose and insulin dynamics, when coupled with the major exercise effects, are given mathematically by
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
The insulin dynamics, Equation (5), have been modified from the Bergman minimal model, Equation (1), by adding the final term. Here, Ie(t) (μU/ml/min) is the rate of insulin removal from the circulatory system due to exercise-induced physiological changes. The plasma glucose dynamics, Equation (7), differ from Equation (3) of the Bergman minimal model by the addition of the following terms: (W/VolG)[Gprod(t) – Ggly(t)] – (W/VolG)Gup(t). Variables Gup(t) (mg/kg/min) and Gprod(t) (mg/kg/min) represent the rates of glucose uptake and hepatic glucose production induced by exercise, respectively. W (kg) represents the weight of the subject. Variable Ggly(t) (mg/kg/min) represents the decline of the glycogenolysis rate during prolonged exercise due to the depletion of liver glycogen stores. The dynamics of hepatic glucose production, glucose uptake, and plasma insulin removal induced by exercise are represented in Equations (8), (9), and (10), respectively.
The rate of glycogenolysis [Ggly(t)] starts to decrease when the energy expenditure exceeds a critical threshold value (ATH), which is a function of exercise intensity and duration. ATH can be represented mathematically as
| (11) |
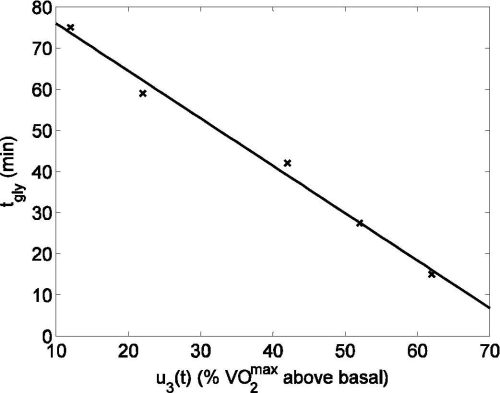
where tgly(u3(t)) is the duration of exercise that can be performed at intensity u3(t) before the rate of hepatic glycogenolysis starts to decrease. The rate of hepatic glycogen depletion increases with increasing exercise intensity.9,22 Hence, tgly(u3(t)) is a function of exercise intensity, as shown in Figure 2. A linear equation, decreasing with increasing work intensity, captures the dependence of tgly(u3(t)) on u3(t) as follows:
| (12) |
Figure 2.
Dependence of glycogen depletion commencement time, tgly, on exercise intensity (u3(t)). Published data (cross) from Pruett22 and linear fit (solid line) [R2 = 0.991].
By substituting Equation (12) into Equation (11),
| (13) |
Hence, the dynamics of glycogenolysis during prolonged exercise can be represented mathematically as follows:
| (14) |
where A(t) is the integrated exercise intensity, u3(t), which is calculated by the following set of equations:
| (15) |
With the onset of exercise (u3(t) > 0), A(t) will increase at a rate proportional to u3(t). At the end of physical activity (u3(t) = 0), A(t) will quickly return to its initial condition (which is zero). As long as A(t) is less than the critical threshold value (ATH), enough glycogen is still available to maintain a sufficient rate of hepatic glucose release. However, once A(t) reaches ATH, the rate of change of glycogenolysis rate starts to decline at a rate given by k because of the depletion of available liver glycogen stores. The end of exercise (when u3(t) returns to zero), which is also the beginning of the recovery period, marks the commencement of repletion of glycogen stores via a continued elevation in the rate of hepatic gluconeogenesis. The time required for Ggly to return to its basal value after exercise is governed by the pseudo-time constant T1.
Parameter Estimation
Parameters for the minimal exercise model were estimated using nonlinear least squares, as described elsewhere.24 The normalized residual is obtained as
| (16) |
Here yi is the measured data at time ti, which has standard deviation σi. The model prediction is given by y(ti,a1…aM), where aj represent model parameters, with j ∈ [1,M]. Equation (16) can be considered a weighted minimization over N data points using (1/σi)2 as weights. χ2 is often denoted as “weighted sum squared error,” and the aim is to estimate aj such that χ2 is minimized.
The quality of the model fits was assessed by measuring the statistical correlation between experimental data and model predictions using the R2 technique. R2 can be defined as
| (17) |
where χ2 is the weighted sum squared error from Equation (16) and SST is the weighted sum of squares about the data mean. SST can be calculated using the following equation:
| (18) |
where N is the number of data points and y is the grand mean of all data points. R2 takes values between 0 and 1, with a value closer to 1 indicating a better fit. Calculated R2 values for every model fit and validation are provided in the figure legends.
Experimental Data from Literature Used in Parameter Estimation
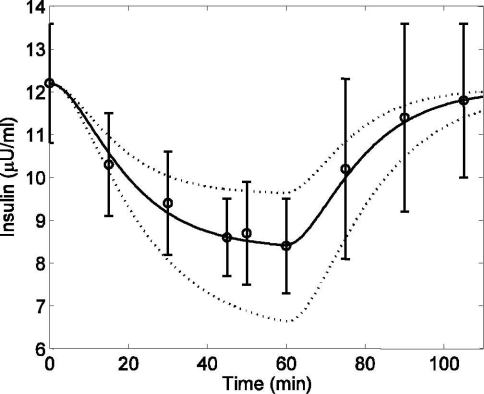
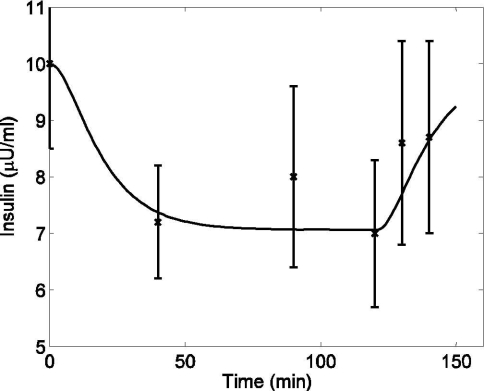
Data from Wolfe and colleagues16 were used to investigate the plasma insulin dynamics during exercise, where healthy subjects performed a continuous bicycle exercise for 60 minutes (PVO2max = 40). Blood samples were taken at regular intervals to measure the plasma insulin level. In order to capture the depletion of plasma insulin during exercise and its repletion during the recovery period, parameters a5 and a6 in Equation (10) were estimated (Figure 3). After fixing a5 and a6, 95% confidence intervals (CI) were calculated by using the nlparci.m function from the MATLAB Statistics Toolbox (©2006 The MathWorks Inc., Natick, MA). Data from a separate study by Ahlborg et al.20 were used to validate the insulin model (see Figure 4), where healthy subjects performed light exercise (PVO2max = 30) for 120 minutes, and the removal of plasma insulin from the circulatory system was observed.
Figure 3.
Plasma insulin concentration in response to mild exercise (PVO2max = 40) lasting from tex = 0 to 60 minutes. Published data (circles) (mean ± SD) from Wolfe et al.,16 model fit (solid line) [R2 = 0.994], and 95% confidence interval of the model output (dotted line).
Figure 4.
Plasma insulin concentration in response to mild exercise (PVO2max = 30) lasting from tex = 0 to 120 minutes. Model simulation validation (solid line) and published data (cross) (mean ± SD) from Ahlborg and co-workers20 [R2 = 0.856].
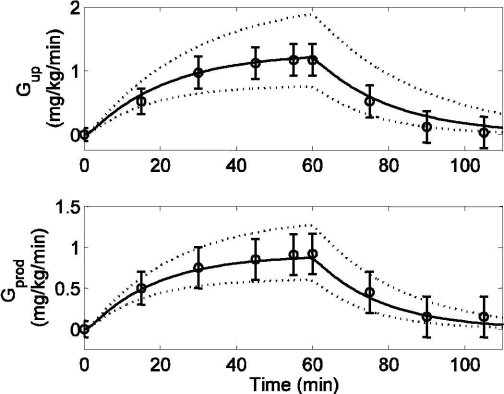
In the glucose model, parameters a3 and a4 for the Gup [Equation (9)], along with their 95% CIs (calculated using the nlparci.m MATLAB function), were estimated from data collected by Wolfe and colleagues16 (see Figure 5, top). In this study, healthy subjects performed mild bicycle exercise (PVO2max = 40) for 60 minutes. Blood samples were obtained at regular intervals to measure the changes in glucose uptake rate (Gup, mg/kg/min) and hepatic glucose production rate (Gprod, mg/kg/min) during and after exercise. After fixing a3 and a4, parameters a1 and a2 for Gprod [Equation (8)] were estimated from the same data set16 (see Figure 5, bottom). Using the same technique as for a3 and a4, 95% CIs were calculated for a1 and a2. After fixing parameters a1–6 and their 95% CIs, model estimation of plasma glucose was compared with data obtained from the same study16 (see Figure 6).
Figure 5.
Model simulation (solid lines), 95% confidence intervals of model outputs (dotted lines), and published data (circles) (mean ± SD) from Wolfe et al.16 in response to mild exercise (PVO2max = 40) lasting from tex = 0 to 60 minutes. (Top) Glucose uptake rate (Gup) [R2 = 0.984]. (Bottom) Hepatic glucose production rate (Gprod) [R2 = 0.992]. Both Gup and Gprod are plotted in deviation form.
Figure 6.
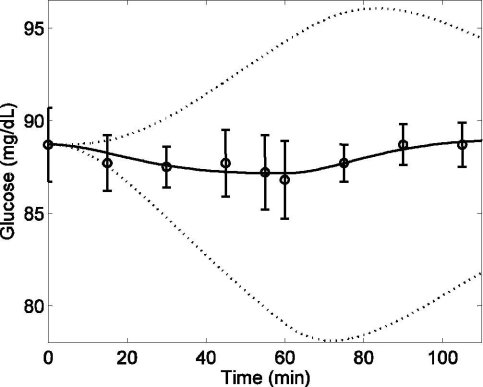
Plasma glucose concentration (G) in response to mild exercise (PVO2max = 40) lasting from tex = 0 to 60 minutes. Model simulation (solid line) [R2 = 0.84], 95% confidence intervals of model output (dotted lines), and published data (circles) (mean ± SD) from Wolfe and colleagues16
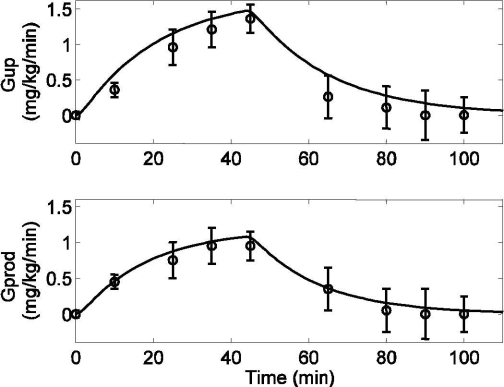
For validation of the glucose model, model predictions of Gprod, Gup, and G were compared with data from another exercise study performed by type 1 diabetes mellitus (T1DM) patients conducted by Zinman and colleagues25 (see Figures 7 and 8). Here, T1DM patients performed moderate level exercise on a bicycle ergometer for 45 minutes at PVO2max = 50. Blood samples were taken at regular intervals to measure Gup, Gprod, and G.
Figure 7.
Response to moderate exercise (PVO2max = 50) by type 1 diabetic patients lasting from tex = 0 to 45 minutes. Model simulation validation (solid lines) and published data (circles) (mean ± SD) from Zinman et al.25 (Top) Glucose uptake rate (Gup) [R2 = 0.939]. (Bottom) Hepatic glucose production rate (Gprod) [R2 = 0.989].
Figure 8.
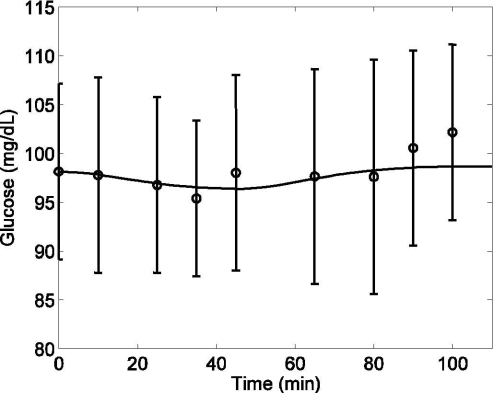
Plasma glucose concentration (G) in response to moderate exercise (PVO2max = 50) by type 1 diabetic patients lasting from tex = 0 to 45 minutes. Model simulation validation (solid line) [R2 = 0.85] versus published data (circles) (mean ± SD) from Zinman et al.25
Finally, the effects of glycogen depletion during prolonged exercise and recovery were modeled. In order to capture these effects, data from Ahlborg and colleagues20 were used to estimate the parameters k and T1 only, from Equation (14) (see Figure 9). In this study, 12 healthy subjects underwent mild exercise (PVO2max = 30) on a bicycle ergometer for 2 hours. Plasma glucose was measured throughout the course of exercise and during a 40-minute postexercise recovery period. After estimating T1 and k, the MATLAB function nlparci.m was used to calculate 95% CIs for these parameters. For further validation of the model during prolonged exercise, plasma glucose concentration was compared with data from another study performed by Ahlborg et al.,19 where healthy subjects performed exercise at a higher intensity (PVO2max = 60) (see Figure 10). Blood samples were taken during and after the exercise to measure plasma glucose concentration. All the parameter values, along with their 95% CIs for the minimal exercise model, are given in Table 2.
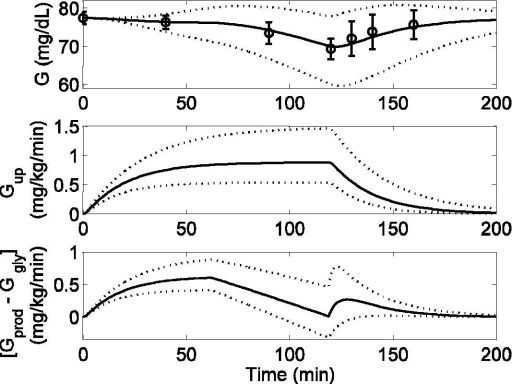
Figure 9.
Model response to mild exercise (PVO2max = 30) lasting from tex = 0 to 120 minutes. Published data (circles) (mean ± SD) from Ahlborg et al.,20 model fit (solid line), and 95% confidence interval of fit (dotted lines). (Top) Model prediction of plasma glucose (G) [R2 = 0.964]. (Middle) Model prediction of glucose uptake rate (Gup). (Bottom) Model prediction of net liver glucose production. Both Gup and [Gprod − Ggly] are shown in deviation form.
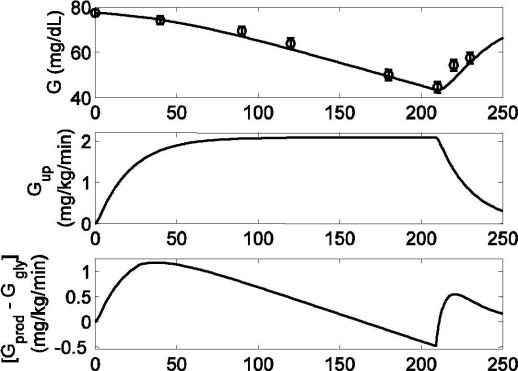
Figure 10.
Model response to moderate exercise (PVO2max = 60) lasting from tex = 0 to 210 minutes. Published data (circles) (mean ± SD) from Ahlborg and co-workers19 and model prediction validation (solid line). (Top) Model prediction of plasma glucose (G) [R2 = 0.94]. (Middle) Model prediction of glucose uptake rate (Gup). (Bottom) Model prediction of net liver glucose production. Both Gup and [Gprod − Ggly] are shown in deviation form.
Table 2.
Parameters of the Minimal Exercise Model with 95% Confidence Intervals (CI), in Addition to Those in Table 1
| Parameter | Value | Lower limit 95% CI | Upper limit 95% CI | Unit |
|---|---|---|---|---|
| a1 | 0.00158 | 0.0013 | 0.0019 | mg/kg·min2 |
| a2 | 0.056 | 0.0441 | 0.0679 | 1/min |
| a3 | 0.00195 | 0.0015 | 0.0024 | mg/kg·min2 |
| a4 | 0.0485 | 0.0355 | 0.0617 | 1/min |
| a5 | 0.00125 | 0.001 | 0.0015 | μU/ml·min |
| a6 | 0.075 | 0.0588 | 0.0912 | 1/min |
| k | 0.0108 | 0.0085 | 0.0131 | mg/kg·min2 |
| T1 | 6.0 | 1.86 | 10.14 | min |
Simulations in Figures 3, 5, 6, and 9 include confidence interval bounds (dotted lines) on the output profile of interest (e.g., I, G, Gup, Gprod, and [Gprod − Ggly]). These bounds are “worst case” bounds, in that the induced effect of multiple parameter uncertainty was maximized by selecting parameter pairs that lead to the largest possible deviation from the nominal profile.
Results
Plasma Insulin Dynamics during Exercise
A simulation study of mild exercise (PVO2max = 40) for 60 minutes was performed to evaluate the physiological effects of exercise on plasma insulin concentration. With the onset of exercise, plasma insulin declined from its basal level (12.2 μU/ml) and continued to do so along a first-order-type response trajectory until the end of the experiment, as shown in Figure 3. During the recovery period (t > 60 minutes), the plasma insulin concentration climbed back to its basal level. Quantitatively, model predictions were consistently within one standard deviation of the mean of experimental data16 from which the relevant parameters (a5 and a6) were estimated. The 95% CI bounds of plasma insulin concentration were simulated by choosing a set of parameter values from Table 2 that had the maximum overestimation (a5 = 0.001, a6 = 0.0912) and maximum underestimation (a5 = 0.0015, a6 = 0.0588) of insulin concentration, as shown in Figure 3 (dotted lines).
For validation of the model, a separate simulation study was performed by keeping the parameter values of a5 and a6 unchanged and using a different exercise intensity level (PVO2max = 30) and a longer time duration (tex = 0 to 120 minutes). With the onset of exercise, the insulin level declined well below the basal level (10.2 μU/ml); this hypoinsulinemic state persisted until the end of the experiment. A comparison between model prediction of insulin and experimental data20 on the same exercise protocol is shown in Figure 4. Plasma insulin gradually returned back to the basal level during the recovery period (t > 120 minutes). Overall, the insulin model fits the experimental data sets.
Plasma Glucose Dynamics during Exercise
To evaluate the exercise effects on plasma glucose concentration, a 60-minute simulation study of mild exercise was performed (PVO2max = 40). With the onset of exercise, Gup increased from its basal state to 1.15 mg/kg/min.
During the recovery period (t > 60 minutes), Gup returned to its basal level. Model prediction of Gup, along with experimental data16 on the same exercise protocol from which parameters a3 and a4 were estimated, is shown in Figure 5 (top). The 95% CIs of Gup were simulated by choosing a set of parameter values from Table 2 that had the maximum underestimation (a3 = 0.0015, a4 = 0.0617) and maximum overestimation (a3 = 0.0024, a4 = 0.0355) of glucose uptake rate, as shown by the dotted lines in Figure 5 (top). In order to maintain plasma glucose homeostasis, the hepatic glucose production rate (Gprod, mg/kg/min) also increased from its basal level to 0.95 mg/kg/min for the duration of exercise. In conjunction with the glucose uptake rate, Gprod decreased to its basal level after the end of exercise. Parameters a1 and a2 were estimated to fit the data, as shown in Figure 5 (bottom). Again, 95% CIs of Gprod were simulated by choosing a set of parameter values from Table 2 that had the maximum underestimation (a1 = 0.0013, a2 = 0.0679) and maximum overestimation (a1 = 0.0019, a2 = 0.0441) of glucose production rate, as shown by the dotted lines in Figure 5 (bottom). Both Gup and Gprod are represented in deviation form in Figure 5.
The accelerated glucose uptake rate during exercise is compensated for by enhanced hepatic glucose production; hence, normoglycemia is maintained throughout the course of physical activity. A comparison between the model prediction of glucose concentration, including Gup plus Gprod effects, and experimental data16 is provided in Figure 6. The predictions of the glucose model are in good accordance with published data. In order to simulate the 95% CIs for plasma glucose concentration, a combination of parameter values were chosen from Table 2 that generated the maximum underestimation (a1 = 0.0013, a2 = 0.0679, a3 = 0.0024, a4 = 0.0355, a5 = 0.001, a6 = 0.0912) and maximum overestimation (a1 = 0.0019, a2 = 0.0441, a3 = 0.0015, a4 = 0.0617, a5 = 0.0015, a6 = 0.0588) of plasma glucose, as indicated by the dotted lines in Figure 6.
For validation of the glucose model, another simulation test was performed using a 45-minute bout of moderate-level exercise (PVO2max = 50). Again, with the onset of exercise, both Gup and Gprod increased. During the recovery period (t > 45 minutes), Gup and Gprod gradually declined to their respective basal levels. Model validation simulations (i.e., no model parameter changes) are plotted alongside experimental data of T1DM patients25 in Figure 7, top and bottom (both in deviation form). Figure 8 shows the model prediction of plasma glucose concentration, including the combined effects of Gup and Gprod during exercise, along with experimental data.16
To evaluate the plasma glucose dynamics during prolonged exercise, data from Ahlborg et al.20 were considered (see Figure 9). With the onset of exercise, both Gup and Gprod rates were elevated from the basal level; this resulted in the maintenance of glucose homeostasis during the first hour of exercise. As the integrated exercise intensity exceeded a critical threshold (which is a function of exercise intensity and duration), the hepatic glycogenolysis rate started to decline as a result of which net liver glucose production rate, [Gprod − Ggly], decreased until the end of exercise (Figure 9, bottom). However, Gup remained elevated because of continuing physical activity (Figure 9, middle). This mismatch between Gup and Gprod resulted in a net decrease of plasma glucose level (Figure 9, top). During the postexercise recovery period, lactate consumption by the liver increased significantly, serving as a substrate for accelerated postexercise gluconeogenesis.23 It is believed that the purpose of this elevated gluconeogenesis is to replete the liver glycogen stores and restore normoglycemia.21 Keeping parameters a1-6 unchanged, parameters k and T1 from Equation (14) were adjusted to capture the dynamical behavior of plasma glucose concentration. To simulate the 95% CIs for plasma glucose concentration during prolonged exercise, the same combination of parameter values was chosen from Table 2 as in Figure 6, with the addition of (k = 0.0131, T1 = 10.14) for maximum underestimation and (k = 0.0085, T1 = 1.86) for maximum overestimation, as shown by the dotted lines in Figure 9 (top). To simulate the CIs for Gup, the same parameter value sets as those used in Figure 5 (top) were chosen (see Figure 9, middle). Finally, to simulate the 95% CIs of net liver glucose production rate, a combination of parameter values were chosen from Table 2 to generate the maximum underestimation (a1 = 0.0013, a2 = 0.0679, k = 0.0131, T1 = 10.14) and maximum overestimation (a2 = 0.0019, a2 = 0.0441, k = 0.0085, T1 = 1.86) of [Gprod − Ggly], as shown by the dotted lines in Figure 9 (bottom).
In order to validate the model during prolonged exercise, a separate simulation study was performed where exercise was performed for 3 hours at a moderate exercise intensity (PVO2max = 60). Because of the higher exercise intensity, glycogen stores depleted at a faster rate; the result is an inability to maintain glucose homeostasis beyond tex = 30 minutes (see Figure 10, top). A comparison between model simulations (without changing any parameters) and data19 is given in Figure 10.
Discussion
A model of exercise effects on plasma glucose–insulin dynamics was developed. The principal goal was to extend the Bergman minimal model7 by adding suitable dynamics to capture the observed physiological phenomenon induced by exercise. Based on validation data, the extended model is able to predict plasma glucose and insulin concentrations in response to mild-to-moderate exercise challenges. All the added equations in the proposed model are linear in nature, thus maintaining the simplistic approach of the original minimal model.7 The model successfully captured the effects of mild-to-moderate aerobic exercise on plasma glucose and insulin concentrations. Inclusion of separate dynamics in the model for glucose uptake [Equation (9)] and hepatic glucose production [Equation (8)] made it possible to capture the simultaneous rise of these rates with the onset of short-term exercise in order to maintain glucose homeostasis. These equations were also successful in capturing the dynamics of glucose fluxes during the postexercise recovery period. As the integrated exercise intensity extends beyond a critical threshold (which is a function of exercise intensity and duration), a decline in splanchnic glucose release is expected. As glucose uptake rate remains elevated, maintenance of glucose homeostasis is no longer possible. Because of this, plasma glucose continues to decline until the end of physical activity. At the end of prolonged exercise, the hepatic gluconeogenesis rate is increased, which facilitates the repletion of glycogen stores and helps achieve normoglycemia.21 A substantial amount of lactate is released from the postexercising muscles during the recovery period, which serves as a substrate for gluconeogenesis. To capture the dynamics of plasma glucose during the various stages of prolonged exercise, Equation (14) was incorporated. The model also successfully captured the clearance of plasma insulin from the circulatory system during physical exercise due to the addition of Equation (10).
With a focus on closed-loop insulin delivery systems for type 1 diabetic patients, it is necessary to develop models that can accurately predict plasma glucose concentration during rest, as well as during physical exercise. Hence, this model provides the control community with an alternative benchmark problem in glucose control for diabetic patients by allowing the analysis of meal and exercise disturbances alone or in combination. The exercise model can also be used to predict the duration of exercise at a given intensity that can be executed while keeping plasma glucose within the normoglycemic range. However, a prospective validation of the components of the minimal exercise model is necessary before the model, or a model-based controller, is employed in any clinical setting.
Acknowledgment
Support for this work was provided by University of Pittsburgh School of Engineering CNG Faculty Fellowship.
Abbreviations
- CI
confidence interval
- T1DM
type 1 diabetes mellitus
References
- 1.The Diabetes Control and Complications Trial Research Group. The effect of intensive treatment of diabetes on the development and progress of long-term complications in insulin-dependent diabetes mellitus. N Engl J Med. 1993 Sep 30;329(14):977–986. doi: 10.1056/NEJM199309303291401. [DOI] [PubMed] [Google Scholar]
- 2.The Diabetes Control and Complications Trial Research Group. The absence of a glycemic threshold for the development of long-term complications: The perspective of the Diabetes Control and Complications Trial. Diabetes. 1996 Oct;45(10):1289–1298. [PubMed] [Google Scholar]
- 3.American Diabetes Association. Standards of medical care for clients with diabetes mellitus. Diabetes Care. 2003;26(1):S33–S50. doi: 10.2337/diacare.26.2007.s33. [DOI] [PubMed] [Google Scholar]
- 4.Parker RS, Doyle FJ, III, Peppas NA. A model-based algorithm for blood glucose control in type 1 diabetic patients. IEEE Trans Biomed Eng. 1999 Feb;46(2):57–148. doi: 10.1109/10.740877. [DOI] [PubMed] [Google Scholar]
- 5.Hovorka R, Canonico V, Chassin LJ, Haueter U, Massi-Benedetti M, Orsini Federici M, Pieber TR, Schaller HC, Schaupp L, Vering T, Wilinska ME. Nonlinear model predictive control of glucose concentration in subjects with type 1 diabetes. Physiol Meas. 2004 Aug;25(4):905–920. doi: 10.1088/0967-3334/25/4/010. [DOI] [PubMed] [Google Scholar]
- 6.Bolie VW. Coefficients of normal blood glucose regulation. J Appl Physiol. 1961 Sep;16:783–788. doi: 10.1152/jappl.1961.16.5.783. [DOI] [PubMed] [Google Scholar]
- 7.Bergman RN, Phillips LS, Cobelli C. Physiologic evaluation of factors controlling glucose tolerance in man: measurement of insulin sensitivity and beta-cell glucose sensitivity from the response to intravenous glucose. J Clin Invest. 1981 Dec;68(6):1456–1467. doi: 10.1172/JCI110398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cobelli C, Pacini G, Toffolo G, Sacca L. Estimation of insulin sensitivity and glucose clearance from minimal model: new insights from labeled IVGTT. Am J Physiol. 1986 May;250(5 Pt 1):E591–E598. doi: 10.1152/ajpendo.1986.250.5.E591. [DOI] [PubMed] [Google Scholar]
- 9.Cobelli C, Caumo A, Omenetto M. Minimal model SG overestimation and SI underestimation: improved accuracy by a Bayesian two-compartment model. Am J Physiol. 1999 Sep;277(3 Pt 1):E481–E488. doi: 10.1152/ajpendo.1999.277.3.E481. [DOI] [PubMed] [Google Scholar]
- 10.Hovorka R, Shojaee-Moradie F, Carroll PV, Chassin LJ, Gowrie IJ, Jackson NC, Tudor RS, Umpleby AM, Jones RH. Partitioning glucose distribution/transport, disposal, and endogenous production during IVGTT. Am J Physiol Endocrinol Metab. 2002 May;282(5):E992–E1007. doi: 10.1152/ajpendo.00304.2001. [DOI] [PubMed] [Google Scholar]
- 11.Astrand I. Aerobic work capacity in men and women with special reference to age. Acta Physiol Scand Suppl. 1960;49(169):92–101. [PubMed] [Google Scholar]
- 12.Felig P, Wahren J. Fuel homeostasis in exercise. N Engl J Med. 1975 Nov 20;293(21):1078–1084. doi: 10.1056/NEJM197511202932107. [DOI] [PubMed] [Google Scholar]
- 13.Ahlborg G, Felig P, Hagenfeldt L, Hendler R, Wahren J. Substrate turnover during prolonged exercise in man. J Clin Invest. 1974 Apr;53(4):1080–1090. doi: 10.1172/JCI107645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wasserman DH, Geer RJ, Rice DE, Bracy D, Flakoll PJ, Brown LL, Hill JO, Abumrad N. Interaction of exercise and insulin action in humans. Am J Physiol. 1991 Jan;260(1 Pt 1):E37–E45. doi: 10.1152/ajpendo.1991.260.1.E37. [DOI] [PubMed] [Google Scholar]
- 15.Wasserman DH, Williams PE, Lacy DB, Goldstein RE, Cherrington AD. Exercise-induced fall in insulin and hepatic carbohydrate metabolism during muscular work. Am J Physiol. 1989 Apr;256(4 Pt 1):E500–E509. doi: 10.1152/ajpendo.1989.256.4.E500. [DOI] [PubMed] [Google Scholar]
- 16.Wolfe RR, Nadel ER, Shaw JH, Stephenson LA, Wolfe MH. Role of changes in insulin and glucagon in glucose homeostasis in exercise. J Clin Invest. 1986 Mar;77(3):900–907. doi: 10.1172/JCI112388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wasserman DH, Cherrington AD. Hepatic fuel metabolism during muscular work: role and regulation. Am J Physiol. 1991 Jun;260(6 Pt 1):E811–E824. doi: 10.1152/ajpendo.1991.260.6.E811. [DOI] [PubMed] [Google Scholar]
- 18.Wahren J, Felig R, Ahlborg G, Jorfeldt L. Glucose metabolism during leg exercise in man. J Clin Invest. 1971 Dec;50(12):2715–2725. doi: 10.1172/JCI106772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ahlborg G, Felig P. Lactate and glucose exchange across the forearm, legs, and splanchnic bed during and after prolonged leg exercise. J Clin Invest. 1982 Jan;69(1):45–54. doi: 10.1172/JCI110440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ahlborg G, Wahren J, Felig P. Splanchnic and peripheral glucose and lactate metabolism during and after prolonged arm exercise. J Clin Invest. 1986 Mar;77(3):690–699. doi: 10.1172/JCI112363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Horton ES, Terjung RL. Exercise, nutrition and energy metabolism. New York: Macmillan; 1988. [Google Scholar]
- 22.Pruett ED. Glucose and insulin during prolonged work stress in men living on different diets. J Appl Physiol. 1970 Feb;28(2):199–208. doi: 10.1152/jappl.1970.28.2.199. [DOI] [PubMed] [Google Scholar]
- 23.Wasserman DH, Lacy DB, Green DR, Williams PE, Cherrington AD. Dynamics of hepatic lactate and glucose balances during prolonged exercise and recovery in the dog. J Appl Physiol. 1987 Dec;63(6):2411–2417. doi: 10.1152/jappl.1987.63.6.2411. [DOI] [PubMed] [Google Scholar]
- 24.Carson E, Cobelli C. Modelling methodology for physiology and medicine. San Diego: Academic Press; 2001. [Google Scholar]
- 25.Zinman B, Murray FT, Vranic M, Albisser AM, Leibel BS, McClean PA, Marliss EB. Glucoregulation during moderate exercise in insulin treated diabetes. J Clin Endocrinol Metab. 1977 Oct;45(4):641–652. doi: 10.1210/jcem-45-4-641. [DOI] [PubMed] [Google Scholar]