Use of Fourier Models for Analysis and Interpretation of Continuous Glucose Monitoring Glucose Profiles

Abstract

Background

The introduction of continuous glucose monitoring (CGM) devices has dramatically increased the amount of information available about each patient. While CGM has become a useful diagnostic tool for the individual patient, interpretive issues including noise reduction remain and further analytical work is needed to fully utilize the data richness.

Method

We applied discrete Fourier transform methodology to CGM data to obtain an overall statistical model providing the dimension reduction necessary for insightful analyses of the whole function and explored some properties and possible applications of this technology.

Results

The following example applications are shown. Discrete Fourier transform allows reduction of noise using an objective statistical criterion and may, as a first step, possibly enhance the value of various measures of variability through this noise reduction. Average functions of groups in a prospective randomized clinical are demonstrated and the aggregate function is readily visualized. Second and third harmonic amplitudes at baseline correlate with hemoglobin A1c after a 6-month treatment period. The time points of most rapid glucose decreases are identified easily with the functional through the second derivative, and its correlation with subsequent reported symptomatic hypoglycemia is shown.

Conclusions

Discrete Fourier transform offers an attractive analytical methodology for CGM data given the achievable dimension reduction without loss of essential information as well as its ability to eliminate noise.

Introduction

Continuous glucose monitoring (CGM)¹ has become a useful diagnostic tool in the treatment of the individual patient,² and substantial efforts have gone into developing derived variables that can be related to meaningful clinical outcomes. Because of the importance of hypoglycemia prediction, particular attention has been given to measures of variability where CGM provides dramatically more information than has been available previously. Researchers have applied previously developed measures of variability—standard deviation,³ M value,⁴ mean amplitude of glycemic excursions,^5,6 J value, low glucose risk index,⁷ and blood glucose (BG) rate of change⁸—and come up with new ones, including continuous overall net glycemic action.⁹ When derived directly from raw data, each of these variables contains both signal and noise from the measurement technology, and inherent in this data reduction to a single number is an incorporation of measurement-related variability not attributable to the patient's condition.

We proposed applying the standard data reduction methodology of the discrete Fourier transform to CGM data that, among other benefits, addresses those issues. The Fourier approximation method provides the following.

• An overall statistical model for assessing the patient's whole blood glucose profile providing the dimension reduction necessary for insightful analyses of the whole function.

• The ability to smooth out extraneous variability in CGM plots by filtering out the high-frequency noise inherent in the CGM measurement process. A useful attribute is that the degree of noise reduction is adaptable to any particular analysis.

• Partitioning the blood glucose profile into a 24-hour mean and component harmonic oscillations about the mean.

• Definitions of new parameters based on 24-hour Fourier profiles, which may have clinical utility.

While individual parameters from discrete Fourier transformation may prove useful as predictors of morbidity, such transformation initially may enhance the utility of the variables mentioned earlier due to the noise elimination it can provide. Furthermore, because the function after discrete Fourier transformation still retains most of the meaningful information about the individual CGM curve, it can be utilized in relation to any clinical outcome whether related to average glycemic exposure, precipitous glucose decreases, low glucose values, or perhaps for oxidative stress, particularly high glucose values.^10,11 No a priori assumptions about pathogenesis have to be made.

In this article, we applied the discrete Fourier transform to CGM data and explored some of the possible utilities with data primarily from adolescent type 1 diabetes patients.

Methods

Model Considerations

Discrete Fourier transformation requires selection of the longest possible cycle for which there are data. In this article, 24-hour periods were selected as the longest cycle because whole function summaries were made based on cohorts of patients, many of whom had only one continuous 24-hour period of usable data. Also, because of the circadian cycle of 24 hours, this cycle time made physiologic sense. When CGM devices with longer sample times become available, a 7-day cycle due to changed food and exercise behavior during the weekend or even a monthly cycle to account for menstrual cycle impact on glycemic control may yield additional information.

The start/end time of a 24-hour cycle can be designated at any time since the CGM monitor continues. It is convenient to select the start/end time of the 24-hour cycle to be midnight so that the horizontal scale begins at midnight (hour 0) and ends at midnight (hour 24 = hour 0). Hence, the date of the 24-hour session becomes the key identification in data analysis. Patients with more than one contiguous 24-hour session would then have, in effect, more than one data “point” (i.e., whole 24-hour function) for the analysis. These can be averaged so that each patient contributes one “point” per specified visit, or the sampling unit can be identified as each individual 24-hour session and patient effects can be accounted for in mixed models.

Fourier Model

Suppose the function obtained from the CGM monitor has the form

$$G=f(t),$$ (1)

where t is in hours from 0 (midnight) to 24 (midnight) and G is the observed CGM BG sensor reading at time t. Here it is convenient to assume that G is observed for every time t even though in reality it is generally observed every 5 minutes. The Fourier approximation to this function has the form

$$G=fh(t)=m+{\displaystyle \sum _i{\text{cycle}}_i(t),}$$ (2)

where cycle_i(t) is a periodic function that runs through exactly i complete cycles in 24 hours.¹² In other words, its frequency of oscillation is i and the time required to complete one cycle is 24/i hours, which is called the period. The function cycle_i(t) is called the ith harmonic component of the overall function, and two parameters are needed to completely define the ith harmonic, the amplitude and phase shift.

Index i runs from 1 to the number of cycles used for the approximation, hence the Fourier model is a linear combination of a constant m and several harmonic curves where each component curve oscillates at a regular integral number of cycles per 24 hours.

It turns out that the intercept term, m, equals the 24-hour mean of blood glucose readings from the 24-hour CGM profile and can be expressed as

$$m=\text{AUC/24}$$

The constant m is also the mean of the Fourier approximating function fh because the 24-hour mean of each of the harmonic functions is zero. This is an important characteristic of the Fourier approximation, namely apart from the overall mean m the rest of the approximating function is modeling only the BG variability and is decomposing this variability into harmonic components.

There is another important characteristic of the cycles cycle_i(t). These cycles are mutually orthogonal in the sense that they are uncorrelated, that is, the integral or sum of the product of any two of them over 24 hours is zero (provided all CGM readings are present over 24 hours and spaced equally). The very important consequence of this is that the fitted coefficients for an individual cycle do not depend on other cycles within the multiple regressions. Each individual estimated cycle remains unchanged regardless of the number of cycles chosen for the model.

The full definition of the harmonic function cycle_i(t) is

$${\text{cycle}}_i(t)={\text{A}}_i\cos (2\pi i(t-{\text{PHS}}_i)/24),$$ (3)

where A_i is the amplitude and PHS_i is the phase shift; both are determined based on obtaining the best approximation to the observed CGM BG function f.

Amplitude A_i is the maximum value that the harmonic cycle_i(t) will ever achieve over 24 hours. If the amplitude of a harmonic is zero, then that frequency of oscillation does not exist in the BG curve, and if all harmonic amplitudes were zero, then the curve would be flat, namely the constant m for all times t.

For CGM sessions yielding 288 readings per 24 hours, if the amplitudes from all 144 harmonics are squared and summed, the result is proportional to the ordinary sample variance of the 288 CGM BG readings [the sum of the squared amplitudes multiplied by 1/(144*287) equals the sample variance]. Hence, A_i values represent a decomposition of the total variation of the BG curve across the oscillation harmonics of the curve.

The phase shift PHS_i moves the cosine curve to the right or left in order to locate the maximum and minimum values of the harmonic to best represent the overall BG curve.

The harmonic determined by cycle_i(t) is linear in amplitude A_i but not linear in the phase shift-PHS_i. This would appear to eliminate the standard multiple regression statistical software for estimating the parameters of the harmonic functions. However, the cosine function is converted readily to another form that is linear in the unknown parameters that must be estimated. Hence, the ith harmonic can be written as

$${\text{cycle}}_i(t)=C_i\cos (2\pi it/24)+{\text{S}}_i\sin (2\pi it/24),$$ (4)

which is an equivalent expression for the ith harmonic function, with

$$\begin{array}{l}{\text{A}}_i={({\text{C}}_i^2+{\text{S}}_i^2)}^{1/2}\\ {\text{PHS}}_i={\tan }^{-1}({\text{S}}_i/{\text{C}}_i).\end{array}$$ (5)

Hence, the Fourier approximation to G = f(t) starts with

$$G=fh(t)=m+{\displaystyle \sum _i\left\{{\text{C}}_i\cos (2\pi it/24)+{\text{S}}_i\sin (2\pi it/24)\right\},}$$ (6)

which is a multiple linear regression in the terms cos(2π i t/24) and sin(2π i t/24).

Statistical Test for Zero Amplitude

After a Fourier transformation of individual CGM data sets, it is useful to aggregate data across patients to a group function when assessing the impact, for example, of a treatment intervention within a clinical trial. This is done simply by calculating the means of the individual patient C and S values for each cycle. A critical consideration is whether this sample size is adequate to detect the given cycles.

Let Cbar and Sbar be sample means of cosine and sine regression coefficients for cycle i from a sample of n patients' 24-hour CGM system profiles, as in Equation (6). Let Cvar, Svar, and COV be sample variances and covariance of patient C and S values for cycle i. Then the statistic

$$\begin{array}{l}\text{Fstat\hspace{0.17em}=}\left\{\left(\text{n\hspace{0.17em}}-2\right)/2\right\}\{\left(\text{Svar}\right){\text{Cbar}}^2+\left(\text{Cvar}\right){\text{Sbar}}^2-\\ 2\left(\text{COV}\right)\text{Cbar\hspace{0.17em}Sbar}\}/\left\{\text{Cvar\hspace{0.17em}Svar\hspace{0.17em}}-{\text{COV}}^2\right\}\end{array}$$ (7)

has an F distribution with 2 df, n – 2 df assuming that the population amplitude = 0 for this cycle (the null hypothesis that both C and S are zero in the population for this cycle). In other words, Fstat is a test statistic that can be applied to each cycle for determining whether there is sufficient precision or sufficient sample size for detecting the presence of a particular harmonic cycle. This statistic is Hotelling's T² test.¹³

The resulting p value should be adjusted to take into account the multiple tests, one for each cycle. There are many ways this can be done, and one procedure utilizes a standard multiple comparison method at each cycle, the idea being that if cycle k is being tested, then this must be the kth test so that significance at the p = 0.05 level should take this into account. This yields a procedure where higher cycles are subjected to a successively more stringent criterion. This adjustment is given by

$$\text{Adjusted\hspace{0.17em}}p\text{\hspace{0.17em}value\hspace{0.17em}}=\text{\hspace{0.17em}cycle}\times p,$$ (8)

where p is obtained from the Hotelling T² test. This adjustment uses the Bonferonni method.¹⁴

Use of Derivatives to Identify Maxima for Rate of Change

One advantage of representing the 24-hour CGM with defined mathematical functions is the ability to obtain stable estimates of rates of change at specific times. One such parameter, termed average steepest descent, can be defined only after the raw CGM curve has been approximated by a smooth function. The average steepest descent is defined in the following two-step process using a smooth (Fourier) approximation to a patient's 24-hour CGM function.

1. Solve for the relative minima of the first derivative of the CGM approximation (find the times at which the curve has its greatest local descent).

2. Average the resulting steepest descents (the first derivative values at these times).

Because the Fourier approximation involves only sines and cosines, it is relatively easy to perform step 1 and hence step 2 using the Newton–Raphson method.¹⁵ Applications where descents of relatively long duration are desired require a Fourier approximation of no more than five cycles.

Results

Illustrative Example of Individual CGM Trace Transformation

Figures 1A and 1B illustrate a 24-hour CGM curve from a patient with type 2 diabetes treated with a combination of metformin, glipizide, and insulin glargine at bedtime. Superimposed on the curve is graphic representation of the functions derived by Fourier transformation with 5 and 20 cycles, respectively. The higher frequency residuals, or differences from the approximation and the actual BG readings, are also depicted.

Figure 1.

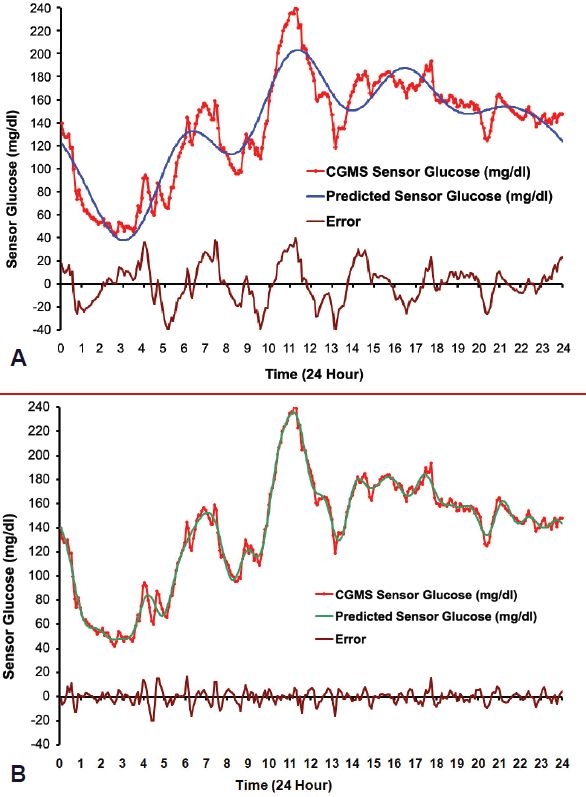
Individual CGM midnight to midnight tracing (red line) from a patient with type 2 diabetes treated with metformin, glipizide, and bedtime insulin glargine with superimposed discrete Fourier transform function (blue line) and residual error (black line) with 5 (A) and 20 (B) cycles, respectively.

The use of just 5 cycles (11 degrees of freedom) in Figure 1A captures the essence of this particular patient's glucose curve with apparent nighttime hypoglycemia and relatively early breakfast and lunch with relatively steep decreases after those two meals. However, the 5 cycles are not sufficient to catch the extremes of the peaks and valleys with deviations from the original curve of up to 40 mg/dl, and the error plot reveals some regular oscillations remaining, suggesting that higher frequency harmonics may be required.

When using 20 harmonic functions (41 degrees of freedom) the model curve, except for some minor spikes, essentially retraces the original curve and the error plot no longer reveals a periodic pattern, possibly indicating it is now reduced to random noise. Furthermore, note that the approximating Fourier model converges uniformly to the observed CGM curve over all times within the 24-hour period (except at times 0 and 24). This uniform convergence is a well-known and useful property of Fourier approximations.

Example of Test for Zero Amplitude

The following examples are drawn from a prospective clinical trial of girls and boys between 9 and 17 years of age with a Tanner stage of ≥2 who had a diagnosis of type 1 diabetes mellitus for at least 1 year for which they were treated with neutral protamine Hagedorn (NPH) as the basal insulin. They had a C-peptide concentration ≤0.5 nmol/liter and 7.0% ≤ hemoglobin A1c (HbA1c) ≤ 9.5% at screening and were randomized to either continue on their previous insulin regimen or be treated with insulin glargine in combination with insulin lispro in a typical multiple daily injection regimen.

The test for zero amplitude on the baseline sample of 90 patients with CGM recordings is shown in Table 1. According to the adjusted p values, there is strong evidence for detecting nonzero amplitudes for cycles 1 through 5. However, because the unadjusted p value for cycle 9 was under 0.05, there may be some evidence of higher frequencies, which perhaps would be detected readily with larger sample sizes.

Table 1.

Test for Existence on Cycles in a Sample of 90 Type 1 Adolescents with Type 1 Diabetes Treated with Insulin NPH in Combination with Fast-Acting Insulin^a

Cycle	Sample Size	Mean cosine	Mean sine	Hotelling's T2	p value	Adjusted p value
1	90	−149.029	−52.813	4.3226	0.01619	0.01619
2	90	75.418	−185.775	11.7284	0.00003	0.00006
3	90	118.59	57.466	12.1072	0.00002	0.00007
4	90	−60.136	−10.945	4.8573	0.00998	0.03991
5	90	42.096	−76.279	11.5319	0.00004	0.00018
6	90	−14.069	12.592	1.2102	0.30304	1.0
7	90	−1.651	−6.43	0.2022	0.81728	1.0
8	90	−12.575	−15.433	2.8423	0.06366	0.50925
9	90	10.762	15.935	3.2471	0.04359	0.39235
10	90	−5.792	−1.066	0.4786	0.62125	1.0

^aThe longest cycle time (cycle 1) is set to 24 hours. Determined parameter estimates for each cycle are shown along with Hotelling's T² test statistic value, the unadjusted p value, and the p value after Bonferonni adjustment for multiple tests.

Group Comparison Example: Individual Harmonic Components and Graphical Representation

Table 2 shows baseline estimates and estimates of changes from baseline for the treatment group randomized to glargine in combination with lispro multiple daily injection therapy of the five cycles demonstrated earlier to be adequately supported by the amount of data available. The estimates were not sample means, but were generated from a mixed repeated measures model of the 11 Fourier parameters.

Table 2.

Fourier Coefficients for Five Cycles with Longest Cycle Time Set to 24 Hours in a Sample of Type 1 Adolescents Treated with Insulin Glargine in Combination with Insulin Lispro at Week 12^a

Summary	Cycles / 24 hours	Combined baseline estimate (SE) (N = 90)	Week 12 glargine estimate (SE) (N = 45)	Week 12 glargine – baseline estimate (SE) (N = 45)	p value
Mean sensor BG (mg/dl)		193.91 (4.61)	176.38 (7.61)	−17.53 (8.88)	NS: 0.05 < p < 0.1
Amplitude (mg/dl)	1	44.11 (1.94)	38.96 (2.96)	−5.15 (3.50)	NS: p > 0.1
	2	34.09 (1.49)	26.77 (2.27)	−7.32 (2.69)	p = 0.007
	3	26.07 (1.04)	20.73 (1.58)	−5.34 (1.88)	p = 0.005
	4	19.03 (0.75)	15.75 (1.14)	−3.28 (1.36)	p = 0.017
	5	14.82 (0.65)	13.25 (0.98)	−1.58 (1.17)	NS: p > 0.1
Phase (hours)	1	12.02 (0.50)	10.85 (0.75)	−1.16 (0.90)	NS: p > 0.1
	2	6.91 (0.27)	6.71 (0.41)	−0.21 (0.49)	NS: p > 0.1
	3	3.58 (0.18)	4.08 (0.28)	0.49 (0.34)	NS: p > 0.1
	4	2.91 (0.13)	3.02 (0.19)	0.11 (0.23)	NS: p > 0.1
	5	2.79 (0.11)	2.79 (0.17)	−0.00 (0.20)	NS: p > 0.1

^aThe baseline, week 12, and difference as well as p value for that difference are shown. Note changes in the cycle times 12, 8, and 6 hours roughly corresponding to the prolonged postprandial glucose in these patients and compare with Figure 2.

There was a nonsignificant reduction of 18 mg/dl in the 24-hour mean BG level. While it may be surprising that this apparently substantial change is not statistically significant, it should be kept in mind that the standard measure of average glycemic control HbA1c is inherently an average over time and therefore can be suspected to be much more stable than a single or a couple of days worth of CGM. Regarding the harmonic amplitudes, the amplitudes decline with increasing frequency. A numerical decrease in the largest amplitude and significant reductions in the amplitudes for harmonics 2, 3, and 4 were observed, and surprisingly the estimated reductions for harmonics 2 and 3 were larger than for harmonic 1. The phase shifts for each harmonic are approximately half of the harmonic period and are not changed much.

Results are easily plotted in Figure 2 to facilitate comprehension for nonmathematicians. Dotted line curves represent one standard error of the week 12 baseline difference at each time t, and it is evident that the curve separation is small when judged by the precision at each individual time point. Summaries of the curves, such as the 24-hour means or individual harmonic amplitudes, utilize the whole curve and hence carry more precision so that some differences between 12 weeks and baseline do achieve statistical significance. However, it is clear that more than 45 patients are required to separate the curves. Even with this sample size limitation, it is clear that the observed reductions in harmonics 2 through 4 reflect a diminished postbreakfast glycemic surge. Despite similar average trough glucose during the night of about 170 mg/dl, the peak postbreakfast glucose is diminished from about 235 to 205 mg/dl.

Figure 2.

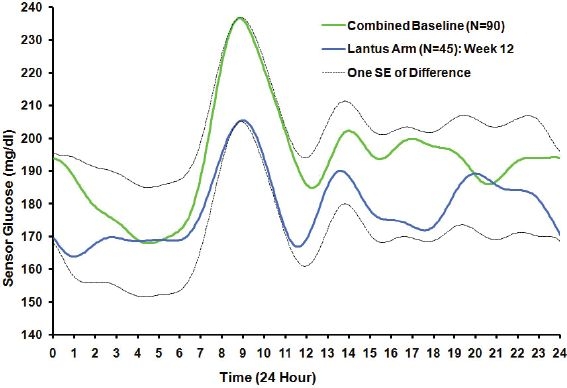
Estimated group function of patients randomized to insulin glargine in combination with insulin lispro (blue curve) after 3 months (N = 45) compared with estimated group function at baseline (green curve) from all subjects (N = 90) based on a general linear model analysis of Fourier coefficients of adolescent type 1 diabetes. Plus or minus one SE of the difference in means is depicted from the average of the curves at each time. The insulin glargine reduction from baseline in the 24-hour mean did not quite achieve statistical significance (NS: 0.05 < p < 0.1). However, the reduction from baseline in the CGM 24-hour standard deviation was statistically significant (p = 0.002).

Clinical Results: Effect of Harmonics 2 and 3 on HbA1c

Each of the patients in the aforementioned study had HbA1c values determined at baseline and at week 24. It was therefore possible to determine whether any of the Fourier parameters had additional prognostic value for predicting the mean week 24 HbA1c after taking into account the effects of the usual baseline predictors, particularly baseline HbA1c. The patient's postbaseline randomized study arm was also taken into account in the model, with 45 patients in the glargine arm and 45 patients in the intermediate-acting insulin arm.

Cycle 2 and cycle 3 amplitudes at baseline each had a statistically significant association with the week 24 HbA1c, after accounting for baseline HbA1c. Further investigation revealed that this association was particularly strong when cycle 2 and cycle 3 harmonic functions were combined, and the amplitude of the resulting sum was used as one prognostic factor. This amplitude was

$$\text{Amp23\hspace{0.17em}=\hspace{0.17em}sprt\hspace{0.17em}}\left\{{\left({\text{A}}_2\right)}^2+{\left({\text{A}}_3\right)}^2\right\}$$ (9)

The multiple linear regression of the 90 patients had week 24 HbA1c as the dependent variable and the following terms as independent variables: baseline HbA1c, baseline mean 24-hour BG (from the CGM records), the amplitude of the first cycle (A₁), the combined amplitudes of cycles 4 and 5, patient age, and study arm (which had little effect for these patients). Results of this model indicated that larger values of Amp23 at baseline yielded larger mean week 24 HbA1c levels for the same baseline HbA1c (p < 0.001). Baseline HbA1c was a significant predictor of week 24 HbA1c (p < 0.05), but the other terms did not achieve statistical significance.

To illustrate the effect graphically, patients were categorized as having low, medium, or high values of Amp23 at baseline, and these categories were entered into the model rather than the single linear term. Values defining low, medium, and high were chosen to divide the cohort of 90 patients into approximately equal groups, and patients classified as having a high amplitude for their 2nd + 3rd harmonic functions had a significantly higher mean HbA1c at week 24 (p = 0.003). Results are depicted in Figure 3A. Because the 24-hour mean BG is known to be correlated with HbA1c, perhaps either the mean BG or HbA1c should have been in the model, but not both. However, the result was the same regardless of which combination of baseline HbA1c, mean BG was used. The scatter plots of week 24 HbA1c versus baseline Amp23 (adjusted for the other baseline factors) in Figure 3B show that this relationship was generally linear across all points, so the original linear model provided a reasonable fit. The low, medium, and high values from Figure 3A do not apply directly to the x axis of Figure 3B, as both the x and the y axes from Figure 3B were obtained by adjusting for the other factors in the model.

Figure 3.

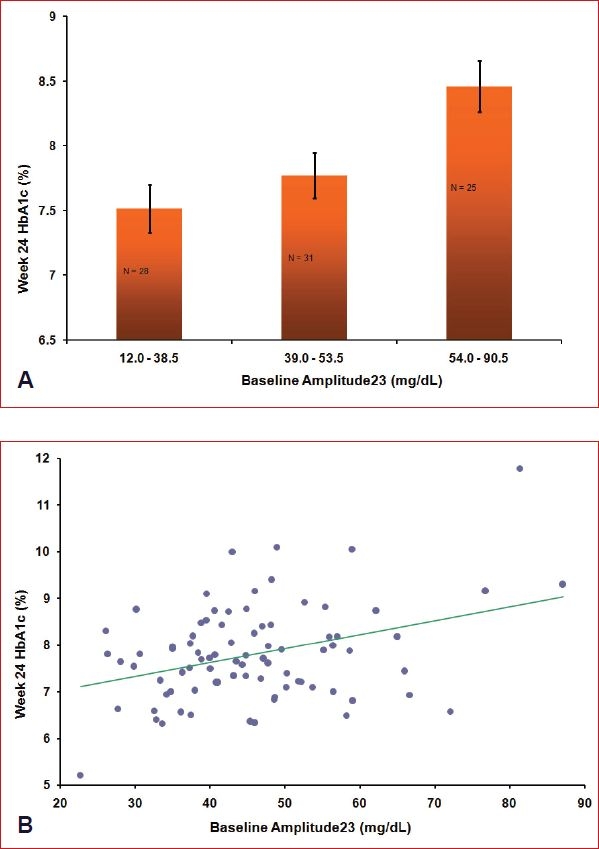
(A) Baseline CGM 2nd + 3rd harmonic amplitude relation to subsequent HbA1c. HbA1C least-squares means at 24 weeks after adjustment for baseline HbA1c (p = 0.03), age (p = 0.06), and study arm (p > 0.3) are shown for each tertile of the 2nd + 3rd harmonic amplitude (p = 0.003). (B) Baseline CGM 2nd + 3rd harmonic amplitude relation to subsequent HbA1c appears linear across all points. Week 24 HbA1c values and baseline 2nd + 3rd harmonic amplitude values have been adjusted by other independent variables in the model. The adjusted slope estimate = 0.03% (mg/dl) (SE = 0.009) (p < 0.001).

Clinical Results: Effect Average Steepest Descent on Hypoglycemia

A measure of average steepest descent for each 24-hour profile obtained at baseline from a cohort of 90 type 1 pediatric patients was used in conjunction with the study arm and other baseline parameters to predict the rate of subsequently reported symptomatic hypoglycemia confirmed with BG <50 mg/dl occurring between the hours of 6 AM and noon during the 24 study weeks. The log-linear relationship between the average steepest descent and the reported hypoglycemia rate by treatment group is depicted in Figure 4. Patients with steeper average descents had higher rates of hypoglycemic events occurring. This relationship was statistically significant for patients in the NPH insulin group with the hypoglycemia rate estimate doubled for every decline of −9 mg/dl in average steepest descent (p < 0.005), while it was in the same direction but not statistically significant (p > 0.1) in the insulin glargine group.

Figure 4.

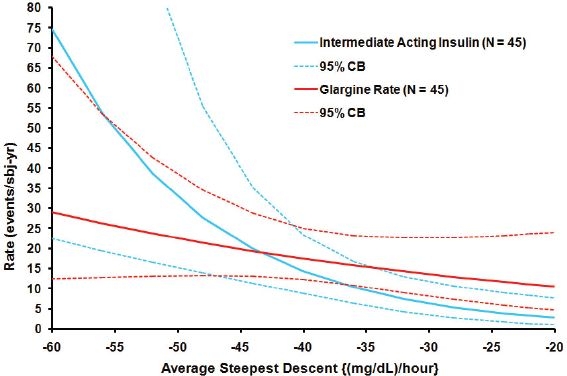
Estimated hypoglycemia rate (symptoms confirmed with BG <50 mg/dl) versus baseline average steepest descent (three cycles), by study arm, for events occurring from 6 AM to noon. The log-linear model is depicted for each treament group as a solid line with 95% confidence bounds shown as dashed lines. The estimated NPH hypoglycemia rate doubles for every −9 mg/dl-hour decline in average steepest descent (p < 0.005). The estimated glargine rate doubles for every −28 mg/dl-hour decline in average steepest descent (NS, p > 0.15). The difference between study arms was statistically significant at p < 0.03.

Discussion

Studying CGM 24-hour plots for different patients suggests characteristics that need to be present for a useful functional approximation. First, the glucose rises and falls cyclically in relation to a baseline as expected with diet and physical activity as well as drug action. Second, there appears to be a relatively high-frequency, low-amplitude oscillation (up and down) motion in the plots. This article considers the latter white noise originating from the CGM meter measurement of the signal and not from fluctuations in the actual BG. Useful functional approximations of BG concentration must be able to filter out this high-frequency noise. What remains is a curve that still rises, falls, and returns to approximately the original starting point as expected. In other words, a typical CGM curve is not some linear or monotonic function amenable to a low-degree polynomial approximation, but something suggesting a combination of sine and cosine functions. These considerations make the Fourier model a method of choice in developing approximating functions for CGM assessments.

For analysis of groups of patients, this methodology has the advantage of making the determination of the required number of cycles depend on a standard objective statistical criterion. When approximating an individual patient trace the number of cycles chosen would depend on the error the user is willing to accept and therefore is a matter of choice evaluating not only the size, but also any possible structure in the residual error (compare Figures 1A and 1B).

From a theoretical point of view the discrete Fourier transform therefore appears to be a very attractive functional description of CGM data, if for nothing else as a noise reduction procedure before calculating already established measures of variability.

While advocates of transformed data for glucose values such as M value and “low blood glucose index”⁷ may be “right” given the skewed distribution of glucose concentrations in diabetes patients, transforming raw data also transforms the noise. While it may be necessary at times to transform the blood glucose signal that can vary exponentially because of among-patient variation, the white noise component from the measurement itself may not require transformation. This again suggests that the high-frequency noise be filtered out prior to transformation, but more research is required to determine whether the Fourier transform for this purpose is of benefit for improving prediction clinical outcomes.

For analysis of clinical trial data, dimension reduction across groups without loss of essential information is of critical importance. In this context, the three chosen examples demonstrate a few of the possible applications of the discrete Fourier transform. Dimension reduction enables a unified comparison of the full group functional forms rather than a comparison of isolated derived variables that by nature fragment and eliminate critical information. The third example shows a particularly useful application of the smooth functional expression of CGM data because the symptoms of hypoglycemia physiologically involve a counterregulatory response that may be precipitated as much by the change in glucose as by the absolute glucose value itself. While rate of change has been used previously to describe glucose curves,⁸ it is relevant that reference to the smooth functional approximation of the CGM profile was made only after failure to demonstrate any hypoglycemia predictive value from measures of low glucose at baseline. Smooth functional approximation of data permitted identification of the time points with the highest velocity downward simply by finding the point where the second derivative of the function was zero using undergraduate level mathematics. Further research will relate the exact time point of symptomatic hypoglycemia reported by the patient to CGM data. From this and empirical data we should be able to determine to what degree reported hypoglycemia by patients is related to the absolute blood glucose level, to the rate of changing glucose, or even to the rapidity with which the rate of change changes or, in other words, the acceleration.

This article focused on one data set from a prospective randomized comparative trial of adolescent type 1 diabetes patients. While space prohibits demonstration of further data, the discrete Fourier transform as a method of analysis has additionally been tested in a database of healthy volunteers, two type 2 diabetes prospective randomized treatment intervention trials, and finally an adult type 1 diabetes study and has shown equal promise there reproducing some of the findings from this article. Further work is needed to further validate this approach, and ultimately only application in morbidity and mortality trials will truly define the value of such methodology.

Abbreviations

BG

blood glucose

CGM

continuous glucose monitoring

HbA1c

hemoglobin A1c

NPH

neutral protamine Hagedorn