Statistical Approach of Assessing the Reliability of Glucose Sensors: The GLYCENSIT Procedure

Abstract

Background

In healthcare, patients with diabetes are instructed on how to apply intensified insulin therapy in an optimal manner. Tight blood glucose control is also performed on patients treated in the intensive care unit (ICU). Different blood glucose meters and glucose monitoring systems (GMSs) are used to achieve this goal, and some may lack reliability.

Methods

The GLYCENSIT procedure is a statistical assessment tool we are proposing for evaluating the significant difference of paired glucose measurements. The performance of the GlucoDay^® system in the ICU is analyzed with GLYCENSIT.

Results

The GLYCENSIT analysis comprises three phases: testing possible persistent measurement behavior as a function of the glycemic range, testing the number of measurement errors with respect to a standard criterion for binary assessment of glucose sensors, and computing the tolerance intervals that indicate possible test sensor deviations for new observations. The probability of the tolerance intervals directly reflects the number of samples and additionally improves current assessment techniques. The method can be tuned according to the clinician's preferences regarding significance level, tolerance level, and glycemic range cutoff values. The measurement behavior of the GlucoDay sensor is found to be persistent but inaccurate and returns wide tolerance intervals, suggesting that the GlucoDay sensor may not be sufficiently reliable for glycemia control in the ICU.

Conclusions

The GLYCENSIT procedure aims to serve as statistical guide for clinicians in the assessment of glucose sensor devices.

Introduction

Frequent and accurate monitoring of glycemia is an important keystone for intensive insulin treatment in critically ill patients and patients with diabetes. Both blood glucose meters (resulting in time-discrete measurements) and glucose monitoring systems (GMSs, resulting in near-continuous measurements) are used to achieve this goal.¹ Some blood glucose meters and GMSs, however, show insufficient reliability. Moreover, no generally accepted procedure for testing reliability exists to date.^1,2 In the literature, analytical and clinical approaches have been described to evaluate the quality of glucose measurements.

The first approach measures the analytical accuracy by using classical statistical techniques. Such techniques are analyses based on regression (or correlation), mean absolute or relative difference, Bland-Altman,^3,4 and analysis of variance (ANOVA).⁵ Although most of these techniques are frequently used for comparing sensor readings with reference observations, they show some weaknesses that have been previously debated. Regression typically measures the strength of a relation between two variables but not their numerical agreement.^4,6 Wide measurement ranges also give large correlation coefficients compared to narrow ranges, easily leading to artificial conclusions.⁴ Difference measures are often skewed⁷ such that their result can sometimes be misleading. The method proposed by Bland and Altman,⁴ in a format favored by clinical users, relies on equal severity of measurement errors for the entire blood glucose range (e.g., 20 mg/dl measurement error in hypo/hyperglycemic range is equally severe).⁸ One also relies on the normal distribution assumption of these errors. This assumption, often not satisfied in clinical practice, is also required when performing classical (parametric) ANOVA tests. In general, it is hard to satisfy all imposed statistical conditions as present in these techniques and to transform statistical results into clinical use.

The second approach evaluates the measurements from a clinical point of view but typically lacks statistical evidence. Most known are the error grid analysis (EGA)^9–11 and the related continuous glucose-EGA.¹² Both techniques are based on systematic and comprehensive graphical display assessments, which have been debated before^7,13–14 (e.g., using specific regions in the grid pattern leads to different results for only slightly different glucose observations). Parkes et al. developed an alternative graphical analysis¹⁵ that shows similar drawbacks as EGA. Since then, the diabetes error test model (DETM) has been developed.¹⁶ In this novel concept, the impact of different factors that may affect postprandial glycemic excursions is simulated giving a clinical evaluation of “treatment” errors rather than “measurement” errors. Though the DETM in its current form is useful in evaluating glucose sensors, its simulations are based on assumptions/simplifications, and the model is restricted to a specific group of patients with type I diabetes.

At present, no consensus exists about the technique or combination of techniques that should be applied when assessing glucose sensors, since both analytical and clinical approaches show some weaknesses; so one (or a selection) of the techniques described earlier are applied for evaluating the sensor reliability.^9,10,17–21

Therefore, we present the GLYCENSIT analysis (GLYCemia sENSor IT), which offers a statistically sound assessment procedure comprising three complementary phases. The methodology is a first step toward combined statistically based and clinically supported assessment techniques for both blood glucose meters and GMSs. The proposed procedure aims to guide the user in appropriately evaluating a glucose sensor based on statistical and clinical knowledge. Instead of returning a simple “yes/no” answer, this methodology helps to interpret the information hidden in the data and gives a certain degree of freedom (in terms of design parameters) to the user.

Methods

Preprocessing and Assumptions

First, a systematic study approach to shift blood glucose over the whole clinically relevant range, by using glucose clamps,¹ can solve the typical problem that few hypo/hyperglycemic data are available.²² However, the recommended use of (temporary) glucose clamps is not suitable for specific patient groups (e.g., critically ill patients) for ethical reasons.^23,24 Second, the received data need to be preprocessed in advance. In the case of GMSs, calibration is required to convert the received (electric) signal into glucose readings (often performed by the supplied software). Further preprocessing is necessary to remove time shifts (e.g., time delay between measurements in venous blood and interstitial glucose,²⁵ possible additional physiological delays (“alternate site testing” phenomenon²⁶), and systematic analytical error²⁷ by appropriately reshifting the data. Next, filters can reduce noise.²⁸ Third, the data are transformed into sets of paired glucose measurements such that test blood glucose meters and test GMSs can be evaluated against reference blood glucose meters (gold standard sensor).

We assume that the measurement errors are sufficiently statistically independent, meaning that no correlation exists between successive errors (identically/independently distributed errors). Therefore, we advise researchers to concomitantly measure glycemia with a minimum 1 h time interval, which is sufficiently large to meet this assumption. The same condition is imposed in other well-known statistical assessment tools like Bland–Altman⁴ or ANOVA.⁵ However, the GLYCENSIT procedure could be adapted when correlation between successive errors would be present. Still, we chose to adopt the no-correlation assumption (by taking at least 1 h for the reference sensor intervals) for clarity of this exposition.

The developed GLYCENSIT procedure comprises three complimentary phases in which possible persistent measurement behavior, total number of measurement errors, and tolerance intervals that are valid for new measurements are successively studied. The full procedure does not directly answer the question of whether a sensor is reliable or not (because of the dependency on the clinician's preferences regarding the design parameters, but rather statistically guides the clinician in assessing test sensor devices.

Normalization

The problem of evaluating a glucose sensor is framed in a statistical setting by considering the sensor under study as a random variable. Starting with a sample of n paired glucose sensor observations y_ref,t and Y_test,t (with t=1,…,n), the gold standard or reference sensor is called y_ref,t, whereas the test sensor is denoted by Y_test,t The latter can be formulated as follows:

$$Y_{\text{test,}t}=y_{\text{ref},t}+e_t,$$

where e_t denotes a stochastic error between test and reference value at time instant t. In this step, errors of the set of paired glucose measurements are normalized using the International Organization for Standardization (ISO) criterion.²⁹ This criterion (which should be fulfilled for 95% of the observations and which is similar to Zone A of the EGA^9–11) can be summarized as follows:

• for reference values ≤75 mg/dl, test sensor values fall within ±15 mg/dl limits

• for reference values >75 mg/dl, target variability is ±20%

The errors are normalized to make the severity of error independent of glycemia. The used normalization function is formulated as

$$\{\begin{array}{ll}{u}_t=f\left(y_{\text{ref,}t}-Y_{\text{test,}t}\right)=1/15\times \left(y_{\text{ref,t}}-Y_{\text{test,}t}\right)\hfill & \text{if\hspace{0.17em}}{y}_{\text{ref,}t}\le 75\text{\hspace{0.17em}mg/dl}\hfill \\ u_t=f\left(y_{\text{ref,}t}-Y_{\text{test,}t}\right)=5\times \left(y_{\text{ref,t}}-Y_{\text{test,}t}\right)/y_{\text{ref,}t}\hfill & \text{if\hspace{0.17em}}{y}_{\text{ref,}t}>75\text{\hspace{0.17em}mg/dl}\hfill \end{array}$$

such that errors violating the ISO criterion return to absolute normalized errors larger than 1. We proceed with normalized errors in Phase 2/3 of the GLYCENSIT procedure. In Figures 1 and 2, y_ref,t and Y_test,t are symbolized by G_R and G_T, respectively.

Figure 1.

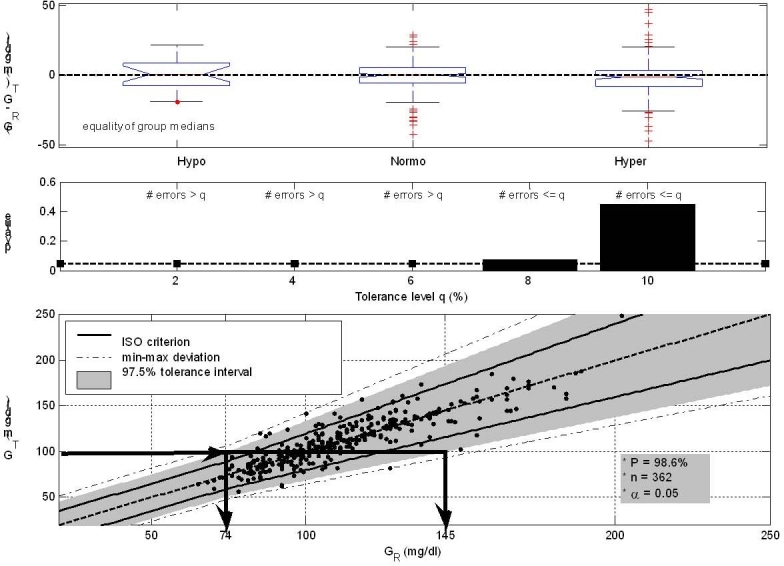
GLYCENSIT analysis of the GlucoDay sensor. The top panel (Phase 1) shows persistent measurement behavior (p ≥ .05) as a function of blood glucose. The G_R = G_T dashed line crosses all generated boxplots, and both under/overestimated (extreme) errors are observed over all ranges. When less than 8% errors in comparison to the ISO criterion are permitted (Phase 2), the sensor does not perform accurately (middle panel, p < .05 for tolerance levels <8% indicating the sensor is “inaccurate”). The significance level (α = 0.05) is represented by the dashed line. The # symbol indicates “frequency of.” Finally, the bottom panel (Phase 3) displays the observed 97.5% tolerance intervals (shaded area), meaning that 95 new measurements obtained from the test sensor out of 100 (α = 0.05) lie in this area with a high probability of 98.6% (related to the high number of uploaded measurements and indicating that the conclusions are statistically reliable). The solid and dashed line illustrate the ISO-criterion limits and the G_T = G_R axis, respectively. The dash-dotted lines denote the min/max deviation present in the data (given by points). The size of the tolerance intervals determines possible future sensor deviations. For example (illustrated with the arrows), when 100 mg/dl is measured with the test sensor (G_T), the real (reference) glycemia (G_R) lies between 74 and 145 mg/dl in 95% of the cases, which indicates that the intervals are too wide to be clinically acceptable. Moreover, these intervals are wider than the ISO limits in both under- and overestimation direction. Together with the large min–max deviations, this may lead to no acceptance of the sensor for use in the ICU.

Figure 2.

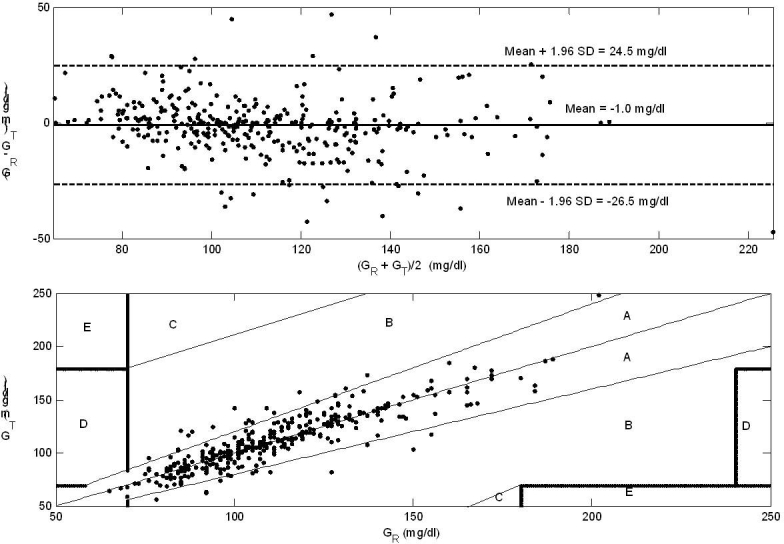
Bland–Altman (top panel) and EGA (bottom panel) analysis of the GlucoDay sensor device. The mean difference (standard deviation) between G_R and G_T equals –1.0 mg/dl (13.0 mg/dl), and the relative number of points in the A and B regions are 90.9% and 9.1%, respectively. The large limits of agreement and the high number of measurements in the B zone may lead to disapproval of the GlucoDay sensor for use in the ICU.

GLYCENSIT Procedure Phase 1: Persistent Measurement Behavior

Measurement behavior that is persistent in the full glycemic range is preferable to nonpersistent behavior from a clinical point of view, as it allows the interchange between sensors with only one conversion factor (valid for the full glycemic range). In this first phase, the sensor performance is assessed by comparing the medians of the errors that belong to the hypo/normo/hyperglycemic range. Therefore, hypo/hyperglycemic cutoff values are chosen a priori, and the full set of paired glucose measurements are divided accordingly (with respect to reference values). The Kruskal—Wallis test,⁵ which may be used when the normality assumption is not met, performs a nonparametric one-way ANOVA for comparing the medians of two or more groups of data. Since distributions are often skewed, median rather than mean values are used.⁷ The null hypothesis H₀ that the distribution functions of the errors per glycemic group are equal is tested resulting in a p-value.³⁰ If p ≥ α (where α denotes the significance level), we cannot reject H0. If p < α, we can reject H₀ with a probability of at least 1 − α. Further, boxplots of measurement errors per glycemic range illustrate the over- and under-estimated measurement behavior, interquartile ranges, presence of outliers, and symmetry/skewness of the distribution.

GLYCENSIT Procedure Phase 2: Number of Measurement Errors

The statistical test used in this phase determines whether or not normalized residual values violate the ISO criterion too often: in other words, whether or not the sensor under study is “accurate” with respect to this criterion. This is expressed in the number of times that the absolute value of the normalized difference does not exceed 1. The acceptable rate of error is defined as the tolerance level q (between 0 and 1). As an example, a tolerance level of q = 0.04 indicates that the sensor is allowed to make, at most, 4 inaccurate (based on the ISO criterion) measurements out of 100. Mathematically, this hypothesis testing is represented in terms of a null hypothesis H₀ and an alternative hypothesis H₁:

$$\begin{array}{cc}{H}_0:\frac{1}{n}{\displaystyle \sum _{t=1}^{n}I\left(\left|u_t\right|>1\right)\le q}& \text{versus\hspace{0.17em}}{H}_1:\end{array}\frac{1}{n}{\displaystyle \sum _{t-1}^n\left(\left|u_t\right|>1\right)>q,}$$

where $I\left(\left|u_t\right|>1\right)=1\text{\hspace{0.17em}\hspace{0.17em}if\hspace{0.17em}}\left|u_t\right|>1$ and 0 otherwise.

The estimated parameter is $\widehat{\theta }=\frac{1}{n}{\displaystyle \sum _{t-1}^{n}I\left(\left|u_t\right|>1\right).}$. The test statistic is a pivot⁵ and is defined as $T_n=\frac{\widehat{\theta }-q}{{\widehat{\sigma }}_{\theta }},$ where $\widehat{\theta }$ is an estimate of θ, and ${\widehat{\sigma }}_{\theta }$ is the standard error of $\widehat{\theta }$.

The computation of the necessary sample quantities is based on the bootstrap technique. This technique estimates the test statistic distribution by resampling the data with replacement.³¹

Based on the selected significance and tolerance level and the critical p-value resulting from this procedure, the test decides whether the sensor device under study passes the second GLYCENSIT phase. If p ≥ α, we cannot reject H₀. If p < α, we can reject H₀ with a probability of at least 1 – α. In the last case, the test sensor does not suit the stated requirements.

GLYCENSIT Procedure Phase 3: Tolerance Intervals

In the last phase, distribution-free tolerance intervals⁵ for reference glucose values are computed, aiming to estimate the future sensor performance. The tolerance intervals estimate a quantile range (with quantiles r and s) in which values that would have been obtained with the reference device lie with a certain probability when a new test measurement is introduced. Unlike other techniques that only retroactively apply to hypothetical situations, this phase informs the user about possible measurement errors corresponding to new test sensor readings under three statistical assumptions. First, the new data follow an identical probability law underlying given observations. Second, the normalized residuals have a similar distribution over the three glycemic ranges. Third, the new test sensor readings are obtained under similar conditions as the current data. In contrast to existing (retroactive) techniques and Phases 1 and 2, Phase 3 provides knowledge about future behavior.

Statistically, the computed normalized residual values, which have a common cumulative distribution function F_u, are sorted with u₍₁₎ < … < u_(n) as order statistics. Let the amount of probability mass in the interval F(u_(s)) – F(u_(r)) be denoted by Q_rs with 1 ≤ r < s ≤ n, where r and s equal 0.0125n and 0.9875n, respectively, when an A = 97.5% tolerance interval is considered. For a confidence coefficient γ = 1 – α with 0 ≤ α ≤ 1, the probability that more than 100γ% of the probability mass is contained in the range is P(Q_rs > γ) = 1 – β_γ(s – r, n – s + r + 1), where β_γ(a, b) is the incomplete beta function.³² The computed tolerance interval can be retransformed with the inverse normalization function, f^-1(y_ref,t – Y_test,t), yielding the desired tolerance intervals for given glucose values.

Crucial elements in Phase 3 are the size of the intervals and their probability. The first parameter denotes the clinical interpretability of the sensor under study. Large tolerance intervals indicate that reference observations may significantly deviate from test readings, resulting in a clinically unacceptable test sensor performance. The second parameter is the computed probability (P) that reference measurements effectively lie in these aforementioned tolerance intervals. This probability reflects the (in)sufficient number of paired glucose measurements that are submitted to the GLYCENSIT analysis. To the best of our knowledge, this important parameter is not considered in other published glucose sensor assessment techniques.

Clinical Trial Procedure

The GlucoDay^® system (A. Menarini Diagnostics test sensor, a portable instrument provided with a micropump and a biosensor coupled to a microdialysis system) is validated against the ABL glucose analyzer (Radiometer Medical reference sensor) by applying the Bland–Altman, EGA, and GLYCENSIT approaches. The GlucoDay system is an amperometric sensor that consists of an enzymatic membrane with immobilized glucose oxidase and a platinum electrode used to measure glucose in subcutaneous interstitial fluid. The ABL glucose analyzer is an amperometric sensor that measures glucose in whole blood using the glucose dehydrogenase method. After informed consent from the next of kin, we implanted a microfiber in 20 ventilated adult patients who were admitted to the intensive care unit (ICU) of the University Hospital Katholieke Universiteit Leuven (see Table 1). Blood glucose could not be artificially shifted because of the specific type of patients.^23,24 After implantation of the fiber in periumbilical subcutaneous tissue, we recorded near-continuous subcutaneous glucose levels during 48 h. Every 3 min, the mean value of the past 3 min was exported. During the first 24 h, arterial blood glucose was measured concomitantly every hour, using the ABL machine; during the next 24 h, arterial blood glucose was measured every 4 h. A 2-point (at 12 and 20 h) retroactive calibration of the test sensor was performed following the supplied software algorithm. The study protocol was approved by the Institutional Ethical Review Board (ML2637). Due to the retroactive calibration, we restricted the preprocessing phase to the transformation of near-continuous test data and time-discrete reference data into sets of paired glucose measurements.

Table 1.

Patient Population (Coming from a Surgical Intensive Care Unit)

Variable	Value
Male sex—number (%)	14 (70.0)
Age—year (standard deviation)	61.3 (13.5)
Body Mass Index—kg/m2 (standard deviation)	27.4 (5.1)
Reason for Intensive Care—number (%)
Cardiac Surgery	10 (50.0)
Noncardiac Indication	10 (50.0)
Neurologic Disease, Cerebral Trauma, or Brain Surgery	2 (10.0)
Thoracic Surgery, Respiratory Insufficiency, or Both	3 (15.0)
Abdominal Surgery or Peritonitis	2 (10.0)
Vascular Surgery	1 (5.0)
Multiple Trauma or Severe Burns	1 (5.0)
Other	1 (5.0)
APACHE II Score (Day 1) (standard deviation)	17.0 (5.9)
APACHE II Score (Day 2) (standard deviation)	17.1 (5.8)
Glycemia (reference sensor device)
Mean Glycemia—mg/dl (standard deviation)	111 (23)
Minimal Glycemia—mg/dl	65
Maximal Glycemia—mg/dl	202
Glycemia (test sensor device)
Mean Glycemia—mg/dl (standard deviation)	112 (25)
Minimal Glycemia—mg/dl	56
Maximal Glycemia—mg/dl	249

We want to stress that the GlucoDay data analyzed in this manuscript are mainly used to illustrate the GLYCENSIT procedure, as conclusions may depend on the predefined clinical design parameters (α, q, and hypo/hyperglycemic cutoff value). In this work, we cannot reject H₀ when p-values are larger than α = 0.05, q varies from 2% to 10%, and glycemia values below 80 mg/dl are called hypoglycemic, and glycemia values above 110 mg/dl are called hyperglycemic because of the ICU origin of the data.^23,24

Results

The GLYCENSIT procedure (Figure 1) shows that the medians of the measurement errors are similar (0.74, 0.028, and –1.3 mg/dl for the hypo/normo/hyperglycemic range, respectively), explaining the obtained persistent measurement behavior (Phase 1, p ≥ .05). A tolerance level of at least 8% is required for not rejecting the null hypothesis (thus the relative number of measurement errors is smaller than the tolerance level) in Phase 2 (p = .075 for q = 0.08 and p = .45 for q = 0.10). When smaller tolerance levels are preferred, the null hypothesis can be rejected (p < .05) with a probability of at least 95%, indicating that the test sensor does not suit the predefined accuracy requirements. The computed tolerance intervals (presented by the shaded area) inform the user of possible measurement errors for new test values. This area contains 97.5% of the data (A = 97.5%) and, as expected from Phase 2, is much wider than the ISO criterion in under- and overestimated direction (Phase 3). The computed probability (P) that 95 new measurements out of 100 (α = 0.05) lie in these (A = 97.5%) observed tolerance intervals equals 98.6%, indicating that the number of available paired glucose data is sufficient to rely on the obtained results.

The Bland–Altman approach (Figure 2) results in –26.5 mg/dl and 24.5 mg/dl for the limits of agreement of G_R – G_T with –1.0 mg/dl as mean bias, whereas applying EGA (Figure 2) leads to 90.9% and 9.1% as relative number of points in the A and B zone, respectively.

Discussion

Existing methods used for evaluating blood glucose meters (time-discrete) and GMSs (near-continuous) often show weaknesses. Here we present the GLYCENSIT procedure: a new assessment tool for glucose sensors. The procedure comprises three analyses that each, independent of each other, approach the data from a different side: (1) testing possible persistent measurement behavior as a function of the glycemic range, (2) testing number of measurement errors with respect to the ISO criterion, and finally (3) computing the tolerance intervals for new test sensor observations and the probability of those intervals. In the end, the precise way of integrating (or “weighting”) all findings must be made by the expert (user). The GLYCENSIT procedure aims to guide and provide motivation to the evaluation process rather than returning a “yes/no” analysis. The method c an be tuned according to expert specifications regarding the design parameters: significance level, tolerance level, and glycemic range cutoff values. Moreover, the analysis is founded on (nonparametric) statistical techniques necessary to draw statistically reliable conclusions.

Besides the application (type of patients, hospital use versus home use, etc.) and the clinician's requirements concerning size of tolerance intervals (Phase 3), approval or rejection of a glucose sensor device depends on the selected values of the design parameters. Accordingly, these values must be clearly mentioned in clinical reports.

The GLYCENSIT procedure applied to the GlucoDay data demonstrates the (relatively) high error rate in comparison to the ISO criterion (Phase 2), which explains the wide tolerance intervals (much wider than the ISO limits) for the full glycemic range (Phase 3). Although the general measurement behavior is persistent (Phase 1), some measurement errors are unacceptably large (Phase 1), leading to broad minimum and maximum deviations (Phase 3). In view of the preferred design parameters (discussed earlier), the GlucoDay sensor may not be sufficiently reliable for glycemia control in the ICU.

A similar conclusion (however, with less statistical evidence) can be made when considering the Bland– Altman and EGA approaches. For the Bland–Altman approach, the limits of agreement are too wide, but the average bias is negligible. The EGA approach illustrates that 9.1% (>5%) of the measurements fall in the B zone, which is too much to be clinically acceptable.¹¹

Three points should be underscored. First, a sensor device should always be validated under conditions similar to its (future) use. Accordingly, results from the GlucoDay data (attained from critically ill patients) are only related to the performance of this sensor device in the critically ill. Possibly different results are obtained when testing the sensor in another patient setting (e.g., outpatients with diabetes). Second, though the same conclusion concerning the GlucoDay device is formulated here irrespective of the selected approach (GLYCENSIT versus Bland–Altman/EGA), this similarity cannot be considered as generally valid (shown with hypothetical examples discussed later). Indeed, statistical pitfalls typical of current standard evaluation techniques may mislead sensor assessments. The GLYCENSIT procedure has already shown its statistical value in practical real-life sensor evaluations.³³ Third, the estimates of the future sensor performance (Phase 3) are only valid under the condition of meeting the three assumptions described earlier.

The currently proposed GLYCENSIT procedure requires the upload of paired measurements independent of type of test signal (time-discrete or near-continuous test sensor). Future research is focusing on the design of statistical procedures, especially developed for evaluating near-continuous test sensors, by taking into account temporal dynamics of the test glucose signal. These specific dynamics are not incorporated into GLYCENSIT's current format, as the necessary presence of a near-continuous (or very frequently measured) gold standard is not yet available (or not always feasible).

The proposed GLYCENSIT procedure is implemented as a web-based assessment tool, freely available at http://www.esat.kuleuven.be/GLYCENSIT. This website also illustrates some hypothetical examples that further clarify the presented procedure. Additionally, these examples show the clinical interpretation of the results, which is particularly of interest if any one of the three phases generates a different assessment(s). Further, the necessary number of uploaded paired glucose observations can be determined (before starting the study) based on the required probability level (Phase 3) and the selected significance level (see also the figures at the GLYCENSIT website). Furthermore, the higher the number of paired glucose measurements (ideally spread over the full glycemic range), the more powerful the assessment tool will be (i.e., higher statistical evidence).

In conclusion, the GLYCENSIT procedure (Phase 1: persistency of the measurement behavior; Phase 2: number of measurement errors; Phase 3: magnitude of new measurement errors) statistically guides the clinician in appropriately assessing the reliability of blood glucose meters and GMSs. The probability measure for the tolerance intervals, computed in Phase 3, is indicative of the statistical evidence for the data under study. The GLYCENSIT procedure will be indispensable as a supplemental tool to existing evaluation techniques to assess the performance of glucose sensors.

Abbreviations

ANOVA

analysis of variance

DETM

diabetes error test model

EGA

error grid analysis

GLYCENSIT

GLYCemia sENSor IT

GMS

glucose monitoring system

ICU

intensive care unit

ISO

International Organization for Standardization