Contributions of Mathematical Modeling of Beta Cells to the Understanding of Beta-Cell Oscillations and Insulin Secretion

Abstract

Mathematical modeling of pancreatic beta cells has contributed significantly to the understanding of the mechanisms involved in glucose-stimulated insulin secretion (GSIS). Early models of insulin secretion built in the 1970s were phenomenological with little biological foundation for the proposed mechanisms. In the 1980s, models focused on identifying the regulation of bursting electrical activity known to be important for insulin secretion. The main result was to reject proposed mechanisms as new data emerged, but important results of the role of cell-to-cell coupling were also established. New models have been proposed that provide possible explanations for the occurrence of various patterns of bursting and calcium oscillations. In addition, modeling has played an important role in comparing competing effects of calcium on both NADH and adenosine 3′-5′-cyclic monophosphate levels. Models including modern cell biological results of the regulation of insulin containing granules and cell heterogeneity have appeared, providing updated versions of the early models proposed in the 1970s. These models, when coupled to electrophysiological- and calcium-based ones, have the prospect to aid in understanding the overall picture of GSIS. In addition, they might be useful for estimating in vivo beta-cell functioning. Beta-cell modeling will likely move closer to clinical applications, where it can be expected to play an important role, as it has and will, in understanding the complex oscillatory phenomena observed in beta cells and islets.

The Beta Cell

The pancreatic beta cells are responsible for the secretion of insulin in response to elevated plasma glucose levels, and the malfunction of these cells is a major contributor to the development of diabetes. The beta cells are, however, social cells living in micro-organs called islets of Langerhans, and coupling between beta cells within islets is important for the proper function of beta cells.¹

The major pathway of glucose-stimulated insulin secretion (GSIS) involves metabolism of the sugar, which raises the intracellular adenosine-5′-triphosphate (ATP) concentration and lowers adenosine diphosphate (ADP) concentration. The higher ATP-to-ADP ratio closes ATP-sensitive potassium [K(ATP)] channels in the plasma membrane, which depolarizes the cell and triggers electrical activity. Voltage-sensitive calcium channels contribute to the electrical pattern, and when they are open, calcium flows into the cell, where it triggers the fusion of insulin-containing granules with the plasma membrane. This allows insulin to escape to the extracellular space and eventually enter the blood stream. Besides this “triggering pathway,” another less understood “amplifying pathway” modifies the amount of insulin that is secreted in response to a glucose challenge.² Insulin is released in distinct pulses with a period of ∼5 min,³ probably as a result of oscillations in beta-cell metabolism, membrane potential, and calcium levels.⁴

Modeling of Bursting Electrical Activity

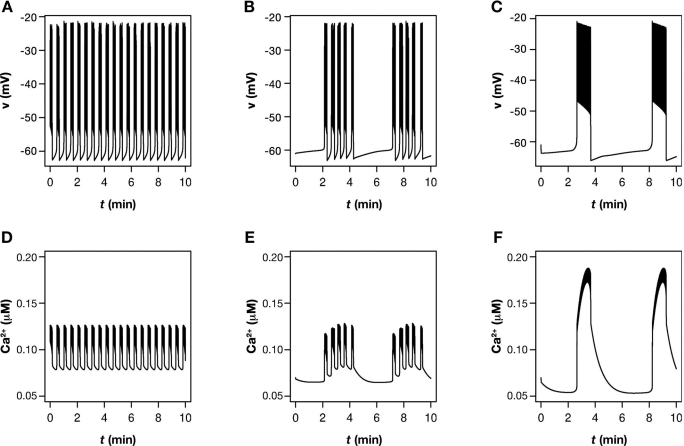
The central role of the electrophysiology of the beta cells has led not only biologists, but also mathematicians to study this particular part of the triggering pathway. Due to the complex bursting patterns exhibited by the membrane potential (Figure 1), electrical activity in the beta cells has provided interesting mathematical problems to be analyzed in addition to understanding its role in GSIS. The bursting electrical behavior in beta cells consists in an alternating pattern between a quiescent, hyperpolarized phase and an active phase, where voltage spikes depart from an elevated plateau. These “square-wave” oscillations are paralleled by periodic modulations of [Ca²⁺]_i and insulin secretion, since calcium, the trigger of insulin release, flows into the cytoplasm during the active phase and is pumped out of the cell during the silent phase.

Figure 1.

Typical patterns of (A–C) bursting electrical activity and (D–F) calcium oscillations observed in beta cells located in islets. These patterns were simulated using the model by Bertram et al.,²² which can produce (from left to right) either intermediate bursting (fast Ca²⁺ oscillations), compound bursting (mixed Ca²⁺ oscillations), or slow, glycolytic bursting (slow Ca²⁺ oscillations).

All current existing mathematical models are basically modifications of the first model of bursting patterns typically observed in islets with a period of 10–30 s (Figure 1A), by Chay and Keizer,⁵ constructed from ideas by Atwater et al.⁶ As first analyzed by Rinzel,⁷ the mechanism underlying bursting is a separation of timescales, where a fast subsystem consisting of the membrane potential and delayed rectifier potassium channels creates the spikes during the active phase, while one or more slow variables are responsible for switching between active and silent phases. The first proposal for the slow variable was [Ca²⁺]_i,^5,6 which modified a calcium-sensitive potassium current [I_K(Ca)].

Simulations predicted that the resulting calcium pattern would be a sawtooth-shaped oscillation, but when it became experimentally possible to measure [Ca²⁺]_i, the observed pattern was found to be closer to a square wave than a sawtooth.⁸ The slow variable was therefore unlikely to be intracellular calcium. In this way, the mathematicians returned the question to the biologists: if not [Ca²⁺] _iand I _K(Ca), then what is driving bursting with a period of tens of seconds? The resulting electrophysiological studies revealed another calcium-sensitive potassium channel that activated on a slower timescale.^9,10 However, my own (unpublished) observations and simulations done by other groups (e.g., Reference ¹¹) have revealed that the electro-physiological components and [Ca²⁺]_i are insufficient in reproducing bursting behavior with a timescale of tens of seconds as observed in beta cells located in islets. I refer the reader to review articles for a fuller account of the history of the role of [Ca²⁺]_i in beta-cell bursting.^12,13

Chay^14,15 introduced the calcium concentration in the endoplasmic reticulum (ER) as a second slow variable in addition to [Ca²⁺]_i. The concept of two slow variables was then generalized in the “phantom burster” idea by Bertram et al.,¹⁶ where is was further analyzed how the interaction of a variable with a timescale of a few seconds (here [Ca²⁺]_i) with another variable with a timescale of minutes can lead to the appearance of bursts with a period of tens of seconds as seen in islets, although no variables are acting on this timescale (hence “phantom”). It should be remarked that the ER calcium concentration is unlikely to be the (only) second slow variable, since preventing filling of the ER does not interrupt or modify [Ca²⁺]_i oscillations substantially, though a slightly different profile is observed.¹⁷ Adenosine triphosphate (or the ATP/ADP ratio) acting on K(ATP) channels^18,19 and sodium²⁰ have been suggested to be other slow variables. Bertram and Sherman¹³ give further details on these aspects.

By varying the relative strength of the two slow processes, bursting with a period ranging from a few seconds to several minutes can be observed. This was hypothesized¹⁶ to account for the difference between isolated beta cells, which often spike or burst with a period of less than a couple of seconds,²¹ the intermediate tens of seconds islet bursting, and the very slow oscillations seen both in membrane potential and calcium recordings from both islets and isolated cells.^22–24 However, it was shown that ion channel fluctuations are likely to disrupt slow oscillations driven by a phantom burster mechanism and change them into a rather fast pattern.²⁵ Nonetheless, the phantom mechanism, a result of mathematical modeling, has suggested a plausible way of obtaining bursting behavior with the right timescale, even though [Ca²⁺]_i is acting too fast.

The Role of Coupling

The difference between single, isolated beta cells and beta cells in situ coupled to their neighbors within the islet has been another area where mathematical modeling has tested and provided possible explanations. Atwater et al.²⁶ suggested that stochastic fluctuations (noise) of single ion channels can disrupt the underlying bursting behavior in single cells, but when the cells are coupled within the islets, the noise intensity is reduced because of the effective sharing of the channels between cells due to electrical coupling by gap junctions. Numerical simulations of stochastic versions of the early bursting models confirmed the possibility of the “channel-sharing hypothesis,”^27,28 and I helped to confirm these findings analytically.²⁹ For the phantom burster model, it was found that noise has a much stronger effect than for bursters with only one slow variable and, in particular, that slow bursting in single cells is unlikely to be driven by a phantom burster mechanism,²⁵ a result that would be hard to discover without a mathematical model and analysis.

Another possible explanation for the emergent intermediate bursting seen in islets is the so-called “heterogeneity hypothesis.”³⁰ Since the parameters of model bursters need to be finely tuned in order to burst, it was suggested that most cells have parameters that fall slightly outside the bursting region, and they will therefore either be silent or spike continuously. When coupled, the cells will behave as if they had some average parameter values, often within the region of bursting. Hence the coupled cell cluster would burst, although very few of the isolated cells did. The heterogeneity hypothesis was later extended to phantom bursting.³¹ Here the mathematical modeling was also used to support and formulate the basic idea, which was recently used to interpret experimental data.³²

Modeling Metabolism

Another candidate, rather than feedback by Ca²⁺ or another slow variable, for a pacemaker of slow bursting, slow calcium oscillations, and pulsatile insulin secretion is an endogenous glycolytic oscillator.^33,34 Oscillations in extracellular glucose levels and oxygen tension,³³ reduced nicotinamide adenine dinucleotide (phosphate) [NAD(P)H] concentrations,³⁵ and ATP levels³⁶ have been observed and are suggestive of a metabolic pacemaker. However, when calcium influx is interrupted, these oscillations can disappear,^35,37 which could suggest that periodic modulation of metabolic variables is driven by calcium oscillations. On the other hand, oscillations in ATP have been observed in calcium-free media.³⁸ Stronger evidence against a glycolytic oscillator is the fact that mitochondrial substrates, which bypass glycolysis, can produce slow calcium oscillations²³ and that islets with very low levels of the muscle form of the enzyme phosphofructokinase (PFK), believed to be responsible for the creation of oscillations in glycolysis, also exhibit slow calcium oscillations and pulsatile insulin secretion.³⁹ However, these observations do not rule out the possibility of an oscillator with mitochondrial origin.⁴⁰

Bertram et al.^22,41,42 suggested that beta cells possess both a glycolytic and a calcium-driven (phantom) oscillator, which communicate through the mitochondria and ATP levels. Adenosine triphosphate inhibits PFK and blocks K(ATP) channels, while pumping Ca²⁺ lowers the ATP concentration. Depending on the parameters, this “dual oscillator”⁴ model can produce various kinds of bursting. Slow “glycolytic” bursting (Figure 1C) occurs when glycolysis is oscillatory, and the calcium system is either stable (at fixed glycolytic input) or bursts with a period close to that of the glycolytic oscillator. Intermediate bursting with a tens-of-seconds period appears when glycolysis is stable, and the calcium system is oscillatory (Figure 1A). Finally, the model can reproduce so-called compound bursting (Figure 1B), where bursts of intermediate period appear periodically interspersed with silent phases with a period of minutes. This occurs when both the glycolytic and the calcium subsystems are oscillatory. Glycolysis is then responsible for the slow modulation of the bursting system.^4,22 All these patterns have been observed experimentally.²² Thus, using a mathematical model, it has been possible to unify the two proposed burst mechanisms and explain complex patterns such as compound bursting, which are hard to understand from a single underlying burst mechanism.

By including noise in the model,²⁵ it was shown that in contrast to bursting driven by electrophysiological mechanisms, glycolytic bursting is stable to ion channel fluctuations. This suggests that the slow (∼4 min) bursting activity and calcium oscillations observed in single cells^24,43 is indeed driven by a metabolic oscillator. It also provides an explanation for the fact that compound bursting is mostly seen in islets. The individual bursts driven by calcium feedback are disrupted by noise, as in the original channel-sharing hypothesis,²⁶ while the slow envelope survives since it has a metabolic origin.

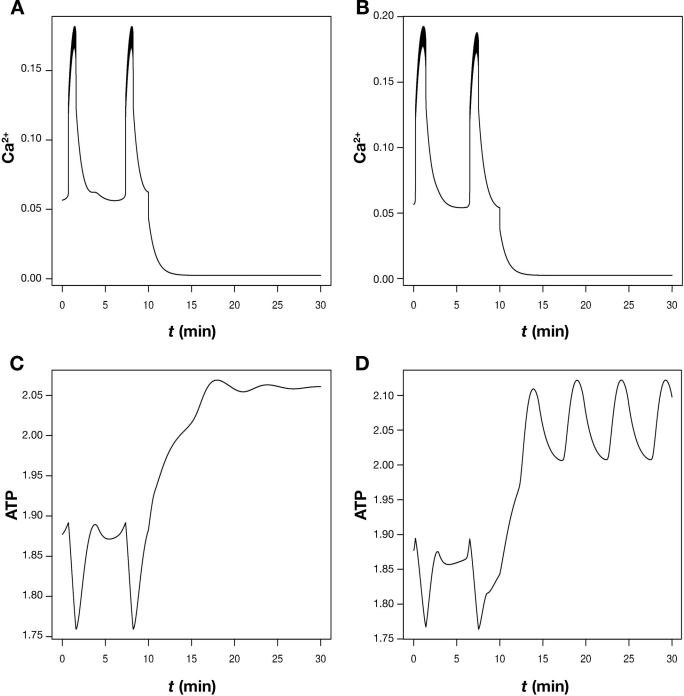
But what about the objections coming from the experiments investigating the effects of blocking calcium entry mentioned eariler? I have previously helped to show⁴¹ that the glycolytic oscillator can become stable when calcium influx is blocked (Figure 2). The reason is that less calcium needs to be pumped, so the ATP concentration rises, which, in turn, inhibits PFK to an extent where glycolysis is no longer oscillatory. This explanation for the experimental results^35,37 would be hard to find without the mathematical model. Interestingly, with other parameters, the model can continue to show metabolic oscillations although calcium is low and stable after blocking influx (Figure 2). This is obtained when ATP inhibition of PFK is weaker, and the glycolytic system therefore continues to oscillate despite the raised, and now oscillatory, ATP concentration, in agreement with Reference ³⁸.

Figure 2.

Blocking calcium entry can, but does not necessarily, stop metabolic oscillations. Simulations using the model by Bertram et al.²² The upper panels, A and B, show slow calcium oscillations, which are interrupted by blocking Ca²⁺ channels. The conductance of these channels was lowered by 90% at t = 10 min. These oscillations are driven by oscillations in glycolysis and ATP levels as shown in the lower panels, C and D. However, when PFK has a high affinity for ATP (A and C), the metabolic oscillations die out when calcium influx is blocked (C). In contrast with a five-times lower ATP affinity, PFK-driven oscillations continue (D) although calcium is low and stable (B). The parameters are as Figure 7 in Bertram et al.²²

Modeling the mitochondria has allowed an understanding of other experiments. Luciani et al.³⁵ found that calcium raises NAD(P)H levels in a bath with low glucose concentration, while it lowers NAD(P)H when the cell is exposed to a stimulating glucose level. I helped to explain this using a submodel of the mitochondria,⁴⁴ which is itself a simplification of a previous model.⁴⁵ Calcium influx has a dual effect on the mitochondria. On one hand, a raised mitochondrial calcium concentration activates dehydrogenases, which produce NADH. On the other hand, the current carried by the calcium influx lowers the mitochondrial membrane potential, which increases the consumption of NADH. Since the effect on dehydrogenases is stronger than the membrane potential effect at a low glycolytic input to the mitochondria, but lower at a high glycolytic rate, the two different kinds of behavior can be explained.

Fridlyand and colleagues⁴⁶ presented a model of the interaction between calcium and adenosine 3′-5′-cyclic monophosphate (cAMP). They reproduced the fact that calcium and cAMP oscillations are synchronous and in phase when stimulated by the incretin hormone glucagon-like peptide-1 (GLP-1), which activates cAMP production by adenylyl cyclases (ACs), but are in antiphase at low AC activity. Calcium, via calmodulin, activates both ACs and phophodiesterases (PDEs), which degrade cAMP. It was proposed that calcium oscillations drive cAMP oscillations but in the absence of GLP-1, and hence low AC activity mainly through the effect on PDEs, resulting in antiphase oscillations, while in GLP-1-stimulated cells, the Ca²⁺ effect on ACs dominates, and the oscillations are in-phase. Biologically, this is beneficial since cAMP potentiates calcium-induced insulin release,^47,48 and for maximal efficacy of the incretins, the oscillations should therefore be in-phase. I remark that a qualitative model⁴⁶ helped in analyzing the two competing regulation mechanisms of calcium on cAMP levels and, more generally, in studying the effect of GLP-1 as it did when studying the competing positive and negative effects of calcium on mitochondrial metabolism as explained earlier.⁴⁴

But What about Insulin?

Considering that the task of the beta cell is to secrete insulin, it might be surprising how little work there has been on modeling insulin secretion compared to the focus on other aspects of beta cell physiology described earlier. However, already in the 1970s, Grodsky and colleagues^49,50 and Cerasi et al.⁵¹ did model the pancreatic insulin response to various kinds of glucose stimuli. Due to the limited knowledge of beta-cell biology at that time, these models were phenomenological. Our knowledge of the control of the movement and fusion of insulin granules has increased to a level where we have started to formulate mechanistically based models.

Cerasi and co-workers⁵¹ suggested that the dynamics of insulin secretion was due to time-dependent inhibitory and potentiating signals, still unidentified,⁵² that act on insulin secretion at different times. For biphasic insulin secretion, inhibition is responsible for creating the nadir after the first phase peak, while potentiation acts later to produce the second phase.

As an alternative, Grodsky⁴⁹ proposed that insulin was located in “packets,” plausibly the insulin containing granules but also possibly entire beta cells. Some of the insulin was stored in a reserve pool, while other insulin packets were located in a labile pool, ready for release in response to glucose. The labile pool is responsible for the first phase of insulin secretion,^49,53 while the reserve pool is responsible for creating a sustained second phase. This basic distinction has been at least partly confirmed when the packets are identified with granules.^54,55 Grodsky⁴⁹ moreover assumed that the labile pool is heterogeneous in the sense that the packets in the pool have different thresholds with respect to glucose, beyond which they release their content. This assumption was necessary for explaining the so-called staircase experiment, where the glucose concentration was stepped up, each step giving rise to a peak of insulin. There has been no support of granules having different thresholds,⁵² but already Grodsky⁴⁹ mentioned that cells apparently have different thresholds based on electrophysiological measurements.⁵⁶ Later, Jonkers and Henquin⁵⁷ showed that the number of active cells is a sigmoidal function of the glucose concentration, as assumed by Grodsky⁴⁹ for the threshold distribution. I have helped to show how to unify the threshold distribution for cells with the pool description for granules,⁵⁸ thus providing an updated version of Grodsky's model, which takes into account more of the newer knowledge of beta-cell biology.

It appears that Grodsky's pool model has gained stronger cell biological support than the signal model by Cerasi, but it also has shortcomings, in particular in simulating the refractive period occurring after the glucose concentration is lowered from a stimulating level^50,58 in contrast to the model by Cerasi et al.,⁵¹ where refractiveness is due to the inhibitory signal. By including time-dependent signals in Grodsky's model, the refractory state can be simulated.⁵⁹ Modeling has thus indicated that the determining the nature of, in particular, the inhibitory signal would contribute to our understanding of dynamic insulin secretion.

Another property of the pancreas that was implicitly included in Grodsky's model is so-called derivative control, i.e., the fact that the pancreas senses not only the glucose concentration but also the rate of change. Modeling the whole body system has shown that this property is necessary for explaining data from in vivo studies.⁶⁰ Derivative control arises from the threshold hypothesis as explained by Grodsky⁴⁹ and in greater detail by Licko.⁶¹ We are currently investigating how derivative control arises in our mechanistic model⁵⁸ and how the subcellular parameters relate to those of the in vivo model. The aim is to be able to predict from in vivo measurements, for example, which steps of GSIS are impaired in diabetes patients. Such indirect knowledge of in vivo beta-cell functioning is virtually impossible without a mathematical model.

Two recent models go into greater detail with respect to the different pools of granules in single cells.^62,63 Both models include calcium, a necessity for coupling the granule model to models of bursting and calcium handling, in this way obtaining a model that includes all steps from glycolysis via calcium dynamics to exocytosis and insulin release. Another aspect to include is the so-called highly calcium-sensitive pool,^64,65 which consists of granules with a lower calcium affinity at the expense of a lower fusion rate. Modeling might play a significant role in identifying the character and function of these granules.

Conclusions

Mathematical modeling has significantly contributed to the understanding of the mechanisms underlying the various patterns of bursting electrical activity in response to different glucose stimuli (for reviews, see References ⁴ and ¹³). The inclusion of a detailed description of insulin granules has allowed modeling of events closer to secretion.^58,62,63 However, these models are based on data from rodents. It has been realized that human beta cells and islets differ substantially from rodent preparations.^66,67 Thus, to gain an understanding of the beta cell in diabetes, these models should be updated as more knowledge on human beta cells appears. Fridlyand and colleagues⁴⁶ studied the incretin effect on the oscillatory behavior. An important extension would be to include the effect of incretins on insulin secretion. One aim is to use the models to interpret in vivo data more accurately, as outlined earlier. Another could be to construct insulin pumps that follow the dynamics of the natural pancreas more closely, for example, with respect to derivative control and pulsatile secretion. For such an “artificial pancreas,” it would be important to include paracrine interactions between alpha, beta, and delta cells in the models.⁶⁸ Beta-cell modeling will likely move closer to clinical applications, where it can be expected to play an important role, as it has and will, in the understanding of the complex oscillatory phenomena observed in beta cells and islets.

Abbreviations

AC

adenylyl cyclase

ADP

adenosine diphosphate

ATP

adenosine-5'-triphosphate

cAMP

adenosine 3′-5′-cyclic monophosphate

ER

endoplasmic reticulum

GLP-1

glucagon-like peptide-1

GSIS

glucose-stimulated insulin secretion

[I_K(Ca)]

calcium-sensitive potassium current

[K(ATP)]

adenosine-triphosphate-sensitive potassium channels

[NAD(P)H]

nicotinamide adenine dinucleotide (phosphate)

PDE

phophodiesterase

PFK

phosphofructokinase