Intermediary Variables and Algorithm Parameters for an Electronic Algorithm for Intravenous Insulin Infusion

Abstract

Background

Algorithms for intravenous insulin infusion may assign the infusion rate (IR) by a two-step process. First, the previous insulin infusion rate (IR_previous) and the rate of change of blood glucose (BG) from the previous iteration of the algorithm are used to estimate the maintenance rate (MR) of insulin infusion. Second, the insulin IR for the next iteration (IR_next) is assigned to be commensurate with the MR and the distance of the current blood glucose (BG_current) from target. With use of a specific set of algorithm parameter values, a family of iso-MR curves is created, each giving IR as a function of MR and BG.

Method

To test the feasibility of estimating MR from the IR_previous and the previous rate of change of BG, historical hyperglycemic data points were used to compute the “maintenance rate cross step next estimate” (MR_csne). Historical cases had been treated with intravenous insulin infusion using a tabular protocol that estimated MR according to column-change rules. The mean IR on historical stable intervals (MR_true), an estimate of the biologic value of MR, was compared to MR_csne during the hyperglycemic iteration immediately preceding the stable interval. Hypothetically calculated MR_csne-dependent IR_next was compared to IR_next assigned historically. An expanded theory of an algorithm is developed mathematically. Practical recommendations for computerization are proposed.

Results

The MR_true determined on each of 30 stable intervals and the MR_csne during the immediately preceding hyperglycemic iteration differed, having medians with interquartile ranges 2.7 (1.2–3.7) and 3.2 (1.5–4.6) units/h, respectively. However, these estimates of MR were strongly correlated (R² = 0.88). During hyperglycemia at 941 time points the IR_next assigned historically and the hypothetically calculated MR_csne-dependent IR_next differed, having medians with interquartile ranges 4.0 (3.0–6.0) and 4.6 (3.0–6.8) units/h, respectively, but these paired values again were correlated (R² = 0.87). This article describes a programmable algorithm for intravenous insulin infusion. The fundamental equation of the algorithm gives the relationship among IR; the biologic parameter MR; and two variables expressing an instantaneous rate of change of BG, one of which must be zero at any given point in time and the other positive, negative, or zero, namely the rate of change of BG from below target (rate of ascent) and the rate of change of BG from above target (rate of descent). In addition to user-definable parameters, three special algorithm parameters discoverable in nature are described: the maximum rate of the spontaneous ascent of blood glucose during nonhypoglycemia, the glucose per daily dose of insulin exogenously mediated, and the MR at given patient time points. User-assignable parameters will facilitate adaptation to different patient populations.

Conclusions

An algorithm is described that estimates MR prior to the attainment of euglycemia and computes MR-dependent values for IR_next. Design features address glycemic variability, promote safety with respect to hypoglycemia, and define a method for specifying glycemic targets that are allowed to differ according to patient condition.

Introduction

Intravenous (IV) insulin infusion therapy has a long history of use in the management of hyperglycemia during the treatment of diabetic ketoacidosis (DKA), hyperglycemic hyperosmolar state, and labor and delivery, exhibiting a favorable safety and efficacy profile compared to subcutaneous insulin therapy.^1,2 A reduction of mortality and morbidities during the utilization of intravenous insulin infusion among cardiac surgery patients in Portland, Oregon, and critically ill patients in the surgical intensive care unit (SICU) in Leuven, Belgium, has led to an explosion of interest in this method of delivery of insulin therapy.^3–8 In recent randomized controlled studies targeting blood glucose (BG) 80–110 mg/dl, however, the mortality rate was not reduced.^9–12 Recognition of hypoglycemia as a complication of therapy without an apparent outcome advantage led to the closure of two randomized trials of IV insulin therapy.^10–12

The relationship between hypoglycemia and adverse outcomes has not been fully defined. Among critically ill patients and hospitalized patients in general, hypoglycemia has been shown to be associated with increased mortality. Hypoglycemia simply may be a marker of clinical severity or the consequence of comorbidities.^13–15 However, cardiac arrest, fatality, and other morbidities have been attributed to regimens that attempt attainment of strict glycemic control.^16–18 A recent case control study suggests that severe hypoglycemia is an independent predictor of mortality in the critical care setting.¹⁹ The possibility cannot be discounted that even mild hypoglycemia is detrimental to the well-being of patients from selected populations. Sympathetic and other counterregulatory activation is likely to occur as BG approaches 70–72 mg/dl.²⁰ Among patients having acute myocardial infarction or left ventricular failure, observational studies suggest that a J-shaped relationship may exist between glucose control and mortality.^21–24

Undeniably, differences dependent on the source of blood and variability of measurement of blood glucose are limiting factors that restrict our ability to achieve target range control.^25–33 For different conditions, such as DKA or hyperglycemic hyperosmolar state,³⁴ the target glucose range may differ from that advocated for the surgical ICU.³⁵ The algorithms available to an institution may perform optimally only for restricted populations or specific target ranges of BG.³⁶ If the desired range of glycemic control could be achieved through the use of carefully engineered insulin infusion algorithms without fear of hypoglycemia, and with adaptability of target range to various populations, researchers might safely investigate glycemic targets necessary for the attainment of specific outcomes among critically ill patients and caregivers might approach the demonstrably optimal target ranges with confidence. The nursing burden may be reduced. Use might be extended safely to general wards. Applicability of the design principles may extend to continuous subcutaneous insulin therapy in the ambulatory setting. For these reasons, engineering of an insulin algorithm to achieve a given target range that avoids hypoglycemia is a high priority. The purpose of this article is to describe the evolution of the algorithm “I, Pancreas.”

Background

The maintenance rate (MR) seeking or “MR” algorithm is a family of functions giving the insulin infusion rate (IR) as a function of current BG (BG_current) and the maintenance rate of insulin infusion, such that each function differs from the other members of the family only according to MR, multiplier, or column assignment when expressed as a function of BG.^37,38 In one published graphical display, curves differ according to multiplier,³⁹ whereas in another differ according to column assignment.³⁶ If the parameters of the algorithm, such as target BG or ideal rate of change at given BG, were revised to match the needs of a different population, then the algorithm would generate a new family of functions.

After each iteration, an MR algorithm assigns the insulin infusion rate in two steps. Using the previous insulin infusion rate (IR_previous) or previous multiplier, the previous blood glucose (BG_previous), the BG_current, and the time between tests (Δ time_previous), the algorithm first determines the next MR, the next column assignment, or the next multiplier. Using the distance from target of BG_current, the second step of the algorithm defines the IR for the next iteration of the algorithm (IR_next). The IR is an increasing function of BG. At any given BG the rate of change of IR with respect to BG, or d(IR)/d(BG), is an increasing function of MR. The algorithm also states the time for the next blood glucose measurement.

The principal input and output are shared by all available algorithms: BG_current, BG_previous, IR_previous, current test time (test time_current), and previous test time (test time_previous). The use of intermediary variables may make the logic of the algorithm more transparent. In the first step, an MR algorithm is likely to compute the previous rate of descent of blood glucose (ROD_previous) or the change or fractional change of blood glucose, which are functions of input data. In the second step, again intermediary variables may be expressed as functions of BG_current, such as the ideal change or rate of change of blood glucose for the next iteration. Unless other features are added to allow user input, the algorithm response to changes of carbohydrate exposure or other patient conditions is reactive, but the design allows rediscovery of MR with changing conditions.

Three Predecessor Tabular Columnar Protocols

The Markovitz algorithm was designed to seek the MR and, in assigning IR, to make corrections commensurate to the MR.⁴⁰ A strategy from ambulatory medicine requires use of the “insulin sensitivity factor” (ISF) and total daily dose of insulin (TDDI) for correction dosing during hyperglycemia, where the ISF is computed to be equal to one of the following :

$$\begin{array}{l}1500/\text{TDDI}=\text{drop\hspace{0.17em}of\hspace{0.17em}BG}/1\text{\hspace{0.17em}unit\hspace{0.17em}of\hspace{0.17em}insulin}\hfill \\ 1800/\text{TDDI}=\text{drop\hspace{0.17em}of\hspace{0.17em}BG}/1\text{\hspace{0.17em}unit\hspace{0.17em}of\hspace{0.17em}insulin}\hfill \\ 1720/\text{TDDI}=\text{drop\hspace{0.17em}of\hspace{0.17em}BG}/1\text{\hspace{0.17em}unit\hspace{0.17em}of\hspace{0.17em}insulin}\hfill \end{array}$$

The parameter 1500, 1800, or 1720 in milligrams per deciliter might be called the glucose per daily dose of insulin exogenously mediated (G-per-DIEM) parameter. In order to compute the correction dose of short- or rapid-acting subcutaneous insulin, the rule holds that in addition to the TDDI, the correction dose of short- or rapid-acting insulin equals (BG current – BG target)/ISF. Problems with the method that must be acknowledged are stated as follows: (a) saturation behavior at higher BG and higher insulin doses is not acknowledged under the rule, (b) the true value of the parameter “1800 mg/dl” is not well established for various populations or patient conditions, (c) the time course of BG response is poorly documented, and (d) the true needed TDDI may be a “moving target.”

The rule can be converted to a rule for IV insulin therapy that apportions the infusion rate during hyperglycemia between maintenance rate and correction rate (CR).

$$\begin{array}{l}\text{IR}=\text{MR}+\text{CR}\hfill \\ \text{TDDI}=24\text{\hspace{0.17em}h}*\text{MR}\hfill \\ \text{ISF}=\left(1800,1500,1720,\text{\hspace{0.17em}or\hspace{0.17em}true\hspace{0.17em}G-per-DIEM}\right)/\text{TDDI}\hfill \\ \text{CR}*\Delta \text{\hspace{0.17em}time}=\left({\text{BG}}_{\text{current}}-{\text{BG}}_{\text{target}}\right)/\text{ISF}=\text{correction\hspace{0.17em}dose}\hfill \\ \text{CR}=\left({\text{BG}}_{\text{current}}-{\text{BG}}_{\text{target}}\right)/\left(\Delta \text{\hspace{0.17em}time}\right)*\text{\hspace{0.17em}ISF}\hfill \\ \text{CR}=\left(\text{ideal\hspace{0.17em}next\hspace{0.17em}rate\hspace{0.17em}of\hspace{0.17em}descent\hspace{0.17em}of\hspace{0.17em}BG}\right)/\text{ISF}\hfill \\ \text{IR}=\text{MR}+\text{MR}*24\text{\hspace{0.17em}h}*\left(\text{ideal\hspace{0.17em}next\hspace{0.17em}rate\hspace{0.17em}of\hspace{0.17em}descent\hspace{0.17em}of\hspace{0.17em}BG}\right)/\text{G-per-DIEM}\hfill \end{array}$$

Using these concepts, the Markovitz tabular dose-defining, column-based algorithm was created for implementation by nurses, assigning the threshold for column adjustment (BG_{critical high}) to be 200 mg/dl, assigning the target for correction rates of insulin infusion (BG_{upper target}) to be 180 mg/dl, and using as G-per-DIEM the value of 1500 mg/dl. A lower target BG (BG_{lower target}) of 120 mg/dl was assigned. Several MR values were selected typical for the population, specifically 1, 1.5, 2, 3, and 4 units per hour. The recommended IR values ( = MR + CR values) were computed from MR values and were rounded off for display in the cells of the table. Each column was identified with an MR. Rows were displayed in order of ascending BG. Arbitrary column-changing rules were applied reactive to rate of change of blood glucose, and for BG below BG_{lower target} or prolonged time within target, a column down-changing rule was applied.

The protocol targeted full correction to BG_{upper target} within the time frame of every iteration, be it 1 or 2 hours. During hyperglycemia, full correction was not achieved consistently by the next test time, despite delivery of the entire correction insulin dose by IV infusion. Alternatively, overshoot occurred. Below BG_{upper target}, because the algorithm lacked any specific theory for management on the euglycemic range, decrements of IR were arbitrary.

The Clinical Management Committee at the University of North Carolina in 2002 requested development of an IV insulin protocol to facilitate and standardize the management of intravenous insulin infusion therapy. Pilot sites included the cardiothoracic ICU and the operating room. The BG_{upper target} was 150 mg/dl, BG_{lower target} was 100 mg/dl, and G-per-DIEM was 1800 mg/dl. The MR values selected to be typical for the population were 1, 1.5, 2, 3, 4, and 6 units per hour, as shown in the second appendix published by Bode, Braithwaite, et al.²

The surgical trauma service at the University of North Carolina requested an IV insulin protocol that would safely target the range identified with improved outcomes in the SICU.⁸ The pilot population would be trauma service ICU patients. The BG_{upper target} was 110 mg/dl, BG_{lower target} was 80 mg/dl, and G-per-DIEM was 1800 mg/dl. The MR values selected to be typical for the population were 1, 2, 3, 4, 6, and 8 units per hour. The initial MR (MR_initial) was 2 units/h. During hyperglycemia, column up-titration was required if ROD_previous for the preceding 2 hours failed to reach ROD_{@BGcritical high} or 30 mg/dl per hour for BG_current ≥ BG_{critical high}, or 180 mg/dl. The rule for correction of hyperglycemia was tolerated perhaps in part because MR had not yet been assigned at its true value. During hyperglycemia, above upper target BG_{upper target} 105 mg/dl, full correction was attempted within the time frame of every iteration:

$${\text{IR}}_{\text{next}}=\text{MR\hspace{0.17em}}*\left[1+24\text{\hspace{0.17em}h}*\left({\text{BG}}_{\text{current}}-{\text{BG}}_{\text{upper\hspace{0.17em}target}}\right)/1800\text{\hspace{0.17em}mg}/\text{dl}\right].$$

To minimize hypoglycemia, a permissive strategy for the euglycemic ascent of BG _current to BG _{true target} was devised. On the euglycemic range, IR _next would be exponentially dependent on the fractional completeness of the ascent of BG (FCABG) from 70 to 105 mg/dl, defining a range between hypoglycemia and the true target blood glucose (BG _{true target} ), assigning IR = 0.1 units/h for BG 70 mg/dl and IR = MR at BG_{true target}. An implicit assumption was that the maximum rate of ascent of blood glucose (ROA_max) for the population at blood glucose 70 mg/dl during negligible insulin infusion might be about 17.5 mg/dl per hour. The BG_{true target} was 105 mg/dl, and FCABG was given by

$$\text{FCABG}=\left({\text{BG}}_{\text{current}}-70\text{\hspace{0.17em}mg}/\text{dl}\right)/\left({\text{BG}}_{\text{true\hspace{0.17em}target}}-70\text{\hspace{0.17em}mg}/\text{dl}\right).$$

For BG_current between 70 and 105 mg/dl, the IR_next was given by

$${\text{IR}}_{\text{next}}={\text{IR}}_{@\text{BG}70}*e^{\text{ln}\left(\text{MR}/{\text{IR}}_{@\text{BG}70}\right)*\text{\hspace{0.17em}FCABG}}$$

Between BG 105 and 109 mg/dl, IR_next = MR. Use of the algorithm spread quickly from the pilot population to other SICU patients and to burn unit patients.^41,42

The University of North Carolina now had two tabular columnar paper protocols for IV insulin infusion in critical care units. These infusion protocols are not applicable for all patients, such as those having DKA or a hyperglycemic hyperosmolar state, pediatric patients, or special situations requiring a revision of parameters, including glycemic targets.³⁶ Another problem was the cost of ICU care and the potential burden on the nursing staff, preventing extension to general wards. In addition, problems that required resolution included glycemic variability within the treatment course, failure of the protocol targeting BG 80–110 mg/dl to preserve target range control even half of the time, and occasional hypoglycemia. At a given column assignment, the column-change rules that were used to define the MR required conservative holding periods at a given column assignment that might span many hours before column up-titration was permitted. Correction rates correspondingly were aggressive, designed to seek full correction to BG _{upper target} within the time frame of each iteration. Perhaps these aggressive correction rates, added to the MR, had been tolerated only because of tardiness in defining the true maintenance rate. The combined problems of underestimation of MR and overestimation of CR perhaps led to excessive oscillation of BG.

The design, performance, and applicability of an MR algorithm across populations may be improved by the introduction of three innovations, each requiring computerization:

• MR computation after each iteration

• Special algorithm parameters having values that exist in nature

• User-defined parameters

Computerization is expected to show superiority to manual methods, as has been shown in studies from other centers.^43–45

The immediate research questions were whether assignments of MR could be made by methods that are not arbitrary; whether assignments of the IR and CR, both commensurate to MR, give reasonable values; and whether true maintenance requirements for insulin can be predicted by the computation of MR prior to the attainment of euglycemia. This article presents a simple statement of design elements of the algorithm; then the methods used in feasibility studies that tested the output of the algorithm against historical time points; and finally results of the feasibility studies and an expanded statement on design and theory of the algorithm, followed by discussion and comments on future implementation.

Methods

Feasibility Studies for Computing Maintenance Rate Cross Step Next Estimate (MR_csne) and MR_csne-Dependent IR

To prepare for creation of an electronic protocol, we began analyzing the feasibility of computing MR_csne as a precedent for computing IR. A formula for MR was derived by rearrangement of the equation for IR, applied to the previous iteration. The computed MR was called the “maintenance rate cross step next estimate.”

A tabular paper protocol, the predecessor to the protocol under evaluation, had been used in the treatment of a published series of trauma service patients.⁴¹ Institutional review board approval was obtained for a waiver of consent to review data from cases treated under the historical protocol. Historical data points from that series were used in which blood glucose determinations were plasma correlated. User-definable parameters were retained that are implicit in the management of hyperglycemia under the predecessor paper protocol,⁴¹ appropriate to surgical ICU patients (BG_{true target} = 105 mg/dl, BG_{upper target} = 110 mg/dl, BG_{critical high} = 180 mg/dl, ROD_{@BGcritical high} = 30 mg/dl per hour, MR_initial = 2 units/h), with additional provisions that the maximum assignable value for ideal rate of descent of BG for the next iteration (ROD_{ideal,next,max}) = 70 mg/dl per hour, IR_max = 36 units/h, and rehydration time = 0. The G-per-DIEM parameter for the population, although not confirmed by experimentation and not user assignable, for purposes of testing the algorithm was estimated as G-per-DIEM = 1800 mg/dl, as in the predecessor paper protocol.

Comparison of IR_next by Historical Column Assignment and MR_csne-Dependent IR_next

The equations of the new algorithm for MR_csne, ideal rate of descent of BG for the next iteration (ROD_ideal,next), and IR_next are shown in Table 1. The equations were applied to time points for which historical data were present that would permit calculation of MR_csne and hypothetical MR_csne-dependent values for the IR for the next iteration (MR_csne-dependent IR_next). To determine ROD_ideal,next, the segmented linear method was used (Table 1).

Table 1.

Equations of the First and Second Steps of the Algorithm^a

Assignment of MR
MRinitial	= population value for initial MR		units/h
RODprevious	= (BGprevious – BGcurrent)/(Δ timeprevious),	for BGprevious ≥ BGtrue target
	= 0,	for BGprevious < BGtrue target	mg/dl per hour
RODprevious, revised	= – ln (1 + |RODprevious|),	for RODprevious ≤ 0;
	= RODprevious,	for RODprevious > 0	mg/dl per hour
MRcsne	= (IRprevious)/[1 + 24 h * (RODprevious,revised) /G-per-DIEM],	for BGprevious ≥ BGtrue target
	The MRcsne is not computed by this formula if BGprevious < BGtrue target (see text)		units/h
MR	For initial iterations and until rehydration time has elapsed,
	MRinitial is assigned as MR;
	thereafter, if BGprevious ≥ BGtrue target, MRcsne is computed and used as MR; or
	if BGprevious < BGtrue target, the MR used to compute IR for the preceding iteration is carried forward unmodified as MR or, according to criteria of the algorithm designed for hypoglycemia prevention, the MR is modified by arbitrary reduction rules to a new value.
Assignment of IRnext, for 70 ≤ BGcurrent < BGtrue target
FCABG	= (BGcurrent – 70 mg/dl)/(BGtrue target – 70 mg/dl)
	for BG ≥ BGtrue target, the FCABG = FRROAideal,next = 1)		unitless
Asymptote for IRnext and function-defining points for (FCABG, IRnext)	The exponential function is defined by asymptote IR = 0 and the points:(0, IR@BG70)
	(1, MR)		units/h
IRnext	= IR@BG70 * e[ln(MR/IR@BG70)] * FCABG		units/h
Assignment of IRnext, for BGtrue target ≤ BGcurrent < BGupper target
IRnext	= MR		units/h
Assignment of IRnext, for BGcurrent ≥ BGupper target
Function-defining points and maximum RODideal,next value or asymptote for (BGcurrent, RODideal,next)	The segmented linear or bounded decaying exponential function is defined by:
	(BGupper target, zero)
	(BGcritical high, ROD@BG critical high),
	and maximum or asymptotically approached value RODideal,next,max
FEBG	= (BGcurrent – BGupper target)/(BGcritical high – BGupper target)		unitless
RODideal,next, by segmented linear method	= (ROD@BGcritical high) * FEBG, or
	= RODideal,next,max,
	whichever is the smaller number		mg/dl per hour
RODideal,next, by bounded decaying exponential method	= RODideal,next,max * {1 – e–ln[RODideal,next,max/(RODideal,next,max – ROD@BGcritical high)] * (FEBG) }		mg/dl per hour
IRnext	= MR * (1 + 24 h * RODideal,next/G-per-DIEM)		units/h
Alternatively,
CRmax	= 24 h * MR * RODideal,next,max/G-per-DIEM
CR@BGcritical high	= 24 h * MR * ROD@BGcritical high/G-per-DIEM
CR	= CRmax * {1 – e–ln[CRmax/(CRmax – CR@BGcritical high)] * (FEBG) }
IR	= MR + CR
Data input after hypoglycemia (also see text)
Hypoglycemia <70 mg/dl is treated with concentrated dextrose until correction occurs
If BGprevious exceeded BGupper target and if BGcurrent is <70 mg/dl, then the BGcurrent value measured prior to treatment of hypoglycemia is used to compute RODprevious and MRcsne
After administration of concentrated dextrose, the BG value is retested within 10 minutes. Even if the BG upon retesting exceeds 70 mg/dl, the pretreatment value BG = 70 mg/dl is used in the equation for IRnext to serve as the value of BGcurrent
In the equation for FCABG and IRnext, the reassigned value BGcurrent = 70 mg/dl is used
Tentative MR after hypoglycemia = 80% of last MR carried forward

^aIn the first step, the MR is assigned. In the second step, IR_next is computed. During euglycemia the FCABG is the fractional completeness of ascent of BG from 70 mg/dl to BG_{true target}, equaling the fractional reduction of the ideal rate of ascent of blood glucose from ROA_max for the next iteration (FRROA_ideal,next). During hyperglycemia the FEBG is the fractional elevation of BG_current above BG_{upper target} in relation to the elevation of BG_{critical high} above BG_{upper target}. During hyperglycemia the segmented linear method for the determination of ROD_ideal,next was used in feasibility studies, but the bounded decaying exponential method will be used in actual implementation.

Computation of Mean IR on Stable Intervals (MR_true) as Estimate of MR

Historical stable intervals of at least 8 hours in duration, initiated by BG <110 mg/dl, were identified that were preceded by hyperglycemia of at least 2 hours of duration. Inclusion and exclusion criteria for time points, including a requirement for consistency of carbohydrate exposure prior to the stable interval, were established to ensure that time points immediately prior to the stable interval were evaluable. Criteria for termination of a stable interval included the following:

• any BG ≥180 mg/dl

• two consecutive BG values ≥140 mg/dl

• any BG <70 mg/dl

• percentage <80% of BG value falling within range 70 mg/dl ≤ BG < 140 mg/dl

• documented change of carbohydrate exposure

During each stable interval, the mean historical value for IR_next (MR_true) was calculated as an estimate of the biologic value of MR, i.e., the maintenance requirement for insulin over that time interval, or MR.

Ability of MR_csne to Estimate MR_true

The hypothetical value of MR_csne upon entry to a stable interval was compared to the averaged hourly requirement for insulin during the ensuing stable interval. In the formula for MR_csne, the last BG ≥110 mg/dl prior to the interval was used as BG_previous, and the first BG <110 mg/dl was used as BG_current. The time between them (1 or 2 hours) was used as Δ time_previous. Because the algorithm was not applied sequentially during historical treatment courses, not the entire sequence of hyperglycemic iterations but only the terminal hyperglycemic iteration prior to euglycemia was used to compute MR_csne. MR_csne was compared pair wise to MR_true on the subsequent stable interval.

Statistical Analyses

Pearson correlation coefficients were computed. The two-sided Wilcoxon signed rank test was used for comparison of units of insulin per hour to test the null hypothesis. Results with P < 0.05 were considered statistically significant.

Proposal for Computerized Algorithm “I, Pancreas”

An expanded theory of an algorithm was developed mathematically, and practical recommendations for computerization were proposed.

Results

Feasibility Studies for Computing MR_csne and MR_csne-Dependent IR_next

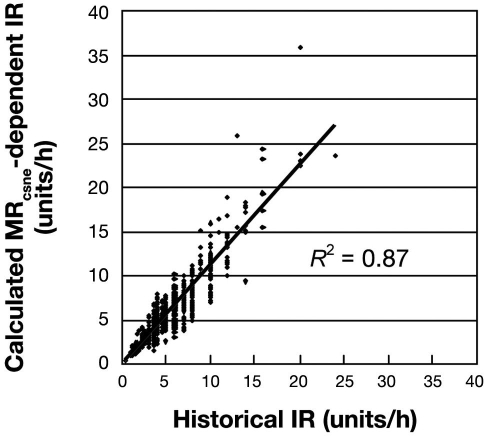
At 941 evaluable hyperglycemic historical time points, medians and interquartile ranges in insulin units per hour were MR_csne 3.9 (2.66–5.81), MR_csne-dependent IR_next4.6 (3.0–6.8), and historical IR_next 4.0 (3.0–6.0). Paired data MR_csne-dependent IR_next and historical IR_next differed significantly according to the two-sided Wilcoxon signed rank test, but the MR_csne-dependent IR_next and historical value for IR_next were correlated (R² = 0.87), as shown in Figure 1. When a subgroup of 244 evaluable hyperglycemic historical time points prior to first reaching upper target BG <110 mg/dl was selected, among 20 treatment courses that did reach target and 2 that never reached target, the medians (with interquartile ranges) in insulin units per hour were MR_csne 4.24 (3.16–6.97), MR_csne-dependent IR_next 5.6 (3.9–9.0), and historically assigned IR_next 5.0 (3.5–8.0). Paired data MR_csne-dependent IR_next and historical IR_next differed significantly according to the two-sided Wilcoxon signed rank test (Z = 14.482, P < 0.0001).

Figure 1.

Comparison of calculated MR_csne-dependent IR_next and IR_next assigned historically under a protocol that estimated MR by column assignment rules, plotted for 941 time points. Medians with interquartile ranges for MR_csne-dependent IR_next and IR_next assigned historically were 4.6 (3.0–6.8) and 4.0 (3.0–6.0) units/h, respectively.

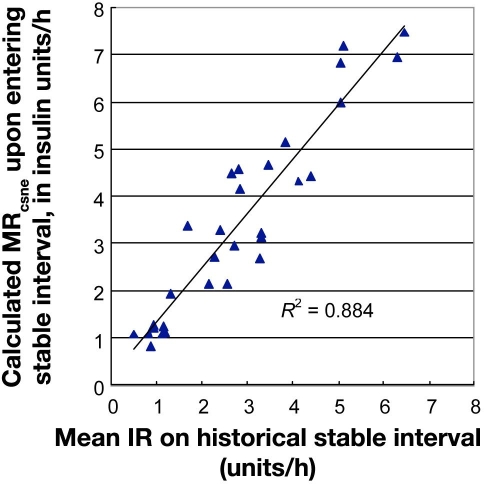
Eighteen treatment courses were identified containing 30 qualifying stable intervals of at least 8 hours of duration, each initiated by the attainment of normoglycemia, following a preceding interval of hyperglycemia. The median (with interquartile ranges) of the mean BG on individual stable intervals was 112.5 mg/dl (106.3–117.6, n = 30 stable intervals). At 30 stable intervals, the medians (and interquartile ranges) in insulin units per hour were MR_csne 3.2 (1.5–4.6) and IR_{mean, stable interval} 2.7 (1.2–3.7).

Paired data MR_csne and IR_{mean, stable interval} differed significantly according to the two-sided Wilcoxon signed rank test (Z = -3.538, P = 0.0004), but the values were correlated (R²= 0.88), as shown in Figure 2.

Figure 2.

Ability of MR_csne to estimate MR_true. The mean IR on stable intervals (MR_true) is compared to MR_csne upon entry to stable intervals. The hypothetical value of MR_csne upon attainment of euglycemia was calculated from the final iteration of a series in which each iteration was initiated during hyperglycemia. Medians for MR_csne and MR_true with interquartile ranges were 3.2 (1.5–4.6) and 2.7 (1.2–3.7) units/h, respectively.

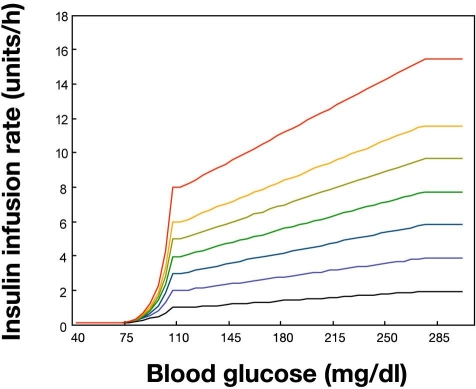
The family of functions created by the algorithm is shown in Figure 3.

Figure 3.

Insulin infusion rate as a function of blood glucose at given values of the maintenance rate. After each iteration, the first step of the algorithm is determination of a value for MR, which then becomes a parameter value for the second step of the algorithm. The second step is determination of IR as a function of BG and MR, displayed as a family of iso-MR curves. For computation of the ideal rate of descent of BG for the next iteration (ROD_ideal,next) as a function of BG, the segmented linear method is used. The ROD_ideal,next is used as an intermediary variable in the computation of IR.

Proposal for Computerized Algorithm “I, Pancreas”

An expanded theory of the algorithm is presented, together with guidelines for nurse implementation, in Table 1 and Appendices 1–3. Guidelines issued by the computerized algorithm for the next BG test time are shown in Appendix 2.

“Opening Screen and Returning Screen”

The nurse will use a computer “opening screen” for the initial input of data. There will be a “returning screen” for use at the time of scheduled retesting of blood glucose. The “returning screen” may also be used between scheduled test times because of hypoglycemia, or perception of risk for hypoglycemia, such that IR and test time reassignment should be considered under the algorithm.

“Opening screen” accepts:

• population data, from which glycemic targets are inferred and presented to user

• user-defined glycemic targets, if defaults are rejected

• BG_current

• maintenance fluids containing dextrose, together with infusion rate (riders containing dextrose will not be entered)

• dextrose content of total parenteral nutrition (TPN) together with infusion rate

• tube feed formula with infusion rate

• insulin concentration in TPN

• “Yes” or “No” response about use of continuous venovenous hemodialysis (CVVHD)

“Returning screen” presents and requests confirmation of:

• previously given information about carbohydrate exposure, insulin content in TPN, and CVVHD

• IR_previous

“Returning screen” accepts:

• reason for entry [scheduled algorithm test time, hypoglycemia, change of carbohydrate exposure (other than riders), change of insulin in TPN, interruption of CVVHD, or other]

• BG_current (mandatory at algorithm test time, optional otherwise)

• “Yes” or “No” answer to question of whether BG_current is a posthypoglycemic recheck

• for IR_previous = 0, a “Yes” or “No” answer to question of whether IR_previous = 0 for >2 hours

After presenting test time_next, the “returning screen” asks whether any of the carbohydrate information has changed or is about to change before “test time next.” A qualifying reduction of carbohydrate exposure is a sufficient condition to increase the frequency of monitoring to hourly intervals in accordance with Appendix 2. If applicable, the “returning screen” advises reversion from testing at 2-hour intervals to hourly testing. Information about carbohydrate exposure will be used only to set test time_next and potentially reduce the insulin rates. Rules for anticipating an increase of insulin according to carbohydrate exposure will not be actuated during piloting.

“Opening screen” and “returning screen” output:

• test time_next

• IR_next

• reminder to request “returning screen” for low BG, change of carbohydrate (other than riders), change of insulin in the TPN, or interruption of CVVHD

General Equation of the Algorithm

Under the hypothesis of the algorithm, the equation that follows give the relationship among IR, the instantaneous rate of change of BG, and the biologic parameter MR. The instantaneous rate of change of BG is embedded in the equation as two functions of BG, namely the rate of change of BG from below target (rate of ascent, or ROA) and the rate of change of BG from above target (rate of descent, or ROD), one of which must be zero at every point in time. Using input from data observed over finite intervals in past time, specifically the observed rate of change of BG and the previous IR, the equation gives estimates of MR. Using the distance of BG_current from the target to determine the ideal future values of fractional reduction of ROA from ROA_max (FRROA) or ROD, the equation, together with an estimate of MR, gives IR_next. In other words, if the IR from past time and ROA or ROD from past time are provided as input, the MR can be estimated. If the FRROA or ROD projected for future time and an estimate of MR are provided as input, an estimate of IR that will achieve the given future FRROA or ROD can be computed.

The overarching design of the algorithm therefore holds that the IR is a function of BG and MR. In the original concept, a linear rule was used during hyperglycemia, such that IR was linearly dependent on the incremental BG elevation above BG_{upper target} and the MR. An exponential rule was used on the euglycemic range, such that IR rose exponentially as a function of the fractional completeness of ascent of BG and MR. The linear rule now will be replaced during hyperglycemia by a bounded exponential rule. The general equation may be expressed more compactly as follows:

$$\text{IR}=\left({\text{IR}}_{@\text{BG}70}\right)*{\left(\text{MR}/{\text{IR}}_{@\text{BG}70}\right)}^{\left[\text{raised\hspace{0.17em}to\hspace{0.17em}a\hspace{0.17em}power\hspace{0.17em}}\le 1\right]}+\text{CR\hspace{0.17em}}\left(\text{if\hspace{0.17em}any}\right),$$

where MR is the maintenance rate of insulin infusion, CR is the correction rate of insulin infusion for hyperglycemia, and IR_@BG70 is the insulin infusion rate at BG 70 mg/dl.

The modifying language in the equation is explained as follows.

• Exponent for MR/IR_@BG70: during euglycemia, when blood glucose is below true target, the power is the fractional completeness of ascent of current BG, between 70 mg/dl and true target (FCABG), which is equivalent to the fractional reduction of the ROA of BG from the maximum rate of ascent (FRROA); whereas at target and above target, the power is 1

• Calculation of CR: when blood glucose exceeds target, ROD is observed in past time or a desired value for ROD is applicable to future time, and CR is a linear function of MR and ROD; whereas at target or below target, CR is 0

The biologic value of MR varies with patient condition. At the beginning of each iteration of the algorithm, an estimation of MR appears as an algorithm parameter in the equation that assigns the next infusion rate (IR_next).

Three Special Parameters Discoverable in Nature

We propose that three special parameters are discoverable in nature, for which estimates can be developed from measurements made routinely in the course of patient treatment, without special physiologic studies, and for which population averages might be determined, specifically:

• ROA_max

• G-per-DIEM

• MR

The ROA_max is the maximum rate of ascent of BG that can occur spontaneously in the absence of hypoglycemia or a counterregulatory response to hypoglycemia, occurring during negligible insulin infusion at the boundary between euglycemia and hypoglycemia, at BG ∼70 mg/dl. Under given conditions of illness, carbohydrate exposure, and concomitant therapies, the ROA_max is assumed to be a discoverable patient characteristic, independent of insulin therapy, insulin secretory capacity, or insulin resistance. The ROA_max depends on ambient conditions affecting the glucose appearance rate, specifically the rate of carbohydrate exposure and the maximum rate of hepatic glucose output during nonhypoglycemia.

The G-per-DIEM is the insulin-mediated BG disposal per kilogram body weight in response to the total daily dose of exogenously administered insulin, if expressed in grams per kilogram; or, if divided by the total daily dose of insulin and expressed in milligrams per deciliter, the G-per-DIEM is the insulin-mediated drop of BG concentration in response to 1 unit of insulin:

$$\left(\text{G-per-DIEM}\right)/\left(\text{total\hspace{0.17em}daily\hspace{0.17em}dose\hspace{0.17em}of\hspace{0.17em}insulin}\right)=\left(\text{drop\hspace{0.17em}of\hspace{0.17em}BG}\right)/\left(1\text{\hspace{0.17em}unit\hspace{0.17em}insulin}\right)$$

The MR for each treated patient requiring exogenous insulin therapy is defined as the rate of intravenous insulin infusion necessary to preserve euglycemia under ambient conditions. MR is a patient characteristic, having fluctuations of magnitude.

Putative determinants of the values of the special parameters are shown in Table 2.

Table 2.

Putative Determinants of the Value of Principal Parameters of the Algorithm Discoverable in Nature and Not User Defined^a

		Putative determinants of parameter value
Parameter	Units of measure	C6R and HGOmax	Endogenous insulin production	Peripheral and hepatic insulin resistance	Body weight
ROAmax	mg/dl per hour	+	0	0	0
G-per-DIEM	mg/dl	+	+	0	0
MR/kg	units/h per kg	+	+	+	0
MR	units/h	+	+	+	+

^aROA_max, nonhypoglycemic maximum rate of ascent of blood glucose during negligible insulin infusion; G-per-DIEM, glucose flux per daily dose of insulin, exogenously mediated; MR, maintenance rate of insulin infusion; C6R, ambient rate of infusion of carbohydrate per hour; HGO_max, maximum hepatic glucose output during negligible insulin infusion under nonhypoglycemic ambient conditions.

Estimation of the Value of MR

In order to compute IR_next, it is necessary to assign an estimated value for MR. The method of assignment is stated in Table 1 and in Appendix 1. The value of MR is unknown at the beginning of a patient's treatment course. A population value for MR is assigned (MR_initial). During treatment the value of MR is reestimated repeatedly or reassigned arbitrarily. During correction of hyperglycemia, an improved estimate of patient-specific MR, the MR_csne, can be computed after each iteration as an intermediary variable (see later), which then can used a parameter in the equation for IR_next. During euglycemia, MR as a parameter is carried forward or, in case of an excessive downward trend of BG, is reassigned to a lower value by arbitrary rules for use in the equation for IR_next (Appendix 1). The best method of validation of the estimate of the biologic value of MR is to compute MR_true retrospectively, defined as the mean IR on stable intervals.

During initial trialing, it is not envisioned that computation of MR_true will be used in real time for the computation of IR_next or for the estimation of revised values for G-per-DIEM or ROA_max.

Computation of MR_csne and MR_csne-Dependent IR_next

A computational method for estimating MR and assigning IR is described. The estimate of MR is called “MR cross step next estimate,” so named because the MR_csne has “one foot in each iteration.” The BG response and IR during the previous iteration permit estimation of MR_csne. The desired BG change for the next iteration, identified with reference to the distance of BG_current from target, permits assignment of IR_next. The principal equations describing computation of MR_csne are shown in Table 1.

General Equation for MR_csne

For BG_previous > 70 mg/dl, the general equation for MR_csne is given hypothetically as follows, with the provisions that

• for BG_previous ≥ BG_{true target}, ROA_previous = 0

• for BG_previous < BG_{true target}, ROD_previous = 0

$$\begin{array}{l}{\text{MR}}_{\text{csne}}={\text{IR}}_{@\text{BG}70}*\hfill \\ e^{\left\{\text{ln}\left[{\text{IR}}_{\text{previous}}/\left\{\left({\text{IR}}_{@\text{BG}70}\right)*\left[1+24*\left({\text{ROD}}_{\text{prev,rev}}\right)/\left(\text{G-per-DIEM}\right)\right]\right\}\right]*\left[\left({\text{ROA}}_{\max }\right)/\left({\text{ROA}}_{\max }-{\text{ROA}}_{\text{previous}}\right)\right]\right\}}\hfill \end{array}$$

Both ROD_previous and ROA_previous are defined as variables at every BG_current value. Each can take positive or negative values, and one must equal zero. For BG_previous ≥ BG_{true target}, the ROD_previous is positive, negative, or zero, and the ROA_previous is zero. ROD_{previous,revised} (ROD_prev,rev) replaces ROD_previous in the equations for MR_csne, providing for logarithmic transform of ROD_previous in case of rising hyperglycemic BG (Table 1). For BG_previous ≤ BG_{true target}, the ROA_previous is positive, negative, or zero, and the ROD_previous is zero. The general equation for MR_csne reduces to simpler equations because either ROD_previous or ROA_previous is extinguished, depending on the value of BG_previous.

Computation of MR_csne during Hyperglycemia

Computation of MR_csne for a clinical application is expected to be useful only during iterations that are initiated during hyperglycemia.

For BG_previous ≥ BG_{true target},

$${\text{MR}}_{\text{csne}}={\text{IR}}_{\text{previous}}/\left[1+24\text{\hspace{0.17em}h\hspace{0.17em}}*\left({\text{ROD}}_{\text{prev,rev}}\right)*\left(\text{G-per-DIEM}\right)\right].$$

During hyperglycemia, the MR_csne is used as MR in the next iteration to calculate the correction rate above MR, giving IR according to the equation:

$$\text{IR}=\text{MR}+\text{CR}.$$

Computation of MR_csne during Euglycemia

During euglycemia, the definition of MR_csne is of theoretical interest, but for practical purposes, at least with present-day technology and under most conditions, the calculated MR_csne should not be used to determine IR_next during euglycemia. Therefore, MR_csne and ROA_previous are only of hypothetical interest. The fractional reduction of ROA_previous from ROA_max (FRROA_previous) is defined as (ROA_max – ROA_previous)/ROA_max, and its inverse appears in the equation for MR_csne. Negative values of ROA_previous commencing on the euglycemic range could be described using a logarithmic transform. When the patient is stable, however, having BG within target, on the narrow euglycemic BG range, the ROA_previous is not measurably distinguishable from zero. The value is so small compared to the error of measurement that the value is not usable. A physiologically meaningful value of MR_csne is not computable if ROA_max is markedly underestimated or if BG rises from a euglycemic value to a value equal to or greater than BG_{true target}. A discussion of ROA_previous and FRROA_previous is included for completeness of the theory and for possible future application in the computation of MR_csne, for special situations in which the algorithm might seek a higher target range, such that measurement of ROA_previous might become meaningful. A further discussion of restrictions on the computability of MR_csne during euglycemia is beyond the scope of this article.

The equation for MR_csne is expressed in terms of the previously observed ROA between BG_previous and BG_current over the time between measurements using the inverse of FRROA_previous. If expressed in terms of FCABG at the previous test time, the value used for BG would not be the actual BG_previous but the fictitious value at which the ideal ROA would be the same as the observed previous ROA. The usefulness of MR_csne for BG_current below BG_{true target} requires having a value for BG_{true target} high enough that meaningful measurements of ROA are possible. MR_csne as a mathematical entity is defined at the point BG = 70 mg/dl, IR = IR_@BG70 as follows:

$${\text{MR}}_{\text{csne}}={\text{IR}}_{\text{@BG70}}*e^{\left[\left({\text{ROA}}_{\text{max}}/{\text{IR}}_{\text{@BG70}}\right)*\left({\text{dIR}}_{\text{previous}}/{\text{dROA}}_{\text{previous}}\right)\right]}.$$

It is not possible to measure dIR_previous/dROA_previous.

For clinical application, MR_csne will not be used after iterations in which BG_previous was below BG_{true target}, but rather a previously assigned MR value will be carried forward. In the presence of hypoglycemic risk factors or after attainment of BG < lower target BG (BG_{lower target}), an arbitrary reduction of MR will be made. The arbitrary methods used to assign MR when BG_previous < BG_{true target} are listed in Appendix 1.

Assignment of IR_next

The general equation for IR_next requires ROD_ideal,next and the ideal future FRROA (FRROA_ideal,next), such that

• for BG_current ≥ BG_{true target}, FRROA_ideal,next = FCABG = 1 and

• for BG_current < BG_{upper target}, ROD_ideal,next = 0.

$${\text{IR}}_{\text{next}}={\text{IR}}_{@\text{BG}70}*e^{\left(\text{FCABG}\right)*\text{\hspace{0.17em}ln}\left[\text{MR}*\left(1+24\text{\hspace{0.17em}h\hspace{0.17em}}*{\text{ROD}}_{\text{ideal,next}}/\text{G-per-DIEM}\right)/{\text{IR}}_{@\text{BG}70}\right]}$$

The general equation for IR_next reduces to simpler equations because either FCABG = 1 and/or ROD_ideal,next = 0, depending upon the value of BG_current.

For BG_{true target} ≤ BG_current < BG_{upper target},

$${\text{IR}}_{\text{next}}=\text{MR}$$

For BG_current ≥ BG_{upper target},

$${\text{IR}}_{\text{next}}=\text{MR\hspace{0.17em}}*\left(1+24\text{\hspace{0.17em}h\hspace{0.17em}}*{\text{ROD}}_{\text{ideal,next}}/\text{G-per-DIEM}\right)$$

For 70 ≤ BG_current < BG_{true target},

$${\text{IR}}_{\text{next}}={\text{IR}}_{@\text{BG}70}*e^{\text{ln}\left(\text{MR}/{\text{IR}}_{@\text{BG}70}\right)*\text{FCABG}}$$

Management of Hyperglycemia

The algorithm does not directly seek to attain BG_{true target} during descent except by assigning ROD_ideal,next conservatively after each hyperglycemic iteration. The fractional elevation of BG_current above BG_{upper target}, compared to elevation of BG_{critical high} above BG_{upper target}, is defined as an intermediary variable, FEBG:

• For BG_current ≥ BG_{upper target},

  FEBG ≡ (BG_current – BG_{upper target})/

  (BG_{critical high} – BG_{upper target}).

• For BG_current < BG_{upper target}, FEBG = 0.

For BG_current ≥ BG_{upper target}, the model for the rate of descent as it first was envisioned, and as it was used in the feasibility studies, held that the ideal ROD_ideal,_next was the ideal ROD at critical high BG (ROD_{@BGcritical high}) multiplied by the FEBG. The model relating insulin infusion rate IR_next to ROD_ideal,next above BG_{upper target} is linear. Estimation of MR_csne utilizes BG_current. However, when MR was given as an algorithm parameter in the expression for IR_next, then for BG_current ≥ BG_{upper target}, the IR_next in the feasibility studies was a linear function of BG_current (see Figure 3 showing linear method with maximum allowed value).

The linear model has a long history of practical application in subcutaneous insulin therapy in the ambulatory setting (the “rule of 1500” or “rule of 1800”), when BG is not elevated greatly. In reality, however, saturation kinetics exist, such that at extremely high insulin exposure, as the linear rule may require for extremely high BG elevations, a declining incremental response occurs.^46,47 One way to acknowledge saturation behavior would be to define a bounded relationship between the infusion rate of insulin and ROD. Another way to acknowledge saturation behavior is to posit a maximum value for the ROD_ideal,next as a function of BG.

The linear method used to compute ROD_ideal,next in the feasibility studies will be replaced by a method that creates a horizontal asymptote for ROD_ideal,next. For BG_current ≥ BG_{upper target}, the model for the rate of descent will hold that the ideal ROD_ideal,_next is a bounded exponential function of the FEBG. For BG_current ≥ BG_{upper target}, the model relating insulin infusion rate IR_next to ROD_ideal,next remains linear, but IR_next will be a bounded decaying exponential function of BG_current. At hyperglycemic BG values, IR = MR + CR will approach a maximum value asymptotically or, in other words, CR will approach a maximum value, CR_max.

Management of Euglycemic Ascent to Target

The algorithm does not directly seek to attain BG_{true target} during euglycemic ascent to target, but rather to restrain the ROA in proportion to both ROA_max and the proximity of BG_current to target. For BG < BG_{true target}, the linear function (BG_current, ROA_ideal,next) giving the ideal rate of ascent of BG for the next iteration (ROA_ideal,next) is defined by the points:

(70 mg/dl, ROA_max)

(BG_{true target}, 0).

• For BG < BG_{true target}, the ROA_ideal,next is defined as:

  ROA_ideal,next ≡ ROA_max * (BG_{true target} – BG_current)/

  (BG_{true target} – 70 mg/dl).

• For BG ≥ BG_{true target}, the ROA_ideal,next ≡ 0.

The fractional reduction of ROA_ideal,next from ROA_max is defined as an intermediary variable FRROA_ideal,next:

• For BG < BG_{true target},

  FRROA_ideal,next ≡ (ROA_max – ROA_{ideal, next} )/ROA_max

• For BG ≥ BG_{true target}, the FRROA_ideal,next ≡ 1.

The model states that if ROA_ideal,next is achieved by appropriate assignment of the insulin infusion rate, then time to target during the ascent of BG is the same for any BG_current such that 70 mg/dl ≤ BG_current < BG_{true target}:

• time to target = (BG_{true target} – 70 mg/dl)/ROA_max.

For 70 ≤ BG_current ≤ BG_{true target}, the FRROA_ideal,next is the same as the fractional completeness of the ascent of BG_current from 70 mg/dl to BG_{true target} (FCABG):

• FCABG = (BG_current – 70 mg/dl)/(BG_{true target} – 70 mg/dl).

FCABG is restricted such that 0 ≤ FCABG ≤ 1.

The model relating insulin infusion rate IR_next to FRROA holds that between BG 70 mg/dl and BG_{true target}, an exponentially increasing value of IR_next as a function of BG_current will deliver a value for FRROA for the coming iteration that declines approximately as a linear function of BG_current. Estimation of MR may utilize BG_current. However, when MR is given as an algorithm parameter in the expression for IR_next, then the IR_next is an exponential function of BG_current for 70 ≤ BG_current ≤ BG_{true target}.

Prevention of Hypoglycemia

Blood glucose test times under the algorithm occur on the hour, every 1 or 2 hours. Based on changes of carbohydrate exposure, insulin in TPN, or CVVHD, between protocol BG test times nursing staff may recognize that an indication for downward reassignment of MR has occurred. Without necessity for retesting BG, the MR is reassigned immediately to 50% of MR_initial, according to the hypoglycemia risk-adjusted MR rate rules outlined in Appendix 1, and IR is recalculated dependent on the new MR. The insulin rate adjustment should not be delayed until the next scheduled BG test time. After such adjustment, the next BG test time occurs on the hour at the next hour, as described later and in Appendix 2.

Management of Hypoglycemia and Interpretation of Algorithm Rules after Hypoglycemia

Hypoglycemia may be recognized at algorithm test times or may be suspected and detected because of patient manifestations occurring between algorithm test times. The time of hypoglycemia occurring between algorithm test times is assigned, under the algorithm, to the nearest hour on the hour. Institutional protocols are used for the treatment of BG <70 mg/dl. An acceptable protocol for treatment of BG <70 mg/dl is administration of a bolus infusion of 12.5 grams dextrose given as 25 cc of 50% dextrose in water, followed by repeat BG testing after 10 minutes. Retreatment and further retesting occur as often as required by symptoms, by manifestations, or by evidence of relapse.

If BG_previous had been above BG_{upper target}, then to compute ROD_previous, a value of BG_current <70 mg/dl at an algorithm test time is accepted as unmodified data. For all computational purposes other than determination of ROD_previous, detection of BG_current <70 mg/dl results in reassignment of the value of BG_current to equal 70 mg/dl. Immediate rebound BG elevations above 70 mg/dl may occur after treatment of hypoglycemia. Any interval BG values collected for safety, obtained by retesting after the treatment of hypoglycemia but before the next algorithm hourly test time, are not used to determine MR or IR; BG_current, reassigned to be 70 mg/dl, is used to mandate that IR = IR_@BG70 for the next hour or the remaining fraction of the hour. After treatment of hypoglycemia, the next BG value eligible for use in the determination of IR_next is the BG obtained at the subsequent hourly test time under the algorithm. IR_@BG70 is infused from the real time at which hypoglycemia occurred until completion of the hour following the algorithm time to which the hypoglycemic event was assigned. At that time, the tentative MR equals 80% of the last MR carried forward, and rules for assigning MR are applied (Appendix 1).

Real Time and Algorithm Times: Practical Programming Suggestions

Algorithm times assigned to BG results are restricted so as to occur on the hour. To determine the time of BG_previous, BG_current, Δ time_previous, and ROD_previous or to determine Δ time_next for the future, the real times of BG tests are rounded to the nearest algorithm time. For BG tests occurring exactly on the half-hour, the assigned algorithm time is the real test time rounded to the next hour.

If hypoglycemia occurs or if there is recognition between algorithm test times that a criterion for hypoglycemia risk-adjusted MR reassignment has occurred, then between algorithm times, by opening a “returning screen,” a nurse should use the algorithm to request a reassignment of IR (see Appendix 1). If a nurse opens the “returning screen” to request a reassignment of IR between algorithm times without entering a new value for BG_current, the start time for the new IR must be identified with an algorithm time. The time of initiation of the new IR is stated to be the nearest algorithm time, on the hour; continuing from this time, the next test time_next is given according to the rules of the algorithm, using Δ time_next = 1 hour.

If a BG test, done between algorithm times, is used in the “returning screen” to request a reassignment of IR and if the nearest algorithm time was the previous hour on the hour, then the value of the new BG replaces the previously determined BG value that had been assigned to correspond to an algorithm time at the previous hour on the hour. If a BG test done between algorithm times is used in the “returning screen” to request a reassignment of IR and if the nearest algorithm time is the next hour on the hour, then the new BG becomes the BG that corresponds to the next algorithm time. The availability of this value eliminates the need to redetermine the BG at the next hour on the hour. Although starting in real time between algorithm times, the newly assigned IR will be understood within the algorithm to have started at the algorithm time that was assigned to the newly determined BG.

At the beginning of the next iteration, a computation of MR_csne may have to be made. If so, the ROD_previous is calculated by taking the irregularly timed BG as BG_previous, associated with a previous algorithm time rather than real time, and by taking the current BG as BG_current, the Δ time as 1 hour, and the start time for IR_previous as the previous algorithm time.

Segmented Asymmetric Nearly Sigmoidal Curve

At a given MR, when the entire domain of BG is considered, an asymmetric nearly sigmoidal function IR of BG will be created, segmented into parts below BG_{true target} (an exponential relationship between IR_next and BG_current), between BG_{true target} and BG_{upper target} (a constant relationship), and above BG_{upper target} (a bounded decaying exponential relationship) (Figure 4). The effect is that the equation for IR_next as a function of MR and BG_current will resemble an asymmetric doubly sigmoidal curve.

Figure 4.

(A) Algorithm with parameters assigned for a surgical intensive care unit. The IR equals MR for BG 105–110 mg/dl. For computation of the intermediary variable ROD_ideal,next, the bounded decaying exponential method is used. (B) Algorithm with parameters assigned for diabetic ketoacidosis in an adult. The IR = MR at BG 184–200 mg/dl. The default initial maintenance rate is used until rehydration time has elapsed and then computation of MR_csne commences. (C) Effect of parameter assignment according to population. A single curve showing IR at differing BG levels from each of two families of curves is compared for a SICU patient and a DKA patient, each having MR = 3 units/h.

Application to Populations

For a given set of parameter values, a family of iso-MR equations giving IR as a function of BG is created. One such family of curves is shown, appropriate for a population such as a surgical ICU in which BG_{true target} may be 105 mg/dl, BG_{upper target} 110 mg/dl, BG_{critical high} 180 mg/dl, ROD_{@BGcritical high} 30 mg/dl per hr, ROD_{ideal,next,max} 70 mg/dl, and IR_@BG70 = 0.1 units/h (Figure 4A). For a patient belonging to a different population, the family of curves may be shifted to the right or shifted up or down (Figure 4B). For purposes of comparing two populations, at given MR the function is shown for a patient who may be a surgical ICU patient and another who may be under treatment for ketoacidosis (Figure 4C).

Hypotheses about Algorithm Parameters Discoverable in Nature

Methods are suggested for the verification of estimated values of three algorithm parameters (Table 3). By definition, MR_true is the mean IR on stable intervals. MR_true reflects actual insulin delivery on intervals of stability close to target range BG control and thus estimates the biologic value of MR. It is hypothesized that MR_csne, computed during the correction of hyperglycemia, will estimate MR_true.

Table 3.

Hypotheses on How to Verify Estimates of Values of Parameters

Parameter	Estimation of the value of parameter	Verification
MR	Calculation of patient mean IR on stable intervals (MRtrue)	By definition
G-per-DIEM	Calculation using MRtrue and IRprevious during hyperglycemia	By ability of MRcsne to estimate MRtrue
ROAmax	Calculation using MRtrue and IRprevious during euglycemia	By ability to predict time to target during euglycemic ascent of BG

Hypothesis about G-per-DIEM

The G-per-DIEM will be assigned arbitrarily as 1800 mg/dl during initial trialing. The hypothesis holds that replacement of the default G-per-DIEM with the estimated population average value of G-per-DIEM will improve the ability of MR_csne to estimate MR_true. The estimation of G-per-DIEM requires making a first estimate of MR_true for a stable time interval. The computation requires analysis of correction of hyperglycemia during immediately antecedent hyperglycemic iterations:

$$\text{G-per-DIEM}=\left({\text{ROD}}_{\text{previous}}\right)*\left({\text{MR}}_{\text{true}}*24\text{\hspace{0.17em}h}\right)/\left({\text{IR}}_{\text{previous}}-{\text{MR}}_{\text{true}}\right)$$

During retrospective studies, multiple stable intervals will be identified, such that MR_true can be determined, and ROD_previous can be captured over the antecedent hyperglycemic 4 hours prior to entry to each qualifying stable interval. Population averages, dependent in part on the level of carbohydrate exposure, then can be determined for the G-per-DIEM parameter. There is reason to believe that the G-per-DIEM parameter at a given level of carbohydrate exposure may be a higher number for type 1 diabetes than for stress hyperglycemia or type 2 diabetes.⁴⁸ The future possibility of a real-time determination of patient values for G-per-DIEM during the individual course of treatment is not discounted.

Hypothesis about ROA_max

The ROA_max is defined at BG = 70 mg/dl, equaling the observed ROA during a subsequent iteration in which IR = IR_@BG70. At euglycemic BG values >70 mg/dl, it is likely to be infrequent that the multiple necessary conditions can be met for the computation of ROA_max. The equations would be as follow:

$$\begin{array}{l}{\text{ROA}}_{\max }={\text{ROA}}_{\text{previous}}*\left[\ln \left({\text{MR}}_{\text{true}}/{\text{IR}}_{@\text{BG}70}\right)/\ln \left({\text{MR}}_{\text{true}}/{\text{IR}}_{\text{previous}}\right)\right],\hfill \\ \text{for\hspace{0.17em}}70\text{\hspace{0.17em}mg}/\text{dl}<{\text{BG}}_{\text{previous}}<{\text{BG}}_{\text{true\hspace{0.17em}target}}\hfill \\ {\text{ROA}}_{\max }={\text{ROA}}_{\text{previous}}\text{\hspace{0.17em}for\hspace{0.17em}}{\text{BG}}_{\text{previous}}=70\text{\hspace{0.17em}mg}/\text{dl\hspace{0.17em}and\hspace{0.17em}}{\text{IR}}_{\text{previous}}={\text{IR}}_{@\text{BG}70}.\hfill \end{array}$$

If MR_true had been available in real time to compute IR_previous, then under the model IR_previous should have delivered ROA_previous, such that ROA_max could be identified more simply as

$$\begin{array}{l}{\text{ROA}}_{\max }={\text{ROA}}_{\text{previous}}*\left({\text{BG}}_{\text{true\hspace{0.17em}target}}-70\text{\hspace{0.17em}mg}/\text{dl}\right)/\left({\text{BG}}_{\text{true\hspace{0.17em}target}}-{\text{BG}}_{\text{previous}}\right),\\ \text{if\hspace{0.17em}}{\text{MR}}_{\text{true}}\text{\hspace{0.17em}was\hspace{0.17em}used\hspace{0.17em}to\hspace{0.17em}assign\hspace{0.17em}}{\text{IR}}_{\text{previous}}.\end{array}$$

It is doubtful whether ROA_max can be estimated by either of the previously suggested methods, but the possibility will be studied.

The model holds that replacement of the default ROA_max with the discovered population average value of ROA_max will improve the ability to predict time to target during the euglycemic ascent of BG.

User-Assigned Parameters

The following population types may prove to have differing parameters: adult surgical ICU, standard adult not critically ill, children <18 years, diabetic ketoacidosis, diabetic ketoacidosis in children <18 years, hyperglycemic hyperosmolar state, chronic renal failure, and patients having BG <50 within 24 hours prior to initiation of the algorithm or having a perceived high risk for hypoglycemia (Appendix 3). In such cases, the algorithm parameters might be assigned with differing default values by computer, according to patient condition, with rates given in units per kilogram per hour for children. User-assignable algorithm parameters preferably may be selected as a panel by indicating the patient population or, alternatively, may be adjusted singly from default values:

• lower target (BG_{lower target})

• true target (BG_{true target})

• upper target (BG_{upper target})

• critical high BG (BG_{critical high})

• ideal rate of descent of BG for next iteration at critical high blood glucose (ROD_{@BGcritical high})

• ideal maximum rate of descent of BG for next iteration (ROD_{ideal,next,max} )

• minimum insulin infusion rate at BG= 70 mg/dl (IR_@BG70)

• initial maintenance rate (MR_initial)

• maximum insulin infusion rate (IR_max)

• rehydration time

• rate of delivery of hypoglycemic action of insulin, onset time (HR onset time)

• rate of delivery of hypoglycemic action of insulin, cessation time (HR cessation time)

• offset time for BG response to enteral delivery of carbohydrate (C6R offset time)

• other, dependent on model

At this time, models for the rate of delivery of the hypoglycemic action of insulin (HR) and rate of exposure to carbohydrate (C6R) are not in place. HR onset and offset times are identical to the times of onset and cessation of IR, and the simplification is made that HR = IR. Although arbitrary reductions of MR are made for the reduction of C6R, the response to C6R otherwise is not calculated. Hypoglycemia <70 mg/dl is treated with concentrated dextrose until correction occurs. Intravenous dextrose is not required on the nonhypoglycemic BG range.

Discussion

Feasibility Studies

Limitations of the study include the fact that steady-state conditions of insulin infusion and BG response were not met between BG samples. Because the mean IR on stable intervals was taken to be an approximation of the true MR, it is necessary to explain why the MR_csne systematically overestimated the mean IR on stable intervals. One possibility is that an imperfect estimate of maintenance requirements may be provided by the formula for MR_csne. Another possibility is that, on average, less than true maintenance requirements may have been delivered during stable intervals. A third possibility is that during stable intervals, ongoing improvement of acute glucotoxicity may have been occurring. A fourth possibility is that for the trauma patient population, the value “1800 mg/dl” used in the algorithm may be inappropriate to the calculation of the insulin sensitivity factor. A fifth possibility is that despite rounding of times for purposes of charting, actual test times and infusion rate change times may not have occurred on the hour punctually.

The benefits to be anticipated are a reduction in oscillations of the BG, safety with respect to hypoglycemia, and attainment of targets that may be specified to differ according to population. The ability of an algorithm to deliver these benefits could not be evaluated without conducting patient trials. The principal limitation of the study is that the response to the algorithm cannot be predicted by a hypothetical application to successive time points within a treatment course that was, in fact, conducted under the rules of the predecessor protocol.

Proposal for Computerized Algorithm “I, Pancreas”

A programmable algorithm is described for intravenous insulin infusion. The new algorithm, as well as its predecessor protocol of proven safety,⁴¹ employ similar rules for the assignment of IR, dependent on discovery of an approximate MR and use of an exponential rule for euglycemic ascent. Whereas the predecessor protocol relies on cumbersome column-change rules to select the best of six possible values for MR, the new algorithm calculates an intermediary continuous variable, the MR_csne. Prior to attainment of normoglycemia, although the feasibility study suggests that the new algorithm would assign slightly higher IR values at isolated historical time points, the respective IR values under the old protocol and new algorithm are tightly correlated. Although the MR_csne upon entry to a stable interval in the feasibility study is slightly higher than the estimated hourly maintenance insulin requirement (historical mean IR on the ensuing stable interval), the two values are tightly correlated.

In contrast to the column-based method of selection from six possible values for MR, calculation of MR_csne by the new algorithm allows for a continuous spectrum of values for MR, and each hyperglycemic iteration provides an opportunity for the adjustment of MR. In future applications we will replace the linear rule for the correction of hyperglycemia, used in the feasibility studies, with a bounded decaying exponential rule. We believe that the method of correction of hyperglycemia, as well as the management of euglycemia, determine the safety of an algorithm with respect to hypoglycemia prevention. The exponential rule for the management of euglycemia, an important feature of the predecessor protocol, will be preserved in the new algorithm.

Future Directions

Using data from stable intervals for calculation, future work will attempt to determine special parameter values in a population-dependent manner. To optimize protection against hypoglycemia, concepts of the rate of delivery of the hypoglycemic action of insulin in units per hour (HR) and the rate of delivery of carbohydrates in grams per hour (C6R) in the future will be incorporated into the assignment of IR_next. Figure 4 uses the simplifying assumption that the pharmacodynamic delay for intravenous insulin is negligible, i.e., that the onset and cessation time for HR is zero, or HR = IR. Future algorithm revisions may invoke HR. Administration of a priming bolus of insulin will be prohibited. At the time of algorithm initiation, the use of HR to calculate IR will account for the lack of insulin during the preceding hour. If computations indicate a need to neutralize the hypoglycemic action of insulin already delivered, the algorithm will calculate a “negative” rate of insulin delivery for IR_next, and the response recommended under the algorithm will be an infusion of dextrose. Otherwise, the pharmacodynamic delay of insulin already administered will be factored into the computation of MR_csne and IR_next. At this time, because a model for HR is not in place,^49–51 the simplest assumption is used, HR = IR.

Adaptation to a change of carbohydrate exposure under the present design is either reactive or arbitrary. In order to match carbohydrate exposure, C6R, together with a matching rule for the discovery of insulin-to-carbohydrate requirements, may be incorporated into future versions of the algorithm.

For a given value of MR, the relationship between IR_next and BG_current is presently based on models using intermediary variables, the FRROA_ideal,next and ROD_ideal,next, which in turn depend on the distance of BG_current from target BG. The segmented curves are defined by upper and lower asymptotes and by four shaping points within the function (BG, IR), namely:

Asymptotes:

• IR = zero at BG = “– ∞”

• IR = MR + CR_max at BG “+ ∞”

Two points defining the boundaries of the domain on which IR_next = MR:

• (BG_{true target}, MR)

• (BG_{upper target}, MR)

Two additional “shaping points” for two exponential curves:

• (70 mg/dl, IR_@BG70)

• (BG_{critical high}, IR_{@BGcritical high}),

where IR is a function of the intermediary variables MR, FRROA_{ideal, next}, and ROD_ideal,next, and where ROD_ideal,next at BG_{critical high} is specified as an algorithm parameter.

A long-range goal is to describe the IR-defining second step of the algorithm as a continuous, strictly increasing, differentiable function on the entire MR and BG domain, giving IR_next as a function of MR and BG_current without using other intermediary variables. The two asymptotes and the MR will be preserved as algorithm parameters, and the shaping points will be retained, giving IR_@BG70 and IR_{@BG critical high} at BG 70 mg/dl and at BG_{critical high}, respectively. There will be three inflection points, assigned such that BG_{target minus} corresponds to BG_{true target} and that BG_{target plus} corresponds to BG_{upper target}:

• (BG_{target minus}, MR_minus)

• (BG_{mid target}, MR)

• (BG_{target plus}, MR_plus)

Although the exact values need to be determined, initial pilot studies on the behavior of the segmented curve will give evidence on the appropriateness of choices that may be made for asymptotes, inflection points, and shaping points. The appearance will be that of an asymmetric doubly sigmoidal curve.

Conclusion

In summary, an algorithm is described that seeks patient MR and assigns commensurate IR. As a replacement for column-change rules of paper protocols, the electronic version of our MR algorithm will add computation of MR_csne to the design of those predecessor algorithms. With the intent of reducing risk for hypoglycemia, the exponential rule of a predecessor protocol for the management of euglycemia is preserved. Computerization is expected to facilitate adaptation of the algorithm to various patient populations by assigning a population-dependent panel of default parameter values in response to user input. Computerization will reduce conceptual burden and errors of column-change rules. It is possible that data collected during use of the algorithm will permit investigators to refine population averages for algorithm parameters and even to propose the real-time revision of parameters during the treatment course of an individual patient. The design features define a method for specifying glycemic targets that are allowed to differ according to patient condition. It is hoped that these effects will translate into the advantages of a reduction of glycemic variability and of hypoglycemia and will enable the algorithm to perform with flexibility across populations.

Abbreviations

BG

blood glucose

C6R

rate of exposure to carbohydrate

CR

correction rate

CVVHD

continuous venovenous hemodialysis

DKA

diabetic ketoacidosis

FEBG

fractional elevation of BG

FCABG

fractional completeness of ascent of BG

FRROA

fractional reduction of ROA

G-per-DIEM

glucose per daily dose of insulin exogenously mediated

HR

hypoglycemic action of insulin delivery rate

ICU

intensive care unit

IR

infusion rate

ISF

insulin sensitivity factor

IV

intravenous

MR

maintenance rate

MR_csne

MR cross step next estimate

ROA

rate of ascent

ROD

rate of descent

SICU

surgical intensive care unit

TDDI

total daily dose of insulin

TPN

total parenteral nutrition

Appendix 1. Rules for Assigning Maintenance Rate (MR)a

Initial iterations

• If the coming iteration is the initial iteration, then MR = population parameter MR_initial

• If interruption of insulin infusion for ≥2 hours preceded the coming iteration, then MR = MR_initial

Tentative MR for subsequent iterations

• If BG_previous ≥ BG_{true target}, then the following apply:

  • If rehydration time has not elapsed, tentative MR = MR_initial,

    unless BG_current < BG_{lower target}, in which case tentative MR = 80% of MR_initial

  • Otherwise, tentative MR = MR_csne

• If BG_previous < BG_{true target}, or if BG is unavailable at the time of last change of IR, then the last MR is carried forward to become the tentative MR, unless BG_current < BG_{lower target}, in which case tentative MR = 80% of last MR carried forward.

Maintenance rate for subsequent iterations

The MR for any subsequent iteration is the minimum of the tentative MR, the TPN-adjusted tentative MR, and the hypoglycemia risk-adjusted tentative MR, where

• Tentative MR is defined as described earlier

• TPN-adjusted tentative MR is defined as follows: if insulin additive to TPN will be increased, then TPN-adjusted tentative MR = tentative MR – (24-hr increment of insulin added to TPN)/24 h

• Hypoglycemia risk-adjusted MR is defined as follows: if tube feed interruption, ≥ 50% reduction of dextrose-containing maintenance fluid infusion rate (from rate at least 40 cc/h of 5% dextrose-containing maintenance fluids, 20 cc/h of 10% dextrose-containing maintenance fluids, or 10 cc/h of TPN or equivalent), or interruption of CVVHD will occur within the next iteration or has occurred at the present time, then hypoglycemia risk-adjusted tentative MR = 50% of MR_initial.

Appendix 2. Rules for Next Blood Glucose Test Timea

Indications for initial BG monitoring every 1 hour

Hourly monitoring is required for each condition:

• Algorithm initiation

• Time elapsed <4 hours since algorithm initiation

• Time elapsed <4 hours since resumption of insulin infusion, following interruption of ≥2 hours duration.

Indications for monitoring every 2 hours

• Nurse acknowledges that no interruption of enteral feedings and no decrement of at least 40 cc/h of 5% dextrose-containing maintenance fluids, 20 cc/h of 10% dextrose-containing maintenance fluids, or 10 cc/h of TPN will occur within the next iteration or have occurred at the present time and that no rate reduction by ≥50% of dextrose-containing maintenance fluid infusion (from rate >40 cc/h 5% dextrose or equivalent) or interruption of CVVHD will occur within the next iteration or has occurred at the present time.

• MR must be stable as defined below, where MR(n) refers to the nth iteration of the algorithm (each condition necessary):

  • ≥ 4 hours have elapsed since algorithm initiation

  • for each of the past three iterations “n,” 0.67 ≤ [MR (n - 1)/MR (n)] ≤ 1.25

  • within the past 4 hours, no BG < BG_{lower target} has occurred

Once the time interval has been adjusted to every 2 hours, the default for Δ time_next = 2 hours.

Indications for reversion to hourly monitoring

Reversion from 2-hour monitoring to hourly monitoring is required if any one of the following occurs:

• Provider override of IR_next occurs to a higher value than identified by the algorithm

• Nurse acknowledges that interruption of enteral feedings, a decrement of at least 40 cc/h of 5% dextrose-containing maintenance fluids, 20 cc/h of 10% dextrose-containing maintenance fluids, or 10 cc/h of TPN will occur within the next iteration or has occurred at the present time; or that a ≥50% rate reduction of dextrose-containing maintenance fluid infusion (from rate >40 cc/h 5% dextrose or equivalent) or interruption of CVVHD will occur within the next iteration or has occurred at the present time.

• Destabilization of glycemic control or insulin infusion occurs

  • BG_current > BG_{upper target} × 8 hours

  • BG_current > BG_{critical high} × 2 hours, and BG not falling at ROD_ideal,next or faster

  • BG_current < BG_{lower target}

  • IR_next >50% of IR_max

  • MR reassignment to ≤50% of MR_initial for any reason.

Appendix 3. Proposed Population Parameters^a

Population	Adult ICU	Standard adult not critically ill	Children <18 years	DKA	DKA, children <18 years	Hyperglycemic, hyperosmolar coma	Chronic renal failure	Hypoglycemia risk
Rate of change of BG, mg/dl per hour
ROD@BGcritical high	30	30	30	75	75	75	30	30
RODideal,next,max	70	70	70	150	150	150	70	70
ROAmax, default	17.5	17.5	17.5	70	70	70	17.5	17.5
G-per-DIEM, mg/dl, population default	1800	1800	1800	1800	1800	1800	1800	1800
BG, mg/dl
BGlower target	80	81	84	150	150	250	84	84
BGtrue target	105	110	120	183.75	227.5	271.25	120	120
BGupper target	110	116	127	200	250	300	127	127
BGcritical high	180	196	227	427.5	565	702	227	227
Rehydration time, hour	0	0	0	4	4	4	0	0
Insulin rates	units/h	units/h	units/kg per hour	units/h	units/kg per hour	units/h	units/h	units/h
MRinitial	2	1	0.015	3	0.045	3	1	1
IR@BG70	0.1	0.1	0.002	0.1	0.002	0.1	0.1	0.1
IRmax	24	24	0.1–0.2	24	0.1–0.2	24	24	24

^aThe “hypoglycemia risk” population is defined by having BG <50 mg/dl within 24 hours prior to algorithm initiation or during the treatment course or by nursing staff acknowledgment of perceived hypoglycemia risk. Within each group, type 1 diabetes might constitute a subgroup. Population values for G-per-DIEM will be discovered in the future, possibly differing for the subgroups of patients having type 1 diabetes compared to values assigned to other members of the same groups. ROD_{@BGcritical high} is ROD_ideal,next at a defined value of BG_current, considered to be a critical high BG for the population. BG_{lower target} is the value of BG_current at which arbitrary MR reduction is required. BG_{true target} is the value of BG_previous above which the ROD_previous may assume nonzero values; it is the value of BG_current below which ROA_ideal,next >0 and FRROA_ideal,next <1. BG_{upper target} is the value of BG_{current above} which FEBG > 0 and ROD_ideal,next > 0. BG_critical high is the value of BG_current associated with a specific value for ROD_ideal,next, namely ROD_{@BGcritical high}. Rehydration time is the time that must elapse before MR_csne may replace MR_initial. IR_max is a value that replaces computed IR_next, if computed IR_next > IR_max. Other parameters are defined in the text. Pediatric values have not been tested in pilot studies. In a future upgrade of the algorithm, a time delay for onset of the delivery of the hypoglycemic action of insulin (HR) will be specified, and a cessation time for HR will be identified as a population parameter, having a distinct value in the presence of renal failure differing from the value assigned to other populations.