Tremor-related motor unit firing in Parkinson's disease: implications for tremor genesis

Abstract

Muscle tremors reflect rhythmical motor unit (MU) activities. Therefore, the MU firing patterns and synchrony determine the properties of the parkinsonian force tremor (FT) and the neurogenic components of associated limb tremors. They may also be indicative of the neural mechanisms of tremor genesis which to date remain uncertain. We examined these MU behaviours during isometric contractions of a finger muscle in 19 parkinsonian subjects. Our results reveal that the parkinsonian FT is abnormally large. Like the physiological FT, it is accompanied by in-phase rhythms in all MU activities. However, there exist two important differences. Firstly, the synchrony during the parkinsonian FT is stronger than the normal one and therefore contributes to the FT enhancement. Secondly, the synchronous MU components partly represent rhythmical sequences of spike doublets and triplets whose incidences directly reflect the differences of the MU firing rates to the FT frequency. According to our analyses, the latter frequency coincides with the MU recruitment rate. Consequently, the numerous medium- and small-sized active MUs contribute rhythmical twitch doublets and triplets, i.e. large force pulses, to the parkinsonian FT. The impact of this effect on the FT amplitude is found to predominate over the impact of the augmented synchrony. Importantly, apart from the rule governing the occurrence of doublets/triplets, the mean interspike intervals within such spike events are fairly fixed around 50 ms. Such regularities in MU activities may reflect properties of the neural input underlying the FT, and thus represent a basis for more focused studies of the generator(s) of parkinsonian tremors.

Introduction

Force tremor (FT) is a ubiquitous characteristic of muscle contractions (Stephens & Taylor, 1974; Hömberg et al. 1986; Christakos et al. 2006). It represents oscillations in the muscle force signal which are caused by unfused twitches contributed by active motor units (MUs) to the muscle force. This tremor is also manifested as rhythmically grouped MU action potentials in the electromyogram (EMG). FT is measured during quasi-isometric voluntary contractions against a force transducer, and is then termed isometric tremor (Deuschl et al. 1998). In all cases, FT is a reflection of neural rhythmicity which may be of central or spinal/peripheral origin.

The formation and properties of FT depend on the way MUs fire and combine their activities (Christakos et al. 2006). At the same time, the MU population level is the site of convergence of both central and peripheral neural influences. Therefore, detailed information on the MU firing patterns and synchrony, as well as their dependencies, is essential for understanding the mechanisms of FT, including the generation of the underlying neural rhythm.

Muscle FTs are clearly the source of the neurogenic tremor components of body segments in health and various movement disorders. In Parkinson's disease (PD), postural tremor, but also rest tremor evaluated while the patient tries to relax, exhibit coherence to rhythmical electromyographic (EMG) activities of participating muscles (Vaillancourt & Newell, 2000; Sturman et al. 2004). This indicates that these tremors indeed have components which share a common origin with muscle force oscillations (FTs) reflecting coherent neural rhythms.

Postural and rest tremor, being common signs of PD, have been extensively studied (Findley et al. 1981; Elble & Koller, 1990; Bain, 2002). There is significant evidence implicating supraspinal centres and associated neural loops in the generation of parkinsonian tremors. These include the basal ganglia (Bergman & Deuschl, 2002; Liu et al. 2002; Brown, 2003) and the thalamus (Lenz et al. 1988). Other findings argue for the participation of proprioceptive input in this process (Rack & Ross, 1986; Spiegel et al. 2002). There also exist observations suggesting the involvement of peripheral loops (Burne, 1987) and spinal motor systems (Rivlin-Etzion et al. 2008) in tremor generation. Overall, however, the neural mechanisms underlying these tremors are poorly understood.

As mentioned above, the analysis of the MU firing properties during parkinsonian FT could facilitate the study of such limb tremors. The experimental conditions of the quasi-isometric FT resemble those of postural tremor which also involves voluntary muscle contractions. An important difference between FT, which can only be measured under quasi-isometric conditions, and postural tremor is that the mechanical properties of the freely moving limb are expected to influence the properties of the latter tremor. However, as explained in the Discussion (final section), there is evidence suggesting that this influence is limited in PD, postural tremor being primarily neurogenic, i.e. resulting from muscle FTs (Stiles & Pozos, 1976; Hömberg et al. 1987; Palmer & Hutton 1995). Similarly, even in the complete absence of voluntary muscle contractions, a component of isometric FT, analogous to the rest tremor, is present (Burne et al. 2004).

The FT-related firing behaviours of MUs in PD have been examined in relatively few early studies, later tremor research having predominantly focused on cerebral activities. These early studies have described abnormal firing patterns exhibiting rhythmical pairs of spikes separated by 20–80 ms in individual MUs, and considered the impact of these spike doublets on the tremor (Das Gupta, 1963; Dietz et al. 1974; Dengler et al. 1986, 1989; Elek et al. 1991); they have also examined the short-term correlation between MUs (Baker et al. 1992). The employed analyses in these pioneering studies have provided a first description of MU firing behaviours and their consequences for the parkinsonian FT.

In order to gain further insight into these behaviours, we systematically investigated in the human first dorsal interosseus (FDI) muscle the characteristics and dependencies of (1) the MU firing patterns during parkinsonian FT, particularly the doublet (or even triplet) occurrences, using higher-order interspike interval (ISI) analyses (Perkel et al. 1967; Christakos et al. 1988), and (2) the FT-related firing synchrony of the MUs, in particular the extent, strength and unit phase-relations of this population synchrony, using an experimentally and computationally efficient method (Christakos, 1997; Christakos et al. 2006). We also compared these MU behaviours to those during physiological FT in age-matched subjects.

We subsequently addressed three main issues. Firstly, we questioned the prominent role for the rhythmical MU synchrony in determining the abnormally large parkinsonian tremors, as is often assumed on the basis of observed highly synchronized supraspinal networks in PD (see Brown & Williams, 2005). Secondly, we examined the impact of the spike doublets and triplets on the FT amplitude. Notably, a coexistence of doublets and overt FT has previously been noticed and examined (Dengler et al. 1986, 1989; Elek et al. 1991). However, the demonstration of a quantitative relationship between the two phenomena has been complicated by difficulties relating to representative measures of doublet incidence in individual MUs and, more so, in the population of active MUs (see Methods and Discussion). Thirdly, we used our observations on the doublet/triplet incidences, the interspike intervals (ISIs) within such spike events, and the overall MU firing synchrony to draw conclusions regarding the input provided by the tremor generator to the MU population. We further related our observations to the mechanisms underlying postural and rest tremor in PD.

A preliminary report has been given in an abstract (Erimaki et al. 2007).

Methods

Patients and control subjects

Nineteen patients with idiopathic Parkinson's disease of tremor-dominant type participated in the study (Table 1). Most patients displayed short disease durations (mean 38.2 months, range 6–120), and their disease stage was 1, 2 or 3 on the Hoehn and Yahr scale. The clinical severity was assessed using the motor part of the UPDRS scale (mean 17, range 7–37). Rest and postural tremor of the patients’ upper limbs was mostly asymmetrical, and at the time of the recordings scored ≤ 2 on the Webster scale. Recordings were obtained from the most severely affected side. In all patients the clinical evaluation and the recordings were performed at least 10 h after the administration of the last dopaminergic medication.

Table 1.

Summary of conditions for, and experimental observations of, the subjects’ isometric muscle contractions

	PS	CS	P
Subjects	19	19
Age (years)	55–80	49–78	0.110
Mean (s.d.)	69.5 (7.6)	64.3 (8.1)
Male:female	11:8	12:7
No. of contractions	46	32
No. of MUs	50	39
ContrLev (%MVC)
Range	2–40	2–45
Mean (s.d.)	13.7 (8.7)	12.3 (9.2)	0.510
FR (Hz)
Range	5.0–19.5	6.0–17
Mean (s.d.)	9.2 (3.1)	10.3 (2.4)	0.085
MU/FCoh
Range	0.08–0.91	0.08–0.87
Mean(s.d.)	0.50 (0.25)	0.36 (0.20)	0.005*
TF (Hz)
Range	4.5–8	6.0–9.0
Mean (s.d.)	6.0 (1.1)	7.0 (0.9)	<0.001*
eBW (Hz)
Range	1.4–6.8	1.9–9.8
Mean (s.d.)	3.6 (1.6)	5.3 (1.7)	<0.001*
TreAmpl (%VC)
Range	0.4–34.3	0.3–6.9
Mean (s.d.)	10.2 (8.9)	2.1 (1.5)	<0.001*

The contraction level (ContrLev) is measured as a percentage of maximal voluntary contraction (%MVC); the MU firing rate (FR), the peak tremor frequency (TF) and the effective bandwidth (eBW) are given in Hz; and the tremor amplitude (TreAmpl) is measured as a percentage of the level of the voluntary contraction (%VC). For the number of segments used in our study, MU/force coherences (MU/FCoh) ≥ 0.08 are significant. The independent-samples t test was used for statistical evaluation; P values with asterisks indicate statistically significant differences. PS, parkinsonian subjects; CS, control subjects.

Nineteen age-matched, neurologically normal volunteers were the control subjects of this study (Table 1). Both patients and control subjects gave informed consent. The study conformed to the standards set by the latest version of the Declaration of Helsinki, and was approved by the Ethical Committee of the University of Athens.

Measurements

In the recording sessions, the subjects assumed a comfortable sitting position in front of a force transducer (WPI-Fort1000; measured stiffness 50 N mm⁻¹).Their most affected hand and arm were secured on the lab bench. The subjects exerted abduction force on the transducer, within a vertical plane, using the lateral side of the horizontally extended index finger. This finger was firmly attached to the transducer, while digits 3–5 were constrained in full flexion.

The subjects were instructed to follow with the nearly isometric force of the FDI muscle of the hand a horizontal target line that was displayed on the oscilloscope and represented a constant force level. The oscilloscope was at a distance of 70 cm from the subject, and in most recordings 1.0 N of force caused a 1.0 cm displacement of the oscilloscope trace. Wide ranges of mean force level were used for both the parkinsonian and the control subjects: 2–40% of maximal voluntary contraction (MVC) for the patients and 2–45% MVC for the control subjects (Table 1).

Simultaneous 2 min records were obtained of the muscle force, the surface EMG (using Ag–AgCl disc electrodes; Kendall ARBO) and the intramuscular EMG (using disposable monopolar needle electrodes; TECA, 0.36 mm, 28G). The data were digitized and stored using the program LabView.

Data analysis

Discrimination of single-MU spike trains in the intramuscular electrical activity was performed by combining a threshold operation and manual sorting. It provided one and, in a few cases, two MUs per recording. Spike trains were represented as sequences of zeroes and ones. All recorded signals, including the sequences that represented spike trains, were originally sampled at 5 kHz. After low-pass filtering at 250 Hz, they were resampled at 500 Hz for analysis. The filtering was digital and introduced no time shifts (Christakos et al. 1984).

Analyses were performed in both the time- and the frequency-domain using MATLAB (Math Works, Natick, MA, USA).

Time-domain analysis included computations of:

1. MU firing rates per record. The (mean) firing rate of an MU, termed intrinsic in what follows, corresponds to a particular mean level of muscle force, according to the MU recruitment and rate coding mechanisms (Henneman, 1979; Glendinning & Enoka, 1994); it is the same for a steady and a time-varying contraction around the same force level (Iyer et al. 1994).

2. First- to third-order ISI histograms of MU spike trains. By definition, nth-order intervals represent intervals from each spike in a train to the nth following spike; the interval histograms (densities) of various orders are the constituents of the auto-correlogram of a spike train (Perkel et al. 1967). Higher-order ISI analyses have proved useful in cases of firing patterns resulting from combination of different neural rhythms (Christakos et al. 1988).

3. Cross-correlograms of pairs of activities.

The frequency analysis method has previously been described in detail (Christakos et al. 2006). A brief description follows.

Spectral computations, performed via the fast Fourier transform (FFT) on pairs of recorded activities, included (Wang et al. 2004): (a) segmentation of the 2 min time-series in 60 segments, combined with mean removal and windowing (Hanning) for each data segment; (b) computation of the auto-spectra and the cross-spectrum from each segment; (c) final estimation of the auto-spectra and the cross-spectrum of the activity pair by averaging the estimates from the individual segments.

The coherence spectrum was subsequently estimated as the squared modulus of the cross-spectrum divided by the product of the individual auto-spectra. This function represents a measure of the degree of correlation between two signals at each frequency, and is normative (values between 0 and 1.0). For the 60 segments used in the spectral analyses of this study, and for the smooth data tapering that was employed for leakage suppression, the threshold for a significant coherence at the 99% confidence level is approximately 0.08 (Rosenberg et al. 1989). It is represented by a horizontal dotted line in the coherence plots.

The tremor amplitude in all studied contractions was estimated as the square root of the total power (integral) in the frequency band of the corresponding auto-spectral deflection. The relative tremor amplitude was subsequently obtained as a percentage of the force level of the voluntary contraction (%VC).

The tremor regularity was expressed in terms of the effective tremor bandwidth (eBW). This is estimated as the reciprocal of the ratio of the auto-spectral component at the peak tremor frequency to the sum of all components forming the tremor auto-spectral deflection (Christakos et al. 2006). It is inversely related to the concentration of the tremor power around the peak tremor frequency. Thus, for a nearly regular tremor (approaching a sine wave) eBW corresponds to one frequency bin; for a perfectly irregular tremor having uniform power within a band covering n frequency bins, eBW corresponds to n bins.

Analysis of synchrony

The employed method for detection and quantification of rhythmical population synchrony has been presented in Christakos (1994) and (1997) and applied to detailed analyses of MU synchrony in Christakos et al. (2006) and Erimaki & Christakos (2008). This method, being experimentally and computationally efficient, is easy to use in patients with movement disorders. In brief, coherence computations performed on samples of pairs of simultaneously recorded MU/force signals were used for:

1. Detection of synchrony, since the occurrence of a non-zero coherence in a sample indicates the presence of a correlated MU subset to which the given unit belongs.

2. Estimation of the extent of the synchrony within the population (proportion of correlated MUs), as the fraction of non-zero coherences in the sample. For example, if 20 of 50 MUs show coherence to the force, the estimate of the extent is 40%.

3. Obtaining information on the strength of the synchrony and its distribution within the active population – importantly, under conditions of widespread and in-phase synchrony, which was the case in the present study, the MU/MU coherence value approaches the squared value of the MU/force coherence.

Further, (4), MU/force cross-correlation computations for the coherent MUs in the sample were used for estimation of MU phases, in terms of MU delays relative to the muscle force signal (common reference signal). It is noteworthy that the information provided by this analysis on individual MU phases could not be obtained from MU/MU analysis (yielding estimates of MU phase differences).

In the relatively few cases where the MU/force coherence was near this threshold, additional computations of coherence between the rectified EMG and the muscle force signal, i.e. an aggregate-to-aggregate coherence, were performed solely for verification of the presence of synchrony and determination of its frequency.

As previously described (Christakos, 1997; Christakos et al. 2006), this coherence analysis, although experimentally and computationally simple, yields a complex index reflecting all three above-mentioned characteristics of the population synchrony. Moreover, for widespread and in-phase synchrony, this index greatly overestimates the true coherence between units. Therefore, such analysis could only be used with great caution for assessment of the strength of population synchrony.

Statistical analyses

All data were analysed using the SPSSv13.0 statistical package. The normality of the distributions of the variables was examined using the one-sample Kolmogorov–Smirnov test. Estimates of the Pearson correlation coefficient were used to examine possible relationships between such variables as MU firing rate, mean level of contraction and MU/force coherence. The independent-samples t test was used to assess the differences between the values of such variables for the parkinsonian and the control subjects. The linear regression procedure was performed to assess the effect of the MU/force coherence on the tremor amplitude. The difference in these regression coefficients between the two groups was evaluated by the t test (Zar, 1999). All tests were performed at the P < 0.05 level.

Computer simulations

In the study of the incidences of (A) the tremor-related doublets that were interchanged with single spikes (singlets) and (B) the triplets that were interchanged with doublets we employed higher-order interval analyses. Specifically, we noted that in (A) the short ISI within each doublet and the following, longer ISI added up to one tremor period, whereas in (B) the same applied to the two short ISIs within each triplet and the following longer ISI. Therefore, we assumed that the second-order interval histogram in (A) and the third-order histogram in (B) would show peaks around the tremor period; also that the fraction of intervals within these peaks would be an index suitably describing the incidence of doublets and triplets, respectively.

Simulations of rhythmical doublets and triplets

In order to verify this assumption, we simulated (MATLAB) long series of (a) doublets randomly interchanged with singlets and (b) triplets interchanged with doublets, all occurring at rhythmical markers representing successive tremor minima.

The sequences of markers were quasi-periodic. In accord with our observations, they were ‘free-running’, i.e. the intervals between markers were serially uncorrelated (Christakos, 1982b); furthermore, such intervals had the Gaussian distribution with mean value, P, corresponding to a frequency in the range 4.5–8.0 Hz, and s.d.= 0.15P (see e.g. Fig. 7C and F). In (a), the occurrence of a doublet at any given marker was determined at random with a certain probability representing doublet incidence; otherwise a singlet was placed instead. An analogous procedure was used to locate spike triplets interchanged with doublets.

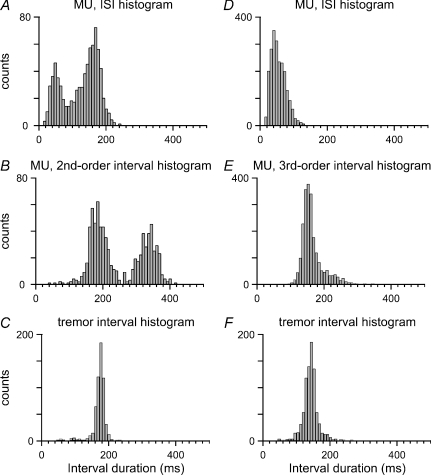
Figure 7. Higher-order interval analyses for MUs belonging to categories II and III.

A, ISI histogram; B, second-order interval histogram; and C, tremor interval histogram, for the case of the MU of Fig. 1. Note in the second-order histogram the high concentration of intervals around the tremor period, which indicates that two successive ISIs often combined so as to form one tremor interval. D, ISI histogram; E, third-order interval histogram; and F, tremor interval histogram, for the case of the MU of Fig. 2. Note in the third-order histogram the high concentration of intervals around the tremor period, which indicates that three successive ISIs often added up to one tremor interval.

We studied the ratio of the number of intervals (integral) within the peak around the tremor period to the total number of intervals in second- and in third-order histograms. In the following this ratio is termed D or T, respectively.

The simulations revealed a linear relationship between D, or T, and the incidence of doublets, or triplets, in the model. In the typical example of Fig. 1 (top), D is plotted against the predetermined doublet incidence. The latter variable (abscissa) is in the range 0–1.0, where 0 represents the absence of doublets and 1.0 the presence of one doublet in every tremor cycle; intermediate values denote the existence of doublets in a fraction of the tremor cycles. As the best-fit line in this figure has a slope of 1, D seems to be an appropriate index of doublet incidence. A best-fit line with slope 1 in Fig. 1 (bottom) also relates T to the predetermined incidence of triplets. T seems therefore to be an appropriate index of triplet incidence.

Figure 1. Indices D and T as estimators of incidence of simulated doublets and triplets.

Top: D plotted against the predetermined probability of doublet occurrence per tremor cycle. Bottom: T plotted against the predetermined probability of triplet occurrence per tremor cycle. Note in both cases the best-fit straight line with slope 1, which indicates that D and T represent appropriate measures of the incidence of doublets and triplets, respectively.

As an example, when doublets occur in 50% of the tremor cycles, and D from Fig. 1 is, correctly, close to 0.50, there exist three types of ISI, each type having a 0.33 probability of occurrence. Clearly, the percentage of short ISIs (0.33), as used by Dengler et al. (1989), is then a false estimate of doublet incidence.

Results

Firing patterns and FT-related synchrony of motor units in PD

Force tremor, manifested as a clear local peak, or deflection, in the force auto-spectrum (e.g. Figs 2 and 3) was present in all 46 constant-force contractions of the 19 patients of this study, with frequencies between 4.5 and 8.0 Hz (mean 6.0, s.d. 1.1; Table 1). For each patient, the FT frequency was generally the same in the different contractions, within the 0.5 Hz spectral resolution. Over the entire set of contractions, the FT frequency was not related to the force level (P= 0.550).

Figure 2. Firing pattern and synchrony for MUs of category II (parkinsonian subject No. 4).

Left column (top to bottom): time record of force signal, intramuscular EMG and discriminated MU spikes; interspike interval (ISI) histogram; and normalized MU/force cross-correlogram. The MU/force time record shows rhythmical spike doublets and singlets near successive FT minima at 5.5 Hz (overall spike rate 9.0 Hz); the ISI histogram exhibits a dual peak representing the ca 50 ms ISIs within doublets and the longer ISIs that separate doublets and/or singlets; the oscillatory MU/force cross-correlogram has its central trough at zero lag, reflecting the tendency for the MU spike events to occur near the FT minima. Right column (top to bottom): auto-spectra and coherence of simultaneous MU spike activity and muscle force signal. The MU auto-spectrum shows a large component at 5.5 Hz (vertical dashed line), and harmonic components, manifesting the FT-related MU spike events. The force auto-spectrum exhibits a dominant component at 5.5 Hz, representing the tremor. The MU/force coherence spectrum shows a large component at 5.5 Hz, and harmonic components, indicative of MU spike event correlations at the FT frequency (the horizontal dashed line represents the threshold level of significance).

Figure 3. Firing pattern and synchrony for MUs of category III (parkinsonian subject No. 1).

All columns as in Fig. 1. Note: in the MU/force time record, the rhythmical spike triplets and doublets, all occurring near successive FT minima at 7.0 Hz (overall spike rate 19.5 Hz); in the ISI histogram, the main peak representing the ca 40 ms ISIs within triplets and doublets, and the small deflections near 60 ms and 90 ms, representing the longer ISIs that follow triplets and doublets; in the oscillatory MU/force cross-correlogram, the central trough at zero lag, which reflects the tendency for the MU spike events to occur near the FT minima; in the force auto-spectrum the dominant component at 7.0 Hz (vertical dashed line), which represents the tremor; in the MU auto-spectrum, the component at the FT frequency and harmonics (arrowheads), and the component at 26.0 Hz (arrow), which reflects the rhythm within the triplets; in the MU/force coherence spectrum, the very large component at 7.0 Hz which indicates the presence of MU correlations at the FT frequency.

In agreement with previous observations, our MU/force records had epochs of category I where the MUs showed rhythmical spikes at their intrinsic discharge rates; these epochs were randomly interchanged with category II epochs, where the same MUs exhibited FT-related doublets and triplets and the FT was overt. In all epochs of each record, FT had the same frequency and was accompanied by corresponding rhythms in the activities of all 50 MUs, irrespective of the MU firing rates. Importantly, the observed MU rates (range 5.0–19.5 Hz; Table 1) were always higher than, or equal to, the frequency of the parkinsonian FT.

The FT-related MU rhythms, whether strong enough to be evident in the MU auto-spectra, or not, exhibited coherence to the FT and hence to the rhythmical components of other active MUs; furthermore they were always locked to the FT minima, as indicated by MU/force cross-correlation analysis (Methods). These rhythmical components represented various MU firing patterns, as outlined below.

Type-1 firing pattern

During the category I epochs, each MU fired rhythmically at its intrinsic rate (type–1 pattern) and showed a dominant auto-spectral component at this frequency, in addition to the component that was locked to the tremor. The same applied during the category II epochs to 9 MUs which fired near (up to 1.25 times) the FT frequency, while for 8 MUs which fired at the FT frequency the two components coincided. In all these cases, the studied MUs only showed coherence to the force at the FT frequency (and its harmonics), indicating that each such MU belonged to a correlated MU subset at the particular frequency. The type–1 pattern is typical of MU discharges during physiological tremor in healthy subjects (see example of Fig. 4).

Figure 4. MU firing pattern and synchrony in normal subjects (control subject No. 2).

All columns as in Fig. 1. Note: in the MU/force time record, the rhythmical spikes at a rate of 9.0 Hz, a fraction of which occur near tremor minima at 6.5 Hz; in the ISI histogram, the main peak around the intrinsic MU period (110 ms), and the additional ISIs between 130 and 160 ms; in the oscillatory MU/force cross-correlogram, the central trough at zero lag, which reflects the tendency for some MU spikes to occur near the FT minima; in the force auto-spectrum, the large component at 6.5 Hz (vertical dashed line), which represents the tremor; in the MU auto-spectrum, the small deflection at the FT frequency, and the large component at 9.0 Hz (arrow), representing the intrinsic rhythm of the MU; in the MU/force coherence spectrum, the clear peak at 6.5 Hz, which indicates the presence of MU correlations at the FT frequency.

Type-2 firing pattern

During the category II epochs, all 27 MUs with intrinsic rates between 1.25 and two times the FT frequency exhibited rhythmical doublets interchanged with singlets (type–2 pattern), that all occurred near successive tremor minima. Thus, the FT-related components of these MUs represented rhythmical sequences of two kinds of spike event. For four of these MUs the contraction level was only 2–5% MVC.

In the typical example of a type–2 pattern in Fig. 2 the MU rate is 9.0 Hz and the FT frequency is 5.5 Hz. As seen in the 2 s time record of this figure, and the ISI histogram (obtained from the entire 2 min record), the short interval between the spikes of each doublet is ca 50 ms. It is followed by a longer ISI, of the order of 130 ms, until the following FT minimum (such minima are 180.0 ms apart). Thus, the ISI histogram shows a peak representing the short ISIs within doublets (mean 50.3, s.d. 13.7), and a broad deflection from ca 110 to 200 ms, which reflects the longer ISIs following the doublets as well as the ISIs separating singlets locked to the FT minima.

The rhythmical MU spike events are manifested in the MU auto-spectrum as a clear peak at the FT frequency, 5.5 Hz (vertical dashed line), accompanied by smaller harmonic peaks; the locking of these events to the FT minima is reflected in a large MU/force coherence value (0.87) at 5.5 Hz and a main trough at zero lag in the oscillatory MU/force cross-correlogram (Methods). The high MU/force coherence indicates that this MU belongs to a subset of correlated MUs at the FT frequency.

As in the case of Fig. 2, the activities of all 27 MUs with type–2 patterns showed a distinct component at the FT frequency, which was locked to the FT minima. Their firing exhibited a variety of ISIs. The average short ISIs for the different MUs were highly concentrated around ca 50 ms (mean 50.3; s.d. 8.6; range 42.0–64.0). No statistically significant relationship existed between the average short ISI and the MU rate (P= 0.499) or the contraction level (P= 0.617); nor, between this ISI and the FT frequency (P= 0.815) or the MU/force coherence (P= 0.812).

Type-3 firing pattern

During the category II epochs, all six MUs with intrinsic rates between two and three times the FT frequency exhibited rhythmical triplets interchanged with doublets (type–3 pattern), that all occurred near successive FT minima. Thus, the FT-related components of these MUs again represented sequences of two kinds of spike event. Interestingly, for one of these MUs the contraction level was only 3% MVC.

In the example of Fig. 3 the MU rate and the FT frequency are 19.5 Hz and 7.0 Hz, respectively. For the MU of this figure, the two ISIs within each triplet are of the order of 40 ms (average/s.d.: 40.8/7.3, 38.5/7.2), and are followed by a longer ISI (ca 60 ms) until the next FT minimum (such minima are 140.0 ms apart). The ISI within doublets is also ca 40 ms (average/s.d.: 39.1/13.2), while the following longer ISI is of the order of 90 ms. These features are reflected in the broad ISI histogram showing a main peak at 40 ms and small deflections near 60 and 90 ms.

The MU auto-spectrum in Fig. 3 shows components at the FT frequency (7.0 Hz, vertical dashed line) and its harmonics (arrowheads), representing the rhythmical MU events (triplets and doublets). It also exhibits (i) a strong component near 26.0 Hz (arrow), representing the rhythm of the spikes (at ca 40.0 ms) within each triplet, (ii) one side-band component (Sanderson, 1980) at 26.0 − 7.0 = 19.0 Hz, mixed with the third harmonic of the 7 Hz rhythm, and (iii) another side-band component at 26.0 + 7.0 = 33.0 Hz, mixed with the fourth harmonic of the 7 Hz rhythm. The MU/force coherence shows a large component (0.80) at 7.0 Hz, indicating that the given MU again belongs to a subset of correlated MUs at the FT frequency; the oscillatory MU/force cross-correlogram has its main trough at zero lag, reflecting the time-locking of the triplets and doublets to the FT minima.

As in the case of Fig. 3, all six MUs with type–3 firing patterns showed a distinct component locked to the FT minima, and a second component representing the rhythm within triplets. The firing of these MUs again exhibited a variety of ISIs. For the different MUs, the average ISIs within triplets were in the range 40.0–62.2 ms, and they again showed a significant concentration around ca 50 ms (mean 49.7, s.d. 8.1). The ones within doublets exhibited a similar range of values and degree of concentration around ca 50 ms (mean 51.3, s.d. 10.7). The small size of the sample did not allow more statistical analyses.

The occurrences of the different MU patterns are summarized in Table 2.

Table 2.

Summary of MU firing patterns during parkinsonian force tremor

	FR ≈ TF	TF < FR ≤ 2TF	2TF < FR ≤ 3TF
Epoch I	Type-1 pattern	Type-1 pattern	Type-1 pattern
Epoch II	Type-1 pattern	Type-2 pattern	Type-3 pattern

Note in category I epochs, the occurrence of the type-1 pattern of MU firing, irrespective of the MU firing rate. Also note in category II epochs the occurrence of type-1, -2 and -3 patterns of MU firing, depending on the relation of the MU rate to the parkinsonian force tremor frequency. FR, MU firing rate; TF, peak tremor frequency.

Firing pattern and FT-related synchrony of MUs in the control subjects

Force tremor existed in all 32 contractions of the 19 control subjects (frequency range 6.0–9.0 Hz; Table 1). The activities of all 39 recorded MUs exhibited rhythmical components phase-locked to the FT, irrespective of the MU firing rates. These rates (range 6.0–17.0 Hz; Table 1) were equal to the FT frequency for six MUs, but they were much higher than this frequency for the majority of the remaining MUs.

Type-2 and -3 firing patterns were not found in the MU records of the control subjects. In the example of Fig. 4, no doublets can be seen in the 2 s record, even though the firing rate of the MU is significantly higher than the FT frequency (9.0 vs. 6.5 Hz). Clearly, the pattern is type–1, but some spikes occur near successive FT minima and this is reflected in the spectra and the cross-correlogram of Fig. 4.

Characteristics of the MU synchrony in relation to the FT amplitude

Since all 50 MUs in the contractions of the 19 patients showed coherence to the FT, it seems highly likely that the correlated subset in each contraction consisted of nearly all active MUs (Methods), i.e. the FT-related MU synchrony in PD is widespread. Further, the locking of the rhythmical MU components to the FT minima reveals that the MU synchrony is in-phase.

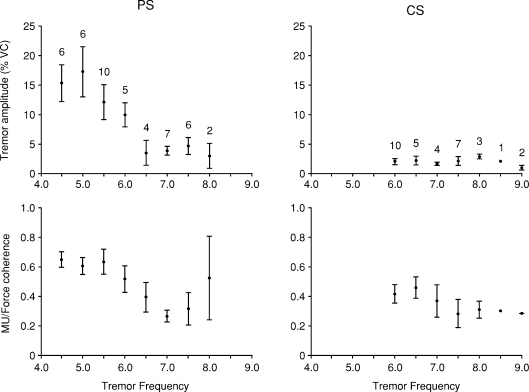
For the sample of 50 MUs, the range of the estimated MU/force coherences at the FT frequency was very broad (0.08–0.91; mean 0.50, s.d. 0.25; Table 1). Analysis performed on this sample did not reveal a significant relationship (P= 0.482) between the MU/force coherence and the mean force level of a muscle contraction, pointing to separate mechanisms underlying the particular MU synchrony and the gradation of muscle force. Further, an inverse relationship existed between the MU/force coherence and the FT frequency in the sample of the patients’ contractions (r=−0.464; P= 0.001). In contrast, no such significant relationship was found in the control subjects (P= 0.761). These behaviours are depicted in Fig. 5 (bottom row).

Figure 5. Dependence of the FT amplitude and the strength of the FT-related MU synchrony on the tremor frequency, for the parkinsonian (PS) and the control subjects (CS).

Top row: distribution for the tremor amplitude. Bottom row: distribution for the strength of the synchrony. Bars represent mean ±s.e.m. The values above bars indicate the number of contractions for each frequency. Note in the PS group the significant decrease of both amplitude and strength for tremor frequencies above 6 Hz. These relationships are not observed in the CS group.

Finally, in the four pairs of simultaneous MUs in the patients contractions, the estimated MU/force coherences were similar for each pair (within 10% of their mean value), suggesting a fairly uniform strength for the FT-related synchrony. To further study this issue, we examined in the entire sample of the 50 MUs the relation between the MU/force coherence and the MU firing rate which characterizes an MU (Methods). The analysis did not reveal a significant relationship (P= 0.746), and this argues further for a fairly uniform strength of the MU synchrony during parkinsonian FT.

Given the widespread and in-phase nature of the FT-related synchrony, its strength in the different contractions of the patients was found in terms of MU/MU coherence by squaring the MU/force coherence estimates in the sample (Methods). Accordingly, the MU/MU coherences were in the range 0.0064–0.83 (mean 0.31, s.d. 0.25). This square rule was verified in the four pairs of simultaneously recorded MUs.

It is worth noting that the FT-related synchrony in the 19 control subjects was also widespread and in-phase. The MU/force coherence again ranged from very low to very high (values between 0.08 and 0.87, mean 0.37, s.d. 0.20; Table 1). The MU/MU coherence was in the range 0.0064–0.76 (mean 0.17, s.d. 0.15).

It should also be noted that the MU/force coherence in the patients was on average larger than that in the control subjects (0.50 vs. 0.37; P= 0.005), even though its ranges were very similar for the two groups. Furthermore, the large harmonic components of this coherence and the large oscillations in the corresponding MU/force cross-correlograms in Figs 2 and 3, as compared to those in Fig. 4, suggest a higher regularity of the tremor rhythm in the patients. This was verified by a comparison of the tremor eBW between patients and controls (Table 1).

Impact of the MU synchrony on the parkinsonian FT amplitude

As expected, the strength of the FT-related synchrony influenced the FT amplitude in both the patients and the control subjects. These dependencies are shown in Fig. 6, on the basis of the entire data sets for the two groups. As seen in this figure, the amplitude of both the parkinsonian (filled squares) and the physiological (open circles) FT increased with increasing MU/force coherence. However, the slope of the best-fit straight line for the parkinsonian group in this figure (continuous line) is much steeper (P < 0.001) than that for the control group (dashed line). Thus, the amplitude of the parkinsonian FT is ca 3.5 times larger than that of the physiological FT. At the same time, in Fig. 6 the rate of increase in both amplitudes is relatively low. For example, a 0.13 coherence rise (similar to the observed average difference between patients and normal subjects) leads to a < 50% tremor amplification. Therefore, such coherence differences could only partially account for the abnormally large parkinsonian FT which thus seems to primarily reflect the MU doublets and triplets.

Figure 6. Dependence of the FT amplitude on the strength of the tremor-related MU synchrony.

Parkinsonian subjects: ▪, continuous line; control subjects: ○, dashed line. Note in the scatter diagrams for both groups the increase in tremor amplitude as the strength of the synchrony increases. Also note the much steeper slope of the best-fit straight line for the parkinsonian group.

This conclusion is corroborated by another observation depicted in Fig. 5: Like the MU/force coherence, the amplitude of the patients’ FT was smaller the higher the FT frequency (r=−0.468; P= 0.001). This was not the case for the control subjects (P= 0.761). As seen in Fig. 5, the inverse relationships between the amplitude, or the coherence, and the frequency of the parkinsonian FT mainly reflected a drastic reduction of both variables above 6.0 Hz: average amplitude 5.7% VC vs. 13.3% VC; average coherence 0.37 vs. 0.60. Importantly, the 0.37 average coherence above 6.0 Hz in the patients equalled the average coherence in the control subjects (FT frequencies between 6.0 and 9.0 Hz). Yet, the corresponding FT amplitude in the patients was 2.7 times larger than that in the control subjects (5.7% MVC vs. 2.1% MVC), and this difference is clearly due to the spike-doublets and triplets during parkinsonian FT.

Doublets and triplets in relation to the MU firing rates and the FT amplitude

To study the occurrence of rhythmical MU spike doublets and triplets we applied higher-order interval analyses (Methods) to the spike events of the epochs of category II. In the example of Fig. 7, the second-order interval histogram (Fig. 7B), from the case of Fig. 2, shows a clear concentration around the 180.0 ms tremor period (Fig. 7C). The same applies to the third-order histogram in Fig. 7E, from the case of Fig. 3, where the tremor period is 140.0 ms (Fig. 7F). The first-order histograms in these two cases (Fig. 7A and D) show a variety of ISIs. However, the peak in Fig. 7B indicates that, often, two successive ISIs, corresponding to the doublets, combined so as to form one tremor interval. The same applies to the peak in Fig. 7E and the three successive ISIs that corresponded to the triplets.

Using indices D and T (Methods), respectively, we estimated the incidences of doublets and triplets in our MU records. Our analyses revealed a simple linear relationship between doublet incidence and firing rate for all 27 MUs exhibiting type–2 patterns. In Fig. 8 (top), as the ratio of the firing rate to the FT frequency increases from about 1.25 to near 2.0, D also increases in a linear fashion and tends to 1.0 (doublets in all tremor cycles). Analogous behaviours were exhibited by the 6 MUs showing type–3 patterns. In Fig. 8 (bottom), as the same ratio increases from 2.0 to near 3.0, T also increases linearly and reaches a value close to 1.0 (triplets in all tremor cycles). Importantly, this strict rule was observed for all the different FT frequencies and for MU synchrony ranging from very weak to very strong.

Figure 8. Occurrence of spike doublets and triplets in relation to the MU firing rate.

Index D (top) and T (bottom) plotted against the ratio of the MU firing rate (FR) to the tremor frequency (TF). Note the linear relationship between D, or T, and the difference of the MU firing rate to the tremor frequency, or to twice its value.

The above behaviours represent a clear difference in the rhythmical MU firing pattern of our control subjects, which did not exhibit doublets or triplets. The second- and third-order interval histograms for these MUs simply showed peaks at multiples of the period of the intrinsic MU rhythms. It therefore seems that, unlike the case of the physiological FT, the oscillatory force contributions of MUs to the parkinsonian FT, to some degree, represent rhythmical sequences of twitch doublets and triplets which contribute to the large amplitude of the latter tremor.

Discussion

The present findings provide a broad and detailed view of the MU firing patterns and rhythmical synchrony during parkinsonian FT. This information is indicative of the way this tremor is generated. It may also have implications regarding the generation of other tremor types in PD.

The main results of our study demonstrate in PD:

1. An FT-related MU synchrony having similar characteristics to those of the synchrony during physiological tremor, but showing a larger strength.

2. Spike doublets and triplets in the synchronous MU components, with incidences directly reflecting the difference of the MU firing rate to the FT frequency (strict rule).

3. The coincidence of the MU recruitment rate and the FT frequency, whereby the MUs showing doublets and triplets are the majority in the active population.

4. Fairly fixed (ca 50 ms) mean ISIs within doublets and triplets.

5. An abnormally large FT amplitude, where the impact of the MU spike doublets and triplets on it is much stronger than the impact of the synchrony.

Rhythmical synchrony of MU activities during parkinsonian FT

As in the case of the physiological FT (Christakos et al. 2006), MU activities during parkinsonian FT, irrespective of mean firing rate, exhibit rhythmical components locked to the FT minima. These MU firing components are thus mutually coherent and in-phase, and the same applies to the corresponding MU force oscillations which through superimposition form the aggregate tremor oscillation.

One difference to the normal case is that the FT-related synchrony shows on average a larger strength than that during the tremor of elderly (present observations) and younger normal individuals (Christakos et al. 2006). The observed ranges of values are, however, very broad for all three groups, and show a virtually complete overlap among these groups (see also Semmler et al. 2003, 2006, for comparisons between elderly and younger normal individuals).

It is worth noting that the present analysis has detected the augmented synchrony during parkinsonian FT because it used a sensitive measure of the strength of the rhythmical MU synchrony, namely the coherence instead of the previously used short-term correlation (see Semmler et al. 2003; see also comment in Discussion of Baker et al. 1992). In fact, the latter analysis, which provides an index of approximate spike coincidences, has not revealed any consistent differences to the normal case (Baker et al. 1992).

Over variable epochs, the coherent firing components of the MUs represent sequences of rhythmical spike events which, apart from single spikes, can also be pairs, or triplets, of spikes separated by ca 50 ms. They thus exhibit another clear difference to the components composing physiological FT in elderly (present observations) and younger (Christakos et al. 2006) individuals, where MUs do not show such spike events.

The observed widespread and in-phase synchrony of the MUs during parkinsonian FT is in accord with the notion of a rhythmical synaptic input provided by the tremor generator to the motoneuron (MN) population. Further, the lack of a significant relationship between the broadly distributed strength of this synchrony and the muscle force level suggests that this rhythmical input is distinct from the common supraspinal drive underlying the generation of voluntary muscle force (De Luca & Erim, 1994).

The augmented strength of the MU synchrony during parkinsonian FT could partly reflect a stronger and more regular rhythmical input, and this is in accord with our observations on the bandwidth of this FT. It could also partly reflect a reduced Ib-mediated autogenic inhibition on the MNs (see Delwaide et al. 1991; Burne & Lippold, 1996; Pötter et al. 2004). Notably, Baker et al. (1992) have hypothesized a disordered bulbospinal system, which would normally inhibit synchronizing presynaptic inputs to MNs, as a possible cause of enhanced MU synchrony.

Finally, in view of the observed very weak synchrony in a number of the studied contractions, it should be stressed that a component of force tremor is expected even when the strength of the rhythmical MU synchrony is minimal (Christakos et al. 2006). This tremor component reflects the (auto-)spectral contents of the rhythmical MU activities, and is additional to the one that reflects the synchrony and the MU cross-spectral contents (Christakos, 1986). In the case of the parkinsonian FT, it is analogous to the physiological tremor caused by uncorrelated large MUs exhibiting a rhythmical grouping of spikes (Taylor, 1962; Allum et al. 1978; Christakos, 1982a,b;). Therefore, small-amplitude tremors in PD are expected even when the MUs are essentially uncorrelated.

The occurrence of rhythmical doublets and triplets follows a strict rule

As our observations indicate, a strict rule governs the occurrence of rhythmical spike doublets and triplets in MU activities, irrespective of the frequency of the parkinsonian FT and the strength of the MU synchrony. Thus, MUs firing at relatively high mean rates, as required for a given force level, exhibit a slower rhythm (of spike events) imposed by the tremor-related synaptic input.

This rule of doublet and triplet occurrences was revealed by our analyses because of the use of appropriate measures of incidence of such spike events. As explained in Methods, the previously used indices (e.g. Dengler et al. 1989; Elek et al. 1991) for single MUs, or small groups of MUs, were non-representative.

Importantly, the rhythmical doublets and triplets were observed in our study for various FT frequencies between 5.0 and 7.5 Hz, i.e. typical frequencies of parkinsonian tremors (Bain, 2002). In contrast, such MU events are very uncommon in healthy individuals (present observations; Dengler et al. 1986; Christakos et al. 2006; Christie & Kamen, 2006; Barry et al. 2007).

The FT frequency represents the recruitment rate of MUs

In our records, no MU was found to fire below the parkinsonian FT frequency. Accordingly, the recruitment rate of MUs (Henneman, 1979) in PD coincides with the FT frequency, as it does in the contractions of elderly (present observations) and younger healthy individuals (Christakos et al. 2006; Erimaki & Christakos, 2008). This property is in agreement with the observation of MU recruitment rates below 6.0 Hz in PD (Dietz et al. 1974; Glendinning & Enoka, 1994), where the tremor frequencies can be as low as 4.0 Hz.

Given the size principle governing MU recruitment and rate coding (Henneman, 1979; Glendinning & Enoka, 1994), the MUs showing doublets/triplets are therefore expected to be medium- and small-sized ones. The above strict regularity seems thus to characterize the firing behaviour of the great majority of the active MUs.

The mean ISIs within doublets/triplets show narrow distributions around 50 ms

According to our observations, the ca 50 ms mean ISIs within spike doublets and triplets do not show a significant relationship to the force level and the MU firing rate, i.e. to parameters characterizing the muscle contraction and the underlying common drive. There is also no significant relationship of these ISIs to the FT frequency and the corresponding MU/force coherence, i.e. to parameters characterizing the synaptic input provided by the tremor generator to the MN population. These behaviours are of particular interest, as they might reflect other features of this input.

Specifically, the doublets and triplets could simply represent modulated MN discharges resulting from the rhythmical synaptic input to the cells, in a manner analogous to the modulations that occur during voluntary slow force variations (De Luca & Erim, 1994; Erimaki & Christakos, 1999). However, the mean ISI would then be shorter the higher the mean (carrier) rate of an MU (Sanderson, 1980). This seems to contradict the lack of a significant relationship between these two variables in our sample of 27 MUs showing doublets; also, the observation that in two of these MUs, which were recorded simultaneously, the mean ISIs were nearly identical, even though the rates of the MUs were 1.3 and 1.6 times the FT frequency.

It therefore seems more likely that the particular patterns of doublets/triplets manifest features of the rhythmical synaptic input to the MNs. One such possibility is a rhythmical input exhibiting multiple local peaks at ca 50 ms, similar to the observed patterns, in each cycle of its oscillatory trajectory. Another possibility is that of a gated 20 Hz rhythm riding on top of this oscillatory trajectory (the observed mean ISIs in our study correspond to frequencies in the range 16–25 Hz). Both possibilities are in agreement with the original view that the doublets do not reflect MN properties but rather represent ‘responses to successive facilitatory stimuli’ (Das Gupta, 1963).

In the above-considered cases, the efficacy of the tremor-related synaptic input in causing spike doublets and triplets could again reflect the size and regularity of this input and/or the reduced autogenic inhibition in PD.

The MU firing pattern is the main factor contributing to the large parkinsonian FT

As our observations reveal, between the two factors that determine the amplitude of the parkinsonian FT, namely the firing pattern and the synchrony of the MUs, the pattern shows a clear deviation from the one during physiological FT. In contrast, the strength of the synchrony has the same range in parkinsonian and in physiological FT, and the observed average difference in strength could not account for the large amplitude difference between the two tremors (Table 1; also see Forssberg et al. 2000). The spike doublets and triplets during parkinsonian FT seem therefore to underlie its abnormally large amplitude.

Specifically, the time to the twitch-peak (contraction time) for medium-sized and small MUs in human hand muscles is several tens of milliseconds (e.g. Milner-Brown et al. 1973). Therefore, for such MUs, even linear superposition of pairs, or triplets, of twitches at ca 50 ms results in force pulses that can be up to two, or three times, as large as the single MU twitch. The MU force oscillations composing parkinsonian FT are thus expected to be much larger than the ones composing physiological tremor (see also Elek et al. 1991).

In previous investigations, the non-linear superposition of paired MU twitches was assumed to be the main determinant of the large parkinsonian FT amplitude (e.g. Dengler et al. 1989; Baker et al. 1992), on the basis of results from animal studies (Burke et al. 1976; Stein & Parmiggiani, 1979; Niemann et al. 1986). According to observations in humans (Elek et al. 1991; Thomas et al. 1999), for twitches separated by 50 ms, the size of the second twitch is increased by only 20–50%, i.e. the non-linear effects seem weaker than the linear ones.

It should be noted that, given the observed regularity characterizing the occurrence of MU doublets and triplets, their total incidences in three to four simultaneously recorded MUs may not be considered representative of the overall occurrences of such spike events in the active MU population. The reason is that, for any given FT, a small group of randomly selected MUs represents one of many possible combinations of MUs firing at rates equal to, or higher than, the tremor frequency and thus exhibiting variable numbers of doublets and triplets. Therefore, the correlation of such total incidences with the FT amplitude (Dengler et al. 1989; Elek et al. 1991) could not lead to any reliable estimates of the impact of the doublets and triplets on this amplitude.

Finally, the observed inverse relationship between the MU/force coherence and the frequency of the parkinsonian FT is clearly one cause for the small FT amplitude at high frequencies. However, the occurrence of rhythmical force pulses in the majority of the active MUs is another major factor underlying this behaviour. Apart from being large, these force pulses have much longer rise times and durations than the single MU twitches. This results in a significant fusion of successive force pulses and a reduced amplitude of the parkinsonian FT when its frequency is high.

Implications for parkinsonian tremor generation

As argued in the Introduction, our observations on the parkinsonian FT and the related MU firing properties may be relevant for postural and rest tremor. There is specific evidence from different studies that supports this view.

In a systematic investigation of postural (acceleration) tremor by Hömberg et al. (1987), changes in the limb's mechanical properties by added mass did not alter the frequency of the tremor and the corresponding EMG component, strongly suggesting that the particular tremor is largely neurogenic. The same is suggested by the finding that the tremor and EMG frequencies coincide (Palmer & Hutton, 1995). Evidence for a partly neural origin of postural tremor in PD is also provided by the observations of Stiles & Pozos (1976).

A link between FT and rest tremor in PD was revealed by the observations of Burne et al. (2004): isometric FT was present while the muscle had no voluntary activity, i.e. under conditions similar to those of rest tremor. As follows from our results, even in the complete absence of voluntary muscle activity, there is a rhythmical input from the tremor generator to the MUs, which is distinct from the common drive underlying muscle contractions. The resulting MU firing rhythms cause weak mechanical muscle activity (force) and a superimposed force tremor component.

The frequencies of parkinsonian FT between 4.5 and 8.0 Hz observed here lie within the ranges reported for postural and rest tremor (Lance et al. 1963; Palmer & Hutton, 1995; Bain, 2002). Furthermore, the MU spike doublets and triplets did occur even for very weak muscle contractions (levels as low as 2% MVC). In fact, our unpublished preliminary observations from three parkinsonian subjects during postural and rest tremor revealed the presence of synchronous MU doublets and triplets. The doublets/triplets seem therefore to be a common behaviour in PD and to primarily underlie the large amplitudes of parkinsonian tremors.

Most studies of the parkinsonian tremor generator have so far focused on oscillations at supraspinal sites, showing frequencies in the tremor range. These brain regions include nuclei of the basal ganglia (e.g. Nini et al. 1995; Hutchison et al. 1997; Levy et al. 2002; Moran et al. 2008), the thalamus (e.g. Lenz et al. 1988; Guehl et al. 2003) and the motor cortex (Timmermann et al. 2003). In such regions, oscillatory cell activities exhibiting coherence to the tremor were found in relatively few cases (Zirh et al. 1998; Hurtado et al. 1999; Timmermann et al. 2003; Amtage et al. 2008). At the same time, according to other studies (Burne, 1987; Rivlin-Etzion et al. 2008), the generator could be located at spinal/peripheral levels.

As described above, the patterns of spike doublets and triplets could represent responses of MNs to a rhythmical synaptic input that exhibits multiple local peaks per cycle or an additional, gated 20 Hz component. These possibilities may facilitate the exploration of the parkinsonian tremor generator, whether this represents an oscillating supraspinal network/loop or spinal–peripheral loop. For example, in the oscillatory action of the spinal stretch reflex loop (Windhorst, 2007), the rhythmical input to the MNs shows multiple local peaks per cycle, representing the acceleration, velocity and displacement components of the spindle Ia discharges (Matthews & Stein, 1969). On the other hand, synchronized 11–30 Hz components are known to exist in activities of supraspinal and spinal centres that have been implicated in tremor generation (Kilner et al. 1999; Levy et al. 2002; Brown, 2003).

Conclusions

The present analyses of MU firing patterns and synchrony during muscle force tremor in PD have revealed important mechanisms underlying the formation and properties of this tremor. The same applies to the neurogenic components of postural and rest tremor. The observed MU firing patterns consisting of spike doublets and triplets are clearly different to the one during physiological tremor, and might even prove characteristic of parkinsonian tremors. Furthermore, the regularities exhibited by these patterns provide a basis for the study of the neural generator(s) of such tremors. More generally, a similar approach could facilitate the investigation of tremors associated with other movement disorders.

Glossary

Abbreviations

eBW

effective bandwidth

FDI

first dorsal interosseus

FT

force tremor

ISI

interspike interval

MN

motoneuron

MU

motor unit

MVC

maximal voluntary contraction

PD

Parkinson's disease

VC

voluntary contraction.

Author contributions

All authors contributed to the conception and design of experiments, generation and analysis of data as well as the drafting and revision of the manuscript. All recordings were performed at the Laboratory of Physiology and Clinical Neurophysiology, University of Athens.