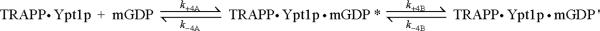Summary
The TRAPP complexes, large multimeric assemblies that function in membrane traffic, are guanine nucleotide exchange factors (GEF) that activate the Rab GTPase Ypt1p. Here we measured the rate and equilibrium constants that define the interaction of Ypt1p with guanine nucleotide (GDP and GTP/GMPPNP) and the core TRAPP subunits required for GEF activity. These parameters allowed us to identify the kinetic and thermodynamic basis by which TRAPP catalyzes nucleotide exchange from Ypt1p. Nucleotide dissociation from Ypt1p is slow (~ 10-4 s-1) and accelerated greater than 1000-fold by TRAPP. Acceleration of nucleotide exchange by TRAPP occurs via a predominantly Mg2+-independent pathway. Thermodynamic linkage analysis indicates that TRAPP weakens the nucleotide affinity by < 80-fold and vice-versa, in contrast to most other characterized GEF systems that weaken nucleotide binding affinities by four to six orders of magnitude. The overall, net changes in nucleotide binding affinities are small because TRAPP accelerates both nucleotide binding and dissociation from Ypt1p. The weak thermodynamic coupling allows TRAPP, Ypt1p and nucleotide to exist as a stable, ternary complex, analogous to strain-sensing cytoskeleton motors. These results illustrate a novel strategy of guanine nucleotide exchange by TRAPP that is particularly suited for a multifunctional GEF involved in membrane traffic.
Keywords: GTPase, GEF, nucleotide exchange, vesicle trafficking, kinetics
Introduction
Small GTPase proteins of the Ras superfamily are chemical switches that regulate diverse cell biological processes ranging from vesicle trafficking and nuclear transport to signaling pathways.1 Ras with bound GTP activates downstream effector proteins and is inactive when GDP is bound. The intrinsic rate of GDP dissociation (t1/2 >100 min) is extremely slow, and in vivo the Ras GTPases are activated by guanine nucleotide exchange factors (GEFs), which accelerate this step. Intracellular nucleotide concentrations, where GTP concentrations are ten times higher, then favor exchange of bound GDP for GTP. A number of GEFs have now been characterized both structurally and biochemically. Though structurally diverse, they use the same general strategy for accelerating nucleotide exchange. GEF activity is driven by allosteric competition between GEF and GDP binding that results in GDP affinity that is weakened 104 to 106 times by GEF binding.2
Members of the Rab subfamily of Ras GTPases play critical roles in regulating vesicle traffic between membrane-bound compartments.3; 4 A vesicle carrying cargo buds from the donor compartment, and travels to a specific target compartment, where it is recognized and then fuses to deliver its cargo. Each trafficking pathway involves numerous protein components, including the Rab proteins as well as large multisubunit tethering complexes. These complexes tether transport vesicles to their target compartment as the vesicle is recognized at the target membrane.5
In the yeast Saccharomyces cerevisiae, the Rab Ypt1p is involved in regulating vesicle transport to the Golgi apparatus. Ypt1p is activated by a large multisubunit complex called TRAPP that also functions in tethering.5 TRAPP is found in two forms6: TRAPPI mediates traffic from the ER to the early Golgi, while TRAPPII plays a role in transport to the late Golgi.7; 8 The two TRAPP complexes share seven subunits (Bet3p, Bet5p, Trs31p, Trs33p, Trs23p, Trs20p, and Trs85p), of which four (Bet3p, Bet5p, Trs23p, Trs31p) are required for the activation of Ypt1p.8; 9 TRAPP is thus an unusual GEF in that its activity does not reside in a single subunit but instead requires a minimal five-subunit subcomplex comprising four different proteins.
We recently described the crystal structure of nucleotide-free Ypt1p bound to a TRAPP subcomplex that is minimally needed to activate Ypt1p.10 A concurrent preliminary kinetic analysis of GTP binding and GDP exchange from wild type and mutant TRAPP suggested that the acceleration of nucleotide exchange from Ypt1p by TRAPP occurs through a strategy distinct from other characterized GEFs. In this study, we perform a complete kinetic and equilibrium analysis of the interaction of Ypt1p with TRAPP and guanine nucleotides. We also determine the Mg2+-dependence of TRAPP GEF activity that suggests an exchange mechanism that occurs independent of Mg2+ displacement. Our results and analysis indicate that TRAPP functions differently from the majority of characterized GEFs in that allosteric weakening of GDP affinity does not completely account for activation. The kinetic and thermodynamic adaptations of TRAPP are suited for a multifunctional GEF involved in vesicle tethering.
Results
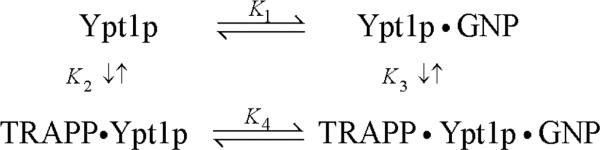
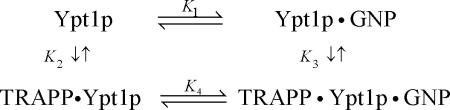
The interaction of Ypt1p with guanine nucleotides (GDP or GTP) and TRAPP, as with other GTPases and exchange factors,2 is defined by the following closed, cyclic reaction scheme of linked equilibria (Scheme 1): where GNP represents either GDP or GTP and Ki represent the overall dissociation equilibrium constants for binding of a given ligand. The results in the following sections are discussed in terms of this Scheme, which has been used in characterizing other exchange factors.2; 11
Scheme 1.
We measured guanine nucleotide (GTP, GDP, GMPPNP) binding to Ypt1p (K1 and K4) using fluorescently modified N-methylanthraniloyl (mant) analogs. Previous measurements demonstrate that the mant fluorophore has negligible effects on the Ypt1p nucleotide binding kinetics and affinity, and that mant-nucleotide analogs can be used to reliably measure guanine nucleotide binding to Ypt1p and related GTPases.11; 12
TRAPP activation of mantGDP dissociation from Ypt1p
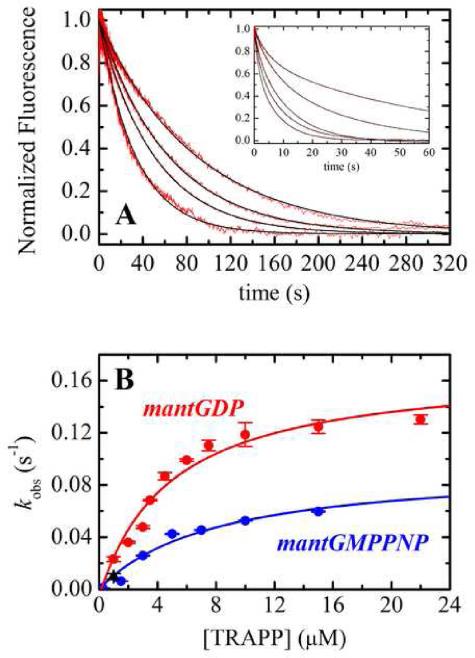
TRAPP activates Ypt1p under in vivo conditions by accelerating exchange of bound GDP for free, cytosolic GTP. We measured TRAPP-catalyzed dissociation of bound mantGDP from Ypt1p by monitoring the reduction in fluorescence intensity after mixing an equilibrated mixture of Ypt1p and mantGDP (i.e. high-fluorescence Ypt1p-mantGDP complex) with excess unlabelled GDP or GTP13 and a range of [TRAPP]. Time courses of irreversible mantGDP dissociation from Ypt1p (in the presence of TRAPP) follow double exponentials with a slow phase that dominates the transient and a fast phase that comprises ~10% of the total amplitude (Figure 1A inset). We interpret the fluorescence changes to reflect nucleotide dissociation. In support of this interpretation, dissociation of radiolabeled GDP from Ypt1p measured by filter binding10 yielded comparable (within a factor of two) observed rate constants as fluorescence (Figure 1B). We do not consider the possibility that a fluorescence change arises from fast TRAPP binding to Ypt1p-mantGDP because there is no fluorescence change upon mixing Ypt1p-mantGDP with TRAPP in the presence of excess mantGDP (data not shown), a condition in which mantGDP dissociation does not result in a change in fluorescence.
Figure 1. TRAPP activation of nucleotide exchange from Ypt1p.
(A) Time courses of mantdGDP dissociation from 0.25 μM Ypt1p in the presence of (right to left) 1 μM, 1.5 μM, 2 μM or 2.5 μM TRAPP. Inset. Time courses of mantGDP dissociation from 0.25 μM Ypt1p in the presence of (right to left) 1 μM, 3 μM, 4.5 μM, 6 μM or 15 μM TRAPP. The smooth black lines through the data (red) represent the best fits to single (panel) or double (inset) exponentials. (B) [TRAPP]-dependence of the observed rate constant for nucleotide dissociation. The smooth line is the best fit of the data to Eq. 1 with k-4 = 0.17 s-1, and K3 = 4.8 μM for mantGDP (red) and k-4 = 0.095 s-1, and K3 = 8 μM for mant-GMPPNP dissociation (blue). Dissociation of [3H]GDP from Ypt1p
MantGDP exists as an equilibrium mixture of 2'- and 3'- labeled isomers, and the observed double exponential time courses could arise from different dissociation kinetics of the two isomers. We therefore measured the exchange of single isomer, 2'-deoxy mantGDP (mantdGDP) from Ypt1p. Time courses of mant-dGDP dissociation from Ypt1p follow single exponentials (Figure 1A) with observed rate constants (kobs) comparable to the slow phase of mant-GDP dissociation (Figure 1A), consistent with the interpretation that the biphasic time courses result from differential binding of the mixed 2' and 3' isomers. We therefore focus our analysis and discussion of mant-GDP to the predominant slow phase that comprises ~90% of the fluorescence transient.
The observed rate constants for irreversible mant-dGDP and mant-GDP dissociation depend hyperbolically on the [TRAPP] (Figure 1B), indicating a two-step scheme for the acceleration of nucleotide exchange from Ypt1p by TRAPP in which TRAPP binding to Ypt1p-GDP (K3) is treated as a rapid equilibrium because it equilibrates more rapidly than GDP dissociates (Scheme 2): According to this scheme, the [TRAPP]-dependence of kobs is given by:
| (Eq. 1) |
The best fit of the data to Eq. 1 yields a rate constant for GDP dissociation from the Ypt1p-TRAPP complex (k-4) of 0.17 s-1 and an affinity for TRAPP binding to Ypt1p-GDP (K3) of 4.8 μM (Table 1). The intercept value defines GDP dissociation from Ypt1p and is indistinguishable from the origin, consistent with a rate constant for GDP dissociation from Ypt1p (k-1) of 0.00012 s-1,10 comparable to the value obtained by others under slightly different buffer conditions (k-1 = 6×10-5 s-1)11. Thus, TRAPP accelerates GDP dissociation from Ypt1p by more than three orders of magnitude from 0.00012 s-1 to 0.17 s-1 (i.e. k-4/k-1 = ~ 1400; Table 3).
Scheme 2.
Table 1.
Rate and equilibrium constants for TRAPP and nucleotide binding to Ypt1p.
| Parameter | Value | Source |
|---|---|---|
| GDP | ||
| k+1 | 0.096 (±0.004) μM-1 s-1 | mant-dGDP binding |
| 0.05 (±0.01) μM-1 s-1 | mantGDP binding10 | |
| k-1 | 0.00012 (±0.00002) s-1 | [H3]GDP Filter binding10 |
| K1 | 1.2 (±0.2) nM | Ratio of rate constants |
| K3 | 4.8 (±1.2) μM | mant-GDP/mant-dGDP (Figure 1) |
| k+4A | 2.4 (±0.1) μM-1 s-1 | Linear fit (Figure 2) |
| 2.5 (±0.1) μM-1 s-1 | Global fit (Figure 2) | |
| k-4A | 22.1 (±2.0) s-1 | Linear fit (Figure 2) |
| 15.7 (±5.3) s-1 | Global fit (Figure 2) | |
| k+4B | 20.7 (±2.2) s-1 | Hyperbolic fit (Figure 2) |
| 11.7 (±12.0) s-1 | Global fit (Figure 2) | |
| k-4B | 0.17 (±0.01) s-1 | mantGDP/mant-dGDP (Figure 1) |
| K4A = (k-4A/k+4A) | 9.2 (±0.9) μM | Ratio of rate constants |
| 6.3 (±2.1) μM | Ratio of rate constants (global fit) | |
| K4B = (k-4B/k+4B) | 0.01 (±0.001) | Ratio of rate constants |
| K4,overall | 75 (±10) nM | Calculated using Eq. 5 |
| K2 | 77 (±25) nM | Detailed balance of Scheme 1 |
| GTP/GMPPNP | ||
| k+1 | 0.10 (±0.01) μM-1 s-1 | mantGTP binding10 |
| k-1 | 0.00005 s-1 | GTP and mant-GMPPNP dissociation11 |
| K1 | 0.5 (±0.1) nM | Ratio of rate constants |
| K3 | 8 (±2) μM | mant-GMPPNP (Figure 1) |
| k-4 | 0.095 (±0.017) s-1 | mant-GMPPNP (Figure 1) |
| k+4 | 3.2 (±0.1) μM-1 s-1 | mantGTP binding10 |
| K4 | 30 (±5) nM | Ratio of rate constants |
| K2 | 133 (±48) nM | Detailed balance of Scheme 1 |
Table 3.
Thermodynamic and kinetic coupling of GTPase exchange factors with GDP.
| Thermodynamic Coupling | Kinetic Coupling | ||||||
|---|---|---|---|---|---|---|---|
| GTPase:GEF | K4 (nM) | K1 (nM) | (K4/K1)a | k-4 (s-1) | k-1 (s-1) | (k-4/k-1)b | Ref. |
| Ran:RCC1 | 3300 | 0.006 | 5.5×105 | 21 | 2.3×10-5 | 9×105 | 13 |
| Ras:Cdc25 | 500 | 0.004 | 1×105 | 1.78 | 6×10-6 | 3×105 | 23; 50 |
| Rab8:Mss4c | 100000 | 0.1 | 1×106 | 0.23 | 7.2×10-4 | 320 | 51 |
| Sec4:Sec2 | 4200 | 0.6 | 7×104 | 15.3 | 6.3×10-4 | 2.4×104 | 42 |
| Ypt51p:Vps9p | 38 | 0.3 | 125 | 0.012 | 2×10-5 | 600 | 11 |
| Ypt1p:TRAPP | 75 | 1.2 | 62.5 | 0.17 | 1.2×10-4 | 1400 | This study |
Defined as ratio of GDP affinity in presence of GEF divided by nucleotide affinity in absence, or equivalently K3/K2 due to detailed balance of equilibrium constants from Scheme 1.
Defined as ratio of rate constant for GDP dissociation in presence versus absence of GEF; also indicative of fold acceleration of nucleotide exchange due to GEF binding.
Rab8:Mss4 is unique in that thermodynamic coupling is much greater than kinetic coupling due entirely to extremely weak nucleotide affinity in the ternary complex (K4).
GDP binding to Ypt1p and Ypt1p-TRAPP
GDP binding was measured by rapidly mixing mant-GDP with nucleotide-free Ypt1p or Ypt1p-TRAPP complex. Time courses of fluorescence change after mixing Ypt1p with mantdGDP follow single exponentials with observed rate constants that depend linearly on [mantdGDP], yielding the second order association rate constant for mant-dGDP binding to Ypt1p (k+1,app) of 0.1 μM-1 s-1 from the slope of the best fit line (Figure 2D, triangles). We did not observe saturation of the observed rate constant as reported for unlabeled GDP11 due to the limited range of [mant-GDP] examined, so k+1,app describes the overall two-step binding reaction including the non-specific collision complex (i.e. k+1,app = K0 k+1 where K0 is the equilibrium constant for Ypt1p-GDP collision complex formation). The intercept is indistinguishable from the origin, consistent with the slow GDP dissociation rate constant of k-1 = 1×10-4 s-1 measured previously by filter binding and mant-GDP dissociation10 (Table 1).
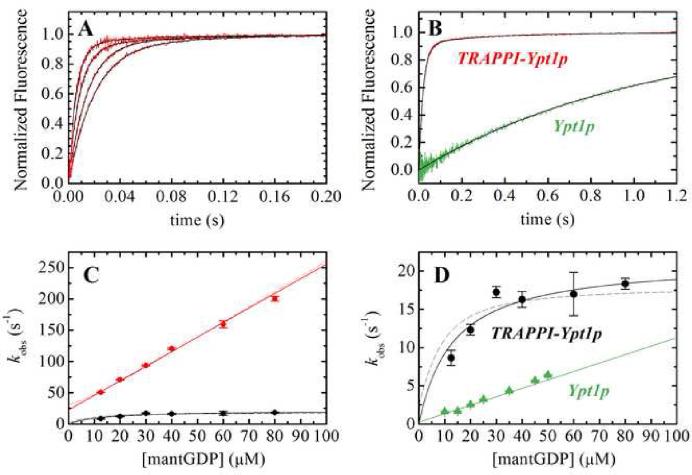
Figure 2. MantGDP binding Ypt1p and TRAPP-Ypt1p.
(A) Time courses of (right to left) 12.5, 20, 40 or 60 μM mantGDP binding Ypt1p-TRAPP complex. (B) mantGDP binding to nucleotide-free Ypt1p (green) or nucleotide-free TRAPP-Ypt1p (red). The smooth black lines through the data in panels A and B represent the best fits to single (Ypt1p) or double (TRAPP-Ypt1p) exponentials. (C) [Mant-GDP]-dependence of the observed rate constant for mantGDP binding to Ypt1p-TRAPP complex. (D) Concentration-dependence of slow phase for mantGDP binding Ypt1p-TRAPP complex. The solid lines through the data in panels C and D represent the best fit to a straight line (Eq. 3) and hyperbola (Eq. 4) for fast and slow phases, respectively. The dashed lines represent the global fit for all data to the quadratic rate equation (Eq. 2). MantGDP binding to Ypt1p alone (green triangles) with the best fit of data to a straight line10 is shown for comparison.
To determine the effect of TRAPP on GDP association, we measured the kinetics of mant-GDP and mant-dGDP binding to the nucleotide-free Ypt1p-TRAPP complex. Time courses of mant-GDP and mant-dGDP binding to the complex follow double exponentials with fast phase observed rate constants (kfast) that depend linearly on the mant-GDP concentration over the range examined (Figure 2C) and slow phase observed rate constants (kslow) that depend hyperbolically on the mant-GDP concentration (Figures 2C and 2D). The biphasic time courses and mant-GDP concentration dependence of the fast and slow phases indicate that mant-GDP binding to Ypt1p-TRAPP complex follows a sequential, two-step reaction mechanism (Scheme 3), with population of two high fluorescence TRAPP-Ypt1p-mant-GDP states (indicated by * and ') that exist in a reversible equilibrium14; 15: It is likely that a diffusion-limited, non-specific collision complex in rapid equilibrium with free complex and nucleotide11; 16; 17 precedes formation of the first high fluorescence state, but is omitted from Scheme 2 for simplicity.
Scheme 3.
Global fitting of the [mant-GDP]-dependence of fast and slow observed rate constants to the general solution of the differential equations defining the two-step binding mechanism depicted in Scheme 3 as given by the following quadratic equation 18:
| (Eq. 2) |
yields a mant-GDP association rate constant (k+4A) of 2.5 μM-1s-1 a dissociation rate constant (k-4A) of 16 s-1, a forward isomerization rate constant (k+4B) of 11 s-1 and a reverse isomerization rate constant (k-4B) approaching zero, consistent with a rate constant for mant-GDP dissociation from the Ypt1p-TRAPP complex of 0.17 s-1 (i.e. considerably smaller than k+4B; Figure 1B; Table 1). The isomerization equilibrium constant (K4B = k-4B /k+4B) obtained from the ratio of isomerization rate constants is 0.01, indicating that TRAPP-Ypt1p with bound mantGDP essentially populates only the second, high fluorescence state (indicated by ') at equilibrium. The lack of a detectable fast phase of dissociation from Ypt1p-TRAPP-mant-dGDP (Figure 1A) is consistent with GDP dissociation exclusively from the TRAPP-Ypt1p-mantGDP' state (i.e. if the TRAPP-Ypt1p-mantGDP* state was populated at equilibrium, a fast GDP dissociation at ~20 s-1 would be observed14; 18). Independent fitting of the fast and slow phases to linear and hyperbolic equations, which apply when k+4A[mant-GDP] >> k+4B 14; 15:
| (Eq. 3) |
| (Eq. 4) |
yielded comparable results (k+4A = 2.4 μM-1 s-1, k-4A = 22 s-1, k+4B = 21 s-1; Table 1).
The overall TRAPP-Ypt1p-mantGDP binding affinity (dissociation equilibrium constant K4,overall), accounting for the equilibrium population of both high fluorescence states, can be calculated from15:
| (Eq. 5) |
where the coefficient K4B/(1 + K4B) accounts for contributions of the isomerization equilibrium to the overall affinity. The overall affinity for mant-GDP binding to TRAPP-Ypt1p (K4,overall) is 75 nM (Table 1), <100-fold weaker than the affinity of mant-GDP for Ypt1p in the absence of TRAPP (K1 = 1 nM; Table 1).
Interaction of Ypt1p-TRAPP with GTP and GMPPNP
Since activation of GTPases by GEFs is a process comprising dissociation of bound GDP as well as binding of GTP, we determined the effects of TRAPP on GTP binding and GMPPNP binding and dissociation from Ypt1p.10 We previously reported values of 0.1 μM-1 s-1 and 3.2 μM-1s-1 for GTP binding to Ypt1p and TRAPP-Ypt1p, respectively10 (Table 1). Due to the intrinsic rate of hydrolysis of GTP by Ypt1p, we measured dissociation of the slowly hydrolyzing GTP analog, mant-GMPPNP, from Ypt1p as reported above for mant-GDP. It has been shown that GMPPNP behaves similarly to GTP in binding to GTPases, including Ypt1p11, although the GMPPNP conformation may differ in some aspects from the GTP conformation (see 19;18).
Mant-GMPPNP dissociates slowly from Ypt1p with a rate constant of 5 × 10-5 s-1.11 TRAPP accelerates mant-GMPPNP exchange from Ypt1p with observed dissociation rate constants that depend hyperbolically on the [TRAPP] (Figure 1B). The best fit of the data to Eq. 1 yields a dissociation rate constant from the ternary complex (k-4) of 0.09 s-1, which represents a ~2,000-fold acceleration over the rate of dissociation in the absence of TRAPP, comparable to the ~1400-fold acceleration of GDP dissociation from Ypt1p by TRAPP (Table 1; Table 3). The affinity of TRAPP binding to Ypt1p-GMPPNP (K3 is 8 μM (Table 1).
Affinity of TRAPP for nucleotide-free Ypt1p
Four equilibrium constants define the interaction of Ypt1p with nucleotide and TRAPP (Scheme 1). Knowledge of the equilibrium constants (Table 1) for nucleotide binding to Ypt1p (K1 in Scheme 1) and Ypt1p-TRAPP (K4), and TRAPP binding to Ypt1p with bound nucleotide (K3) allows us to calculate the affinity of TRAPP for nucleotide-free Ypt1p (K4) from the principle of detailed balance. The product of the equilibrium constants of a closed, cyclic reaction scheme with no external energy input (e.g. Scheme 1) must be equal to unity. Therefore, K2 = K1 K3/K4 when the affinities are expressed as dissociation equilibrium constants. The value of K2 calculated from the experimentally determined equilibrium constants for GDP and GTP/GMPPNP cofactor binding agree within a factor of two (77 nM for GDP parameters and 133 nM for GTP/GMPPNP parameters; Table 1) and indicate that bound nucleotide weakens the affinity of TRAPP for Ypt1p ~ 80-fold. Conversely, TRAPP weakens the affinity of Ypt1p for nucleotide by the same amount. The <2-fold discrepancy in K2 calculated from GDP versus GTP/GMPPNP parameters could be attributed, at least in part, to use of the mant-GMPPNP analog to measure K3 and k-4 for GTP.
Mg2+-dependence of GDP dissociation from Ypt1p
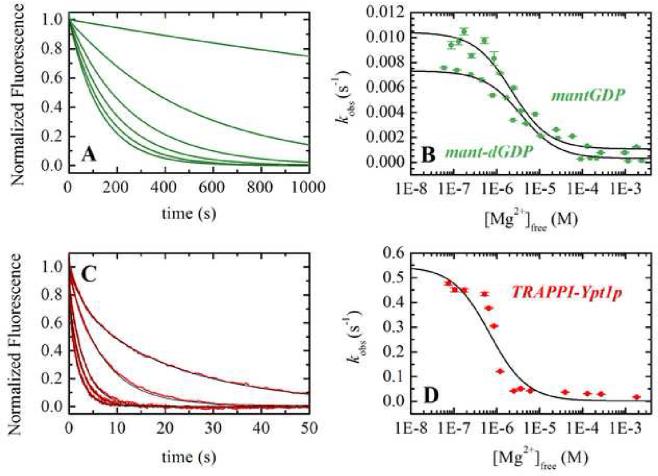
Numerous guanine and adenine nucleotide binding protein exchange factors, including GEF's for GTPases 20, actin filaments for myosin V 15, microtubules for kinesin21 and profilin for actin monomers22, accelerate nucleotide exchange by disrupting coordination of the nucleotideassociated magnesium cation. Two of these exchange factors (profilin-actin and actin-myosin V) do not accelerate nucleotide exchange in the absence of Mg2+. To determine if nucleotide and TRAPP binding are linked through the bound Mg2+ and if TRAPP accelerates nucleotide exchange from Ypt1p by disrupting Mg2+ coordination, we measured the Mg2+-dependence of mant-GDP dissociation from Ypt1p and TRAPP-Ypt1p.
The observed rate constant of mant-dGDP and mant-GDP dissociation from Ypt1p (Figure 3A and 3B) depends on the [Mg2+], dissociating more rapidly at low free [Mg2+]. We assume the observed effect of Mg2+ arises from interaction with the nucleotide, though secondary binding sites on the protein(s) cannot be excluded, and modeled the data according to the following reaction scheme: Mg2+ binding () equilibrates more rapidly than GDP dissociates from Ypt1p and is treated as a rapid equilibrium. The best fits of the [Mg2+]-dependence of the observed mant-dGDP dissociation rate constant to Eq. 6 (see Appendix):
| (Eq. 6) |
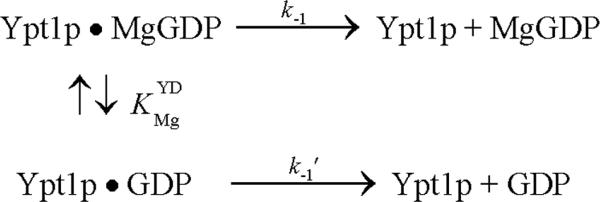
yields a rate constant for divalent cation-free mant-GDP dissociation (k-1') of ~0.01 s-1, ~10-fold more rapid that the Mg-mant-GDP dissociation rate constant (k-1 ~0.001 s-1-1), and an affinity () of ~2 μM for Mg2+ binding to Ypt1p-mant-GDP (Table 2). The value of k-1 determined from the best fit of the data compares within a factor of 3 to the value measured using radiolabeled nucleotide.10 Measurements with mant-dGDP yielded parameters that differed by less than a factor of 2 (Table 2).
Figure 3. Mg2+-dependence of GDP dissociation from Ypt1p and TRAPP-Ypt1p.
(A) Time courses of mant-dGDP dissociation after mixing 250 nM Ypt1p-mdGDP with excess GDP in buffer containing (left to right), 0.06, 0.44, 0.8, 7.9, 26.6, or 90.3 μM free Mg2+ (final). (B)[Mg2+]-dependence of the observed rate constants for mant-dGDP (squares) or mantGDP (circles) dissociation from Ypt1p. The smooth black lines through the data (green) represents the best fit to a hyperbola (Eq. 6) yielding , k-1' = 0.0073 s, k = 0.00032 s-1-1 for mant-dGDP and , k-1' = 0.0104 s-1, k-1 = 0.0011 s-1-1 for mantGDP. (C) Time courses of mantGDP dissociation after mixing 500nM Ypt1p-mGDP with excess GDP2 in buffer containing (left to right) 0.87, 2.5, 4.9, 10.5, or 130 μM free Mg2+ (final) and 2.5 μM TRAPP. The smooth black lines through the data (red) represent the best fits to double exponentials; the small fast phase shows little [Mg2+]-dependence and is observed only with mixed 2' and 3'-mant isomers. (D) [Mg2+]-dependence of mantGDP dissociation from Ypt1p in the presence of 2.5 μM TRAPP. The smooth black lines through the data (red) represents the best fit to a hyperbola (Eq. 7) yielding K0.5 = 1.0 μM, k∞ = 0. 0014 s-1, and k0 = 0.55 s-1 for mant-GDP.
Table 2.
Rate and equilibrium constants for Mg2+-dependent GDP exchange.‡

| Parameter | Value | Source |
|---|---|---|
| K1 | 1.2 (±0.2) nM | Ratio of rate constants (Table 1) |
| K3 | 4.8 (±1.2) μM | mant-GDP/mant-dGDP (Figure 1;Table 1) |
| K4 | 75 (±10) nM | Calculated using Eq. 5 (Table 1) |
| 842 (±32) μM | Isothermal titration calorimetry | |
| 2.2 (±0.5) μM | mantGDP (Figure 3B) | |
| 3.7 (±1.1) μM | mant-dGDP (Figure 3B) | |
| 1.0 (±0.3) μM | mantGDP (Figure 3D) | |
| K1' | 460 (±130) nM | Detailed balance () |
| k-1' | 0.0073 (±0.0004) s-1 | mant-dGDP (Figure 3B) |
| 0.0104 (±0.0004) s-1 | mantGDP (Figure 3B) | |
| k+1' | 0.02 (±0.006) μM-1 s-1 | Calculated from ratio |
| K3' | ~5 μM | Detailed balance () |
| K4' | ~30 μM | Detailed balance () |
| k-4' | 1.6 (±0.3) s-1 | Eq. A11 (Figure 3D) |
| k+4' | 0.05 μM-1 s-1 | Calculated from ratio |
Equilibrium constants K1-K4 are the same as in Scheme 1, while the K1'-K4' represent corresponding equilibriums in the absence of Mg2+. The equilibrium constants representing Mg2+ binding are indicated with subscript Mg and superscript representing binding to GDP (D), Ypt1p-GDP (YD), and TRAPP-Ypt1p-GDP (TYD).
As with Ypt1p alone, mant-GDP dissociation from TRAPP-Ypt1p depends hyperbolically on the [Mg2+] and dissociates more rapidly at low free [Mg2+] (Figure 3C and 3D). The best fit of the data acquired in the presence of 2.5 μM TRAPP to the following equation (Appendix):
| (Eq. 7), |
yields values of 0.55 s-1 for k∞, 0.0014 s-1 for k0 and 1.0 μM for K0.5. These observed fitting parameters can be used to extract the fundamental rate and equilibrium binding constants (see Appendix). The observation that the K0.5 value (i.e. apparent Mg2+ affinity) is similar, within experimental uncertainty, in the presence and absence of TRAPP indicates that the Mg2+ binding affinity of Ypt1p is not affected by TRAPP (Eq. A10 of Appendix; Table 2). The dissociation rate constant of divalent cation-free mant-GDP from TRAPP-Ypt1p (k-4', calculated using Eq. A11) is ~1.6 s-1, ~10-fold more rapid than dissociation of Mg-mant-GDP (k-4 ~0.17 s-1; Table 1). A ten-fold acceleration of GDP release from Ypt1p by EDTA is also observed in the absence of TRAPP (Table 2), consistent with Mg2+ binding to Ypt1p being independent of TRAPP interactions.
Discussion
Mechanism of Nucleotide Exchange Catalysis by TRAPP Differs from Other Characterized GEFs
GEFs activate GTPases by accelerating dissociation of bound nucleotide up to several orders of magnitude. For the large majority of GTPase-GEF systems examined, GEF binding significantly weakens the nucleotide binding affinity of the associated GTPase, and a general exchange strategy has been proposed in which nucleotide exchange is catalyzed through an allosteric mechanism thermodynamically driven by a GEF-linked reduction in nucleotide binding affinity and reciprocal nucleotide-dependent reduction in GEF affinity.2; 23 In most cases, the thermodynamic linkage is similar whether GDP or GTP is bound, and exchange of GDP for GTP is favored by the higher concentration and chemical potential of cytosolic GTP. Nucleotide binding to the GTPase-GEF complex is weak because the GEF alters the configuration of the nucleotide-binding pocket—typically in the conformations of switches I or II, the regions of GTPase nucleotide binding pocket that differ in the active and inactive conformations.24 In many instances, as revealed by structural studies of GEF-GTPase complexes25; 26; 27, this is accomplished by insertion of a structural element from the GEF, a “wedge”, into the nucleotide-binding pocket of the GTPase to either directly inhibit the binding of nucleotide, or to indirectly inhibit binding by blocking the Mg2+ required for coordination of its negatively-charged phosphates.
The crystal structure of nucleotide-free Ypt1p with bound TRAPP10 shows that, like all known GEFs, TRAPP reorganizes the nucleotide binding pocket of Ypt1p. Both switch I and switch II have altered conformations as compared with the nucleotide-bound state (in the absence of TRAPP), and as a result of the switch I rearrangement, the nucleotide binding pocket is opened to solvent. The C-terminus of one of the TRAPP subunits, Bet3p, is inserted into the Ypt1p nucleotide binding site10, where it occupies a position that is partially occupied by switch I in nucleotide bound forms of Ypt1p. The Bet3p C-terminus is unusual as a wedge, however, in that it is not a rigid structural element, and in the absence of Ypt1p it is unstructured (see, for example, PDB entries 2J3W and 2J3T).9 Although the Bet3p C terminus is essential for activity10, it is likely that it assumes the position observed in the structure only after the initial encounter of Ypt1p with TRAPP and does not function as a typical wedge, to sterically displace bound nucleotide. It is also worth noting that with one exception, switch I residue Tyr33 which forms an aromatic-aromatic interaction with the guanosine base of bound nucleotide, few of the GTPase residues that interact with nucleotide directly are perturbed in the Ypt1p-TRAPP complex.10 We had therefore previously hypothesized that TRAPP facilitates nucleotide exchange not by weakening the nucleotide affinity of Ypt1p, but rather by opening the nucleotide binding pocket and making it easier for nucleotides to bind and dissociate.10 The biochemical solution studies completed in this study support this hypothesis and favor a mechanism in which TRAPP GEF activity occurs with weak thermodynamic linkage through a Mg2+-independent pathway.
The TRAPP-Ypt1p thermodynamic linkage is weak because TRAPP accelerates both dissociation and association of nucleotide, allowing a) Ypt1p to equilibrate more rapidly with free GTP in solution (kinetic basis of GEF activity), but also b) yielding small net changes in overall nucleotide binding affinity (thermodynamic basis of GEF activity). Such a considerable acceleration in nucleotide binding to GTPases when bound to GEFs is uncommon and suggests a unique pathway for TRAPP modulating the Ypt1p nucleotide binding site.
Theoretical values for the maximum association rate constant for a diffusion-limited reaction can be approximated from the Smoluchowski equation (Eq. 8) 28:
| (Eq. 8), |
where kcollision is the collision rate constant, DA and DB are the translational diffusion coefficients (in cm2 s-1) for the two species, rA and rB are the interaction radii (in cm), and N0 is Avogadro's number (the factor 10-3 is required for conversion to units of M-1). The diffusion coefficient and radius for GDP can be approximated by those values calculated for Mg2+-ATP29; 30 as rGDP = 4 × 10-8 cm, with corresponding D = 6.13 × 10-6 cm2 s-1 at 25 °C. The translational diffusion coefficient for Ypt1p estimated from the Stokes-Einstein relation using the radius approximated from the crystal structure10 is 1.2 × 10-6 cm2 s-1, and the radius of the nucleotide binding site is estimated to be approximately equal in size to GDP. These values yield a value of ~4.5 × 109 M-11 s-1 for kcollision, which is more than 4 orders of magnitude greater than the rate constant for GDP binding to Ypt1p. This means that ~1 in 50,000 random collisions between nucleotide and the Ypt1p nucleotide-binding site results in productive binding.
Binding constants this far below the diffusion limit often arise from multi-step binding and/or an inaccessible ligand binding site (see 31;32; 16; 17; 33). The latter could result if nucleotide-free Ypt1p were partially denatured and adopted a conformation incapable of readily binding nucleotide. Multi-step nucleotide binding to Ypt1p has been observed; GDP and GTP binding follow a two-step mechanism with formation of a low affinity, nonspecific collision complex (Kcoll = ~300 μM) that isomerizes slowly (kisom ~40s-1, where kisom = k+isom + k-isom and k-isom ≈ k ≈ 10-4 s-1) to a conformation that binds nucleotide strongly,11 yielding an overall association rate constant (k+isom/Kcoll) of ~0.1μM -1s-1 as reported in this study. The value of Kcoll is in the same range as other proteins that bind nucleotide rapidly (see for example 34;16), and is an order of magnitude tighter than proteins that equilibrate between states with accessible and inaccessible nucleotide binding site conformations (see for example 35;16; 17). In contrast, an isomerization rate constant of 40 s-1 is very slow when compared to other nucleotide binding proteins (see for example 34;17). These characteristics suggest that an inactive conformation of nucleotide-free Ypt1p does not account for the slow Ypt1p-nucleotide association kinetics. Rather, they indicate that slow nucleotide binding to Ypt1p arises because of a slow isomerization rate constant.
The rate constant for GDP binding to Ypt1p is >20-fold more rapid in the presence of TRAPP, increasing the number of productive collisions to ~1 in every 1000 and the overall association rate constant to ~2 μM-1s-1, comparable to values observed for other nucleotide binding proteins.14; 17; 18; 30; 36 Acceleration of nucleotide binding would arise if TRAPP made Kcoll tighter and/or accelerated kisom. The observation that the rate of nucleotide binding to TRAPP-Ypt1p is considerably faster than 40s-1 at sub-saturating nucleotide concentrations (Figure 2C) indicates that TRAPP increases kisom by at least an order of magnitude. It is possible that Kcoll could also be tighter when TRAPP is bound, thereby also contributing to faster nucleotide binding. However, Kcoll for nucleotide binding to TRAPP-Ypt1p is >100 μM as indicated by the lack of a hyberbolic dependence of kobs on nucleotide concentrations up to 80μM (Figure 2C). These observations indicate that TRAPP promotes nucleotide binding to Ypt1p by accelerating the weak to strong nucleotide binding isomerization (k+isom) from ~ 40s-1 to > 200s-1. Because TRAPP also accelerates the reverse isomerization rate constant (k-isom), which precedes and limits nucleotide dissociation, it can be viewed as effectively lowering the transition state energy barrier between weak and strong nucleotide-binding states.
The Mg2+-dependence of GDP dissociation (Figure 3) also supports the interpretation that catalysis of nucleotide exchange by TRAPP differs from the mechanism of other characterized GEFs, including Tiam1 (Rho GEF)37, Trio (Rho GEF)38, Sos (Ras GEF)26, Rabex-5 (Rab GEF)39, Sec2 (Rab GEF)40, and Sec7 (Arf GEF)27. Binding of GEFs typically results in structural rearrangements in the nucleotide-binding pocket of the associated GTPase that competes with bound Mg2+, either through the use of a GEF “glutamate finger”27 or residues from the GTPase itself that are shifted into the Mg2+-binding site26; 37; 40, thereby weakening the overall Mg2+ and, consequently, GDP binding affinities.38 The Mg2+ affinity for Ypt1p-mantGDP is unaffected by TRAPP (Table 2), indicating that the TRAPP and nucleotide binding sites do not communicate allosterically by weakening the Mg2+ affinity as observed for other GEFs20; 24 and adenine nucleotide exchange factors15; 21; 22. In fact, TRAPP is better than EDTA at dissociating GDP from Ypt1p, indicating that TRAPP activation is not due to preventing rebinding of Mg2+ at the nucleotide-binding site. Contributions to acceleration of nucleotide dissociation via a Mg2+-independent pathway have been reported for H-Ras nucleotide exchange by Cdc2541 and Rac1 nucleotide exchange by Trio38. We provide here the evidence that a GEF can function without any perturbation of the Mg2+ affinity. Since disruption of Mg2+ coordination is not the source of allostery and acceleration of nucleotide exchange, TRAPP GEF activity must be mediated through an alternative mechanism. Although perturbation of bound Mg2+ coordination may occur, it does not account for the acceleration of GDP dissociation, and additional factors, such as reorganization of switch I must also contribute to acceleration of nucleotide binding and dissociation.
Kinetic versus Thermodynamic Control of Nucleotide Exchange
Catalysis of nucleotide exchange from Ypt1p by TRAPP occurs without a large overall weakening of the nucleotide binding affinity (Table 1 and 3). While most GEFs significantly weaken GDP affinity >10,000-fold from < nM to μM affinities (Table 3, columns 2 & 3), TRAPP weakens the affinity by only ~100-fold. However, GDP dissociation from Ypt1p is accelerated > 1000-fold by TRAPP (Table 1), making TRAPP an efficient nucleotide exchange factor. Therefore, whereas thermodynamics drives nucleotide exchange for most GEFs by weakening the affinity of the GTPase for nucleotides, a strong energetic coupling of linked nucleotide and GEF binding sites does not drive TRAPP GEF activity. Thus, TRAPP GEF activity can be viewed as under kinetic, rather than thermodynamic, control. The nucleotide exchange factor for actin monomers, profilin, also functions using similar principles.36
Degree of Thermodynamic Coupling & Biological Consequences
Nucleotide exchange can be considered from the viewpoint of energetic coupling between nucleotide and exchange factor binding to the GTPase (Scheme 1) such that GEF binding weakens affinity for nucleotide, and consequently, nucleotide weakens the affinity for GEF.2 In other words, GEF and nucleotide binding are linked and acceleration of nucleotide exchange is a consequence of strong coupling between nucleotide and GEF binding. The degree of thermodynamic coupling is given by the ratio of K4/K1, or equivalently K3/K2 (Scheme 1). A high thermodynamic coupling ratio (Table 3) indicates strong coupling and is a measure of how much binding of one ligand weakens the affinity of the other.
The affinity of mantGDP for Ypt1p is reduced ~100 fold with TRAPP binding (thermodynamic coupling ratio ~100). The corresponding coupling ratio for most other characterized GEF's is ~104 to 106 (Table 3). In many of these cases, the weaker nucleotide affinity largely scales with the acceleration in exchange rate (k-4). That is, there is a correlation between the degree of thermodynamic coupling indicated by K4/K1 and the degree of “kinetic coupling” or “kinetic effectiveness”2 (i.e. acceleration of nucleotide dissociation) indicated by k-4/k-1. Thus, for these systems, acceleration of nucleotide exchange is a consequence of strongthermodynamic and kinetic coupling between GEF and nucleotide binding. This is not the case for TRAPP, where the kinetic coupling is considerably stronger than the thermodynamic coupling, thereby allowing TRAPP to function as an effective exchange factor due to kinetic destabilization of bound nucleotide. Such a mechanism for an effective GEF with weak thermodynamic coupling was hypothesized from a theoretical perspective, though no examples had been documented.2
Another notable exception is the Rab Ypt51p and associated GEF, Vps9. In this system, the nucleotide affinity is weakened ~100-1000 fold.11 There is a corresponding acceleration of nucleotide dissociation of ~600 fold which accounts for the weakened affinity. In this case also, binding of Vps9 does not reduce nucleotide affinity as much as with other Ras-like GTPases; that is the thermodynamic coupling is low. This situation differs from the Ypt1p-TRAPP system, however, in that the kinetic and thermodynamic coupling ratios are similar. It is interesting to note that both of these systems with weak thermodynamic coupling are Rabs involved in membrane trafficking pathways, raising the possibility that a relationship between the mechanism of nucleotide exchange and vesicle transport has evolved (discussed below). However, another Rab Sec4p, which functions in exocytosis, and its GEF, Sec2p, have similar thermodynamic and kinetic coupling ratios42, in keeping with parameters observed for other Ras subfamilies of GTPases (Table 3).
Most characterized GTPases have high thermodynamic coupling ratios and, in consequence, exist as one of the two binary complexes (with bound nucleotide or bound to GEF in the nucleotide-free state), with the ternary complex comprising a negligible fraction of the total GTPase pool. The direct consequence of weak coupling between nucleotide- and TRAPP-binding to Ypt1p is that the ternary (TRAPP-Ypt1p-nucleotide) complex is stable and can be populated to a significant extent under physiological conditions. In support of this prediction, TRAPP is capable of binding both GDP- and GTP-bound forms of Ypt1p in yeast cell lysates as determined from pull-down assays.10 As a result of the weak coupling, TRAPP can activate Ypt1p by accelerating GDP dissociation and GTP binding without destabilization of the complex. DSS4, another protein that accelerates nucleotide dissociation from Ypt1p, also forms a stable complex with Ypt1p, but in this case, the nucleotide-free DSS4-Ypt1p is significantly favored.11 In addition, DSS4 is a far less efficient exchange factor than TRAPP, so weak that it is generally not considered to be a bona fide GEF.
Weak coupling between nucleotide binding and exchange factor binding is demonstrated in other systems in which population of the ternary complex is important for biological function. Most notably, the degree of coupling between ADP and actin binding correlates with biological function of myosin motors.43; 44 Myosin motors with weak thermodynamic coupling populate the ternary actomyosin-ADP complex and operate as tension sensors and processive transporters. Myosin motors with strong thermodynamic coupling do not populate the ternary complex and operate as “fast movers” that generate rapid contractions and transport.
In a similar manner, formation of the ternary Ypt1p-TRAPP-nucleotide complex could potentially reflect an adaptation for the biological activity of TRAPP. GEF activity of TRAPPI and activation of Ypt1p is critical for the fusion of ER-derived COPII transport vesicle fusion with the Golgi. Upon activation of Ypt1p, the weak thermodynamic coupling ensures that a significant fraction of the activated Ypt1p-GTP remains bound to the TRAPP complex. The stable ternary complex of TRAPP with GTP-bound Ypt1p would permit effector proteins that are substrates for Ypt1p to be recruited within the vicinity of the site of vesicle fusion, thereby allowing all components required for fusion to be co-localized around the TRAPP tethering complex; if the ternary complex affinity were very weak, Ypt1p could potentially recruit components of membrane fusion at sites where TRAPP is not localized. In this manner, TRAPP GEF activity is kinetically tuned to be an effective GEF activator of Ypt1p and thermodynamically adapted to localize activated Ypt1p at sites of membrane fusion, in accordance with TRAPP functioning as a tethering complex with GEF activity.
Clearly, this behavior relies on the ability to form a ternary TRAPP-Ypt1p-nucleotide complex. Although the measured Kd of TRAPP to GTP-bound Ypt1p is ~ 5μM while estimates of the cellular concentration of TRAPP are ~ 100 nM (based on TRAPP comprising 0.01% of the diameter; S.F-N. unpublished observation), local effective concentrations of TRAPP can be considerably higher due to the association of these proteins to membranes, as suggested for other Rabs with their GEFs.42 It is also possible that subunits of TRAPP-I and -II that are absent in the TRAPP subcomplex used in this study may further increase the affinity for nucleotide-bound Ypt1p, as could crowded cellular conditions.45
Materials and Methods
Reagents
All reagents were the highest purity commercially available. Mixed 2'- and 3'-mant (N-methylanthraniloyl)-nucleotides were purchased from Invitrogen and single 2'-deoxy mant-GDP and 2'-deoxy mant-GTP isomers were purchased from Jena Biosciences. One molar equivalent of MgCl2 was added to nucleotide immediately before use.
Protein Expression and Purification
TRAPP proteins and Ypt1p were expressed and purified as described.10 TRAPP subcomplexes were comprised of Bet3p, Bet5p, Trs23p, Trs31p, and Trs20p (without Trs33p) that contained all essential TRAPP subunits and is indistinguishable from intact TRAPPI in guanine nucleotide-exchange activity.8; 9 Briefly, for overexpression of TRAPP subcomplexes, three Duet plasmids harboring genes for BET3, BET5, TRS23, TRS31, and TRS20 were cotransformed into E. coli BL21(DE3) cells by electroporation, and protein expression was induced with 0.5 mM IPTG. Cells were harvested 18 hr after induction. TRAPP subcomplex was purified by Ni-NTA chromatography (QIAGEN). Gel filtration over a Superdex-200 column (GE Healthcare) removed the Bet3p/Trs31p heterodimer.
An N-terminal His tagged Ypt1p construct truncated at aa180 (His6-Yptp 1-180) was overexpressed in E. coli BL21(DE3) cells at 25°C and purified using Ni-NTA resin (QIAGEN). Nucleotide-free Ypt1p was prepared with EDTA13; 46 or with alkaline phosphatase treatment for 12 h at 16 °C 47 to remove bound GDP. Essentially identical results were obtained with both preparation methods. Nucleotide-free Ypt1p was used immediately after preparation, as it became inactive if stored overnight on ice. Ypt1p with bound mantGDP was prepared by mixing labeled nucleotide and 5 mM Mg2+ (free) with nucleotide-free Ypt1p. Excess mant-nucleotide was removed by gel filtration over a Zeba desalt spin column (Pierce).
Nucleotide binding kinetics
Mant-nucleotide binding to Ypt1p was measured from the fluorescence enhancement associated with Förster resonance energy transfer from Ypt1p tryptophan residues (λex=280 nm) to bound fluorescent mant-nucleotide.10; 11; 48 Kinetic measurements were made using an Applied Photophysics SX.18MV-R stopped-flow apparatus thermostatted at 25 (± 0.1) °C. Fluorescence was monitored at 90° through a 400-nm, long-pass colored glass filter. Final buffer conditions were 50 mM Tris-HCl (pH 8.0), 100 mM NaCl, 5 mM MgCl2, 1 mM DTT. Multiple (2-3) time courses were averaged and fitted to a sum of exponentials by nonlinear least-squares regression. Uncertainties are reported as standard errors in the fits unless otherwise stated. Concentrations stated are final after mixing.
Association kinetics were measured by mixing 250 nM nucleotide-free Ypt1p in the presence or absence of 5 μM TRAPP complex under pseudo-first-order conditions with [nucleotide] >> [Ypt1p] or [Ypt1p-TRAPP]. GDP exchange from Ypt1p is limited by dissociation of bound GDP and was measured by mixing equilibrated samples of Ypt1pmantGDP with excess (300 μM- 2 mM) unlabeled GDP and the indicated [TRAPP].
The Mg2+-dependence of nucleotide exchange was measured by mixing Ypt1p-mantGDP (0.5 μM) with varying concentrations of EDTA and excess (300 μM - 2 mM) unlabelled GDP. The final free-[Mg2+] was calculated by the web-based MaxCHELATOR program.
Kinetic Simulations
Simulated time courses of TRAPP-accelerated nucleotide exchange (Figure 1), mantGDP binding to Ypt1p and TRAPP-Ypt1p (Figure 2), and the Mg2+-dependence of GDP dissociation from Ypt1p and TRAPP-Ypt1p (Figure 3) using the experimental binding parameters (Tables 1 and 2) and the corresponding reaction schemes carried out using KinTek Global Explorer confirm that the rate and equilibrium constants accurately account for the experimental data (data not shown). KinTek Global Explorer is based on the kinetic simulation and fitting programs, KINSIM and FITSIM, developed by Frieden and colleagues.49
Isothermal Titration Calorimetry
An affinity of 842 (± 32) μM for Mg2+ binding to GDP was measured at 25 (±0.1) °C in 50 mM Tris-HCl (pH 8.0), 100 mM NaCl, 1 mM DTT buffer with a MicroCal (Northampton, MA) MCS isothermal titration calorimeter. Data analysis was done with Origin software accompanying the instrument.
Scheme 4.
Acknowledgement
This work is supported by grants from the Hellman Family to E.M.D.L.C. and the Mathers Foundation and the National Institutes of Health (GM080616) to K.M.R. S. F-N. is an Investigator of the Howard Hughes Medical Institute and S. M. is a postdoctoral associate of the Howard Hughes Medical Institute. E.M.D.L.C. is an American Heart Association Established Investigator (0940075N) and a National Science Foundation CAREER Award recipient (MCB-0546353). E.M.D.L.C. acknowledges additional support from the National Institutes of Health under award GM071688. H.F.C. is supported by NIH predoctoral fellowship F31 DC009143-01 and in part by grants from the American Heart Association (0655849T) and Yale Institute for Nanoscience and Quantum Engineering to E.M.D.L.C. We thank the anonymous referees for insightful comments.
Appendix
The [Mg2+]-dependence of irreversible GDP dissociation (exchange) from Ypt1p was analyzed according to the following reaction mechanism, which is adapted from the scheme in Table 2: Since the dissociation of GDP from any of these four starting complexes of Ypt1p.GDP with Mg2+ and/or TRAPP (k-1, k-1', k-4, and k-4') is at least an order of magnitude slower than Mg2+ or TRAPP binding and dissociation, equilibrium among these complexes is maintained throughout the course of the experiment (i.e. , , K3, and K3' can be treated as rapid equilibria). Under our experimental conditions, free [Mg2+] is constant and can be calculated based on total [MgCl2], [GDP] and [EDTA] according to the respective equilibrium constants for Mg2+ binding.
The observed rate constant of GDP dissociation in the presence of TRAPP represents the weighted average of dissociation from all four nucleotide-bound states and is given by the following differential equation:
| (Eq. A1), |
which can be rewritten in terms of any of the four starting complexes of Ypt1p.GDP (plus [TRAPP] and [Mg2+]free) and three of the four equilibrium equations in Scheme A1:
| (Eqs. A2-5), |
where all K's represent overall dissociation equilibrium constants.
Scheme A1.
Rewriting Eq. A1 in terms of [Ypt1p.Mg.GDP], the biochemical state populated at the start of the experiment (i.e. at t = 0) yields:
| (Eq. A6), |
assuming [Mg2+]free and [TRAPP]free are constant with respect to time, which they are under our conditions with [TRAPP]>>[Ypt1p]. The solution to differential Eq. A6 is a single exponential with an observed relaxation rate constant, kobs, given by the term in parentheses on the right hand side of Eq. A6.
In the absence of TRAPP (Figure 3A), GDP dissociation occurs through k-1 and k-1', and kobs of nucleotide exchange depends on [Mg2+] according to:
| (Eq. A7), |
which simplifies to:
| (Eq. A8), |
predicting a hyperbolic dependence of kobs on [Mg2+ (Figures 3B) with intercept value (k0, extrapolation to [Mg2+] = 0) of k-1', saturating value (k∞, achieved at [Mg2+]→ ∞ [Mg2+] at half maximal saturation (K0.5) of .
We measured the [Mg2+]-dependence of nucleotide exchange from Ypt1p at a constant, non-saturating [TRAPP] (Figures 3C and 3D). Under these conditions, the value of kobs depends hyperbolically on [Mg2+] according to:
| (Eq. A9), |
with the following parameters:
| (Eq. A10), |
| (Eq. A11), |
| (Eq. A12). |
The term k0 (Eq. A11) represents the [TRAPP]-dependence of the observed GDP dissociation rate constant in the absence of Mg2+ and presence of TRAPP (Figure 3C and 3D), predicting a hyperbolic dependence on [TRAPP] with intercept value (i.e. [TRAPP] = 0) of k-1', saturating value (i.e. [TRAPP] → ∞) of k-4', and K0.5 value of (due to detailed balance). k∞ represents the dependence of the observed rate constant for GDP dissociation in the presence of saturating Mg2+ and presence of TRAPP (Figure 1), yielding a hyperbolic [TRAPP]-dependence of kobs equivalent to that given in Eq. 1 in the text. Therefore, the intrinsic rate and equilibrium constants, and k-4', can be determined using Eqs. A10-A12 and the experimentally determined values of (Figure 3A and 3B), k-1' (Figure 3A and 3B), and K3 (Figure 1).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Bourne HR, Sanders DA, McCormick F. The GTPase superfamily: a conserved switch for diverse cell functions. Nature. 1990;348:125–32. doi: 10.1038/348125a0. [DOI] [PubMed] [Google Scholar]
- 2.Goody RS, Hofmann-Goody W. Exchange factors, effectors, GAPs and motor proteins: common thermodynamic and kinetic principles for different functions. Eur Biophys J. 2002;31:268–74. doi: 10.1007/s00249-002-0225-3. [DOI] [PubMed] [Google Scholar]
- 3.Grosshans BL, Ortiz D, Novick P. Rabs and their effectors: achieving specificity in membrane traffic. Proc Natl Acad Sci U S A. 2006;103:11821–7. doi: 10.1073/pnas.0601617103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Stenmark H, Olkkonen VM. The Rab GTPase family. Genome Biol. 2001;2 doi: 10.1186/gb-2001-2-5-reviews3007. REVIEWS3007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cai H, Reinisch K, Ferro-Novick S. Coats, tethers, Rabs, and SNAREs work together to mediate the intracellular destination of a transport vesicle. Dev Cell. 2007;12:671–82. doi: 10.1016/j.devcel.2007.04.005. [DOI] [PubMed] [Google Scholar]
- 6.Sacher M, Barrowman J, Wang W, Horecka J, Zhang Y, Pypaert M, Ferro-Novick S. TRAPP I implicated in the specificity of tethering in ER-to-Golgi transport. Mol Cell. 2001;7:433–42. doi: 10.1016/s1097-2765(01)00190-3. [DOI] [PubMed] [Google Scholar]
- 7.Cai H, Zhang Y, Pypaert M, Walker L, Ferro-Novick S. Mutants in trs120 disrupt traffic from the early endosome to the late Golgi. J Cell Biol. 2005;171:823–33. doi: 10.1083/jcb.200505145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cai H, Yu S, Menon S, Cai Y, Lazarova D, Fu C, Reinisch K, Hay JC, Ferro-Novick S. TRAPPI tethers COPII vesicles by binding the coat subunit Sec23. Nature. 2007;445:941–4. doi: 10.1038/nature05527. [DOI] [PubMed] [Google Scholar]
- 9.Kim YG, Raunser S, Munger C, Wagner J, Song YL, Cygler M, Walz T, Oh BH, Sacher M. The architecture of the multisubunit TRAPP I complex suggests a model for vesicle tethering. Cell. 2006;127:817–30. doi: 10.1016/j.cell.2006.09.029. [DOI] [PubMed] [Google Scholar]
- 10.Cai Y, Chin HF, Lazarova D, Menon S, Fu C, Cai H, Sclafani A, Rodgers DW, De La Cruz EM, Ferro-Novick S, Reinisch KM. The structural basis for activation of the Rab Ypt1p by the TRAPP membrane-tethering complexes. Cell. 2008;133:1202–13. doi: 10.1016/j.cell.2008.04.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Esters H, Alexandrov K, Iakovenko A, Ivanova T, Thoma N, Rybin V, Zerial M, Scheidig AJ, Goody RS. Vps9, Rabex-5 and DSS4: proteins with weak but distinct nucleotide-exchange activities for Rab proteins. J Mol Biol. 2001;310:141–56. doi: 10.1006/jmbi.2001.4735. [DOI] [PubMed] [Google Scholar]
- 12.Hutchinson JP, Eccleston JF. Mechanism of nucleotide release from Rho by the GDP dissociation stimulator protein. Biochemistry. 2000;39:11348–59. doi: 10.1021/bi0007573. [DOI] [PubMed] [Google Scholar]
- 13.Klebe C, Prinz H, Wittinghofer A, Goody RS. The kinetic mechanism of Ran--nucleotide exchange catalyzed by RCC1. Biochemistry. 1995;34:12543–52. doi: 10.1021/bi00039a008. [DOI] [PubMed] [Google Scholar]
- 14.Henn A, De La Cruz EM. Vertebrate myosin VIIb is a high duty ratio motor adapted for generating and maintaining tension. J Biol Chem. 2005;280:39665–76. doi: 10.1074/jbc.M507667200. [DOI] [PubMed] [Google Scholar]
- 15.Hannemann DE, Cao W, Olivares AO, Robblee JP, De La Cruz EM. Magnesium, ADP, and actin binding linkage of myosin V: evidence for multiple myosin V-ADP and actomyosin V-ADP states. Biochemistry. 2005;44:8826–40. doi: 10.1021/bi0473509. [DOI] [PubMed] [Google Scholar]
- 16.Robblee JP, Olivares AO, de la Cruz EM. Mechanism of nucleotide binding to actomyosin VI: evidence for allosteric head-head communication. J Biol Chem. 2004;279:38608–17. doi: 10.1074/jbc.M403504200. [DOI] [PubMed] [Google Scholar]
- 17.Robblee JP, Cao W, Henn A, Hannemann DE, De La Cruz EM. Thermodynamics of nucleotide binding to actomyosin V and VI: a positive heat capacity change accompanies strong ADP binding. Biochemistry. 2005;44:10238–49. doi: 10.1021/bi050232g. [DOI] [PubMed] [Google Scholar]
- 18.Henn A, Cao W, Hackney DD, De La Cruz EM. The ATPase cycle mechanism of the DEAD-box rRNA helicase, DbpA. J Mol Biol. 2008;377:193–205. doi: 10.1016/j.jmb.2007.12.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Yengo CM, De la Cruz EM, Safer D, Ostap EM, Sweeney HL. Kinetic characterization of the weak binding states of myosin V. Biochemistry. 2002;41:8508–17. doi: 10.1021/bi015969u. [DOI] [PubMed] [Google Scholar]
- 20.Bos JL, Rehmann H, Wittinghofer A. GEFs and GAPs: critical elements in the control of small G proteins. Cell. 2007;129:865–77. doi: 10.1016/j.cell.2007.05.018. [DOI] [PubMed] [Google Scholar]
- 21.Cheng JQ, Jiang W, Hackney DD. Interaction of mant-adenosine nucleotides and magnesium with kinesin. Biochemistry. 1998;37:5288–95. doi: 10.1021/bi972742j. [DOI] [PubMed] [Google Scholar]
- 22.Kinosian HJ, Selden LA, Gershman LC, Estes JE. Interdependence of profilin, cation, and nucleotide binding to vertebrate non-muscle actin. Biochemistry. 2000;39:13176–88. doi: 10.1021/bi001520+. [DOI] [PubMed] [Google Scholar]
- 23.Guo Z, Ahmadian MR, Goody RS. Guanine nucleotide exchange factors operate by a simple allosteric competitive mechanism. Biochemistry. 2005;44:15423–9. doi: 10.1021/bi0518601. [DOI] [PubMed] [Google Scholar]
- 24.Vetter IR, Wittinghofer A. The guanine nucleotide-binding switch in three dimensions. Science. 2001;294:1299–304. doi: 10.1126/science.1062023. [DOI] [PubMed] [Google Scholar]
- 25.Renault L, Kuhlmann J, Henkel A, Wittinghofer A. Structural basis for guanine nucleotide exchange on Ran by the regulator of chromosome condensation (RCC1) Cell. 2001;105:245–55. doi: 10.1016/s0092-8674(01)00315-4. [DOI] [PubMed] [Google Scholar]
- 26.Boriack-Sjodin PA, Margarit SM, Bar-Sagi D, Kuriyan J. The structural basis of the activation of Ras by Sos. Nature. 1998;394:337–43. doi: 10.1038/28548. [DOI] [PubMed] [Google Scholar]
- 27.Goldberg J. Structural basis for activation of ARF GTPase: mechanisms of guanine nucleotide exchange and GTP-myristoyl switching. Cell. 1998;95:237–48. doi: 10.1016/s0092-8674(00)81754-7. [DOI] [PubMed] [Google Scholar]
- 28.Berg OG, von Hippel PH. Diffusion-controlled macromolecular interactions. Annu Rev Biophys Biophys Chem. 1985;14:131–60. doi: 10.1146/annurev.bb.14.060185.001023. [DOI] [PubMed] [Google Scholar]
- 29.De La Cruz EM, Pollard TD. Nucleotide-free actin: stabilization by sucrose and nucleotide binding kinetics. Biochemistry. 1995;34:5452–61. doi: 10.1021/bi00016a016. [DOI] [PubMed] [Google Scholar]
- 30.Talavera MA, De La Cruz EM. Equilibrium and kinetic analysis of nucleotide binding to the DEAD-box RNA helicase DbpA. Biochemistry. 2005;44:959–70. doi: 10.1021/bi048253i. [DOI] [PubMed] [Google Scholar]
- 31.De La Cruz EM, Pollard TD. Transient kinetic analysis of rhodamine phalloidin binding to actin filaments. Biochemistry. 1994;33:14387–92. doi: 10.1021/bi00252a003. [DOI] [PubMed] [Google Scholar]
- 32.De La Cruz EM, Pollard TD. Kinetics and thermodynamics of phalloidin binding to actin filaments from three divergent species. Biochemistry. 1996;35:14054–61. doi: 10.1021/bi961047t. [DOI] [PubMed] [Google Scholar]
- 33.Cao W, Goodarzi JP, De La Cruz EM. Energetics and kinetics of cooperative cofilin-actin filament interactions. J Mol Biol. 2006;361:257–67. doi: 10.1016/j.jmb.2006.06.019. [DOI] [PubMed] [Google Scholar]
- 34.De La Cruz EM, Wells AL, Rosenfeld SS, Ostap EM, Sweeney HL. The kinetic mechanism of myosin V. Proc Natl Acad Sci U S A. 1999;96:13726–31. doi: 10.1073/pnas.96.24.13726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.De La Cruz EM, Ostap EM, Sweeney HL. Kinetic mechanism and regulation of myosin VI. J Biol Chem. 2001;276:32373–81. doi: 10.1074/jbc.M104136200. [DOI] [PubMed] [Google Scholar]
- 36.Vinson VK, De La Cruz EM, Higgs HN, Pollard TD. Interactions of Acanthamoeba profilin with actin and nucleotides bound to actin. Biochemistry. 1998;37:10871–80. doi: 10.1021/bi980093l. [DOI] [PubMed] [Google Scholar]
- 37.Worthylake DK, Rossman KL, Sondek J. Crystal structure of Rac1 in complex with the guanine nucleotide exchange region of Tiam1. Nature. 2000;408:682–8. doi: 10.1038/35047014. [DOI] [PubMed] [Google Scholar]
- 38.Zhang B, Zhang Y, Wang Z, Zheng Y. The role of Mg2+ cofactor in the guanine nucleotide exchange and GTP hydrolysis reactions of Rho family GTP-binding proteins. J Biol Chem. 2000;275:25299–307. doi: 10.1074/jbc.M001027200. [DOI] [PubMed] [Google Scholar]
- 39.Delprato A, Lambright DG. Structural basis for Rab GTPase activation by VPS9 domain exchange factors. Nat Struct Mol Biol. 2007;14:406–12. doi: 10.1038/nsmb1232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Dong G, Medkova M, Novick P, Reinisch KM. A catalytic coiled coil: structural insights into the activation of the Rab GTPase Sec4p by Sec2p. Mol Cell. 2007;25:455–62. doi: 10.1016/j.molcel.2007.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lenzen C, Cool RH, Prinz H, Kuhlmann J, Wittinghofer A. Kinetic analysis by fluorescence of the interaction between Ras and the catalytic domain of the guanine nucleotide exchange factor Cdc25Mm. Biochemistry. 1998;37:7420–30. doi: 10.1021/bi972621j. [DOI] [PubMed] [Google Scholar]
- 42.Itzen A, Rak A, Goody RS. Sec2 is a highly efficient exchange factor for the Rab protein Sec4. J Mol Biol. 2007;365:1359–67. doi: 10.1016/j.jmb.2006.10.096. [DOI] [PubMed] [Google Scholar]
- 43.De La Cruz EM, Ostap EM. Relating biochemistry and function in the myosin superfamily. Curr Opin Cell Biol. 2004;16:61–7. doi: 10.1016/j.ceb.2003.11.011. [DOI] [PubMed] [Google Scholar]
- 44.Nyitrai M, Geeves MA. Adenosine diphosphate and strain sensitivity in myosin motors. Philos Trans R Soc Lond B Biol Sci. 2004;359:1867–77. doi: 10.1098/rstb.2004.1560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Frederick KB, Sept D, De La Cruz EM. Effects of solution crowding on actin polymerization reveal the energetic basis for nucleotide-dependent filament stability. J Mol Biol. 2008;378:540–50. doi: 10.1016/j.jmb.2008.02.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Wang W, Sacher M, Ferro-Novick S. TRAPP stimulates guanine nucleotide exchange on Ypt1p. J Cell Biol. 2000;151:289–96. doi: 10.1083/jcb.151.2.289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.John J, Sohmen R, Feuerstein J, Linke R, Wittinghofer A, Goody RS. Kinetics of interaction of nucleotides with nucleotide-free H-ras p21. Biochemistry. 1990;29:6058–65. doi: 10.1021/bi00477a025. [DOI] [PubMed] [Google Scholar]
- 48.Alexandrov K, Scheidig AJ, Goody RS. Fluorescence methods for monitoring interactions of Rab proteins with nucleotides, Rab escort protein, and geranylgeranyltransferase. Methods Enzymol. 2001;329:14–31. doi: 10.1016/s0076-6879(01)29062-4. [DOI] [PubMed] [Google Scholar]
- 49.Barshop BA, Wrenn RF, Frieden C. Analysis of numerical methods for computer simulation of kinetic processes: development of KINSIM--a flexible, portable system. Anal Biochem. 1983;130:134–45. doi: 10.1016/0003-2697(83)90660-7. [DOI] [PubMed] [Google Scholar]
- 50.John J, Rensland H, Schlichting I, Vetter I, Borasio GD, Goody RS, Wittinghofer A. Kinetic and structural analysis of the Mg(2+)-binding site of the guanine nucleotide-binding protein p21H-ras. J Biol Chem. 1993;268:923–9. [PubMed] [Google Scholar]
- 51.Itzen A, Pylypenko O, Goody RS, Alexandrov K, Rak A. Nucleotide exchange via local protein unfolding--structure of Rab8 in complex with MSS4. EMBO J. 2006;25:1445–55. doi: 10.1038/sj.emboj.7601044. [DOI] [PMC free article] [PubMed] [Google Scholar]