An integrated system for planning, navigation and robotic assistance for skull base surgery

Abstract

Background

We developed an image-guided robot system to provide mechanical assistance for skull base drilling, which is performed to gain access for some neurosurgical interventions, such as tumour resection. The motivation for introducing this robot was to improve safety by preventing the surgeon from accidentally damaging critical neurovascular structures during the drilling procedure.

Methods

We integrated a Stealthstation^® navigation system, a NeuroMate^® robotic arm with a six-degree-of-freedom force sensor, and the 3D Slicer visualization software to allow the robotic arm to be used in a navigated, cooperatively-controlled fashion by the surgeon. We employed virtual fixtures to constrain the motion of the robot-held cutting tool, so that it remained in the safe zone that was defined on a preoperative CT scan.

Results

We performed experiments on both foam skull and cadaver heads. The results for foam blocks cut using different registrations yielded an average placement error of 0.6 mm and an average dimensional error of 0.6 mm. We drilled the posterior porus acusticus in three cadaver heads and concluded that the robot-assisted procedure is clinically feasible and provides some ergonomic benefits, such as stabilizing the drill. We obtained postoperative CT scans of the cadaver heads to assess the accuracy and found that some bone outside the virtual fixture boundary was cut. The typical overcut was 1–2 mm, with a maximum overcut of about 3 mm.

Conclusions

The image-guided cooperatively-controlled robot system can improve the safety and ergonomics of skull base drilling by stabilizing the drill and enforcing virtual fixtures to protect critical neurovascular structures. The next step is to improve the accuracy so that the overcut can be reduced to a more clinically acceptable value of about 1 mm.

Introduction

Neurosurgery has undergone tremendous technological innovation over the past half-century. The introduction of the operating microscope, stereotactic surgery, modern neuroimaging, neuroendoscopy, technologically demanding implants and image-guided surgery have enabled advancements while also challenging the limits of human dexterity. The continued advancement of image-guided surgery and the limitations of human dexterity motivate the application of robotic assistance to neurosurgery. Neurosurgery is well suited to the use of image-guided robots, due to the static nature of the human skull and locally fixed segments of the spine, the complex anatomy, and the critical nature of adjacent neural and vascular structures. Complications include vascular injury, direct injury to critical neural structures or indirect injury to critical neural structures, through retraction or inadequately gentle surgical manipulation. Sawaya et al. reported that neurological deficit occurs in approximately 20% of craniotomies for intraparenchymal brain tumours (23). Many of these tumours seated in the deep anterior, middle and posterior cranial fossae require complex bone removal for complete tumour resection. Such resection may be complicated by vascular or neural injury. For example, when drilling the posterior wall of the internal auditory canal in acoustic neuroma surgery, critical structures such as the semicircular canals, the cochlea, facial nerve and jugular bulb are within millimeters. Even when using an established surgical approach, the surgeon may damage the inner ear, vestibular apparatus, adjacent nerves or jugular bulb (24).

Currently available image-guidance systems use the patient’s MR or CT images for precise intraoperative navigation. Image guidance, although of dramatic benefit to the surgeon, does not overcome the limits of fatigue and dexterity, and cannot prevent surgical error. We developed a system combining intraoperative navigation with robotics to assist with skull base surgery, based on previous work (1). Using a preoperative image, the surgeon delineates the portion of the skull base that can be safely drilled, thereby defining a virtual fixture that is enforced by the robot. The robot and surgeon share control of the cutting tool in a cooperative control mode. A shared-control robotic system that is validated to the satisfaction of surgeons may dramatically improve patient safety and reduce procedure times by allowing the surgeon to perform the drilling with confidence that critical structures are protected.

We believe that the novelty of this work is the use of a cooperatively controlled robot for skull base drilling. Nevertheless, prior work exists in the use of cooperatively controlled robots for cutting bone (2,3), in the use of robots for drilling the skull (4–8), and in the area of navigated control (9–11). For a more extensive review of recent developments in surgical robotics, see (12).

The Acrobot robot is the best-known example of a cooperatively controlled robot for bone cutting. It uses Active Constraint Control™ (a form of cooperative control) to keep the cutting tool within the region of bone that must be removed to accommodate a knee prosthesis. The knee prosthesis is represented by a 2.5D volume, i.e. a two-dimensional (2D) outline extruded in the third dimension.

Prior work at Johns Hopkins University (JHU) (3) employed a constrained optimization framework to enable a robot system to move its milling tool along a complex path inside the sinus of a skull phantom, while avoiding contact of the tool shaft with the surrounding anatomy. Path-following experiments (i.e. without actual milling) were performed using cooperative control or teleoperated control, with reported accuracies of 0.99 and 0.72 mm, respectively.

In (5), a modified six-degree-of-freedom (DoF) industrial robot was integrated with a navigation system to perform transsphenoidal skull base surgery. The navigation system uses a dynamic reference frame connected to a mouthpiece. The authors reported fully automated, as well as telemanipulatory (using a spaceball), sphenoidotomy operations on cadaveric heads. They measured a mean robot stereotactic accuracy of 1.53 mm. This does not include errors due to the drilling procedure, which were up to 1 mm.

Several generations of a hexapod robot for skull base surgery, called ‘NeuRobot’ (4), ‘NeuroBot’ (7) and NIRS (Neuroscience Institute Robotic System) (8), have been developed at the Nanyang Technological University in Singapore. These systems can position a tool guide or can autonomously remove bone by following the specified path. The surgeon identifies the ‘no go’ regions on the 2D image slices that are processed to create a Voronoi map that identifies the largest ‘go’ path.

In (6), an industrial robot fitted with a force sensor was applied to bone milling in otoneurosurgery. The goal of the robot system was to automatically prepare the implant bed for a cochlear implant. Milling results are reported for oak wood and for human cadaver temporal bones.

Several researchers have developed systems for navigated control, where a tracked hand-held cutting tool is controlled (e.g. turned on or off) based on its location with respect to a desired cut region identified in a preoperative image (9–11). While this approach does not provide the benefits of mechanical support (e.g. to stabilize the drill), it can improve the safety and accuracy of skull base drilling procedures.

Materials and methods

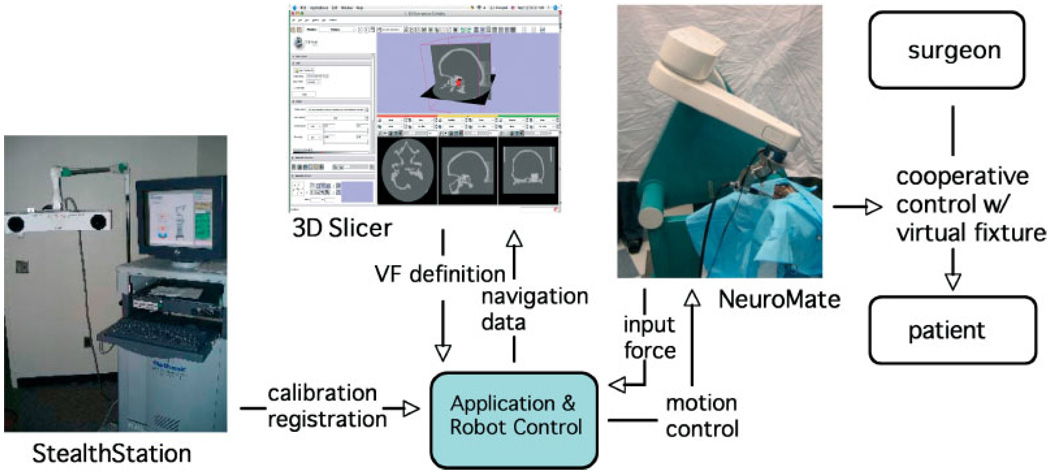
The current system (see Figure 1) consists of the following major components: a modified NeuroMate robot; a StealthStation Navigation System; a workstation running the 3D Slicer software; and a second workstation running the application logic and high-level robot control.

Figure 1.

System overview of the image-guided robot for skull base surgery. System components include: modified NeuroMate^® robot in cooperative control mode; StealthStation^® navigation system; 3D Slicer software for intraoperative visualization; and workstation for application logic and robot control

NeuroMate robot

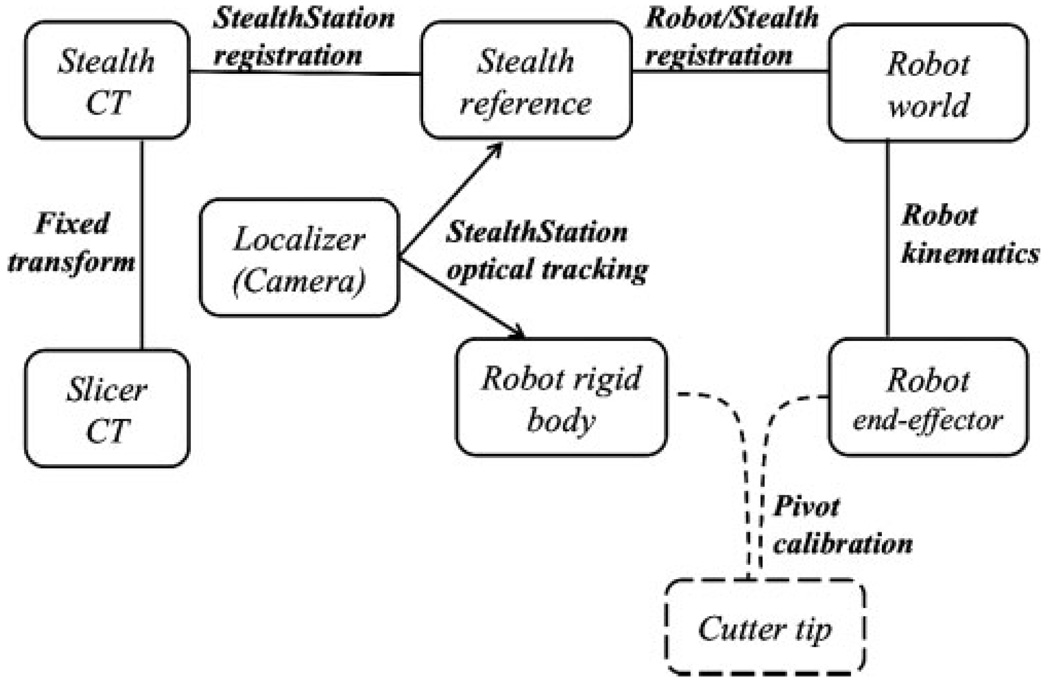
The NeuroMate robot (Integrated Surgical Systems, Sacramento, CA) is an FDA-cleared image-guided robotic system designed for stereotactic procedures in neurosurgery. The rationale for using this robot includes its mechanical stiffness, good accuracy (13) and convenient workspace for cranial procedures. While the robot was originally designed for positioning and orientating surgical tools, we converted the NeuroMate into a cooperatively-controlled robot by attaching a six-DoF force sensor (JR3 Inc., Woodland, CA, USA) at the end-effector, between the final axis and the surgical instrument (Anspach eMax drill, Palm Beach Gardens, FL, USA). Forces and torques exerted by the surgeon are translated into joint motions to move the instrument in the direction of the applied force. The system can allow unimpeded motion of the instrument or can impose ‘virtual fixtures’ (14) to guide the surgeon’s hand and/or enforce safety constraints, as described in the section on Virtual fixture implementation. The robot kinematic equations, including tool calibration, provide the location of the cutter tip relative to the Robot world frame (see Figure 5).

Figure 5.

Transformation map for the coordinate frames

StealthStation navigation system

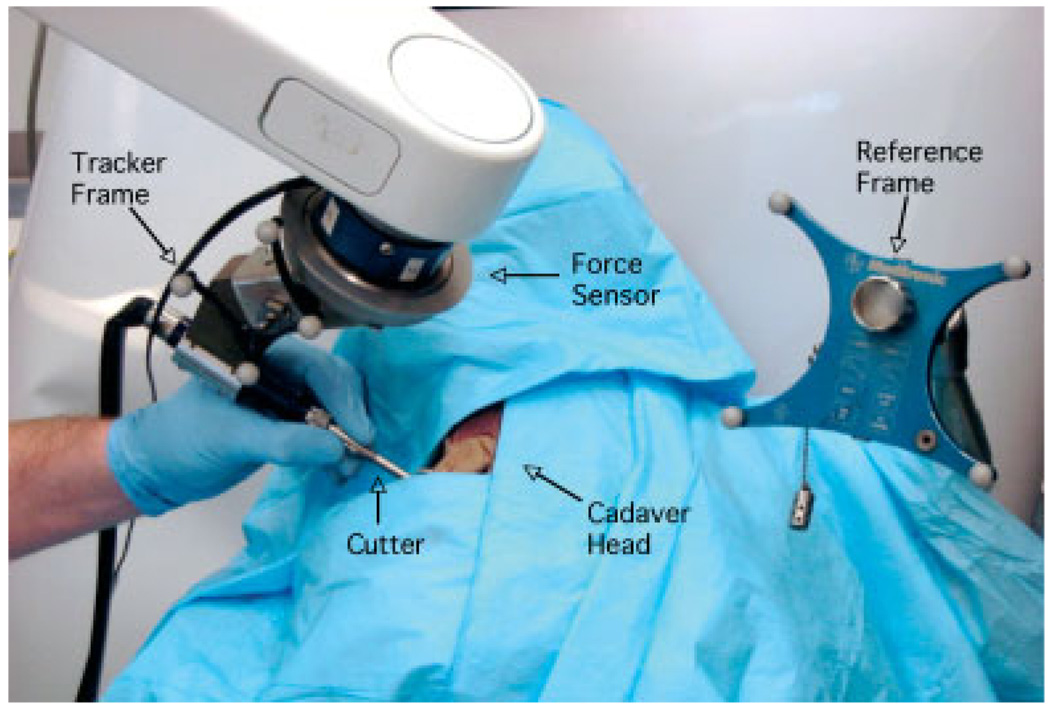
The StealthStation is a commercial navigation system marketed byMedtronic Navigation (Louisville, Colorado). The StealthLink interface enables researchers to obtain data from the StealthStation via Ethernet. The Stealth-Station tracks the position and orientation of sets of optical markers arranged in a precisely-known geometry, i.e. a rigid body. We adopt the conventional approach of expressing positions and orientations relative to a dynamic reference frame (rigid body) attached near the operative site, which defines the Stealth reference frame. This technique is robust with respect to camera motion, because the relationship between the tracked instrument and the fixed reference frame would not change (within the accuracy threshold). We use the StealthStation, with a standard pointer probe, to register the anatomy to the preoperative CT image (i.e. the transformation between the Stealth reference frame and the Stealth CT frame; see Figure 5). We used the StealthStation’s paired-point registration method, with a combination of fiducials and anatomical points, for our experiments. We also mounted a rigid body on the robot cutting tool (see Figure 1, Figure 2), which enables us to co-register the robot and Stealth-Station and provides intraoperative visualization of the cutting tool.

Figure 2.

Set-up for cadaver experiment. The surgeon operates the robot-mounted surgical drill in cooperative control mode

3D Slicer

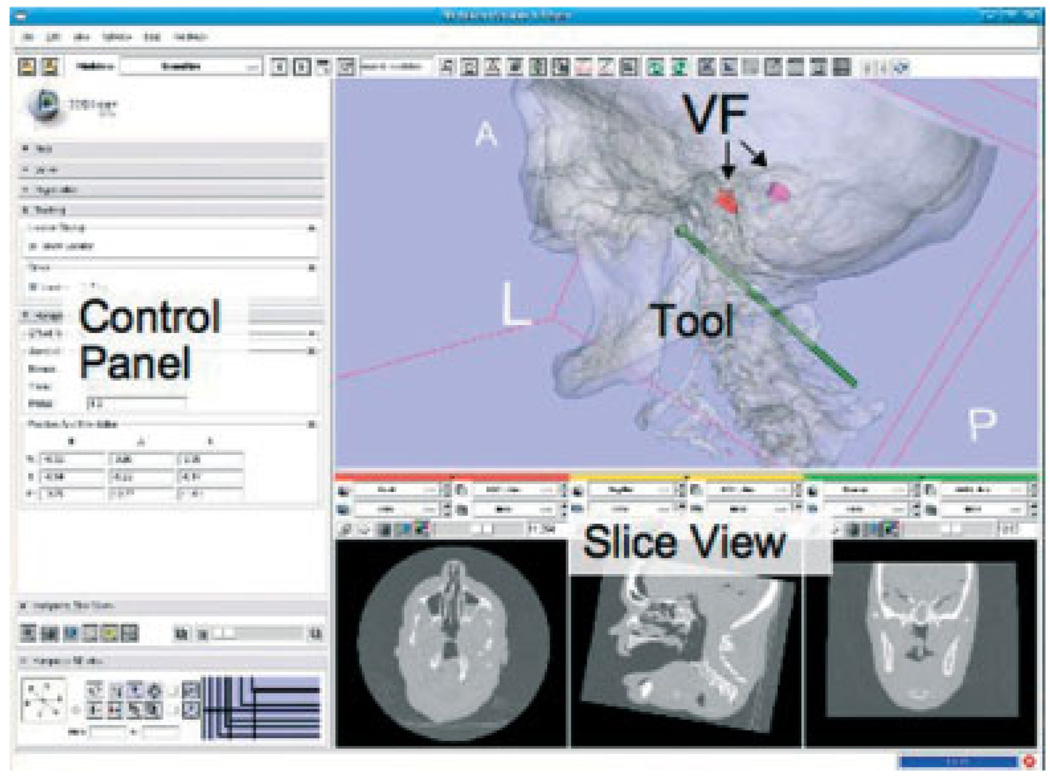
3D Slicer (www.slicer.org) is an open-source, cross-platform application for visualizing and analysing-medical image data (Figure 3). We use Slicer as the planning system because it enables us to create complex virtual fixtures and export them in an open file format (e.g. VTK polydata). We also use Slicer for intraoperative visualization of the cutting tool with respect to the preoperative CT image because, in contrast to the StealthStation visualization, it displays the 3D model of the virtual fixture and includes a more realistic model of the cutting tool. The robot software provides periodic updates of tool position and orientation to Slicer via a network interface (see Figure 4).

Figure 3.

Slicer display for intraoperative visualization, showing the location of the cutter relative to the bilateral virtual fixtures

Figure 4.

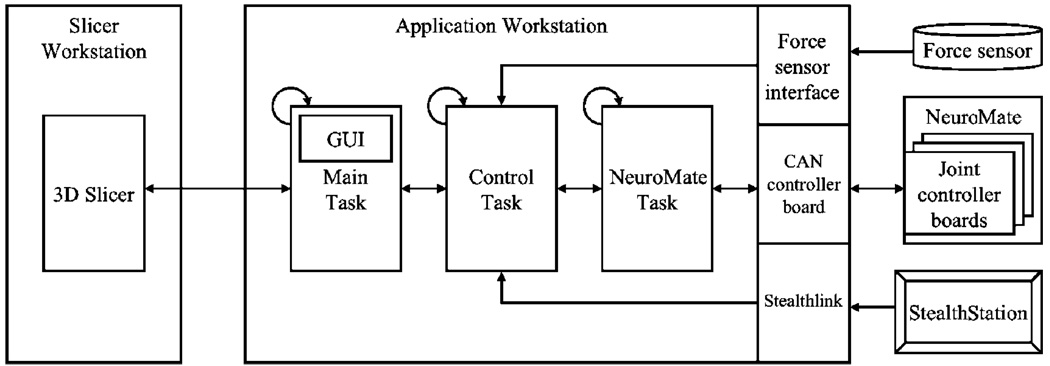
System block diagram showing workstation tasks and interfaces to external systems

Application controller

The application control software, which includes the high-level robot control, runs on a workstation that contains the Real-Time Application Interface (RTAI, www.rtai.org) for Linux. The software uses the cisst package (www.cisst.org/cisst), an open source medical robot controller framework developed at our research centre (15). The application is partitioned into the Main, Control and Robot tasks, as shown in Figure 4. The Robot task communicates with the NeuroMate robot via the Controller Area Network (CAN) bus and performs basic functions, such as receiving joint feedback and sending joint setpoints. The Control task implements the supervisory control layer. Its primary functions are to provide cooperative force control and virtual fixture computation during drilling. It also provides the interfaces to the force sensor and the StealthStation. The Robot and Control tasks both require periodic, real-time execution, which is provided by RTAI. The Main thread handles the graphical user interface (GUI), implemented using the Fast Light Toolkit (FLTK, www.fltk.org), and drives the application procedural flow. It also provides the data to Slicer for intraoperative visualization.

Registration and calibration

In this application, the surgeon uses Slicer to define the ‘safe zone’, also known as the virtual fixture, in the preoperative CT image. This information is loaded into the application control software, which must ultimately use it to affect motion in the Robot world frame. The complete set of transformations is shown in Figure 5. While the StealthStation and Slicer both read the CT data, they use different conventions for the CT coordinate system; therefore, we require a fixed transformation between the Slicer CT frame and the Stealth CT frame. The transformation between the Stealth CT frame and the Stealth reference frame is obtained using registration methods provided by the StealthStation. For the current experiments, we used a point-based registration, where a tracked, hand-held pointer probe is used to touch at least four features (e.g. skin fiducials, craniofacial screws, or anatomical points) attached to the skull prior to the CT scan. The transformation between the Robot world frame and the Stealth reference frame is obtained by moving the robot to six different positions, recording the cutter tip position in each coordinate system, and applying a standard paired-point registration method (16,17).

Because the virtual fixture is intended to constrain motion of the cutter tip, it is necessary to calibrate the tool so that the cutter tip is known with respect to the Robot world frame and in the Stealth reference frame. The robot kinematics already provides the location of the end-effector with respect to the world frame, so it is only necessary to measure the offset (translation) between the origin of the end-effector frame and the cutter tip. Similarly, for the StealthStation, it is only necessary to measure the offset between the cutter tip and the rigid body attached to the robot. Both of these offsets are obtained simultaneously via a standard pivot calibration method.

The virtual fixture computations can be performed in either of the intraoperative reference frames: Stealth reference frame or Robot world frame. The advantage of the former is that the virtual fixture position is updated if the skull is moved (assuming that the reference frame moves with the skull). The advantage of the latter is that it eliminates the requirement for maintaining a clear line-of-sight to the StealthStation camera during cutting. In the experiments reported here, we chose the latter approach because we did not anticipate significant motion of the skull. In more recent work, we perform the computations in the Stealth reference frame, using the tracked position of the robot cutting tool to compensate for patient motion (25).

Virtual fixture implementation

Virtual fixture definition

To generate a virtual fixture, we use Slicer to segment regions of interest from the CT images and create a surface model (e.g. a VTK polydata file). We simplify the model by creating a six-sided convex hull and removing one or two sides to enable cutter entry. Justification for the simplification is based on clinical input that a ‘box-like’ virtual fixture is sufficient for many skull-base procedures, such as the suboccipital approach for acoustic neuroma resection, as simulated in our phantom and cadaver experiments.

Virtual fixture algorithm

Virtual fixtures enforce position limitations on the robot manipulator and restrict its motion into forbidden regions (14). The method we are using is similar to the Acrobot system reported for knee surgery (2). The workspace of the robot is divided into three regions:

1. A safe zone in which the robot is free to move.

2. A boundary zone between the safe region and the forbidden region. Here, motion of the robot may be restricted, as described below.

3. The forbidden region, which the cutting tool should not penetrate.

We use the following admittance control law:

$$\dot{q}=J^{-1}(q)\times K(d)\times G(f)\times \left[\begin{array}{c}{F}_w\hfill \\ T_w\hfill \end{array}\right]$$ (1)

where q̇ is the goal velocity in joint space and K(d) and G(f) are the diagonal matrices of scale factor and admittance gain, respectively. J is the Jacobian matrix resolved at the cutter tip. Its inverse, J⁻¹, transforms the Cartesian velocities into joint velocities. F_w and T_w are the measured forces and torques in the Robot world frame.

The admittance gains are non-linear, exponential functions, which depend on the measured force, f. This was done to enable high-speed motion for coarse positioning, while preserving the capability for fine motion control (18). The parameters for this non-linear function were experimentally determined. In addition, deadband near the origin of the measured force f serves to suppress noisy measurements, while cut-off at high forces keeps the goal velocity below the physical limits of the robotic mechanism.

The virtual fixture algorithm imposes motion constraints by modifying the scale factor K(d). In the safe zone, K(d) is set to the identity matrix, so the robot is able to move freely. The boundary zone is defined by a distance, D, from the forbidden zone. The velocity of motions towards the forbidden zone are scaled down by a factor proportional to the computed distance, d, to the forbidden zone. Motions away from the forbidden zone are not modified. If the robot enters the forbidden zone, only motion towards the safe/boundary zone is permitted.

In our current method for computing K(d), we compute the distance d_i to the virtual fixture planes in each of the Robot world frame coordinate directions (i = X, Y, Z):

$$d_i=\frac{(C-P)·N}{\left|N_i\right|}$$ (2)

where C is the robot Cartesian position vector and and N are P the unit normal and a point on the virtual fixture plane, respectively. Adopting the convention that the unit normal points in the direction of the ‘safe zone,’ the distance d_i is positive if the robot is on the safe side of the plane. If d_i is negative for any plane, the robot is in the forbidden zone, and only motions toward the safe/boundary zone are permitted. If d_i is positive for all planes, the software determines the minimum value, which corresponds to the closest plane in the i direction. If the cutter is moving towards this plane and is within the safety boundary, D, then K(d) = d_i/D. This reduces the robot velocity as it approaches the boundary.

This implementation is effective at preventing the cutter from penetrating the virtual fixture boundary, even when the cutter is at a corner formed by two or more planes. However, it provides a limited ability to move tangential to the virtual fixture boundary. Although this was not a major problem in our experiments, we plan to improve this by using a constrained optimization framework, as described in (3).

Phantom experiments and results

Accuracy of robot and navigation subsystems

Procedure

The first set of experiments used an aluminium plate with 13 small conical divots at different positions and heights. This plate was machined on a Computer Numerical Control (CNC) machine with a known accuracy of 0.0005 inches (0.0127 mm) and was originally used to validate an image-guided robot for small animal research (19,21). The test was performed by placing the robot in cooperative control mode and guiding the cutter tip (5 mm diameter sphere) into each divot. The software then recorded the position of the cutter in the Robot world frame and in the Stealth reference frame.

We characterized the accuracy by computing the fiducial registration error (FRE) (20), as described in (21). Specifically, the FRE was computed by registering all 13 robot (or tracker) positions to the CNC positions, which served as the ‘gold standard.’ For the robot, the FRE was 0.64 mm and for the navigation system, the FRE was 0.74 mm. As noted in the Discussion, we obtained more accurate results after installing a better mounting platform on the robot base.

Accuracy of integrated system

These experiments were performed using a plastic skull with an embedded fixture for inserting foam blocks that represent the target anatomy. The experiments verify the robotic-assisted surgical procedure and measure the accuracy and repeatability of the integrated system.

Procedure

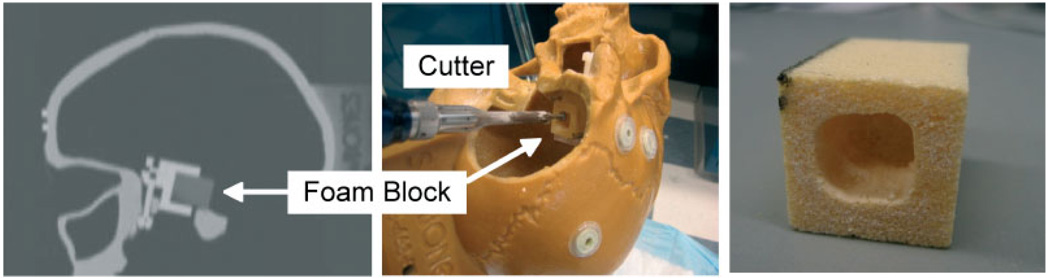
The phantom consists of a plastic skull, with adhesive fiducials, that contains an embedded fixture for holding a precisely machined foam block (Figure 6, middle). The phantom was CT scanned with 2 mm slice spacing (Figure 6, left). For the virtual fixture, we defined a box whose edges are offset from the fixture (block) edges by a specific amount. We performed the registrations described in the section on Registration and calibration, and machined the foam block in cooperative-controlmode with the robot (Figure 6, right). The block was then removed from the fixture and the distances between the machined edges and block edges were measured using calipers. The experiment was repeated for six foam blocks: the first three were cut with the same registrations, whereas each of the last three were cut with the skull in a different location/orientation and with all registrations repeated.

Figure 6.

Phantom experiments. (Left) CT slice view of phantom with foam block; (middle) experimental set-up; (right) machined foam block

Results

For each machined block, two individuals used calipers to make measurements of the distance between the machined edges and block edges at different depths of the cut volume. The averaged measurements are used for analysis. The results are summarized in Table 1. For the X and Y directions, we computed a placement error, E_p, defined by the difference in the centroids of the actual and desired cut volumes. The dimensional error, E_d, is defined by the difference between the actual and desired cut volume dimensions. A positive value of E_d indicates an overcut, i.e. cutting beyond the boundary of the virtual fixture. The total overcut error, due to both placement and dimensional error, is equal to |E_P| + E_d/2. The depth error (Z) cannot be separated into placement and dimensional errors because there is no opposing side on the virtual fixture.

Table 1.

Results of phantom experiments (errors in mm); Dimensional error is positive for overcut (more bone removed)

	Placement		Dimensional		Depth
Foam	X	Y	X	Y	Z
1	0.17	1.12	0.54	0.25	1.16
2	0.04	1.08	0.50	0.20	1.06
3	0.49	0.96	0.25	0.05	1.19
Mean1	0.23	1.05	0.43	0.17	1.14
SD1	0.23	0.09	0.16	0.10	0.07
3	0.49	0.96	0.25	0.05	1.19
4	1.28	1.11	0.70	0.33	0.51
5	−0.44	0.79	0.99	0.35	1.39
6	1.04	−0.62	0.54	0.10	1.85
Mean2	0.59	0.56	0.62	0.21	1.23
SD2	0.76	0.80	0.31	0.15	0.56

The mean and standard deviation (SD) for trials 1, 2 and 3 are ‘Mean 1’ and ‘SD1’. The low values of SD1 (<0.25 mm) demonstrate that the robot system had excellent repeatability when the same registrations were used to machine the first three blocks. For the four foam blocks cut with different registrations, the results are ‘Mean 2’ and ‘SD2’. These latter results are more indicative of the overall system performance, although additional trials are required to achieve statistical significance.

Cadaver experiments and results

For the cadaver experiments, we performed drilling of the bone surrounding the internal auditory canal (IAC), as would be done to resect an acoustic neuroma via a suboccipital approach. We performed this procedure on the left and right sides of three cadaver heads, for a total of six trials. The first trial was unsuccessful due to an implementation error and was excluded from further analysis. We obtained and analysed postoperative CT scans for three of the remaining five trials.

Procedure

For each specimen, we generated the virtual fixtures for the IAC from a CT scan of the cadaver heads at 0.5 mm slice spacing, through manual segmentation (a combination of thresholding and freehand drawing) using 3D Slicer. The virtual fixture encompasses the IAC’s posterior wall, as shown in Figure 7. The virtual fixture was shaped so that we could observe the anatomical structure of the fundus, as typically done in a real surgical procedure. Prior to positioning into the robot field, a retrosigmoid craniectomy using standard surgical techniques gained access to the cerebellopontine angle. The cadaver specimen was secured to a three-point Mayfield skull clamp in the lateral position. The Mayfield clamp was secured to the base of the NeuroMate robot to avoid relative motion.

Figure 7.

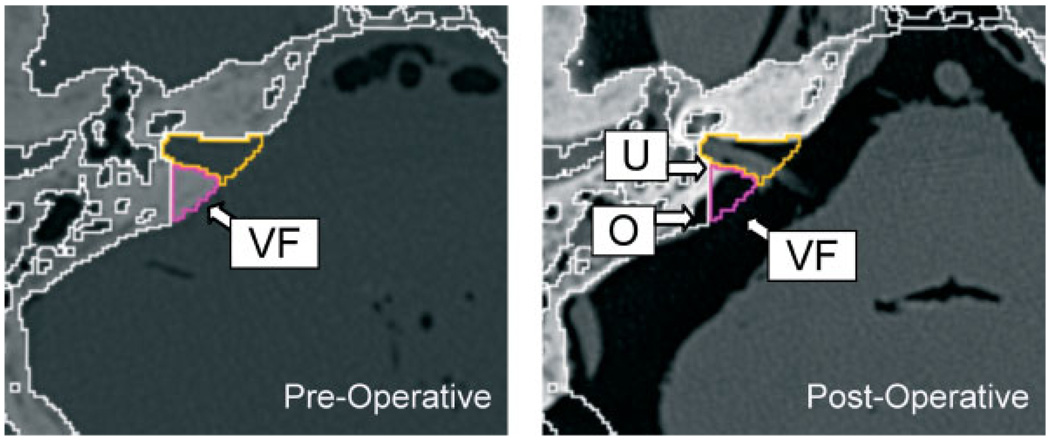
Specimen 1. (Left) Preoperative CT cross-section showing virtual fixture (VF). (Right) Postoperative CT cross-section showing uncut bone (U) and overcut (O)

We used the StealthStation to register the Stealth reference frame to the Stealth CT frame. We only accepted the registration if the residual error displayed by the StealthStation was <1 mm. We then registered the Stealth reference frame to the Robot world frame, as described above, and only accepted this registration if the residual error (FRE) was <0.5 mm(see Table 2).

Table 2.

Registration residual errors in cadaver experiments

Trial No.	Cadaver	Procedure	StealthStation-to-CT residual error (mm)	StealthStation-to-robot residual error (mm)
1	A	Left porus	0.61	0.36
2	B	Right porus	0.86	0.48
3	B	Left porus	0.94	0.33

Results

The NeuroMate proved to have sufficient workspace and dexterity to perform the procedure, which is not surprising given that this robot was designed for neurosurgical procedures. It was, however, necessary to carefully position the robot with respect to the head to avoid the kinematic singularities, where it becomes difficult to control the robot. The neurosurgeon operating the system noted that it improved the efficiency and ergonomics by stabilizing the drill and by maintaining its position when released.

We used 3D Slicer to register the preoperative and postoperative CT scans for two cadaver heads, where the drilling procedure was performed on one side of the first head and on both sides of the second head. We then transformed the preoperatively-defined virtual fixtures (and simplified convex hulls) to the postoperative CT scans. This enabled us to visualize both uncut bone (i.e. bone inside the virtual fixture that was not cut) and overcut bone (i.e. bone outside the virtual fixture that was cut). Figure 7 and Figure 8 show representative 2D cross-sections and 3D views, respectively, for the two cadaver heads. There were areas of uncut bone (U), but we note that the objective of this procedure is to remove enough bone to access the tumour – it is not clinically necessary to remove all bone inside the virtual fixture. A more critical measure is the amount of overcut bone (O), because this can affect the safety of the procedure if the overcut area includes critical neurovascular structures. We measured the overcut in several CT cross-sections for both specimens and found that it was typically 1–2 mm, with occasional excursions up to 3 mm.

Figure 8.

Specimen 2. (Left) Postoperative CT with VFs (original and simplified) in place, showing the overcut (O) and uncut bone (U) of the left side IAC. (Right) The overcut (O) of the right side IAC procedure

Discussion

The cadaver experiments indicate that a cooperatively-controlled robot system could feasibly be used in a clinical setting, although a significant amount of engineering effort would be required to bring this prototype to clinical use. In these experiments, the cutting tool often penetrated the virtual fixture by 1–2 mm, with occasional excursions up to 3 mm. The phantom experiments produced better results, most likely due to the more favourable experimental conditions and the use of foam rather than bone. These experiments showed a mean placement error of 0.6 mm and a mean dimensional error of 0.6 mm, which implies a mean overcut error of about 0.9 mm. There are many possible causes of placement error, including registration error (CT-to-Stealthstation and Stealthstation-to-NeuroMate), calibration error (cutter-to-NeuroMate and cutter-to-Stealthstation), robot kinematic error, and undetected motion of the skull. The most likely causes of dimensional error are compliance in the system and anomalies in the machining process [such as the ‘imperfect drilling characteristics’ noted in (5)], but robot kinematic error or skull motion can also be factors. One approach for reducing the effect of system compliance is to use telemanipulation rather than cooperative control because it eliminates the deflection due to surgeonapplied forces, as demonstrated in (3). On the other hand, telemanipulation requires additional hardware and may not provide the surgeon with the same feeling of direct control.

We believe that the error can be reduced and are actively working on corrective methods (25). We expect to improve the placement accuracy to about 1 mm, which is consistent with experimental results reported for similar skull-base systems (3,5) and in orthopaedics (22). Nevertheless, even with a higher inaccuracy, the system can still provide useful mechanical assistance to the surgeon by stabilizing the drill. Because the surgeon monitors the drilling via the microscope or endoscope, he or she can provide the final safety check. One possible enhancement is to provide a means for the surgeon to adjust the virtual fixture intraoperatively if it appears to be malpositioned. This is the 3D equivalent to setting a mechanical stop that limits drilling depth along a single (1D) axis. It may also be possible to use intraoperative sensing, including video, to verify or update the position of the virtual fixture. The dimensional error can be reduced by improving cutting tool stiffness and utilizing an active compensation method. For example, deflection of the tool tip can be estimated from the measured force. Similarly, anomalies in the cutting procedure can be subtracted. These methods should enable submillimeter dimensional errors similar to those achieved by automated robotic milling systems, e.g. 0.4 mm for ROBODOC^® (22). Recent mechanical improvements to the mounting platform on the robot base (where the head clamp is attached) produced encouraging results. We repeated the robot and navigation system accuracy testing described above, with the aluminium plate attached to the new mounting platform. In this configuration, the mean fiducial registration errors (FREs) for the robot and navigation system were 0.38 mm and 0.45 mm, respectively, which represent about a 40% improvement over their respective prior values of 0.64 mm and 0.74 mm. Although there is little glamour in the development of mounting hardware, our experiences have taught us that proper fixation is crucial. Furthermore, even with rigid fixation, it is still advisable to at least monitor, and preferably track, relative motion between the patient and robot (25).

Conclusion

This study reports the development of a cooperatively-controlled robotic system for skull base surgery with virtual fixture motion constraints. The system has the potential to enable surgeons to more quickly perform skull base drilling with greater safety. The placement and dimensional errors were measured in phantom experiments, where the robot drilled box shapes in foam blocks that were subsequently measured using calipers. The placement error is the difference in the centroids of the desired and measured box shapes; its mean value was 0.6 mm. The mean dimensional error was 0.6 mm, which means that the linear dimensions of the box cut with the robot were 0.6 mm larger than desired. In the cadaver experiments, accuracy was measured by registering a postoperative CT to the preoperative CT and identifying the overcut areas, which are areas where bone outside the virtual fixture was (erroneously) drilled. Qualitatively, the mean overcut appeared to be 1–2 mm, with a maximum value near 3 mm. We are currently investigating methods to reduce this error.

Other areas for improvement include support for more complex virtual fixture models (instead of the six-sided convex hull), a better virtual fixture control algorithm (3), and tools for postoperative assessment that can characterize the placement and dimensional error by comparing 3D models of the virtual fixture (from preoperative CT) and cut cavity (from postoperative CT).