The Tensor Distribution Function

Abstract

Diffusion weighted magnetic resonance imaging is a powerful tool that can be employed to study white matter microstructure by examining the 3D displacement profile of water molecules in brain tissue. By applying diffusion-sensitized gradients along a minimum of six directions, second-order tensors (represented by three-by-three positive definite matrices) can be computed to model dominant diffusion processes. However, conventional DTI is not sufficient to resolve more complicated white matter configurations, e.g., crossing fiber tracts. Recently, a number of high-angular resolution schemes with more than six gradient directions have been employed to address this issue. In this article, we introduce the tensor distribution function (TDF), a probability function defined on the space of symmetric positive definite matrices. Using the calculus of variations, we solve the TDF that optimally describes the observed data. Here, fiber crossing is modeled as an ensemble of Gaussian diffusion processes with weights specified by the TDF. Once this optimal TDF is determined, the orientation distribution function (ODF) can easily be computed by analytic integration of the resulting displacement probability function. Moreover, a tensor orientation distribution function (TOD) may also be derived from the TDF, allowing for the estimation of principal fiber directions and their corresponding eigenvalues.

In the past decade, diffusion magnetic resonance imaging (dMRI) has become a powerful tool for studying the structure of fibrous materials, including white matter connectivity and integrity in the living brain. By applying diffusion-sensitized gradients (1–3), dMRI characterizes the particle diffusivity profile in various tissues (see, e.g., 4–6 for early approaches).

When the duration of the applied diffusion sensitization δ is much smaller than the time between the two pulses, the MR signal attenuation is related to the displacement probability function using a Fourier integral relationship with respect to a wave vector q (7,8).

As water Brownian motion is constrained by the underlying tissue microstructure, measurements of the displacement probability function of water molecules thus provide great insight into this microstructure. In brain imaging, dMRI can be advantageous over conventional nondiffusion-weighted MRI as it can reveal the configuration and orientation of fiber tracts in white matter. This can allow virtual tractography to be conducted and brain connectivity inferred (9–14).

In diffusion tensor MRI (DT-MRI) (15,16), the water displacement probability function is modeled using a zero-mean 3D Gaussian distribution whose covariance matrix, a second-order symmetric positive definite tensor, thus represents the principal directions of diffusion or the orientation of local fiber tracts. Here, eigenvectors represent the three principal orthogonal directions of water diffusion at each point in the image, and the associated eigenvalues denote the relative mobility along these three directions. Thus, local fiber tract orientation is considered parallel to the eigenvector associated with the largest eigenvalue. Although extremely powerful and easy to compute, DT-MRI relies on strong assumptions including an unrestricted environment and homogeneity of diffusion within voxels [i.e., no partial volume effect; also see (17) for more discussion] to correctly model displacement probability functions as 3D Gaussian distributions. As a result, DT-MRI has some disadvantages. First, despite major hardware improvements, the spatial resolution of dMRI images is still suboptimal compared with the size of the fiber bundles, and thus partial volume effects are inevitable in regions where multiple fiber tracts cross. Unfortunately, any Gaussian probability distribution function has at most one orientational mode, and thus can not resolve fiber crossing. To address this issue, multicompartment models have been proposed (18–21). Unfortunately, the numerical fittings of these models are generally highly nonlinear and/or unstable. As a result, the number of tensors often needs to be specified a priori. More recently, high-order tensor (HOT) fitting, as first pioneered in (22) and further studied in (23–25), has also been proposed to account for fiber crossing, although the direct physical relevance of high-order tensors to the water diffusion process is less straightforward and yet to be fully explored.

In addition to the partial volume effect, the issue of whether non-Gaussianity of the displacement profile results from intra- or extra-cellular exchange or restriction remains unresolved (17). To bypass the Gaussian assumption, the q-space imaging (QSI) technique (26) seeks to provide a model-free reconstruction of the displacement probability function by sufficient sampling of the q vectors and exploiting their Fourier integral relationship using the fast Fourier transform (FFT). Although theoretically possible, q-space imaging requires a large amount of data to be acquired, leading to high gradient strengths and long acquisition times, and thus is not feasible in clinical settings without compromise (e.g., under-sampling and suboptimal spatial resolution).

More recently, high-angular resolution diffusion imaging (HARDI) seeks to address the issue of long acquisition time in QSI by sampling the q-space on one or more shells with fixed radii. As a result, HARDI is in general considered to contain less information than that which is required for the full recovery of the displacement probability function. Thus, methods such as the q-ball imaging technique (27, also see Refs. 28 and 29), the Persistent Angular Structure (PAS) technique and MESD (30,31), the DOT transform (32), and deconvolution-based techniques (33–36; also Ref. 37 where a unified framework of deconvolution was proposed and studied) have been proposed to recover partial information on the displacement probability function, while still allowing the underlying fiber orientations to be inferred. For example, the q-ball imaging technique (QBI) as proposed in (27–29) provides a model-free reconstruction of the orientation distribution function (ODF), the radial integral of the water displacement probability function, by applying the Funk-Radon transform. This scheme provides an approximation to the true radial integral because the result is a convolution of the probability values with a 0-th order Bessel function. This may give rise to an undesirable contamination of the probability along one direction with probabilities from other directions. The spherical deconvolution methods, on the other hand, reconstruct the fiber orientation distribution by deconvolving the diffusion-weighted signal in the q space using a model of the response function of a single fiber tract (i.e., the deconvolution kernel). In these methods (e.g., 33 and 36; also Ref. 38 where this kernel takes the form of a Wishart distribution), however, prior assumptions on the fibers are usually imposed and all fiber tracts are considered to have the same anisotropy profile.

In this article, we propose a new approach, the computation of the tensor distribution function (TDF), to model fiber crossing and non-Gaussianity in diffusion MR images. By using Gaussian distributions as basis functions, we expand the unknown displacement probability function with the weights given by the TDF. This may also be viewed as a natural, probabilistic extension of multicompartmental models. With the computation of the TDF, the water displacement probability function, orientation distribution function, tensor orientation distribution, and their corresponding anisotropy measures may all be obtained through simple analytic relations. In the following sections, we discuss in detail the theory and implementation of the proposed TDF approach.

THEORY

In standard dMRI, images are acquired using the Stejskal-Tanner pulsed gradient spin-echo method (2). With some simplifications (rectangular pulse profiles), measured image intensities S are linked to p, the displacement probablity function of water molecules, via the following Fourier transform

$$S(q)=S(0)\int p(x)exp(iq·x)\text{d}x$$ [1]

Here the wave-vector q = rδG, where r, δ, and G are the gyromagnetic ratio, the duration of the diffusion sensitization, and the applied magnetic gradient vector, respectively. Without loss of generality, let us assume the constant S(0) is 1.

Assuming a simple one-tensor Gaussian diffusion model, the displacement probability function evaluated at position x (given diffusion tensor D and diffusion time t) is

$$p(x)={({(4\pi t)}^{3}det(D))}^{-\frac{1}{2}}exp\left(-\frac{x^T{D}^{-1}x}{4t}\right)$$ [2]

Thus, the measured diffusion MR image intensities in this one-tensor case are simply S(q) = exp(−tq^TDq). It is often useful to use the normalization q̃ = q/|q| and the notation b = t|q|². In this case, we have

$$S(\stackrel{\sim }{q})=exp(-b{\stackrel{\sim }{q}}^{T}D\stackrel{\sim }{q})$$ [3]

The Tensor Distribution Function

Let us first denote the space of symmetric positive definite three-by-three matrices as . We seek a probabilistic ensemble of tensors, as represented by a tensor distribution function (TDF) P, defined on the tensor space , that best explains the observed diffusion-weighted images. If we estimate that the TDF should be P for a particular voxel, then the (calculated) image intensity should be

$$S_{\text{calculated}}(q)=\underset{D\in \mathbb{D}}{\int }P(D)exp(-t{q}^{T}Dq)\text{d}D$$ [4]

Notice that this equation is the same as Eq. [4] in (38), although in (38) this probability density function takes the form of a mixture of Wishart distributions, whose shape parameter and corresponding tensor eigenvalues are fixed (i.e., all fibers are assumed to have the same anisotropy profile). Thus, the method proposed in (38) is essentially a deconvolution-based technique.

To solve for an optimal TDF P*, we apply multiple diffusion-sensitized gradient directions q_i and arrive at P* using the least-squares principle

$$P^{\ast }={\text{argmin}}_P\sum _i{(S_{\text{obs}}(q_i)-S_{\text{calculated}}(q_i))}^2$$ [5]

To simplify our derivations, we define the error vector E(q_i) = S_obs(q_i) − S_calculated(q_i) to be the contribution to the total error with respect to q_i. For P(D) to be a true TDF, we have to enforce two constraints, i.e., (1) the non-negativity constraint: P(D) ≥ 0 for every D and (2) the probability density constraint: ∫ P(D)dD = 1.

To enforce the first constraint, we utilize the nonnegativity property of the exponential function and let P(D) = exp(R(D)). The minimization problem as proposed above is now optimized in the associated R space instead of the original P space, ensuring the nonnegativity of the resulting TDF. To this end, the gradient descent in the R space for this minimization problem is:

$$\frac{\text{d}R}{\text{d}\tau }(D)=\sum _{i}2E(q_i)exp(R(D))F(D,q_i)$$ [6]

Here, τ is an artificial time, and $F(D,q_i)=exp(-t{q}_i^{T}D{q}_i)$.

Let us now turn to address the second constraint. We first rewrite this constraint in the R space: ∫_D∈ exp(R(D))dD = 1, and modify the gradient direction in Eq. [6] by gradient projection onto the constraint space. This gives us the following modified gradient descent equation:

$$\frac{\text{d}R}{\text{d}\tau }(D)=\sum _{i}E(q_i)exp(R(D))F(D,q_i)+Lexp(R(D))$$ [7]

where L is the Lagrange multiplier

$$L=-\frac{{\int }_{D\in \mathbb{D}}exp(R(D)){\sum }_{i}E(q_i)exp(R(D))F(D,q_i)\text{d}D}{{\int }_{D\in \mathbb{D}}exp{(R(D))}^2\text{d}D}$$

Please refer to the Appendix for detailed derivations.

Parametrizing the Tensor Space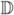

As the solution space 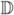is a six-parameter space, some reduction may be helpful for numerical optimization purposes. Here, we follow the ideas in (36) and assume that fiber tracts are cylindrical, thus enforcing two eigenvalues (out of three) to be equal for each individual tensor in 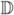. With this assumption, we only need to specify, for each tensor, one unit direction (defined on the unit sphere), which we associate with the third eigenvalue. Thus, each tensor is now represented by two scalars (specifying three eigenvalues) and one unit direction, allowing us to reduce 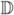to a four-dimensional space. In the rest of this article, every diffusion tensor D is expressed using D(λ, θ), with the eigenvalues λ = (λ₁, λ₂) (with λ₂ the repeated eigenvalue) and θ= (θ₁, θ₂) the azimuthal and polar angles associated with λ₁. Notice that here we do not specify whether the two equal eigenvalues are smaller or greater than the third eigenvalue, thus allowing more types of tensors to be included. This may be advantageous when comparing our TDF approach with the deconvolution methods where a standard analytic fiber response function is usually assumed.

From TDF to ODF and Beyond

Once the optimal TDF is calculated, the displacement probability function p is simply:

$$p(x)=\underset{D\in \mathbb{D}}{\int }P(D){({(4\pi t)}^{3}det(D))}^{-\frac{1}{2}}exp\left(-\frac{x^T{D}^{-1}x}{4t}\right)\text{d}D$$ [8]

Moreover, the ODF can be analytically computed by radial integration:

$$\text{ODF}(\stackrel{\sim }{x})=C\underset{r=0}{\overset{\infty }{\int }}p(r\stackrel{\sim }{x})\text{d}r=C\underset{D\in \mathbb{D}}{\int }P(D){(det(D){\stackrel{\sim }{x}}^T{D}^{-1}\stackrel{\sim }{x})}^{-\frac{1}{2}}\text{d}D$$ [9]

Here C is a normalizing constant. To determine dominant fiber directions, we propose the tensor orientation distribution function (TOD), a scalar-valued function defined on the unit sphere, by computing the marginal density function of the TDF with the eigenvalues λ = (λ₁, λ₂) integrated out.

$$\text{TOD}(\theta )=\underset{\lambda }{\int }P(D(\lambda ,\theta ))\text{d}\lambda$$ [10]

Here, the TOD directly encodes orientational information by computing, along any direction θ, the probability that we observe the principal fiber direction. As a result, the TOD has very sharp and distinctive peaks.

Once the dominant fiber direction θ* is determined, one can further estimate their corresponding eigenvalues (λ*) by computing the expected values of λ along this direction.

$${\lambda }^{\ast }=\frac{\int P(D(\lambda ,{\theta }^{\ast }))\lambda \text{d}\lambda }{\int P(D(\lambda ,{\theta }^{\ast }))\text{d}\lambda }$$ [11]

Exponential Isotropy via Shannon Entropy

To provide a complete presentation of the TDF framework, here we seek a measure, similar to fractional anisotropy or generalized fractional anisotropy, which quantifies the overall anisotropy of any given voxel. First, we observe that the Shannon entropy (H) of any TDF P measures the randomness of this probabilistic ensemble, and thus is inversely related to the certainty with which we can estimate dominant fiber directions.

$$H(P(D))=-\underset{D\in \mathbb{D}}{\int }P(D)\mathit{logP}(D)\text{d}D$$ [12]

In other words, here the Shannon entropy measures the isotropy of diffusion in any given voxel, and thus we propose the exponential isotropy (EI) as follows.

$$\text{EI}(P(D))=e^{-\underset{D\in \mathbb{D}}{\int }P(D)\mathit{logP}(D)\text{d}D}$$ [13]

To motivate the concept of EI, we observe that in an ideal one-fiber system [i.e., P(D) = 0 everywhere except for one point in the tensor space ], the Shannon entropy is 0 and the EI is 1. For an ideal two-fiber system with equal weights [P(D) = 0 everywhere except for two points in the tensor space , each of which takes a value of 0.5], the Shannon entropy is ln2 and the EI is 2. Thus, in general, we expect EI to take a value that is approximately proportional to the number of dominant fibers.

As indicated by its name [and opposite to the fractional anisotropy (FA) or the generalized FA (GFA) (27)], the EI is a measure of isotropy instead of anisotropy, and thus takes greater values in gray matter tissue than in white matter. As will be shown in the results section, EI is a natural analog of FA or GFA in the TDF framework.

Numerical Implementations

To implement the descent equation Eq. [7], the unit sphere is initially parameterized using the n diffusion-sensitized gradient directions q_i. The rationale behind this particular discretization is twofold. First, the angular resolution of computed fiber tracts should be monotonically increasing with the number of independent diffusion-sensitized gradients employed when acquiring HARDI. Second, explicit discretization of the unit sphere allows for the discrete sampling of the corresponding TOD, and thus straightforward determination of dominant fiber directions using simple thresholding. To further refine the angular resolution (beyond that given by the number of diffusion-sensitizing gradient directions), we employ a multiresolution strategy and locally include new unit directions, at each resolution, around the maximal values of the TOD in our discretization of the unit sphere. This step allows us to increase angular resolution without much compromise in computation speed by only upsampling regions on the unit sphere where dominant fiber directions are located. In this article, these new directions are selected from icosahedron-based triangulations approximating the unit sphere (up to the 7th order tessellation with n = 642 directions).

Image Acquisition

In this article, a 94-direction diffusion-sensitized gradient protocol was employed to generate simulations and acquire real human dMRI data. The timing of the diffusion sequence was optimized for SNR (signal-to-noise ratio) according to the scheme proposed in (39). For human data, the dMRI of an individual subject was acquired on a Bruker Medspec 4 Tesla MRI scanner, with a transverse electromagnetic (TEM) headcoil. This protocol used a total of 105 scans (94 diffusion-sensitized gradient directions plus 11 baseline scans with no diffusion sensitization) and the acquisition parameters were (b-value: 1159 sec/mm²; TE/TR: 92.3/8,250 msec; FOV = 230 × 230; in-plane resolution: 1.8 mm × 1.8 mm; 55 × 2 mm² contiguous slices; acquisition time 14:30 min).

RESULTS

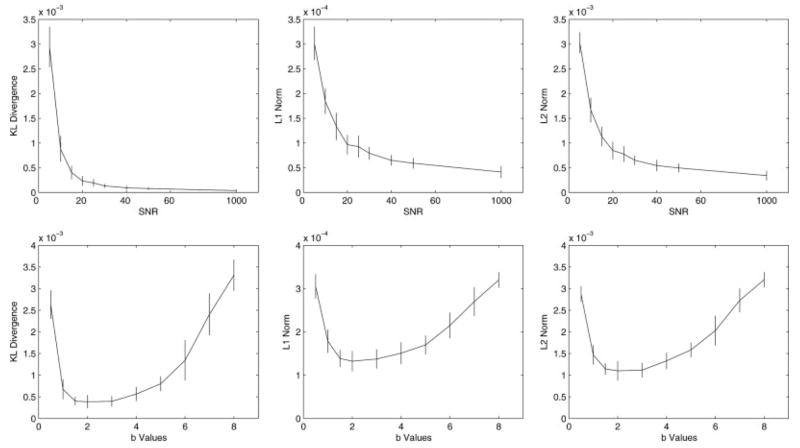
In this section, we present experimental results to validate the proposed TDF approach. To assess the performance of the TDF approach, we first simulate various configurations of two-fiber systems, crossing at 90° with equal volume fractions, using different b values and SNR ratios (similar to those seen in real HARDI data). To quantitatively compare the proposed TDF approach with other methods in the literature, we compare the calculated ODF and the true ODF using the well-known Kullback-Leibler (KL) divergence, as employed in the original QBI (27), and the L2 norm or squared error as in (29). The KL divergence is a non-negative, nonsymmetric divergence or measure of the difference between two probability density functions, and takes the value zero if and only if the two density functions are identical. Given any two probability density functions p₁ and p₂, the KL divergence of p₁ over p₂ is $KL(p_1\mid \mid p_2)=\int p_1(x)\mathit{log}\frac{p_1(x)}{p_2(x)}dx$. For completeness, we also included the L1-norm between the computed and true ODF (as a variety of different natural distance metrics may be defined between ODFs).

Here, we chose λ₁ = 10 and λ₂ = 2 (×10⁻¹⁰ m² s⁻¹) as the eigenvalues for each individual tensor (FA = 0.77) and employed complex Gaussian noises as in (33) (with a standard deviation of S(0)/SNR) when generating simulations using discrete mixtures of Gaussian distributions based on Eq. [3] (i.e., $S(q)/S(0)={\sum }_{i=1}^2{w}_{i}exp(-t{q}^T{D}_{i}q)+\text{noise}$; w₁ = w₂ = 0.5). The ODFs were rendered using 642 points, as determined using a seventh-order icosahedral approximation of the unit sphere.

Table 1 and Fig. 1 (first row) compare the mean and standard deviation of the three performance measures with a fixed b value (1,200 sec/mm²) and different SNRs of 5, 10, 15, 20, 25, 30, 40, 50, and 1,000 using the 94-direction protocol (100 simulations were computed for each SNR value). As expected, the accuracy of the computed ODF improves as SNR increases.

Table 1.

Means and Standard Deviations (Std) of the Three Metrics (KL Divergence, L1 Norm, and L2 Norm) as Functions of SNR

SNR	5	10	15	20	25	30	40	50	1,000
KL (Mean)	2.94e-3	8.83e-4	4.03e-4	2.33e-4	1.93e-4	1.33e-4	9.48e-5	7.82e-5	3.84e-5
KL (Std)	4.07e-4	2.60e-4	1.35e-4	9.80e-5	7.87e-5	3.93e-5	3.96e-5	2.63e-5	2.23e-5
L1 (Mean)	3.01e-4	1.84e-4	1.33e-4	9.67e-5	9.28e-5	7.93e-5	6.50e-5	5.91e-5	4.13e-5
L1 (Std)	3.35e-5	2.56e-5	2.74e-5	1.96e-5	2.22e-5	1.27e-5	1.05e-5	1.04e-5	1.23e-5
L2 (Mean)	3.03e-3	1.67e-3	1.13e-3	8.49e-4	7.76e-4	6.50e-4	5.44e-4	4.97e-4	3.41e-4
L2 (Std)	2.11e-4	2.47e-4	1.93e-4	1.77e-4	1.58e-4	9.68e-5	1.15e-4	8.71e-5	9.43e-5

For each SNR, 100 simulations of two-tensor systems (equal volume fractions; 90° crossing) were computed with a b value of 3,000 sec/mm². Please also refer to Fig. 1 for more details.

FIG. 1.

The means and standard deviations of the three distance measures: KL divergence (left column), L1 norm (middle column), and L2 norm (right column) between the computed ODF (using Eq. [9]) and the true ODF as functions of SNR (top) and b value (bottom). Here, b values are scaled by 1,000 sec/mm² (i.e., a value of 2 represents 2,000 sec/mm²). For each experiment, a 94-direction HARDI acquisition scheme as described in the theory section was used, and 100 simulations were computed using two-fiber systems with equal volume fractions and 90° crossing (the FA for each individual fiber is 0.77). As expected, the accuracy of the computed ODF improves as SNR increases. All three measures decrease as the b value increases from 500 sec/mm² to around 1,500 sec/mm², and remain relatively stable before increasing again around 3,000 sec/mm².

In Table 2 and the second row of Fig. 1, we investigated the influence of the b value, ranging from 500 sec/mm² to 8,000 sec/mm², on the three performance measures. Our results indicated that all three measures decrease as the b value increases from 500 sec/mm² to around 1,500 sec/mm² and remain relatively stable before increasing again starting around 3,000 sec/mm². This finding is consistent with the literature where optimal b values were reported to be from around 2,000 sec/mm² to 4,000 sec/mm² (29).

Table 2.

Means and Standard Deviations (Std) of the Three Metrics (KL Divergence, L1 Norm, and L2 Norm) as Functions of b Values

b	0.5	1	1.5	2	3	4	5	6	7	8
KL (Mean)	2.63e-3	6.75e-4	4.01e-4	3.86e-4	3.96e-4	5.65e-4	8.01e-4	1.34e-3	2.40e-3	3.31e-3
KL (Std)	3.30e-4	2.30e-4	9.86e-5	1.53e-4	1.18e-4	1.62e-4	1.70e-4	4.67e-4	4.84e-4	3.61e-4
L1 (Mean)	3.05e-4	1.79e-4	1.39e-4	1.32e-4	1.37e-4	1.51e-4	1.70e-4	2.15e-4	2.70e-4	3.20e-4
L1 (Std)	2.84e-5	2.68e-5	1.93e-5	2.35e-5	2.20e-5	2.51e-5	2.20e-5	2.98e-5	3.34e-5	1.81e-5
L2 (Mean)	2.88e-3	1.47e-3	1.14e-3	1.10e-3	1.12e-3	1.33e-3	1.58e-3	2.03e-3	2.72e-3	3.21e-3
L2 (Std)	1.82e-4	2.25e-4	1.32e-4	2.24e-4	1.66e-4	1.86e-4	1.68e-4	3.42e-4	2.77e-4	1.71e-4

For each b value, 100 simulations of two-tensor systems (equal volume fractions; 90° crossing) were computed with a SNR of 15. Here, b values are scaled by 1,000 (i.e., a value of 2 represents 2,000 sec/mm²). Please also refer to Fig. 1 for more details.

In the next experiment, we investigated the angular resolution of the TDF approach using simulated two-fiber systems (equal volume fractions; the FA for each individual fiber is 0.77) crossing at different angles (i.e., angular separations). As the TDF approach provides a probabilistic estimation of the underlying fiber distributions, we need new measures to quantify the angular resolution. To this end, here we introduce the maximal spread and the weighted spread. The maximal spread was defined as the largest angular separation among all recovered peaks of the TOD (defined as any unit direction with a TOD value greater than 0.15). We then clustered these peaks into two groups, depending on which simulated fiber direction each peak was closer to, and calculated the weighted mean fiber directions for these two groups (weights given by the corresponding TOD values). We then obtained the weighted spread by computing the angular separation between the two weighted mean fiber directions. Table 3 shows the means and standard deviations (in parentheses) of the maximal spread and the weighted spread as functions of SNR (20, 30, and 40) and the angular separation (30, 45, 60, and 90°) used for simulating these two-fiber systems. For each angular separation, the 94-direction HARDI protocol as described in the theory section was used (with a b value of 3,000 sec/mm²) and 20 simulations were computed. Our results indicate that, in general, a smaller angular separation (less than 45°) coupled with a reduction in SNR translates to a larger bias for both maximal and weighted spreads in recovering the angular separation, although the TDF approach was still able to recover probabilistic ensembles at 30° (i.e., more than one peaks were identified in the corresponding TOD; notice that, in the case of 30°, the ground truth ODF has only one peak). For fibers crossing at 45 and 30°, both maximal and weighted spreads under-estimate the angular separation at low-SNR values (for noise-free simulations with 30° of separation, maximal and weighted spreads were 36 and 22°). For 60°, the maximal spread over-estimates and the weighted spread under-estimates the angular separation. To put our results in perspective, the angular resolution of our discretization of the unit sphere (icosahedron-based; n = 642 directions) is approximately 9°.

Table 3.

Means and Standard Deviations (in Parentheses) of the Maximal Spread and the Weighted Spread for the Recovered Dominant Fiber Directions as Functions of SNR (20, 30, and 40) and the Angular Separation (30, 45, 60, and 90°) Used for Simulating Two-Fiber Systems (Equal Volume Fractions; FA = 0.77)

Angular separation (°)	30	45	60	90
Maximal spread
SNR = 40	17.6 (4.6)	50.5 (6.0)	66.7 (5.7)	89.6 (0.5)
SNR = 30	13.0 (3.2)	47.0 (4.9)	68.0 (5.7)	89.7 (0.5)
SNR = 20	10.4 (2.5)	40.1 (7.3)	63.9 (5.1)	89.5 (0.3)
Weighted spread
SNR = 40	13.0 (2.7)	36.5 (3.1)	57.2 (3.0)	90.2 (1.5)
SNR = 30	10.2 (2.7)	38.0 (2.2)	55.0 (6.3)	90.0 (1.7)
SNR = 20	8.5 (1.2)	31.5 (5.6)	52.6 (6.1)	89.6 (1.9)

For each angular separation, the 94-direction HARDI protocol described in the theory section was used (with a b value of 3,000 sec/mm²), and 20 simulations were computed. Our results indicate that, in general, a smaller angular separation (less than 45°) coupled with a reduction in SNR translates to a larger bias for both maximal and weighted spreads, although the TDF approach was still able to recover probabilistic ensembles at 30° (i.e., more than one peaks were identified in the corresponding TOD; notice that in the case of 30° the ground truth ODF has only one peak). For fibers crossing at 45 and 30°, both maximal and weighted spreads under-estimate the angular separation at low SNR values. For 60°, the maximal spread over-estimates and the weighted spread under-estimates the angular separation.

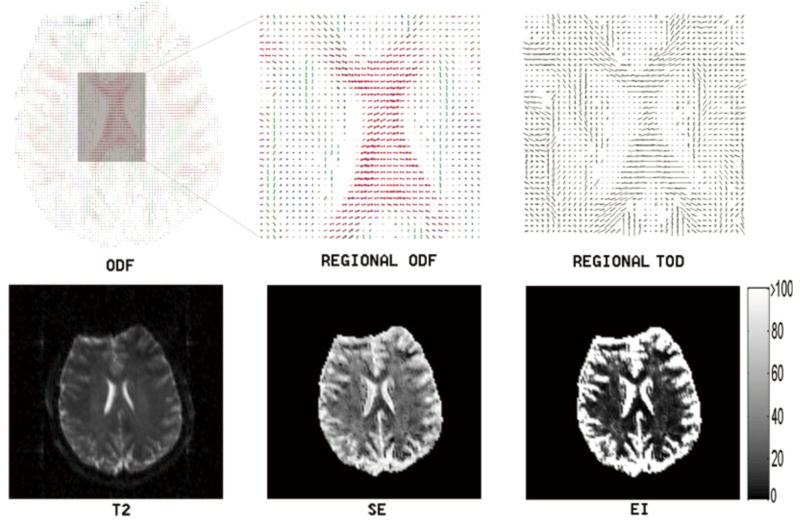
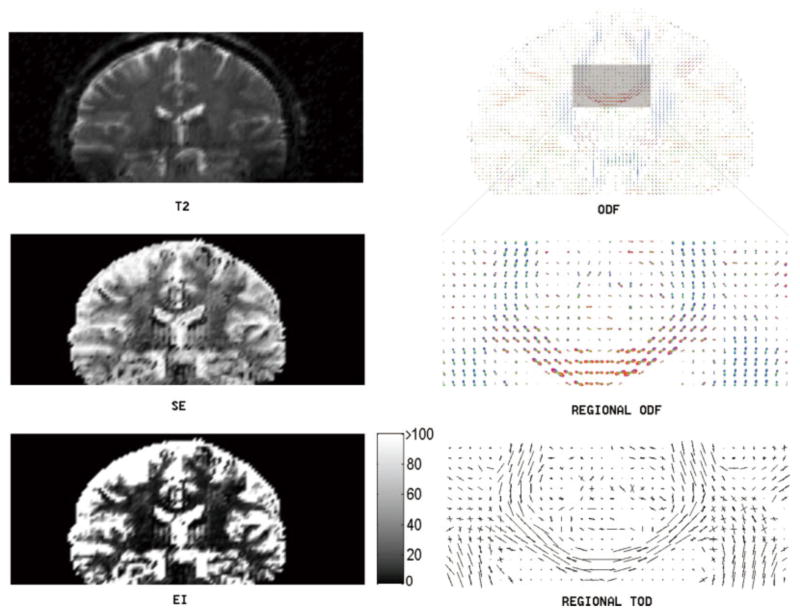
To validate the TDF approach using real imaging data, the dMRI of a normal control subject was acquired using the 94-direction protocol. Figures 2 and 3 illustrate the proposed TDF approach applied to two slices (one axial and one coronal) showing the complex white matter microstructure in the centrum semiovale, a predominantly white matter core in the interior of the cerebral hemispheres. For the visualization of ODFs, we adopted a conventional color coding scheme in which red corresponds to medial-lateral (i.e., left–right), green to anterior-posterior, and blue to superior–inferior orientation. Here, visual inspections suggest that the EI plot provides a clear separation between gray matter and white matter (colorbars are included in the EI plots to illustrate typical EI values obtained using the proposed numerical implementations), and that the TOD and ODF plots complement each other to provide better fiber orientation information at a voxel level. Here, voxel-wise ODFs were min–max normalized and scaled using their generalized fractional anisotropy (GFA), whereas no normalization or rescaling was necessary in the TOD plots (TOD is itself normalized as it is the marginal density function of the TDF).

FIG. 2.

This figure illustrates the TDF approach applied to the dMRI (axial view of the centrum semiovale) of a normal subject using the 94-direction HARDI scheme as described in the theory section. Here, the computed Shannon entropy (SE), exponential isotropy (EI), and ODF plots are shown along with the structural image (T2). The detailed ODF and TOD plots are also included for the highlighted region to show the complex local fiber orientation geometries. Voxel-wise ODFs were min–max normalized and scaled using their GFAs, whereas no normalization or rescaling was necessary when plotting TOD (TOD is itself normalized as it is the marginal density function of the TDF). For the visualization of ODFs, we adopted a conventional color coding scheme in which red corresponds to medial-lateral, green to anterior–posterior, and blue to superior–inferior orientation. Notice the clear separation between gray and white matter in the EI plot (here we include a colorbar for this plot to illustrate typical EI values obtained using the proposed numerical implementations). [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

FIG. 3.

This figure illustrates the TDF approach applied to a coronal slice of the dMRI data in Fig. 2. Here, the computed Shannon entropy (SE), exponential isotropy (EI), and ODF plots are shown along with the structural image (T2). The detailed ODF and TOD plots are also included for the highlighted region to show local fiber orientations. In this regional TOD plot, we notice the complex fiber-crossing geometries between the corpus callosum and the corona radiata (i.e., between the red or left–right oriented fibers and the blue or superior-inferiorly oriented fibers in the regional ODF plot). [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

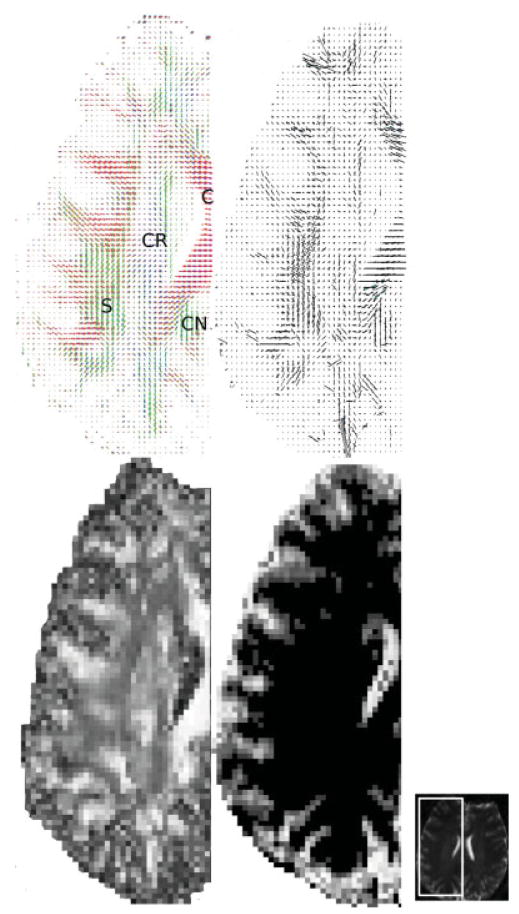
To further illustrate the TDF approach and compare the recovered fiber morphology with known neuroanatomical structures, we examined more closely the transverse section of the right centrum semiovale in Fig. 2. Figure 4 shows the detailed GFA, ODF, TOD, and EI plots of this region, along with the nondiffusion weighted structural MRI. Here, the detailed ODF plot reveals the left–right oriented corpus callosum (C), the superior-inferiorly oriented corona radiata (CR), and the anterior-posteriorly oriented superior longitudinal fasciculus (S) and cingulum (CN). Also notice that compared with the gray matter, the white matter region has higher GFA values but lower EI values.

FIG. 4.

The detailed ODF (top left), TOD (top right), GFA (bottom left), and EI (bottom right) plots of the right centrum semiovale (axial view) in Fig. 2. On the far right is the corresponding nondiffusion weighted structural image, showing where this region was extracted. Here, the ODF plot reveals the left–right oriented corpus callosum (C), the superior-inferiorly oriented corona radiata (CR), and the anterior-posteriorly oriented superior longitudinal fasciculus (S) and cingulum (CN). Notice that the white matter has higher GFA values but lower EI values compared with the gray matter, and that the TOD and ODF plots complement each other to provide better fiber orientation information at a voxel level. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

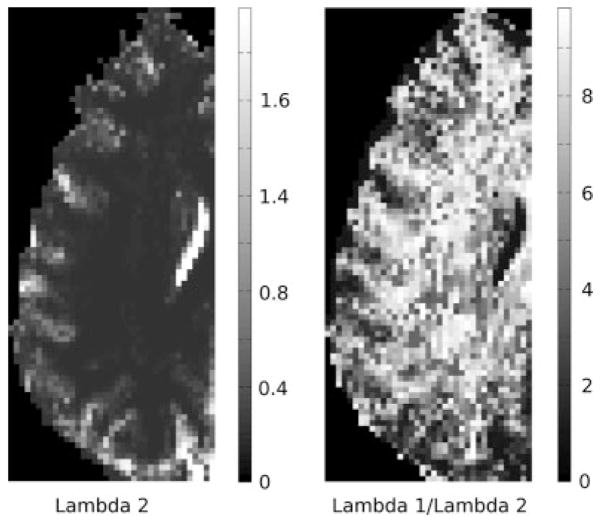
In Fig. 5, we plot the computed λ₂ (values scaled by 10⁻⁹ m² s⁻¹) and λ₁/λ₂ ratio maps, using Eq. [11], for the brain region in Fig. 4. As λ₂ value differs more than λ₁ between gray and white matter, the ratio map (instead of the λ₁ map) is shown here to better visualize the separation between gray and white matter. Although no spatial constraint was employed when computing these maps (to ensure neighboring voxels to have similar λ values), we notice that the TDF approach still produced maps that are spatially relatively smooth, with a visually identifiable gray/white matter junction and values consistent with those reported in the literature.

FIG. 5.

The computed voxel-wise λ₂ and λ₁/λ₂ ratio maps, using Eq. [11], of the brain region in Fig. 4. As the λ₂ value differs more than λ₁ between gray and white matter, the ratio map (instead of the λ₁ map) is shown here to better visualize the separation between gray and white matter. Although no spatial constraint was employed when computing these maps (to ensure neighboring voxels to have similar λ values), the TDF approach still produced maps that are spatially relatively smooth, with visually identifiable gray/white matter junction and values consistent with those reported in the literature. The values in the λ₂ map are scaled by 10⁻⁹ m² s⁻¹.

To more closely examine fiber crossing, two regions of interest were identified (Fig. 6): the first region (top row) covered the crossing of the corona radiata (CR) and corpus callosum (C), and the second region (bottom row) was obtained from the dispersion of the superior longitudinal fasciulus (S). In both cases, the proposed TDF approach was successful in resolving the complex fiber geometries consistent with known neuroanatomy.

FIG. 6.

The detailed ODF (left) and TOD (right) plots showing: (top row) the crossing between the left–right oriented corpus callosum commissural fibers (C) and the superior–inferior oriented corona radiata (CR), and (bottom row) the dispersion of the superior longitudinal fasciculus (S) in the centrum semiovale region of Fig. 4. The selected regions show where the complex fiber crossing/dispersion geometries are most evident. The corresponding nondiffusion weighted structural images indicating where the data were extracted (marked in white) are shown on the right. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

DISCUSSION

In this article, we propose to compute the tensor distribution function as a novel method for simultaneously recovering the water displacement probability function, dominant fiber orientations and their corresponding eigenvalues, and the orientation distribution function in dMRI. We also propose the exponential isotropy, an inverse measure of anisotropy, by taking the exponential of the Shannon entropy of the computed tensor distribution function. The TDF approach can be considered a hybrid methodology as it has theoretical similarities to other approaches. First, the TDF approach provides a probabilistic fitting of multiple tensors, and thus may be thought of as a natural extension of multitensor models. However, here we observe a major difference between the TDF approach and multitensor fitting. In TDF, a weight is being assigned to any tensor whose anisotropic properties are consistent with human physiology (i.e., in the solution space); while in conventional multitensor estimation, the physiological properties of the tensors are considered unknown variables that remain to be determined. This difference explains the advantages of TDF fitting from a computational perspective. For example, multitensor fitting requires certain constraints to be imposed to guarantee the positive definiteness of the computed tensors. In contrast, only positive definite second-order three-by-three tensors are included in the solution space of the TDF approach, thus excluding nonphysiological tensors. Moreover, by using the logarithmic transform along with projected gradient descent, the proposed algorithm naturally yields positive weights for all tensors in the solution space, without the need for extra constraints or numerical procedures.

Alternatively, the TDF approach also shares similarities with deconvolution-based techniques, as 3D Gaussian diffusion functions may be simply viewed as basis functions with which we expand the water displacement probability function. Here, let us point out an interesting observation that 3D Gaussian distributions, as basis functions, are not orthogonal to one another in the traditional sense, and thus in theory may introduce redundancy in the solution space and ambiguity in tensor representations. We suggest that this explains why Gaussian mixture models in multitensor fitting are well known to be unstable and ill-posed, and thus the number of compartments usually needs to be predetermined in advance. The TDF approach, by introducing a probabilistic interpretation into tensor fitting, provides a numerically stable solution.

To point out the difference between spherical-deconvolution methods and the TDF approach, we observe that, in the former, a single fiber response function in the q space is usually assumed to be applicable to all fiber bundles and thus MR signals must be explained as a linear combination of this response function, whereas in the latter, no prior knowledge on axonal water diffusion is assumed and different fiber tracts are allowed to have different anisotropic properties (i.e., different tensor eigenvalues). Thus, the TDF approach may potentially be advantageous for studying regional differences or recovering longitudinal changes in white matter anisotropy. Last, as discussed at length in (37), realizing non-negative weights during the deconvolution operation is not a trivial task for these methods, and advanced optimization techniques such as non-negative least squares using quadratic programming and active set strategy were employed in (37).

Comparing the TDF approach with the QBI and PAS methods, we notice that the TDF approach directly computes the water displacement probability function, whereas only partial information on the water displacement probability function is recovered in QBI (the ODF) or PAS (the angular structure). Moreover, although state-of-the-art analytic ODF reconstruction methods (28,29) through spherical harmonics are much faster and require fewer directions, these methods still employ the Funk-Radon transform, which merely provides a numerical approximation to the true ODF.

Although the TDF approach is based on the Gaussian diffusion assumption, we point out that a different diffusion model can be used, as Eq. [4] can be thought of as the weighted response function (in the q space) with respect to the discretized solution space. In theory, one can also sharpen the computed TDF using a regularizing prior similar to the entropy penalty term in the PAS approach. Mathematically, this means that, instead of minimizing Eq. [5], we minimize the following combined cost function:

$$\sum _i{(S_{\text{obs}}(q_i)-S_{\text{calculated}}(q_i))}^2+\underset{D\in \mathbb{D}}{\int }-P(D)\mathit{log}(P(D))\text{d}D$$ [14]

Numerically, our experimental results indicate that the TDF approach performs well when coupled with the 94-direction HARDI protocol. Moreover, as the TDF directly encodes information on the orientation of the dominant fibers (through the tensor orientation distribution) as well as their corresponding anisotropy measures, we envisage that the TDF approach will make it easier to develop a simple and elegant fiber-tracking technique. We are currently investigating TDF-based probabilistic tractography and we intend to report our results in future studies.

Last, one may generalize the proposed approach by relaxing the constraint on the tensor space in the section on Parametrizing the Tensor Space Section, and compute the TDF with respect to the full six-dimensional space. However, with its current solution space of four dimensions, the TDF approach is already computationally expensive. To tackle this issue, we proposed a multiresolution scheme to compute the TDF more efficiently, although we acknowledge that our computation speed is still slow compared with other methods (e.g., analytic Q-ball imaging via Funk-Radon transform), and the convergence of the proposed numerical solution is yet to be analytically In the future, we will further investigate this issue, at a software (numerical) and hardware (machine) level.

CONCLUSION

In this article, we introduced the computation of the as a novel method to resolve intravoxel fiber in HARDI. We presented mathematical formulations the TDF and proposed a projected gradient descent rithm for the numerical computation of TDF. With constraints on the diffusion process and the of individual tensors, the proposed approach solves an underlying tensor ensemble that best describes observed diffusion-weighted MR images. Moreover, offers some advantages relative to other as the displacement probability function, orientation tribution function, and principal fiber directions (or tensor orientation distribution function) may all be derived from TDF through simple analytic relations.

APPENDIX

Let us first define the notation RHS = Σ_i E(q_i) exp(R(D)) F(D, q_i), we then have the projected gradient descent equation $\frac{\text{d}R}{\text{d}\tau }(D)=\text{RHS}+Lexp(R(D))$, where L is a Lagrange multiplier. To determine L, we differentiate the probability density constraint ∫_D∈ exp(R(D))dD= 1 with respect to the artificial time τ, followed by switching the order of differentiation and integration:

$$\begin{array}{l}\frac{\text{d}}{\text{d}\tau }\underset{D\in \mathbb{D}}{\int }exp(R(D))\text{d}D=\underset{D\in \mathbb{D}}{\int }\frac{\text{d}}{\text{d}\tau }exp(R(D))\text{d}D\\ =\underset{D\in \mathbb{D}}{\int }exp(R(D))\frac{\text{d}R(D)}{\text{d}\tau }\text{d}D\\ =\underset{D\in \mathbb{D}}{\int }exp(R(D))\text{RHS}+Lexp{(R(D))}^2\text{d}D=0\end{array}$$ [A1]

Thus, we obtain

$$L=-\frac{{\int }_{D\in \mathbb{D}}\text{RHS}exp(R(D))\text{d}D}{{\int }_{D\in \mathbb{D}}exp{(R(D))}^2\text{d}D}$$ [A2]

By invoking the Cauchy-Schwarz inequality, it is straightforward to show that this projected direction is still a gradient descent direction.