Abstract
The Ω-loop of TEM β-lactamase is involved in substrate recognition and catalysis. Its dynamical properties and interaction with water molecules were investigated by performing multiple molecular dynamics simulations of up to 50 ns. Protein flexibility was assessed by calculating the root mean-square fluctuations and the generalized order parameter, S2. The residues in secondary structure elements are highly ordered, whereas loop regions are more flexible, which is in agreement with previous experimental observations. Interestingly, the Ω-loop (residues 161–179) is rigid with order parameters similar to secondary structure elements, with the exception of the tip of the loop (residues 173–177) that has a considerably higher flexibility and performs an opening and closing motion on the 50-ns timescale. The rigidity of the main part of the Ω-loop is mediated by stabilizing and highly conserved water bridges inside a cavity lined by the Ω-loop and residues 65–69 of the protein core. In contrast, the flexible tip of the Ω-loop lacks these interactions. Hydration of the cavity and exchange of the water molecules with the bulk solvent occurs via two pathways: the flexible tip that serves as a door to the cavity, and a temporary water channel involving the side chain of Arg164.
Introduction
Plasmid-encoded TEM β-lactamases are the main cause for resistance against β-lactam antibiotics in Gram-negative bacteria (1). They efficiently hydrolyze the β-lactam ring and therefore render the antibiotic inactive. First isolated in 1965 from Escherichia coli (2), the TEM β-lactamases within a few years have spread worldwide and are now found in many pathogenic organisms (3). TEM β-lactamases (EC 3.5.2.6) belong to the class A β-lactamases and are globular enzymes with a molecular mass of 29 kDa. Their structure is composed of two domains that are closely packed together: An all-α-domain consisting of eight α-helices, and an α-/β-domain, consisting of three α-helices and five β-strands (4). The active site cavity, with the catalytic residues Ser70, Lys73, and Lys234, is located at the interface between the two domains and is limited by the Ω-loop. The Ω-loop (residues 161–179) is a conserved structural element in all class A β-lactamases and mediates their catalytic function because it positions the catalytic Glu166 and is involved in substrate binding. Its conformation is stabilized by a highly conserved salt bridge formed between Arg164 and Asp179 (5–7) (Fig. 1).
Figure 1.
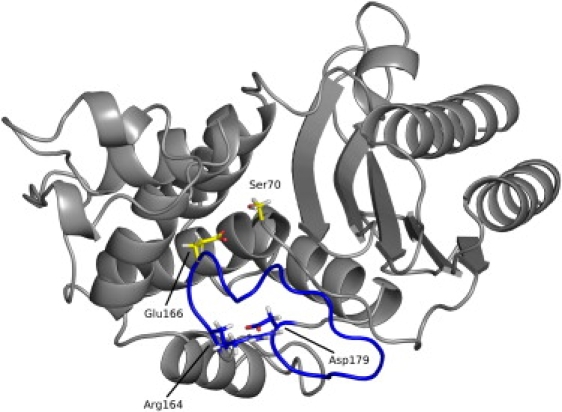
Structure of the TEM β-lactamase (gray). The Ω-loop (highlighted in blue) is anchored by a salt bridge formed between Arg164 and Asp179 and positions Glu166 toward the active Ser70 (yellow).
Because of their importance in antibiotic resistance, the structure and catalytic function of TEM β-lactamases are well studied and characterized (8,9), but only a few studies addressed the dynamical features of the TEM β-lactamases and the catalytically relevant Ω-loop. Computational analysis of the TEM β-lactamases using molecular dynamics (MD) simulations (10,11) showed a stable enzyme that does not exhibit large structural rearrangements. This was experimentally confirmed by a recently published nuclear magnetic resonance (NMR) study of the TEM β-lactamase from which it is evident that the protein is one of the most ordered proteins (12). However, the flexibility of the Ω-loop is still under debate: From structural analysis, it was found that the Ω-loop has only few contacts with the rest of the protein and therefore was speculated to be a flexible element (13). This is supported by the molecular dynamics study of Roccatano et al. (11), in which a flaplike motion of the Ω-loop was observed. In contrast, in the MD simulation of Diaz et al. (10) as well as in the NMR study of Savard and Gagne (12), no indication of an increased flexibility of the Ω-loop in the picosecond-to-nanosecond timescale was found.
In a comparative study of 49 high-resolution structures of class A β-lactamases, we previously identified six highly conserved crystal water molecules located in a narrow, tunnel-shaped cavity lined by the Ω-loop and residues 65–69 of the protein core (14). By mediating hydrogen bonds between the Ω-loop and the protein core, these water molecules provide an explanation for the stability and low flexibility of the Ω-loop.
To study the dynamical properties of the Ω-loop, the formation of water bridges near the Ω-loop, and the paths of water molecules into and out of the Ω-loop cavity, multiple molecular dynamics simulations of the TEM β-lactamase were performed. This approach has been used because it has been shown that due to insufficient sampling of the conformational space by simulations on the nanosecond timescale (15–17), in general MD simulations with different initial conditions result in slightly different values for the system properties (18). To overcome this limitation, it has been demonstrated that averaging over multiple MD simulations can improve the sampling of conformational space considerably (19–23).
To assess the effect of the presence of crystal water molecules to the outcome of a simulation, two protein-water systems were compared: One system with the crystal water included, and the other without crystal water. By performing multiple simulations for each system and—as a further validation—using different water models, we were able to estimate the reproducibility of our results and the significance of differences between the two systems.
Methods
MMD simulations of TEM β-lactamase
A high-resolution crystal structure of TEM-1 β-lactamase (Protein Data Base (PDB) entry 1M40, resolution 0.85 Å) (24) was used as a starting point for multiple molecular dynamics (MMD) simulations. Protonation states of titratable groups were determined using PDB2PQR (25), retaining existing hydrogen atoms in the crystal structure. Two different lactamase-water systems were prepared: One including the crystal water molecules (referred to as MMDwat) and one without the crystal water molecules (referred to as MMDnowat). For each system, a truncated octahedron periodic water box of TIP3P waters was used with a minimum distance of 10 Å between the box boundary and the protein, with or without crystal water for the MMDwat and MMDnowat system, respectively. Thus, the total amount of water molecules was 10,302 for the MMDwat system and 8168 for the MMDnowat system. The net charge of −7 for both systems was neutralized by adding seven sodium counterions. The total system size was 34,974 and 28,572 atoms for the MMDwat and MMDnowat system, respectively.
The PMEMD program of AMBER 8.0 (26) with the all-atom ff03 force field (27) was used for energy minimization and MD simulations. The SHAKE algorithm (28) was applied to all bonds containing hydrogen atoms, and a time step of 1 fs was used. The Berendsen method was used to couple the systems to a constant temperature of 300 K and a pressure of 1 bar (29). The electrostatic interaction was evaluated by the particle-mesh Ewald method (30), and Lennard-Jones interactions were evaluated using a 8.0 Å cutoff. Each system was subjected to 50 steps of energy minimization by steepest descent to remove repulsive van der Waals contacts, followed by 150 steps of energy minimization by conjugate gradient. For each system, 10 MD simulations with different initial velocity distributions were performed. In the first 150 ps, the backbone and side-chain atoms were restrained using a harmonic potential with a gradually decreasing force constant from 5 to 0.1 kcal/mol for the backbone atoms and 1.0 to 0.1 kcal/mol for the side-chain atoms. This was followed by an unrestrained simulation of 5 ns in which snapshots were saved every picosecond. For both systems, one simulation of 50 ns was performed.
Furthermore, two similar lactamase-water systems were prepared using the SPC/E water model (31) instead of the TIP3P water model, but otherwise identical parameters. The total system size was 34,965 and 2854 atoms with 10,298 and 8161 water molecules for the SPC/Ewat and SPC/Enowat system, respectively. Both systems were equilibrated and subsequently simulated for 5 ns as described above.
Analysis of protein structure and dynamics
Analysis was performed using the PTRAJ program of AMBER 8.0 on the last 2 ns of each MMD trajectory, unless stated otherwise. From the extended 50-ns simulations, the last 47 ns were analyzed. All protein figures were created using VMD (32) or PyMOL (33). The surface of the Ω-loop cavity seen later in Fig. 6 was created with the program HOLLOW (34). Results obtained on a per-residue basis were averaged for the 10 MMDwat and the 10 MMDnowat 5-ns simulations and standard deviations were calculated.
Figure 6.
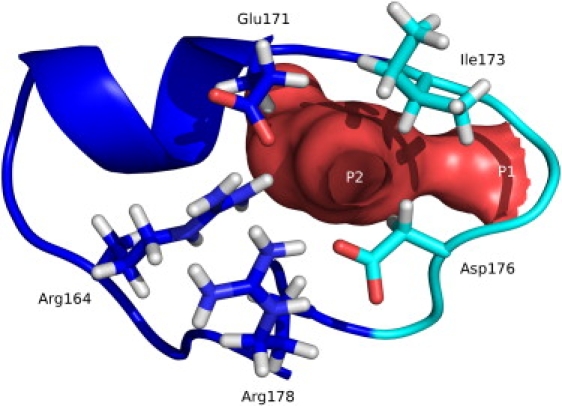
Entry and exit points of the Ω-loop cavity (red surface). Entry and exit point P1 is located at the flexible tip of the Ω-loop (cyan). Entry and exit point P2 is a temporarily formed opening lined by Ω-loop residues Arg164, Glu171, Ile173, Asp176, and Arg178.
The stability of the simulations was analyzed by calculating the root mean-square deviation (RMSD) of the backbone atoms between each conformer and the initial conformation (RMSD) and between all conformers (2D-RMSD). The root mean-square fluctuation (RMSF) of the backbone atoms was calculated after removal of the overall translational and rotational motion of the protein by superimposition onto a common reference frame.
Order parameters S2 were calculated applying the model-free approach of Lipari and Szabo (35) to the normalized time-correlation functions of the N-H internuclear vectors after overall rotation was removed. Order parameters of residues for which time-correlation functions did not reach a plateau value in more than six MMD simulations were treated as “not determined.”
A principal component analysis of all concatenated trajectories was performed using programs from the GROMACS software package (36). Eigenvectors and eigenvalues were obtained from the diagonalization of the covariance matrices of the Cα atoms, and the principal components were generated by projecting the trajectories on the respective eigenvectors (37). The cosine content of the principal components was calculated to estimate whether they describe random diffusion (38).
Analysis of water binding and water exchange at the Ω-loop
Water bridges were identified and characterized using the software ANKUSH (39). Only water molecules within a maximum distance of 4.0 Å to any non-water polar atom of the Ω-loop and its adjacent residues were considered (residues 65–75, 161–180, 237–244, and 266–269). For water bridges that were formed for at least 30% of the trajectory, the occupancies and number of unique water molecules involved in a particular water bridge were averaged and the exchange rate was calculated.
Water molecules entering and leaving the Ω-loop cavity were monitored throughout the complete trajectories as previously described (40). The region of interest was defined as a bounding sphere with its center located at the Cα atom of Met68 and a radius of 10.0 Å. Thus the complete Ω-loop cavity was included. All water molecules entering the region of interest were tracked until they left the region of interest, and the number of consecutive frames during which the water stayed inside the region was recorded. The resulting pathways consist of the routes that individual water molecules take when they move from the bulk solvent into the Ω-loop cavity and back to the bulk solvent. Pathways with a length of <100 consecutive frames (100 ps) were excluded from further analysis, as their visual inspection revealed that those water molecules just touched upon the region of interest and then moved back into the bulk solvent.
Results
Multiple molecular dynamics (MMD) simulations of TEM-1 β-lactamase, comprising a total simulation time of over 200 ns, were performed. Two different lactamase-water systems were studied: One including the crystal water molecules (referred to as MMDwat), and one without the crystal water molecules (referred to as MMDnowat). For each system, 10 independent MD simulations with a length of 5 ns each and a different initial velocity distribution were performed. For further validation of the results, one simulation of each system was extended to 50 ns, and both systems were additionally simulated using the SPC/E water model.
Stability of the simulation
For each simulation, the stability of the simulation was assessed by monitoring the root mean-square deviation (RMSD) with respect to the minimized starting structure (see Fig. S1, Fig. S2, Fig. S3, and Fig. S4 in the Supporting Material). All 20 MMDwat and MMDnowat simulations were stable and showed only a small deviation of the protein backbone to the initial conformation. Over the last 2 ns of the trajectories, the average RMSD was 0.93 ± 0.06 Å and 0.95 ± 0.11 Å for the MMDwat and MMDnowat simulations, respectively. The two systems using the SPC/E water model had an average RMSD of 0.85 ± 0.06 Å and 0.84 ± 0.06 Å for the simulation with and without the initial crystal water, respectively. The extended trajectories showed a slightly increased RMSD over the course of the 50-ns simulation, with an average RMSD of 1.35 ± 0.17 Å and 1.23 ± 0.16 Å in the simulation with and without crystal water, respectively.
2D-RMSD plots of each simulation revealed that in most MMDwat or MMDnowat simulations the protein backbone kept its initial conformation throughout the complete simulation, whereas in six simulations the protein backbone underwent small conformational changes (Fig. S5, Fig. S6, Fig. S7, and Fig. S8). Simulations with changes in protein backbone conformation were present in simulations of both systems, with no particular preference for MMDwat or MMDnowat simulations. Snapshots were extracted from those regions of the 2D-RMSD plots where a conformational change was observed. Superimposition of the snapshots showed that the conformational changes occurred mainly in the hinge region between the all-α and the α/β domain (residues 216–229), a short part of the Ω-loop (residues 173–177), other solvent-exposed loops, and the C- or N-terminal amino acids. In particular, the conformational changes at these positions occurred during the extended 50-ns simulations, and are the main reason for the higher RMSD values.
Dynamics of the TEM β-lactamase
The backbone of the TEM β-lactamase is characterized by a low overall flexibility, as indicated by the residue-averaged RMSFs (Table 1 and Fig. 2 A). Residues located in secondary structure elements show less flexibility than residues located in solvent-exposed loops and turns. Although the majority of the Ω-loop residues have RMSF values similar to residues located in secondary structure elements, the residues 173–177 have much higher RMSF values and thus are referred to as flexible tip of the Ω-loop.
Table 1.
Dynamical features of the TEM β-lactamase: root mean-square fluctuations and order parameters S2 show less flexible residues in secondary structure elements and flexible residues in loops and turns
| MMDwat | MMDnowat | Extendedwat | Extendednowat | SPC/Ewat | SPC/Enowat | |
|---|---|---|---|---|---|---|
| RMSFs in Å | ||||||
| All residues | 0.51 ± 0.14 | 0.53 ± 0.14 | 0.76 ± 0.33 | 0.71 ± 0.35 | 0.50 ± 0.16 | 0.48 ± 0.14 |
| α-Helices | 0.47 ± 0.10 | 0.48 ± 0.10 | 0.65 ± 0.18 | 0.63 ± 0.23 | 0.44 ± 0.10 | 0.44 ± 0.09 |
| β-Sheets | 0.39 ± 0.06 | 0.41 ± 0.06 | 0.54 ± 0.12 | 0.48 ± 0.09 | 0.39 ± 0.06 | 0.39 ± 0.05 |
| Loops | 0.59 ± 0.15 | 0.61 ± 0.14 | 0.95 ± 0.38 | 0.86 ± 0.43 | 0.58 ± 0.18 | 0.55 ± 0.15 |
| Ω-Loop rigid part | 0.43 ± 0.05 | 0.45 ± 0.05 | 0.63 ± 0.30 | 0.56 ± 0.49 | 0.39 ± 0.12 | 0.40 ± 0.12 |
| Ω-Loop flexible part | 0.69 ± 0.15 | 0.74 ± 0.16 | 0.99 ± 0.02 | 1.28 ± 0.04 | 0.59 ± 0.02 | 0.58 ± 0.03 |
| Order parameter S2 | ||||||
| α-Helices | 0.90 ± 0.02 | 0.90 ± 0.02 | 0.90 ± 0.02 | 0.90 ± 0.02 | 0.91 ± 0.02 | 0.90 ± 0.02 |
| β-Sheets | 0.90 ± 0.02 | 0.90 ± 0.02 | 0.90 ± 0.02 | 0.90 ± 0.02 | 0.91 ± 0.02 | 0.90 ± 0.04 |
| Loops | 0.86 ± 0.05 | 0.86 ± 0.04 | 0.85 ± 0.05 | 0.85 ± 0.05 | 0.88 ± 0.03 | 0.88 ± 0.04 |
| Ω-Loop rigid part | 0.90 ± 0.02 | 0.90 ± 0.01 | 0.90 ± 0.02 | 0.90 ± 0.02 | 0.90 ± 0.02 | 0.90 ± 0.02 |
| Ω-Loop flexible part | n.d. | 0.83 | 0.72 ± 0.05 | n.d. | 0.85 ± 0.02 | 0.84 ± 0.02 |
MMDwat and MMDnowat values represent the averages over 10 simulations.
Figure 2.
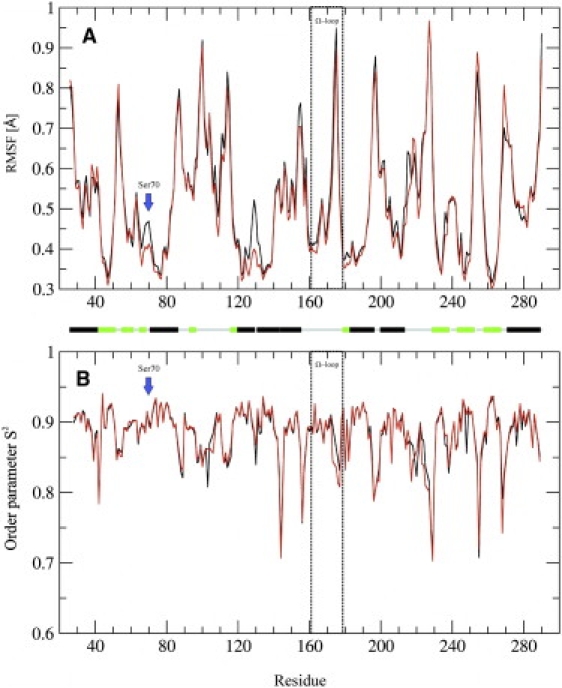
Dynamical features of the TEM β-lactamase: (A) RMSF and (B) order parameter S2 of the MMDwat (red) and MMDnowat (black) simulations. The catalytic Ser70 and the residues forming the Ω-loop are marked and the secondary structure is annotated (helices, black; sheets, green; loops, gray). Residues for which no order parameter could be determined are missing in the graph.
In addition, the flexibility of the protein backbone was characterized by calculating the order parameter S2 from the time-correlation functions of the N-H bond vectors (Table 1 and Fig. 2 B). Consistent with the results obtained by the RMSF calculations, the residues with a high order parameter (S2 > 0.90) are mostly located in secondary structure elements of the protein, while residues in loops have a lower order parameter. It should be noted that the time-correlation function of eight residues in MMDwat did not reach a plateau value in seven or more simulations, and therefore no order parameter could be determined. Catalytic residues (Ser70, Lys73, and Lys234) are highly ordered (S2 > 0.90), with the exception of Ser130. Consistent with the results of the RMSF analysis, the Ω-loop is rigid with order parameters similar to residues located in secondary structure elements, while the residues in the tip of the Ω-loop show remarkably lower order parameters.
The essential dynamics analysis of the combined 200-ns trajectory showed that the first 20 eigenvectors constitute 70% of the overall protein motion. The largest correlated motion was a movement of the two domains relative to each other, which could be best described as contracting and stretching motion, as well as a flaplike motion of the flexible Ω-loop tip. The principal component associated with this motion had a cosine content of 0.31, indicating that it partly describes random diffusion due to insufficient sampling. The focused essential dynamics analysis of the Ω-loop showed that the first five eigenvectors constitute 79% of the overall motion of the Ω-loop and that the movement of the flexible tip was the largest correlated motion within the Ω-loop. The cosine content of the first five principal components was <0.13, indicating sufficient sampling.
To further analyze the higher flexibility of the residues in the tip of the Ω-loop, the distance between the center of mass of the Cα atoms of these residues and the center of mass of the Cα atoms of the oppositely located residues 65 and 66 of the protein core was measured. The average distance in MMDwat and MMDnowat simulations (8.4 ± 0.6 Å and 8.2 ± 0.5 Å, respectively), as well as in SPC/Ewat and SPC/Enowat simulations (8.4 ± 0.3 Å and 8.7 ± 0.4 Å, respectively), was similar to the initial distance in the crystal structure (8.2 Å). In most of the snapshots of the 5-ns trajectories, the distance was within 1 Å of the distance of the crystal structure. On average, in only 10% of the snapshots of each trajectory, the distance changed for >1 Å with respect to the crystal structure. In seven MMDwat and five MMDnowat simulations the distance increased, while in two simulations of each system the distance decreased.
As the residues of the flexible tip contribute to the entrance of the Ω-loop cavity, an increase in the distance to the protein core can be referred to as an opening movement, a decrease as a closing movement. A complete opening and subsequent closing movement was not observed in any 5-ns MMDwat and MMDnowat simulation, as an increase and decrease in the distance seemed to be mutually exclusive in an individual simulation at this short timescale. However, in one of the extended 50-ns simulations a complete opening and closing movement was observed (Figs. 3 and 4). While the tip of the Ω-loop stays in the open conformation for ∼20 ns, the conformational change associated with the opening and closing movement is fast and takes place in <100 ps. The analysis of the Ω-loop backbone dihedral angles over the 50-ns trajectory revealed that only the residues of the flexible tip exhibited dihedral angle changes that were correlated with the changes in the distance to the protein core.
Figure 3.
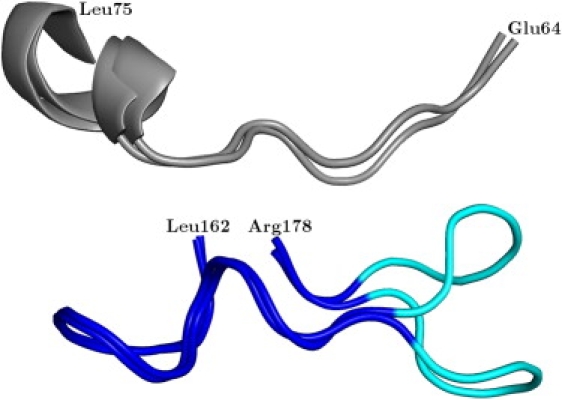
Flexibility of the Ω-loop. Whereas most of the residues of the Ω-loop are rigid during the simulations (dark blue), the flexible tip of the Ω-loop (cyan) performed an opening and closing movement by increasing and decreasing its distance to the protein core (gray). Shown are the two snapshots of the extended 50-ns simulation with the minimum and maximum distance.
Figure 4.
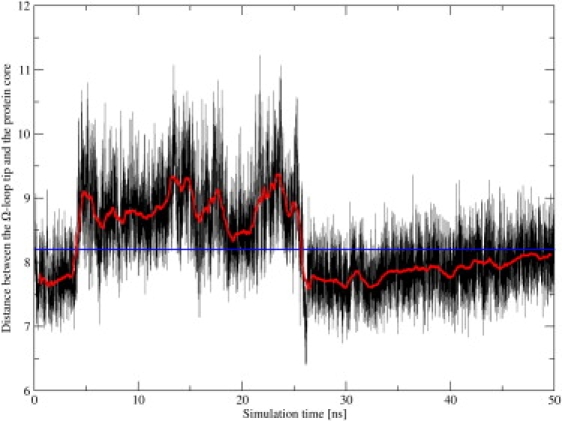
Distance between the Ω-loop tip and the residues of the protein core. Compared to the distance in the crystal structure (blue line), the distance in the extended 50-ns simulation shows an opening movement that lasts for ∼20 ns. Shown are the distance from the MD simulation sampled at 1-ps intervals (black line) and the running average over 1 ns (red line).
A change of ψAla172 from 0° to 30° at 5 ns initiated the opening movement and led to a concerted displacement of the subsequent residues 173–177 away from the protein core. At 12 ns, a sudden concerted change of ϕAla172 from 60° to −100° and of ψAla172 from 30° to 150° occurred. In addition, ψGlu171 changed from −30° to 100°. These changes had no major impact on the conformation of the flexible tip and thus the distance between the flexible tip and the protein core remained unchanged. At 23 ns, the simultaneous change in ϕPro174 and ψAsn175 from 140° to −30° and from 80° to −80°, respectively, marked the beginning of the closing movement. In consequence, residues 173–175 started to bend back toward the protein core. Two nanoseconds later, with changes in the backbone dihedral angles of Asp176 (ψ from 130° to −20°), Glu177 (ϕ from −90° to 90°), and Glu171 (ψ from 100° to 0°), the closing movement was completed (Fig. S11).
Water binding at the Ω-loop
To characterize the interaction of water molecules with the Ω-loop and adjacent residues, water bridges (WB), defined as a set of two or more non-water polar atoms of different residues that interact with a particular water molecule, were calculated. This allows us to derive temporal information like occupancies (in percent of analyzed simulation time) and exchange rates (number of different water molecules involved in forming a certain water bridge during the analyzed simulation time).
Three water bridges could be distinguished inside the Ω-loop cavity (Fig. 5), which are among the highest occupied water bridges detected and which form hydrogen bonds exclusively to main chain atoms of the adjacent residues (Table 2). WB1 connects residues Met68 and Met69 of the protein core to residues Leu169 and Asp179 of the Ω-loop and is highly occupied in all simulated systems with a low rate of exchange. WB2 connects residues Leu169 and Ala172 of the Ω-loop and is also highly occupied in all simulated systems with the exception of the extended 50-ns simulation, in which the Ω-loop changed its conformation. The exchange rate is similar to WB1. WB3 resides between residues Ile173 and Asp176 at the entrance of the Ω-loop cavity. In contrast to the other water bridges, it has a lower occupancy and a considerably higher exchange rate.
Figure 5.
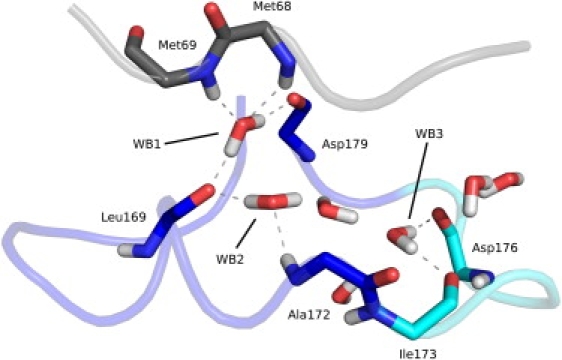
Formation of water bridges (WB1–WB3) inside the Ω-loop cavity by hydrogen bonding of water molecules to main chain atoms of the Ω-loop (blue, with flexible tip in cyan) and the protein core (gray).
Table 2.
Highly occupied water bridges in the Ω-loop cavity
| MMDwat | MMDnowat | Extendedwat | Extendednowat | SPC/Ewat | SPC/Enowat | |
|---|---|---|---|---|---|---|
| Occupancies (in percent of analyzed simulation time) | ||||||
| WB1 | 90.80 ± 5.62 | 91.11 ± 6.67 | 86.25 | 90.52 | 95.25 | 88.80 |
| WB2 | 87.49 ± 29.28 | 96.62 ± 3.37 | 93.13 | — | 99.85 | 99.90 |
| WB3 | 81.20 ± 10.51 | 81.11 ± 7.65 | 82.68 | 39.95 | 91.40 | 97.75 |
| Number of different water molecules (during the analyzed simulation time) | ||||||
| WB1 | 1.2 ± 0.4 | 1.3 ± 0.7 | 5 | 1 | 1 | 1 |
| WB2 | 1.5 ± 0.7 | 2 ± 1.4 | 16 | — | 1 | 1 |
| WB3 | 25.0 ± 6.7 | 23.8 ± 6.7 | 249 | 296 | 8 | 16 |
MMDwat and MMDnowat values represent the averages over 10 simulations.
Exchange of water molecules with the bulk solvent
During the simulations, an exchange of the water molecules in the Ω-loop cavity with bulk solvent occurs. Therefore, the paths of all water molecules that moved into the spherical region of interest were tracked. Two entry and exit points to the cavity were observed. The first entry and exit point is located at the entrance of the Ω-loop cavity near the flexible tip and was permanently present in all simulations. The second entry and exit point is located at a gap between the residues Arg164, Glu171, Ile173, Asp176, and Arg178. This water channel was temporarily formed during the simulations and was not obvious from visual inspection of the initial crystal structure (Fig. 6).
In all simulated systems, on average 90% of all water paths had a length of <1 ns, regardless of the simulated system, the solvent model, and the simulation length. These water molecules in general did not penetrate deeply into the Ω-loop cavity, but diffused from the bulk solvent to one of the two entrance points described above, where they stayed for a short amount of time before again diffusing back into the bulk solvent. However, in each simulation a small number of water paths with a length between 1 ns and 5 ns in the MMD simulations and between 1 ns and 41 ns in the 50-ns simulations was observed. These water molecules moved deeply into the inside of the Ω-loop cavity, where some of them stayed at well-defined positions corresponding to the location of the water bridges for the remainder of the trajectory (Fig. S9), while others left the Ω-loop cavity again by one of the two exit points (Fig. S10).
Although all possible combinations of entry and exit points were observed for water molecules to enter and leave the Ω-loop cavity, water entrance and exit was fourfold and 1.5-fold, respectively, more frequent via the first rather than the second entry and exit point.
Hydration of the Ω-loop cavity in simulations starting without crystal water
In the MMDnowat simulations, the crystal water molecules were excluded from the initial system preparation and therefore the Ω-loop cavity initially did not contain any water molecule. To gain insight into the process of Ω-loop solvation, all trajectories starting without crystal water molecules were visually analyzed. It was observed that the Ω-loop cavity was already solvated at an early stage of the simulations, and that the solvation process was similar in all simulations: At 20 ps, the first water molecule entered the opening of the Ω-loop cavity formed by residues 65 and 66 of the protein core and the flexible tip (residues 174–176). Soon after, further water molecules followed (Fig. 7). After 400 ps, the Ω-loop cavity was fully solvated, and the water bridges were established. From now on, water bridges in the Ω-loop cavity were identical in the MMDnowat and MMDwat simulations.
Figure 7.
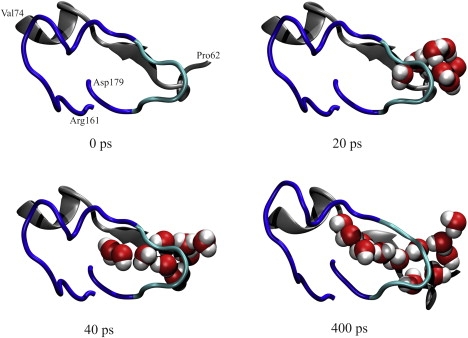
Gradual solvation of the Ω-loop cavity consisting of the Ω-loop (residues 161–179, dark blue) and residues of the protein core (residues 62–74, gray) at four different time steps of simulation MD1nowat. The first water molecules enter the cavity at 20 ps near the flexible tip (residues 173–177, cyan).
Discussion
Influence of the crystal water molecules
The comparison between simulations of the TEM β-lactamase starting either with or without crystal water molecules did not indicate any influence of the missing initial crystal waters on the MD simulations. The studied properties of protein flexibility, Ω-loop dynamics, and water binding were similar in both systems. Discrepancies in the average RMSF values around residues 70 and 130 were not significant, when taking into account the standard deviation (Ser70: RMSFnowat = 0.47 ± 0.11 Å and RMSFwat = 0.41 ± 0.06 Å; Ser130: RMSFnowat = 0.49 ± 0.09 Å and RMSFwat = 0.39 ± 0.04 Å). Regardless of the initial starting conditions, within the timescale of 1 ns, the water binding patterns at the Ω-loop of TEM β-lactamase were established, and the dynamics of the protein and of the Ω-loop were similar in both systems.
Dynamics of the TEM β-lactamase
All MD simulations performed in this work have shown that the TEM β-lactamase was stable during the timescale of the simulation. It deviated only slightly from the initial crystal structure and did not undergo significant conformational rearrangements. The dynamics and the flexibility of the protein were probed by analyzing the RMSF and S2 order parameters. From both properties, it is evident that residues located in secondary structure elements had a low flexibility and were highly ordered, in contrast to residues located in loop regions, which were more flexible and less ordered. This is in agreement with a previous short 1-ns MD simulation of the TEM β-lactamase, in which only small structural changes occurred during the simulation (10). However, a more recent 5-ns MD simulation using a different force field and water model describes a motion of one domain relative to the other by essential dynamics analysis (11). We acknowledge the observation of similar motions in our 5-ns simulations; however, the associated principal component had a considerable amount of cosine content. Thus, the adequate description of the complete global motions and dynamics of the TEM β-lactamase protein requires longer simulation times.
It was shown that the order parameter S2 for the backbone amide N-H bond vectors from NMR can be reproduced by MD simulations for residues exhibiting motions on a short timescale (41). In a recent NMR study of the TEM β-lactamase, an average generalized order parameter S2 of 0.90 ± 0.02 was determined for the complete protein, thus giving experimental evidence for a highly ordered protein (12). The average S2 for all residues calculated from our MMD simulations showed agreement with the experimental data (MMDnowat: 0.89 ± 0.04, MMDwat: 0.88 ± 0.04). The highly ordered N- and C-terminal residues and the highly ordered residues in secondary structure elements, as well as the high order of active site residues, are reproduced by the MMD simulations. With the agreement between the calculated and experimental S2, our study further strengthens the picture of the TEM β-lactamase and its overall dynamical behavior as a very compact and rigid protein. Since all other members of the class A β-lactamases have a very similar structure, this overall rigidity might be a common property of the whole protein family. While the main part of the Ω-loop is rigid with S2 comparable to residues in the protein core, the tip of the Ω-loop (residues 173–177) has a considerably higher flexibility. As observed in one of the extended simulations and indicated by the essential dynamics analysis and the distance measurements, the tip of the Ω-loop performs an opening and closing motion.
Thus, the MMD simulations can consistently explain results from previous MD simulations in the timescale of up to 5 ns, which seemed to be contradictory: Although Diaz et al. (10) observed only slight deviations from the crystal structure, in the MD simulation of Roccatano et al. (11) the tip of the Ω-loop moved closer to the core of the enzyme. Both events, the unchanged Ω-loop tip conformation and the closing movement of the tip, are part of the opening and closing motion and have also been observed in different individual 5-ns MD simulations of this work. However, the complete opening and closing motion was observed only in one of the extended 50-ns simulations, which indicates that this motion occurs on a longer timescale. This is supported by the NMR study of Savard and Gagne (12), who observed the presence of motions of the Ω-loop in the microsecond timescale. The high flexibility of the Ω-loop tip residues is also supported by the NMR analysis, which demonstrates that S2 drops from 0.91 ± 0.04 for the rigid part of the Ω-loop to 0.84 ± 0.01 for the flexible tip region (12).
The role of water in stabilizing the Ω-loop
Water is known to have a crucial role in protein structure, dynamics, and activity (42–45). The analysis of 49 of high-resolution TEM β-lactamase structures derived from proteins crystallized under different conditions led to the finding that six highly conserved crystal water molecules are associated with the Ω-loop (14). In the MD simulations of the TEM β-lactamase, only three water molecules, buried in the Ω-loop cavity, were identified to form water bridges between residues of the Ω-loop and between residues of the Ω-loop and the protein core. The location of these water bridges corresponds to the location of three conserved water molecules detected also in x-ray structures (14). The other three conserved crystal water molecules were not detected in the MD simulations and are located at the entrance of the Ω-loop cavity, close to the flexible tip of the Ω-loop. These water molecules might not have been detected by the water bridge analysis, as suitable residues are too far away to form stable water bridges or are too flexible to be occupied for a longer time.
The high residence time of the water molecules inside the Ω-loop cavity, forming highly occupied water bridges even in simulations starting without crystal water, together with their high conservation at well-defined positions in multiple crystal structures, led us to the conclusion that these water molecules are involved in stabilizing of the Ω-loop conformation and in packing the Ω-loop to the protein core. This conclusion is supported by the results of previous studies on crystallographic data of other proteins that have shown the involvement of conserved water molecules in packing loops to β-strands (46), stabilization of hairpin structures (46), and stabilization of twisted β-turns (47). It is further supported by an analysis of high-resolution protein structures, which concluded that well-resolved, internal water molecules preferentially reside near residues that are not part of an α-helix or a β-strand, and help to saturate intramolecular hydrogen-bond donors and acceptors of the protein backbone (48). Indeed, in our simulations the hydrogen bonds of the water bridges are exclusively formed by backbone atoms. It was shown experimentally that water can directly interact with the protein backbone and side chains in the protein interior (49) and that the residence times of buried water molecules are much longer than those of water molecules at the protein surface (50). A differential scanning calorimetry study has indicated that buried water molecules contribute to protein stability (51). Therefore, the water molecules packed between the Ω-loop and the protein core can provide an explanation for the rigidity of the Ω-loop and the flexibility of the tip. Whereas the main part of the Ω-loop is stabilized by water molecules, which act as structural glue, the tip of the Ω-loop lacks these interactions and thus shows an increased flexibility.
The calculation of path lines to track those water molecules that enter or leave the Ω-loop cavity led to the observation that some water molecules leave the Ω-loop cavity through a temporarily formed opening lined by the side chains of Arg164, Ile173, Asp176, and Arg178. This may help to understand the effect of the Arg164Ser or Arg164His substitution that is often observed in extended-spectrum β-lactamases. Arg164 is part of a salt bridge (Arg164-Asp179) that anchors the Ω-loop. It has been shown that substituting Arg164 by uncharged amino acids disrupts the salt bridge and the structure of the Ω-loop breaks down. As a consequence, more bulky substrates can bind to the active site (6), which leads to extended spectrum β-lactamases activity of these mutants. A conformational change of the Ω-loop in the region between residues 167 and 175 is seen in the crystal structure of variant TEM 64 (52), in which the salt bridge is disrupted by an Arg164Ser substitution and almost all conserved water molecules at the Ω-loop are missing. Taking into account our observation that conserved water molecules help to stabilize the Ω-loop, a possible explanation for the effect of the Arg164Ser or Arg164His substitution could be that the smaller side chains promote the opening of the temporary water channel and in consequence this could lead to an increase in the exchange rate of bound water molecules in the Ω-loop cavity and thus to a destabilization of the Ω-loop. However, this assumption needs further verification by detailed MD simulation studies of the mutant protein.
Acknowledgments
The authors thank Michael Lerner for providing the Python script for the order parameter calculation.
Support by the German Research Foundation (Deutsche Forschungsgemeinschaft) within the priority program “Directed Evolution to Optimize and Understand Molecular Biocatalysts” (grant No. SPP1170) is gratefully acknowledged.
Supporting Material
References
- 1.Bradford P.A. Extended-spectrum β-lactamases in the 21st century: characterization, epidemiology, and detection of this important resistance threat. Clin. Microbiol. Rev. 2001;14:933–951. doi: 10.1128/CMR.14.4.933-951.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Datta N., Kontomichalou P. Penicillinase synthesis controlled by infectious R factors in Enterobacteriaceae. Nature. 1965;208:239–241. doi: 10.1038/208239a0. [DOI] [PubMed] [Google Scholar]
- 3.Poole K. Resistance to β-lactam antibiotics. Cell. Mol. Life Sci. 2004;61:2200–2223. doi: 10.1007/s00018-004-4060-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Jelsch C., Lenfant F., Masson J.M., Samama J.P. Beta-lactamase TEM1 of E. coli crystal structure determination at 2.5 Å resolution. FEBS Lett. 1992;299:135–142. doi: 10.1016/0014-5793(92)80232-6. [DOI] [PubMed] [Google Scholar]
- 5.Vakulenko S.B., Toth M., Taibi P., Mobashery S., Lerner S.A. Effects of Asp-179 mutations in Tem(Puc19) β-lactamase on susceptibility to β-lactams. Antimicrob. Agents Chemother. 1995;39:1878–1880. doi: 10.1128/aac.39.8.1878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Vakulenko S.B., Taibi-Tronche P., Toth M., Massova I., Lerner S.A. Effects on substrate profile by mutational substitutions at positions 164 and 179 of the class A TEMpUC19 β-lactamase from Escherichia coli. J. Biol. Chem. 1999;274:23052–23060. doi: 10.1074/jbc.274.33.23052. [DOI] [PubMed] [Google Scholar]
- 7.Majiduddin F.K., Palzkill T. An analysis of why highly similar enzymes evolve differently. Genetics. 2003;163:457–466. doi: 10.1093/genetics/163.2.457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Matagne A., Lamotte-Brasseur J., Frere J.M. Catalytic properties of class A β-lactamases: efficiency and diversity. Biochem. J. 1998;330:581–598. doi: 10.1042/bj3300581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fisher J.F., Meroueh S.O., Mobashery S. Bacterial resistance to β-lactam antibiotics: compelling opportunism, compelling opportunity. Chem. Rev. 2005;105:395–424. doi: 10.1021/cr030102i. [DOI] [PubMed] [Google Scholar]
- 10.Diaz N., Sordo T.L., Merz K.M., Jr., Suarez D. Insights into the acylation mechanism of class A β-lactamases from molecular dynamics simulations of the TEM-1 enzyme complexed with benzylpenicillin. J. Am. Chem. Soc. 2003;125:672–684. doi: 10.1021/ja027704o. [DOI] [PubMed] [Google Scholar]
- 11.Roccatano D., Sbardella G., Aschi M., Amicosante G., Bossa C. Dynamical aspects of TEM-1 β-lactamase probed by molecular dynamics. J. Comput. Aided Mol. Des. 2005;19:329–340. doi: 10.1007/s10822-005-7003-0. [DOI] [PubMed] [Google Scholar]
- 12.Savard P.Y., Gagne S.M. Backbone dynamics of TEM-1 determined by NMR: evidence for a highly ordered protein. Biochemistry. 2006;45:11414–11424. doi: 10.1021/bi060414q. [DOI] [PubMed] [Google Scholar]
- 13.Massova I., Mobashery S. Kinship and diversification of bacterial penicillin-binding proteins and β-lactamases. Antimicrob. Agents Chemother. 1998;42:1–17. doi: 10.1128/aac.42.1.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bös F., Pleiss J. Conserved water molecules stabilize the Ω-loop in class A β-lactamases. Antimicrob. Agents Chemother. 2008;52:1072–1079. doi: 10.1128/AAC.01035-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hess B. Convergence of sampling in protein simulations. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2002;65:031910. doi: 10.1103/PhysRevE.65.031910. [DOI] [PubMed] [Google Scholar]
- 16.Straub J.E., Thirumalai D. Theoretical probes of conformational fluctuations in S-peptide and RNase A/3′-UMP enzyme product complex. Proteins. 1993;15:360–373. doi: 10.1002/prot.340150404. [DOI] [PubMed] [Google Scholar]
- 17.Caves L.S., Evanseck J.D., Karplus M. Locally accessible conformations of proteins: multiple molecular dynamics simulations of crambin. Protein Sci. 1998;7:649–666. doi: 10.1002/pro.5560070314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Elofsson A., Nilsson L. How consistent are molecular dynamics simulations? Comparing structure and dynamics in reduced and oxidized Escherichia coli thioredoxin. J. Mol. Biol. 1993;233:766–780. doi: 10.1006/jmbi.1993.1551. [DOI] [PubMed] [Google Scholar]
- 19.Carlson M.L., Regan R.M., Gibson Q.H. Distal cavity fluctuations in myoglobin: protein motion and ligand diffusion. Biochemistry. 1996;35:1125–1136. doi: 10.1021/bi951767k. [DOI] [PubMed] [Google Scholar]
- 20.Daggett V. Long timescale simulations. Curr. Opin. Struct. Biol. 2000;10:160–164. doi: 10.1016/s0959-440x(00)00062-2. [DOI] [PubMed] [Google Scholar]
- 21.Gorfe A.A., Ferrara P., Caflisch A., Marti D.N., Bosshard H.R. Calculation of protein ionization equilibria with conformational sampling: pKa of a model leucine zipper, GCN4 and barnase. Proteins. 2002;46:41–60. doi: 10.1002/prot.10027. [DOI] [PubMed] [Google Scholar]
- 22.Likic V.A., Gooley P.R., Speed T.P., Strehler E.E. A statistical approach to the interpretation of molecular dynamics simulations of calmodulin equilibrium dynamics. Protein Sci. 2005;14:2955–2963. doi: 10.1110/ps.051681605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Legge F.S., Budi A., Treutlein H., Yarovsky I. Protein flexibility: multiple molecular dynamics simulations of insulin chain B. Biophys. Chem. 2006;119:146–157. doi: 10.1016/j.bpc.2005.08.002. [DOI] [PubMed] [Google Scholar]
- 24.Minasov G., Wang X., Shoichet B.K. An ultrahigh resolution structure of TEM-1 β-lactamase suggests a role for Glu166 as the general base in acylation. J. Am. Chem. Soc. 2002;124:5333–5340. doi: 10.1021/ja0259640. [DOI] [PubMed] [Google Scholar]
- 25.Dolinsky T.J., Nielsen J.E., McCammon J.A., Baker N.A. PDB2PQR: an automated pipeline for the setup of Poisson-Boltzmann electrostatics calculations. Nucleic Acids Res. 2004;32:W665–W667. doi: 10.1093/nar/gkh381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Case D., Darden T., Cheatham T., III, Simmerling C., Wang J. University of California; San Francisco, CA: 2004. AMBER 8. [Google Scholar]
- 27.Duan Y., Wu C., Chowdhury S., Lee M.C., Xiong G.M. A point-charge force field for molecular mechanics simulations of proteins based on condensed-phase quantum mechanical calculations. J. Comput. Chem. 2003;24:1999–2012. doi: 10.1002/jcc.10349. [DOI] [PubMed] [Google Scholar]
- 28.Ryckaert J.P., Ciccotti G., Berendsen H.J.C. Numerical integration of Cartesian equations of motion of a system with constraints—molecular dynamics of n-alkanes. J. Comput. Phys. 1977;23:327–341. [Google Scholar]
- 29.Berendsen H.J.C., Postma J.P.M., Vangunsteren W.F., Dinola A., Haak J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984;81:3684–3690. [Google Scholar]
- 30.Darden T., York D., Pedersen L. Particle mesh Ewald: an N · log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993;98:10089–10092. [Google Scholar]
- 31.Berendsen H.J.C., Grigera J.R., Straatsma T.P. The missing term in effective pair potentials. J. Phys. Chem. 1987;91:6269–6271. [Google Scholar]
- 32.Stone, J.E., J. Gullingsrud, and K. Schulten. 2001. A system for interactive molecular dynamics simulation. In I3D '01: Proceedings of the 2001 Symposium on Interactive 3D Graphics. ACM Press, New York, NY.
- 33.DeLano, W. 2002. The PyMol Molecular Graphics System. http://www.pymol.org. DeLano Scientific, Palo Alto, CA.
- 34.Ho B.K., Gruswitz F. HOLLOW: generating accurate representations of channel and interior surfaces in molecular structures. BMC Struct. Biol. 2008;8:49. doi: 10.1186/1472-6807-8-49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Lipari G., Szabo A. Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 1. Theory and range of validity. J. Am. Chem. Soc. 1982;104:4546–4559. [Google Scholar]
- 36.Spoel D.V.D., Lindahl E., Hess B., Groenhof G., Mark A.E. GROMACS: fast, flexible, and free. J. Comput. Chem. 2005;26:1701–1718. doi: 10.1002/jcc.20291. [DOI] [PubMed] [Google Scholar]
- 37.Amadei A., Linssen A.B., Berendsen H.J. Essential dynamics of proteins. Proteins. 1993;17:412–425. doi: 10.1002/prot.340170408. [DOI] [PubMed] [Google Scholar]
- 38.Hess B. Similarities between principal components of protein dynamics and random diffusion. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 2000;62:8438–8448. doi: 10.1103/physreve.62.8438. [DOI] [PubMed] [Google Scholar]
- 39.Sanjeev B. Indian Institute of Science; Bangalore: 2004. ANKUSH software. [Google Scholar]
- 40.Bidmon K., Grottel S., Bös F., Pleiss J., Ertl T. Visual abstractions of solvent pathlines near protein cavities. Comput. Graph. Forum. 2008;27:935–942. [Google Scholar]
- 41.Philippopoulos M., Mandel A.M., Palmer A.G., Lim C. Accuracy and precision of NMR relaxation experiments and MD simulations for characterizing protein dynamics. Proteins. 1997;28:481–493. [PubMed] [Google Scholar]
- 42.Mattos C. Protein-water interactions in a dynamic world. Trends Biochem. Sci. 2002;27:203–208. doi: 10.1016/s0968-0004(02)02067-4. [DOI] [PubMed] [Google Scholar]
- 43.Despa F. Biological water: its vital role in macromolecular structure and function. Ann. N.Y. Acad. Sci. 2005;1066:1–11. doi: 10.1196/annals.1363.023. [DOI] [PubMed] [Google Scholar]
- 44.Prabhu N., Sharp K. Protein-solvent interactions. Chem. Rev. 2006;106:1616–1623. doi: 10.1021/cr040437f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Helms V. Protein dynamics tightly connected to the dynamics of surrounding and internal water molecules. ChemPhysChem. 2007;8:23–33. doi: 10.1002/cphc.200600298. [DOI] [PubMed] [Google Scholar]
- 46.Loris R., Stas P.P.G., Wyns L. Conserved waters in legume lectin crystal structures—the importance of bound water for the sequence-structure relationship within the legume lectin family. J. Biol. Chem. 1994;269:26722–26733. [PubMed] [Google Scholar]
- 47.Ogata K., Wodak S.J. Conserved water molecules in MHC class-1 molecules and their putative structural and functional roles. Protein Eng. 2002;15:697–705. doi: 10.1093/protein/15.8.697. [DOI] [PubMed] [Google Scholar]
- 48.Park S., Saven J.G. Statistical and molecular dynamics studies of buried waters in globular proteins. Proteins. 2005;60:450–463. doi: 10.1002/prot.20511. [DOI] [PubMed] [Google Scholar]
- 49.Ernst J.A., Clubb R.T., Zhou H.X., Gronenborn A.M., Clore G.M. Demonstration of positionally disordered water within a protein hydrophobic cavity by NMR. Science. 1995;267:1813–1817. doi: 10.1126/science.7892604. [DOI] [PubMed] [Google Scholar]
- 50.Otting G., Liepinsh E., Wüthrich K. Protein hydration in aqueous solution. Science. 1991;254:974–980. doi: 10.1126/science.1948083. [DOI] [PubMed] [Google Scholar]
- 51.Takano K., Yamagata Y., Yutani K. Buried water molecules contribute to the conformational stability of a protein. Protein Eng. 2003;16:5–9. doi: 10.1093/proeng/gzg001. [DOI] [PubMed] [Google Scholar]
- 52.Wang X., Minasov G., Shoichet B.K. Noncovalent interaction energies in covalent complexes: TEM-1 β-lactamase and β-lactams. Proteins. 2002;47:86–96. [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


