A Simple and Highly Sensitive Method for Magnetic Nanoparticle Quantitation Using ¹H-NMR Spectroscopy

Abstract

Iron oxide superparamagnetic nanoparticles (SPIONs) have drawn significant attention because of their potential impact on medical diagnosis and therapy. However, the difficulty of achieving reliable and standardized quantification of these nanoparticles has limited the uniform study of nanoparticle systems. Current measurement techniques have limited sensitivity, and are sophisticated and subject to individual instrumental settings. Here, a characterization method using proton nuclear magnetic resonance (¹H-NMR) spectroscopy is presented that can quantify SPIONs regardless of surface modification. In addition to routine quantification of SPIONs during nanoparticle development, the method can also be used with in vitro nanoparticle assays and potentially with tissue samples for biodistribution studies. Specifically, measurement of water relaxivity shifts (R₁ or R₂) of dissolved SPION samples is correlated with nanoparticle concentration. Unmodified and dextran- and poly(ethylene glycol)-coated SPIONs gave linear correlations between SPION concentration and R₁ and R₂ relaxivities over five orders of magnitude, to below 10 ppb iron. Quantification of SPION concentration was also demonstrated in the presence of RAW 264.7 macrophage cells. A linear correlation between the SPION concentration and relaxivities was observed to <10 ng Fe/mL. This method is a rapid and inexpensive approach for quantitation of SPIONs and exhibits a number of advantages over many of the current methods for quantitative SPION analysis.

Introduction

The development of superparamagnetic iron oxide nanoparticle (SPION) systems has been widely pursued in recent years because of their successful use as biomedical imaging (1–5) and therapeutic (6–9) agents. The preparation of SPIONs with specific coatings (e.g., dextran (10,11), polyethylene glycol (12)), surface-bound bioligands (e.g., TAT peptide (13) and transferrin (14)), and cell markers (e.g., fluorochromes) has relied upon the accurate and routine quantification of SPION concentration. In addition, nanoparticle quantification is essential for assessing SPION localization in target tissue, which is necessary to establish SPION efficacy in vivo.

To evaluate SPION concentration and uptake by cells and tissue, iron oxide nanoparticles have been labeled with near-infrared (NIR) optical tags (11,15) or radiolabels (16–18) for indirect nanoparticle quantification. Optical assessments are strictly semiquantitative, and radiolabels require highly monitored procedures for SPION preparation and use. Magnetic resonance imaging (MRI) phantoms have also been prepared for indirect nanoparticle detection, but they require tedious sample preparation, expensive equipment, and user-intensive image processing. Alternatively, the iron component of the nanoparticles can be directly detected by elemental analyses, including inductively coupled plasma atomic emission spectroscopy (ICP-AES) (19), atomic absorption spectroscopy (AAS), isotope dilution assay (IDA) by mass spectroscopy (20), and colorimetric assays (e.g., ferrozine-iron complexation (21)). Although these methods can accurately quantify iron, they require a laborious standard curve assessment each time a sample is tested (ICP-AES, AAS, and ferrozine), significant sample handling (ferrozine and colorimetric assays), or expensive, complicated systems for sample analysis (mass spectroscopy).

In addition to these basic restrictions, quantification of SPIONs in biological tissue poses additional challenges. For example, NIR fluorometry suffers from nanoparticle-related quenching effects, optical scattering, and limited sensitivity due to sample autofluorescence. The acids that are typically used during tissue homogenization can spoil a colorimetric analysis of cell/SPION samples, limiting the uniformity of the tested samples. ICP-AES, AAS, and mass spectroscopy can be complicated by iron contamination between samples, necessitating routine cleaning procedures. Lastly, IDA requires sample purification and argon matrix adjustments to ensure accurate observation of sample iron during analysis.

In the work presented here, we provide an alternative, standardized methodology that utilizes proton nuclear magnetic resonance (¹H-NMR). In this method, dissolved nanoparticles are quantified by correlating the effect of iron on the reduction of water's characteristic longitudinal (R₁) and transverse (R₂) relaxation rates with sample iron quantity. Specifically, SPIONs and tissue samples are digested and their water relaxivity is measured. The sensitivity of the method was demonstrated to 10 ppb with linear correlations of at least five orders of magnitude. This technique can be applied to routine quantification of nanoparticles, the study of in vitro samples, and tissue assessment for nanoparticle biodistribution analysis.

Materials and Methods

SPION sample preparation

Polyethylene glycol (PEG)-coated SPIONs (NP-PEG) were synthesized and coated as previously described (12), and Feridex SPIONs were commercially purchased (Advanced Magnetics, Cambridge, MA). The NP-PEG and Feridex nanoparticles were exchanged from their synthesis and storage buffers, respectively, into water by means of PD-10 columns (GE Healthcare, Piscataway, NJ). The initial SPION concentrations were determined by ICP-AES. Dilutions of each SPION system were made with deionized water, and final volumes of 200 μL were prepared with the addition of water. For the dissolved SPION samples, 100 μL DCl (Sigma, St. Louis, MO) were added to the nanoparticles at room temperature for 30 min, followed by the addition of 700 μL D₂O. Nanoparticles were confirmed as dissolved by means of dynamic light scattering analysis. Alternatively, 800 μL D₂O were added to untreated SPION NMR samples. Deuterated solvents were used to assist with NMR shimming and locking. The final sample iron concentrations of each particle system were 0, 0.01, 0.05, 0.1, and 0.5, 1, 10, 50, and 100 μg Fe/mL (500 μg Fe/mL samples were prepared for the Feridex and NP-PEG systems). Sample mixtures (800 μL) were placed in 300 MHz, 5 mm outer-diameter NMR tubes (Wilmad Lab Glass, Buena, NJ).

NMR quantitation

A standard T₁ inversion recovery pulse sequence was used to record the magnetization recovery after a 180° square pulse as a function of relaxation delay τ in ranges of 0.2–50.0, 0.01–2.5, and 0.005–0.25 s for SPION concentrations of 0–0.5, 1–50.0, and 100–500 μg Fe/mL, respectively. A standard three-parameter exponential recovery model was fitted to the data to extract the T₁ relaxation time. T₂ measurements were carried out using a standard Carr-Purcell-Meiboom-Gill (CPMG) pulse train, employing a 90° pulse followed by a delay d, at the end of which a train of 180° pulses were applied; the 180° pulses were separated in time by 2 × d. Magnetization decay data from the CPMG pulse sequence was generated by recording the free induction decay signal after progressively increasing the number of 180° pulses in the CPMG pulse train. A plot of the total time elapsed during the 180° pulse train versus the intensity recorded at the end gave a monotonic decay curve. A two-parameter monoexponential decay model was found to accurately fit the decay curve thus generated, and T₂ was obtained as one of the two parameters that describe the exponential curve. Data analysis was completed using the curvefit routine (CurveFit ©Art Palmer), as well as the Levenberg-Marquardt algorithm using the Kaleidagraph software package (Synergy Software, Reading, PA).

In vitro cell sampling

Cy5.5-NHS ester (3 mg; GE Healthcare) was dissolved in anhydrous dimethyl sulfoxide (100 μL; DMSO) and mixed with 5 mg amino-terminated NP-PEG in 100 mM Na bicarbonate, pH 8.0. Nanoparticles were mixed for 2 h at room temperature and purified by Sephacryl S-200 chromatography (GE Healthcare) against water to yield NP-PEG-Cy5.5. RAW 264.7 macrophages (ATCC, Manassas, VA) were cultured in Dulbecco's modified Eagle's medium supplemented with 10% fetal bovine serum and 1% penicillin/streptomycin. To prepare the RAW/NP-PEG-Cy5.5 standards, cells were rinsed with deionized water three times, dislodged by cell scraping, and counted with a hemacytometer. The cells were divided into samples of 1 million cells, pelletized by centrifugation, dissolved in 100 μL DCl (12 h at 60°C), and mixed with dilutions of NP-PEG-Cy5.5 as determined by ICP-AES (total volume: 400 μL SPION). Nanoparticles were allowed to dissolve for 2 h before 500 μL D₂O were added to each sample. Samples with final iron concentrations of 0, 0.01, 0.05, 0.5, 1, 10, 50, 100, and 500 μg Fe/mL were prepared. To test each cell sample by NMR, mixtures (800 μL) were placed in 300 MHz, 5 mm outer-diameter NMR tubes (Wilmad).

Fluorescence imaging

Fluorescence quantitation was completed with the use of an Odyssey infrared imaging system (Li-Cor, Lincoln, NE). For this process, 10⁶ cells of each sample were mixed with NP-PEG-Cy5.5 in 200 μL PBS, placed in a 96-well plate, and imaged at 700 nm. Absorbance intensity was measured across each well with NIH ImageJ software and plotted in arbitrary units.

Magnetic resonance imaging

MRI phantom samples were prepared by suspending 10⁶ cells treated with NP-PEG-Cy5.5 in 50 μL of 1% low-melting agarose (BioRad, Hercules, CA). Cell mixtures were loaded into a 12-well agarose sample holder and allowed to harden at 4°C. A 4.7 T Varian spectrometer (Palo Alto, CA) equipped with a Bruker magnet (Karlsruhe, Germany) and a 5 cm volume coil was used to image the MR phantom with a spin-echo multisection pulse sequence. A repetition time of 3000 ms and variable echo time of 15–90 ms were used. Imaging parameters were as follows: acquisition matrix of 256 × 128, field of view of 4 × 4 cm, section thickness of 1 mm, and two averages. Sample regions of interest were quantified by averaging the R₂ (1/T₂) signal intensity over the 5.0 mm diameter regions of interest using NIH ImageJ software.

Results

¹H-NMR for SPION analysis

Iron quantification systems typically evaluate iron content by direct analyte detection (ICP-MS, ICP-AES, etc.), whereas alternative methods increase the system signal/noise ratio (SNR) by using sample iron to catalyze the reaction of a substrate found in large quantities (e.g., N,N-dimethyl-p-phenylenediamine (22)). The latter approach can increase system sensitivity, but is limited by ligand interference and tedious sample processing. Alternatively, NMR characterization of water hydrogens in a SPION sample retains an inherently larger SNR compared to direct iron probing. Because sample water content remains consistently high between samples, the same quantity of analyte protons is observed in high (Fig. 1 a) and low (Fig. 1 b) iron concentration samples, providing NMR analysis with excellent sensitivity.

Figure 1.

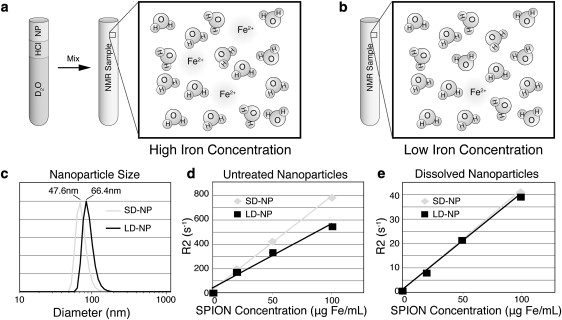
SPION sample preparation for NMR. Dissolved nanoparticle samples retain the same analyte (water protons) concentration for samples with (a) high and (b) low iron concentrations. SPION samples of (c) different hydrodynamic size have (d) different R₂ relaxation rates due to magnetic susceptibility variation. (e) Dissolved SPIONs of different sizes show similar relaxivity curves.

The magnetic susceptibility of SPIONs suspended in water can be affected by variations in size, surface coating, and functionalization (i.e., attachment of bioligands and fluorochromes). Additionally, aggregation of nanoparticles in the cellular endosome, SPION digestion by the lysosome, and complexation between the nanoparticle and cell similarly limit direct correlations between nanoparticle quantity and the sample relaxivity. This was illustrated by comparing the R₂ relaxation rates of water in the presence of small-diameter (SD-NP, 48 nm) and large-diameter (LD-NP, 66 nm) SPIONs (Fig. 1 c). Here, significant relaxivity variation was observed with a change in nanoparticle size (Fig. 1 d), as was previously demonstrated (23). To limit the effects of SPION size, or possible agglomerate contaminants in a sample, the SPIONs were dissolved in acid before analysis (Fig. 1 e). By dissolving the nanoparticle samples in acid, a single linear relaxation curve was produced, which allowed consistent iron concentration measurements to be made regardless of the original SPION sample size. All subsequent NMR studies were performed on similarly dissolved samples.

¹H-NMR parameters and data processing

Relaxivity analyses of unmodified SPION samples (bare nanoparticles without any coating) dissolved in acid are given in Fig. 2. The R₁ and R₂ values of water from each sample were generated from data collected using the inversion-recovery and CPMG pulse sequences, respectively. Here, water resonance peaks at 4.7 ppm of the pulse sequence scans were integrated to provide the raw data for relaxivity analysis. The SNR variation across different samples was found to be unnoticeable, and with the particularly low scatter observed in the raw data due to the substantial SNR of water, a three-parameter exponential recovery curve was applied to describe the R₁ data (24,25). Similarly, a two-parameter exponential decay curve described the R₂ relaxivity characterizations accurately. This feature makes the technique more robust compared to conventional analytical methods, as the characterization sensitivity is effectively unchanged over a wide range of nanoparticle concentrations that span at least five orders of magnitude (10 ng/mL to 500 μg/mL). R₁ values were obtained by fitting the model to data using the routine curvefit. In addition to performing a parameter optimization by minimizing the X² error, this fitting routine also calculates reliable statistical scatter in the fitted parameters using the Monte Carlo algorithm. To confirm accurate data fitting, the same R₁ and R₂ raw data analysis was repeated using the Levenberg-Marquardt algorithm. No noticeable differences in the values of R₁ and R₂ calculated by both methods were observed. Of interest, linear fits for both R₁ and R₂ were reasonably accurate across the entire range of data points (1 ng to 100 μg Fe/mL) (see Fig. S1 in the Supporting Material). In addition, when samples were tested with NMR machines with different field strengths (Larmor frequencies between 200–500 MHz), the R₁ values did not change significantly, and R₂ values increased moderately (Fig. S2).

Figure 2.

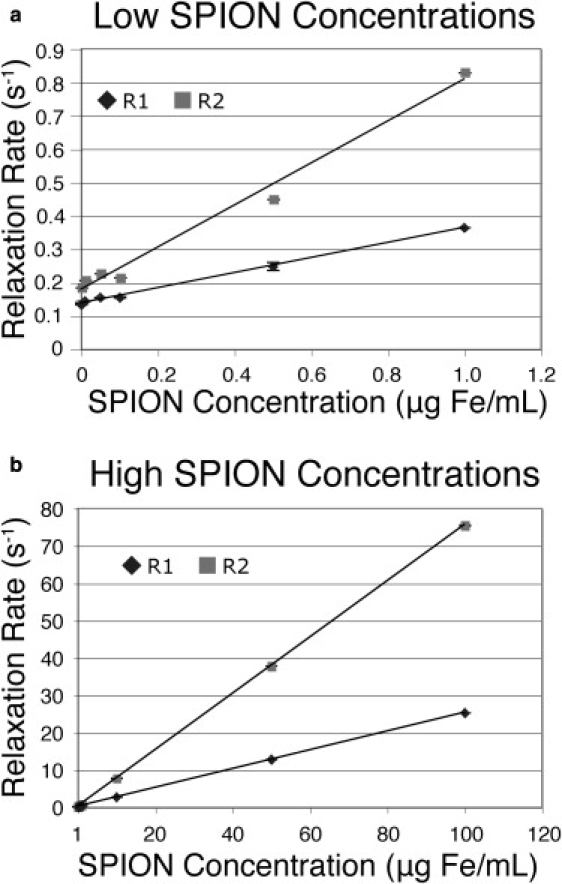
Analysis of unmodified SPIONs. Linear correlations between the concentration of dissolved, uncoated iron-oxide nanoparticles and the R₁ and R₂ of sample water were observed at both (a) low concentration (0–1 μg Fe/mL) and (b) high concentration (1–100 μg Fe/mL).

Functionalized SPION analysis

After we demonstrated the usefulness of this approach for analyzing bare iron oxide nanoparticles, we also tested its ability to analyze nanoparticle samples with coatings. SPION systems are typically modified with coatings for improved biocompatibility, steric stability, and functionalization. Feridex (an FDA-approved dextran-coated SPION) and NP-PEG were similarly prepared and analyzed to demonstrate quantitation of modified SPIONs. R₁ and R₂ analyses, as in the unmodified SPION systems, produced linear fits at high and low concentration ranges for both nanoparticle systems (Fig. 3). The slope of the Feridex nanoparticle system remained similar to that of uncoated SPIONs, whereas the NP-PEG response was lower in both the R₁ and R₂ studies. Variation in water relaxivity of these samples could be due to the dynamic equilibrium of the active silane under the acidic sample conditions that are unique to the NP-PEG system. Here, the correlations between relaxation rate and SPION concentration remained highly linear in both the high and low SPION concentration ranges, though the slopes of the linear fits varied slightly. The consistently linear behavior exhibited by relaxation of water in different systems with changing analyte concentration clearly suggests the potential of these linear graphs as standard calibration curves unique to each nanoparticle system. In this work, the measured R₁ or R₂ values of water for samples of known SPION quantity were used to accurately determine the concentration of particles for a given particle system. Standard curve sets were prepared for both nanoparticle types (Table 1). However, data fitting with a single slope across the entire range of nanoparticle samples did not provide accurate fitting for the low-concentration samples (1–500 ng Fe/mL; Fig. S3).

Figure 3.

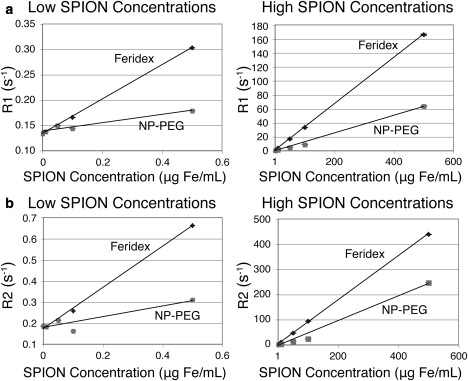
Analysis of coated SPIONs. Linear correlations of SPION concentration with (a) R₁ and (b) R₂ are observed at varying concentration ranges. SPIONs coated with dextran (Feridex) and PEG (NP-PEG) were individually tested.

Table 1.

Standard linear fit analyses of dissolved SPION systems

	R1: Standard curves
	0–500 ng/mL	1–500 μg/mL
Uncoated SPION	[Fe] = 4.518 × R1 − 0.624 (0.989)	[Fe] = 3.979 × R1 − 0.630 (1.000)
Feridex	[Fe] = 2.943 × R1 − 0.390 (0.999)	[Fe] = 3.017 × R1 − 0.435 (1.000)
NP-PEG	[Fe] = 11.27 × R1 − 1.542 (0.935)	[Fe] = 7.722 × R1 + 12.30 (0.995)

	R2: Standard curves
	0–500 ng/mL	1–500 μg/mL
Uncoated SPION	[Fe] = 1.907 × R2 − 0.978 (0.978)	[Fe] = 1.328 × R2 − 0.231 (1.000)
Feridex	[Fe] = 1.021 × R2 − 0.174 (0.997)	[Fe] = 1.144 × R2 − 2.694 (0.999)
NP-PEG	[Fe] = 3.271 × R2 − 0.558 (0.832)	[Fe] = 1.960 × R2 + 20.38 (0.989)

Iron concentration (μg Fe/mL) is given as a function of the R₁ and R₂ relaxivity of the sample water.

Correlation constants (R²) are provided in parentheses.

It should be noted that the relaxation rate for each sample is an inherent property, and thus established standard curves can be universally applied between analytical systems for samples prepared in the same manner. As such, the system is unencumbered by baseline shifts or system drift, unlike other analytical systems.

In vitro SPION uptake analysis

In vitro cell samples labeled with nanoparticles, which typically are quantified by MR phantom or fluorescence imaging, were evaluated by R₂ NMR analysis. First, the R₂ standard curves of a sample cell/SPION system were generated. RAW 264.7 macrophage cells were harvested, rinsed with water, and added to samples of increasing SPION concentration “spikes”. The tested nanoparticles were NP-PEG to which the NIR fluorophore Cy5.5 was attached (yielding NP-PEG-Cy5.5). The physical mixture of cells and nanoparticles was then dissolved in acid and prepared for R₂ quantification. A linear fit was observed between the iron concentration present and the R₂ value across high and low iron concentrations (Fig. 4 a). The linearity of the fit remained highly regular above 50 ng Fe/mL, providing a RAW/NP-PEG-Cy5.5 standard curve. The same undissolved cell/SPION samples were also analyzed by MR phantom (Fig. 4 b) and optical fluorescence (Fig. 4 c) imaging for comparative study. Quantitation by R₂ measurement with MR phantom imaging showed significant signal saturation at 100 μg Fe/mL and above, causing erratic readings (i.e., hypointense/white readings). Similarly, the optical imaging had a narrow range of linearity between 10 and 500 μg Fe/mL, with little to no signal sensitivity below 10 μg Fe/mL. The notable linearity of the NMR analysis, on the other hand, demonstrated its ability to quantify over a wider linear range with similar or better sensitivity compared to the conventional MR and optical analysis techniques.

Figure 4.

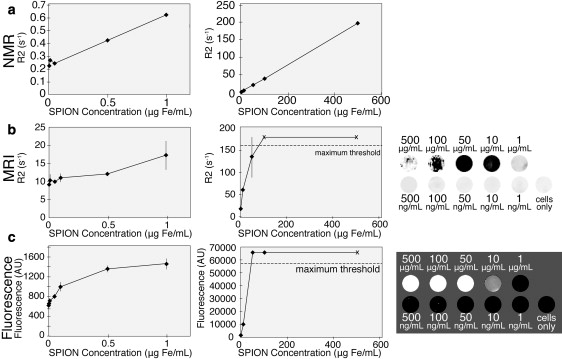
In vitro SPION analysis. (a) NMR R₂ analysis of dissolved samples of RAW macrophage cells spiked with Cy5.5-labeled nanoparticles (NP-PEG-Cy5.5). All of the samples were assessed at both low (0–1 μg Fe/mL) and high (1–500 μg Fe/mL) particle concentration ranges. (b) R₂ maps of macrophage cells and NP-PEG-Cy5.5 mixed together and cast in agarose. R₂ readings were saturated at higher nanoparticle concentrations and caused erratic, hypointense readings. (c) Optical fluorescence quantification of NP-PEG-Cy5.5 mixed with macrophage cells. Fluorescent readings were saturated at higher nanoparticle concentrations.

Discussion

In this study we have introduced a new method for quantifying SPIONs using ¹H-NMR. This technique can be applied to bare iron oxide nanoparticles, as well as SPIONs modified with different coatings and surface ligands. Nanoparticles can also be quantified in vitro with cell samples. SPIONs are typically quantified by MRI using agarose-cast phantoms, by elemental analysis, and, when modified with an optical label, by fluorescence detection (e.g., microscopy and flow cytometry). MRI has been used in the past to quantify iron content by monitoring the change in R₂ of local regions of a sample as a function of iron concentration. Applying the same principle, we found that changes in the R₁ and R₂ of the sample's solvent (i.e., water) can be used as a sensitive indicator of the quantity of paramagnetic materials, such as SPIONs and iron ions. As can be seen from the results presented here, the particularly large SNR afforded by the single NMR resonance of water in these samples makes this technique especially well suited to quantify nanoparticles in the parts-per-billion range.

The observed variation in relaxivity between dissolved samples of nanoparticles with different coatings (i.e., PEG versus dextran), and when dissolved with cells, warrants further consideration. All of these NMR analyses rely on the linear dependence of the relaxation rate on dissolved magnetic nanoparticles, utilizing the solvent relaxation rate as an indicator of solute (i.e., dissolved paramagnetic ion) concentration. This concept builds upon earlier studies of both aqueous (26,27) and organic (28) mediums. Although a rigorous theoretical model that quantitatively explains the observed NMR relaxivity changes, accounting for all possible molecular interactions, is beyond the scope of this work, a simplified physical interpretation of observed data is viable based on existing proven theoretical models of solvent molecule relaxation in the presence of paramagnetic ions and other chemical species, as outlined comprehensively in the classic review by Lauffer (29).

Two distinct relaxation mechanisms contribute to the total R₁ and R₂ relaxation enhancement of the solvent: inner- and outer-sphere relaxation. The former phenomenon is mediated primarily by chemical exchange of water, which transfers fully relaxed water protons between the volume of metal coordination sphere immediately surrounding each metal ion and the volume of solvent that is predominantly unbound with the ions (30,31). Outer-sphere relaxation is a loose term that is used to describe two relaxation mechanisms: 1), the relaxation of the layer of water molecules that are hydrogen-bonded to the inner layer of bound-water molecules (also called the “second coordination sphere”); and 2), the relaxation of bulk water molecules that move into the proximity of the metal ion by self-diffusion and remain there long enough to relax faster than what is accounted for by Brownian motion alone. Of importance, the ¹H relaxation of the water molecules that comprise the second coordination sphere is dependent on both the type and concentration of the metal ions, and also on other dissolved chemical species. In our study, these species include dissolved particle coatings and cellular debris, which affect relaxivity, as observed in Figs. 3 and 4.

To describe this observed relaxivity dependence, we will specifically evaluate R₁, which can be expressed as

$$R_1^{total}=R_1+R_{1p},$$ (1)

where R₁ denotes the relaxation rate of water molecules exclusively in the bulk (by a conventional Brownian motion mediated relaxation process), and R_1p denotes the relaxation rate of water due to the presence of paramagnetic ions. R_1p can be further expanded into

$$R_{1p}=R_1^{inner}+R_1^{outer}\text{.}$$ (2)

As is the convention, R₁^outer comprises the “second sphere” relaxation rate and the relaxation mediated by self-diffusion. The term R₁^inner is given by

$$R_1^{inner}=\frac{P_{m}q}{T_{1M}+t_M},$$ (3)

where t_M is the average residence time of water protons bound to the metal ion, P_m is the molar fraction of metal ions, q is the number of water molecules in the inner coordination sphere of the metal ion, and T_1M is the relaxation time of the solvent molecules bound directly to the metal ion, expressed by the Solomon-Bloembergen (SB) equations (26,32). From this model, we note that the inner water shell is not affected by dissolved species, including nanoparticle coat materials. Indeed, a model that is dependent only on inner sphere water relaxation and the conventional R₁ mediated through the dynamic modulation of proton-proton dipolar coupling due to Brownian motion can provide a universal linear relationship between the relaxation rate of water and the dissolved concentration of Fe³⁺. On the other hand, the quantitative expression of R₁^outer is influenced by the presence of added materials to an aqueous paramagnetic solution. Specifically, R₁^outer is given by

$$R_1^{outer}=\frac{{CN}_S{g}_1^2{g}_s^2{h}^{2}S(S+1)}{4{pd}^3{t}_D}\left[7I\left(w_s{t}_D{T}_{1e}\right)+3I\left(w_I{t}_D{T}_{1e}\right)\right],$$ (4)

where N_S is the number of metal ions per cubic centimeter, d is the distance of the closest approach of the solvent molecule to the metal-inner-sphere water complex that could include the molecules from the coat material, and t_D is the relative translational diffusion time. The other variables are not directly impacted by the addition of other chemical species in the NMR sample. Of importance, t_D is defined by the following relation:

$$t_D=\raisebox{1ex}{$d^2$}\!\left/ \!\raisebox{-1ex}{$3\left(D_I+D_S\right)$}\right.\text{.}$$ (5)

Here, D_I and D_S are the diffusion coefficients of water and the metal complex, respectively. It should be noted that R₁^outer is directly proportional to N_S scaled by the cube of d, the distance between the closest outer-shell water molecules and the metal ion. Together, the term N_S/d³ (Eq. 4) represents an “average concentration” of metal ions that is directly determined by the volume defined by the length scale, d. With the addition of other molecules (i.e., coating materials) to the metal ion and water mixture, the term d can fluctuate due to “interference” caused by the third component. Based on the change in relaxivities observed in Figs. 3 and 4, it is reasonable to see the effect that dissolved coatings and cellular debris can have on the average d, thereby weighting the effective concentration of the dissolved metal ions.

We can therefore see that the total relaxation rate of solvent molecules due only to the presence of paramagnetic centers (R_1p) is linearly scaled by the effective concentration of the dissolved paramagnetic ions, which can differ between varying, dissolved SPION preparations. This model describes the relaxivity data observed in this work, as well as the linear dependence of the relaxation rates of solvent molecules over the range of SPION concentrations analyzed.

Although alternative quantitative systems can be affected by problems such as system drift (elemental analysis) and quenching (fluorescence reporting), the ¹H-NMR method of nanoparticle quantification given here provides linear curves that are not affected by similar issues. The highly linear correlations between iron content and R₁ and R₂ below 10 ppb indicate that this technique provides exquisite sensitivity while also retaining the flexibility to quantify varying SPION systems. A similar strategy using acid-digested cell samples was reported in previous studies that employed ferrous chloride iron standards to create a standard curve (33,34). However, our study demonstrates that sample relaxivity is sensitive to sample impurities, such as the dissolved SPION coating and cellular debris, which means that calibration curves must be prepared using the same nanoparticle construct employed in test samples and with cell digests for in vitro cell samples. With these precautions, we believe that this method could be further expanded to analysis of tissue samples drawn from in vivo SPION testing, and anticipate its practical integration into automated NMR systems in future investigations.

Relaxivity analysis by ¹H-NMR retains key benefits that are important for nanoparticle quantification, including 1), highly linear and “permanent” standard curves for diverse SPION systems; 2), large SNR at all sample concentrations; 3), direct measurement of SPIONs (i.e., with no need for chemical labels); 4), the ability to quantify coated or conjugated SPIONs; 5), no system contamination issues; and 6), the ability to use homogenized samples and signal averaging, which limits spectral heterogeneity. Although the solvent relaxation rates in the presence of paramagnetic ions do depend on the Larmor frequency, the variation for the SPION systems studied here was found to be rather small, within the usual range of NMR spectrometer frequencies routinely employed as analytical tools (Fig. S2). This implies that quantitative assessments based on R₁ measurement can be made with NMR machines of varying size, and standards can be used between analytical systems. The implementation of standardized characterizations for emerging nanotechnologies will be reliant on sensitive, flexible analytical methodologies that are widely available, such as ¹H-NMR.