Counteraction of Urea by Trimethylamine N-Oxide Is Due to Direct Interaction

Abstract

Trimethylamine N-oxide (TMAO) is a naturally occurring osmolyte that stabilizes proteins, induces folding, and counteracts the denaturing effects of urea, pressure, and ice. To establish the mechanism behind these effects, isotopic substitution neutron-scattering measurements were performed on aqueous solutions of TMAO and 1:1 TMAO-urea at a solute mole fraction of 0.05. The partial pair distribution functions were extracted using the empirical potential structure refinement method. The results were compared with previous results obtained with isosteric tert-butanol, as well as the available data from spectroscopy and molecular-dynamics simulations. In solution, the oxygen atom of TMAO is strongly hydrogen-bonded to, on average, between two and three water molecules, and the hydrogen-bond network is tighter in water than in pure water. In TMAO-urea solutions, the oxygen atom in TMAO preferentially forms hydrogen bonds with urea. This explains why the counteraction is completed at a 2:1 urea/TMAO concentration ratio, independently of urea concentration. These results strongly support models for the effect of TMAO on the stability of proteins based on a modification of the simultaneous equilibria that control hydrogen bonding between the peptide backbone and water or intramolecular sites, without any need for direct interaction between TMAO and the protein.

Introduction

Trimethylamine N-oxide (TMAO) is a naturally occurring osmolyte that counteracts the denaturing effects on proteins of urea (1), pressure (2), and ice (3); induces folding (at least at pH values above its pKa (4.7) (4)); and increases attractive intermolecular interactions in protein solutions, whereas urea decreases them. These effects, which may have different causes, could have significant applications because the protective osmolytes reduce endoplasmic reticulum stress, which is an important factor in diseases such as Type II diabetes (5).

Thermodynamic studies on the influence of TMAO on protein stability (6), folding (7), and crystallization (8), and its counteraction of urea over a wide range of concentrations have led to the conclusion that counteraction is a property of the solvent system. TMAO/water is a poorer solvent for the polypeptide backbone than buffered water, whereas urea/water is a better solvent (7). However, the mechanism of counteraction of urea and TMAO, which are generally assumed to act independently, has remained elusive and there is no consensus regarding interpretation of the experimental data or the results of molecular-dynamics (MD) simulations. Direct interactions between TMAO and urea have been considered, but were hitherto not clearly established. The effect of TMAO on the dilution heat of urea was interpreted as a sign of direct interaction, confirming contact data in MD simulations, but this was not considered to be the major cause of counteraction (9). Although crystals of a 4:1 urea-TMAO complex were obtained from an aqueous solution, albeit in narrowly defined conditions, it was assumed that urea-TMAO complexes can only exist in anhydrous organic solvents (6).

NMR spin relaxation measurements indicate that TMAO (0.35 M) nearly uniformly increases protein rigidity in the presence of denaturant (0.7 M GuHCl) (10), and that specific protein binding is not involved, as was previously concluded on the basis of binding studies (1) and MD simulations (9). NMR data on water self-diffusion also indicate that the structure of water is more compact and rigid in TMAO solutions at concentrations up to 6 M (11). In contrast, however, a ²H-NMR study on separate solutions of TMAO or tetramethylurea, made at concentrations of <0.22 M to avoid hydration shell overlap and solute-solute interactions, indicated that the two osmolytes have virtually the same effect on the dynamics of their first hydration shell, as monitored by the relaxation times of water (12). This was taken as an indication that TMAO and tetramethylurea, a strong denaturant, do not act indirectly via solvent perturbation, but rather by direct interaction with the protein.

A number of MD simulations of aqueous solutions of TMAO or urea, and of the interaction between them (13,14) or with proteins (see Beck et al. (15) and references therein) have also sometimes yielded contradictory results. Therefore, the aim of the experiments presented here was to establish the influence of TMAO on the average structure of water, and to verify to what extent it is counteracted by urea. The results indicate that TMAO considerably alters the structure of water and preferentially interacts with urea, providing an important benchmark for MD simulations. They also lend strong support to a model for the effect of TMAO on protein stability based on a modification of the simultaneous equilibria that control hydrogen bonding between the peptide backbone and water or intramolecular sites, without any need for direct interaction between TMAO and the protein (7).

Materials and Methods

Solutions were prepared by accurately weighing H₂O, D₂O, and oven-dried (CH₃)₃NO (TMAO; Aldrich, Gillingham, UK), (CD₃)₃NO (TMAO-D9; Cambridge Isotope, Andover, MA), (H₂N)₂CO (urea; Aldrich) and (D₂N)₂CO (urea-D4; Aldrich). Their densities were determined before the measurements by weighing 1 mL of solution, and checked after the measurements with an Anton Paar DMA58 densitometer. The pH values of the TMAO and 1:1 TMAO-urea solutions were 9.2 and 9.1, respectively, at 298 K. The osmolyte concentrations were chosen to obtain a fraction of substituted hydrogen sites above 10% of the total number of atomic sites in the mixture as required to obtain an ∼1% second-order difference signal. The compositions of the different solutions used are given in Table 1. Samples A1–A3 give access to the TMAO-TMAO correlations via the pair distribution function of the methyl hydrogen sites, whereas the combination of B4, B5, and A2 yields the water-water correlations via the pair distribution function of the water hydrogen sites. The additional measurements C6 and C7 can be combined with A2, and subtraction of the results obtained in the two previous series yields the TMAO-water interactions via the pair distribution function of the TMAO methyl hydrogens and the water hydrogens.

Table 1.

Composition of the TMAO and TMAO-urea solutions used for neutron scattering

TMAO series			TMAO-urea series
Sample	Solute	Solvent	Sample	Solute	Solvent
A1	2.5 M TMAO	D2O	D1	2.5 M TMAO + 2.5 M urea-d4	D2O
A2	2.5 M d-TMAO	D2O	D2	2.5 M d-TMAO + 2.5 M urea-d4	D2O
A3	1.25 M TMAO 1.25 M d-TMAO	D2O	D3	1.25 M TMAO + 1.25 M d-TMAO + 2.5 M urea-d4	D2O
B4	2.5 M d-TMAO	H2O	E4	2.5 M d-TMAO + 2.5 M urea	H2O
B5	2.5 M d-TMAO	1:1 H2O/D2O	E5	2.5 M d-TMAO + 1.25 M urea + 1.25 M urea-d4	1:1 H2O/D2O
C6	2.5 M TMAO	H2O	F6	2.5 M TMAO + 2.5 M urea	H2O
C7	1.25 M TMAO 1.25 M d-TMAO	1:1 H2O/D2O	F7	1.25 M TMAO + 1.25 M d-TMAO 1.25 M urea + 1.25 M urea-d4	1:1 H2O/D2O

Similarly, for the TMAO-urea-water system, the TMAO-TMAO correlations are obtained from samples D1–D3, and the water/urea-water/urea correlations are obtained from the combination of E4 and E5 with A2. The TMAO-water/urea correlations in this system are obtained from the results of F6 and F7 combined with those of A2, and subtraction of the results of the D and E samples.

The neutron-scattering patterns of the solutions were measured on the Small Angle Neutron Diffractometer for Amorphous and Liquid Samples (SANDALS) at the ISIS Pulsed Neutron Facility of the Rutherford Appleton Laboratory (Chilton, UK). The samples were contained in flat 1 mm thick cells with 1 mm thick Ti_0.68Zr_0.32 alloy walls with a zero coherent neutron-scattering cross section, and placed in a thermostated (313 ± 1 K) sample-changer. Data were collected for each sample in two periods of 4 h. Vanadium calibration samples, empty instrument samples, and empty cells were each collected for 3 h. Scattering data were collected in the range of 3° ≤ 2θ ≤ 40° (2θ: scattering angle) and analyzed using neutron wavelengths between 0.05 and 3.5 Å to cover the range of momentum transfer (Q) 0.175 ≤ Q ≤ 50 Å⁻¹.

The experimental data were corrected for absorption and multiple and inelastic scattering, and normalized to the incoherent scattering of vanadium using the GUDRUN program package (16), which yields the total structure factors S(Q). Single atom scattering and inelasticity corrections were made as previously described by Soper and Luzar (17). Scattering lengths of C = 6.646 fm, N = 9.36 fm, O = 5.803 fm, H = −3.739 fm, and D = 6.671 fm were used in the calculations.

The empirical potential structure refinement (EPSR) method (18) was used to obtain an ensemble of structural models for the solutions containing only TMAO, and another one for the solutions containing TMAO and urea. Each ensemble simultaneously fits all seven measured structure factors for the corresponding set of solutions. Atomic partial pair distribution functions (PPDFs), g(r)_X-Y (where the label X-Y corresponds to the distribution of atoms of type Y around those of type X), were extracted for the two systems. The atom types are referred to by the symbols in Table 2.

Table 2.

Lennard-Jones and charge parameters used for the reference potentials that seed the EPSR models of the TMAO-water and TMAO-urea-water solutions

	Atom type	E, kJ/mole	σ, Å	q, e	q, e∗
TMAO	CM	0.39	3.70	−0.26	−0.2068
	HM	0.065	1.80	0.11	0.1845
	N	0.711	3.25	0.44	−0.4521
	O	0.585	3.08	−0.65	−0.5883
H2O	Hw	0.0	0.0	0.4238	0.410
	Ow	0.65	3.17	−0.8476	−0.820
Urea	Cu	0.439	3.75	0.142	−1.157
	Ou	0.878	2.96	−0.39	−0.701
	Nu	0.711	3.25	−0.542	−1.034
	Hu	0.0	0.0	0.33	0.403

Note that the charges are the same as in Paul and Patey (13), but differ significantly from those in the last column, which were used in other works (9,27). The MCY potential (47) was used for the water-water interactions by Noto et al. (27).

^∗Values taken from previous studies (12,23).

The geometry of TMAO was obtained by averaging equivalent bond distances in the crystallographic model (19) (distances C-H: 0.969 Å, C-N: 1.492 Å, N-O: 1.403 Å, with all bond angles equal to 109.5°) and the charges were taken from the literature (20). The geometry of urea was optimized with the program Ghemical (http://www.bioinformatics.org/ghemical) (distances C-N: 1.39 Å, N-H: 1.01 Å, C-O: 1.22 Å and angles H-N-H: 118.9° and N-C-N: 117.0°). For water, OH distances of 0.976 Å and an H-O-H angle of 104.2° were used. The Lennard-Jones parameters and charges used to seed the EPSR models are given in Table 2. The boxes of molecules used to model the TMAO-water and TMAO-urea-water solutions had side lengths of 34.25 Å and 35.53 Å, respectively, which were set to give an atomic density for the solutions of 0.103 atoms Å⁻³. The TMAO-water simulation consisted of 60 TMAO molecules in 1100 water molecules, whereas the TMAO-urea-water simulation consisted of 60 TMAO molecules, 60 urea molecules, and 1100 water molecules.

Results and Discussion

Structural information on the TMAO and TMAO-urea solutions was extracted by hydrogen-deuterium substitution by measuring neutron scattering from the 14 solutions in Table 1. The experimental structure factors S(Q) and the fits obtained with the EPSR method (18) for all solutions are shown in Fig. 1. The poorer fit for Q < 2.5 Å⁻¹ is due to inaccuracies in the inelasticity correction, which introduces significant uncertainties for samples that contain hydrogens. An accurate correction would require a good model of the dynamic scattering law over a very wide range of energy transfers, which is not generally available. However, recent calculations of the inelastic scattering using a realistic model of the vibrational and librational motions (21) clearly demonstrate that, after the results from many detectors at different scattering angles are merged, as is done on SANDALS, the inelasticity effect is rather monotonic with increasing Q. It is thus unlikely to cause structure-like features in the data that could significantly prejudice the outcome of further data analysis. Needless to say, the EPSR method, which is based on models using three-dimensional arrays of atoms and molecules, cannot fit such unphysical features. Consequently, the discrepancy between fit and data emerges particularly at low Q, where the inelasticity effect is most pronounced on a time-of-flight neutron source. Inelastic effects certainly intrinsically limit the accuracy of the experimental data, but since they cannot be quantified, it is impossible to say what the systematic uncertainty actually is. Given the difficulty of removing inelasticity effects, the fits at low Q are in this case quite good. The only other significant uncertainty is statistical in nature, but this is too small to be visible on the scale of the graphs.

Figure 1.

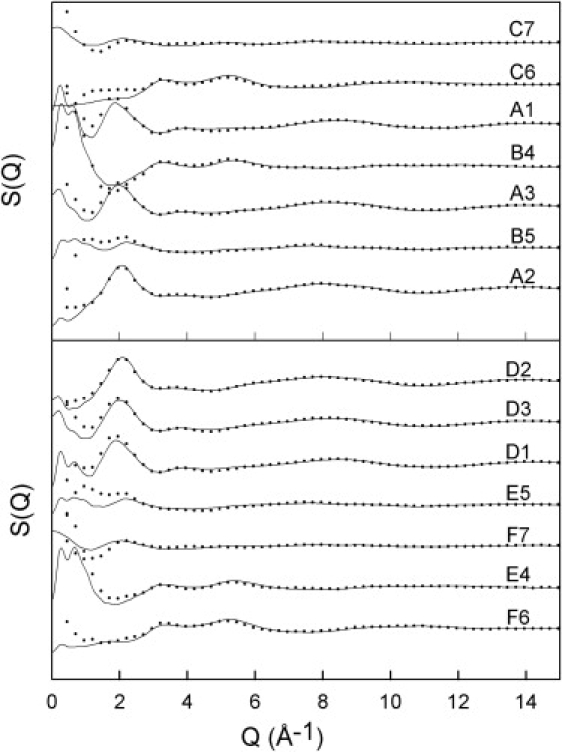
Structure factors S(Q) for the TMAO and 1:1 TMAO-urea solutions in water obtained by neutron scattering (dots) and corresponding EPSR fits (solid lines) for the samples in Table 1. The errors on the experimental data and on the fits are smaller than the size of the dots. The poorer fit for Q < 2.5 Å⁻¹ is due to uncertainties in the corrections for the inelastic scattering contributions, and to the finite size of the integration box in the simulations.

Isotopic substitution provides a degree of structural contrast within the set of experimental data. This helps us separate partial structure factors (S_XY) corresponding to the contribution to the total scattering of all pairs of atoms of types X and Y, corresponding to the symbols in Table 2 (22). If ρ is the atomic number density of the sample, the partial structure factors are related to the corresponding PPDFs, g_XY(r), by:

$$S_{XY}\left(Q\right)-1=4\pi \rho \underset{0}{\overset{\mathrm{\infty }}{\int }}{r}^2(g_{XY}\left(r\right)-1)\frac{\sin Qr}{Qr}dr$$

The g_XY(r) is related to the probability of finding an atom of type Y at a distance r from an atom of type X located at the origin. The average number of atoms (n_XY) of type Y with concentration c_Y surrounding the central X-atom in a shell extending from r₁ to r₂ can be readily obtained by integrating the PPDFs:

$$n_{XY}=4\pi c_Y\rho {\int }_{r_1}^{r_2}{g}_{XY}\left(r\right)r^{2}dr$$

Integration of the first peak of the g(r) gives the number of nearest neighbors or the coordination number. Note that because the discrepancies between experimental and calculated S(Q) only occur at Q < 2.5 Å⁻¹, any error that they might introduce will not contribute to oscillations in the g(r) at short and middle distances, on which the conclusions of this work are based.

The first two shells in the g(r)_Ow-Ow of TMAO and (1:1) TMAO-urea solutions are very similar, but the second shell differs significantly from that of pure water (Fig. 2). The first maximum of g(r)_Ow-Ow is slightly higher for the solutions than for pure water, whereas the second shell is broader, with a somewhat bimodal appearance. This result is compatible with a water structure that is more compact but has less long-range order. The g(r)_Ow-Hw (see Fig. S1 in the Supporting Material) also suggests that the local structure of water is more compact, and that addition of urea to a TMAO solution has little influence. The g(r)_Ow-Hw and g(r)_Hw-Hw are less affected by the presence of solute than g(r)_Ow-Ow. A similar effect was previously observed with a 9 M urea solution; however, in that case the g(r)_Ow-Ow clearly indicated an expansion of the second shell (see Fig. 4 in Soper et al. (23)). The effects observed here are not due to the difference of temperature between the water and solution data. If anything, the g(r)_Ow-Ow of water would be expected to be shifted to slightly higher distances at 313 K than at 298 K (24).

Figure 2.

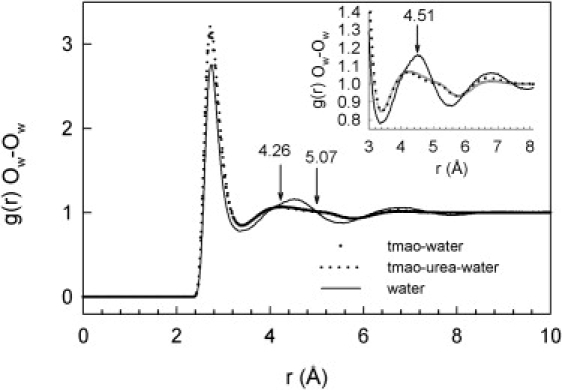
PPDF of the water oxygens, g(r)_Ow-Ow, in pure water at 298 K (24) and in aqueous solutions of TMAO and 1:1 TMAO-urea at 313 K.

These results can be compared with those obtained with tert-butanol (TBA), which is isosteric with TMAO but has quite different properties (25). In particular, unlike TMAO, it has a tendency to aggregate in solution at mole fractions above 0.025 (26). The changes between first-neighbor distances in water and TMAO or TBA solutions are very limited (Fig. 3) and the coordination numbers (n_Ow-Ow = 4.3) confirm that the tetrahedral coordination of water is not significantly affected. In contrast, there are very significant differences in the distribution of second neighbors. The number of neighbors in the second shell of TBA (3.5Å ≤ r ≤ 5.5 Å) is 12.9, whereas for TMAO it is 18.3 and the shell extends both to shorter distances, consistent with the shift of the O_w-H_w distribution to shorter distances than in water (Fig. S1), and to longer distances (3.4 Å ≤ r ≤ 5.9 Å).

Figure 3.

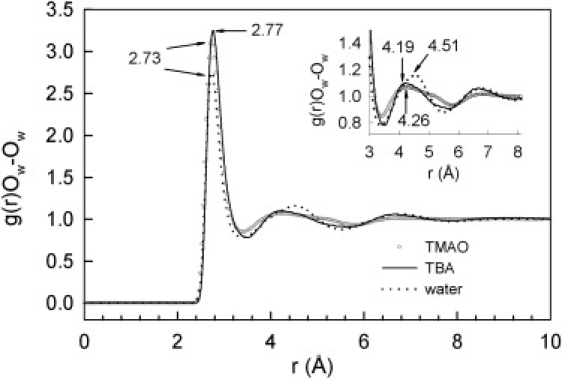
Comparison of the g(r)_Ow-Ow of the oxygen atoms in water in aqueous solutions of TBA or TMAO at similar concentrations (mole fraction TMAO: 0.05; TBA: 0.06 (25)) with that of pure water (24). The TBA curve was linearly interpolated to 313 K using the data obtained at 298 K and 338 K (25).

Hydrogen bonding between the TMAO oxygen and water (Fig. 4) gives a characteristic peak in the g(r)_O-Hw at shorter distances than the first maximum of g(r)_O-Ow (2.67 Å). The first peaks in the g(r)_O-Ow and g(r)_O-Hw for TMAO are higher than those for TBA, and the coordination numbers (n_O-Ow = n_O-Hw = 2.5 ± 0.1) indicate that on average between two and three water molecules donate a hydrogen to the oxygen atom in TMAO. For TBA, n_O-Hw = 1.3 (25), but because the hydroxyl group of TBA donates a hydrogen to a water molecule, n_O-Ow = 2.2. Similar ratios of the first maxima for TBA and TMAO solutions were found in some previous MD simulations (9,27). Infrared studies on TBA and TMAO solutions at mole fractions up to 0.05 indicated that the TMAO oxygen forms stronger hydrogen bonds with two water molecules than TBA (26), as confirmed by the relative positions of the first peaks in the g(r)_O-Hw of TMAO and TBA solutions (Fig. 4).

Figure 4.

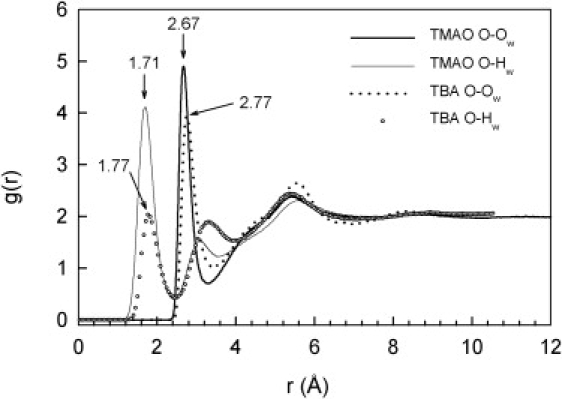
Comparison of the PPDFs of the oxygen atoms (g(r)_O-Ow) and hydrogen atoms (g(r)_O-Hw) of water around the oxygen atom of TMAO or TBA in aqueous solutions (mole fraction TMAO: 0.05; TBA: 0.06).

In MD simulations, the threefold coordination of the TMAO oxygen was interpreted as a single site reflecting the symmetry of the molecule (15), although in the crystals of TMAO dihydrate (19) and the urea-TMAO complex (28) the TMAO oxygen is involved in two or three hydrogen bonds, respectively, in a pyramidal arrangement. In the crystal structure of TMAO dihydrate (19) the TMAO oxygen is coordinated to two water molecules through nearly linear hydrogen bonds with O-H_w distances of 1.83 Å and O-O_w distances of 2.68 Å and 2.71 Å. The O-H_w distances to the second hydrogen atoms in the two water molecules are 2.99 Å and 3.09 Å, corresponding to the position of the second maximum in the g(r)_O-Hw.

The first maximum in the N-H_w distribution (Fig. S2) is at too large a distance (2.79 Å) to correspond to a hydrogen bond. As expected, no short distance peak is observed in a comparison of the CM-O_w and CM-H_w PPDFs (Fig. S3), confirming the preferential orientation of the water oxygens toward the methyl groups, which maximizes hydrogen bonding. This effect is also responsible for the slower reorientation dynamics of water in the solvation shell of hydrophobic moieties observed for amphiphilic molecules such as TMAO in previous NMR (12) and mid-infrared pump-probe experiments (29).

Fig. 5 illustrates that urea interacts directly and nearly quantitatively (n_O-Hu ≈ 0.9) with TMAO through somewhat longer O^…H-N hydrogen bonds (1.83 Å). It is expected that adding another equivalent of urea to the solution would completely eliminate strong direct interactions between the TMAO oxygen and water.

Figure 5.

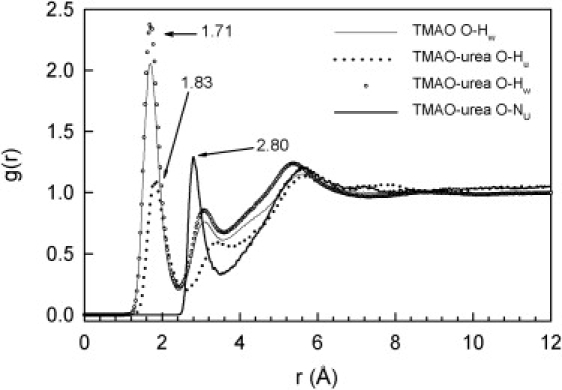
PPDF around the oxygen atom in TMAO of the water hydrogen atoms in aqueous solutions of TMAO and 1:1 TMAO-urea (mole fraction TMAO: 0.05) and of the urea hydrogen atoms in a 1:1 TMAO-urea solution (mole fraction TMAO: 0.05).

When comparing PPDFs with the results of MD simulations, one can test the reliability of the simulations by assessing their ability to reproduce the PPDFs for pure water. The g(r)_Ow-Ow values for pure water calculated from synchrotron radiation x-ray scattering data obtained by real-space methods, and neutron-scattering data obtained by EPSR (24) with SPC/E (30) as the reference potential, are in excellent agreement (31), as are the results of simulations performed with different empirical force fields (16). The F3C model, which is popular among biophysicists, reproduces the main features of g(r)_Ow-Ow, in particular below the third maximum, but predicts a first coordination shell at somewhat shorter distances than those experimentally observed (32). A comparison of the F3C model (D. A. C. Beck and V. Daggett, University of Washington, S. Paul and G. N. Patey, University of British Columbia, personal communication, 2009) and the SPC/E model (Paul and Patey, personal communication) used in recent MD simulations on TMAO solutions is given in Fig. S4. The height of the first shell is somewhat overestimated in both models, whereas the second maximum is broader than in the experimental data and the F3C model significantly deviates from the experimental data above the second shell. The agreement between the results for water obtained in a recent MD study (11) of TBA and TMAO solutions at mole fractions of 0–0.1, using the TIP3P model of water (Fig. S5), is much poorer. In that study, it was concluded that the g(r)_Ow-Ow is unaffected by the presence of the solutes (see Fig. S6 and Fig. S7), in clear contradiction to the neutron-scattering data for TBA/water mixtures (25) and our results for TMAO/water. The PPDFs g(r)_N-Ow, g(r)_CM-Ow, g(r)_N-N, and g(r)_CM-CM (Fig. S8, Fig. S9, Fig. S10, and Fig. S11), also do not agree with those obtained by isotopic substitution. In another comparison of the effects of TBA and TMAO on the structure of water, it was found that neither of the two solutes significantly changes the structure of water (33). The compaction of the water structure found experimentally for TBA (g(r)_Ow-Ow) is not reproduced, but the main features of g(r)_O-Hw and the ratios of peak heights (including the fact that the height of the first peak for TMAO is about twice that of TBA) are. Although interaction energies are more favorable for TMAO-water than TBA-water hydrogen bonds in this simulation, the maxima of the first peak in the g(r)_O-Hw for TBA and TMAO occur at a very similar distance (1.7 Å).

A previous MD study on the counteraction of urea by TMAO (9) also concluded that TMAO does not significantly affect the structure of water, but for very different reasons: the correct g(r)_Ow-Ow of the F3C water model (Fig. S2) was unfortunately substituted for another curve. However, this mishap, which was also propagated in a recent review article (15), should not affect other results and conclusions in these studies (V. Daggett, University of Washington, personal communication, 2009). When compared with the experimental water curve or the correct F3C water model, there are some differences between the PPDFs of water oxygens in pure water and TMAO/water (Fig. 6). The simulation overestimates the amplitude of the first maximum, whereas the second shell, which also has a somewhat bimodal appearance, is less extended to shorter distances than in the experimental data. Other MD simulations for a 7.4 M urea/3.7 M TMAO mixture (13) also revealed an increase in the first maximum of the g(r)_Ow-Ow (Fig. S12), but none of the significant differences in the second water shell observed here for the TMAO-urea solution or in other simulations (15) were reproduced.

Figure 6.

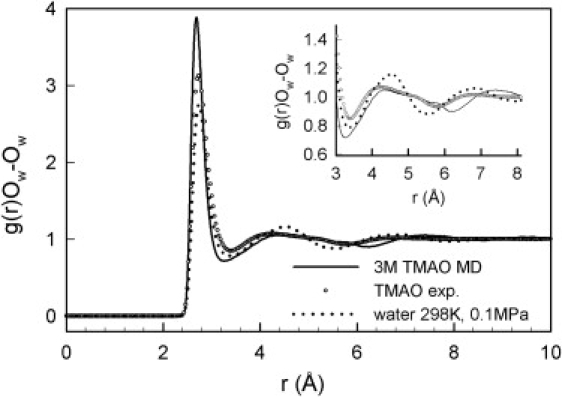
Comparison of experimental PPDF of the water oxygens (g(r)_Ow-Ow) of pure water and of a 2.5 M aqueous solution of TMAO (mole fraction TMAO: 0.05) with the results of MD simulations of a 3 M TMAO solution using the F3C model for water (15).

An independent check of the plausibility of the simulations is provided by a comparison with neutron-scattering data for concentrated (9 M) urea solutions (23), which indicates that all three site-site PPDFs of water (O_wO_w, O_wH_w, and H_wH_w) are significantly affected by the presence of urea. In the experimental data (23), the first shell is enhanced and the second one is destroyed and shifted to higher r-values, but further shells do not seem to be affected (Fig. 7). The results of the first set of simulations are not very sensitive to urea concentration (see, e.g., Fig. 22.2 in Beck et al. (15)). The distances in the first water shell are somewhat too short, whereas the third shell appears at too large distances. The second set of simulations (13) fails to reproduce the changes in the second shell, also when compared to the simulated pure water.

Figure 7.

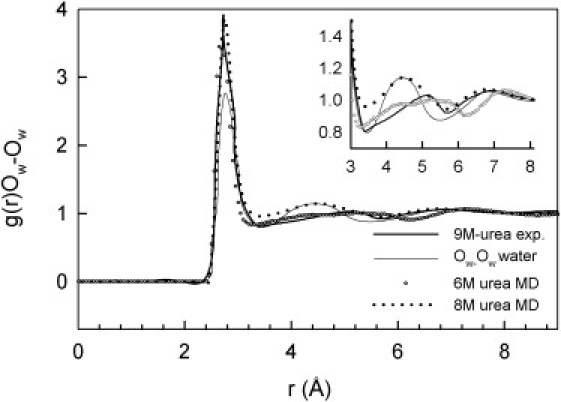
Comparison of the experimental g(r)_Ow-Ow of the oxygen atoms in pure water and in 9 M urea (23) with the results of MD simulations for 6 M urea (15) and 8 M urea (13).

Because the MD simulations of various groups are based on two very different sets of charges, the EPSR calculations were run with the two sets in Table 2 (Fig. S13, Fig. S14, Fig. S15, Fig. S16, and Fig. S17). Although there are significant differences between the g(r) values, none of these affect the main conclusions of this work. The inability of MD simulations to reproduce the individual PPDFs, and hence also the experimental neutron-scattering data S(Q) in Fig. 1, casts some doubt on their ability to reliably predict the dynamical properties of solutions. However, a comparison with the experimental evidence remains useful if only because the simulations quite consistently predict that TMAO 1), slightly increases the number of hydrogen bonds per water; 2), leads to stronger water hydrogen bonds, with the length of water hydrogen bonds shifting to <1.8 Å in 1 M TMAO; and 3), induces long-range spatial ordering of the water structure (9). The g(r)_Ow-Hw in Fig. 3 suggests that the first effect is indeed very small. The neutron-scattering results verify the second effect, and the broadening of the second maximum of the g(r)_Ow-Ow indeed suggests longer-range correlations than in pure water, although the water structure appears to be less ordered than in pure water or in the presence of TBA.

The higher strength of hydrogen bonds is also confirmed by a number of independent observations. NMR measurements on 0.25 M TMAO solutions (12) indicate that at higher concentrations the overlap between hydration shells of neighboring solute molecules increases the relaxation times of the first hydration shell from 2.5 ps in pure water to 4 ps. With urea, the relaxation times become slightly shorter (2.4 ps). At these concentrations, urea usually has no significant denaturing effect and may in some cases even stabilize proteins (34,35). Dielectric relaxation measurements on aqueous solutions of urea (1–2 M) also indicate that the relaxation times of coordination water molecules are close to those of pure water (36), whereas they are longer in TMAO solutions (<1 M) (37).

Because the neutron data clearly indicate that the main changes occur in the second shells, techniques that probe only the first hydration shell are probably less useful in the context discussed here than, for example, infrared spectroscopy, which records signals from all bonds of a given type in the system. Recent mid-infrared pump-probe experiments showed that TMAO reduces the reorientation time of the mobile fraction of water (i.e., the fraction that is not involved in the solvation of hydrophobic groups) (29). This effect, which is reversed by the addition of urea, is particularly strong at concentrations above 2.5 M. It has been suggested on this basis that TMAO destabilizes the water network by creating defects, mainly due to the presumed threefold coordination of the oxygen of TMAO. The difficulty of relating this phenomenon to physiological effects lies (in addition to the fact that it occurs mainly in a concentration range (2.5–10 M) that is well outside the presumed physiological conditions) in the expectation that destabilization of the water network would lead to denaturation rather than stabilization of proteins.

A Raman spectroscopy study also indicated that hydrogen bonds stronger than the average water-water bonds are formed in the presence of TMAO but not in the presence of TBA (38). That study also concluded, however, that there is no direct correlation between the effects of a solute on the structure of water and the stability of proteins. This was also suggested by NMR results obtained with tetramethylurea, a strong denaturant that increases the relaxation times in the first hydration shell of water to the same value as TMAO (4 ps) (12). A similar view was reached on the basis of a recent pressure perturbation calorimetry study of 17 cosolutes, which showed that there was no correlation between their denaturing or counteracting properties and their ability to “make” or “break” the structure of water (39). Note, however, that although these properties are well defined in thermodynamic terms by the positive or negative sign, respectively, of ${({\overline{\partial C}}_p/\partial P)}_T$ (where ${\overline{C}}_p$ is the partial molar heat capacity, P is the pressure, and T is the temperature), they are not well defined in structural terms. Indeed, in most cases studied so far, it appears that the first hydration shell of water is hardly affected by the presence of cosolutes, and that entropy changes that occur upon hydration are mainly related to perturbations of the second shell (25). In this respect, it is interesting that alcohols have been found to dehydrate proteins in crystals, especially in their second hydration shell (40).

The effect of TMAO on protein stability has been explained with the use of several complementary thermodynamic approaches. The different ways used to partition the various energetic contributions make it difficult to compare these methods, which essentially yield similar conclusions. In one study (1), increased protein stability was related to the preferential exclusion of TMAO from the surface of proteins (i.e., preferential hydration of the protein surface), and the stability of proteins in the presence of cosolutes has more generally been well explained by a balance between contact interactions and exclusion volume effects (41). In this second approach, preferential hydration is attributed to the dominance of effects due to the volume excluded to the cosolute by the protein. Similarly, the effect of cosolutes was also very successfully explained by using the transfer free energy of the protein backbone and side chains (42).

Replacement of water molecules in the hydration layer by a TMAO molecule would require not only their transfer to a tighter water network compared to that in a usual buffer, which should be entropically unfavorable, but also very favorable interactions between TMAO and the protein surface to compensate for the loss of its two strong O-water hydrogen bonds. MD simulations suggest that, unlike the case of urea, there are few strong interactions between polar side chains of proteins and TMAO, even if the number of TMAO molecules within the hydration layer is roughly proportional to its concentration (43). If TMAO effectively exists as a di- or trihydrate in solution, its larger effective volume would correspondingly increase the gap in Schellman's (41) notation, and hence the excluded volume, more than would be expected for a molecule of its size. The strong interactions between the TMAO oxygen and water reduce the number of hydrogen-bond partners available to the protein backbone. Moreover, the more rigid water network should make backbone-water hydrogen bonds entropically less favorable, which in turn should promote the formation of intramolecular hydrogen bonds and thus stabilize the native state to satisfy the multiple equilibria involved, in agreement with the recent analysis of Bolen and Rose (7). It is thus a combination of features—strong hydrogen bonds to water and the lack of favorable interactions with side chains—that make TMAO such an effective protecting osmolyte.

The behavior of urea is quite different. Neutron-scattering experiments at high urea concentration (9 M) have shown that there is no preference between water and urea in the formation of hydrogen bonds to water, and that urea easily fits into the water structure (23). Several urea molecules are often found in the hydration layer of proteins crystallized in the presence of urea. This hydration layer is denser than bulk water and is characterized by the presence of five-membered rings of water molecules (44). The structures of lysozyme crystals containing up to 4 M urea clearly indicate, however, that these specific binding sites are occupied even at low urea concentrations (35,45) and that their number does not significantly increase with concentration. However, these tightly bound molecules are not responsible for denaturation; rather, they illustrate the strong interactions between the cosolute and protein surfaces. Preferential solvation of lysozyme by urea (i.e., an excess urea in the hydration shell of lysozyme compared to the bulk solvent) was recently observed by neutron small-angle scattering (46). In contrast, it appears that binding of TMAO used for crystallization does not occur frequently; however, since few examples are available, a systematic study would be required to resolve that issue. Exclusion of TMAO from the hydration shell of proteins should be clearly detectable using combinations of H- and D-substituted proteins and cosolutes, and H₂O/D₂O contrast variation.

The softening of the TMAO-water network by urea observed in the infrared pump-probe experiments (27), the 2:1 urea-TMAO concentration ratio required for full counteraction, and the additivity of the effect of the two cosolutes are all well explained by the direct interactions between urea and TMAO reported here. The discussion above also illustrates that, despite obvious shortcomings in the description of long-range structural effects, MD simulations catch many of the important features of the interactions of cosolutes with water. Clearly, molecular-level interpretations of the effects of cosolutes will require a more integrated approach than has hitherto been the case.