Collective Dynamics of Periplasmic Glutamine Binding Protein upon Domain Closure

Abstract

The glutamine binding protein is a vital component of the associated ATP binding cassette transport systems responsible for the uptake of glutamine into the cell. We have investigated the global movements of this protein by molecular dynamics simulations and principal component analysis (PCA). We confirm that the most dominant mode corresponds to the biological function of the protein, i.e., a hinge-type motion upon ligand binding. The closure itself was directly observed from two independent trajectories whereby PCA was used to elucidate the nature of this closing reaction. Two intermediary states are identified and described in detail. The ligand binding induces the structural change of the hinge regions from a discontinuous β-sheet to a continuous one, which also enhances softness of the hinge and modifies the direction of hinge motion to enable closing. We also investigated the convergence behavior of PCA modes, which were found to converge rather quickly when the associated magnitudes of the eigenvalues are well separated.

Introduction

Investigations into the complex nature of macromolecular movements are of outstanding importance for the understanding of their biological roles and functioning. Conformational changes are known to be crucial in catalysis, signaling, allosteric regulation, complex formation, and substrate binding.

A natural need that arises is to be able to predict macromolecular motion from structural information typically originating from x-ray crystallography. Various successful approaches for characterizing global motion have been reported in the literature (1–3). Common tools are the MolMOV database (2,4,5), which uses morphing technology to create smooth animated pictures, and DynDom (6–8), which computes the possible rigid and flexible parts of a protein. Anisotropic elastic network models (ANM) (9–11), on the other hand, have been shown to crudely predict macromolecular movements from single crystal structures.

The link between the structure of a molecule and its function is dynamics. Molecular dynamic (MD) simulation techniques can help in sampling the complicated energy landscape of biomolecules and their global movements. Analysis methods like normal mode analysis (12) or principal component analysis (13) ((PCA), essentially the same as the quasi-harmonic method (14) and the effective normal mode analysis (15) but also known as essential dynamics (16) and other names in different communities but eventually going back to work from Pearson (17)), may be applied to dissect them into a linear combination of independent, one-dimensional movements and categorize them.

ATP binding cassette (ABC) transporters can be found across the three kingdoms of archaea, eubacteria, and eukarya (18,19). In Escherichia coli they make up of almost 5% of the genome comprising of ∼80 known transporters. They are involved in many physiological roles, making them highly interesting for medical as well as commercial applications. Most ABC transporters show high specificity for their substrate whereas some others bind to a wider variety of ligands, but transporters exist for virtually any molecule that needs to permeate the membrane.

X-ray structures for complete transport systems have become available only since recently (20). The core structure of ABC transporters consists of four domains: two α-helical transmembrane domains spanning the membrane multiple times, and two domains for the ATP or nucleotide binding domain in the cytoplasm. Auxiliary domains in the periplasm (periplasmic binding protein or pBP) may be used for specific functions like binding the substrate. In Gram-positive bacteria these are covalently bound to the outside of the cell due to the absence of an outer membrane, whereas the pBPs of Gram-negative transporters move freely in the periplasm (see Fig. S14 in the Supporting Material for illustration). The pBP superfamily may be divided into two classes, I and II, based on the number of β-strands (21) per domain. The general structural fold consists of two domains connected by a common hinge, which is located near the substrate's binding site.

The ABC transporter of interest for this work is the glutamine transport system GlnHPQ (EC 3.6.3.21, polar-amino-acid-transporting ATPase). The structures for GlnP and GlnQ have not been determined yet but GlnH (referred to as GlnBP in the following) has been studied by nuclear magnetic resonance (22–24) and x-ray (25,26). Likewise, the mechanism of association between GlnH and GlnP is unknown but it is suspected that it is the changed conformation after ligand binding that is recognized by the membrane receptor and initiates transport (see Fig. S14). Kinetical data for both binding and transport have been measured (27,28) and the influence of various pH and salt concentrations on stability and transport has been reported (29). In addition, the role of the ligand on the thermostability was subject of a recent study (30) as well as the folding behavior (31).

In theoretical work, the glutamine binding protein has been subject to molecular dynamics studies earlier. Six-nanosecond MD simulation have been carried out to elucidate interdomain dynamics and ligand binding of the closed-ligand, closed-apo, and open-apo states (32). However, one of the main findings suggested that the dominant global movement of the open-apo form would be a twist-type motion and not a hinge-type motion, which was ranked as second most important. Shorter simulations were carried out in later work (33). Domain movements of the closed-ligand, closed-apo, and open-apo states were investigated (34) with the help of the Gaussian network model and the anisotropic network model, which suggested a hinge motion to be most dominant and a twist motion to be second.

In related work, MD simulations have been carried out on the ligand-binding region of ionotropic glutamate receptors (35,36). This region is closely related, structurally, to GlnBP, and Mendieta et al. have used 1WDN and 1GGG structures to model missing loops in GluR2 (35). Stockner et al. observed the opening/closing mechanism of the maltose binding protein from MD (37) and Kandt et al. observed the Vitamin B₁₂ binding protein in a 480-ns multicopy MD simulation (38). The opening/closing mechanism of the ribose binding protein was studied via umbrella sampling molecular dynamics, and a free energy landscape as a function of the hinge and twist angles was proposed (39). The leucine/isoleucine/valine binding protein was studied by targeted molecular dynamics as part of the structure resolution (40).

In this work, we want to shed light on the closing mechanism and on the domain motions of GlnBP. We studied the protein by MD and subsequent PCA analysis. The principal modes revealed that a hinge-type movement is the dominant mode, which corresponds to the biological function of the protein, i.e., the closing of GlnBP upon ligand binding. The closure has been observed in two independent MD simulations by use of PCA mode analysis, and these results are discussed in detail below.

Methods

Initial structures

Four states of GlnBP—closed-liganded (CL), open-unliganded (OU), closed-unliganded (CU), and open-liganded (OL)—have been constructed from crystal structures, as described in this section. The CL (PDB id 1WDN (25)) and OU (PDB id 1GGG (26) chain A) x-ray crystal structures have been taken from the PDB database (41).

The class II pBP (21) is composed of a small domain (residues 90–180) and a large domain (1–84 and 186–226) containing both N- and C-termini (Fig. 1) connected by a hinge region (85–89 and 181–185) (26). The ligand, zwitterionic glutamine, binds with high specificity (K_d = 3 × 10⁻⁷ M at 5°C and pH 7.2) (27) into the cleft near the hinge region, invoking a large conformational change from an open to a closed state. The x-ray structures suggest a hinge-type motion of >50°, as visually demonstrated by morphing videos (4,5,42). Almost all contacts between ligand and hinge region are indirect (25).

Figure 1.

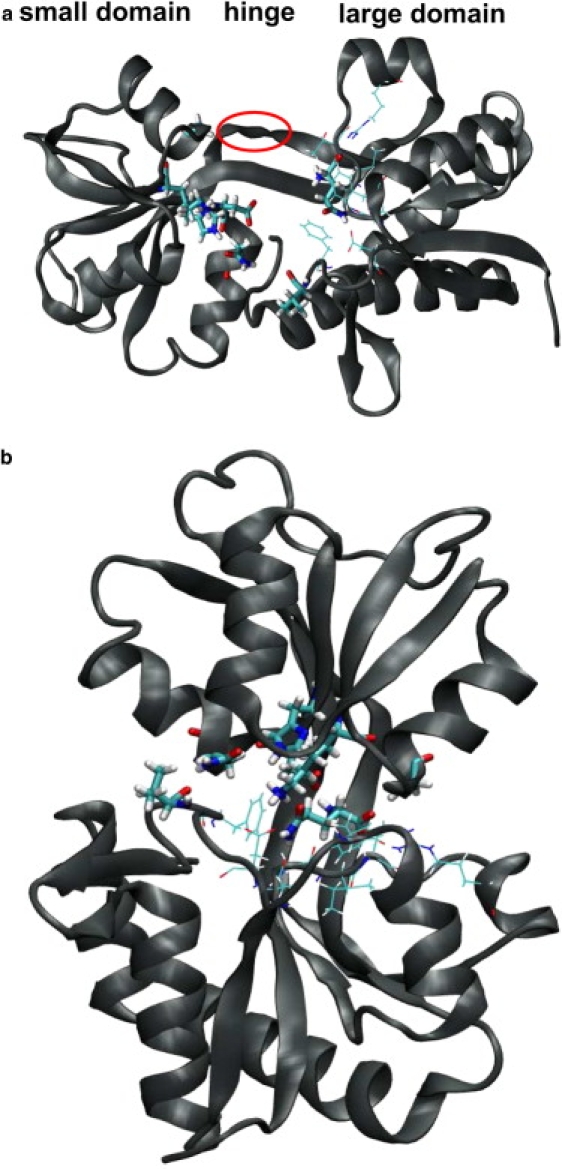
The structure of GlnBP. The top panel shows the modeled open-liganded GlnBP while the bottom panel shows the final structure from the OL/N simulation (see Analysis of Closing Trajectories in the main text). The circle marks the secondary structure (as discussed in Secondary Structure and Hydrogen Bonds of Hinge Region in the main text). Key residues (Val¹⁴, Asn¹⁶⁰, Lys¹¹⁵, Gly¹¹⁹, His¹⁵⁶, and Asp¹⁵⁷) forming H-bonds to the ligand (compare to Fig. S16) are drawn as stick models. Key residues between ligand and large domain (Asp¹⁰, Phe¹³, Phe⁵⁰, Ala⁶⁷, Gly⁶⁸, Ile⁶⁹, Thr⁷⁰, and Arg⁷⁵) are drawn as lines.

Missing hydrogens and the missing carboxy-O of the ligand in 1WDN were added. In both structures, N- and C-terminal residues were unresolved by x-ray crystallography (25,26); these were residues 1–3 in 1WDN, and residues 1–4 and 225–226 in 1GGG, in both chains. These residues were added and the structures obtained were subjected to brief minimizations with the coordinates from the frozen PDBs. The N- and C-terminal residues were acetylated and amidated according to the AMBER standard database. The protonation states, valid for a pH range of 6.6–7.2, were determined with H++ (43,44). Experiments have shown that ligand binding is unaffected over a pH range of 5–8 and is relatively insensitive to salt concentrations between 0 and 1.0 M KCl (29). H++ suggested protonated Glu¹⁷, Asp¹⁰⁶, and ɛ-protonated His¹⁵⁶. Whereas the first two residues are at some distance to the ligand, His¹⁵⁶ may be directly involved in hydrogen-bonding to the glutamine zwitterionic ligand N_ɛ156–O_ɛ227 (25). The closed-liganded crystal could be grown at pH 4.6 where His¹⁵⁶ is expected to be fully protonated, but could not be grown at higher pH. In contrast, the open-unliganded crystal structure was obtained at pH 8.5 (26).

Because the AMBER standard database does not include charges for zwitterions, these were computed with the RESP method (45,46) for the AMBER ff03 force field (47). In addition to the crystal structure of the glutamine ligand, two additional minimum structures obtained from preliminary MD simulations were included in the final fit to the electrostatic potential.

The CU and OL structures were not available and therefore had to be modeled. For CU we replaced the ligand with five water molecules. The OL structure was constructed by superimposing 1GGG with 1WDN by least-square fitting of the binding site, i.e., residues 10, 13, 50, 67–70, 75, 183, and 185 (all large domain), and then transferring the ligand to the open structure. The large domain is the most likely binding site (48) because of the higher number of interactions with the large domain and the perfect fit of the ligand into the binding site, as determined from the solvent-accessible surface. To check this, we performed two MD simulations with the ligand attached to the small domain, but neither led to a stable complex.

MD simulations

The initial structures were solvated in a rectangular TIP3P water box and crystal waters retained (all waters within 4.0 Å of chain A in the case of 1GGG). A single chloride ion was added to neutralize the system. The four simulation boxes (closed-liganded, open-unliganded, closed-unliganded, and open-liganded) contained ∼62,500 atoms (≈77 × 85 × 95 ų on average during constant pressure simulation) in the case of CL, CU, and OL, and 61,160 atoms in the OU case. In the two CL and OL cases, an additional larger box size with ∼140,000 atoms was created (≈106 × 122 × 109 ų). To reach a reasonable starting structure, the systems were slowly heated over a period of ∼100,000 steps in several steps of constant temperature with harmonic positional restraints applied (force constant 25 and 20 kcal mol⁻¹ Å⁻²). Fifty-thousand additional steps were performed to switch from constant volume to constant pressure. Both temperature and pressure were controlled by the Berendsen algorithm (49) with coupling constants of 0.2 ps⁻¹ and 1.0 ps⁻¹, respectively. Over the course of several hundred thousand steps, the positional restraints were stepwise-lowered and eventually switched off. The first five nanoseconds of unrestrained MD simulations were not included in computing statistical properties, unless specified.

All hydrogen bonds were constrained with the SHAKE algorithm (50), allowing a timestep of 2 fs. Coordinates and energies were written every 1 ps. Total unrestrained simulation times comprised 30 ns in each state and box size unless pointed out below.

Principal component analysis (PCA)

Principal component analysis (13–17) (PCA) is a powerful technique to assess collective motions by analyzing the (mass-weighted) covariance-variance matrix of atomic displacements over time. An element a_ij of the second moment, matrix A is given as

$$a_{\text{ij}}=\langle \left(x_{\mathrm{i}}-\langle x_{\mathrm{i}}\rangle \right)\left(x_{\mathrm{j}}-\langle x_{\mathrm{j}}\rangle \right)\rangle ,$$ (1)

where x_i and x_j are the Cartesian coordinates of atoms i and j, and the angle brackets denote an average over time. Diagonalizing the matrix leads to eigenvectors from each column vector in W describing the directions of the collective motion of all atoms, and the associated eigenvalue in the diagonal matrix ζ carries information about the magnitude of motions along the corresponding eigenvector

$$\text{AW}=\mathrm{W}\varsigma \text{.}$$ (2)

The sum over the diagonal elements of ζ is a measure for the overall movement. We can assess the similarity between different simulations of states and of modes by comparing eigenvectors of individual modes and computing their dot product. The projection vector σ_m of an eigenvector w_m onto the trajectory T can be computed as

$${\mathit{\sigma }}_{\mathrm{m}}\text{=}\mathbf{T}\prime {\mathbf{w}}_{\mathrm{m}},$$ (3)

where the prime denotes a transposed matrix. The trajectory T is a 3N × K matrix, where N is the number of atoms and K the number of simulation steps.

Results

Stability and fluctuation of simulated structures

To assess the basic reasonableness of the simulations, analysis of the root mean-square deviations (RMSD) and root mean-square fluctuations (RMSFs) have been carried out. The general picture is that the RMSDs of all simulations develop into a stable plateau (see Fig. S1 for the total RMSD and Fig. S2 for per-domain RMSDs) indicating sufficient stability of the trajectories for further analysis. The RMSD data shows that the open states fluctuate more strongly than the closed states, hinting at larger-scale motions. The larger box simulations behave very similarly to the smaller box simulations. Analysis of the two individual domains suggests that the small domain deviates less from the crystal structure than the large domain. In both cases, however, fluctuations are quite small compared to the total RMSD, meaning that the two domains move as rather rigid bodies against each other. RMSD statistics is summarized in Table S1.

The RMSF analysis (see Fig. S3) shows that individual residue fluctuations are quite similar in the four states with larger motions in the loop regions of the small domain and smaller fluctuations in the residues binding to the ligand. The hinge region also shows relatively small RMSFs, but the fluctuations of the OU simulation and the OL simulations too, are larger than the others, indicating a less stable anti-parallel β-sheet. Somewhat larger residue fluctuations were found in the simulations with the larger box size.

Major collective motions: hinge and twist

PCA was applied to decompose the complex motions into simpler-to-understand, one-dimensional modes. It is necessary to establish sufficient convergence of PCA modes (51–54) and thus the reliability of the results for the subsequent analysis of the global motions in the closure of GlnBP. We also wish to explore whether certain modes are more dominant than others, and whether these modes are linked to the biological functioning of GlnBP.

Table 1 lists the relative contributions of individual, first three, and first 25 modes to the overall motions of the simulation systems, which reveal that dominant modes are present in some cases (see Fig. S4). In general, open states display larger motions and the first mode dominates over all other modes. The closed states do not show this clear dominance, and the motion is more evenly distributed over the first few modes. Both effects are more pronounced in the larger box sizes, i.e., the first mode of the OL big-box simulation accumulates ∼47% (10% for the second) of all motion, whereas the CL big-box simulation only shows 20% for the first mode (16% for the second).

Table 1.

List of MD simulations and contribution of individual, first three, and first 25 PC modes to the total motion

Simulation setup	Abbrev.	Box size	Final structure	Contribution (%)
				1st	2nd	3rd	First 3	First 25
Closed-liganded	CL	Normal	Closed	21.3	12.6	7.3	41.1	79.0
	CL big	Big	Closed	19.9	16.3	7.0	43.1	79.8
Closed-unliganded	CU	Normal	Closed	17.1	14.5	8.3	39.9	78.8
Open-liganded	OL	Normal	Open	29.9	13.5	7.3	50.7	82.1
	OL big	Big	Open	46.7	10.2	6.3	63.2	86.5
	OL/N∗	Normal	Closed	87.3	2.0	1.6	90.9	96.7
	OL/N2∗	Normal	Closed	85.0	3.0	2.0	90.0	96.6
Open-unliganded	OU	Normal	Open	42.6	12.2	6.0	60.7	86.0

^∗For these two cases, restraint MD simulations were done before production. The percentages are computed from PCA analysis over the entire trajectory. See Analysis of Closing Trajectories in main text for details.

Pairwise comparison of individual modes via dot products (see Table S2) shows that both first mode and second modes are not very similar to each other. Visual inspection with VMD (55) and IED (56) shows that the first mode of the open states is of hinge type, whereas the second mode is of twist type. The first mode of the closed states is of twist type and the second mode is hinge type. However, hinge and twist types between the open and closed states are not very similar to each other, as is obvious from the dot products and cross correlations (see Table S2 and Table S3).

Further analysis of dot products and cross correlations on subtrajectories of 5-ns length (see Table S4, Table S5, Table S6, Table S7, Table S8, Table S9, Table S10, Table S11, Table S12, Table S13, Table S14, and Table S15) reveals that for the open state simulations, the direction of the first mode, and to a lesser extent the second mode, is maintained in shorter simulation times. In contrast, eigenmodes of the closed state simulations are not very well reproduced in shorter simulations.

Secondary structure and hydrogen bonds of hinge region

In general, the predictions of the MD simulations agree very well with the x-ray crystallographic data (25,26). A notable exception, however, is the secondary structure in the hinge region (see Fig. 1). Using the DSSP algorithm (57) as implemented in AMBER's ptraj utility, we find that the β-sheet formed by the two hinge strands is effectively broken in both crystal structures, as residues 89, 181, and 182 cannot be categorized as having secondary structure.

Interestingly, however, in the CL (both box sizes) and CU simulations, the secondary structure around these residues is, in fact, a continuous β-sheet. On the other hand, the open-state simulations exhibit a secondary structure similar to the two crystal structures over the entire simulation period.

We tested the stability of the secondary structure in this region with a few short simulations using a shorter setup protocol that also used smaller restraints. Two additional simulations starting from 1WDN (closed-liganded) showed similar behavior to the CL simulations: in the first, the continuous β-sheet formed very early, whereas in the second simulation, the broken β-sheet was maintained for ∼3 ns. Another simulation starting from 1GGG (open-unliganded) confirmed the result from the OU simulation. We also performed a simulation of 1GGG with a continuous β-sheet throughout the simulation. Here we find the first PCA mode to be very close to the open-liganded simulations (dot products > 0.8) but different from the OU simulation (dot product = 0.62).

We also removed the ligand from the OL simulation and carried out two simulations: one starting structure taken from after the release of the restraints, and the other from after 15 ns of OL simulation. The secondary structure in the hinge region remained unchanged in both cases as in the original OL simulation. The dot products of the first PCA mode between the latter two simulations and the OU simulation are 0.83 and 0.94, respectively.

In summary, from these test calculations we confirmed that binding of the ligand modifies the direction of the hinge motion. This motion is very different in the unliganded GlnBP, but becomes more similar to the liganded protein when the anti-parallel β-sheet becomes continuous in the hinge region.

Two different H-bond patterns were found in the hinge region Fig. S15. Whereas Leu⁹⁰:N makes a H-bond to Leu¹⁸⁰:O in the crystal structure and the open state simulations, the closed state simulations make a H-bond to one residue farther away, that is, to Glu¹⁸¹:O. This also leads to a more closed structure, as determined from average RMSD distances (calculated for the small domain after the large domain had been fixed). In the case of the continuous β-sheet (Leu⁹⁰:N–Glu¹⁸¹:O), the RMSDs are ∼15.4 Å, while they are larger than 16.7 Å for the broken β-sheet.

Analysis of closing trajectories

As outlined above, the hydrogen-bonding pattern in the backbone of the hinge region in the two OL simulations (both smaller and larger box size) is different from the closed state simulations. To assess what would happen if we had the same H-bond pattern, we performed an additional restraint MD simulation with force constant k = 100 kcal/mol applied to the six ϕ- and ψ-angles of residues 89, 181, and 182 to force the region into β-conformation. The restraints were released after 1 ns and then the simulation (OL/N) was continued without any restraints. In another simulation (OL/N2), we kept restraints with k = 10 kcal/mol for another 100 ps before release.

We find that both OL/N and OL/N2 simulations start closing after ∼18 ns and 30 ns, respectively. The β-structure in the three residues 89, 181, and 182 appears to be weaker in the earlier stage, but is fully formed in the later stage of the open state (see Table S16). In contrast, neither do the OL or OU simulations reach the closed state nor do the CL or CU simulations reach the open state.

The closing of the protein can be analyzed through PCA. The projections of the first three principal modes are shown in Fig. 2 for both simulations. The most dominant mode corresponds naturally to the closing motion itself (see Table 1). The second and third modes do not show a clear trend in any of the two simulations, although the projections become somewhat less variable after closure. It can be seen that the onset of closure is ∼18 ns for the OL/N simulation. The projection suggests that closure is complete at ∼20 ns, i.e., the total timespan to close is roughly 2–3 ns. In the case of the OL/N2 simulation, the protein attempts to close first at ∼28 ns, but opens again at 30 ns. From this time on, the projection progresses toward closure in two steps. In the first step between 30 ns and 32.5 ns, the projection decreases only slightly on average, reaching, temporarily, a deep minimum at 31 ns. In the second step, the projection between 32.5 ns and 37.5 ns reaches a plateau, which eventually leads to final closure.

Figure 2.

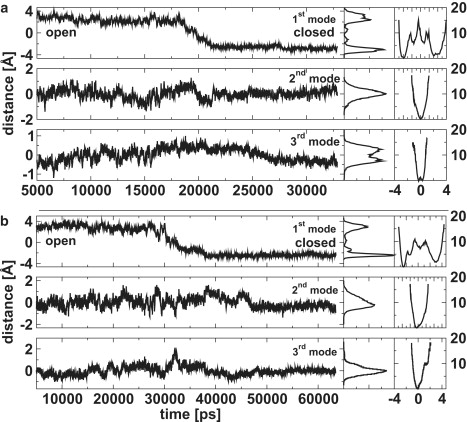
The projections of the first three modes of the OL/N (top) and OL/N2 simulations (bottom). The central panel shows the probability distribution and the right panel shows the free energy G = −kT ln p in kJ/mol along the corresponding principal mode.

The probability distributions for the projections in Fig. 2 clearly show the locations of both the open and the closed states along the reaction coordinate, i.e., the first principal mode. However, the free energy profile is too rugged in the intermediate regions to allow an estimate of the activation free energy.

In Table 2 we summarize cross correlations for the first three modes between the three OL simulations. The two closing simulations OL/N and OL/N2 match each other very well. The comparison of PCA vectors of the initially open states with the OL simulation also shows quite high similarity between the first two modes.

Table 2.

Eigenmode cross-correlations between OL simulation and the OL/N and OL/N2 simulations while still open

Mode	OL/N versus OL/N2	OL/N∗ versus OL	OL/N2† versus OL
First	0.97	−0.91	0.86
Second	0.84	0.69	0.70
Third	0.62	0.19	−0.38

^∗First 15 ns.

^†First 20 ns.

In Table 3 we summarize cross correlations for the first three modes between the open liganded and open unliganded simulations. The coordinates of the ligand have been removed from the eigenvectors to enable comparison. We find low similarity between the initially open states and the open-unliganded OU simulation in all three modes.

Table 3.

Eigenmode cross-correlations between open liganded and open unliganded simulations

Mode	OU versus OL	OU versus OL/N∗	OU versus OL/N2†
First	−0.47	−0.54	−0.49
Second	0.13	0.09	0.04
Third	0.04	0.38	−0.22

Note that the coordinates of the ligand have been ignored in this comparison.

^∗First 15 ns.

^†First 20 ns.

Fig. 3 plots the first PCA vector (x axis) versus the second PCA vector (y axis) together with the probability distributions. Moving from the open (left) to the closed (right) state along the first mode (hinge motion, see discussion above), we find four relatively well-separated patches in the OL/N simulation. These patches correspond to the plateaus found in the projection of the first mode (Fig. 2). The first patch corresponding to the open state shows a larger variance in both dimensions. The two intermediate patches as well as the last patch are confined to a smaller space.

Figure 3.

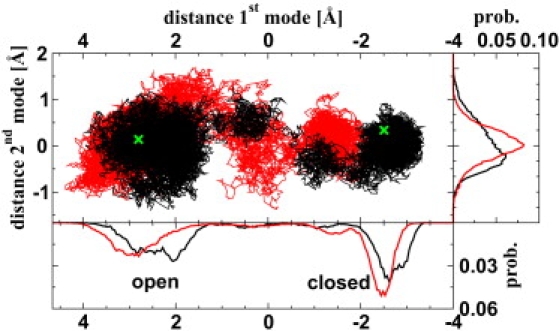
The projections of the first two modes of the OL/N (black) and OL/N2 (red) simulations plotted against each other. The locations of the x-ray structures are marked in green. The probability distributions are shown on the bottom for the first mode and on the right for the second mode.

The OL/N2 simulation also displays four patches, but the second one from the right is less well separated from the other intermediate patch, indicating a smaller barrier between these two substrates. The open state patch is quite spread out along the second mode dimension, similar to the second patch.

Fig. S16 shows the formation of the hydrogen bonds between the Gln ligand and the residues Lys¹¹⁵, Gly¹¹⁹, His¹⁵⁶, and Asp¹⁵⁷ from the small domain in the closing simulations. The first new H-bond that is created between the small and the large domain in the closing event, however, is between Asn¹⁶⁰:ND2 (helix VI, residues 158–167) and Val¹⁴:O. Correspondingly, the distance between helix VI and helix VIII increases (residues 212–220), which is necessary to achieve closure. The Tyr¹⁶³:CA–Phe²²¹:CA distance has been chosen as a measure, and this distance increases from ∼5.5 Å to ∼9.5 Å, indicating the progress of closure.

Asp¹⁵⁷, the residue spatially closest to the ligand in the open state, forms the H-bond ∼1 ns later than Val¹⁴:O–Asn¹⁶⁰:ND2 in both simulations. Lys¹¹⁵ forms a very strong H-bond ∼1 ns later than Asp¹⁵⁷ in the OL/N case, but several nanoseconds later in the OL/N2 case. The backbone of Lys¹¹⁵ also appears to be more rigid than other lysines, i.e., the residue's side chain points away from the small domain in a rather constant angle, which could possibly facilitate hydrogen-bond formation. His¹⁵⁶ stays at positions of ∼4.0 Å and comes closer only temporarily, thus not really forming a H-bond. Gly¹¹⁹ arrives at similar distances but only long after closure, due to a local rearrangement in the backbone in the OL/N case but much earlier in the OL/N2 case.

A key vdW interaction has been identified (26) between Gln²²⁷:N and Tyr¹⁸⁵:CE with a distance of 3.62 Å in the crystal structure (26). We also find this interaction in our simulations with average distances of 3.69 Å in the CL simulation and 3.85 Å in the OL simulation (the two equivalent ɛ-Cs switch position after 4 ns). The difference in fluctuations of Tyr¹⁸⁵ in the OU and OL simulations, however, seems to be not too large, i.e., the ligand obviously fixes the Tyr¹⁸⁵ location only a little. In addition, there appears to be only a small effect on the Tyr¹⁸⁵ backbone when comparing CL and OL simulations. OL tends to be larger by 6° on average in both backbone dihedrals.

Comparison of the open-unliganded and closed-liganded crystal structures (25) suggests that the hinge motion is centered around residue 89 on one strand and residue 181 on the other strand. The most significant changes in backbone dihedral angles were found in the ϕ-angle of Gly⁸⁹ with 41.1° and the ψ-angle of Glu¹⁸¹ with 34.3°.

A rigid body analysis with DynDom (6–8) suggests that the hinge angle of the first mode is 54° in both simulations, based on the respective average structures of open and closed states. The hinge residues are 87–89 and 180–183 (OL/N) and 88–89 and 180–183 (OL/N2). Table S17 compares DynDom with the MD simulations. The torsions most strongly affected in MD are in residues 89, 90, and 181–183. For comparison, an ANM analysis has been carried out (see Table S13) to estimate mean-square deviations (MSDs) in the hinge region. The data shows that residues 181–186 are least flexible in the OL simulation whereas residues 85–89 show very similar MSDs for the three simulations OL, OL/N, and OL/N2.

The MD simulations results were obtained from the differences in the average dihedral of open and closed states. In some cases, dihedrals fluctuated quite strongly and thus, are only rough estimates. However, we also find a clear stiffening in some torsions after closure in agreement with the closed-state simulations. In general, DynDom and MD simulation results compare quite well (see Table S16).

Discussion

In this article, we have used molecular dynamics and principal component analysis to investigate the dynamics and closure of glutamine binding protein. We have shown that PCA is a valuable tool in understanding global motions of proteins including transitions between different states, e.g., from open to closed state.

Size effects appear to play a role for the global domain motions. The large amplitude motions of the larger box sizes and hence slower domain movements may indicate that closure is less likely to be observed. However, this effect is only minor, and it is therefore reasonable to assume that the simulations with the smaller box sizes are sufficient to describe global motions and closure.

Convergence of collective motions

We have demonstrated that even relatively short simulations may yield plausible PCA modes in the case of the 226-residue GlnBP. However, this appears to depend on several factors like the separation of the magnitudes of eigenvalues from each other or the size of the simulation system. Other influences may come from the choice of the starting structure as well as the simulation length. This would explain why Pang et al. have found the most dominant mode of the open-unliganded protein not to be of hinge-type motion in their recent 6-ns MD simulation on GlnBP (32).

In the open cases, whether liganded or not, the first mode is very well separated from the second mode. It is in these simulations where we also observe the fastest convergence, i.e., even short 5-ns patches would be able to predict motions very similar to the ones obtained from much longer simulations.

In the closed simulations, the first modes do not separate so clearly from each other, i.e., their eigenvalues are of very similar magnitude. In these cases, their associated eigenvectors are more likely to be dissimilar on comparison of short trajectory patches. In other words, achieving reliable results is more difficult even on longer timescales.

Closing mechanism

PCA suggests that the hinge-type motion is the dominant one in the open states. However, the direction of the hinge motion was found to be different in the simulations depending on the secondary structure in the hinge region and the presence of the ligand. The crystal structures 1WDN and 1GGG (25,26) suggest a discontinuous anti-parallel β-sheet in the hinge area with a bend at residue 181. Interestingly, the structurally very closely related glutamate/aspartate binding protein (also of pBP type II) with a sequence identity of only 24% was recently found to have a continuous anti-β-sheet in the closed-liganded x-ray structure (58).

This hinge motion was found to be very similar in the open-liganded simulations OL, OL/N, and OL/N2. OL displayed a broken β-sheet in the hinge area while OL/N and OL/N2 have a continuous β-sheet. The binding of the ligand obviously modifies the direction of the hinge motion toward closure. Although the OU simulation with broken β-sheet showed a hinge motion that was very different from the hinge motion of the open-liganded simulations, with a continuous β-sheet the observed dominant motion was very similar to the open-liganded simulations. The RMSF (see Fig. S3) suggests a more flexible hinge region, and thus, a less stable secondary structure in the OU and OL simulations. The role of the ligand is to induce the formation of a continuous β-sheet by switching the hydrogen bond from Leu⁹⁰:N–Leu¹⁸⁰:O to Leu⁹⁰:N–Glu¹⁸¹:O, and thereby to stabilize the structure.

The first modes of the CL, CU, and OU state simulations were found not to resemble each other, which implies that previous findings from ANM analysis (34) are not correct. The CL and CU simulations were not found to show a preferred dominant mode.

The ligand has only indirect connections to the hinge residues Tyr¹⁸⁵ and Gln¹⁸³ through hydrogen bonds. Gln¹⁸⁴ and Ala¹⁸² point away from the ligand, and hence, their side chains do not contribute to the closure. Glu¹⁸¹ shows only weak H-bonding (25%) to the backbone of Ala¹⁸² in the continuous β-sheet simulations. It appears, therefore, that the hinge side chains probably play a minor role, at most, in closure, and therefore the information from ligand binding propagates through the backbone. The detailed interactions between the ligand and the protein (see Fig. 1) were not found to be significantly different in the three open-liganded simulations.

Two closures of GlnBP starting from two independent trajectories were observed. However, to achieve this we had to force three backbone residues into a certain backbone pattern leading to a continuous anti-β-sheet in the hinge region. The question is whether the closure in the OL/N and OL/N2 simulations is not simply an artifact of the initially applied restraints. However, the two closures occurred at 18 ns and 30 ns, respectively, after the release of the restraints. This allows for sufficient time to attain a new equilibrium.

Comparing the PCA of the closing reaction to the small domain RMSD after fixing the large domain in space, and the projection of the first mode in the two closure simulations, shows very close correspondence. This suggests that the reaction coordinate could indeed be approximated by either measure. However, the detailed reaction mechanism is more complicated. Ravindranathan et al. (39) described the closing and opening of the ribose binding protein in terms of a two-dimensional free energy landscape as a function of the hinge and twist angles. Our plot of the first two modes against each other also shows that the dominant hinge motion is accompanied by a twist motion.

The statistics from only two closure events is not sufficient for furnishing enough detailed information about the mechanism. E.g., the analysis of ϕ- and ψ-angles turned out to be rather noisy, although reasonable agreement with rigid body analysis (Table S17) was found when average dihedral angles were compared. In addition, no estimate of the reaction rate of the process can be given. This will be left to subsequent studies.

The two closure simulation presented here do, however, give some insights. The two-dimensional projection plot (see Fig. 3) suggests that there are two intermediate states. The OL/N2 simulation exhibits larger amplitude twist motions in the second intermediate state and less well-separated states. In addition, the transitions between the open and first intermediate state are located at different positions along the y axis, but the two other transitions are located at very similar positions. The hydrogen bonds do close in a certain order (see Fig. S16) in both simulations, but this is a natural consequence from the change in spatial distances between small and large domains during closure.

Summarizing the picture drawn from the closing event above, it appears that the mechanism of closure is the sum of tiny statistical events. The hinge motion is the natural motion of GlnBP and the ligand steers the movements toward the closed state. The free energy hyper surface is thereby modified in such a way that the likelihood of closure is larger when the ligand is present than when it is not. From the viewpoint of principal component modes, the open state must pass through several low dimensional funnels to reach the closed state. These funnels are well presented by the first few dominant PCA modes.