Abstract
Topical microbicide products are being developed for the prevention of sexually transmitted infections. These include vaginally-applied gels that deliver anti-HIV molecules. Gels may also provide partial barriers that slow virion diffusion from semen to vulnerable epithelium, increasing the time during which anti-HIV molecules can act. To explore the barrier function of microbicide gels, we developed a deterministic mathematical model for HIV diffusion through realistic gel distributions. We applied the model to experimental data for in vivo coating distributions of two vaginal gels in women. Time required for a threshold number of virions to reach the tissue surface was used as a metric for comparing different scenarios. Results delineated how time to threshold increased with increasing gel layer thickness and with decreasing diffusion coefficient. We note that for gel layers with average thickness >∼100 μm, the fractional area coated, rather than the gel layer thickness, was the primary determinant of time to threshold. For gel layers <∼100 μm, time to threshold was brief, regardless of fractional area coated. Application of the model to vaginal coating data showed little difference in time to threshold between the two gels tested. However, the protocol after gel application (i.e., with or without simulated coitus) had a much more significant effect. This study suggests that gel distribution in layers of thickness >100 μm and fractional area coated >0.8 is critical in determining the ability of the gel to serve as a barrier to HIV diffusion.
Introduction
Mathematical models of pharmacokinetics and pharmacodynamics have provided insights for the development of antiretroviral therapy (1,2) and informed our understanding of acquired immune deficiency syndrome (AIDS) pathology and the immune system (3–5). However, there have been few attempts to create analogous mathematical models for topical microbicides for human immunodeficiency virus (HIV) prevention.
Microbicides are agents applied topically to prevent transmission of sexually transmitted infections, including HIV (6–8). Microbicide development has been motivated by the lack of a prophylactic vaccine for HIV/AIDS (9) and the lack of female-controlled methods of HIV prevention (10). First-generation microbicide candidates acted via nonspecific mechanisms of action. These included vaginal defense enhancers, surfactants, and entry and fusion inhibitors. To date, clinical trials of first-generation products have not demonstrated efficacy for HIV prevention (11–14). Subsequent microbicide development has shifted toward active pharmaceutical agents (APIs) with HIV-specific mechanisms of action (15).
Mathematical models have the potential to contribute to microbicide design and evaluation. To date, two approaches have been employed to mathematically describe the functioning of microbicides: stochastic models of infectivity and deterministic transport models. Tuckwell et al. developed a stochastic approach (16) derived from clinical data linking semen viral load and likelihood of infection (17). An advantage of the stochastic approach is that it can incorporate data for rates of infection provided by epidemiological studies and clinical trials. Model predictions can provide insights for clinical trial design. However, one limitation of stochastic modeling is that it provides limited insight into microbicide product functioning and biological mechanisms underlying HIV infection. Parameters that describe microbicide efficacy and likelihood of infection are empirically derived, and summarize complex underlying phenomena.
An alternative modeling approach, used by our group, is to develop deterministic models of HIV and microbicide transport and neutralization processes (18,19). These models consider parameters relevant to the development of topical microbicide formulations, such as rates of drug delivery, rates of HIV diffusion, and spatial deployment of drug delivery vehicles. The advantage of this approach is that these mathematical models can serve as tools for microbicide developers, helping them to interpret product characteristics. However, this approach is hampered by limited experimental data linking model parameters to clinical outcomes.
Models embodying parameters relevant to drug delivery can be used in design of microbicide products, e.g., in specifying drug loading and release rates from the dosage form, and determining the optimal timing for product application in relation to exposure to sexually transmitted infection pathogens. Dosage forms for microbicides have included semisolid gels, intravaginal rings, quick-dissolve films, and tablets (20,21). Intended methods of use may be coitus-dependent or coitus-independent. Different mathematical models are necessary for different microbicide product scenarios. Microbicide developers may have different goals for drug delivery, depending on the API, the dosage form, and the intended method of use. For example, APIs may focus on neutralizing HIV in fluids of the vaginal lumen (e.g., HIV-targeted entry inhibitors) or within the vaginal epithelium (e.g., reverse transcriptase inhibitors). Different mathematical models are needed to characterize different microbicide products.
In this study, we used transport theory to describe HIV virions diffusing from semen through microbicide gel to vulnerable vaginal epithelial surfaces. The biological context of our analysis is the time interval after ejaculation during which HIV virions introduced in semen are deposited in the lower female reproductive tract. We were interested in the functioning of microbicide gels as semipermeable barriers to HIV and in how the spatial deployment of gels in vivo affects this function.
To date, the functional significance of hindering HIV transport through semisolid microbicide products has not been comprehensively studied. Barrier methods such as condoms are known to be an effective means of preventing HIV transmission (10). Moreover, biological physical barriers, such as epithelial tissue and mucus, comprise the first line of an imperfect innate immune defense. However, it is less clear how barriers created by semisolid microbicide products could contribute to preventing HIV transmission. Our previous work suggested that hindrance of virion diffusion is crucial to allowing APIs the time necessary to neutralize virions in the vaginal lumen before they reach vulnerable tissue surfaces (18). Furthermore, HIV has a finite infectious lifetime in vitro and presumably in vivo, thus, hindering HIV transport rates could reduce the infectious viral inoculum arriving at vulnerable tissue surfaces. This might also provide innate host defenses extended time in which to neutralize the virus. Overall, hindering HIV transport could potentially reduce the inoculum of infectious virions that reaches tissue surfaces in vivo, which provides motivation for further studies of the potential barrier effects of microbicide products.
We use here the time required for a threshold number of virions to reach the tissue compartment as a metric for comparing different scenarios. This allowed us to study the barrier function of gels without limiting ourselves to specific microbicide APIs. Thus, although this model does not address neutralization by APIs, it provides a foundation for future models that will include specific mechanisms of action by APIs. Results here provide a useful first approximation of the lower bound of time required for virions to diffuse from infectious semen, through vaginal gels, to tissue.
In this study, we also considered realistic deployment of vaginal gels in vivo. Previously, we modeled an idealized geometry in which vaginal tissue was coated completely by a layer of constant thickness (18). However, optical imaging experiments performed by our lab have shown that vaginal coating by gels in women is not so uniform: coating thickness varies spatially, and not all tissue is covered (22–24). Depending upon gel properties, and a woman's posture and activity after gel application, as much as one-third of the epithelial surface area has been found to be devoid of detectable coating (22,23). The distribution of coating thickness likely affects transport and interactions between HIV virions and APIs and, thus, the prophylactic functioning of the gel. Algorithms based upon how coating details affect actual HIV and API transport kinetics would enhance the biological interpretations of imaging studies.
The goal of this study was to define and understand parameters salient to the functioning of a semisolid microbicide gel as a barrier to HIV diffusion. We developed a mathematical model for HIV diffusion from semen, through realistically-deployed microbicide gel, to vaginal epithelial surfaces where early events of infection occur. Our results provide insights about the time required for virions to contact vaginal epithelium, and how that is influenced by viral mobility in epithelial coating with a gel, as well as details of that coating.
Materials and Methods
Mathematical model of 1-D HIV diffusion through semen and microbicide gel
Fig. 1 illustrates our model. Microbicides formulated as gels are applied topically to the vagina. Previous in vivo studies have found that vaginal gels deploy to partially coat the epithelium, forming layers ∼100 μm thick (23,24). These layers may then be challenged by semen containing infectious HIV. We model HIV-virion transport from semen, through coating layers (where present), to vaginal tissue as an unsteady one-dimensional diffusion process in two compartments (semen, gel) (Fig. 2). First, we create a model of local HIV diffusion from semen to tissue that is partially coated by a gel layer of constant thickness. Then, we expand the analysis to transport to a partially coated surface with a distribution of coating thicknesses measured in human in vivo vaginal imaging experiments. Table 1 contains variable definitions and parameter values.
Figure 1.

Schematic of female reproductive tract showing how microbicide gel and semen may be deployed after coitus. (Inset) Idealized scenario for mathematical modeling of a semen layer on top of a microbicide gel layer.
Figure 2.
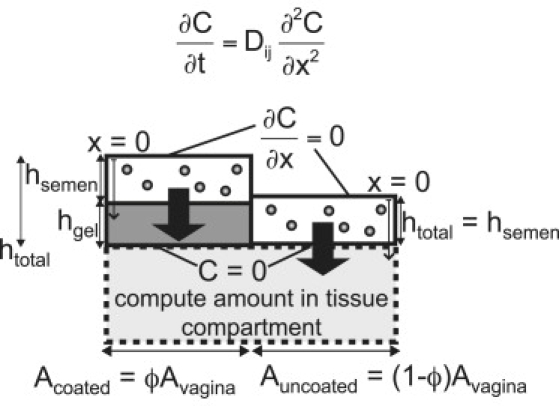
Schematic of mathematical model of HIV migration from semen layer, through microbicide gel layer, into tissue compartment.
Table 1.
Variable and parameter definitions, with reference conditions
| Variable | Definition | Reference condition |
|---|---|---|
| CHIV | Concentration of HIV | — |
| DHIV, semen | Diffusion coefficient of HIV in semen | 3.63 × 10−8 cm2/s |
| dHIV | Diameter of HIV virion | 125 nm |
| μsemen | Viscosity of semen | 1 cP |
| T | Temperature | 37°C |
| DHIV, gel | Diffusion coefficient of HIV in microbicide gel | 0.5 Dsemen |
| ΦHIV | Partition coefficient between semen and gel layers | 1 |
| C0 | Initial concentration of HIV in semen | 5 × 104 virions/ml = 8.3 × 10−17 M |
| hsemen | Thickness of semen layer | 340 μm |
| hgel | Thickness of microbicide gel layer | 300 μm |
| htotal | Total thickness of semen and microbicide gel layers, | 640 μm |
| Mtissue | Amount of HIV in tissue compartment | — |
| Vsemen | Volume of semen | 3.4 ml |
| Vgel | Volume of microbicide gel | 3.0 ml |
| Avagina | Surface area of vaginal epithelium | 100 cm2 |
| ϕ | Fractional area coated by gel of given thickness | 1 |
| threshold | Threshold number of virions in tissue compartment | 1.7 × 104 virions |
Values were input to the model unless otherwise specified.
Governing equations
The transport equations for HIV diffusion in the semen and gel layers are
| (1) |
| (2) |
The assumption of one-dimensional diffusion is reasonable, because vaginal coating thickness is generally small compared to the lateral scale over which it varies.
Boundary conditions
The vagina is treated as a collapsed flat tube (26) with symmetry about x = 0 (Fig. 2). The symmetry boundary condition at x = 0 is
| (3) |
At the interface of the semen and gel layers, standard concentration and flux boundary conditions are represented by
| (4) |
| (5) |
Here, hsemen+ and hsemen− are positions infinitesimally above and below the semen-gel interface, respectively.
The boundary condition between gel and tissue compartments is not well understood. Virions likely accumulate on the vaginal epithelial surface because the squamous epithelial cells form a physical barrier (27). Recent work by Hope et al. suggests that HIV virions can diffuse through intact epithelial tissue in vivo, presumably by moving through gaps between cells (28). Given this current lack of quantitative understanding, we apply a zero-concentration boundary condition at the gel/tissue interface:
| (6) |
This condition maximizes flux into the tissue compartment and provides conservative estimates for times needed to reach threshold levels of infectious virus at the tissue surface.
Initial conditions
At time zero, HIV is introduced at concentration C0 in the semen. The concentration within the microbicide gel layer is zero:
| (7) |
| (8) |
Numerical methods
The partial differential equations are solved using the MATLAB (The Mathworks, Natick, MA) partial differential equation solver “pdepe” to obtain concentration profiles of HIV in the semen and gel compartments over time from the onset of semen-gel contact. These profiles are integrated throughout the depths of the layers and multiplied by area coated for each coating thickness to determine the total amount of virus in the semen and gel compartments. The time-dependent amount of HIV in the tissue compartment, Mtissue(t), is calculated by a mass balance, subtracting the amounts of virus in the semen and gel compartments from the initial amount of virus in the semen. For a constant gel coating thickness, hgel,
| (9) |
Using the results for M(t), we find the times necessary for defined threshold numbers of virions to migrate to the tissue compartment. These times, tthreshold, are used as metrics to evaluate the effects of different model parameters, e.g., diffusion coefficients in semen and gel, layer thicknesses, and fraction of surface coated by gel. The rationale for choosing tthreshold is described below.
Model parameters
Our model contains both biophysical parameters (e.g., diffusion coefficients in semen and gel) and biological and human use parameters (e.g., gel and semen volumes). Values from Table 1 are input to the model unless otherwise noted.
Diffusion coefficients
The diffusion coefficient of HIV in semen (DHIV,semen) is estimated using the Stokes-Einstein equation (29). HIV is taken as a sphere of diameter 125 nm (30). Semen is treated as a Newtonian fluid with viscosity 1 cP. Then, DHIV,semen = 3.6 × 10−8 cm2 s−1. Human semen is a heterogeneous material, and measurements of its viscosity have produced results typically within the range 3–7 cP (31). This may be due in part to differences in the viscometric methods employed. Our use of the viscosity 1 cP simulates waterlike semen properties and thus provides the highest, and therefore most conservative, value for DHIV,semen. That is, it leads to the lowest estimates of tthreshold.
There has been little work quantifying diffusion coefficients of HIV in aqueous gels. Recent work indicates that HIV mobility is reduced in human cervical mucus (32). We can also infer that gels have the potential to hinder HIV diffusion from studies of nanoparticles in cervical mucus (33) and studies of small molecules in microbicide gels (34). Further work is needed to characterize likely reductions in diffusion coefficient of HIV in different gel materials. To allow for a range of possible values of viral hindrance in our model, the diffusion coefficient of HIV in vaginal gels (DHIV,gel) is varied relative to the diffusion coefficient of HIV in semen (DHIV,semen): DHIV,gel = DHIV,semen, 0.5DHIV,semen, or 0.1DHIV,semen.
Partition coefficient
We assume that the partition coefficient at the semen/gel interface (ΦHIV) was 1. We expect this to be a reasonable approximation because vaginal gel formulations, like semen, are hydrophilic with high water content. As a result, the semen/gel interface likely becomes indistinct after some time of contact. Furthermore, this provides a conservative estimate, maximizing the number of virions that diffuse from the semen layer into the gel layer.
Gel and semen parameters
Volumes of microbicide gels used in clinical trials range from 2 to 5 ml (35–38). Here, we use an intermediate volume of 3 ml. The average volume of the human ejaculate (Vsemen) is 3.4 ml (31). If the volume of semen is distributed relatively evenly over the area of the vagina, then an effective semen layer thickness is represented by . The shape and surface area of the vagina vary among individuals. Using vinyl polysiloxane casts, Pendergrass et al. found that the surface area of the human vagina ranged from 65.73 to 107.07 cm2 (39). A comparable value was found using MRI (40). Here, an intermediate value of 100 cm2 is used for vaginal surface area (Avagina). This yields an effective value of hsemen = 340 μm.
HIV concentration
HIV viral load in semen varies with stage of infection, antiviral treatment, and co-infection with genital tract infections (41). Risk of HIV transmission is highest during acute HIV infection, during which the level of HIV RNA in semen can reach 5 log10 to 6 log10 copies/ml (42,43). HIV RNA levels have been found to be highest in men within 1 month of infection: in a recent study quantifying HIV RNA levels in seminal plasma, median HIV RNA level in nine acutely infected men was 5.0 log10 copies/ml (44). In our model, we use this value of 105 copies/ml for HIV RNA in semen. There are 2 copies of RNA per HIV virion, so this is equivalent to an initial concentration of 5 × 104 virions/ml.
Threshold number of virions in tissue compartment
The number of virions needed for HIV infection to occur is unknown, and likely varies according to many biological factors related to infectiousness of the virions and condition of their recipient (45). It is not possible to translate HIV RNA copy number to measures of infectiousness (e.g., 50% tissue culture infectious dose), because attempts to isolate HIV from semen are typically unsuccessful. However, Klasse et al. (46) noted that the highest risk of transmission from man to woman per coital act is 10%, which likely reflects the scenario of highest infectiousness of the transmitter and highest susceptibility of the recipient.
These current data are insufficient to link our model results to the clinical outcome of infection. We use a conservative threshold of 1.7 × 104 virions in computing values of tthreshold. This is one-tenth of the virions introduced in an infectious ejaculate, assuming that semen volume is 3.4 ml and initial concentration is 5 × 104 virions/ml. Considering that the highest risk of transmission from man to woman per coital act is 10%, our chosen threshold would approximately correspond to a 1% risk of infection at tthreshold. Microbicides that increase time to threshold may allow more time for HIV virions to be neutralized before virions diffuse to tissue surfaces. Using tthreshold allows us to make comparisons among different scenarios. Although the quantitative biological and clinical implications of our value for tthreshold are uncertain, our model may easily be modified to accommodate new clinical data on the number of virions needed to establish infection.
Application of diffusion model to in vivo vaginal coating distributions
Experiments quantifying in vivo deployment of vaginal gels
Our group developed an optical probe for imaging deployment of vaginal gels in women in vivo (22–24). The imaging technique outputs the spatial distribution of gel coating thickness over vaginal epithelial surfaces, as illustrated in Fig. S1 in the Supporting Material. Gels are fluorescently labeled with U.S.-Pharmacoepia-grade injectable fluorescein powder (typical concentration 0.1% w/w). Coating thickness is linearly related to fluorescence for layers <1.5 mm thick. The resolution of the device is 15–25 μm for gel thickness measurements.
Vaginal coating data were obtained for two commercial vaginal gels: K-Y Jelly (Personal Products, Skillman, NJ), a hydroxyethylcellulose based lubricant, termed gel K; and Replens (Lil' Drug Store Products, Cedar Rapids, IA) a Carbopol-based moisturizer, termed gel R. These were chosen as surrogates for microbicide products. They have different rheological properties, which give rise to different flow rates in fluid mechanical models of vaginal coating (47–51). Imaging studies were performed in the clinic of the Department of Obstetrics and Gynecology, Duke University Medical Center, in a group of women of child-bearing age with no abnormalities of anatomy or physiology of the reproductive tract. The group included both parous and nulliparous women; measurements were performed throughout the menstrual cycle except during menses.
Experiments were performed for two protocols for a woman's activity after gel application: without (−) and with (+) simulated coitus. In both protocols, a 3.5-ml bolus of gel was applied by a syringe-type applicator to the vaginal fornix while the woman was in a supine posture. In the first protocol, the woman remained supine for 20 min before imaging measurements commenced. This simulated precoital conditions of gel use. In the second protocol, the woman simulated coitus: after gel application, she assumed a sitting position (1 min), a standing position (1 min), a sitting position (1 min), and a supine position during which coitus was simulated by applying 30 strokes using an artificial phallus (∼1 min). Imaging measurements were performed 10 min after gel application. These protocols have been followed in a number of prior imaging studies of vaginal gel distribution (52).
A total of eight experiments were performed in different women, with duplicate experiments in each treatment combination (gel × activity). This relatively small sample size is not sufficient to identify statistically significant differences across each combination (gel × activity). However, it is sufficient to exercise our new model of intravaginal HIV transport kinetics, providing initial quantitative insights about HIV transport times in vivo.
Application of the model to in vivo vaginal coating data
Vaginal coating data are discretized (Fig. 3). Gel thicknesses are divided into 12 bins: 0 μm (areas in which no gel is detected), 0–50 μm, 50–100 μm, 100–150 μm, 150–200 μm, 200–250 μm, 250–300 μm, 300–350 μm, 350–400 μm, 400–450 μm, 450–500 μm, and >500 μm. An approximate thickness value is input for hgel for each bin: 0 μm, 25 μm, 75 μm, 125 μm, 175 μm, 225 μm, 275 μm, 325 μm, 375 μm, 425 μm, 475 μm, and 525 μm, respectively. Areas coated by gel layers of these thicknesses are normalized to total area, to determine fractional area (ϕn) coated by a given thickness. The total area of tissue input to the model is 100 cm2. The amount of virus in the tissue compartment versus time is calculated using a modified version of Eq. 9, into which multiple gel thicknesses and their respective fractional coating areas are incorporated:
| (10) |
Here, m is the number of bins, 12. The time to reach the threshold amount of virus in tissue, tthreshold, is then determined.
Figure 3.

Schematic showing how model is applied to in vivo deployment data. Thickness data taken from in vivo experiments are discretized into 12 bins, approximated by constant thickness. The fractional areas coated by each of these approximated thicknesses were also derived from experimental data. These, with the parameters defined in Table 1, were used to calculate the time required to reach the threshold number of virions in the tissue compartment, tthreshold.
Results
Initial modeling for a surface entirely coated at constant thickness
We initially applied the model to a surface fully coated by a gel layer of constant thickness. This illustrated the primary interaction between HIV diffusion coefficients and gel thickness in governing HIV transport times. Fig. S2 shows the amount of virus in the tissue compartment as a function of time. Different combinations of gel thickness and HIV diffusion coefficients are compared. Note that the presence of a gel layer does not provide an absolute barrier to HIV diffusion, i.e., the curves converge at the same maximum, where all of the virions entered the tissue compartment. However, the presence of a gel layer delays entry of HIV into the tissue compartment. Increasing the gel layer thickness shifts the curve to the right and increases time to threshold (Fig. S2 A). Decreasing the diffusion coefficient for virus in gel shifts the curve to the right and increases time to threshold (Fig. S2 B).
Trade-offs between coating thickness and the relative area of gel coating
To investigate trade-offs between the thickness of coating (where it exists) and the area of tissue with coating, we applied a schema in which the volume of gel was conserved (Vgel = 3 ml). Here, the gel coating thickness and fractional area coated are inversely related:
| (11) |
Fig. 4 shows the time to threshold versus fractional area coated. Note that time to threshold increases as fractional area coated increases, even though coating thickness decreases (to conserve gel volume).
Figure 4.

Trade-offs between gel layer thickness and area coated when the volume of gel is conserved, such that . As the fractional area coated increases, time to threshold increases.
Fig. 4 also illustrates how delay of HIV diffusion to the tissue surface can be attributed to the physical presence of the gel layer, which distances the semen from the tissue. This is represented by the scenario Dgel = 1Dsemen, as compared to the scenario in which there is no gel coating. For gel layers a few hundred microns thick, such distancing delays time to threshold by up to 3 h. When the gel layer hinders viral diffusion (versus diffusion in semen), the time to threshold is further increased. For Dgel = 0.1Dsemen (i.e., the greatest degree of reduction in viral diffusion in gel versus semen), there is a pronounced increase in slope of this curve for ϕ ≥ 0.85. When Dgel = 0.1Dsemen, the time to threshold increases to as much as 22 h.
To further explore trade-offs between coating thickness and fractional area coated, we generated a contour plot for time to threshold, in which coating thickness, hgel, and fractional area coated, ϕ, are varied (Fig. 5). The curves in the contour plot exhibit a notable bend at ∼100 μm. This means that, for deployment scenarios where coating thickness is <100 μm, threshold time remains relatively constant for a range of areas coated. For deployment scenarios where coating thickness is >100 μm, fractional area coated is the primary determinant of time to threshold. In the results generated (not shown) for increased semen viscosity (and therefore decreased Dsemen), the shapes of the curves were qualitatively the same, but shifted to the right. That is, trends were similar, but time to threshold increased.
Figure 5.

Contour plot showing values of threshold time for different gel thicknesses and fractional areas coated. Note that fractional area coated is the more important factor for all but the thinnest gel layers.
We also generated a contour plot to explore conditions in which viral hindrance significantly affects time to threshold (Fig. S3). Recognizing from the trends shown in Fig. 5 that the area coated is important in determining time to threshold, we plotted time to threshold varying the level of viral hindrance (Dgel/Dsemen) and fractional area coated for a 300-μm coating layer (Fig. S3). We find that for ϕ ≥ 0.80, the level of viral hindrance contributes to determining time to threshold. For ϕ ≥ 0.95, increasing viral hindrance rapidly increases time to threshold. These results suggest that a significant portion of the tissue must be coated for levels of viral hindrance to contribute to the barrier function of a microbicide gel.
Inputting in vivo vaginal coating data to model showed differences between application protocols
To examine how gels would act to hinder viral diffusion in vivo, we input experimental deployment data to the mathematical model (Fig. 3). Deployment data for a small sample of in vivo data for vaginal coating thickness distributions were selected. These provided a range of fractional areas with detectable coating, and of the distributions of thicknesses within that coating (Table S1). The deployment data were summarized as discretized thicknesses and corresponding fractional areas coated. These experimental inputs and other model parameters were used to calculate the time to threshold for different vaginal gels, application protocols, and levels of viral hindrance by the gel.
Fig. 6 shows the resulting model outputs of tthreshold. There was little difference in tthreshold between gels. Gel application protocol (with or without simulated coitus) had a more significant effect on time to threshold. Simulated coitus increased the fractional area coated from ∼60–87% to nearly 100% (Table S1). Shearing forces of simulated coitus spread the gels over tissue surfaces, and the calculated time to threshold increased as a result. For deployment data from experiments without simulated coitus, there was little difference in tthreshold for different reductions in viral diffusion coefficient; time to threshold was <1.5 h, regardless of the reduction. In contrast, for experiments with simulated coitus, a higher level of viral hindrance (Dgel = 0.1 Dsemen) added hours to tthreshold compared to cases in which diffusion was not hindered (Dgel = 1Dsemen). For gels with Dgel = 0.1Dsemen, calculated time to threshold was nearly 8 h. The Supporting Material (Fig. S4) describes the work we performed to identify a summary measure of gel thickness distribution, the harmonic mean, that is useful for estimating viral transport times.
Figure 6.

Resulting threshold times for application of the mathematical model to experimental data obtained from deployment of vaginal gels in women. The numbers “1” and “2” represent data from two independent experiments for each gel/protocol. K, KY jelly; R, Replens; +, with simulated coitus; −, without simulated coitus. Three levels of viral hindrance were input (Dgel/Dsemen = 0.1, 0.5, and 1).
Discussion
We have developed a mathematical model for in vivo HIV transport in the presence of a microbicide gel. The model analyzes diffusion of HIV virions from semen to tissue in the presence of a biologically realistic vaginal coating, with incomplete coverage and nonuniform thickness. Total HIV transport to tissue occurs over coated and uncoated regions. To compare different scenarios, we use the metric of time required for a threshold number of virions to enter the tissue compartment.
Results indicate that comprehensive coating by microbicide gels is crucial to increasing time to threshold. For example, for a conserved volume of gel, we sought to determine whether it is more important to coat a greater area with thinner layers or a smaller area with thicker layers. We found that time to threshold increases with increasing fractional area coated, even though the thickness of gel layers decreases. Analyzing different deployment scenarios, we also found that there is a cutoff in effective coating thickness: below ∼100 μm, time to threshold was brief, regardless of the fractional area coated. However, for thicknesses >∼100 μm, increasing fractional area coated increased the time to threshold. When coating was incomplete, HIV transport to the epithelium occurred primarily over surfaces in which there was direct contact between semen and uncoated tissue. When fractional area was >∼80%, both gel thickness and level of viral hindrance (i.e., reduced diffusion coefficient) contributed to increasing the time to threshold. Taken together, these results suggest the importance of comprehensive coating in determining the ability of a microbicide gel to function as a barrier to HIV. Microbicide formulators should consider the importance of deployment as they design products that function by preventing or delaying the contact between HIV virions and vulnerable tissue.
The model was also used to provide an objective context for interpreting in vivo data for the extent and thickness of vaginal coating. Our human imaging study was relatively small (n = 8), but it provided insights about differences in vaginal coating, and about how to consolidate coating data. The protocol involving simulated coitus (+) produced a larger coated surface area than that in which women remained supine after gel application (−), and the calculated HIV transport times were longer as a result.
In the state of development presented here, our model does have limitations. Some input parameters were approximations. For example, to our knowledge, the diffusion coefficients of HIV in semen and microbicide gels have not yet been measured. We expect HIV diffusion in a typical viscous vaginal gel to be slower than it is in semen (e.g., due to increased viscous drag, physical obstruction, and electrostatic interactions with polymers). We used the Stokes-Einstein relation to conservatively approximate the diffusion coefficient of HIV in semen, and computations were subsequently performed while varying the ratio Dgel/Dsemen. However, the motion of particles through polymer solutions can be complicated, especially when the particle is comparable in size to the mesh formed by polymer chains. More complex mathematical models for estimating the diffusion coefficients of particles in polymer solutions account for mechanisms such as hydrodynamic drag on particles and physical obstruction by polymer chains (53). Experimental methods are being developed for determining HIV diffusion coefficients in gels (34), semen, and cervical mucus (32), and results of these studies can be readily incorporated into the computational framework presented here. Furthermore, we assumed that diffusion coefficients of virions in semen and gel were constant over time, thereby neglecting possible changes due to dilution of gel with semen and vaginal fluid.
In our model, we also assumed that HIV infection occurs via cell-free virus. However, cell-associated virus may play a role in HIV transmission (54), e.g., via infected immune cells such as lymphocytes, monocytes, and/or macrophages. Such cells are much larger than free virions, with diameters of the order of 10–20 μm, whereas the diameter of an HIV virion is ∼125 nm. Thus, we would expect cell transport via simple diffusion to be much slower than that for free HIV virions. However, unlike free virions, these cells are motile. The analogous diffusion coefficient, or motility coefficient, of cells in semen or gel could be closer to that of free virus. Saltzman et al. found motility coefficients of monocytes in synthetic polymer gels to be ∼10−9–10−10 cm2 s−1 (55). Although further studies will continue to elucidate the roles of cell-associated and cell-free virus, we note that cell-free transmission is consistent with animal models used currently to evaluate microbicide products.
Our model assumed that HIV transport is a result of simple diffusion, and did not consider the possible role of convective transport. Coital activity (viz. shearing by the penis) likely causes movements of fluids within the vagina (including gels) that would give rise to such transport. The work here is thus more relevant to HIV transport after coitus. Moreover, it is unclear whether convective processes would affect transport of HIV at mucosal surfaces. There is, at times, likely some convection of transudate from vaginal tissues, and clearance of fluids out of the vagina. Clearance of virus due to these mechanisms would likely reduce the number of virions reaching the tissue surface, and thus, we believe that our model provides an estimate of the upper bound of the number of virions that could reach tissue surfaces, i.e., a conservative lower-bound estimate of the time to threshold.
To evaluate different scenarios, we used the time needed for a threshold number of virions to enter the tissue compartment. There is currently a lack of experimental data needed to relate this value to measures of clinical outcome. In the future, it may be helpful to incorporate this approach, which addresses the spatiotemporal distributions of virions, with stochastic theory, which incorporates data from clinical trials. This could provide increased understanding of the extent to which factors under developer control (e.g., pharmaceutical agent potency, concentration, and delivery system) determine microbicide product efficacy.
Finally, this study did not account for HIV neutralization by pharmaceutical agents. We made this choice because there are currently >10 microbicides in clinical trials and several agents in the pipeline (56), with several different mechanisms of action and dosage forms among them. This study focused on exploring how gel deployment and transport properties could affect the barrier functions of a microbicide gel. A logical follow-up to the modeling here will be to incorporate the simultaneous transport of specific anti-HIV pharmaceutical agents for a specific microbicide product.
A number of transport processes interact in the functioning of vaginal microbicide gels, including movement of active ingredients and virions. Understanding these processes will contribute to a fundamental understanding of the functioning of microbicide gels, and to the design of gels with improved performance. To date, there have been few attempts to develop mathematical models for topical microbicides. This is probably due to the fact that sexual transmission of HIV is complex and poorly understood. Furthermore, topical microbicides often deliver drugs locally rather than systemically, so the analyses used in traditional pharmacokinetic modeling, where entire organs are treated as single compartments, are less relevant. There is also a lack of experimental pharmacokinetic data for topical microbicides from humans or animal models: biopsies of vaginal tissue are invasive, and there can be high variability in collection and analysis of cervicovaginal lavages and cytobrush specimens. Without these pharmacokinetic data, mathematical models cannot be validated. Additional collaborations among researchers using experimental and mathematical approaches are needed. Ultimately, mathematical models for topical microbicides could serve as valuable tools in understanding mucosal HIV transmission, development of new prevention technologies, and design of clinical trials.
Acknowledgments
We thank Dr. Anthony R. Geonnotti for his thoughtful review of this manuscript.
This work was sponsored by National Institutes of Health grant R01 AI48103 and U19 AI077289 and a National Science Foundation Graduate Research Fellowship for B.E.L.
Footnotes
David Katz's present address is Box 90281, Durham, NC 27708.
Supporting Material
References
- 1.Rosario M.C., Jacqmin P., Dorr P., van der Ryst E., Hitchcock C. A pharmacokinetic-pharmacodynamic disease model to predict in vivo antiviral activity of maraviroc. Clin. Pharmacol. Ther. 2005;78:508–519. doi: 10.1016/j.clpt.2005.07.010. [DOI] [PubMed] [Google Scholar]
- 2.Rosario M.C., Poland B., Sullivan J., Westby M., van der Ryst E. A pharmacokinetic-pharmacodynamic model to optimize the phase IIa development program of maraviroc. J. Acquir. Immune Defic. Syndr. 2006;42:183–191. doi: 10.1097/01.qai.0000220021.64115.37. [DOI] [PubMed] [Google Scholar]
- 3.Davenport M.P., Ribeiro R.M., Zhang L., Wilson D.P., Perelson A.S. Understanding the mechanisms and limitations of immune control of HIV. Immunol. Rev. 2007;216:164–175. doi: 10.1111/j.1600-065X.2006.00485.x. [DOI] [PubMed] [Google Scholar]
- 4.Perelson A.S. Modelling viral and immune system dynamics. Nat. Rev. Immunol. 2002;2:28–36. doi: 10.1038/nri700. [DOI] [PubMed] [Google Scholar]
- 5.Perelson A.S., Neumann A.U., Markowitz M., Leonard J.M., Ho D.D. HIV-1 dynamics in vivo: virion clearance rate, infected cell life-span, and viral generation time. Science. 1996;271:1582–1586. doi: 10.1126/science.271.5255.1582. [DOI] [PubMed] [Google Scholar]
- 6.McGowan I. Microbicides: a new frontier in HIV prevention. Biologicals. 2006;34:241–255. doi: 10.1016/j.biologicals.2006.08.002. [DOI] [PubMed] [Google Scholar]
- 7.Balzarini J., Van Damme L. Microbicide drug candidates to prevent HIV infection. Lancet. 2007;369:787–797. doi: 10.1016/S0140-6736(07)60202-5. [DOI] [PubMed] [Google Scholar]
- 8.Cutler B., Justman J. Vaginal microbicides and the prevention of HIV transmission. Lancet Infect. Dis. 2008;8:685–697. doi: 10.1016/S1473-3099(08)70254-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Johnston M.I., Fauci A.S. An HIV vaccine—evolving concepts. N. Engl. J. Med. 2007;356:2073–2081. doi: 10.1056/NEJMra066267. [DOI] [PubMed] [Google Scholar]
- 10.Padian N.S., Buve A., Balkus J., Serwadda D., Cates W. Biomedical interventions to prevent HIV infection: evidence, challenges, and way forward. Lancet. 2008;372:585–599. doi: 10.1016/S0140-6736(08)60885-5. [DOI] [PubMed] [Google Scholar]
- 11.Honey K. Microbicide trial screeches to a halt. J. Clin. Invest. 2007;117:1116. doi: 10.1172/JCI32291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Skoler-Karpoff S., Ramjee G., Ahmed K., Altini L., Plagianos M.G. Efficacy of Carraguard for prevention of HIV infection in women in South Africa: a randomised, double-blind, placebo-controlled trial. Lancet. 2008;372:1977–1987. doi: 10.1016/S0140-6736(08)61842-5. [DOI] [PubMed] [Google Scholar]
- 13.Tao W., Richards C., Hamer D. Enhancement of HIV infection by cellulose sulfate. AIDS Res. Hum. Retroviruses. 2008;24:925–929. doi: 10.1089/aid.2008.0043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Karim S.A. Safety and effectiveness of vaginal microbicides buffer gel and 0.5% PRO 2000/5 gel for the prevention of HIV infection in women: results of the HPTN 035 trial. Proc. 16th Conf. Retroviruses Opportun. Infect. 2009 [Google Scholar]
- 15.Klasse P.J., Shattock R., Moore J.P. Antiretroviral drug-based microbicides to prevent HIV-1 sexual transmission. Annu. Rev. Med. 2008;59:455–471. doi: 10.1146/annurev.med.59.061206.112737. [DOI] [PubMed] [Google Scholar]
- 16.Tuckwell H.C., Shipman P.D., Perelson A.S. The probability of HIV infection in a new host and its reduction with microbicides. Math. Biosci. 2008;214:81–86. doi: 10.1016/j.mbs.2008.03.005. [DOI] [PubMed] [Google Scholar]
- 17.Chakraborty H., Sen P.K., Helms R.W., Vernazza P.L., Fiscus S.A. Viral burden in genital secretions determines male-to-female sexual transmission of HIV-1: a probabilistic empiric model. AIDS. 2001;15:621–627. doi: 10.1097/00002030-200103300-00012. [DOI] [PubMed] [Google Scholar]
- 18.Geonnotti A.R., Katz D.F. Dynamics of HIV neutralization by a microbicide formulation layer: biophysical fundamentals and transport theory. Biophys. J. 2006;91:2121–2130. doi: 10.1529/biophysj.106.086322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Geonnotti, A., P. Kiser, M. Rosen, K. Barnhart, and D. Katz. 2008. Three-dimensional pharmacokinetic modeling of microbicide delivery by intravaginal rings within an MRI-derived finite-element vaginal compartment. Microbicides Meeting. New Delhi, India.
- 20.Rohan L.C., Sassi A.B. Vaginal drug delivery systems for HIV prevention. AAPS J. 2009;11:78–87. doi: 10.1208/s12248-009-9082-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Justin-Temu M., Damian F., Kinget R., Van Den Mooter G. Intravaginal gels as drug delivery systems. J. Womens Health (Larchmt) 2004;13:834–844. doi: 10.1089/jwh.2004.13.834. [DOI] [PubMed] [Google Scholar]
- 22.Mauck C.K., Katz D.F., Sandefer E.P., Nasution M.D., Henderson M. Vaginal distribution of Replens and K-Y Jelly using three imaging techniques. Contraception. 2008;77:195–204. doi: 10.1016/j.contraception.2007.11.016. [DOI] [PubMed] [Google Scholar]
- 23.Henderson M.H., Couchman G.M., Walmer D.K., Peters J.J., Owen D.H. Optical imaging and analysis of human vaginal coating by drug delivery gels. Contraception. 2007;75:142–151. doi: 10.1016/j.contraception.2006.08.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Henderson M.H., Peters J.J., Walmer D.K., Couchman G.M., Katz D.F. Optical instrument for measurement of vaginal coating thickness by drug delivery formulations. Rev. Sci. Instrum. 2005;76:034302. [Google Scholar]
- 25.Reference deleted in proof.
- 26.Barnhart K., Pretorius E.S., Malamud D. Lesson learned and dispelled myths: Three-dimensional imaging of the human vagina. Fertil. Steril. 2004;81:1383–1384. doi: 10.1016/j.fertnstert.2004.01.016. [DOI] [PubMed] [Google Scholar]
- 27.Greenhead P., Hayes P., Watts P.S., Laing K.G., Griffin G.E. Parameters of human immunodeficiency virus infection of human cervical tissue and inhibition by vaginal virucides. J. Virol. 2000;74:5577–5586. doi: 10.1128/jvi.74.12.5577-5586.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Broliden K., Haase A.T., Ahuja S.K., Shearer G.M., Andersson J. Introduction: Back to basics: mucosal immunity and novel HIV vaccine concepts. J. Intern. Med. 2009;265:5–17. doi: 10.1111/j.1365-2796.2008.02053.x. [DOI] [PubMed] [Google Scholar]
- 29.Truskey G.A., Yuan F., Katz D.F. Pearson Education; Upper Saddle River, NJ: 2009. Transport Phenomena in Biological Systems. [Google Scholar]
- 30.Briggs J.A., Grunewald K., Glass B., Forster F., Krausslich H.G. The mechanism of HIV-1 core assembly: insights from three-dimensional reconstructions of authentic virions. Structure. 2006;14:15–20. doi: 10.1016/j.str.2005.09.010. [DOI] [PubMed] [Google Scholar]
- 31.Owen D.H., Katz D.F. A review of the physical and chemical properties of human semen and the formulation of a semen simulant. J. Androl. 2005;26:459–469. doi: 10.2164/jandrol.04104. [DOI] [PubMed] [Google Scholar]
- 32.Boukari H., Brichacek B., Margolis L., Nossal R. HIV-virions appear to be trapped by human cervical mucus. Biophys. J. 2009;96:35a. doi: 10.1021/bm900344q. (Abstr.) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lai S.K., O'Hanlon D.E., Harrold S., Man S.T., Wang Y.Y. Rapid transport of large polymeric nanoparticles in fresh undiluted human mucus. Proc. Natl. Acad. Sci. USA. 2007;104:1482–1487. doi: 10.1073/pnas.0608611104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Geonnotti A.R., Furlow M.J., Wu T., DeSoto M.G., Henderson M.H. Measuring macrodiffusion coefficients in microbicide hydrogels via postphotoactivation scanning. Biomacromolecules. 2008;9:748–751. doi: 10.1021/bm701018w. [DOI] [PubMed] [Google Scholar]
- 35.Coggins C., Blanchard K., Alvarez F., Brache V., Weisberg E. Preliminary safety and acceptability of a carrageenan gel for possible use as a vaginal microbicide. Sex. Transm. Infect. 2000;76:480–483. doi: 10.1136/sti.76.6.480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.El-Sadr W.M., Mayer K.H., Maslankowski L., Hoesley C., Justman J. Safety and acceptability of cellulose sulfate as a vaginal microbicide in HIV-infected women. AIDS. 2006;20:1109–1116. doi: 10.1097/01.aids.0000226950.72223.5f. [DOI] [PubMed] [Google Scholar]
- 37.Kilmarx P.H., van de Wijgert J., Chaikummao S., Jones H.E., Limpakarnjanarat K. Safety and acceptability of the candidate microbicide Carraguard in Thai women: findings from a phase II clinical trial. J. Acquir. Immune Defic. Syndr. 2006;43:327–334. doi: 10.1097/01.qai.0000243056.59860.c1. [DOI] [PubMed] [Google Scholar]
- 38.Low-Beer N., Gabe R., McCormack S., Kitchen V.S., Lacey C.J. Dextrin sulfate as a vaginal microbicide: randomized, double-blind, placebo-controlled trial including healthy female volunteers and their male partners. J. Acquir. Immune Defic. Syndr. 2002;31:391–398. doi: 10.1097/00126334-200212010-00004. [DOI] [PubMed] [Google Scholar]
- 39.Pendergrass P.B., Belovicz M.W., Reeves C.A. Surface area of the human vagina as measured from vinyl polysiloxane casts. Gynecol. Obstet. Invest. 2003;55:110–113. doi: 10.1159/000070184. [DOI] [PubMed] [Google Scholar]
- 40.Barnhart K., Izquierdo A., Pretorius E.S., Shera D.M. Baseline dimensions of the human vagina. Hum. Reprod. 2006;21:1618–1622. doi: 10.1093/humrep/del022. [DOI] [PubMed] [Google Scholar]
- 41.Coombs R.W., Reichelderfer P., Landay A.L. Recent observations on HIV type-1 infection in the genital tract of men and women. AIDS. 2003;17:455–480. doi: 10.1097/00002030-200303070-00001. [DOI] [PubMed] [Google Scholar]
- 42.Cohen M.S., Gay C., Kashuba A.D., Blower S., Paxton L.A. Narrative review: antiretroviral therapy to prevent the sexual transmission of HIV-1. Ann. Intern. Med. 2007;146:591–601. doi: 10.7326/0003-4819-146-8-200704170-00010. [DOI] [PubMed] [Google Scholar]
- 43.Cohen M.S., Pilcher C.D. Amplified HIV transmission and new approaches to HIV prevention. J. Infect. Dis. 2005;191:1391–1393. doi: 10.1086/429414. [DOI] [PubMed] [Google Scholar]
- 44.Stekler J., Sycks B., Holte S., Maenza J., Stevens C. HIV dynamics in seminal plasma during primary HIV infection. AIDS Res. Hum. Retroviruses. 2008;24:1269–1274. doi: 10.1089/aid.2008.0014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Galvin S.R., Cohen M.S. The role of sexually transmitted diseases in HIV transmission. Nat. Rev. Microbiol. 2004;2:33–42. doi: 10.1038/nrmicro794. [DOI] [PubMed] [Google Scholar]
- 46.Klasse P.J., Shattock R.J., Moore J.P. Which topical microbicides for blocking HIV-1 transmission will work in the real world? PLoS Med. 2006;3:e351. doi: 10.1371/journal.pmed.0030351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Kieweg S.L., Geonnotti A.R., Katz D.F. Gravity-induced coating flows of vaginal gel formulations: in vitro experimental analysis. J. Pharm. Sci. 2004;93:2941–2952. doi: 10.1002/jps.20194. [DOI] [PubMed] [Google Scholar]
- 48.Kieweg S.L., Katz D.F. Squeezing flows of vaginal gel formulations relevant to microbicide drug delivery. J. Biomech. Eng. 2006;128:540–553. doi: 10.1115/1.2206198. [DOI] [PubMed] [Google Scholar]
- 49.Kieweg S.L., Katz D.F. Interpreting properties of microbicide drug delivery gels: analyzing deployment kinetics due to squeezing. J. Pharm. Sci. 2007;96:835–850. doi: 10.1002/jps.20774. [DOI] [PubMed] [Google Scholar]
- 50.Lai B.E., Xie Y.Q., Lavine M.L., Szeri A.J., Owen D.H. Dilution of microbicide gels with vaginal fluid and semen simulants: Effect on rheological properties and coating flow. J. Pharm. Sci. 2007;97:1030–1038. doi: 10.1002/jps.21132. [DOI] [PubMed] [Google Scholar]
- 51.Szeri A., Park S., Verguet S., Weiss A., Katz D. A model of transluminal flow of an anti-HIV microbicide vehicle: combined elastic squeezing and gravitational sliding. Phys. Fluids. 2008;20:083101. doi: 10.1063/1.2973188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Pretorius E.S., Barnhart K., Timbers K., Malamud D. Magnetic resonance imaging to determine the distribution of a vaginal gel: before, during, and after both simulated and real intercourse. Contraception. 2002;66:443–451. doi: 10.1016/s0010-7824(02)00412-2. [DOI] [PubMed] [Google Scholar]
- 53.Amsden B. Modeling solute diffusion in aqueous polymer solutions. Polymer (Guildf.) 2002;43:1623–1630. [Google Scholar]
- 54.Sattentau Q. Avoiding the void: cell-to-cell spread of human viruses. Nat. Rev. Microbiol. 2008;6:815–826. doi: 10.1038/nrmicro1972. [DOI] [PubMed] [Google Scholar]
- 55.Willits R.K., Saltzman W.M. The effect of synthetic polymers on the migration of monocytes through human cervical mucus. Biomaterials. 2004;25:4563–4571. doi: 10.1016/j.biomaterials.2003.11.046. [DOI] [PubMed] [Google Scholar]
- 56.Alliance for Microbicide Development. 2009. July 2009 Pipeline Update. Silver Spring, MD.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


