Abstract
Focal adhesions are clusters of specific receptor-ligand bonds that link an animal cell to an extracellular matrix. To understand the mechanical responses of focal adhesions, here we develop a stochastic-elasticity model of a periodic array of adhesion clusters between two dissimilar elastic media subjected to an inclined tensile stress, in which stochastic descriptions of molecular bonds and elastic descriptions of interfacial traction are unified in a single modeling framework. We first establish a fundamental scaling law of interfacial traction distribution and derive a stress concentration index that governs the transition between uniform and cracklike singular distributions of the interfacial traction within molecular bonds. Guided by this scaling law, we then perform Monte Carlo simulations to investigate the effects of cluster size, cell/extracellular matrix modulus, and loading direction on lifetime and strength of the adhesion clusters. The results show that intermediate adhesion size, stiff substrate, cytoskeleton stiffening, and low-angle pulling are factors that contribute to the stability of focal adhesions. The predictions of our model provide feasible explanations for a wide range of experimental observations and suggest possible mechanisms by which cells can modulate adhesion and deadhesion via cytoskeletal contractile machinery and sense mechanical properties of their surroundings.
Introduction
Most animal cells cannot survive in isolation and must adhere to adjacent cells or extracellular matrix (ECM) through the formation of focal complexes (FXs) or focal adhesions (FAs) (1). FXs are small primordial adhesion clusters of specific membrane-bound receptors and their complementary ligands on ECM formed close to the edge of advancing membrane protrusions of a cell, whereas FAs are more mature, stable, micron-sized bond clusters linking cells to ECM (2). FAs are usually exposed to forces induced by external physical interactions such as blood flow, as well as those generated by cell's own contractile machinery as stress fibers made of bundles of actin filaments and myosin II motors actively pull FAs at an inclined angle with respect to the cell-ECM interface (3). These forces are known to exert significant influences on cell shape, cytoskeleton organization, and intracellular processes such as cell growth, differentiation, motility, and apoptosis (4). Cells react to mechanical signals by producing a series of biochemical processes within the FAs. The feedback loop between mechanical stimuli and biochemical responses is critical to the regulation of cell adhesion.
Several key experiments have suggested that mechanical forces and cell/ECM elasticity play an essential role in FA growth and maintenance. Mature FAs cannot grow unboundedly and are usually subjected to a size limit up to a few microns (5). Stable FAs only form on sufficiently rigid substrates, and cells tend to migrate toward stiffer region when cultured on an elastically nonhomogeneous substrate (6,7). The elastic modulus of cytoskeleton can change over several orders of magnitude in response to different levels of myosin-II-driven contractility (8,9), whereas inhibition of the contractile stress leads to dissolution of cytoskeleton and disappearance of FAs (10). When myosin II activity is suppressed, application of an external force, irrespective of its physical origin, is found to stimulate growth of FAs in the direction of the force (11). Experiments have also shown that the size of mature FAs can reversibly increase or decrease in response to the applied force, with force per unit area (stress) maintained near a constant value at ∼5.5 kPa irrespective of the cell type (12,13).
A number of theoretical studies have been performed to investigate how mechanical stimuli and cell/ECM properties affect the behaviors of cell adhesion. Deshpande et al. (14) have proposed a model of cellular contractility that accounts for dynamic reorganization of cytoskeleton, with prediction that stress fibers are more effectively developed by multiple activation signals than a single prolonged signal. Bruinsma (15) has described the regulation of cytoskeletal force which is generated along actin filaments during the growth stage from initial contacts to FXs. Nicolas et al. (16) have developed a model to investigate the distribution of shear stress along cell-substrate interface, with the postulate that stress gradient in FAs may control their growth or shrinkage. Smith et al. (17) considered force-induced adhesion strengthening aided by the lateral mobility of molecular receptors. Erdmann and Schwarz (18,19) studied the stochastic effects of a cluster of uniformly stressed molecular bonds transiting between open and closed states under the influence of thermal fluctuation. Based on the solutions to a one-step master equation, Erdmann and Schwarz demonstrated that clusters below a critical size behave like a single molecular bond with a finite lifetime whereas those above the critical size survive over a much-prolonged time due to the collective effect of clustering. Therefore, adhesion size can play a very important role in the stability of a bond cluster: small clusters can easily switch between adhesion and de-adhesion, similar to FXs, which are subjected to frequent turnover, whereas large clusters tend to have a much longer lifetime similar to stable FAs. Qian et al. (20) have extended the work of Erdmann and Schwarz to include the effect of elasticity and nonuniform stress distribution on the stability of a single adhesion cluster under a tensile load applied perpendicular to the cell-ECM interface. The results predict a size-dependent transition between uniform and cracklike distributions of interfacial traction as well as a window of cluster size for relatively stable adhesion and an optimal size for maximum strength. Recent analysis by Lin and Freund (21), based on a direct analogy between focal adhesions and periodic cracks, also predicts an optimum cluster size for maximum strength.
Despite these fascinating studies, the physical mechanisms of focal adhesions and mechanosensitivity in general are still a subject of intense speculation and debate. There exist few theoretical studies to synergize different experimental observations of FAs into a coherent understanding. Motivated by the existing experiments and seemingly complex interplay among cluster size, cell/ECM elasticity, receptor-ligand binding/unbinding, and cytoskeletal contractile forces, here we develop a stochastic-elasticity model of a periodic array of adhesion clusters between two dissimilar elastic media subjected to an inclined tensile stress, in which stochastic descriptions of molecular bonds and continuum elastic descriptions of interfacial traction distribution are unified in a single modeling framework. This model can be subjected to rigorous mathematical and numerical analysis to address several important questions including:
Why is there a micron-scale size limit on FAs?
Why do cells prefer stiffer substrates?
Why are cytoskeletal contractile forces necessary to stabilize FAs?
How do lifetime and strength of FAs depend on the stress fiber orientation?
Model
The system under investigation involves a periodic array of adhesion clusters of molecular bonds between two dissimilar elastic media subjected to a tensile stress σ∞ applied at an inclined angle θ with respect to the cell-ECM interface, as shown in Fig. 1. Both cell and substrate are modeled as semi-infinite elastic media with Young's modulus and Poisson's ratio EC, νC, and ES, νS, respectively. It will be convenient to define a reduced elastic modulus E∗ according to the convention of contact mechanics (22)
| (1) |
Figure 1.

Schematic illustration of a periodic array of adhesion clusters between two dissimilar elastic media under an inclined tensile stress.
We consider the situation that interfacial adhesion arises solely from the receptor-ligand bonds modeled as Gaussian chains having a finite stiffness kLR and zero rest length. All bonds are assumed to be closed at the initial state and subsequently can statistically transit between open (broken) and closed (linked) states as described by Bell (23). The bonds are grouped in adhesion clusters of size 2a, which are periodically distributed at a period of along the interface. Within each cluster, the bonds are distributed uniformly at spacing b, corresponding to a bond density of . The average bond density along the interface is . For simplicity, we consider a slice of the system with out-of-plane thickness b, corresponding to the so-called plane strain problem in the theory of elasticity.
We note that the present problem can be considered a combination of the bond dynamics obeying one-step master equation (24) and the periodic crack model in interfacial fracture mechanics (25). In the absence of molecular bonds, our model is reduced to a periodic array of cracks between two elastic media and in the limit of rigid elastic media—i.e., the type of cluster model discussed by Erdmann and Schwarz (18,19).
Due to the periodic nature of the problem, we focus our attention on one cluster and adopt a set of coordinates (x, z) with directions shown in Fig. 1 and origin located at the center of the cluster. In our plane strain model, the total number of bonds within the cluster is Nt = 2a/b. To understand how interfacial traction is distributed within the adhesion domain, let us first consider the initial state when all bonds are closed. In this case, the tangential and normal components of interfacial traction, τ(x) and σ(x), are related to displacement discontinuities across the interface as
| (2) |
where ux and uz are displacements in x and z directions, respectively. Superscripts C and S here denote cell and substrate. Using the elastic Green's function for semi-infinite media (22), it can be shown that τ(x) and σ(x) obey the integral equations
| (3) |
where
| (4) |
| (5) |
The global force balance along the interface requires that
| (6) |
Equation 3 shows that the interfacial traction is governed by two dimensionless parameters α and β, where β can be recognized as one of Dundurs' constants (26) for elasticity problems in a bi-material system (The present problem is in some sense a tri-material system). It has been pointed out before that β plays a rather minor role in interfacial crack problems (27). Biological materials are often modeled as incompressible and the Poisson's ratio would be near one-half, in which case β ≈ 0. Therefore, taking β ≈ 0, we identify α as the unique controlling parameter to determine how the interfacial traction is distributed within the adhesion clusters.
The effects of α can be immediately understood from the solutions to Eqs. 3 and 6 in extreme cases. In the limit when α → 0, the solution is
| (7) |
within the adhesion domain |x| ≤ a, indicating a uniform distribution of interfacial traction independent of the bond location x. In this limit, the interfacial traction is equally shared among all bonds in the adhesion domain. In the opposite limit when α → ∞, the solution becomes
| (8) |
for |x| ≤ a, which is the classical singular solution for a periodic array of interfacial cracks (28). For the intermediate range 0 < α < ∞, the maximum traction generally occurs at the edge of adhesion and the minimum traction occurs at the center. Fig. 2 shows that the interfacial traction is nearly uniform for α-values <0.1, while a cracklike stress concentration emerges near the adhesion edge for α-values >1. Therefore, we shall refer to α as the stress concentration index. Equation 4 shows that α is linearly proportional to the adhesion size, the bond stiffness, and the density, and inversely proportional to the reduced elastic modulus of cell and substrate. These factors all play an essential role in controlling the distribution of interfacial traction within the adhesion domain. In particular, we note that the elastic modulus of both cell and substrate needs to be sufficiently large to keep α small.
Figure 2.
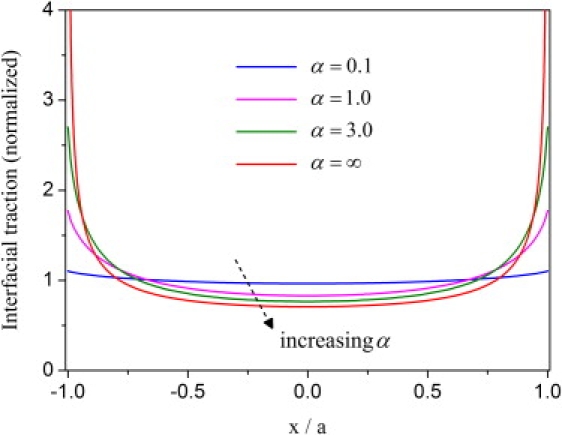
The distributions of the normalized interfacial traction at different values of the stress concentration index while taking β = 0 and c/a = 2. The results indicate a transition between uniform and cracklike singular distributions of interfacial traction.
A similar concept of the stress concentration index has been developed by Qian et al. (20) for a single adhesion cluster between two elastic media. This analysis generalizes this concept to a periodic array of clusters subject to inclined stretching.
From a microscopic point of view, the molecular bonds are subjected to stochastic events of dissociation/association. The bond reaction (dissociation or association) rates are governed by the forces acting on closed bonds and surface separations at open bonds, which can be determined for any instantaneous bond configuration using the appropriate elastic Green's function given in the Appendix. In particular, the dissociation rate koff of a closed bond is assumed to increase exponentially with force F acting on the bond as (23,29–32)
| (9) |
Here k0 is the spontaneous dissociation rate in the absence of an applied force and Fb is a force scale typically in the pN range. For receptor-ligand bonds in focal adhesions, k0−1 falls in the range from a fraction of a second to ∼100 s (33,34). In our model, F depends on the bond location xi, which is generally larger near the adhesion edge than at the center due to stress concentration.
The association rate kon of an open bond is assumed to decrease with the surface separation δ as (20,35,36)
| (10) |
where kB is Boltzmann's constant, T is the absolute temperature (kBT ≈ 4.1 pN · nm at physiological temperature), kon0 is a reference association rate when the receptor-ligand pair are within a binding radius lbind, and Z is the partition function for a receptor confined in a harmonic potential between zero and δ. The surface separation δ is generally larger near the edge than at the center. Consequently, rupture is more likely while rebinding is less likely near the adhesion edge. Under strongly nonuniform distribution of interfacial traction, the failure process is expected to be similar to crack propagation.
Previously, a number of numerical algorithms have been developed for studying bond kinetics in cell adhesion (37,38). In our Monte Carlo simulations, each bond location xi is considered an independent reaction site where the next event will be bond rupture at rate koff (xi) if the bond is currently closed, and bond rebinding at rate kon (xi) if the bond is currently open (20). The reaction rates, kon (xi) and koff (xi), are determined from the computed forces on closed bonds and surface separations at open bonds. The first-reaction method of Gillespie's algorithm (39,40) is used to determine when and where the next reaction will occur through random number generation (18–20). When the binding state of any bond (open versus closed) has undergone a change, an update of the force and surface separation at all bonds is performed using the associated elastic Green's function, and the results are used to determine the subsequent events. This coupling between elastic analysis of interfacial traction/separation and stochastic events starts at the initial state when all bonds are closed and the process proceeds until all bonds within the adhesion domain become open. The total elapsed time T (real time normalized by k0−1) is recorded as the lifetime of the adhesion. The statistical lifetime is obtained from an average of 200 independent simulation trajectories. For relevant physical/biological parameters used in the simulation, we adopt the following typical values: b = 32 nm, c/a = 2, kLR = 0.25 pN/nm, Fb = 4 pN, kon0/k0 = 3200, and lbind = 1 nm, unless stated otherwise.
Results
The lifetime T of the periodic clusters is shown in Fig. 3 as a function of the cluster size Nt for different values of the reduced elastic modulus E∗ between 1 kPa and 300 kPa. The loading angle θ is fixed at 45°. The simulation results indicate that a size-window exists for stable adhesion. In all cases, the traction distribution along the cell-ECM interface is nonuniform and the failure becomes increasingly “cracklike” at increasing cluster size. Very small clusters resemble single molecule behavior with limited lifetime and large clusters fail by severe stress concentration near the adhesion edge. Increasing the reduced elastic modulus tends to stabilize and strengthen the adhesion by alleviating stress concentration within the FAs domain. We observe that the size-window of stable adhesion shifts and broadens as the cell and substrate stiffen, which can be understood from the point of view that large values of E∗ decreases the stress concentration index α toward the regime of uniform interfacial traction. The concept of a size-window for stable adhesion is similar to our previous study on a single cluster under normal tensile load and should be a general feature of molecular adhesion clusters between elastic media because stochastic effects are expected to dominate at small scales and cracklike failure dominates at large scales. Increasing adhesion size or decreasing cell/ECM modulus tends to increase α toward the regime of cracklike stress concentration, hence reducing the lifetime and stability of adhesion.
Figure 3.
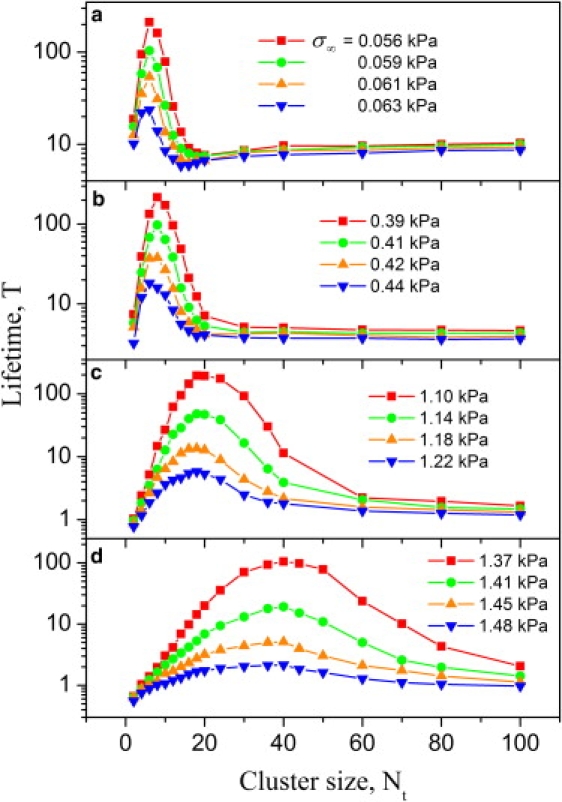
The lifetime T of periodic adhesion clusters as a function of the cluster size Nt for different values of the reduced elastic modulus E∗. The pulling angle θ is fixed at 45°. The selected values of E∗ are (a) 1 kPa; (b) 10 kPa; (c) 100 kPa; and (d) 300 kPa.
Increasing the applied load eventually destabilizes the adhesion. For an example system with Nt = 40, E∗ = 10 kPa, and θ = 45°, Fig. 4 a plots some representative simulation trajectories at three different stress levels. The average lifetime T of 200 simulation trajectories is plotted as a function of the applied stress σ∞ in Fig. 4 b. It is seen that the lifetime asymptotically approaches infinity as the applied stress is reduced to below a critical value. Stresses larger than this critical value dramatically reduce the lifetime and destabilize the adhesion. This suggests that we can define the critical stress at which the cluster lifetime asymptotically approaches infinity as the adhesion strength. To investigate the dependence of the adhesion strength on the pulling angle θ, we have further performed a series of Monte Carlo simulations by varying the value of θ. For a given magnitude of the applied stress, smaller pulling angles with respect to the cell-ECM interface always lead to more stable adhesion. Fig. 4 c shows the adhesion strength as a function of θ for different reduced moduli E∗ ranging from 1 kPa to 300 kPa. Here the cluster size Nt is fixed at 40 bonds. Stiffening cell and ECM leads to dramatic increases in adhesion strength. This can be interpreted again from the point of view that stiffening cell/ECM tends to decrease the stress concentration index α toward the regime of uniform interfacial traction. Fig. 4 d shows the θ-dependence of the adhesion strength for different cluster sizes. Here E∗ is fixed at 100 kPa. As the cluster size is increased from 6 to 20 bonds, the adhesion strength increases due to the collective effect of bond clustering. However, as the cluster size is further increased to 100 bonds, stress concentration effects dominate and cause the adhesion strength to decrease as a consequence of cracklike failure.
Figure 4.

The strength of periodic adhesion clusters. (a) Representative simulation trajectories of the number of closed bonds k versus time τ at three selected stress levels (Nt = 40, E∗ = 10 kPa, and θ = 45°). (b) The adhesion lifetime T as a function of the applied stress σ∞. The lifetime asymptotically approaches infinity as the stress is reduced below a critical value which is defined as the adhesion strength (Nt = 40, E∗ = 10 kPa, and θ = 45°). (c) The adhesion strength as a function of the pulling angle θ for different values of the reduced elastic modulus E∗ from 1 to 300 kPa (Nt = 40). (d) The adhesion strength as a function of the pulling angle θ for different values of the cluster size Nt from 6 to 100 bonds (E∗ = 100 kPa).
The lifetime T of the periodic cluster array is plotted as a function of the pulling angle θ at various stress levels in Fig. 5. Here we fix Nt = 40 and E∗ = 10 kPa in the calculation. We see that, for a given magnitude of the applied stress σ∞, decreasing θ tends to stabilize adhesion. In fact, the adhesion lifetime asymptotically approaches infinity as the pulling angle is reduced to below a critical threshold. This is especially interesting in view of the fact that cells generally flatten when successfully adhering to a substrate, and this immediately suggests a regulation mechanism by which cells can switch between long- and short-lived adhesions by adjusting pulling direction around the critical angle.
Figure 5.

The lifetime T of periodic adhesion clusters as a function of the pulling angle θ at various levels of the applied stress (Nt = 40 and E∗ = 10 kPa).
Discussion
From the basic scaling parameter α, which governs the interfacial traction distribution and detailed Monte Carlo simulations, we observe that the adhesion size, substrate rigidity, cytoskeleton stiffening, and the direction of pulling forces all play important or critical roles in the stability of FAs. In particular, we have shown an elasticity-controlled transition between uniform and cracklike tractions along the cell-ECM interface. Although we do not expect that the present model can fully capture the complexity of real focal adhesions, it seems that the predictions from this model can provide feasible explanations for a wide range of experimental observations and also suggest possible cytoskeletal mechanisms by which cells can control and regulate the growth and stability of FAs via contractility.
Our model suggests that the reason for FAs to lie in a narrow size range from a few hundred nanometers to a few microns might be that the growth of FAs eventually leads to cracklike delamination failure near the adhesion edge. From this point of view, the growth of FAs is self-limiting. Our analyses show that the optimal size-window for stable adhesion is in the submicron-to-micron range, depending on the rigidity of cell and substrate. This is also in qualitative agreement with the experimental observations that stable and large FAs are only formed on sufficiently rigid substrates. The fact that FAs on stiff substrates are more stable provides a driving force for cells to migrate toward the stiffer part of the substrate. The effects of the reduced elastic modulus E∗ on adhesion lifetime and strength imply that very soft substrates tend to diminish the adaptive capability of cells, in that cracklike interfacial traction would persist irrespective of the cytoskeleton stiffness, which may prevent short-lived FXs from maturing into stable FAs. On hard substrates, the reduced elastic modulus E∗ tends to be dominated by the stiffness of cytoskeleton. The cytoskeletal contractile forces can stiffen cytoskeleton by decreasing entropic elasticity of the actin network and therefore alleviate stress concentration at FAs to achieve long-term stability. This is consistent with the experimental observations that cytoskeletal contractile forces are necessary to stabilize cell adhesion. We also demonstrate the dependence of adhesion lifetime and strength on the loading angle θ. Low-angle pulling dramatically increases the adhesion lifetime and strength. Therefore, cell spreading and flattening over a substrate result in low-angle pulling on FAs and benefit stable adhesion. All these results are consistent with experimental observations and suggest multiple mechanisms by which cells can actively control adhesion and deadhesion by modulating the cytoskeleton or adjusting the angle of stress fibers. Generally, rigid substrates, cytoskeleton stiffening, intermediate adhesion size, and low-angle pulling are factors that contribute to stable focal adhesions whereas soft substrates, cytoskeleton softening by dissolution of actin network, extreme adhesion size, and high-angle pulling are factors that tend to destabilize FAs. Our model provides a unique guiding parameter α to understand these phenomena.
Conclusion
This model aims to bridge elastic descriptions of adhesive contact at large scale, and stochastic descriptions of molecular bonds at small scale. A dimensionless stress concentration index α has been identified as a controlling parameter to help us understand the transition between uniform and cracklike traction distributions along the cell-ECM interface. In the Monte Carlo simulations, the choice of parameters is specific but the essential features of the model, e.g., the observed size window for stable adhesion and the angle-dependence of adhesion lifetime and strength, appear to be generic. Finally, we point out some critical assumptions made in our model that can be improved in future work. We have assumed immobile receptor-ligand bonds at the cell-ECM interface, whereas bond diffusion is likely to be important in real biological cells. Cell and ECM are idealized to be purely elastic but in reality they show nonlinear and viscoelastic behaviors. The loading conditions at FAs can also be much more complex than assumed. Despite these limitations, it is encouraging that the predictions of such an idealized model are essentially consistent with relevant experimental observations.
Appendix
Consider a periodic array of concentrated forces with period 2c along the cell-substrate interface. We focus on an arbitrary period and adopt (x,z) coordinates with origin located at the adhesion center and directions shown in Fig. 1. The discontinuity of the displacement u on cell and substrate surfaces at a bond location xi caused by a different bond at location xj (i ≠ j) is given by (41,42)
| (11) |
where Fj is the bond force at xj. To avoid singularity, the self-displacement discontinuity at xi induced by the force array Fi, which is modeled as an equivalent uniform pressure with half-width a0 (a0 = 5 nm in simulations (43)), is given as (41,42)
| (12) |
The compatibility condition at the interface is
| (13) |
where k is the current number of closed bonds within the adhesion domain, h is the cell-substrate surface separation in the absence of elastic deformation and
| (14) |
is the elastic Green's function for a periodic array of forces.
The global force balance requires that
| (15) |
Once the k +1 unknowns (F1, F2, ···, Fk, h) are solved, the surface separation δi between the two elastic media at an open bond location xi can be calculated through
| (16) |
References
- 1.Alberts B., Johnson A., Lewis J., Raff M., Roberts K. Garland Science; New York: 2002. Molecular Biology of the Cell. [Google Scholar]
- 2.Bershadsky A.D., Balaban N.Q., Geiger B. Adhesion-dependent cell mechanosensitivity. Annu. Rev. Cell Dev. Biol. 2003;19:677–695. doi: 10.1146/annurev.cellbio.19.111301.153011. [DOI] [PubMed] [Google Scholar]
- 3.Burridge K., Chrzanowska-Wodnicka M. Focal adhesions, contractility, and signaling. Annu. Rev. Cell Dev. Biol. 1996;12:463–518. doi: 10.1146/annurev.cellbio.12.1.463. [DOI] [PubMed] [Google Scholar]
- 4.Giancotti F.G., Ruoslahti E. Transduction-integrin signaling. Science. 1999;285:1028–1032. doi: 10.1126/science.285.5430.1028. [DOI] [PubMed] [Google Scholar]
- 5.Zamir E., Katz M., Posen Y., Erez N., Yamada K.M. Dynamics and segregation of cell-matrix adhesions in cultured fibroblasts. Nat. Cell Biol. 2000;2:191–196. doi: 10.1038/35008607. [DOI] [PubMed] [Google Scholar]
- 6.Pelham R.J., Wang Y.L. Cell locomotion and focal adhesions are regulated by substrate flexibility. Proc. Natl. Acad. Sci. USA. 1997;94:13661–13665. doi: 10.1073/pnas.94.25.13661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lo C.M., Wang H.B., Dembo M., Wang Y.L. Cell movement is guided by the rigidity of the substrate. Biophys. J. 2000;79:144–152. doi: 10.1016/S0006-3495(00)76279-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Gardel M.L., Shin J.H., MacKintosh F.C., Mahadevan L., Matsudaira P. Elastic behavior of cross-linked and bundled actin networks. Science. 2004;304:1301–1305. doi: 10.1126/science.1095087. [DOI] [PubMed] [Google Scholar]
- 9.Storm C., Pastore J.J., MacKintosh F.C., Lubensky T.C., Janmey P.A. Nonlinear elasticity in biological gels. Nature. 2005;435:191–194. doi: 10.1038/nature03521. [DOI] [PubMed] [Google Scholar]
- 10.Totsukawa G., Wu Y., Sasaki Y., Hartshorne D.J., Yamakita Y. Distinct roles of MLCK and ROCK in the regulation of membrane protrusions and focal adhesion dynamics during cell migration of fibroblasts. J. Cell Biol. 2004;164:427–439. doi: 10.1083/jcb.200306172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bershadsky A., Kozlov M., Geiger B. Adhesion-mediated mechanosensitivity: a time to experiment, and a time to theorize. Curr. Opin. Cell Biol. 2006;18:472–481. doi: 10.1016/j.ceb.2006.08.012. [DOI] [PubMed] [Google Scholar]
- 12.Riveline D., Zamir E., Balaban N.Q., Schwarz U.S., Ishizaki T. Focal contacts as mechanosensors: externally applied local mechanical force induces growth of focal contacts by an mDia1-dependent and ROCK-independent mechanism. J. Cell Biol. 2001;153:1175–1185. doi: 10.1083/jcb.153.6.1175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Balaban N.Q., Schwarz U.S., Riveline D., Goichberg P., Tzur G. Force and focal adhesion assembly: a close relationship studied using elastic micropatterned substrates. Nat. Cell Biol. 2001;3:466–472. doi: 10.1038/35074532. [DOI] [PubMed] [Google Scholar]
- 14.Deshpande V.S., McMeeking R.M., Evans A.G. A bio-chemo-mechanical model for cell contractility. Proc. Natl. Acad. Sci. USA. 2006;103:14015–14020. doi: 10.1073/pnas.0605837103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bruinsma R. Theory of force regulation by nascent adhesion sites. Biophys. J. 2005;89:87–94. doi: 10.1529/biophysj.104.048280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Nicolas A., Geiger B., Safran S.A. Cell mechanosensitivity controls the anisotropy of focal adhesions. Proc. Natl. Acad. Sci. USA. 2004;101:12520–12525. doi: 10.1073/pnas.0403539101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Smith A.S., Sengupta K., Goennenwein S., Seifert U., Sackmann E. Force-induced growth of adhesion domains is controlled by receptor mobility. Proc. Natl. Acad. Sci. USA. 2008;105:6906–6911. doi: 10.1073/pnas.0801706105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Erdmann T., Schwarz U.S. Stability of adhesion clusters under constant force. Phys. Rev. Lett. 2004;92:108102. doi: 10.1103/PhysRevLett.92.108102. [DOI] [PubMed] [Google Scholar]
- 19.Erdmann T., Schwarz U.S. Stochastic dynamics of adhesion clusters under shared constant force and with rebinding. J. Chem. Phys. 2004;121:8997–9017. doi: 10.1063/1.1805496. [DOI] [PubMed] [Google Scholar]
- 20.Qian J., Wang J., Gao H. Lifetime and strength of adhesive molecular bond clusters between elastic media. Langmuir. 2008;24:1262–1270. doi: 10.1021/la702401b. [DOI] [PubMed] [Google Scholar]
- 21.Lin Y., Freund L.B. Optimum size of a molecular bond cluster in adhesion. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2008;78:012109. doi: 10.1103/PhysRevE.78.021909. [DOI] [PubMed] [Google Scholar]
- 22.Johnson K.L. Cambridge University Press; Cambridge, UK: 1985. Contact Mechanics. [Google Scholar]
- 23.Bell G.I. Models for specific adhesion of cells to cells. Science. 1978;200:618–627. doi: 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
- 24.van Kampen N.G. Elsevier Science; Amsterdam, The Netherlands: 1992. Stochastic Processes in Physics and Chemistry. [Google Scholar]
- 25.Rice J.R. In: Fracture: an Advanced Treatise. Liebowitz H., editor. Academic Press; New York: 1968. [Google Scholar]
- 26.Dundurs J. American Society of Mechanical Engineers; New York: 1969. Mathematical Theory of Dislocations. [Google Scholar]
- 27.Hutchinson J.W., Suo Z. Advances in Applied Mechanics. Vol 29. Academic Press; San Diego, CA: 1992. Mixed-mode cracking in layered materials. [Google Scholar]
- 28.Tada H., Paris P.C., Irwin G.R. American Society of Mechanical Engineers; New York: 2000. The Stress Analysis of Cracks Handbook. [Google Scholar]
- 29.Alon R., Hammer D.A., Springer T.A. Lifetime of the P-selectin-carbohydrate bond and its response to tensile force in hydrodynamic flow. Nature. 1995;374:539–542. doi: 10.1038/374539a0. [DOI] [PubMed] [Google Scholar]
- 30.Merkel R., Nassoy P., Leung A., Ritchie K., Evans E. Energy landscapes of receptor-ligand bonds explored with dynamic force spectroscopy. Nature. 1999;397:50–53. doi: 10.1038/16219. [DOI] [PubMed] [Google Scholar]
- 31.Evans E., Ritchie K. Dynamic strength of molecular adhesion bonds. Biophys. J. 1997;72:1541–1555. doi: 10.1016/S0006-3495(97)78802-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Freund L.B. Characterizing the resistance generated by a molecular bond as it is forcibly separated. Proc. Natl. Acad. Sci. USA. 2009;106:8818–8823. doi: 10.1073/pnas.0903003106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Chesla S.E., Selvaraj P., Zhu C. Measuring two-dimensional receptor-ligand binding kinetics by micropipette. Biophys. J. 1998;75:1553–1572. doi: 10.1016/S0006-3495(98)74074-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Evans E.A., Calderwood D.A. Forces and bond dynamics in cell adhesion. Science. 2007;316:1148–1153. doi: 10.1126/science.1137592. [DOI] [PubMed] [Google Scholar]
- 35.Erdmann T., Schwarz U.S. Bistability of cell-matrix adhesions resulting from nonlinear receptor-ligand dynamics. Biophys. J. 2006;91:L60–L62. doi: 10.1529/biophysj.106.090209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Erdmann T., Schwarz U.S. Impact of receptor-ligand distance on adhesion cluster stability. Eur. Phys. J. E. 2007;22:123–137. doi: 10.1140/epje/e2007-00019-8. [DOI] [PubMed] [Google Scholar]
- 37.Tees D.F.J., Coenen O., Goldsmith H.L. Interaction forces between red-cells agglutinated by antibody. IV. Time and force dependence of break-up. Biophys. J. 1993;65:1318–1334. doi: 10.1016/S0006-3495(93)81180-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Long M., Goldsmith H.L., Tees D.F.J., Zhu C. Probabilistic modeling of shear-induced formation and breakage of doublets cross-linked by receptor-ligand bonds. Biophys. J. 1999;76:1112–1128. doi: 10.1016/S0006-3495(99)77276-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Gillespie D.T. General method for numerically simulating stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 1976;22:403–434. [Google Scholar]
- 40.Gillespie D.T. Exact stochastic simulation of coupled chemical-reactions. J. Phys. Chem. 1977;81:2340–2361. [Google Scholar]
- 41.Gao H.J., Chen S.H. Flaw tolerance in a thin strip under tension. J. Appl. Mech. Trans. ASME. 2005;72:732–737. [Google Scholar]
- 42.Qian, J., J. Wang, and H. Gao. 2009. Tension-induced growth of focal adhesions at cell-substrate interface. In The Proceedings of IUTAM Symposium on Cellular, Molecular and Tissue Mechanics. In press.
- 43.Arnold M., Cavalcanti-Adam E.A., Glass R., Blummel J., Eck W. Activation of integrin function by nanopatterned adhesive interfaces. ChemPhysChem. 2004;5:383–388. doi: 10.1002/cphc.200301014. [DOI] [PubMed] [Google Scholar]


