K⁺ current changes account for the rate dependence of the action potential in the human atrial myocyte

Abstract

Ongoing investigation of the electrophysiology and pathophysiology of the human atria requires an accurate representation of the membrane dynamics of the human atrial myocyte. However, existing models of the human atrial myocyte action potential do not accurately reproduce experimental observations with respect to the kinetics of key repolarizing currents or rate dependence of the action potential and fail to properly enforce charge conservation, an essential characteristic in any model of the cardiac membrane. In addition, recent advances in experimental methods have resulted in new data regarding the kinetics of repolarizing currents in the human atria. The goal of this study was to develop a new model of the human atrial action potential, based on the Nygren et al. model of the human atrial myocyte and newly available experimental data, that ensures an accurate representation of repolarization processes and reproduction of action potential rate dependence and enforces charge conservation. Specifically, the transient outward K⁺ current (I_t) and ultrarapid rectifier K⁺ current (I_Kur) were newly formulated. The inwardly recitifying K⁺ current (I_K1) was also reanalyzed and implemented appropriately. Simulations of the human atrial myocyte action potential with this new model demonstrated that early repolarization is dependent on the relative conductances of I_t and I_Kur, whereas densities of both I_Kur and I_K1 underlie later repolarization. In addition, this model reproduces experimental measurements of rate dependence of I_t, I_Kur, and action potential duration. This new model constitutes an improved representation of excitability and repolarization reserve in the human atrial myocyte and, therefore, provides a useful computational tool for future studies involving the human atrium in both health and disease.

accurate representation of the ionic currents of the human atrial myocyte is essential for the ongoing investigation of human atrial electrophysiology and pathophysiology. It is now well established that the elucidation of mechanisms underlying the complex phenomena that occur in highly integrative systems, such as atrial tissue, requires that experimental data be incorporated such that models are both accurate and biophysically based. Within the past decade, advances in experimental methods have resulted in a much-improved characterization of repolarizing currents in the human atria (21, 50, 59–61). New insights into the underlying channel isoforms responsible for these K⁺ currents are also now available (32, 41, 53, 54, 56). However, findings regarding essential repolarization processes in the human atria have been incorporated into none of the available mathematical models of the action potential (AP) (7, 40).

Of particular interest are the recent experimental findings regarding the transient outward K⁺ current (I_t; K_v4.3) and ultrarapid delayed rectifier K⁺ current (I_Kur; K_v1.5). I_t contributes significantly to the early repolarization phase of the human atrial AP, which is analogous to its contribution to phase 1 repolarization in human ventricular myocytes. I_Kur, a sustained outward current that is expressed in human atrial but not ventricular myocytes, contributes to both early and late repolarization in the human atrial myocyte. The rapid and slow delayed rectifier K⁺ currents (I_Kr and I_Ks, respectively), which are essential for late repolarization in the human ventricle, are very small (or even undetectable) in the human atria (18). The inward rectifier K⁺ current (I_K1), which contributes to late repolarization and stabilizes the resting membrane potential (RMP), is expressed at a much lower density in the human atria compared with the ventricles; I_K1 has been measured in the human atria at densities that are 10–50% of those found in the human ventricle (30).

The main goals of the present study were twofold: 1) to create a new model of the human atrial AP that accurately represents repolarization in the human atrial myocyte, which will be accomplished by the reformulation of I_t and I_Kur, and 2) to analyze the contribution of repolarization processes to the rate dependence of the human atrial AP. The result was a well-quantified model of the human atrial myocyte that ensures the availability of a physiologically relevant and robust model for cell-, tissue-, and, eventually, organ-level studies of atrial electrophysiological phenomena, including arrhythmogenesis.

METHODS

Basic Assumptions

Many fundamental aspects of the mathematical model presented in this article are based on a previous model of the adult human atrial myocyte AP, that of Nygren et al. (40). Our model will be referred to as the human atrial myocyte with new repolarization (hAMr) model. It consists of an electric equivalent circuit for the sarcolemma, including ionic currents based on Hodgkin-Huxley formalisms, as well as a fluid compartment model to account for changes in ionic concentrations, as described previously (40). The dimensions and capacitance of the human atrial myocyte are the same as those in the original article (40); specifically, total myocyte volume (Vol_i) and cell membrane capacitance (C_m) were considered to be 5.884 μl and 50 pF, respecitively.

Transmembrane Ionic Currents

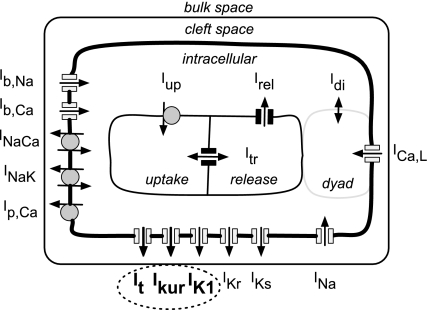
Figure 1 is a schematic of the hAMr model of the human atrial myocyte. The formulation includes all time- and voltage-dependent ion currents that contribute to the generation of the human atrial AP: the Na⁺ current (I_Na), the L-type Ca²⁺ current (I_Ca,L), and the K⁺ currents I_t, I_Kur, I_K1, I_Kr, and I_Ks. In addition, our model includes electrogenic pump and exchanger currents: the sarcolemmal Ca²⁺ pump currrent (I_Ca,P), the Na⁺/Ca²⁺ exchanger current (I_NaCa)_, and the Na⁺-K⁺ pump current (I_NaK), which are responsible for the maintenance of intracellular ion concentrations. Na⁺ and Ca²⁺ time-independent or background currents (I_BNa and I_BCa, respectively) are also included. The K⁺ currents that are the focus of the present study, I_t, I_Kur, and I_K1, are shown in bold and indicated by the dashed ellipse in Fig. 1; the formulations of the remaining currents and ion fluxes are based on the formulation of Ref. 40, with some parameters updated. In the present model, I_t and I_Kur are the transient and sustained components, respectively, of the outward K⁺ current. The significant reformulation and novel contribution of these key repolarization currents are described in detail in the next two sections.

Fig. 1.

Schematic representation of the mathematical model of the human atrial myocyte (hAMr model). Ion channel-mediated currents as well as electrogenic pump and ion exchanger currents are shown. Significant compartments include the extracellular, intracellular, and cleft spaces as well as the uptake and release compartments within the sarcoplasmic reticulum (40). The dashed ellipse indicates the currents that are the main focus of this new model of the human atrial AP. The myocyte was modeled as a cylindrical cell with a length of 130 μm and a diameter of 11 μm. Cell capacitance was 50 pF. See the Glossary for definitions of abbreviations used in this and subsequent figures.

I_t

Due to a lack of experimental data, the Nygren et al. (40) formulation of I_t in the human atrial myocyte was based on experimental data obtained from rabbit atrial myocytes (16). It is now well accepted that the K⁺ channel underlying I_t in the rabbit atria is the K_v1.4 gene product, whereas in the human atria, the α-subunit encoded by K_v4.3 underlies this current (14, 16, 42, 53, 54, 56). In human atria, I_t activates very rapidly (∼10 ms) (46) and then inactivates more slowly (∼20 ms) (56). The recovery from inactivation is strongly voltage dependent (56) and relatively rapid (on the order of 10s of ms) (55, 56). In contrast, in the model of Nygren et al. (40), the time course of recovery was on the order of ∼300 ms at hyperpolarized potentials.

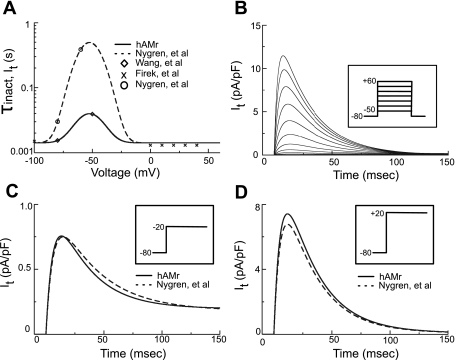
Figure 2 shows the new implementation of I_t in the hAMr model. Figure 2A shows implementations made to achieve improved kinetic descriptions for the time constant of inactivation (τ_s). These were based on newer experimental data from the human atrium (56). Figure 2B shows a family of current traces of I_t generated by our new formulation when subjected to the voltage-clamp protocol shown in the inset; note that the current is both rapidly activating and inactivating. Figure 2, C and D, compare current traces generated by the hAMr model and the model of Nygren et al. when subjected to identical voltage clamps from −80 to −20 and +20 mV, respectively (as indicated in the insets). Note the more rapid decay of the updated I_t compared with the same current in the model of Nygren et al. for negative (Fig. 2C) versus positive (Fig. 2D) holding potentials. A complete mathematical description of the new formulation of I_t can be found in the appendix.

Fig. 2.

Modification of I_t. A: data describing the modification of voltage-dependent kinetics of reactivation in Ref. 40 (○). The time constant of inactivation/recovery (τ_inact) is shown by the dashed trace. The present model is based on more complex recovery data [◊ (56)]. This, combined with inactivation data [“X”s (18)], led to a new formulation for the time constant of inactivation/recovery in the hAMr model (solid trace). B: a family of current recordings of I_t simulated using a holding potential of −80 mV and a series of 750-ms voltage clamp steps from −50 to +60 mV in 10-mV increments applied at 0.1 Hz (as shown in the inset). C: simulated currents after a voltage clamp step from a holding potential of −80 to −20 mV (as shown in the inset) for the hAMr model (solid trace) and the model of Nygren et al. (dashed trace). D: simulated currents after a voltage clamp step from a holding potential of −80 to +20 mV (as shown in the inset) for the hAMr model (solid trace) and the model of Nygren et al. (dashed trace).

I_Kur

In the Nygren et al. (40) model of the human atrial myocyte AP, recovery from inactivation of the “sustained outward K⁺ current” (I_sus) was represented via a time course on the order of ∼300 ms and included a partial inactivation of 40%. I_sus is now known to be I_Kur, a member of the family of ultrarapidly delayed rectifier K⁺ currents encoded by the K_v1.5 gene (13). I_Kur activates very rapidly (<10 ms) (1) and inactivates very slowly (∼3 s) but completely.

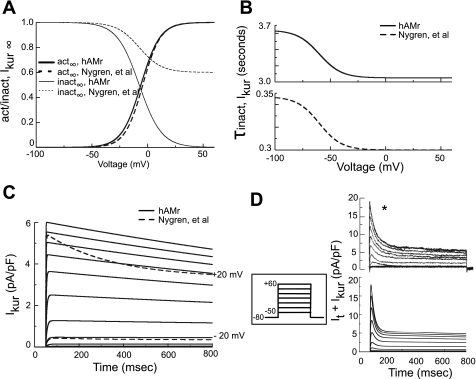
Figure 3 shows the major changes to I_Kur made to accurately simulate the kinetics of inactivation and recovery of this current. Figure 3A shows the new implementations of the steady-state activation and inactivation of I_Kur. Steady-state activation was adjusted to match data from human atrial myocytes (13). The partial steady-state inactivation present in the original model (40) was replaced by a complete inactivation process in the hAMr model (58). Figure 3B shows the new voltage dependence of the time constant of inactivation at hyperpolarized potentials; it was increased by ∼10-fold (15) (Fig. 3B, top, solid black trace). Figure 3C shows current traces of I_Kur generated by the voltage clamp steps shown in the inset. For holding potentials of ±20 mV, current traces of I_sus, the analogous current from the model of Nygren et al., are also shown for comparison (Fig. 3C, dashed traces); note that I_sus decays much more rapidly compared with I_Kur. A comparison of the sum of I_t and I_Kur elicited via the voltage-clamp protocol shown in the inset revealed a close correspondence between the recent experiment (Fig. 3D, top) (21) and hAMr model (Fig. 3D, bottom). A complete mathematical description of the formulation of I_Kur in the present model can be found in the appendix.

Fig. 3.

Modification of I_Kur. A: steady-state activation and inactivation variables for I_Kur. Parameters for both the Nygren et al. and hAMr models are shown. B: time constants for the inactivation of I_Kur for the hAMr model (top) and the model of Nygren et al. (bottom). C: current traces of I_Kur (solid traces) simulated using a holding potential of −80 mV and a series of 750-ms-duration depolarizing steps from −50 to +60 mV applied in 10-mV increments (as shown in the inset between C and D). Additionally, for depolarizing steps to −20 and +20 mV, simulated current traces of I_sus, the analogous current in the model of Nygren et al., are overlaid for comparison (dashed traces). D: a family of currents corresponding to the sum of I_t and I_Kur recorded from experiments [top [*Reprinted from Eur J Pharmacol 497, Gluais P. et al. (21), Risperidone reduces K⁺ currents in human atrial myocytes and prolongs repolarization in human myocardium, p. 215–222, 2004, with permission of Elsevier. Permission also granted by authors (21)]. These results were compared with the same simulated traces (bottom) generated by an identical voltage-clamp protocol in silico (shown in the inset between C and D).

Optimization of Parameters

Individual parameter values in each mathematical formulation in the hAMr model were optimized to reproduce physiologically relevant experimental observations. The specific magnitudes of these changes are discussed in the following section; two prime examples are I_K1 and I_Na. Please reference the appendix for the exact parameter values.

I_K1

While the mathematical formulation of I_K1 remains the same as in Ref. 40, the maximum conductance of I_K1 (g_K1) was increased by ∼3%; this change maintains the RMP at experimentally measured values and results in I_K1 densities within the range of experimentally validated values for the human atria (59, 61).

I_Na

It was necessary to increase the peak magnitude of this current by 12.5% by adjusting the Na⁺ permeability (P_Na) to agree with experimental measurements of the maximum upstroke velocity (dV/dt_max) of the human atrial AP. Specifically, this change increased dV/dt_max from ∼120 to ∼150 V/s when stimulated at 1.5 times the threshold for activation, which falls within the experimentally measured range of values for human atrial myocytes (8).

I_t and I_Kur

The maximum conductance of I_t (g_t) was increased by ∼9% in the hAMr model to match values reported in recent experiments (21, 60). The maximum channel conductance of I_Kur (g_Kur) was decreased by ∼11% in the hAMr model to fit recent experimental data (21).

Material Balance: Elimination of the Electroneutral Na⁺ Influx

The model of Nygren et al. (40) incorporated an electroneutral Na⁺ influx (Φ_en) to achieve long-term stability in ionic concentrations over long periods of stimulation at a specific rate (1 Hz) and stimulus strength (280 pA, or 5.6 pA/pF). A consequence of the incorporation of this flux is a lack of charge conservation as well as the absence of any true mathematical steady states (25). These factors limit the ability of any model to accurately reproduce long-term physiological phenomena and thus decrease its predictive power. In the hAMr model, Φ_en was removed, and the stimulus current delivered to the intracellular space was attributed to the influx of potassium ions, as suggested by Hund et. al. (24). As a result, charge is conserved within the system for the hAMr model for any stimulation protocol.

RESULTS

The simulation results presented here had two goals: 1) to illustrate the effects of incorporation of essential new K⁺ current data and 2) to further explore the mechanisms underlying the repolarization reserve in the human atrial myocyteby by examining both early and late repolarizationin in the hAMr model.

RMP

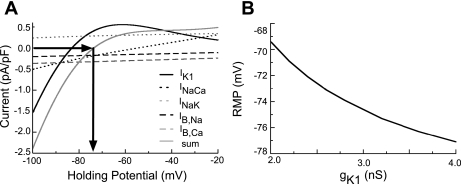
A detailed understanding of the factors that control the RMP is one of the essential elements of any physiologically accurate model (33). This reflects a dynamic balance between the time-independent background, pump, and exchanger currents (I_K1, I_B,Na, I_B,Ca, I_NaK, I_CaP, and I_NaCa). In Fig. 4A, the current-voltage relationships of five of the key ion-trafficking mechanisms that are responsible for determining the RMP in the quiescent atrial myocyte (I_K1, I_NaCa, I_NaK, I_B,Ca, and I_B,Na) are shown. The resulting net current and RMP in our model are also shown. As indicated by the arrows, the net membrane current is zero at approximately −74.0 mV, in agreement with experimental measurements of the RMP (8, 12, 20, 46, 52). We note that RMP exhibits strong dependence on I_K1; for example, a 10% increase in this conductance (g_K1) will cause a decrease in RMP of ∼1 mV in the absence of other alterations in the hAMr model. The dependence of the RMP on g_K1 for a wider range of conductances is shown in Fig. 4B.

Fig. 4.

A: current-voltage relationships of the currents underlying the stability of RMP (I_K1, I_NaCa, and I_B,Na) in the hAMr model along with the sum of these currents (solid shaded trace), which can be used to predict the RMP of the model. B: examination of the sensitivity of RMP to changes in g_K1.

Long-Term Steady State of Simulated Ion Fluxes

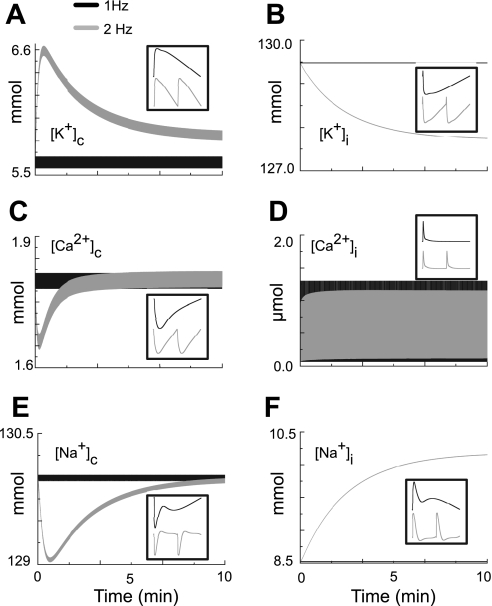
The long-term steady-state ionic concentrations in our model are shown in Fig. 5 for pacing rates of 1 and 2 Hz and for a simulation time of 10 min (600 and 1,200 cycles, respectively). Initial conditions for pacing at both rates were steady-state values following pacing at a rate of 1 Hz. The cleft concentrations of K⁺, Ca²⁺, and Na⁺ (Fig. 5, A, C, and E, respectively, solid traces) showed steady-state ionic balance through the entire time course of stimulation at a pacing rate of 1 Hz. When the pacing rate was elevated to 2 Hz (Fig. 5, A, C, and E, shaded traces), the cleft concentrations initially changed somewhat. [K⁺]_c initially rose by ∼1 mmol/l and then returned to a steady-state value as a result of I_NaK activity and diffusion, consistent with experimental observations (31). The intracellular concentrations of K⁺, Ca²⁺, and Na⁺ (Fig. 5, B, D, and F, respectively, solid traces) also demonstrated steady-state ionic balance through the entire time course of stimulation at a pacing rate of 1 Hz. When the pacing rate was elevated to 2 Hz, [K⁺]_i and [Na⁺]_i (Fig. 5, B and F, respectively, shaded traces) reached steady state within the time course of simulation, decreasing by 2.0 mmol/l and increasing by 1.5 mmol/l, respectively. The peak magnitude of [Ca²⁺]_i (Fig. 5D, shaded trace) decreased slightly by 0.1 μmol/l at steady state for pacing at 2 Hz, and diastolic [Ca²⁺]_i increased by ∼0.025 μmol/l, as observed in experiments (49, 51).

Fig. 5.

Evaluation of the ability of the model to maintain ionic stability when paced at either 1 or 2 Hz (10 min of simulation shown). The insets in A–F are the selected ion concentrations as they change during a single AP when the model is paced at either 1 or 2 Hz. A: [K⁺]_c. B: [K⁺]_i. C: [Ca²⁺]_c. D: [Ca²⁺]_i. E: [Na⁺]_c. F: [Na⁺]_i.

The hAMr model reveals a critical difference with the original model of Nygren et al. in terms of long-term stability of both intracellular and cleft space ion concentrations. The elimination of the constant background flux Φ_Na,en allows the hAMr model to adhere to fundamental physical principles of conservation of charge and ionic species, which results in the existence of long-term mathematical steady states (25). Moreover, the changes in intracellular and cleft ionic concentrations with an increase in pacing frequency to 2 Hz in the hAMr model are consistent with rate-dependent concentration alterations observed in experiments (40).

AP Morphology

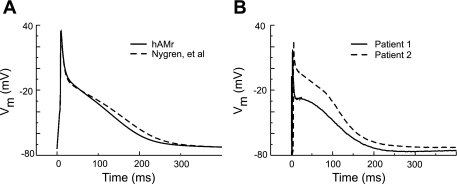
Figure 6A shows the AP waveform generated by our model and the original Nygren et al. model at a rate of 1 Hz. The change to the hAMr model AP was relatively small; the AP in our model had a more rapid rate of late repolarization. We note that in the Nygren et al. model, the AP morphology was tuned to match a subset of recorded data almost exactly. In the hAMr model, in contrast, we chose not to make this requirement upon the AP morphology. This is because recorded traces from human atrial myocytes, even when from the same region of the atria, as shown in Fig. 6B (from the right atrial appendage; unpublished observations by U. Ravens, used with permission), often show heterogeneity in AP morphology from one patient to the next. Thus, rather than require adherence to a single experimental recording, we chose to focus on the reproduction of key kinetic properties of individual K⁺ currents while also requiring AP morphological features that fall well within the range of experimental observations in human atrial myocytes.

Fig. 6.

A: APs generated by the hAMr and Nygren et al. (40) models. B: APs recorded from human atrial myocytes from two different patients (unpublished data from U. Ravens, used with permission) in response to a 1-Hz stimulus train at 37°C. V_m, transmembrane voltage.

Early Repolarization of the AP

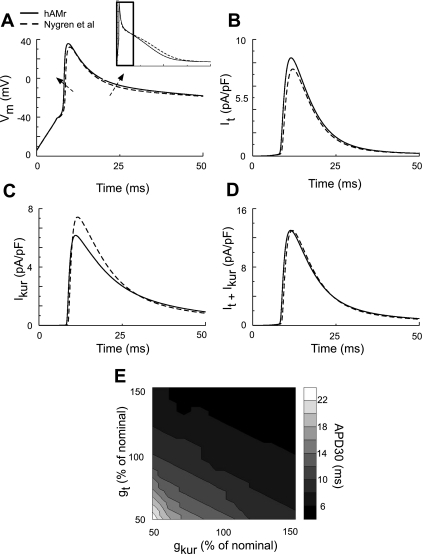
Figure 7 shows early repolarization of the AP in our model. In Fig. 7A, APs from both the Nygren et al. (40) and hAMr models are shown. The AP upstroke and early repolarization are emphasized. The major changes in our model were 1) an increased AP upstroke velocity and 2) a slight decrease in the rate of early repolarization, as indicated by the dashed arrows. The increased rate of rise of the AP is a result of an increase in peak I_Na, as discussed previously; the slight decrease in the rate of early repolarization in the hAMr model can be attributed to the alteration in the net contribution of I_t and I_Kur. Figure 7B shows I_t during the first 50 ms of the cardiac AP for both hAMr and Nygren et al. (40) models. I_t activated more quickly in our hAMr formulation. This was due to the increased rate of rise of the AP; peak I_t density was also larger. In contrast, the peak density of I_Kur (Fig. 7C) was decreased, and the inactivation of this current was slower in the hAMr model than in the original model.

Fig. 7.

Illustration of early AP repolarization in the hAMr model and in the model of Nygren et al. (40). A: comparison of AP morphology during early repolarization in the two models. The inset shows the time course of portion of the AP examined. B and C: traces of both I_t and I_Kur during the first 50 ms of a single AP. D and E: contribution of I_t and I_Kur to early repolarization of the human atrial AP. D: sum of I_t and I_Kur, which was similar for the hAMr and Nygren et al. (40) models. E: APD₃₀ as a function of g_t and g_Kur; nominal values are those used in the hAMr model.

Figure 7D shows the sum of I_t and I_Kur. Although each of the two currents were significantly different in the models, their sum was quite similar. In the hAMr model, the sum of I_t and I_Kur decayed more rapidly and thus resulted in a slightly slower early repolarization. Figure 7E shows the roles of g_t and g_Kur on APD₃₀; g_t and g_Kur are expressed as percentages of the nominal g_t and g_Kur, defined as those in the hAMr model. Note that this AP property is dependent on both g_t and g_Kur; for instance, if g_t and g_Kur are both decreased by 25%, the APD₃₀ lengthens by ∼6 ms; if both g_t and g_Kur increase by 25%, the APD₃₀ decreases by ∼1 ms. Early repolarization in the hAMr model is thus especially sensitive to the collective decrease in I_t and I_Kur.

Late Repolarization of the AP

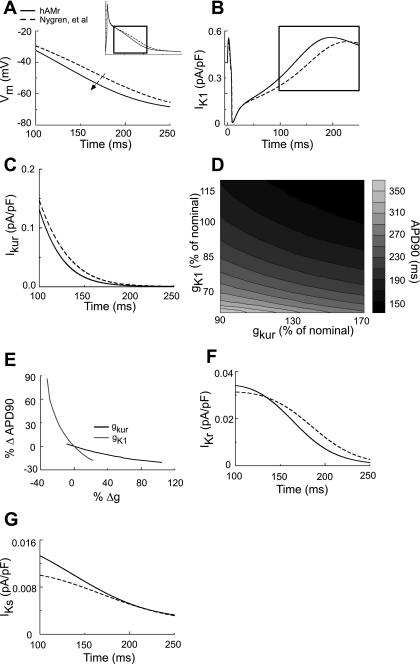
Figure 8 shows the revised simulation of late repolarization of the AP. Figure 8A shows AP traces during late repolarization for each model. The inset shows the entire time course of the APs, whereas the box indicates the latter 150 ms of the cardiac cycle. The major waveform change in the hAMr model compared with the original model of Nygren et al. was an increased rate of late repolarization, as shown by the dashed arrow. I_K1 is shown during the entire time course of the AP in Fig. 8B (the box indicates the last 150 ms of the AP). Although the densities of I_K1 in early repolarization were quite similar between the two models, the density of I_K1 in our modified formulation was, on average, ∼12% greater than that of the parent model during late repolarization. This corresponds to a difference in the average current density of ∼0.06 pA/pF during the last 150 ms of the AP between the two models. Figure 8C shows I_Kur during late repolarization of the AP. Note that I_Kur during late repolarization was decreased in the hAMr model. I_Kur was ∼24% smaller on average in the hAMr model; the difference in average current density during the time course shown was ∼0.007 pA/pF. Although it was an order of magnitude smaller than I_K1 during late repolarization, the density of I_Kur can have a marked influence on APD₉₀.This is shown in Fig. 8D. Here, g_K1 and g_Kur are expressed as percentages of nominal g_K1 and g_Kur in the hAMr model. APD₉₀ is dependent on both g_K1 and g_Kur, as shown in Fig. 8E. Note that a decrease in g_Kur (from its nominal value) has a greater influence on increases in APD₉₀ compared with a similar increase in g_Kur (and subsequent APD₉₀ decreases). For nominal g_K1, a 10% decrease in the nominal value of g_Kur causes an increase in APD₉₀ on the order of 10 ms, whereas a 30% increase in nominal g_Kur is necessary to lengthen the AP by the same amount. Deviations from the nominal value in g_K1 exert a greater influence on APD₉₀ than g_Kur. However, similarly to g_Kur, increases in g_K1 from its nominal value exert less influence on APD₉₀ than decreases: for a nominal g_Kur, a 15% decrease and increase in g_K1 will increase and decrease APD₉₀ by ∼20 and ∼10 ms, respectively.

Fig. 8.

AP waveform of the human atrial myocyte during late repolarization. A: late repolarization occurred more rapidly in the hAMr model compared with the model of Nygren et al. (40), as shown by the arrow. B: note that I_K1 during late repolarization in the hAMr model was increased compared with the model of Nygren et al. (40). C: I_Kur during the late repolarization phase of the AP. The magnitude and time courses of I_Kur in the hAMr and Nygren et al. (40) models were very similar. D: modulation of the time course of late repolarization as a function of the relative conductance of g_K1 and g_Kur. E: percent change in APD₉₀ with changes in g_K1 or g_Kur compared with nominal values (those used in the hAMr model). The relative size and time course of the two additional K⁺ currents active during late repolarization in the human atrial myocyte (I_Kr and I_Ks) are shown in F and G, respectively. Note the small density of these currents compared with I_K1 and I_Kur in B and C.

In addition to I_K1 and I_Kur, the role of smaller K⁺ conductances was examined during late repolarization of the AP. Figure 8F shows the role of I_Kr (human ether-a-go-go-related gene) during late repolarization; the density of this current was ∼31% smaller for the interval of 150–250 ms from the beginning of a single cardiac cycle. However, this corresponds to a difference in the average density of I_Kr in the two models of only ∼0.004 pA/pF (∼0.5% of total membrane current) during the same time course. I_Ks (Fig. 8G) was ∼14% greater in the hAMr model until 200 ms of the AP; this was only a difference of ∼0.001 pA/pF (∼0.2% of total membrane current) in the average current density between the two models for the same time course.

Rate Dependence of the hAMr Model

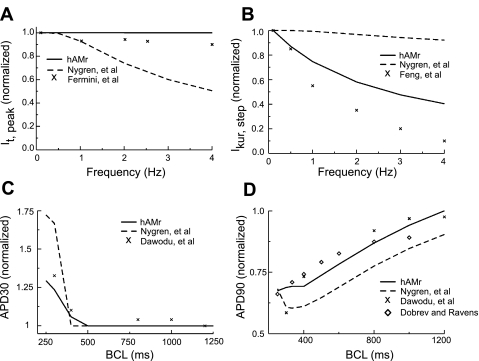
Figure 9 shows the rate dependence of key parameters in our new model compared with experimental data. For reference, we also show the rate dependence of the same parameters in the Nygren et al. model (40). In Fig. 9, A and B, peak I_t and end-pulse (as measured at the end of the voltage clamp) I_Kur were normalized to the peak and step current density, respectively, for a stimulation frequency of 0.1 Hz. Figure 9A shows the rate dependence of peak I_t compared with the experimental data of Fermini et al. (16). I_t as formulated in the original Nygren et al. model (dashed trace) was strongly rate dependent. The reformulation of recovery kinetics in the hAMr model resulted in much less rate dependence of I_t (black trace), resulting in a close match to experimental data. Figure 9B shows the rate dependence of end-pulse I_Kur compared with the experimental results of Feng et al. (15). The alteration of inactivation kinetics in the hAMr model improved the representation of the rate dependence of I_Kur.The new formulation reduced the amount of available I_Kur after an increase in pacing rate (15). The rate dependence of APD₃₀ together with data from the experiments by Dawodu et al. [black “X”s (8)] are shown in Fig. 9C. APD₃₀ was normalized to its value at a basic cycle length of 1,600 ms for the model of Nygren et al., the hAMr model, and the experimental data. While the original model qualitatively replicated the experimental observation that APD₃₀ increases in response to an increase in stimulation rate, the present simulations more closely reproduced experimental results. The rate dependence of APD₉₀ is shown in Fig. 9D and was compared with experiments (8, 9). APD₉₀ was normalized to its value at a rate of 1,200 ms. The rate dependence of APD₉₀ in the hAMr model was a much closer match to the available experimental values; moreover, in the hAMr model, APD₉₀ continued to decrease for pacing rates of >2 Hz, a behavior that has been observed in experiments but was not duplicated by the previous model (40). It is important to note that there was a close agreement between experimental measurements and the improved rate dependence. This is an emergent feature of the hAMr model rather than a pattern of behavior to which the model was fit (see discussion).

Fig. 9.

Changes in K⁺ currents and APD as a function of basic cycle length (BCL). A: rate dependence of normalized peak I_t for both models and experimental data (16). From a holding potential of −60 mV, 100 steps to 0 mV of 200-ms duration were applied at frequencies of 0.1, 0.5, 1, 2, 3, and 4 Hz. The voltage-clamp protocol was identical for the experiment and simulation. B: rate dependence of normalized I_Kur at the end of test voltage pulses for both models and experimental data (15). From a holding potential of −80 mV, 100 steps to +40 mV of 200-ms duration were applied at frequencies of 0.1, 0.5, 1, 2, 3, and 4 Hz. The voltage-clamp protocol was identical for the experiment and simulation. C: rate dependence of APD₃₀ in both models compared with the experiment (8). D: rate dependence of APD₉₀ in both models compared with experiments (8, 9).

Utility of the hAMr Model in Applications

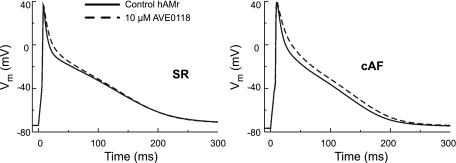
Unlike other models of the human atrial myocyte, the hAMr model features new repolarization kinetics and rate dependence and thus is appropriate for a wide range of cellular, tissue-level, and organ-level studies of the APs in human atria under normal and pathophysiological conditions. Of particular utility at the cellular level is the simulation of pharmacological interventions. Figure 10 shows the results of the use of the hAMr model to reproduce the effects of the I_t/I_Kur/I_K(ACh) blocker AVE0118 on human atrial myocyte APs, as described by Christ et al. (6). For sinus rhythm (or healthy) atrial myocyte APs, simulations used the hAMr model, whereas for chronic atrial fibrillation APs, a version of the hAMr model modified to represent chronic atrial fibrillation based on experimental findings (6, 9) was used. The experimentally measured effects of AVE0118 on diverse K⁺ currents (6) were used in both sets of simulations. The simulations reproduced experimental findings (6) showing that AVE0118 administered in cells at sinus rhythm increased APD₂₀ but not APD₉₀, whereas in cells with chronic atrial fibrillation, both APD₂₀ and APD₉₀ increased with the administration of AVE0118. The increase in APD₉₀ afforded by AVE0118 in human atrial myocytes with chronic atrial fibrillation has been suggested to underlie the efficacy of this compound to convert atrial fibrillation to sinus rhythm in goats (2), but the potential effects in a clinical setting to treat atrial fibrillation is unknown. As a forerunner and complement to clinical testing, the hAMr model could prove a useful tool to investigate the tissue-level effects of AVE0118 as well as numerous other pharmacokinetic therapies targeting human atrial myocytes.

Fig. 10.

Use of the hAMr model to investigate the effects of the drug AVE0118 on the human atrial AP waveform during sinus rhythm (SR) and chronic atrial fibrillation (cAF). The specific differential effects of AVE0118 in SR versus cAF human atrial myocytes described by Ref. 6 are shown here, illustrating the potential utility of the hAMr model in the simulation of pharmacological interventions.

DISCUSSION

The primary goal of the present study was to provide a computational framework in which the repolarization of the human atrial myocyte could be examined. This was achieved via the development of a new human atrial myocyte model based on the model of Nygren et al. (40), which incorporated recent experimental K⁺ current data and then characterized the emergent rate dependence of the new model. The results presented here demonstrate the ways in which select properties of major repolarizing K⁺ currents can result in the ability of the model to reproduce experimental measurements of AP properties of adult human atrial myocytes. In addition, the RMP matches available experimental data from human atrial myocytes. Importantly, our model now satisfies fundamental physical constraints of conservation of charge and ionic species and thereby ensures unique, long-term steady states of ionic concentrations in both the intracellular and cleft spaces. The morphology of the AP in the hAMr model resembles experimental APs from adult human atrial myocytes. This is the case despite the fact that no attempt was made to systematically match any such recordings. APD values for both early and late repolarization more closely approximated those measured in experiments, and an emergent feature of the hAMr model is its improved rate dependence of both individual currents and APD. The model presented in this article provides insight into repolarization processes and results in a much-improved match of current and AP behaviors to available experiments, an essential characteristic for the future use of the model in the context of human atrial rhythm disturbances.

I_K1 and RMP

I_K1 is essential for the maintenance of the resting potential in all myocytes and for late repolarization (17, 43). This is true even though the conductance of I_K1 in the atria (compared with the ventricles) is relatively small (30). Some studies have indicated that I_K1 in the atria does not exhibit strong rectification, i.e., the current-voltage relation shows little, if any, negative slope (30). These studies would suggest that, at high levels of depolarization, I_K1 would maintain a current density close to its maximum value at less depolarized potentials and would remain at this density throughout the time course of the AP. It is possible that limitations in methodology (i.e., seal resistance changes for human atrial myocytes) lead to leakage currents, which may be interpreted as incomplete rectification but are an experimental artifact (39). A strong rectification of I_K1 allows the reproduction of experimentally observed current densities and the maintenance of a stable RMP and has thus been included in the hAMr model.

One important consequence of the relatively small conductance of I_K1 in the human atria is a slower rate of final repolarization as well as a somewhat more depolarized RMP (∼5–10 mV) compared with human ventricular myocytes (45). The RMP maintained in the hAMr model is −74.0 mV, which agrees with the majority of experimental studies using isolated adult human atrial myocytes (8, 21, 45, 46, 52, 60). The model of Courtemanche et al. (7) of the human atrial myocyte has a relatively hyperpolarized RMP of −81.2 mV. This is more typical of the maximum diastolic potential found in recordings from isolated human atrial tissue preparations (20, 45). We believe that accurate representation of the RMP is important not only in the context of steady-state phenomena but in the case of rate accommodation, wherein the maximum diastolic potential is typically depolarized compared with RMP and may affect both the availability and time dependence of ionic currents.

Demonstration of Long-term Pacing and Steady-State Ion Concentrations in the hAMr Model

Intracellular and cleft ion concentrations are at steady states for >10 min of simulation at a pacing rate of 1 Hz in the hAMr model. A small but notable change occurs in the steady-state value of [K⁺]_c in the hAMr model compared with the original model of Nygren et al. (40); basal diastolic [K⁺]_c was increased to 5.6 from 5.4 mmol/l (∼3.7% increase). This may be explained as resulting from the elimination of Φ_Na in the hAMr model: the stimulus current that enters the intracellular space is now carried by potassium ions (24). These potassium ions are then extruded via sarcolemmal ion channels and accumulate in the cleft space surrounding the cell, whereas the bulk K⁺ concentration remains unchanged. Experimental measurements of extracellular ion concentrations are taken from the bulk fluid surrounding the cell or preparation, and there may exist locally higher concentrations of ions in an extracellular cleft space surrounding a myocyte than may be measured in the bulk plasma.

When the stimulation frequency was increased to 2 Hz, [K⁺]_c accumulated, increased to values up to ∼1 mmol/l greater than its basal value (∼18% increase), and then returned to a unique steady state close to its initial value. [Na⁺]_c and [Ca²⁺]_c initially decreased by ∼0.8% and ∼8%, respectively, and then returned to steady-state values. At a stimulation rate of 2 Hz, [Na⁺]_i increased by ∼18% to a new steady-state value. [K⁺]_i reached a new steady-state value, which was a 1.5% decrease. [Ca²⁺]_i, in contrast, underwent very little change in steady-state value at a stimulation rate of 2 Hz: the peak magnitude of the transient was decreased by ∼6% (peak magnitude), and peak diastolic [Ca²⁺]_i increased. It is difficult to provide a comprehensive comparison of our results due of the lack of experimental data for many of these quantities. However, an increase in [K⁺]_c with an increase in stimulation rate to 2 Hz has been recorded in experiments (31). In addition, peak diastolic [Ca²⁺]_i has also been shown to increase with an increase in stimulation frequency in experimental models (49, 51).

The elimination of Φ_Na results in the existence of a mathematical steady state in the hAMr model, as discussed briefly in Jacquemet et al. (25). The concentration of nonspecific, monovalent cations in the intracellular space, constant for any stimulation protocol in the hAMr model, was ∼138.4 mmol/l. Based on the elegant stability analysis provided in Jacquemet et al. (25), it can be determined that the initial condition for the transmembrane potential (initial condition in the appendix) in the hAMr model ensures that the system is dynamically stable for any stimulation protocol.

AP Waveforms

The AP in the hAMr model is characterized by a slightly slowed early (phase 1) repolarization as well as a more rapid late (phase 3) repolarization compared with the model of Nygren et al. (40) and fits well within the range of AP morphologies seen in recordings from experiments with adult human atrial myocytes (U. Ravens, unpublished observations). It is well known that there exist heterogeneities in human atrial AP shape. AP morphology and characteristics can vary both from patient to patient and from region to region in the atria (45) and have variously been classified into “types” or patterns (8, 10, 27, 57). Rather than require that the resultant AP morphology adhere to a specific experimental recording as in previous models of the adult human atrial myocyte (7, 40), we have chosen to arrive at a morphology for which accurate reproduction of observed behaviors of individual currents has been the focus. Although an exact match to an atrial AP shape was not required in our development, the result of the hAMr model is an AP morphology that is markedly similar to many experimental traces.

Repolarization Reserve Revisited

In the human atrial myocyte, I_t and I_Kur, followed by I_K1, are the main time- and voltage-dependent currents responsible for repolarization. I_t is active during phase 1 (early) repolarization of the AP only, whereas I_Kur inactivates very slowly and thus contributes to repolarization during phases 1, 2, and 3 of the human atrial AP. I_K1 figures prominently during late repolarization; because of the small densities of I_Kr and I_Ks compared with I_K1, neither current plays a major role during late repolarization in the hAMr model.

In the human atria, myocytes may have a relatively small safety factor for repolarization due to decreased densities of outward currents compared with ventricular myocytes. “Repolarization reserve” has previously been defined as the ability of myocardial cells to repolarize when normal repolarizing currents are altered or reduced via either physiological perturbations or pathological challenges (22). This concept has been applied as a measure of the safety factor for repolarization (17) and, in practice, has been defined as the sum of the K⁺ currents I_K1, I_Kr, and/or I_Ks, which can be activated under physiological conditions (17). However, the concept needs to be operationally defined with reference to particular contexts and situations. For example, outward currents that are active relatively late in the cardiac cycle may compensate for the low availability of other repolarizing currents when pacing rates increase, due to residual activation (i.e., I_Kur). The comparatively low density of outward K⁺ currents in the human atrial myocyte may result in low repolarization reserve, particularly in the context of drug therapies and pathologies that may interfere with K⁺ currents and repolarization processes. The underlying complexity of outward current remodeling, which contributes to varying degrees of the repolarization reserve, has been demonstrated recently (44). These new findings highlight the dynamic nature of the repolarization reserve and suggest that even outward currents active in early repolarization, i.e., I_t and I_Kur, may be critically important for repolarization in the human atria.

Rate Response of the AP Waveform

As shown in Fig. 9, the rate dependence of both I_t and I_Kur agree closely with experimental data. In addition, the frequency dependence of the AP waveform in the present model reproduces recent experimental results (Fig. 9) (8, 9).This improved representation of current availability and AP behavior at a variety of pacing rates is essential not only for the simulation of behaviors in healthy tissue but for the capacity of the model to lend its predictive power to disease state phenomena.

It is of interest to simulate the behavior of atrial myocytes and tissue at increased rates of stimulation so that atrial tachycardic rhythm disturbances (such as atrial flutter and atrial fibrillation) can be examined. For instance, in both paroxysmal and chronic atrial fibrillation, structural remodeling including progressive fibrosis has been widely implicated in the initiation and maintenance of the arrhythmia (3, 11). However, despite a wealth of investigation in recent years (29, 34, 48), a complete picture of the mechanisms underlying fibrosis-linked atrial arrhythmia has yet to emerge. Recent investigations have suggested that a critical aspect of atrial fibrotic remodeling may be functional: electrotonic coupling between fibroblasts and myocytes may play a crucial role at the cellular level (4, 5, 19, 26, 28, 35, 37, 38). Fibroblasts that are present within and maintain the extracellular matrix adjacent to myocytes can have a large influence on local myocyte activation and repolarization. To appropriately address questions regarding the potential involvement of electronic coupling between fibroblasts and human atrial myocytes in the development and maintenance of atrial arrhythmias, it is essential that the repolarization processes of the latter cell type be realistically represented at a variety of physiological and pathophysiological stimulation rates. The hAMr model was used in a recent study from our group (36) to investigate the effects of fibroblast-myocyte coupling on excitability and repolarization in the adult human atrial myocyte under a variety of conditions, including increased rates of stimulation.

Limitations of This Study

There are important limitations to the present work that should be recognized.

In Fig. 3D, computational traces of the sum of I_t and I_Kur appear to decay more rapidly than the experimental voltage clamp results. A cause of this apparent disparity is that the experimental traces available are from a recent publication (21), which, however, was not used in the new model, as the focus of the study of Gluais et al. was characterization of the AP and steady-state current density properties of human atrial myocytes after treatment with risperidone compared with control. The experimental datasets used to formulate the kinetics included in the model (15, 56) unfortunately did not include multiple voltage-clamp traces of the currents and thus could not be presented for a comparison to the simulated data shown in Fig. 3D.

The use of Hodgkin-Huxley formalism in our model employs first-order kinetics. Activation/deactivation and inactivation/recovery from inactivation are each governed by a single time constant, obtained, where possible, from fits to experimental measurements at a variety of holding potentials. However, many of these processes exhibit very complex kinetics. Markovian models allow for the existence of a multiplicity of channel states, each with specific transitional rate constants; however, these rate constants are often very difficult to determine. In addition, Markovian models often result in comprehensive AP models that are computationally expensive, particularly when more than one channel is involved. Additionally, Markovian models for the ion channels in the human atrium that were the main focus of this study (I_t and I_Kur) have not yet been developed. Future development and incorporation of such models will lead to further accuracy in the representation of ionic currents.

The mathematical formulations that account for Ca²⁺ homeostasis in the model of Nygren et al. (40) remained unchanged in the hAMr model. Although detailed models of Ca²⁺ cycling have emerged in recent years (23, 47), such models focus on ventricular rather than atrial tissue. Because of the lack of appropriate experimental data and because incorporation of a detailed model of Ca²⁺ cycling may be computationally prohibitive, particularly with respect to tissue and organ models, the formulation of Ca²⁺ cycling used in the model of Nygren et al. (40) was maintained in the hAMr model.

GRANTS

The laboratory of N. A. Trayanova gratefully acknowledges support of this work by National Heart, Lung, and Blood Institute Grants R01-HL-063195, R01-HL-082729, and R01-HL-067322 and National Science Foundation Grant CBET-0601935. The W. R. Giles laboratory is funded by the Canadian Institutes of Health Research and the Heart and Stroke Foundation of Canada. In addition, W. Giles holds a Medical Scientist Award from the Alberta Heritage Foundation for Medical Research.

APPENDIX: MODEL EQUATIONS

This section contains all the equations, parameter values, and initial conditions necessary to be the basis for a full and accurate implementation of the hAMr model when combined with the kinetic descriptions available in the model of Nygren et al. (40). Unless otherwise noted, the units are as follows: time (in s), voltage (in mV), concentrations (in mmol/L), current (in pA), conductance (in nS), capacitance (in pF), volume (in nl), and temperature (in K). The stimulus used to evoke an AP was a rectangular current pulse (I_stim) with amplitude of 280 pA and duration of 6 ms.

I_t

• $$I_{\text{t}}=g_{\text{t}}\times r\times s\left(V-E_{\text{K}}\right)$$
• $$\mathrm{d}r/\text{d}t=\left(r_{\infty }-r\right)/{\tau }_{\text{r}}$$
• $$\text{d}s/\text{d}t=\left(s_{\infty }-s\right)/{\tau }_{\text{s}}$$
• $$r_{\infty }=1.0/\left[1.0+e^{\left(v-1.0\right)/-11.0}\right]$$
• $$s_{\infty }=1.0/\left[1.0+e^{\left(v+40.5\right)/11.0}\right]$$
• $${\tau }_{\text{s}}=0.025635\times e^{\left\{-\left[\left(v+52.45\right)/15.8827\right]2\right\}}+0.01414$$
• $${\tau }_{\text{r}}=0.0035\times e^{\left[-\left(v/30.0\right)2\right]}+0.0015$$

I_Kur

• $$I_{\text{Kur}}=g_{\text{Kur}}\times a_{\text{ur}}\times i_{\text{ur}}\times \left(V-E_{\text{K}}\right)$$
• $$\text{d}{a}_{\text{ur}}/\text{d}t=\left(a_{\text{ur,}\infty }-a_{\text{ur}}\right)/{\tau }_{\text{aur}}$$
• $$\text{d}{i}_{\text{ur}}/\text{d}t=\left(i_{\text{ur,}\infty }-i_{\text{ur}}\right)/{\tau }_{\text{iur}}$$
• $$a_{\text{ur,}\infty }=1.0/\left[1.0+e^{-\left(V+6\right)/8.6}\right]$$
• $$i_{\text{ur,}\infty }=1.0/\left[1.0+e^{\left(V+7.5\right)/10.0}\right]$$
• $${\tau }_{\text{aur}}=0.009/\left[1.0+e^{\left(V+5.0\right)/12.0}\right]+0.0005$$
• $${\tau }_{\text{iur}}=0.59/\left[1.0+e^{\left(V+60.0\right)/10.0}\right]+3.05$$

Intracellular Ion Concentrations

• $$\text{d}{\left[{\text{K}}^{+}\right]}_{\text{i}}/\text{d}t=-\left[I_{\text{t}}+I_{\text{Kur}}+I_{\text{K1}}+I_{\text{Ks}}+I_{\text{Kr}}-2\left(I_{\text{NaK}}\right)+I_{\text{stim}}\right]/\left({\text{Vol}}_{\text{i}}\times F\right)$$
• $$\text{d}{\left[{\text{Na}}^{+}\right]}_{\text{i}}/\text{d}t=-\left[I_{\text{Na}}+I_{\text{BNa}}+3\left(I_{\text{NaCa}}\right)+3\left(I_{\text{NaK}}\right)\right]/\left({\text{Vol}}_{\text{i}}\times F\right)$$

Parameter Values

• $$K_{\text{Ca}}=\text{0}\text{.025mmol/l}$$
• $$I_{\text{NaK,max}}=\text{68}\text{.55pA}$$

Maximum Conductance Values

• $$P_{\text{Na}}=\text{0}\text{.0018nl/s}$$
• $$g_{\text{t}}=8.25\text{nS}$$
• $$\text{Mean}{g}_{\text{Kur}}=2.25\text{nS}$$
• $$g_{\text{K}1}=3.1\text{}\text{nS}$$

Initial Conditions

• $$\text{V}=-74.0320\text{mV}$$
• $${\left[{\text{Na}}^{+}\right]}_{\text{c}}=130.0221\text{mmol/l}$$
• $${\left[{\text{K}}^{+}\right]}_{\text{c}}=5.5602\text{mmol/l}$$
• $${\left[{\text{Ca}}^{+}\right]}_{\text{c}}=1.8158\text{mmol/l}$$
• $${\left[{\text{Na}}^{+}\right]}_{\text{i}}=8.5168\text{mmol/l}$$
• $${\left[{\text{K}}^{+}\right]}_{\text{i}}=129.4860\text{mmol/l}$$
• $${\left[{\text{Ca}}^{2+}\right]}_{\text{i}}=6.5000\times {10}^{-5}\text{mmol/l}$$
• $${\left[{\text{Ca}}^{2+}\right]}_{\text{d}}=7.1000\times {10}^{-5}\text{mmol/l}$$
• $${\left[{\text{Ca}}^{2+}\right]}_{\text{rel}}=0.6326\text{mmol/l}$$
• $${\left[{\text{Ca}}^{2+}\right]}_{\text{up}}=0.6492\text{mmol/l}$$
• $$m=3.2890\times {10}^{-3}$$
• $$h_1=0.8772$$
• $$h_2=0.8739$$
• $$d_{\text{L}}=1.4000\times {10}^{-5}$$
• $$f_{\text{L1}}=0.9986$$
• $$f_{\text{L2}}=0.9986$$
• $$r=1.0890\times {10}^{-3}$$
• $$s=0.9486$$
• $$a_{\text{ur}}=3.6700\times {10}^{-4}$$
• $$i_{\text{ur}}=0.9673$$
• $$n=4.3740\times {10}^{-3}$$
• $$p_{\text{a}}=5.3000\times {10}^{-5}$$
• $$F_1=0.4701$$
• $$F_2=0.0028$$
• $$O_{\text{C}}=0.0268$$
• $$O_{\text{Calse}}=0.4315$$
• $$O_{\text{TC}}=0.0129$$
• $$O_{\text{TMgC}}=\mathrm{0.19.4}$$
• $$O_{\text{TMgMg}}=0.7145$$