Abstract
Background
Zipf's discovery that word frequency distributions obey a power law established parallels between biological and physical processes, and language, laying the groundwork for a complex systems perspective on human communication. More recent research has also identified scaling regularities in the dynamics underlying the successive occurrences of events, suggesting the possibility of similar findings for language as well.
Methodology/Principal Findings
By considering frequent words in USENET discussion groups and in disparate databases where the language has different levels of formality, here we show that the distributions of distances between successive occurrences of the same word display bursty deviations from a Poisson process and are well characterized by a stretched exponential (Weibull) scaling. The extent of this deviation depends strongly on semantic type – a measure of the logicality of each word – and less strongly on frequency. We develop a generative model of this behavior that fully determines the dynamics of word usage.
Conclusions/Significance
Recurrence patterns of words are well described by a stretched exponential distribution of recurrence times, an empirical scaling that cannot be anticipated from Zipf's law. Because the use of words provides a uniquely precise and powerful lens on human thought and activity, our findings also have implications for other overt manifestations of collective human dynamics.
Introduction
Research on the distribution of time intervals between successive occurrences of events has revealed correspondences between natural phenomena on the one hand [1], [2] and social activities on the other hand [3]–[5]. These studies consistently report bursty deviations both from random and from regular temporal distributions of events [6]. Taken together, they suggest the existence of a dynamic counterpart to the universal scaling laws in magnitude and frequency distributions [7]–[11]. Language, understood as an embodied system of representation and communication [12], is a particularly interesting and promising domain for further exploration, because it both epitomizes social activity, and provides a medium for conceptualizing natural and biological reality.
The fields of statistical natural language processing and psycholinguistics study language from a dynamical point of view. Both treat language processing as encoding and decoding of information. In psycholinguistics, the local likelihood (or predictability) of words is a central focus of current research [13]. Many widely used practical applications of statistical natural language processing, such as document retrieval based on keywords, also exploit dynamic patterns in word statistics [10], [14], [15]. Particularly important for these applications, and also noticed in different contexts [16]–[21], is the non-uniform distribution of content words through a text, suggesting that connections to the previous discoveries about inter-event distributions may be revealed through a systematic investigation of the recurrence times of different words.
With the rise of the Internet, large records of spontaneous and collective language are now available for scientific inquiry [22]–[24], allowing statistical questions about language to be investigated with an unprecedented precision. At the same time, large-scale text mining and document classification is of ever-increasing importance [25]. The primary datasets used in our study are USENET discussion groups available through Google (http://groups.google.com). These exemplify spontaneous linguistic interactions in large communities over a long period of time. We first focus on the 
words that occurred more than 
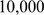times between Sept. 1986 and Mar. 2008 in a (
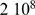-word) discussion group, talk.origins. The data were collated chronologically, maintaining the thread structure (see Text S1, Databases).
Here, we show that long-time word recurrence patterns follow a stretched exponential distribution, owing to bursts and lulls in word usage. We focus on time scales that exceed the scale of syntactic relations, and the burstiness of the words is driven by their semantics (that is, by what they mean). The burstiness of physical events and socially contextualized choices makes words more bursty than an exponential distribution. However, we show that words are typically less bursty than other human activities [26] due to their logicality or permutability
[27], [28], technical constructs of formal semantics that index the extent to which the meanings and usage of words are stable over changes in the discourse context. Our quantitative analysis of the empirical data confirms the inverse relationship between burstiness and permutability. The model we develop to explain these observations shares the generative spirit of local (
-gram) and weakly non-local models of text classification and generation [29]–[31]. However it focuses on long time-scales, picking up at temporal scales where studies of local predictability and coherence leave off [13]. We verify the generality of our main findings using different databases, including books of different genres and a series of political debates.
Methods
We are interested in the temporal distribution of each word 
. All words are enumerated in order of appearance, 
, where 
plays the role of the time along the text. The recurrence time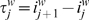 
is defined by the number of words between two successive uses (
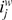and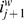 
) of word 
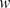(plus one). For instance, the first appearances of the word the in the abstract above are at 
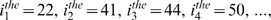leading to a sequence of recurrence times 
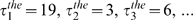. We are interested in the distribution 
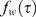of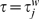 
, 
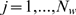. The mean recurrence time, called by Zipf the wavelength of the word [7], is given by 
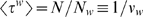[2] (hereafter we drop 
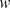from our notation). It is mathematically convenient to consider 
to be a continuous time variable (an assumption that is justified by our interested in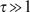 
) and to use the cumulative probability density function defined by 
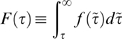, which satisfies 
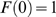and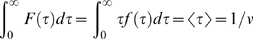 
.
The first point of interest is how the distribution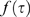 
[or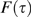 
] deviates from the exponential distribution
 |
(1) |
where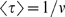 
leads to 
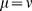. The exponential distribution is predicted by a simple bag-of-words model in which the probability 
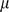of using the word is time independent and equals 
(a Poisson process with rate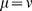 
) [14], [15], [19], [25], [29], as observed if the words in the text are randomly permuted. Deviations are caused by the way that people choose their words in context. Numerous studies, as reviewed in Ref. [32], already demonstrate that the language users dynamically modify their use of nouns and noun phrases as a function of the linguistic and external context. We analyze such modifications for all types of words.
Results and Discussion
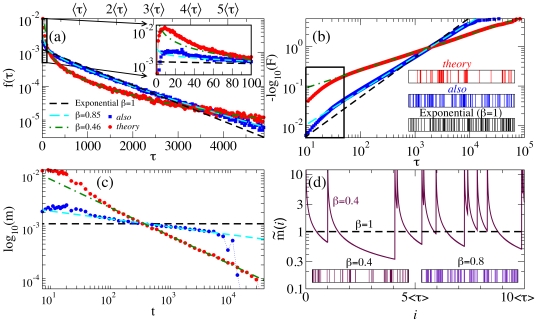
Figure 1 shows the empirical results obtained for the example words theory and also in the talk.origins group of the USENET database. Both words have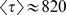 
but are linguistically quite different: while theory is a common noun, also is an adverb that functions semantically as an operator. The deviation from the Poisson prediction (1) is apparent in Fig. 1(a–c): 
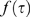is larger than the exponential distribution for distances 
both much shorter and much longer than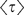 
, while it is smaller for 
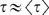. Both words exhibit a most probable recurrence time 
and a monotonically decaying distribution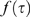 
for larger times [Fig. 1(a)]. Comparing the insets in Fig. 1(b), one sees that the occurrences of theory are clustered close to each other in a phenomenon known as burstiness [6], [14], [15], [19], [21]. Due to burstiness, the frequency of the word theory estimated from a small sample would differ a great deal as a function of exactly where the sample was drawn. Similar but lesser deviations are observed for the word also.
Figure 1. Recurrence time distributions for the words theory (red) and also (blue) in the USENET group talk.origins, a discussion group about evolution and creationism.
Both words have a mean recurrence time of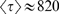 
. (a) Linear-logarithmic representation of 
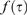, showing that the decay is slower than the exponential 
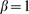prediction (1) (black dashed line) and follows closely the stretched exponential distribution (2) with 
(
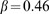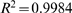) for theory and 
(
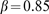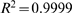) for also. For comparison, 
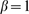yields 
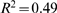for the word theory and 
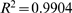for the word also (see Text S1, Fitting Procedures). The inset in (a) shows a magnification for short times. A word-dependent peak at 
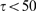reflects the domination of syntactic effects and local discourse structure at this scale. (b) Cumulative distribution function 
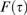in a scale in which the stretched exponential (2) appears as a straight line. The panels in the inset show 
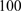occurrences (top to bottom): of the word theory, of the word also, and of a randomly distributed word (
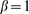). (c) The probability of word usage 
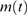for the words theory and also. The data are binned logarithmically and the straight lines correspond to Eq. (4). (d) Illustration of the generative model for the usage of individual words when 
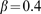, where the spikes indicate the times at which the word is used. The probability 
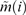of using a word decays as a piece-wise power-law function since its last use, as determined by Eq. (4). The Poisson case corresponds to constant 
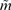. The panels at the bottom show 
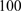occurrences of words generated by the model for 
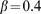and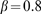 
.
Central to our discussion, Fig. 1 shows that the distributions of both words can be well described by the single free parameter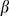 
of the stretched exponential distribution
 |
(2) |
where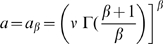 
is obtained by imposing 
, 
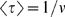is the Gamma function, and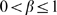 
. Distribution (2), also known as Weibull distribution, and similar stretched exponential distributions describe a variety of phenomena [6], [23], [33]–[35], including the recurrence time between extreme events in time series with long-term correlations [2], [36]. The stretched exponential (2) is more skewed than the simple exponential distribution (1), which corresponds to the limiting case 
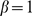, but less skewed than a power law, which is approached for 
.
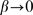A crucial test for the claim that an empirical distribution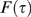 
follows a stretched exponential 
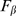is to represent 
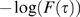as a function of 
in a double logarithmic plot [2]. The straight line behavior for almost three decades shown in Fig. 1(b), which is illustrative of the words in our datasets, provides strong evidence for the stretched exponential scaling (spam-related deviations for long 
are discussed in Text S1, Databases). This is a clear advance over the closest precedents to our results: (i) In Ref. [8] Zipf proposed a power-law decay, which would appear as an horizontal line in Fig. 1b. (ii) Refs. [14], [15] compare two non-stationary Poisson processes for predicting the counts of words in documents (see Text S1, Counting Distribution); (iii) Ref. [19] proposes a non-homogeneous Poisson process for recurrence times, using a mixture of two exponentials with a total of four free parameters; (iv) Ref. [37] uses the Zipf-Alekseev distribution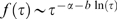 
, which we found to underestimate the decay rate for large 
and to leave larger residuals than our fittings (see Text S1, Zipf-Alekseev Distribution). The stretched exponential distribution was found to describe the time between usages of words in Blogs and RSS feeds in Ref. [24]. However, time was measured as actual time and the same distribution was found for different types of words, suggesting that their observations are driven by the bursty update of webpages, a related but different effect. More strongly related to our study is Ref. [5]'s analysis of email activity, in which a non-homogeneous Poisson process captures the way one email can trigger the next.
Generative Model
Motivated by the successful description of the stretched exponential distribution (2), we search for a generative stochastic process that can model word usage. We consider the inverse frequency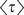 
as given and focus on describing how the words are distributed throughout the text. We assume that our text (abstractly regarded as arbitrarily long) is generated by a well-defined stationary stochastic process with finite 
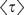for the words of interest. We further assume that the probability 
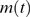of using the word 
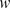depends only on the distance 
since the last occurrence of the word. The latter means that we are modeling the word usage as a renewal process
[34], [36]. The distribution of recurrence times is then given by the (joint) probability of having the word at distance 
and not having this word for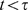 
:
 |
The cumulative distribution function is written as
 |
(3) |
The time dependent probability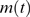 
, also known as hazard function, can be obtained empirically as 
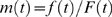(see Text S1, Hazard Function). Equation (3) reduces to the exponential distribution (1) for a time independent probability 
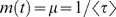. The stretched exponential distribution (2) is obtained from (3) by asserting that [34], [36], [38]
 |
(4) |
This assertion means that in our model, the probability of using a word decays as a power law since the last use of that word. This is further justified by the power-law behavior of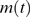 
determined directly from the empirical data, as shown in Fig. 1(c) and Text S1, Fig. 9, and is in agreement with results from mathematical psychology [39], [40] and information retrieval [40]. The Weibull renewal process we propose can be analyzed formally as a particular instance of a doubly stochastic Poisson process [41].
Our model is illustrated in Fig. 1(d) and can be interpreted as a bag-of-words with memory that accounts for the burstiness of word usage. This model does not reproduce the positive correlations between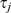 
and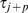 
[2], [6], [20], which are usually small (less than 
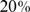% for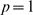 
) but decay slowly with 
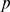(see Text S1, Correlation in
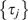). These correlations quantify the extent to which the renewal model is a good approximation of the actual generative process, and show that the burstiness of words exists not only as a departure of 
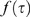from the exponential distribution, but also as a clustering of small (large) 
[6] (see Text S1, Independence of
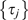). The advantage of the renewal description is that the model (i) can be substantiated to a vast literature describing power-law decay of memory in agreement with Eq. (4), see Refs. [39], [40] and references therein, and (ii) fully determines the dynamics (allowing, e.g., the precise derivation of counting distributions [38], which are used in applications to document classification [14], [15] and information retrieval [40]).
Word Dependence
We have seen in Fig. 1 that the word-dependent deviation from the exponential distribution is encapsulated in the parameter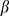 
: the smaller the 
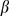for any given word, the larger the deviation (see Text S1, Deviation from the Exponential Distribution). Next we investigate the dominant effects that determine the value of the parameter 
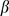of a word. Previous research has observed that frequent function words (such as conjunctions and determiners) usually are closer to the random (Poisson) prediction while less frequent content words (particularly names and common nouns) are more bursty. These observations were quantified using: (i) an entropic analysis of texts [16]; (ii) the variance of the sequence of recurrence times [17]; (iii) the recurrence time distribution [19], [42]; and (iv) the related distribution of the number of occurrences of words per document [14], [15]. Because we have a large database and do not bin the datastream into documents, we are able to go beyond these insightful works and systematically examine frequency and linguistic status as factors in word burstiness.
Our large database allows a detailed analysis of words that, despite being in the same frequency range, have very different statistical behavior. For instance, in the range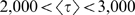 
, words with high 
(
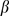) include once, certainly, instead, yet, give, try, makes, and seem; the few words with 
include design, selection, intelligent, and Wilkins. Corroborating Ref. [14], it is evident that words with low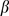 
better characterize the discourse topic. However, these examples also show that the distinction between function words and content words cannot be explanatory. For instance, many content words, such as the adverbs and verbs of mental representation in the list just above, have 
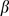values as high as many function words. Here we obtain a deeper level of explanation by drawing on tools from formal semantics, specifically on type theory [27], [43], [44], and on dynamic theories of semantics [45], [46], which model how words and sentences update the discourse context over time. We use semantics rather than syntax because syntax governs how words are combined into sentences, and we are interested in much longer time scales over which syntactic relations are not defined. Type theory establishes a scale from simple entities (e.g., proper nouns) to high type words (e.g., words that cannot be described using first-order logic, including intensional expressions and operators). Simplifying the technical literature in the interests of good sample sizes and coding reliability, we define a ladder of four semantic classes, as listed in Table 1.
Table 1. Examples of the classification of words by semantic types.
| Class | Name | Examples of words |
| 1 | Entities | Africa, Bible, Darwin |
| 2 | Predicates and Relations | blue, die, in, religion |
| 3 | Modifiers and Operators | believe, everyone, forty |
| 4 | Higher Level Operators | hence, let, supposedly, the |
The primitive types are entities e, exemplified by proper nouns such as Darwin (Class 1), and truth values, t (which are the values of sentences). Predicates or relations, such as the simple verb die, and the adjective/noun blue, take entities as arguments and map them to sentences (e.g., Darwin dies, Tahoe is blue). They are classified as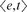 
(Class 2). The notation 
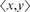denotes a mapping from an element 
in the domain to the image 
[43], [44]. The semantic types of higher Classes are established by assessing what mappings they perform when they are instantiated. For example, everyone is of type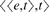 
(Class 3), because it is a mapping from sets of properties of entities to truth values [44]; the verb believe shares this classification as a verb involving mental representation. The adverb supposedly is a higher order operator (Class 4), because it modifies other modifiers. Following Ref. [44] (contra Ref. [43]) words are coded by the lowest type in which they commonly occur (see Text S1, Coding of Semantic Types).
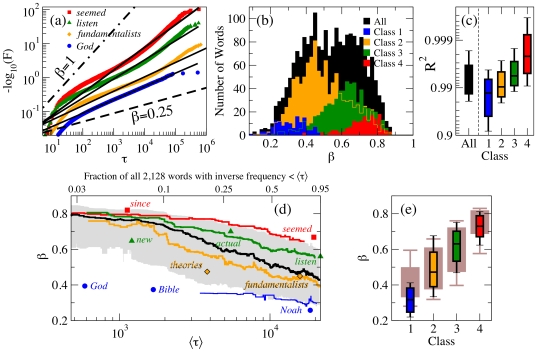
In Fig. 2, we report our systematical analysis of the recurrence time distribution of all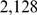 
words that appeared more than ten thousand times in our database (for word-specific results see Table S1). We find a wide range of values for the burstiness parameter 
[
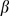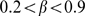, Fig. 2(a,b)] and the stretched exponential distribution describes well most of the words [
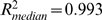, Fig. 2(c)]. The Class-specific results displayed in Fig. 2(a–c) show that words of all classes are accurately described by the same statistical model over a wide range of scales, a strong indication of a universal process governing word usage at these scales. Figure 2(b) also reveals a systematic dependence of 
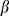on the semantic Classes: burstiness increases (
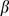decreases) with decreasing semantic Class. This relation implies that words functioning unambiguously as Class 3 verbs should be less bursty than words of the same frequency functioning unambiguously as common nouns (Class 2). This prediction is confirmed by a paired comparison in our database: such verbs have a higher 
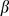in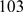 
out of 
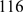pairs of verbs and frequency-matched nouns (sign test, 
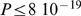). The relation applies even to morphologically related forms of the same word stem (see Text S1, Lemmatization): for 
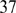out of the 
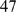pairs of Class 3 adjectives and Class 4 adverbs in the database that are derived with -ly, such as perfect, perfectly, the adverbial form has a higher 
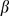than the adjective form (sign test, 
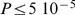). Figure 2(d) shows the dependence of 
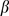on inverse frequency 
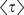. This figure may be compared to the TF-IDF (term frequency-inverse document frequency) method used for keyword identification [14], but it is computed from a single document (see also Refs. [16]–[18]). Figure 2(d) reveals that 
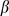is correlated with 
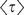and that the Class ordering observed in Fig. 2(b) is valid at all 
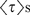s. The detailed analysis in Fig. 2(e) demonstrates that semantic Class is more important than frequency as a predictor of burstiness (Class accounts for 
and log-frequency for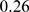 
of the variance of 
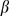, by the test proposed in Ref. [47]).
Figure 2. Dependence of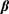 
on semantic Class and frequency for the 
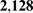most frequent words of the USENET group talk.origins.
Different classes of words (see Table 1) are marked in different colors. (a) Fitting of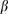 
exemplified for four words with 
(bottom to top): God, Class 1,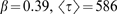 
; fundamentalists, Class 2, 
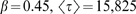; listen, Class 3, 
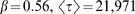; seemed, Class 4, 
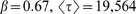. (b) Histogram of the fitted 
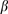, providing evidence that the Class is determinant to the value of 
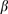. (c) Quality of fit quantified in terms of the coefficient of determination 
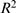between the fitted stretched exponential and the empirical 
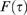(see Text S1, Quality of Fit). The box-plots are centered at the median and indicate the 
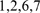octiles. For comparison, an exponential fit with two free parameters yields 
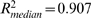(see Text S1, Deviation from the Exponential Distribution). (d) Relative dependence of 
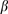on Class and 
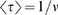(inverse frequency), indicating: running median on words ordered according to 
(center black line) and 
-st and 
-th octiles (boundaries of the gray region); and running medians on words by Class (colored lines, Class 1–4, from bottom to top) with illustrative words for each Class. At each 
, large variability in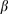 
and a systematic ordering by Class is observed. (e) Box-plots of the variation of 
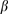for words in a given Class. The box-plots in the background are obtained using frequency to divide all words in four groups with the same number of words of the semantic Classes (first box-plot has words with lowest frequency and last box-plot has words with highest frequency). The classification based on Classes leads to a narrower distribution of 
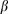's inside Class and to a better discrimination between Classes.
We are now in a position to discuss why burstiness depends on semantic Class. A straw man theory would seek to derive the burstiness of referring expressions directly from the burstiness of their referents. The limitations of such a theory are obvious: Oxygen is a very bursty word in our database (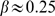
) though oxygen is ubiquitous. A more careful observer would connect the burstiness of words to the human decisions to perform activities related to the words. For instance, the recurrence time between sending emails is known to approximately follow a power law [3], [5]. However, in our database the word email is significantly closer to the exponential (
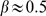) than a power law would predict (
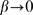). Indeed, a defining characteristic of human language is the ability to refer to entities and events that are not present in the immediate reality [48]. These nontrivial connections between language and the world are investigated in semantics. An insight on the problem of word usage can be obtained from Ref. [27], which establishes that the meaning and applicability of words with great logicality remains invariant under permutations of alternatives for the entities and relations specified in the constructions in which they appear. Here we consider permutability to be proportional to the semantic Classes of Table 1. As a long discourse unfolds exploring different constructions, we expect words with higher permutability (higher semantic Class) to be more homogeneously distributed throughout the discourse and therefore have higher 
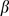(be less bursty). Critical to this explanation is the fact that human language manipulates representations of abstract operators and mental states [49]. However, the overt statistics of recurrence times do not need to be learned word by word. It seems more likely that they are an epiphenomenal result of the differential contextualization of word meanings. The fact that the behavior of almost all words deviate from a Poisson process to at least some extent, indicates that the permutability and usage of almost all words are contextually restricted to some degree, whether by their intrinsic meaning or by their social connotations.
Different Databases
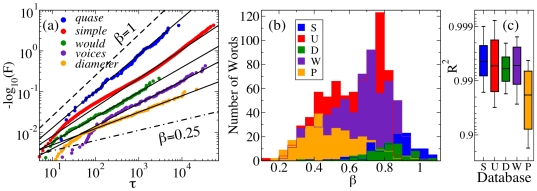
In Fig. 3 we verify our main results using databases of different sizes and characterized by different levels of formality. We analyzed a second example of a USENET group (U), a series of political debates (D), two novels (S,W), and a technical book (P) (for word-specific results see Table S1). The stretched exponential provides a close fit for frequent words in these datasets [Fig. 3(a,c)], and a wide and smoothly varying range of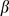 
s is observed in each case [Fig. 3(b)]. The technical book exhibits lower 
values, which can be attributed to the predominance of specific scientific terms. These datasets include examples of texts differing by almost four orders of magnitudes in size, generated by a single author (books), a few authors (debates) or a large number of authors (USENET), in writing and speech (e.g., books vs. debates), and in different languages (e.g., novels), indicating that the stretched exponential scaling is robust with regard to sample size, number of authors, language mode, and language.
Figure 3. Stretched exponential recurrence time distributions observed in different databases.
The databases consist of the documentary novel Os Sertões by Euclides da Cunha (S), in Portuguese (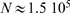
); the USENET group comp.os.linux.misc (U) between Aug. 
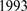and Mar. 
(
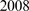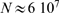); the three Obama-McCain debates of the 2008 United States presidential election (D) arranged in chronological order (
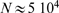); an English edition of the novel War and Peace by Leon Tolstoy (W) (
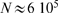); and the first English edition of Isaac Newton's Principia (P) (
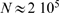). All words appearing more than 
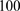times were considered in S (
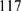words), D (
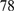words), P (
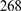words), and W (
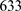words), whereas in U all 
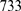words appearing more than 
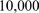times were used (see Text S1, Databases). (a) Recurrence time distributions for the words quase in S (
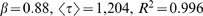), simple in U (
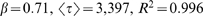), would in D (
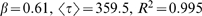), voices in W (
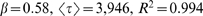), and diameter in P (
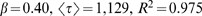). (b) Histograms of the fitted 
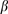for all datasets. Due to sample size limits, the analysis into semantic Classes is not feasible for the smaller datasets. (c) Box-plots of the coefficient of determination 
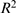of the corresponding stretched exponential fit.
Conclusions
The quest for statistical laws in language has been driven both by applications in text mining and document retrieval, and by the desire for foundational understanding of humans as agents and participants in the world. Taking texts as examples of extended discourse, we combined these research agendas by showing that word meanings are directly related to their recurrence distributions via the permutability of concepts across discourse contexts. Our model for generating long-term recurrence patterns of words, a bag-of-words model with memory, is stationary and uniformly applicable to words of all parts of speech and semantic types. A word's position along the range in the memory parameter in the model,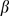 
, effectively captures its position in between a power-law and an exponential distribution, thus capturing its degree of contextual anchoring. Our results agree with Ref. [49] in emphasizing both the specific ability to learn abstract operators and the broader conceptual-intentional system as components in the human capability for language and in its use in the flow of discourse.
Analogies between communicative dynamics and social dynamics more generally are suggested by the recent documentation of heavy-tailed distributions in many other human driven activities [3], [5], [26]. They indicate that tracing linguistic activities in the ever larger digital databases of human communications can be a most promising tool for tracing human and social dynamics [22]. The stretched exponential form for recurrence distributions that derives from our model and the empirical finding it embodies are thus expected to also find applicability in other areas of human endeavor.
Supporting Information
Supplementary information on language analysis, statistical analysis, and counting models.
(0.55 MB PDF)
Detailed information on the statistical analysis of all words that were studied (six databases).
(31.88 MB TAR)
Acknowledgments
We thank Pedro Cano and Seth Myers for piloting supplementary studies of word recurrences, Roger Guimerà and Seth Myers for sharing web mining programs, Bruce Spencer for advice on the statistical analysis, Stefan Kaufmann for his assistance in developing the semantic coding scheme, and Hannah Rohde for validating it. E. G. A. thanks the audiences at the Complex Systems & Language Workshop (The University of Arizona, April 2008) and at the NICO Colloquium (Northwestern University, October 2008) for providing valuable feedback.
Footnotes
Competing Interests: The authors have declared that no competing interests exist.
Funding: This work was supported by JSMF Grant No. 21002061 (J. B. P.) and NSF DMS-0709212 (A. E. M.). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Bak P, Christensen K, Danon L, Scanlon T. Unified scaling law for earthquakes. Phys Rev Lett. 2002;88:178501. [Google Scholar]
- 2.Bunde A, Eichner JF, Kantelhardt JW, Havlin S. Long-term memory: A natural mechanism for the clustering of extreme events and anomalous residual times in climate records. Phys Rev Lett. 2005;94:048701. doi: 10.1103/PhysRevLett.94.048701. [DOI] [PubMed] [Google Scholar]
- 3.Barabási A-L. The origin of burstiness and heavy tails in human dynamics. Nature. 2005;435:207–211. doi: 10.1038/nature03459. [DOI] [PubMed] [Google Scholar]
- 4.Politi M, Scalas E. Fitting the empirical distribution of intertrade durations. Physica A. 2008;387:2025–2034. [Google Scholar]
- 5.Malmgren RD, Stouffer DB, Motter AE, Amaral LAN. A Poissonian explanation for heavy tails in e-mail communication. Proc Natl Acad Sci USA. 2008;105:18153–18158. doi: 10.1073/pnas.0800332105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Goh K-I, Barabási A-L. Burstiness and memory in complex systems. Europhys Lett. 2008;81:48002. [Google Scholar]
- 7.Zipf GK. Boston: Houghton Mifflin; 1935. The Psycho-biology of Language: An Introduction to Dynamic Philology. [Google Scholar]
- 8.Zipf GK. New York: Addison-Wesley; 1949. Human Behavior and the Principle of Least Effort. [Google Scholar]
- 9.Simon HA. On a class of skew distribution functions. Biometrika. 1955;42:425–440. [Google Scholar]
- 10.Baayen RH. Berlin: Springer; 2002. Word Frequency Distributions. [Google Scholar]
- 11.Newman MEJ. Power laws, Pareto distributions and Zipf's law. Contemporary Physics. 2005;46:323–351. [Google Scholar]
- 12.Goodwin C. Action and embodiment within situated human interaction. J Pragm. 2000;32:1489–1522. [Google Scholar]
- 13.Bell A, Brenier J, Gregory M, Girand C, Jurafsky D. Predictability effects on durations of content and function words in conversational English. J Mem Lang. 2009;60:92–111. [Google Scholar]
- 14.Church KW, Gale WA. Poisson mixtures. Nat Lang Eng. 1995;1:163–190. [Google Scholar]
- 15.Katz SM. Distribution of content words and phrases in text and language modelling. Nat Lang Eng. 1996;2:15–59. [Google Scholar]
- 16.Montemurro MA, Zanette DH. Entropic analysis of the role of words in literary texts. Advances in Complex Systems. 2002;5:7–17. [Google Scholar]
- 17.Ortuño M, Carpena P, Beranaola-Galván P, Muñoz E, Somoza AM. Keyword detection in natural languages and DNA. Europhys Lett. 2002;57:759–764. [Google Scholar]
- 18.Herrera JP, Pury PA. Statistical keyword detection in literary corpora. Eur Phys J B. 2008;63:135–146. [Google Scholar]
- 19.Sarkar A, Garthwaite GH, de Roeck A. A Bayesian mixture model for term re-occurrence and burstiness. Proceedings of the 9th Conference on Computational Natural Language Learning. 2005:48–55. [Google Scholar]
- 20.Alvarez-Lacalle E, Dorow B, Eckmann J-P, Moses E. Hierarchical structures induce long-range dynamical correlations in written texts. Proc Natl Acad Sci USA. 2006;103:7956–7961. doi: 10.1073/pnas.0510673103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Serrano MA, Flammini A, Menczer F. Modeling statistical properties of written text. PLoS ONE. 2009;4:e5372. doi: 10.1371/journal.pone.0005372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Watts DJ. A twenty-first century science. Nature. 2007;445:489. doi: 10.1038/445489a. [DOI] [PubMed] [Google Scholar]
- 23.Wu F, Huberman BA. Novelty and collective attention. Proc Natl Acad Sci USA. 2007;104:17599–17601. doi: 10.1073/pnas.0704916104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lambiotte R, Ausloos M, Thelwall M. Word statistics in Blogs and RSS feeds: Towards empirical universal evidence. J of Informetrics. 2007;1:277–286. [Google Scholar]
- 25.Nigam L, McCallum A, Thrun S, Mitchell T. Text classification from labeled and unlabeled documents. Mach Learn. 2000;39:103–134. [Google Scholar]
- 26.Vázquez A, Oliveira JG, Dezsö Z, Goh K-I, Kondor I, et al. Modeling bursts and heavy tails in human dynamics. Phys Rev E. 2006;73:036127. doi: 10.1103/PhysRevE.73.036127. [DOI] [PubMed] [Google Scholar]
- 27.van Benthem J. Logical constants across varying types. Notre Dame J Form Logic. 1989;30:315–342. [Google Scholar]
- 28.von Fintel K. The Formal Semantics of Grammaticalization. Proceedings of NELS 25: Papers from the Workshops on Language Acquisition & Language Change GLSA 2. 1995:175–189. [Google Scholar]
- 29.Shannon CE. A mathematical theory of communication. Bell System Tech J. 1948;27:379–423. [Google Scholar]
- 30.Grosz B, Joshi A, Weinstein S. Centering: A framework for modeling the local coherence of discourse, Comput Linguist. 1995;21:203–226. [Google Scholar]
- 31.Ron D, Singer Y, Tishby N. The power of amnesia: Learning probabilistic automata with variable memory length. Mach Learn. 1996;25:117–149. [Google Scholar]
- 32.Tanenhaus MK, Brown-Schmidt S. Language processing in the natural world. Phil Trans R Soc B. 2008;363:1105–1122. doi: 10.1098/rstb.2007.2162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Laherrere J, Sornette D. Stretched exponential distributions in nature and economy: “Fat tails” with characteristic scales. Eur Phys J B. 1998;2:525–539. [Google Scholar]
- 34.Cox DR. U.K.: Methuen; 1967. Renewal Theory. [Google Scholar]
- 35.Redner S. Cambridge: Cambridge Univ. Press; 2001. A Guide to First-passage Processes. [Google Scholar]
- 36.Santhanam MS, Kantz H. Return interval distribution of extreme events and long term memory. Phys Rev E. 2008;78:051113. doi: 10.1103/PhysRevE.78.051113. [DOI] [PubMed] [Google Scholar]
- 37.Hrebicek L. Text Laws. In: Altmann G, Piotrowski RG, editors. Quantitative Linguistics, an International Handbook. Berlin: Walter de Gruyer; 2005. pp. 348–361. [Google Scholar]
- 38.McShane B, Adrian M, Bradlow ET, Fader P. Count models based on Weibull interarrival times. J Bus Econ Stat. 2008;26:369–378. [Google Scholar]
- 39.Wixted J, Ebbeson EB. On the form of forgetting. Psychol Sci. 1991;2:409–415. [Google Scholar]
- 40.Anderson JR, Milson R. Human memory: An adaptive perspective. Psychol Rev. 1989;96:703–719. [Google Scholar]
- 41.Yannaros Y. Weibull renewal processes. Ann Inst Statist Math. 1994;46:641–648. [Google Scholar]
- 42.Corral R, Ferrer-i-Cancho R, Boleda G, Diaz-Guilera A. Universal complex structures in written language. 2009. pre-print arXiv:physics.soc-ph/0901.2924v1.
- 43.Montague R. The proper treatment of quantification in ordinary English. In: Hintikka J, Moravscik J, Suppes J, editors. Approaches to Natural Language. Dordrecht: Reidel; 1973. pp. 373–398. [Google Scholar]
- 44.Partee BH. Syntactic categories and semantic type. In: Rosner M, Johnson R, editors. Computational Linguistics and Formal Semantics. Cambridge: Cambridge Univ. Press; 1992. pp. 97–126. [Google Scholar]
- 45.Heim I. File Change Semantics and the Familiarity Theory of Definiteness. In: Bäuerle R, Schwartze C, von Stechow A, editors. Meaning, Use and Interpretation of Language. Berlin: De Gruyter; 1983. pp. 164–189. eds. Bäuerle R, Schwartze C, von Stechow A. [Google Scholar]
- 46.Kamp H. A theory of truth and semantic representation. In: Groenendijk J, Janssen T, Stokhof M, editors. Formal Methods in the Study of Language. Amsterdam: Mathematisch Centrum; 1981. [Google Scholar]
- 47.Kruskal W. Relative importance by averaging over orders. Am Stat. 1987;41:6–10. [Google Scholar]
- 48.Hockett CF. The origin of speech. Sci Am. 1960;203:89–97. [PubMed] [Google Scholar]
- 49.Hauser MD, Chomsky N, Fitch WT. The faculty of language: What is it, who has it, and how did it evolve? Science. 2002;298:1569–1579. doi: 10.1126/science.298.5598.1569. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary information on language analysis, statistical analysis, and counting models.
(0.55 MB PDF)
Detailed information on the statistical analysis of all words that were studied (six databases).
(31.88 MB TAR)