Abstract
Dynamic nuclear polarization (DNP) is a method that permits NMR signal intensities of solids and liquids to be enhanced significantly, and is therefore potentially an important tool in structural and mechanistic studies of biologically relevant molecules. During a DNP experiment, the large polarization of an exogeneous or endogeneous unpaired electron is transferred to the nuclei of interest (I) by microwave (μw) irradiation of the sample. The maximum theoretical enhancement achievable is given by the gyromagnetic ratios (γe/γl), being ∼660 for protons. In the early 1950s, the DNP phenomenon was demonstrated experimentally, and intensively investigated in the following four decades, primarily at low magnetic fields. This review focuses on recent developments in the field of DNP with a special emphasis on work done at high magnetic fields (≥5 T), the regime where contemporary NMR experiments are performed. After a brief historical survey, we present a review of the classical continuous wave (cw) DNP mechanisms—the Overhauser effect, the solid effect, the cross effect, and thermal mixing. A special section is devoted to the theory of coherent polarization transfer mechanisms, since they are potentially more efficient at high fields than classical polarization schemes. The implementation of DNP at high magnetic fields has required the development and improvement of new and existing instrumentation. Therefore, we also review some recent developments in μw and probe technology, followed by an overview of DNP applications in biological solids and liquids. Finally, we outline some possible areas for future developments.
I. Introduction/Background
In 1953 Overhauser proposed that the large Boltzmann polarization of unpaired electrons could be transferred to neighboring nuclei by saturating the corresponding electron paramagnetic resonance (EPR) transition. The result of this process would be an enhancement of the signal intensities of the associated nuclear magnetic resonance (NMR) signals by a factor of (γe/γl) ∼ 660 in the case of protons. 1 The validity of this suggestion was vigorously debated until Carver and Slichter reported an experiment in which they polarized Li (Ref. 2) and later 23Na and 1H nuclei,3 achieving signal enhancements of ∼100. This experiment, now known as the Overhauser effect (OE) and widely used in solution NMR experiments for measuring 1H–1H distances, was the first demonstration of dynamic nuclear polarization (DNP).
In the following decade, additional pioneering DNP experiments were performed in both solids and liquids. In 1958 the solid effect (SE) was discovered, which required the use of polarizing agents with a homogeneous EPR linewidth (δ) and an inhomogeneous spectral breadth (Δ) smaller than the nuclear Larmor frequency (δ,Δ < ω0I) 4,5 Subsequently, Kessenikh et al., 6,7 Hwang and Hill, 8,9 and Wollan10 reported 9 GHz DNP experiments on systems with inhomogeneously broadened EPR spectra. The polarization mechanism in this case is the cross effect (CE), which is the dominant continuous wave (cw) mechanism at high magnetic fields. Specifically, the CE is operative when the polarizing agent has an inhomogeneous broadened EPR spectrum whose breadth Δ is larger than the nuclear Larmor frequency ω0I, and, concurrently, the homogeneous linewidth δ remains small (Δ > ω0I > δ). The third regime, where the homogeneous EPR linewidth is larger than the nuclear Larmor frequency (δ> ω0I), is referred to as thermal mixing11 (TM) and requires the existence of a high concentration of paramagnets.
There is currently a renaissance occurring in the development and application of DNP driven by the desire of the spectroscopist to enhance signal intensities in NMR spectra of both solids and liquids. This renaissance began in the 1980s with the appearance of magic angle spinning (MAS) experiments devoted to solids where the necessity of observing low-γ nuclei (13C, 15N, etc.) limits the sensitivity of the experiment. Thus, MAS-DNP methodology was developed to enhance sensitivity in 13C spectra of polymers, carbonaceous, and other materials. These experiments were constrained to low fields (≤60 MHz for 1H) because of the limited frequency range of klystron sources (≤40 GHz) used to produce microwaves. At the same time, solid-state NMR was reaping tremendous benefits from the availability of superconducting magnets operating at fields of ≥5 T (∼200 MHz for 1H), which yields significant improvements in sensitivity and spectral resolution. Thus, today it is not uncommon to record MAS spectra at 16–21 T (700–900 MHz for 1H). The success of these high-field MAS experiments stimulated interest in developing DNP at high frequencies, and this in turn motivated innovations in a number of areas required to buoy the experiments to fruition: technological developments in high-frequency microwave (μw) sources, transmission lines, and low temperature, multiple resonance MAS NMR probes. In addition, there have been important advances in the design of paramagnetic polarizing agents required for DNP. This in turn has enabled MAS experiments on membrane and amyloid proteins that are either difficult or impossible because of limited signal-to-noise. Therefore, high-frequency DNP is yet another example where the development of new instrumentation and methodology enables new areas of scientific inquiry.
In this overview, we focus primarily on the principles and applications of DNP MAS experiments at high magnetic fields and μw frequencies, which we arbitrarily define as ≥5 T corresponding to μw irradiation at frequencies ≥140 GHz (for g∼2). For technical reasons discussed below, μw power levels in the range of ∼10 W are desirable. One μw source that is capable of operating in this frequency regime and producing this level of output power is the gyrotron, a cyclotron resonance maser, and accordingly, we introduced this source into DNP experiments in the early 1990s initially at 140 GHz (Ref. 12) and more recently at 250 GHz (Ref. 13) and 460 GHz.14
In addition, gyrotron technology can also be used to perform pulsed EPR experiments at high μw frequencies,15 which is of particular interest since pulsed DNP schemes potentially do not suffer from the unfavorable field dependence of the classical DNP mechanisms (SE and CE/TM). Several different approaches to time domain experiments—nuclear spin orientation via electron spin locking (NOVEL),6 the integrated solid effect (ISE),17,18 dressed state solid effect19 (DSSE) and rotating frame DNP (RF-DNP) (Refs. 68–70)—have set the stage for future developments in this area of DNP methodology. Because of the availability of gyrotron technology, as well as other innovations, the future of high-field DNP appears very promising.
Although the focus of our efforts is high-field solid-state DNP, we also discuss recent experiments on liquids. Solution-state DNP experiments were first reported by Bennett and Torrey20 and liquids were extensively studied in the early work of Hausser et al.,21 who used the OE to transfer electron polarization to 13C, 19F, and 31P nuclei. Further work was done by Mueller–Warmuth et al.,22 who focused on the influence of molecular motion on the electron OE. More recent efforts to polarize liquids have utilized flow techniques23,24 or approaches where the sample is polarized as a solid at low temperatures and dissolved or melted and the liquid-state spectrum observed.25,26 Finally, we note that high nuclear spin polarizations can also be created by several other methods such as polarization transfer from optically excited states or polarized noble gases. For example, the high spin polarization in para-hydrogen can be used to enhance nuclear polarization in a chemically induced DNP (CIDNP) experiment.27 Another possibility is the use of hyperpolarized xenon in a spin polarization induced nuclear Overhausser effect (SPINOE) experiment described by Bifone et al.28 More recently, it was shown that caged hyperpolarized xenon can be used as a biosensor in magnetic resonance imaging (MRI) experiments.29 The discovery of photochemically induced dynamic electron polarization in chloroplasts30 resulted in a new class of experiments that utilize photochemically induced dynamic nuclear polarization (photo-CIDNP).31 For example, the observation of photo-CIDNP by solution NMR led to the formulation of the radical pair mechanism32 and later to photo-CIDNP in solid-state NMR (ssNMR) MAS spectra.33
An effect similar to the SE can be used to transfer polarization between an excited electronic triplet state and a nucleus via forbidden transitions. This mechanism is referred to as microwave induced optical nuclear polarization and was introduced by Deimling et al.34 Other polarization schemes rely on the use of 3He (Ref. 35) and quantum dots.36–38 These techniques, however, are of a much more specific interest and are beyond the scope of this review.
The remainder of this overview is organized as follows. In Sec. II we discuss cw and time domain polarization mechanisms, and in Sec. III we describe polarizing agents designed to be used in high-field experiments. Section IV is devoted to the most recent developments in μw technology, low temperature probe technology, and other instrumentation that enables DNP. We view these instrumental developments as very important since it is presently progress in this area more than anything else that limits applications of DNP. Some recent successful applications of DNP are described in Sec. V and we close in Section VI with a summary of prospective developments.
There are a number of excellent reviews on solid-state DNP by Jeffries,39 Abragam and Goldman, ,40,41 Atsarkin,42 and Wind et al.,11 and liquid-state experiments are discussed by Hausser et al.21 and Mueller–Warmuth et al.22 Although these reviews focus on the early literature of the field, they are well written and contain much information that is currently useful.
II. Polarizing Mechanisms in DNP Experiments
To understand the polarization transfer mechanisms operative in a DNP experiment, we consider the general static Hamiltonian for an electron-nuclear system of the form
| (1) |
where ω0S and ω0I are the electron and nuclear Larmor frequencies, respectively, Si and Ii are the electron and nuclear spin operators, is the isotropic (Fermi contact) hyperfine interaction between the electron and the nucleus, and is the anisotropic dipolar coupling. The hyperfine coupling HSI is given in a basis where the coefficients A and B denote the secular and pseudosecular hyperfine interactions. Note that this convention is the reverse of that commonly employed in ssNMR literature where I is usually H and S is 13C, 15N. The energy levels that result from this Hamiltonian are shown in Fig. 1(a).
Fig. 1.
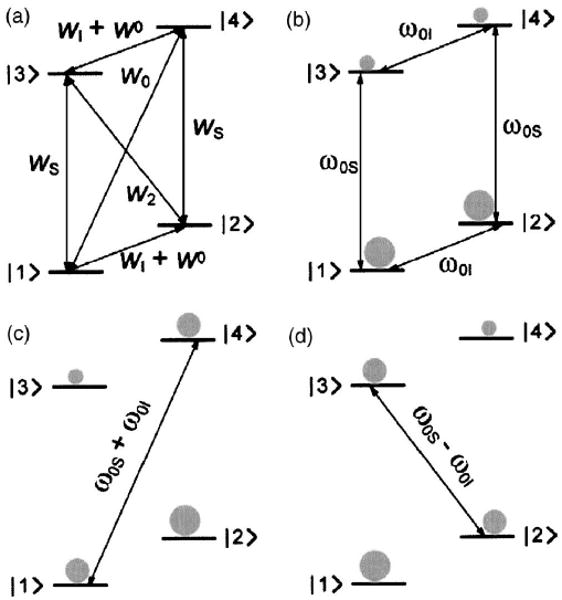
Energy level diagrams for the OE and SE. (a) Transition rates important for the OE. (b) Thermal equilibrium population for a two-level spin system. The spin population is depicted schematically in gray. [(c) and (d)] Saturation of the forbidden zero-quantum and double-quantum transitions leads to negative or positive enhancement through the SE.
Several excellent monographs covering the quantum mechanical treatment of electron-nuclear interactions under the influence of μw irradiation are available43–48 and the interested reader is referred to literature.
A. Continuous wave DNP polarizing schemes
There are presently four cw DNP mechanisms that have been successfully applied to solids and liquids—the OE,1 the SE,4,5,49 the CE,6,8,9 and TM.41 In particular, the OE has also been used extensively in studies of liquids. Most of the applications of these DNP mechanisms have been performed at low magnetic fields, and the theoretical treatments published in the literature reflect this fact. In this section we present a brief overview for each mechanism with an emphasis on high-field theory when available.
1. Overhauser effect
The OE is a DNP mechanism which requires the presence of relaxation processes that simultaneously flip an electron and a nuclear spin. In liquids, these relaxation processes are based on time-dependent dipolar and scalar interactions between the electrons and the nuclei, which are governed by molecular rotational and translational motion in the dipolar case or chemical exchange and/or fast relaxation of one of the spins in the scalar case.50 In solids, the OE requires the presence of mobile electrons such as the electrons in the conduction band of a metal2 one-dimensional (1D) organic conductors such as fluoranthene.51 The success of the OE depends on the condition ω0Sτ< 1 with τ the rotational correlation time of the paramagnetic species. This condition is difficult to satisfy when ω0S becomes large. Thus, the efficiency of the OE decreases at high magnetic fields, even though it likely does not go to zero.52 However, the OE is presently the only practical mechanism for the direct polarization of liquids. The following section outlines the main features of the OE, while a more detailed description can be found in the reviews of Hausser et al.21 and Mueller–Warmuth et al.22 and in the recent publication by Hoefer et al.52
The energy level diagram describing the transitions responsible for the OE is shown in Fig. 1(a). The rates of the zero- and double-quantum transitions are W0 and W2, respectively, while the rates for the EPR transitions are denoted as WS and the corresponding rate for the NMR transitions is WI. W0 is the nuclear relaxation rate in the absence of electrons. In the OE, the allowed EPR transitions are saturated, while the zero- and double-quantum transitions induce changes in the nuclear spin population resulting in the DNP effect, with the observed enhancement defined as ε = 〈IZ〉/〈Ieq〉. A rigorous treatment, which involves solving the rate equations for this system, leads to the following equation for the enhancement:21
| (2) |
with
| (3) |
| (4) |
| (5) |
The coupling parameter ρ depends on the relative contributions of the scalar and dipolar couplings and can range from −1.0 (pure scalar coupling) to 0.5 (pure dipolar coupling). Therefore, the maximum enhancement in a liquid sample, where the dipolar coupling governs the relaxation, is ∼330, whereas in 1D conductors an enhancement of 530 was observed,51 which is very close to the theoretical value of 660.
The couplings on the other hand depend on the electron Larmor frequency ω0S and the degree of molecular motion manifested in the correlation time τ. This dependence is plotted in Fig. 2, which illustrates that the process is inefficient at high magnetic fields. The experimental aspects of determining ρ are discussed in the articles of Hausser et al.,21 Armstrong and Han,53 Grucker et al.,54 and more recently by Hoefer et al.52 he leakage factor f describes the nuclear spin relaxation by the electron spins and can assume a value between 0 (no relaxation due to the electron-nuclear coupling) and 1 (no other relaxation mechanisms). When the electron transitions are saturated completely (〈SZ〉=0), the saturation factor s has a value of 1, although the saturation achieved depends on the number of hyperfine lines in the spectrum. This is important if polarizing agents based on nitroxide radicals are used. Due to the large electron-nitrogen hyperfine coupling (∼50 MHz), the EPR spectrum shows a well-resolved doublet (for 15N, ) or triplet (for 14N, I =1), as opposed to the trityl radical featuring only a single EPR line.
Fig. 2.
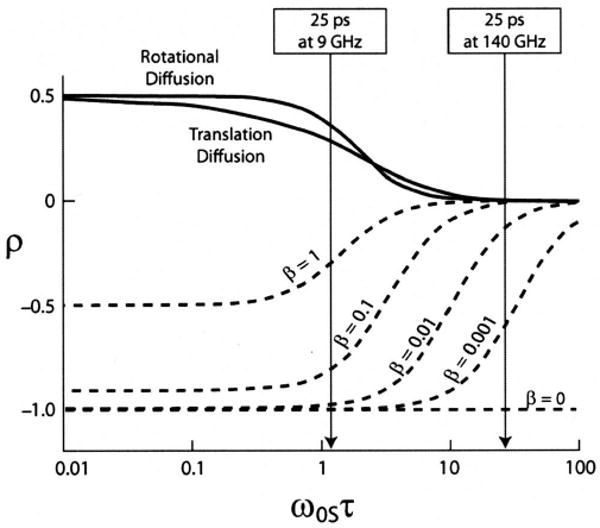
Dependence of the coupling parameter ρ on the electron Larmor frequencyω0S, the correlation time τ, and the factor β. The arrows point out the difference in efficiency at 9 and 140 GHz for τ=25 ps. Figure adapted from Loening et al. (Ref. 50).
The contribution of the scalar coupling can attenuate the enhancement if there is a concurrent time-dependent spin exchange. This can be described by an additional factor β, which can vary between 0 (no contribution of the scalar coupling) and 1 (large contribution of the scalar coupling). This dependence is shown in Fig. 2 for a number of different values of β.
2. Solid effect
The solid effect is a two-spin process, which relies on the mixing of states caused by the nonsecular component B of the hyperfine coupling.41 The Boltzmann population distribution at thermal equilibrium is shown in Fig. 1(b).
The pseudosecular term B in the Hamiltonian contains terms of the form SZI+ and SZI− that lead to a mixing of the states of the system. The new mixed states are |1′〉 = |1〉 + q|2〉, |2′〉=|2〉−q|1〉, |3′〉 = |3〉−q|4〉 and |4′〉 = |4〉 + q|3〉. The coefficient q can be calculated by first order perturbation theory and is given by11
| (6) |
where r, θ, and φ are the polar coordinates describing the electron-nuclear vector. Irradiation at ω0S+ω0I or ω0S−ω0I leads to zero-quantum [Fig. 1(c)] or double-quantum transitions [Fig. 1(d)], the probability of which is proportional to 4q2.41 Since q is proportional to ω0I, the transition probability and the enhancement scale with . This field dependence has thus far restricted the utility of the SE in high-field DNP experiments.
Another issues of a practical nature which affects the applicability of the SE is the fact that it requires a polarizing agent with a relatively narrow EPR spectrum. In particular, the homogeneous width δ and the inhomogeneous breadth Δ of the EPR spectrum have to be much smaller than ω0I to ensure that only one of the forbidden transitions is excited at a time. Simultaneous irradiation of both transitions leads to partial or complete cancellation of the polarization effect caused by each transition, a situation known as the differential solid effect (DSE).17
3. Cross effect/thermal mixing
The CE was first described in the 1960s by Kessenikh et al.,6,7 a few years later by Hwang and Hill8,9 and then by Wollan.10 Unlike the SE, this new mechanism was based on allowed transitions and involved the interaction of electron spin packets in an inhomogeneously broadened EPR line. Treatments of a similar effect, called thermal mixing, in a homogeneously broadened EPR line appeared a few years later. 11,55–57 The intermediate case of an EPR line broadened by both homogeneous and inhomohogeneous interactions was treated by Wollan.10 This early theoretical work considers the CE/TM mechanisms at low magnetic field only, and it is only recently that the CE and TM have been used for DNP at high magnetic fields.15,58–61 Although they are the most efficient cw irradiation mechanisms known today, the theoretical framework describing them is not yet complete.
At high magnetic fields, the CE is defined as a three-spin process, which involves the interaction between two dipolar coupled electrons with EPR frequencies ω0S1 (electron spin 1) and ω0S2 (electron spin 2) that satisfy the relation60
| (7) |
This is the dominant mechanism when the EPR line is inhomogeneously broadened by the g anisotropy and the electrons are weakly coupled via electronic cross relaxation.
The CE requires that the inhomogeneous breadth Δ of the EPR spectrum is larger than the nuclear Larmor frequency ω0I to satisfy the condition that there are two molecular orientations, resulting in two effective EPR resonance frequencies, separated by the correct frequency. At the same time, the homogeneous width must satisfy the condition δ < ω0I. This condition is achieved when biradicals are used as polarizing agents, where the presence of a dipolar coupling between the two electrons can dramatically improve the efficiency of the DNP effect. In contrast, the TM mechanism involves a homogeneously broadened EPR line arising from multiple dipolar coupled electrons. Here, the condition δ > ω0I is satisfied. This condition implies that at high magnetic fields the concentration of the polarizing agent must be high, which could unfortunately compromise the resolution in a MAS NMR experiment.
The thermal equilibrium spin population for a three-spin system is shown in Fig. 3(a). Note that there is no degeneracy present in the general case. However, when the appropriate polarizing agent is used, i.e., when there are two dipolar coupled electrons separated in frequency by ω0I, levels |4〉 and |5〉 or |6〉 and |3〉 become degenerated [Figs. 3(b) and 3(c)]. Irradiation of ω0S1 saturates the EPR transitions for one of the two dipolar coupled electrons, and the CE transitions (ωCE) ensure that there is a negative enhancement of the nuclear polarization [Fig. 3(b)]. Similarly, irradiation of the other EPR transition (ω0S2) leads to positive enhancement [Figure 3(c)].
Fig. 3.
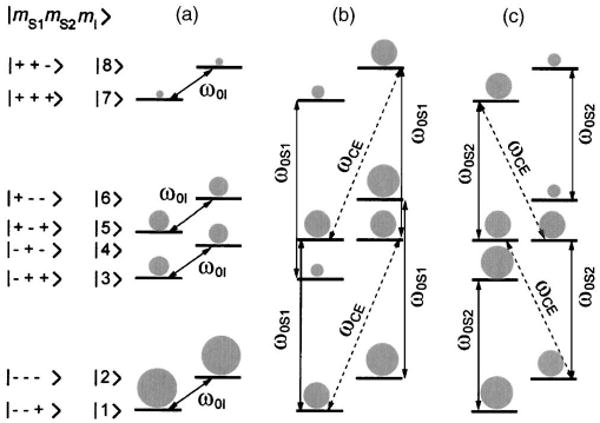
Population distribution at thermal equilibrium for a general three-spin system (a). Saturation of the allowed EPR transitions for one of the dipolar coupled electrons (ω0S1) leads to negative enhancement (b). Saturation of the transition corresponding to the second electron (ω0S2) leads to positive enhancement (c).
Since the linewidth of the EPR spectrum scales with the magnetic field, the degeneracy condition becomes more difficult to satisfy at higher magnetic fields. As a result, enhancements scale as . Despite this unfavorable field dependence, the CE/TM mechanisms have been used successfully to polarize biological solids at high magnetic fields.62,63
The TM effect is usually treated from a thermodynamic point of view, based on the concept of spin temperature.55 The electron-nuclear spin system can be described as a set of three interacting baths, each characterized by a spin temperature: the electron Zeeman system (EZS), the electron dipolar system (EDS), and the nuclear Zeeman system (NZS). Off resonance irradiation of the allowed EPR transition results in a large polarization gradient across the EPR line, which is equivalent to cooling the EDS. This bath is in thermal contact with the NZS, which is also cooled in an energy-conserving three-spin electron-electron-nuclear exchange process, leading to DNP enhancement. The TM process can be direct, i.e., the enhancement is caused by the direct coupling between the NZS and the EDS, or indirect, when both allowed and forbidden transitions are induced.11 However, compared to the CE, the TM effect is less efficient and results in smaller enhancements.
B. Pulsed DNP
In principle, pulsed DNP experiments based on coherent polarization transfer such as the Hartmann–Hahn cross polarization (HHCP) are more efficient and do not show a field dependence of the polarization transfer with increasing magnetic field strengths.64
Currently, HHCP is an essential pillar in the standard repertoire of techniques in ssNMR spectroscopy, where the large polarization of one nucleus (e.g., 1H) is transferred to another nucleus (e.g., 13C, 15N).65,66 This requires irradiating both nuclei with rf fields, and the rotating frame Hartmann–Hahn matching condition, given by
| (8) |
has to be satisfied. In Eq. (8), ω1I/S is the field strength of the applied rf field and I and S denote two different spins. In ssNMR experiments involving nuclei, the rf fields are sufficiently strong that they dominate all other interactions. This permits the excitation of the entire NMR spectrum and efficient spinlocking of both spin species. Therefore, the Hartman–Hahn condition [Eq. (8)] can be easily fulfilled.
In contrast, the g anisotropy and hyperfine interactions can lead to large inhomogeneous broadening of high-field EPR spectra, and their spectral breadth Δ can easily exceed several hundred megahertz. Furthermore, usually, the μw field strengths are one to two orders of magnitude smaller. As a result, the matching condition in a electron-nuclear cross-polarization (eNCP) experiment cannot be achieved by simply adjusting the μw (ω1e) and rf field strengths (ω1I). Thus, off resonance effects of the electron spin must be considered in analyzing the problem.
Another substantial difference with the HHCP scheme used in NMR is related to the relative concentrations of both spin types. NMR-CP experiments are typically performed by transferring polarization from a network of abundant high-γ spins I to dilute low-γ spins S. Thermodynamic arguments suggest67 that efficient CP transfer in a single thermal contact between the I and S spins is possible only if NI≫NS, with NI and NS the spin concentrations of the I and S spins, respectively. In this case, the signal enhancement in HHCP of the S spins is given by67
| (9) |
and the full ratio γI/γS can be transferred. However, in eNCP the concentration of unpaired electrons from the polarizing agent (the high-γ spins) is typically four orders of magnitude lower than the 1H concentration. This leads to an enhancement of ε < 1 and only a small fraction of the H polarization can be transferred in a single CP step. Fortunately, the much shorter electron relaxation time T1e (∼ms) allows for multiple CP contacts within the nuclear relaxation time T1n (∼s, pumping of polarization). This argument is also valid for cw DNP mechanisms such as the SE or TM/CE where a low concentration of electrons is used to polarize a much larger population of nuclear spins.
Pulsed DNP schemes can be divided into two groups: (1) those which involve both coherent μw pulses and cw irradiation and (2) schemes which are based purely on coherent μw pulses.
1. DNP based on pulsed and cw μw irradiation
Rotating frame DNP (RF-DNP)
The idea upon which rotating frame DNP is based originated with experiments performed by Bloembergen and Sorokin on a single crystal of CsBr. In this case, the transverse Cs magnetization was developed by cooling the rare 133Cs spins in the rotating frame with a 133Cs spin lock pulse, while simultaneously irradiating the abundant 79Br spin with a rf field of frequency ω=ωBr± γCsB1,Cs.68
Wind et al. applied this approach to an electron-nuclear system at low magnetic fields (B0 = 1.4 T, ω0S/2π=40 GHz).69,70 Subsequently, rotating frame DNP was shown to function at high magnetic fields (B0 =5 T, ω0S/2π=140 GHz).71
In rotating frame DNP experiments, CE or SE experiments are performed in the nuclear rotating frame, where the transition probabilities of forbidden transitions are greatly enhanced. This results in more efficient polarization transfers from the electron spin system to the nuclear spin system with short electronic/nuclear irradiation times. Furthermore, no Hartmann-Hahn matching condition is required, which is often difficult to achieve for electron-nuclear spin systems due to the large mismatch in gyromagnetic ratios.
Integrated solid effect (ISE)
As mentioned above, the SE becomes inefficient in the case δ≫ω0I, since simultaneous saturation of the forbidden transitions at ω0S± ω0I will cancel the polarization effect. However, if a forbidden EPR transition can be selectively inverted, prior to saturation of an allowed transition, the polarization effect can be recovered. This approach is known as the ISE, introduced by Henstra et al..17,18
ISE experiments can be performed by inversion of the forbidden transition using a selective π pulse, at a frequency ω0S ± ω0I, followed by irradiation on resonance. A second possibility is to perform a magnetic field sweep through the entire EPR line, while simultaneously applying cw microwave irradiation at a constant frequency ω0S. At sufficient μw power, each electron spin packet experiences an adiabatic fast passage, leading to an inversion of the electron spin polarization. Just before this inversion, the condition for the forbidden transition ω0S ± ω0I is fulfilled. This will be referred to as the adiabatic-ISE. To date, ISE experiments were performed at low magnetic fields (9 GHz) using either electrons to polarize 29Si nuclei or transferring the high polarization of a photoexcited triplet to surrounding protons.18,73,74 In Fig. 4 we show an ISE build up curve for the adiabatic-ISE. In this experiment the Si signal in p-type Si at 1.2 K is detected and a factor ∼20 larger enhancement is obtained in an adiabatic-ISE as opposed to the DSE.
Fig. 4.
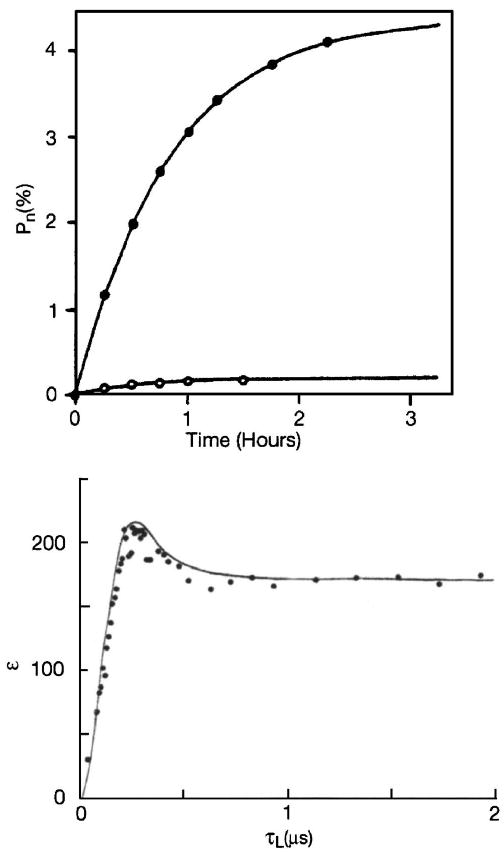
Top: Growth of the nuclear polarization (open circles—DSE, closed circles—ISE). Figure adapted from Henstra et al. (Ref. 17). Bottom: Enhancement of the nuclear spin polarization as a function of the spin locking time τL in a NOVEL experiment. Figure adapted from Henstra et al. (Ref. 72).
However, both the ISE and the adiabatic-ISE have certain limitations. In particular, the ISE requires high-power μw pulses to excite a large number of spin packets, and the appropriate μw sources are currently not available at high μw frequencies. In contrast, the adiabatic-ISE requires a fast magnetic field sweep. Adiabatic field sweeps are easy to perform at low magnetic fields but technically more demanding at high magnetic fields, since superconducting sweep coil couples strongly to the main and shim coils and distort the homogeneity of the magnetic field required for high-resolution spectroscopy. However, despite these current limitations, the ISE is an appealing approach because of the large enhancements that can be achieved.
2. DNP based on coherent pulses
Nuclear spin orientation via electron spin locking
In a NOVEL experiment, the electron magnetization is locked in the electron rotating frame via an electron spin locking sequence. If the field strength of the locking pulse is adjusted such that ω1S=ω0I, the rotating frame/lab-frame Hartmann-Hahn condition is fulfilled and polarization can be transferred to the nuclei in the presence of a dipolar coupling. NOVEL was independently introduced by Henstra et al. and Brunner et al.16,75 Figure 4 (bottom) shows the nuclear polarization buildup curve for a NOVEL experiment in which the electron polarization from pentacene guest molecules in a photoexcited triplet state is transferred to H of the naphthalene host crystal. An enhancement of 220 is achieved after a spin locking time τL<0.5 μs.
So far, NOVEL experiments have only been performed at 9 GHz μw frequencies, where high-power μw sources and amplifiers are available.72,74,76–78 At higher magnetic fields, and therefore higher nuclear Larmor frequencies, much higher μw field strengths are required. For example, at 5 T the 1H Larmor frequency is 211 MHz, which must be matched by ω1S. However, the current technology used in high-field EPR experiments, which is based on Gunn and impact ionization avalanche transit-time (IMPATT) diodes, produces μw field strengths of only a few megahertz. With the availability of high μw power at high frequencies (e.g., provided by extended interaction klystrons79 and gyrotron amplifiers), this method may become more generally useful since it provides a simple polarization scheme without the requirement of additional rf pulses.
Dressed-state solid effect
The Dressed State SolidEffect experiment, introduced by Weis et al.,19,80 is based on simultaneous, near resonant μw and rf irradiations. The selective excitation of dressed state transitions generates nuclear polarization in the nuclear laboratory frame on a time scale of tens of microseconds and polarization transfer to surrounding nuclei is possible even in the absence of nonsecular hyperfine coupling terms.
The DSSE is best understood in a doubly tilted rotating frame. Given the limited μw power at high frequencies, the allowed EPR transitions are in general no longer excited with the same μw field strength resulting in unequal effective fields and (see Fig. 5). As a result, the transformation into the electron (nuclear)-tilted frame is no longer possible with a single angle θS/I per spin type.
Fig. 5.
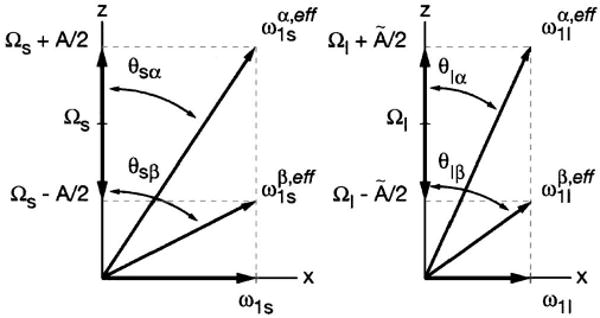
Illustration of the electron (S) and nuclear (I) spin effective fields. The effective fields belonging to the EPR and NMR transitions are no longer equal. Therefore, four effective fields are needed to accurately describe the two-spin system.
As Figure 5 shows, the conditions matched for CP include four effective fields. The general matching condition for the DSSE experiment is given by
| (10) |
with the resonant offsets given by ΩS and ΩI, the μw and rf field strengths given by ω1S and ω̃1I, and the hyperfine coupling constant given by A and Ã, respectively. While the electrons experience the full hyperfine coupling strength A, the nuclei are partially decoupled due to the μw irradiation resulting in a reduced hyperfine coupling Ã.81
As in NMR-CP, the polarization transfer is driven by the zero-quantum (S+I−+S−I+) or the double-quantum operator (S+I+ + S−I−). In the case of on resonance μw irradiation (ΩS=0) but arbitrary hyperfine coupling, the matching condition is given by
| (11) |
In this case, the width of the Hartmann–Hahn condition is determined by the distribution of hyperfine couplings and should allow for hyperfine selective polarization transfer. For |ΩI| ≈ ω1S, only nuclei with weak couplings A < ω1S (bulk nuclei) are expected to be polarized.
Figure 6 shows an example of the high-field DSSE. The eNCP condition was monitored indirectly through the electron spin echo intensity. Two peaks dispersed symmetrically around the H Larmor frequency ω0I are observed at all μw power levels. The positions of the satellites are μw power dependent and shift towards ω0I when ω1S is reduced. The position of the symmetric peaks is in full agreement with the matching condition for weakly coupled nuclei [Eq. (11) for A→0] and on resonance μw irradiation. Furthermore, a change in rf power does not result in a detectable shift or broadening of the CP matching condition. However, a decrease in signal intensity is observed upon reduction of the rf power indicating that the polarization transfer is faster for larger rf fields (Fig. 6, upper trace).
Fig. 6.
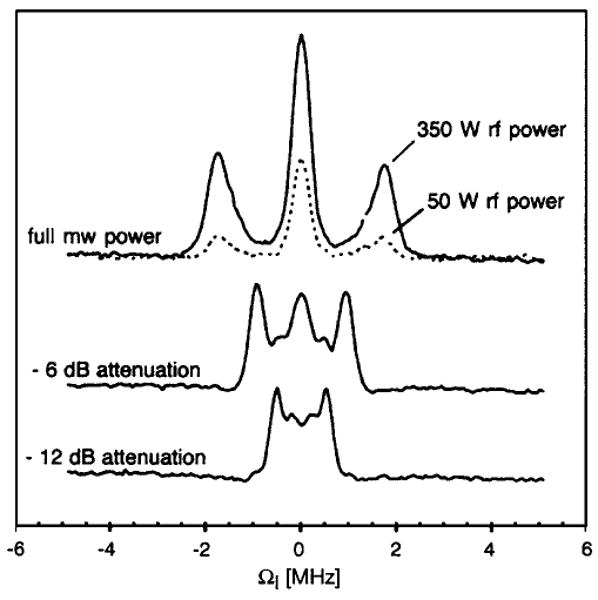
140 GHz eNCP experiment on perdeuterated BDPA for various settings of ω1S (ω1S/2π=1.75,0.9,0.5 MHz) and ω1I (ω1I/2π=100 kHz at 350 W). CP contact time was set to 3 μS. Figure adapted from Ref. 19.
III. Polarizing Agents
The mechanism governing the DNP experiment depends strongly on the choice of the polarizing agent, and is influenced by factors such as the width of the EPR spectrum, the radical solubility, the temperature dependence of relaxation times, etc. In addition, the polarizing agent can be either exogeneous (a mono- or biradical or metal ion added to the system) or, in principle, endogeneous (for example, a stable radical present in a protein). There are many examples of the use of exogeneous radicals as polarizing agents, and, to date, the optimal enhancements in MAS experiments have been achieved with biradicals dispersed in a glassy matrix.59,61 In contrast only photo-CIDNP experiments have utilized endogeneous polarizing agents in solids.82,83 In solution DNP, the polarizing agent can be dissolved in the solvent,50 attached to a support while the solution flows past it,24,84,85 or connected to a bulky particle such Si and suspended in solution.86
Five of the molecules that have been frequently used for polarizing agents in high-field DNP experiments are illustrated in Fig. 7. Two of these, trityl and bis-α, γ-diphenylene-β-phenyl-allyl (BDPA), have either threefold or approximate threefold symmetry and yield EPR spectra that are relatively narrow. This makes them suitable for SE DNP experiments. TEMPO is a nitroxide based radical, which leads to the TM mechanism at sufficiently high concentrations, whereas its biradical derivatives, bis-TEMPO-n-ethylene oxide (BTnE) and 1-(TEMPO-4-oxy)-3-(TEMPO-4-amino)-propan-2-ol (TOTAPOL) induce the CE DNP mechanism. These and similar nitroxide based free radicals/biradicals have been used for both liquid- and solid-state bio-DNP since they are stable, unreactive, and soluble in a wide variety of solvents. For example, TOTAPOL is soluble in glycerol/water solutions and is currently the polarizing agent of choice for experiments involving proteins. In addition to these g ∼ 2 species, very successful DNP experiments have been performed with paramagnetic chromium (V) based compounds, which were used in the preparation of polarized targets for nuclear scattering experiments.87
Fig. 7.
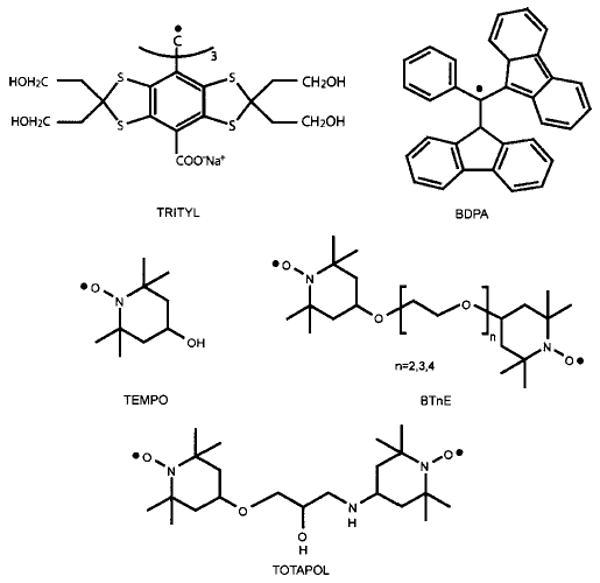
Chemical structures of three mono- and two biradical polarizing agents used in high-field DNP experiments.
A. Polarizing agents for the SE
The resolved SE requires that the homogeneous linewidth, δ of the radical is less than the nuclear Larmor frequency, ω0I. This requirement ensures that the zero- and double-quantum forbidden transitions are not excited simultaneously and there is no cancellation of the positive and negative enhancement. Currently, only two radicals satisfy this property at high magnetic fields, BDPA (Ref. 88) and trityl.89,90 BDPA has an inhomogeneous linewidth of Δ ∼ 20 MHz at 211 MHz 1H Larmor frequency and it was first used to study the SE in a polystyrene matrix.11,12,56,91 However, its utility for biological work is greatly limited by its insolubility in aqueous solutions. In contrast, the trityl radical, developed by Nycomed/Amersham was originally designed for low field OE imaging experiments.90,92 It is very soluble in aqueous media, and because of its symmetry and the absence of large 1H hyperfine couplings, it has a narrow EPR spectrum that supports the SE. Furthermore, trityl has been successfully used together with the HyperSense (Oxford Instruments, UK) to polarize aqueous solutions.25
Figure 8(a) shows the 140 GHz EPR spectrum and the field dependent enhancement profile of trityl (Δ = 42 MHz). The experimental data were obtained in a MAS experiment on 13C-urea dispersed in 2H6-DMSO/2H2O/H2O = 60:34:6 (w/w/w) at 90 K. The positive and negative enhancements correspond to the double- and zero-quantum SE transitions, which are clearly resolved. The maximum enhancement is ∼15, which is relatively small but consistent with data obtained from BDPA and expected from a SE mechanism at high magnetic fields.
Fig. 8.
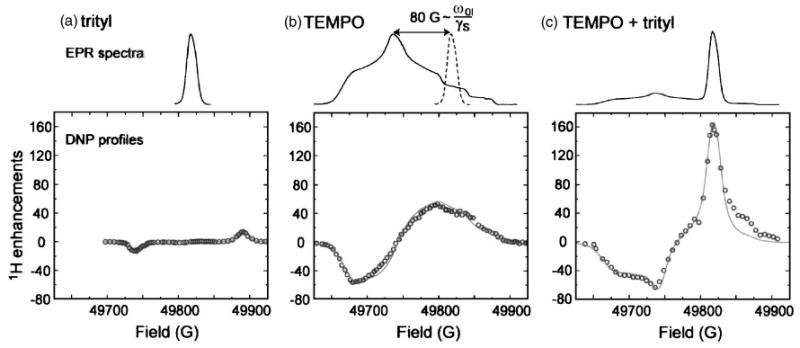
140 GHz EPR spectra and DNP field profiles for (a) trityl, (c) TEMPO, and (c) a mixture of trityl and TEMPO. The EPR spectra were recorded in 2H6-DMSO/2H2O 60:40 w/w (1 mM) at 20 K. The DNP samples were prepared in 2H6-DMSO/2H2O/H2O 60:34:6 w/w/w with a total radical concentration of 40 mM (90 K). The solid line represents a simulation of the experimental data. Figure taken from Hu et al. (Ref. 60).
B. Polarizing agents for TM and CE
The TM and CE mechanisms are the dominant mechanisms when the breadth of the EPR spectrum is large compared to the nuclear Larmor frequency (Δ > ω0I). If the EPR spectrum is homogeneously broadened, the TM governs the DNP process. The CE, on the other hand, is the dominant mechanism when the EPR spectrum is inhomogeneously broadened. Nitroxide based radicals/biradicals are very suitable for these mechanisms since their inhomogeneous EPR spectral width Δ is ∼600 MHz at a 1H Larmor frequency of 211 MHz.
Monomeric TEMPO at high concentrations exhibits partial homogeneous broadening in its EPR spectra,15 and DNP is thought to proceed partially through the TM mechanism. As illustrated in Fig. 8(b), the maximum and minimum enhancements observed are ∼ ± 50 at a magnetic field strength of 5 T (140 GHz) using a TEMPO concentration of ≥40 mM.60 At a magnetic field strength of 9 T (250 GHz), the enhancement factor decreases to ε ∼ 2013. However, above this concentration, the electron-nuclear broadening becomes significant and limits the resolution in the spectra.
In contrast, the CE is the dominant mechanism when the intermolecular electron coupling is small and the intramolecular electron-electron dipole coupling is large (∼22 MHz in the case of TOTAPOL). The biradical polarizing agents shown in Fig. 7 are typically used in CE DNP experiments at low concentrations (∼10 mM). Thus, the CE operates in the limit Δ > ω0I> δ, where strongly coupled electron spin packets are present that effectively communicate with one another and produce larger enhancements than those observed with monoradicals.
The first biradicals used for DNP belonged to the BTnE series and consisted of two TEMPO moieties connected through ehtylene glycol linkages.59 Depending on the length of the tether (n = 2, 3, or 4), the electron-electron dipolar coupling increases from ∼11 to ∼22 MHz, which is a significant improvement over the ∼0.3 MHz intermolecular dipolar coupling observed in a 10 mM solution of monomeric TEMPO. As a result, larger enhancements of ε = 175 ± 25 through the CE have been observed for the shortest member of the series (n = 2). The use of biradicals with stronger dipolar coupling and exhibiting greater enhancements also means that a lower concentration of the polarizing agent can be used, therefore reducing the residual paramagnetic broadening. Thus, while the enhancement obtained with BT2E increases by a factor of ∼4, the overall electron concentration can be reduced by a similar factor from 40 to 10 mM.
The field dependent enhancement profile for BT2E is shown in Fig. 9(a) and it is slightly asymmetric with a positive maximum (175) that is larger than the minimum (−150), which likely reflects the asymmetry in the EPR spectrum. Despite its success, the BTnE series is not sufficiently soluble in glycerol/water mixtures, which are the preferred medium for biological samples and they have been succeeded by TOTAPOL (see Fig. 7).61 This biradical consists of two TEMPO moieties tethered with a three-carbon chain, which leads to an average electron-electron dipolar coupling of ∼22 MHz. Although this biradical has a similar enhancement profile to BT2E [Fig. 9(a)], it offers the very important advantage of being soluble in aqueous media. This is achieved by the hydroxyl and secondary amine moieties on the tether and allows for its use in DNP experiments on biological systems.
Fig. 9.
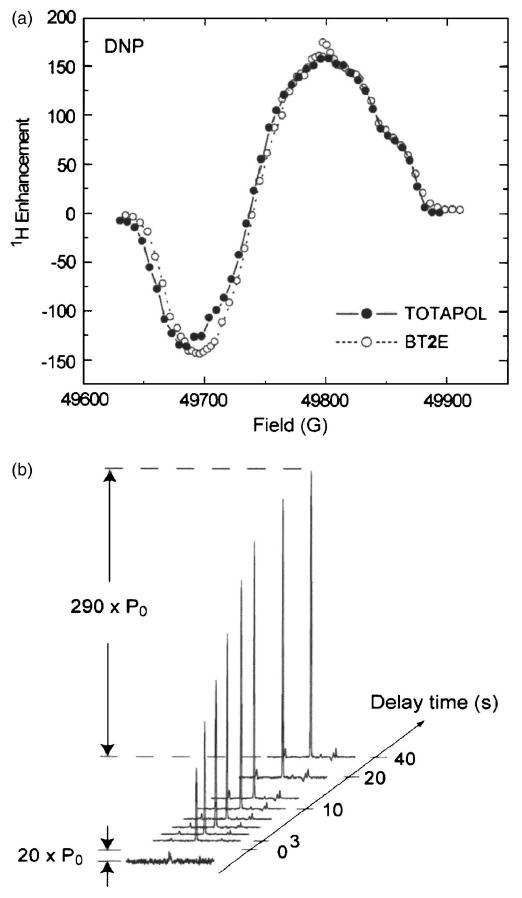
(a) Field profile of TOTAPOL and BT2E recorded at 5 T (90 K, 4 mm rotor). (b) Enhancement profile of 13C-urea (2M) as a function of the MW irradiation time in the presence of 3 mM TOTAPOL (2.5 mm rotor). Figures taken from Song et al. (Ref. 61).
The TOTAPOL tether, like the BT2E biradical tether, is conformationally flexible, even though the tether in TOTAPOL is shorter and more rigid (see Hu et al., this issue). However, the average orientation of the g tensors of the two electrons appears to be improved yielding an enhancement extrapolated to infinite power of ε∞ = 335 ± 65 while the corresponding number for BT2E is ε∞ = 260 ± 55.
Figure 9(b) shows another interesting experimental result, which is the polarization buildup curve as a function of the μw irradiation time for a sample in a 2.5 mm (as opposed to a 4 mm) rotor. The time constant characterizing the buildup curve is ∼9 s, approximately the nuclear T1 of the sample. Note, however, that the maximum enhancement achieved is 290, which is much larger than the enhancement observed in a 4 mm rotor (∼170). This is most likely due to improved μw penetration into the sample.
Finally, we would like to point out a few strategies to further improve polarizing agents available for DNP. The ideal polarizing agent for the CE should have an EPR spectrum consisting of two narrow sharp lines separated by ω0I in order to satisfy the CE matching condition.10,60 Although such a polarizing agent has not yet been reported, Hu et al. proposed to approximate this situation by utilizing a narrow line radical (e.g., trityl or BDPA) tethered to a broad line radical (e.g., TEMPO). This idea can be validated with a physical mixture of trityl and TEMPO,60 where the separation between the trityl line and the gyy component of TEMPO is 225 MHz at 5 T, which closely matches the 1H Larmor frequency of 211 MHz [Fig. 8(b)]. The observed enhancement is ∼160, an improvement of a factor of 4 over the enhancement achieved with TEMPO alone [Fig. 8(c)]. Thus, biradicals utilizing this approach could offer even larger enhancements than are presently observed.
IV. Instrumentation
The implementation of DNP experiments requires the addition of three pieces of instrumentation to existing NMR spectrometers—namely, a suitable μw source, a waveguide to transmit the microwaves from the source to the NMR probe, and a multiple frequency NMR probe (typically 1H, 13C, and 15N) with a waveguide to irradiate the sample. Furthermore, since DNP processes are most efficient at low temperatures, it is necessary to perform MAS at <90 K, and for dissolution or melting experiments, a means must be present to dissolve or melt the sample. Finally, it is necessary to irradiate the EPR spectrum at the position that produces the maximum enhancement. This is conveniently done with either a sweep coil on the magnet or, in principle, by tuning the microwave source. We now discuss each of these topics in more detail.
A. Microwave sources
The μw power requirement for DNP depends strongly on the nature of the experiment to be performed. In DNP experiments on static samples a high Q resonant μw cavity can be used since the sample size can be small compared to the wavelength of the radiation. However, the sizes of conventional MAS rotors (2.5–4.00 mm) used in experiments on biological systems are comparable to the wavelength of the μw (0.65–2.14 mm). Thus, placing a rotor and a rf coil in a cavity significantly lowers its Q. Furthermore, the μw field strength ω1S is directly related to the available μw power P and the quality factor Qμw by
| (12) |
Therefore, high-power μw sources are required for DNP experiments without a resonance structure.
Several excellent reviews are available describing μw sources, outlining the historical developments and giving future directions in μw technology.93–95 In general, two different types of μw sources can be distinguished: solid-state and vacuum electronic devices. Figure 10 provides an overview of high-frequency μw sources available currently. However, not all sources fulfill the requirements necessary for DNP or EPR applications. As we will see below, gyrotrons (cyclotron resonance masers) are high-frequency vacuum electronic devices that have many desirable features for EPR and DNP experiments.
Fig. 10.
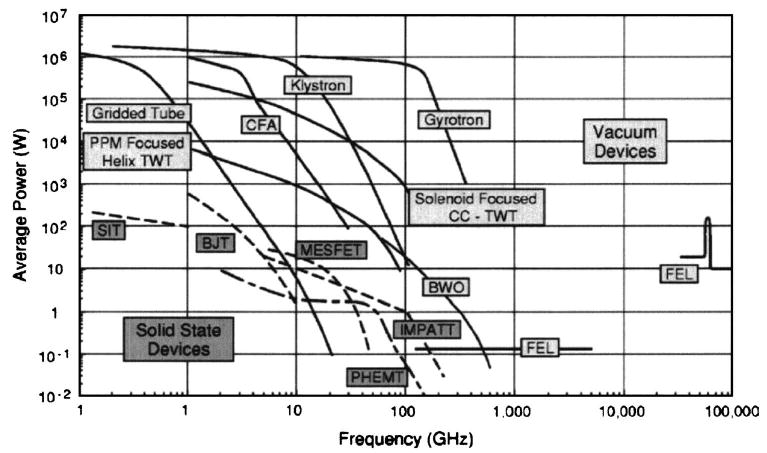
Present state of vacuum electronic devices in terms of the ability of multiple devices types to generate average power at a certain frequency. Figure taken from Granatstein et al. (Ref. 93).
1. Solid-state and other low power devices
Currently, the majority of high-frequency μw sources used in cw, low-power pulsed EPR spectrometers, and in some DNP experiments utilizing μw cavities, are solid-state devices. Typical examples include phase-locked Gunn diodes, IMPATT diodes or CO2 pumped far infrared (FIR) lasers. Phase-locked Gunn diodes provide stable μw irradiation of several tens of milliwatts. However, at higher μw frequencies (>200 GHz), the available output power drops dramatically (e.g., ∼5 mW at 400 GHz, Ref. 96) and IMPATT devices assume a more important role as μw oscillators and amplifiers. They can operate in either cw or pulsed modes and deliver powers of up to 500 mW at 140 GHz. Despite their substantial complexity of operation, CO2 pumped FIR lasers have been used as low-power sources at series of discrete frequencies in the range of 160 GHz–3 THz.96,97 However, DNP/MAS experiments that do not employ a resonant μw structure require several watts of μw power that is available from vacuum electronic devices. Therefore, solid-state sources are not applicable.
2. Vacuum electronic devices
General
Vacuum electronic devices are μw sources that are able to generate high μw power at high frequencies. Extended interaction oscillators (EIOs), extended interaction klystrons (EIKs), backward wave oscillators (BWOs), orotrons, and gyrotrons are several examples; some of them have been used successfully in EPR spectroscopy. EIOs and EIKs have been developed as remarkably powerful sources operating at 95 and 140 GHz in cw and pulsed experiments. They are capable of delivering up to 1.2 kW peak power with pulse widths from a few nanoseconds to several microseconds.79,98
BWOs (or carcinotrons) are μw devices operating in both cw and pulsed modes. At 100 GHz, they can generate more than 10 W in cw mode, and several kilowatts of pulsed power. However, the output power shows a strong frequency dependence and requires highly stabilized high-voltage power supplies. Furthermore, at higher frequencies, the available power drops dramatically93 (see Fig. 10).
Orotrons are nonrelativistic free-electron lasers, where the μw radiation is created when the electron beam passes close to the surface of a metallic grating and moves perpendicular to its periodic rulings. The incoherent and weak μw beam is transformed into coherent and intense radiation in a Fabry–Pérot resonator, and power levels up to 60 mW were achieved at a μw frequency of 360 GHz.99
The vacuum electronic devices described above are also called “slow-wave” devices. In particular, the μw irradiation is created by modulating an electron beam that passes close to a fragile interaction structure, whose size is on the order of the μw wavelength. As the power and frequency increase, so does the power density, and the lifetime of the slow-wave structure decreases since the interaction structure is easily destroyed. This significantly limits the lifetime of the slow-wave structure especially at high-power levels. Although there continue to be advances in technology, the current power levels and lifetimes of these devices limits their use to lower μw frequencies.
Gyrotons
Gyrotron oscillators and amplifiers are “fast-wave” devices that rely on a resonance phenomenon between the modes of an interaction structure and the electron beam in a magnetic field. The resonator can be overmoded and, as such, can have physical dimensions, which are much larger than the operating wavelength. This permits high peak and average power operation even at elevated frequencies without the risk of damage to the interaction structure.100
In the frequency range of interest for DNP/NMR (presently 200–900 MHz for 1H, corresponding to 140–590 GHz for electrons), the gyrotron is the only device demonstrated capable of producing adequate power levels. There are now a number of excellent introductory books on gyrotron technology101–105 as well as several excellent review articles.100,106
A gyrotron is a vacuum electronic device that operates in a static magnetic field. It functions as an electron cyclotron resonance maser that emits coherent radiation near the relativistic electron cyclotron frequency, or its harmonics given by
| (13) |
with B0 the magnetic field strength, e the electron charge, s the harmonics of the operational mode (integer), m the electron mass, c the speed of light, and γ′ a relativistic mass factor (vide infra) given by
| (14) |
with ν the velocity of the electron. When other experimental constraints are satisfied, the μw frequency ωc is primarily determined by the strength of the magnetic field.
The physical layout of a gyrotron oscillator is shown in Fig. 11 (left). The compact design of the tube makes it compatible with operation in close proximity to a NMR spectrometer. Electrons, which are emitted from a cathode located in the electron gun [Fig. 11(1)], are accelerated by a high voltage (10–30 kV) applied between the anode and the cathode and in the presence of an external magnetic field they start to gyrate (rotate) about the magnetic field lines. While they move from the lower magnetic field region at the gun to the high-field region in the center of the magnet along the magnetic field lines, they increase their rotational energy. In the cavity region [Fig. 11(5)], a phenomenon referred to as bunching leads to the generation of microwaves (see Ref. 62 and references therein). The radiation excites a mode of the cavity, causing stimulated emission, which leads to high efficiency emission and output power. The microwaves are then extracted by a step-cut mode converter [Fig. 11(6)] through a cross bore in the magnet dewar and directed to the NMR sample through a waveguide. Finally, the remaining electron beam is collected in a water-cooled collector [Fig. 11(9)].
Fig. 11.

Left: Schematic of a gyrotron tube indicating its key components. Figure taken from Hornstein et al. (Ref. 14). Middle and right: Photographs of the 460 GHz gyrotron.
Currently, two gyrotrons are operating in DNP experiments at 140 GHz (Refs. 12 and 107) and 250 GHz (Refs. 13 and 62) and the application that they have enabled will be discussed below. A third device operating at 460 GHz (corresponding to 700 MHz for 1H) is already operational14,108 and its incorporation into a DNP experiment is under way. Figure 11 shows a photograph of the 460 GHz gyrotron.
B. Microwave waveguides
Low-loss μw transmission lines are crucial for an efficient delivery of the μw irradiation. Unfortunately, fundamental waveguides become very inefficient with increasing μw frequencies (WR-08, >8 dB / m at 140 GHz). To minimize the loss, the μw irradiation can be delivered in an oversized waveguide (e.g., K band, WR-42, 0.7 dB / m at 140 GHz). Near the NMR coil (or cavity), the oversized waveguide is then tapered down to the fundamental waveguide.109 However, the overall loss will still be in the range of several decibels.
With a corrugated waveguide, operating in the circular HE11 mode, which has almost negligible Ohmic losses, the efficiency can be dramatically increased.110 No additional mode converters are necessary, since the gyrotron can be designed to deliver this mode. Corrugated waveguide transmission lines are well-established and currently used in high-frequency EPR as well as in DNP applications.62,111,112 For example, in the 250 GHz DNP spectrometer, the overall loss of the transmission line is as low as 0.7 dB.62 Furthermore, directional couplers are available to monitor the transmitted and reflected μw power.112
C. Probes used for DNP experiments
As mentioned above, DNP experiments on static samples and in some liquid-state experiments can utilize small μw cavities in combination with low-power sources. In contrast, DNP probes used for ssNMR MAS experiments cannot incorporate a μw cavity, since the rotor containing the sample, and the NMR coil spoil the Q of any cavity.
1. Probes with a resonant structure
In liquid-state DNP experiments, the sample size is kept very small to avoid excessive μw absorption by the solvent, especially if the dielectric constant of the solvent is high (e.g., water). At low μw frequencies (e.g., 9 GHz) polarization in a DNP experiment can be performed in a standard TE102 rectangular EPR cavity.24,84 At high frequencies, the cylindrical TE011 cavity first proposed by Grinberg et al.113 is commonly used in EPR experiments. However, the reduced size of the cylindrical resonator (e.g., 2.8 mm inner diameter at 140 GHz) does not allow a NMR rf coil to be mounted inside the resonator. An external rf coil in combination with a slotted cavity, commonly used in high-frequency electron nuclear double resonance (ENDOR),109,114 suffers from a dramatic loss of rf magnetic field strength at the sample position. A more suitable double-resonance design for DNP and ENDOR experiments is shown in Fig. 12 (left side).115 It was originally proposed by Hyde116 and later used for ENDOR experiments at X-band frequencies.117
Fig. 12.
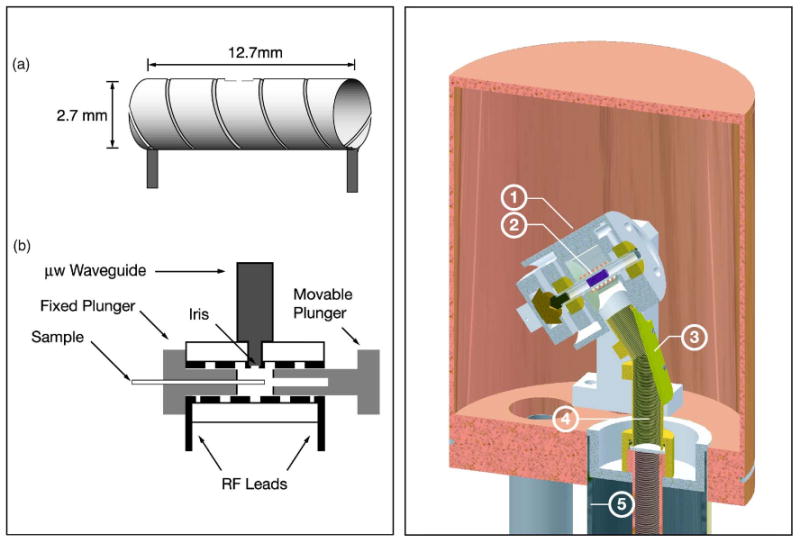
(Color online) Layout of DNP probes. Left: Probe used for DNP in liquids and solids. Figure adapted from Weis et al. (Ref. 115). Right: Low temperature MAS probe for ssNMR DNP experiments. (1) Stator, (2) Sample, (3) Miter bend, (4) Inner conductor, and (5) Outer conductor. Figure adapted from Barnes et al. (Ref. 118).
The metal wall, which serves as a cylindrical cavity operating in the TE011 mode, doubles as the cavity and rf coil. A fixed and a movable plunger with metal plates complete the cavity. Currently, this cavity operates at 140 GHz (Ref. 115) and features a double-tuned rf circuit for irradiation at 1H and 13C frequencies allowing rf field strengths of 100 and 50 kHz, respectively. The μw field strength ω1S is 2.5 MHz at 15 mW μw power. Using this cavity enhancement factors of 400 were achieved in a DNP experiment at low temperatures (20 K).115 The cavity can also be used in liquid DNP experiments, since the electric field at the sample position is minimized.
2. Probes without a resonant structure
Historically, two different designs were used in DNP/MAS experiments. In the design featured by Schaefer and McKay, operating at 40 GHz, the μw irradiation is applied along the rotor axis.91 The same design was later used at 140 GHz.109 However, the μw irradiation is highly attenuated parallel to the sample length, since the length of the rotor is a few centimeters. In current designs, the microwave irradiation occurs perpendicular to the rotor axis.119 A slightly modified design operating at 60 GHz was recently introduced by Cho et al.,120 while in the design of Wind et al. operating at 40 GHz, a horn-antenna/reflector combination was used.119 At higher frequencies (> 140 GHz), the microwaves are usually launched between the turns of the NMR coil due to space restrictions. Figure 12 (right) gives a schematic overview of a DNP probe for MAS-NMR experiments. A saphire rotor containing the sample (shown in purple) resides inside the MAS stator. The inner conductor of the transmission line doubles as a corrugated waveguide, and connects to a mitered, metal-mirrored assembly that terminates perpendicular to the rotor axis 1 cm from the sample. Since the μw are delivered as a Gaussian beam in a corrugated waveguide, the beam can be focused by carefully adjusting the miter bend on top of the probe to achieve optimum enhancements.
One major challenge of the rf circuit of a low temperature probe is to maintain the ability to tune the resonant circuit even at low temperatures. This can be done by locating all variable tuning elements outside the probe at room temperatures and delivering the rf power using a transmission line.121
Low temperature spinning is accomplished by using cold drive and bearing gas, and the excellent thermal conductivity of sapphire at low temperatures insures a uniform sample temperature. The gas is cooled in a heat exchanger and the cold gas is delivered by cryogenic transfer lines.122 Using nitrogen for spinning, temperatures as low as ∼85 K are achieved. To reach temperatures as low as ∼15 K, helium gas is used.58,123,124
D. Superconducting magnets
For DNP experiments, the μw frequency or magnetic field strength is adjusted to maximize the enhancement. Since gyrotrons and other high-frequency μw devices operate at a fixed frequency, it is necessary to sweep the magnetic field. Furthermore, if the field profile of a polarizing agent needs to be recorded, the system should be equipped with a field-lock system.125 In such a system, the NMR signal of a small liquid sample (e.g., water) is monitored, allowing the field determination to very high accuracy.
V. Applications
After the initial experiments demonstrating the ability to enhance nuclear spin polarization, DNP in solids largely became the province of high-energy physics.40 Thus, for many years, the main application of the technique was in experiments performed at low temperatures aimed at producing polarized targets used to investigate the spin dependence of nuclear forces in scattering experiments. These experiments continue today.
A different application of DNP was stimulated by the introduction of Hartmann–Hahn cross polarization to high-resolution ssNMR.64,65 In this case DNP was used to enhance the polarization of 19F in CaF2, and this polarization was subsequently transferred to the rare 43Ca spins for observation.126 This experiment was the predecessor to much of the research currently in progress.
In the 1980s DNP and MAS were integrated into experiments designed to enhance the 13C signal in the studies of several samples including polymers, carbonaceous materials, diamond, etc.11,91,127 However, for reasons outlined above, essentially all of these applications were limited to low frequencies and mostly to experiments that demonstrated the ability to enhance signal-to-noise ratio. Here, we focus on some more recent applications to biological solids, liquids, and pulsed DNP.
A. DNP applications to biological solids
Hall et al.58 reported the first successful application of DNP to enhance ssNMR MAS spectra of biological macromolecules. In this experiment, a sample of 15N-Ala-labeled T4 lysozyme was polarized and the DNP enhanced 15N solid-state CP/MAS spectra was recorded. An enhancement of ∼50 was achieved for the alanine amide 15N signals. The experiments were performed in a frozen, glassy, aqueous solution of glycerol/water (60/40, w/w) using 4-amino-TEMPO as the polarizing agent. Aqueous glycerol solutions form a glass upon cooling and have been successfully used as cryoprotectants for biological samples at low temperatures.128 Thereafter, the method was applied to record 1D spectra of other systems of biological interest—filamentous bacteriophages, purple membranes,129 and membrane and soluble proteins.130
Since the gyrotron provides a stable high-power source for μw irradiation, it is possible to integrate high-field DNP into state-of-the-art multidimensional ssNMR MAS experiments to obtain enhanced sensitivity. This was first demonstrated with two-dimensional (2D) high-field DNP enhanced correlation spectra of [U – 13C, 15N] proline at 140 GHz (211 MHz for 1H) (Ref. 131) and subsequently at 250 GHz (380 MHz for 1H).13
More recent applications have focused on the areas of amyloid and membrane protein spectroscopy where ssNMR MAS experiments are the method of choice for structural studies. As illustrated in Fig. 13, high-field DNP can also be used to enhance NMR spectra of amyloid-forming peptides.63 The samples consist of nanocrystals of the amyloid-forming peptide GNNQQNY7–13, derived from the yeast prion protein Sup35p, dispersed in a glycerol/water matrix containing the biradical polarizing agent TOTAPOL. The crystals have an average width of 100–200 nm, and their known crystal structure132,133 suggests that the size of the biradical precludes its penetration into the crystal lattice. This was confirmed by the observation that 1D 15N spectra of the nanocrystals did not broaden even in the presence of high concentrations of polarizing agent (up to 50 mM TOTAPOL, corresponding to 100 mM electrons). Thus, polarization from the glycerol/water solvent diffuses over the dimensions of the crystal and results in an enhancement of the 13C signals by a factor of ∼120. The large signal enhancement facilitated the acquisition of a 2D 13C – 13C homonuclear correlation spectrum, an experiment that would have been impossible in the absence of DNP. The spectrum, shown in Fig. 13, was acquired with 6 ms spin diffusion time and the total acquisition time was 20 min. The linewidths of the peaks are likely governed by 13C – 13C J couplings and n = 0 rotational resonance effects.134
Fig. 13.
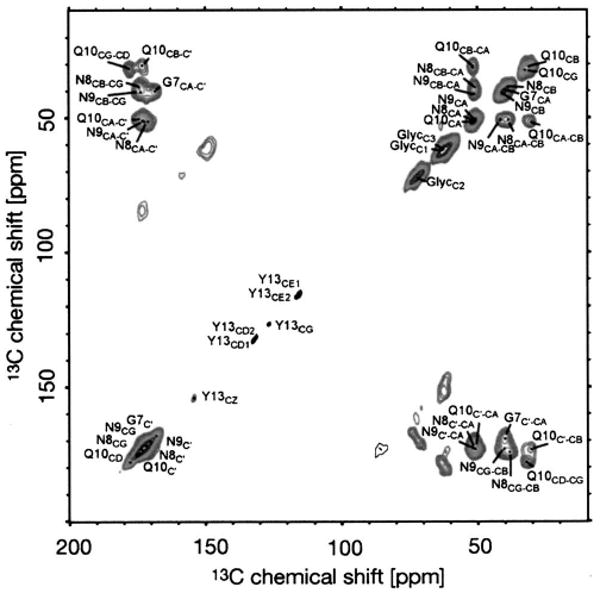
DNP-enhanced 13C – 13C DARR/RAD correlation spectrum of [20% U – 13C, 15N-GNNQ]QNY nanocrystals. Figure adapted from van der Wel et al. (Ref. 63).
More recently, 250 GHz DNP was used to study bacteriorhodopsin (bR), a 248-residue integral membrane protein that functions as a light-driven ion pump.62 The protein encapsulates an all-trans chromophore, which is attached to the protein via a Schiff base linkage lys216. To study a particular photocycle intermediate, the sample is irradiated with the optimal wavelength of light at a suitable low temperature. In the next step, the sample is cooled further to ∼ 90 K where the attenuated electronic and nuclear spin-lattice relaxation renders the polarization transfer more efficient.
Since the instrumentation is very stable, 2D spectra can be recorded over a period of several days. A typical 2D 15N/13C correlation spectrum illustrating this point is shown in Fig. 14. Because of the excellent signal-to-noise ratios, it was possible to observe cross peaks between the 15N Schiff base and C-15, C-14, C-13, and C-20 on the retinal and with Cε and Cδ of lys216. The spectrum in Fig. 14 was recorded in approximately 12 h and allowed the assignment of most retinal resonances in a single experiment. This would not have been possible without the factor of ∼90 signal enhancement. Further experiments on the other photocycle intermediates of bR will be reported elsewhere.
Fig. 14.
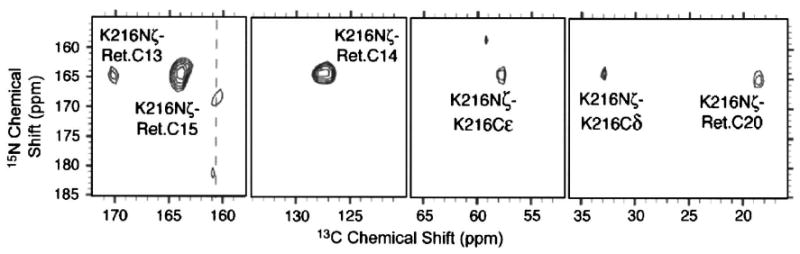
Schiff base region of a typical 2D Lys-Nζ-Ret.-C15-CX correlation spectrum (DAR/RAAD) of [U – 13C, 15N]-bR in the light adapted state (bR568). Multiple chemical shift assignments result from a single experiment. ωr/2π = 7 kHz. Figure taken from Bajaj et al. (Ref. 62).
B. DNP in liquid phase
1. Direct polarization
To date, the OE is the only mechanism available to directly polarize liquids. Since the OE becomes less efficient at higher magnetic field, one strategy to perform DNP on liquid samples is to polarize at low magnetic fields and perform the NMR experiment at high magnetic fields. To transfer the sample between high and low magnetic fields a flow system can be used.
In the late 1980s, the first flow experiments were carried out by Dorn and co-workers. Initially, the polarization and detection was performed in the same magnet, at a frequency of 9.3 GHz (0.35 T, 14 MHz for 1H) and enhancement factors for 1H of up to ε = −90 were obtained.23,84 Later, the detection was performed at a magnetic field of 4.7 T (200 MHz for 1H) in a separate magnet85 yielding enhancement factors of ε = −30. In these experiments, the polarizing agent was either diluted in the sample (liquid-liquid intermolecular transfer, L2IT) or immobilized on silica gel (solid-liquid intermolecular transfer, SLIT). The same technique was shown to yield large enhancements for 13C (Refs. 135 and 136) and 15N (Ref. 137) nuclei.
Recently, McCarney et al. used the SLIT experiment to polarize water for possible use in MRI experiments.24 These experiments showed that the hyperfine coupling of the nitroxide has to be taken into account for an accurate description of the Overhauser effect.53
2. Temperature jump experiments
A different strategy to obtain DNP enhanced spectra of molecules in solution is to perform the polarization at low temperatures in the frozen, solid state and then quickly melt the sample and record the liquid-state NMR spectrum. In this case, the enhancement, defined as ε†, is determined by the intensity of the DNP signal ε at the irradiation temperature (Tμw) relative to the signal due to the Boltzmann polarization recorded at 300 K (Tobs). Specifically since the polarization is generated at low temperature, an additional factor of Tobs/Tμw has to be included in the calculation. Thus, ε† is given by
| (15) |
Currently, there are two experimental protocols that employ this approach—the “dissolution” experiment and the in situ temperature jump (TJ) experiment.
Dissolution experiment
The dissolution experiment was introduced by Ardenkjaer–Larsen et al.25 In this experiment, direct polarization of 13C or 15N is performed at 1.2 K at a μw frequency of 94 GHz using a 200 mW Gunn diode source. Furthermore, the EPR signal as well as relaxation data can be obtained by longitudinal detection138 in the apparatus used for dissolution experiments.
Because of the low temperature, the low μw power, the long T1e of the polarizing agent, and the fact that 13C is polarized directly, the polarization time is very long (≥80 min). Subsequently, the frozen polarized sample is dissolved in superheated water. The sample is then shuttled to a NMR spectrometer, where the liquid-state NMR experiment is recorded. Enhancements of ε = 163 (ε† = 44 400) for 13C and ε = 86 (ε† = 23 500) for 15N are reported for small molecules in a 1D experiment. Recently, the dissolution experiment was combinded with single-scan 2D NMR methods139 to record 2D NMR spectra of liquid within ∼0.1 s.140
Although the dissolution experiment yields large values of ε†, this arises mostly from the Boltzmann temperature factor. In addition, the experiment has other limitations. First, the polarized sample is diluted by a factor of ∼150 when melted. Second, since a direct polarization is performed rather than via the 1H's, it requires long periods. Third, because of the requirement of shuttling to a second magnet, it is not possible to rapidly repolarize the sample for further signal averaging and there is an inherent loss in the sample transfer. Because of the inability to recycle the experiment, many multidimensional liquid experiments are more difficult to implement, especially when the spectra are wide and the gradients required for single-scan experiments are large. However, the method has considerable potential as an analytical tool to study small molecules and may be useful in imaging experiments.
In situ TJ DNP experiment
The in situ TJ experiment introduced by Joo et al.26 is considerably different from the dissolution experiment. Here, the 1H nuclei of the sample are polarized at low temperatures (90 K) using low concentrations of biradical polarizing agents.61 The 1H polarization is then transferred to the low-γ spins in a typical CP step and the sample is melted with an infrared laser pulse. The enhanced signal is observed in the presence of 1H decoupling. This scheme and the respective pulse sequence is summarized in Fig. 15(a). Currently, this method yields enhancements on the order of ε = 133 (ε† = 400) for small molecules such as urea. The entire cycle can be repeated in situ and signal averaging can be performed as is customary in contemporary NMR experiments. This is demonstrated in Fig. 15(d), where a series of 16 spectra acquired over a period of 40 min from a sample of 13C-proline is shown. It illustrates that the instrumentation is sufficiently stable to reproduce the intensities in the spectra to 5%.
Fig. 15.
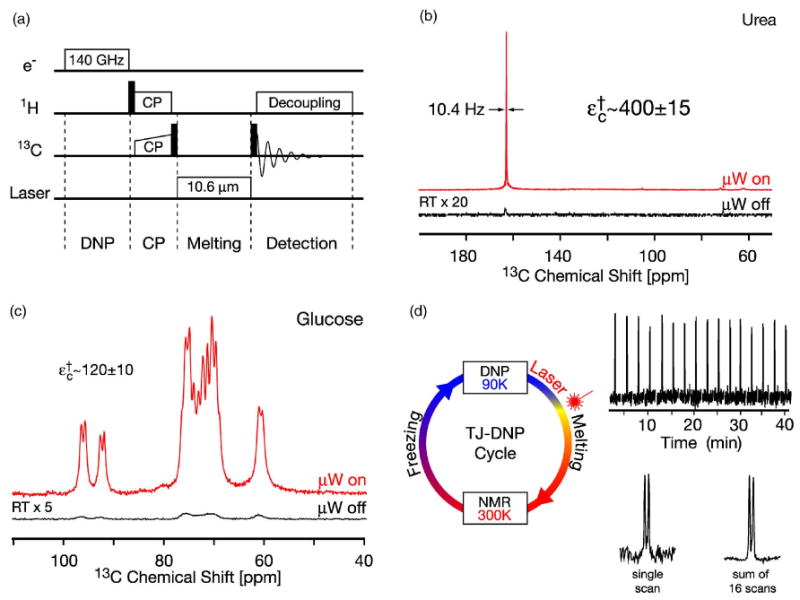
(Color online) In situ TJ-DNP experiment. (a) Pulse sequence. (b) 13C-TJ-DNP NMR spectra of 13C-urea in 50% 2H6-DMSO and 50% water (2H2O/H2O=4/1). (c) 13C-TJ-DNP NMR spectra of [U – 13C6, 2H7]-glucose in H2O. D: 16 spectra of the CO resonance in [U – 13C]-L-proline resulting from a series of TJ-DNP experiments. (Below) average of the 16 spectra giving an improved signal-to-noise ratio. Samples contained 3–5 mM TOTAPOL biradical polarizing agent corresponding to 6–10 mM electrons. The TJ-DNP spectra (the top traces in each figure) were recorded with a single scan, while the RT spectra were recorded with 256 (a) and 512 scans (b).
C. Pulsed DNP
Apart from the pioneering work by Henstra et al. and Brunner et al., there have been few publications using the ISE or NOVEL reported. However, recently, it was shown that NOVEL can be used to enhance the 13C NMR signal in diamonds.76 This was done at 9 GHz, corresponding to a 13C Larmor frequency of 3.5 MHz. It was shown that the polarization rate of the 13C nuclei in natural diamond is severely limited by the spin-diffusion bottleneck created by the slow rate at which flip-flop transitions occur among the diluted 13C spins surrounding a paramagnetic impurity. Furthermore, the concentration of the paramagnetic impurities plays a dominant role in the polarization rate. A comparison of the 13C polarization rates for the SE and NOVEL shows that, for the same microwave power, the polarization rates are comparable at higher impurity concentrations. However, at low impurity concentrations, the SE results in faster polarization of the 13C nuclei.
VI. Future Perspectives
Although high-field DNP has made significant progress towards evolving into a standard technique to study biological macromolecules, it remains a scientific field with a large potential for new developments both in theory and instrumentation.
Currently the water-soluble biradical TOTAPOL remains the only polarizing agent that can be used in high-field DNP to study biological systems. Although the enhancement factors are already very large, there is ample room for improvements, together with a deeper understanding of the DNP processes at high magnetic fields. For example, the synthesis of biradicals with more rigid tethers or radicals with narrower lines could produce even higher enhancements. Furthermore, a large number of biological macromolecules (e.g., electron transport proteins) have intrinsic paramagnetic centers, which have yet to be exploited as potential polarizing agents. In addition, a deeper understanding of the DNP processes at high magnetic fields for these species would be necessary.
The last two decades witnessed significant progress in microwave technology. Many new solid-state sources operating at high microwave frequencies are available with increasing output power and improvements in gyrotron technology will lead to more compact and practical designs.
Liquid DNP will benefit with new cavity designs, which minimize electric field heating and maximize μw penetration. These innovations will also have a large impact on high-field EPR and ENDOR spectroscopy.
Currently solid-state DNP experiments are performed at 90 K because of the experimental convenience of using liquid nitrogen as the cooling gas. However, lowering the temperature can further increase the efficiency of the polarization processes. MAS/NMR experiments at helium temperatures have been reported.123,124 and their incorporation into DNP experiments is in progress.
Finally, since classical cw DNP schemes suffer from an inverse field dependence, the implementation of DNP at higher magnetic fields should stimulate the development of new polarizing mechanisms potentially based on a coherent polarization transfer. In addition to these theoretical developments, time domain experiments will require μw amplifiers such as gyroamplifiers operating at frequencies of 140 GHz and above to provide coherent high-power microwave pulses. With high μw power available, experiments such as the ISE, NOVEL, and DSSE will become possible or more efficient at high magnetic fields.
Acknowledgments
This research was supported by the National Institutes of Health through Grant Nos. EB002084, EB002026, EB009866, EB001965, and EB001035. T.M. acknowledges receipt of a postdoctoral fellowship of the Deutsche Forschungsgemeinschaft. The authors are grateful to Andrew B. Casey and Marvin J. Bayro for careful proofreading the manuscript. We thank Alexander Barnes for supplying Fig. 12 (right side).
References
- 1.Overhauser AW. Phys Rev. 1953;92:411. [Google Scholar]
- 2.Carver TR, Slichter CP. Phys Rev. 1953;92:212. [Google Scholar]
- 3.Carver TR, Slichter CP. Phys Rev. 1956;102:975. [Google Scholar]
- 4.Abragam A, Proctor WG, Hebd CR. Seances Acad Sci. 1958;246:2253. [Google Scholar]
- 5.Erb E, Motchane JL, Uebersfeld J, Hebd CR. Seances Acad Sci. 1958;246:2121. [Google Scholar]
- 6.Kessenikh AV, Lushchikov VI, Manenkov AA, Taran YV. Sov Phys Solid State. 1963;5:321. [Google Scholar]
- 7.Kessenikh AV, Manenkov AA, Pyatnitskii GI. Sov Phys Solid State. 1964;6:641. [Google Scholar]
- 8.Hwang CF, Hill DA. Phys Rev Lett. 1967;19:1011. [Google Scholar]
- 9.Hwang CF, Hill DA. Phys Rev Lett. 1967;18:110. [Google Scholar]
- 10.Wollan DS. Phys Rev B. 1976;13:3671. [Google Scholar]
- 11.Wind RA, Duijvestijn MJ, van der Luat C, Manenschijn A, Vriend J. Prog Nucl Magn Reson Spectrosc. 1985;17:33. [Google Scholar]
- 12.Becerra L, Gerfen G, Temkin R, Singel D, Griffin R. Phys Rev Lett. 1993;71:3561. doi: 10.1103/PhysRevLett.71.3561. [DOI] [PubMed] [Google Scholar]
- 13.Bajaj V, Farrar C, Hornstein M, Mastovsky I, Vieregg J, Bryant J, Elena B, Kreischer K, Temkin R, Griffin R. J Magn Reson. 2003;160:85. doi: 10.1016/s1090-7807(02)00192-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hornstein MK, Bajaj VS, Griffin RG, Kreischer KE, Mastovsky I, Shapiro MA, Sirigiri JR, Temkin RJ. IEEE Trans Electron Devices. 2005;52:798. [Google Scholar]
- 15.Farrar CT, Hall DA, Gerfen GJ, Inati SJ, Griffin RG. J Chem Phys. 2001;114:4922. [Google Scholar]
- 16.Henstra A, Dirksen P, Schmidt J, Wenckebach WT. J Magn Reson. 1988;77:389. [Google Scholar]
- 17.Henstra A, Dirksen P, Wenckebach WT. Phys Lett A. 1988;134:134. [Google Scholar]
- 18.Henstra A, Lin TS, Schmidt J, Wenckebach WT. Chem Phys Lett. 1990;165:6. [Google Scholar]
- 19.Weis V, Bennati M, Rosay M, Griffin RG. J Chem Phys. 2000;113:6795. [Google Scholar]
- 20.Bennett LH, Torrey HC. Phys Rev. 1957;108:499. [Google Scholar]
- 21.Hausser KH, Stehlik D, Waugh JS, editors. Dynamic Nuclear Polarization in Liquids. Vol. 3 Academic; New York: 1968. [Google Scholar]
- 22.Mueller–Warmuth W, Meise–Gresch K, Waugh JS, editors. Molecular Motions and Interactions as Studied by Dynamic Nuclear Polarization (DNP) in Free Radical Solutions. Vol. 11 Academic; New York: 1983. [Google Scholar]
- 23.Gitti R, Wild C, Tsiao C, Zimmer K, Glass TE, Dorn HC. J Am Chem Soc. 1988;110:2294. [Google Scholar]
- 24.McCarney E, Armstrong B, Lingwood M, Han S. Proc Natl Acad Sci USA. 2007;104:1754. doi: 10.1073/pnas.0610540104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ardenkjær–Larsen J, Fridlund B, Gram A, Hansson G, Hansson L, Lerche M, Servin R, Thaning M, Golman K. Proc Natl Acad Sci USA. 2003;100:10158. doi: 10.1073/pnas.1733835100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Joo C, Hu K, Bryant J, Griffin R. J Am Chem Soc. 2006;128:9428. doi: 10.1021/ja0611947. [DOI] [PubMed] [Google Scholar]
- 27.Bowers CR, Weitekamp DP. J Am Chem Soc. 1987;109:5541. doi: 10.1021/ja010572z. [DOI] [PubMed] [Google Scholar]
- 28.Bifone A, Song YQ, Seydoux R, Taylor RE, Goodson BM, Pietrass T, Budinger TF, Navon G, Pines A. Proc Natl Acad Sci USA. 1996;93:12932. doi: 10.1073/pnas.93.23.12932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Schroder L, Lowery T, Hilty C, Wemmer D, Pines A. Science. 2006;314:446. doi: 10.1126/science.1131847. [DOI] [PubMed] [Google Scholar]
- 30.Blankenship R, McGuire A, Sauer K. Proc Natl Acad Sci USA. 1975;72:4943. doi: 10.1073/pnas.72.12.4943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Goldstein RA, Boxer SG. Biophys J. 1987;51:937. doi: 10.1016/S0006-3495(87)83421-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Closs GL, Closs LE. J Am Chem Soc. 1969;91:4549. [Google Scholar]
- 33.Zysmilich MG, McDermott A. J Am Chem Soc. 1994;116:8362. [Google Scholar]
- 34.Deimling M, Brunner H, Dinse KP, Hausser KH, Colpa JP. J Magn Reson (1969-1992) 1980;39:185. [Google Scholar]
- 35.Schuhl A, Maegawa S, Meisel MW, Chapellier M. Phys Rev Lett. 1985;54:1952. doi: 10.1103/PhysRevLett.54.1952. [DOI] [PubMed] [Google Scholar]
- 36.Ono K, Austing DG, Tokura Y, Tarucha S. Science. 2002;297:1313. doi: 10.1126/science.1070958. [DOI] [PubMed] [Google Scholar]
- 37.Ono K, Tarucha S. Phys Rev Lett. 2004;92:256803. doi: 10.1103/PhysRevLett.92.256803. [DOI] [PubMed] [Google Scholar]
- 38.Sanada H, Matsuzaka S, Morita K, Hu CY, Ohno Y, Ohno H. Phys Rev Lett. 2005;94:097601. doi: 10.1103/PhysRevLett.94.097601. [DOI] [PubMed] [Google Scholar]
- 39.Jeffries CD. Dynamic Nuclear Orientation. Interscience; New York: 1963. [Google Scholar]
- 40.Abragam A, Goldman M. Nuclear Magnetism: Order and Disorder. Clarendon, Oxford/Oxford University Press; New York: 1982. [Google Scholar]
- 41.Abragam A, Goldman M. Rep Prog Phys. 1978;41:395. [Google Scholar]
- 42.Atsarkin VA. Sov Phys Usp. 1978;21:725. [Google Scholar]
- 43.Poole CP, Farach HA. Theory of Magnetic Resonance. 2nd. Wiley Interscience; New York: 1987. [Google Scholar]
- 44.Weil JA, Bolton JR, Wertz JE. Electron Paramagnetic Resonance: Elementary Theory and Practical Applications. Wiley Interscience; New York: 1994. [Google Scholar]
- 45.Gordy W. Theory and Applications of Electron Spin Resonance. Wiley; New York: 1980. [Google Scholar]
- 46.Freeman AJ, Frankel RB. Hyperfine Interactions. Academic; New York: 1967. [Google Scholar]
- 47.Schweiger A, Jeschke G. Principles of Pulse Electron Paramagnetic Resonance. Oxford University Press; Oxford, UK: 2001. [Google Scholar]
- 48.Kevan L, Bowman MK. Modern Pulsed and Continuous-Wave Electron Spin Resonance. Wiley; New York: 1990. [Google Scholar]
- 49.Jeffries CD. Phys Rev. 1957;106:164. [Google Scholar]
- 50.Loening N, Rosay M, Weis V, Griffin R. J Am Chem Soc. 2002;124:8808. doi: 10.1021/ja026660g. [DOI] [PubMed] [Google Scholar]
- 51.Denninger G, Stocklein W, Dormann E, Schwoerer M. Mol Cryst Liq Cryst. 1985;120:233. [Google Scholar]
- 52.Hoefer P, Parigi G, Luchinat C, Carl P, Guthausen G, Reese M, Carlomagno T, Griesinger C, Bennati M. Field dependent dynamic nuclear polarization (DNP) with radicals in aqueous solution. J Am Chem Soc. doi: 10.1021/ja0783207. in press. [DOI] [PubMed] [Google Scholar]
- 53.Armstrong B, Han S. J Chem Phys. 2007;127:104508. doi: 10.1063/1.2770465. [DOI] [PubMed] [Google Scholar]
- 54.Grucker D, Guiberteau T, Eclancher B, Chambron J, Chiarelli R, Rassat A, Subra G, Gallez B. (B).J Magn Reson. 1995;106:101. doi: 10.1006/jmrb.1995.1019. [DOI] [PubMed] [Google Scholar]
- 55.Goldman M. Spin Temperature and Nuclear Magnetic Resonance in Solids. Clarendon; Oxford: 1970. [Google Scholar]
- 56.Duijvestijn MJ, Wind RA, Smidt J. Physica B & C. 1986;138:147. [Google Scholar]
- 57.Wenckebach WTh, Swanenburg TJB, Poulis NJ. Phys Rev B. 1974;14:181. [Google Scholar]
- 58.Hall D, Maus D, Gerfen G, Inati S, Becerra L, Dahlquist F, Griffin R. Science. 1997;276:930. doi: 10.1126/science.276.5314.930. [DOI] [PubMed] [Google Scholar]
- 59.Hu K, Yu H, Swager T, Griffin R. J Am Chem Soc. 2004;126:10844. doi: 10.1021/ja039749a. [DOI] [PubMed] [Google Scholar]
- 60.Hu Kan-Nian, Bajaj Vikram S, Rosay Melanie, Griffin Robert G. J Chem Phys. 2007;126:044512. doi: 10.1063/1.2429658. [DOI] [PubMed] [Google Scholar]
- 61.Song C, Hu K, Joo C, Swager T, Griffin R. J Am Chem Soc. 2006;128:11385. doi: 10.1021/ja061284b. [DOI] [PubMed] [Google Scholar]
- 62.Bajaj VS, Hornstein MK, Kreischer KE, Sirigiri JR, Woskov PP, Mak–Jurkauskas ML, Herzfeld J, Temkin RJ, Griffin RG. J Magn Reson. 2007;190:86. doi: 10.1016/j.jmr.2007.09.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.van der Wel P, Hu K, Lewandowski J, Griffin R. J Am Chem Soc. 2006;128:10840. doi: 10.1021/ja0626685. [DOI] [PubMed] [Google Scholar]
- 64.Hartmann SR, Hahn EL. Phys Rev. 1962;5:2042. [Google Scholar]
- 65.Pines A, Gibby MG, Waugh JS. J Chem Phys. 1972;56:1776. [Google Scholar]
- 66.Conte P, Spaccini R, Piccolo A. Prog Nucl Magn Reson Spectrosc. 2004;44:215. [Google Scholar]
- 67.Mehring M. Principles of High-Resolution NMR in Solids. 2nd. Springer-Verlag; Berlin: 1983. [Google Scholar]
- 68.Bloembergen N, Sorokin PP. Phys Rev. 1958;110:865. [Google Scholar]
- 69.Wind RA, Li L, Lock H, Maciel GE. J Magn Reson (1969-1992) 1988;79:577. [Google Scholar]
- 70.Wind RA, Lock H. Adv Magn Opt Reson. 1990;15:51. [Google Scholar]
- 71.Farrar C, Hall D, Gerfen G, Rosay M, Ardenkjaer–Larsen J, Griffin R. J Magn Reson. 2000;144:134. doi: 10.1006/jmre.2000.2025. [DOI] [PubMed] [Google Scholar]
- 72.van den Heuvel DJ, Henstra A, Lin TS, Schmidt J, Wenckebach WT. Chem Phys Lett. 1992;188:194. [Google Scholar]
- 73.Schmidt J, van den Heuvel DJ, Henstra A, Lin TS, Wenckebach WTh. Isr J Chem. 1992;32:165. [Google Scholar]
- 74.Schmidt J, van den Heuvel DJ, Henstra A, Lin TS, Wenckebach WT. Pure Appl Chem. 1992;64:859. [Google Scholar]
- 75.Brunner H, Fritsch RH, Hausser KH, Naturforsch Z. A: Phys Sci. 1987;42:1456. [Google Scholar]
- 76.Reynhardt EC, High GL. J Chem Phys. 1998;109:4100. [Google Scholar]
- 77.Takeda K, Takegoshi K, Terao T. Chem Phys Lett. 2001;345:166. [Google Scholar]
- 78.Henstra A, Wenckebach WT. In: Pulsed Magnetic Resonance: NMR, ESR and Optics. Bagguley DMS, editor. Clarendon; Oxford: 1992. p. 411. [Google Scholar]
- 79.Freed J. Annu Rev Phys Chem. 2000;51:655. doi: 10.1146/annurev.physchem.51.1.655. [DOI] [PubMed] [Google Scholar]
- 80.Weis V, Griffin R. Solid State Nucl Magn Reson. 2006;29:66. doi: 10.1016/j.ssnmr.2005.08.005. [DOI] [PubMed] [Google Scholar]
- 81.Jeschke G, Schweiger A. J Chem Phys. 1997;106:9979. [Google Scholar]
- 82.Diller A, Roy E, Gast P, van Gorkom H, de Groot H, Glaubitz C, Jeschke G, Matysik J, Alia A. Proc Natl Acad Sci USA. 2007;104:12767. doi: 10.1073/pnas.0701763104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Prakash S, Alia A, Gast P, de Groot H, Jeschke G, Matysik J. Biochemistry. 2007;46:8953. doi: 10.1021/bi700559b. [DOI] [PubMed] [Google Scholar]
- 84.Dorn HC, Wang J, Allen L, Sweeney D, Glass TE. J Magn Reson (1969-1992) 1988;79:404. [Google Scholar]
- 85.Dorn HC, Gitti R, Tsai KH, Glass TE. Chem Phys Lett. 1989;155:227. [Google Scholar]
- 86.Dorn HC, Gu J, Bethune DS, Johnson RD, Yannoni CS. Chem Phys Lett. 1993;203:549. [Google Scholar]
- 87.Crabb DG, Meyer W. Annu Rev Nucl Part Sci. 1997;47:67. [Google Scholar]
- 88.Koelsch CF. J Am Chem Soc. 1957;79:4439. [Google Scholar]
- 89.Ardenkjaer–Larsen J, Laursen I, Leunbach I, Ehnholm G, Wistrand L, Petersson J, Golman K. J Magn Reson. 1998;133:1. doi: 10.1006/jmre.1998.1438. [DOI] [PubMed] [Google Scholar]
- 90.Reddy T, Iwama T, Halpern H, Rawal V. J Org Chem. 2002;67:4635. doi: 10.1021/jo011068f. [DOI] [PubMed] [Google Scholar]
- 91.Afeworki M, McKay RA, Schaefer J. Macromolecules. 1992;25:4084. [Google Scholar]
- 92.Anderson S, Golman K, Rise F, Wikstrom H, Wistrand LG. U.S Patent No 5.530.140. 1996
- 93.Granatstein VL, Parker RK, Armstrong CM. Proc IEEE. 1999;87:702. [Google Scholar]
- 94.Abrams RH, Levush B, Mondelli AA, Parker RK. IEEE Microw Mag. 2001;3:61. [Google Scholar]
- 95.Parker RK, Abrams RH, Jr, Danly BG, Levush B. IEEE Trans Microwave Theory Tech. 2002;50:835. [Google Scholar]
- 96.Hassan A, Pardi L, Krzystek J, Sienkiewicz A, Goy P, Rohrer M, Brunel L, Magn J. Reson. 2000;142:300. doi: 10.1006/jmre.1999.1952. [DOI] [PubMed] [Google Scholar]
- 97.Barra AL. Appl Magn Reson. 2001;21:619. [Google Scholar]
- 98.Prisner T, Un S, Griffin R. J Chem Phys. 1992;32:357. [Google Scholar]
- 99.Grishin YA, Fuchs MR, Schnegg A, Dubinskii AA, Dumesh BS, Rusin FS, Bratman VL, Mobius K. Rev Sci Instrum. 2004;75:2926. [Google Scholar]
- 100.Felch KL, Danly BG, Jory HR, Kreischer KE, Lawson W, Levush B, Temkin RJ. Proc IEEE. 1999;87:752. [Google Scholar]
- 101.Nusinovich GS. Introduction to the Physics of Gyrotrons. Johns Hopkins University Press; Baltimore: 2004. [Google Scholar]
- 102.Kartikeyan MV, Borie E, Thumm MKA. Gyrotrons: High Power Microwave and Millimeter Wave Technology. Springer; Berlin: 2004. [Google Scholar]
- 103.Barker RJ, Schamiloglu E. High-Power Microwave Sources and Technologies. IEEE; New York: 2001. [Google Scholar]
- 104.Cairns RA, Phelps ADR. Generation and Application of High Power Microwaves: Proceedings of the Forty Eighth Scottish Universities Summer School in Physics, St Andrews, August 1996. Scottish Universities Summer School in Physics Institute of Physics Publishing; Edinburgh: 1997. [Google Scholar]
- 105.Gaponov–Grekhov AV, Granatstein VL. Applications of High-Power Microwaves. Artech House; Boston: 1994. [Google Scholar]
- 106.Chu KR. Rev Mod Phys. 2004;76:489. [Google Scholar]
- 107.Joye C, Griffin R, Hornstein M, Hu K, Kreischer K, Rosay M, Shapiro M, Siriqiri J, Temkin R, Woskov P. IEEE Trans Plasma Sci. 2006;34:518. doi: 10.1109/TPS.2006.875776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Hornstein M, Bajaj V, Griffin R, Temkin R. IEEE Trans Plasma Sci. 2006;34:524. doi: 10.1109/TPS.2006.875769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Becerra LR, Gerfen GJ, Bellew BF, Bryant JA, Hall DA, Inati SJ, Weber RT, Un S, Prisner TF, McDermott AE, Fishbein KW, Kreischer K, Temkin RJ, Singel DJ, Griffin RG. (A).J Magn Reson. 1995;117:28. [Google Scholar]
- 110.Doane JL. Propagation and Mode Coupling in Corrugated and Smooth-Walled Circular Waveguides. Academic; New York: 1985. [Google Scholar]
- 111.Grinberg OY, Berliner LJ, Grinberg OY, Berliner LJ, editors. Very High Frequency (VHF) ESR/EPR. Vol. 22 Kluwer Academic, Dordrecht/Plenum; New York: 2004. [Google Scholar]
- 112.Woskov PP, Bajaj VS, Hornstein MK, Temkin RJ, Griffin RG. IEEE Trans Microwave Theory Tech. 2005;53:1863. doi: 10.1109/TMTT.2005.848097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Grinberg OY, Dubinskii AA, Lebedev YS. Russ Chem Rev. 1983;52:850. [Google Scholar]
- 114.Burghaus O, Rohrer M, Gotzinger T, Plato M, Mobius K. Meas Sci Technol. 1992;3:765. [Google Scholar]
- 115.Weis V, Bennati M, Rosay M, Bryant J, Griffin R. J Magn Reson. 1999;140:293. doi: 10.1006/jmre.1999.1841. [DOI] [PubMed] [Google Scholar]
- 116.Hyde JS. J Chem Phys. 1965;43:1806. [Google Scholar]
- 117.Gruber K, Forrer J, Schweiger A, Gunthard HH. J Phys E. 1974;7:569. [Google Scholar]
- 118.Barnes A, De Paëpe G, van der Wel PCA, Hu K, Bajaj VS, Mak-Jurkauskas ML, Herzfeld J, Griffin RG. High field dynamic nuclear polarization for solid and solution biological NMR. Appl Magn Reson. doi: 10.1007/s00723-008-0129-1. submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Wind RA, Anthonio FE, Duijvestijn MJ, Smidt J, Trommel J, de Vette GMC. J Magn Reson (1969-1992) 1983;52:424. [Google Scholar]
- 120.Cho H, Baugh J, Ryan C, Cory D, Ramanathan C. J Magn Reson. 2007;187:242. doi: 10.1016/j.jmr.2007.04.012. [DOI] [PubMed] [Google Scholar]
- 121.McKay RA, Grant DM, Harris RK, editors. Probes for Special Purposes. Vol. 6 Wiley; Chichester: 1996. [Google Scholar]
- 122.Allen PJ, Creuzet F, de Groot HJM, Griffin RG. J Magn Reson (1969-1992) 1991;92:614. [Google Scholar]
- 123.Carravetta M, Johannessen OG, Levitt MH, Heinmaa I, Stern R, Samoson A, Horsewill AJ, Murata Y, Komatsu K. J Chem Phys. 2006;124:104507. doi: 10.1063/1.2174012. [DOI] [PubMed] [Google Scholar]
- 124.Macho V, Kendrick R, Yannoni CS. J Magn Reson (1969-1992) 1983;52:450. [Google Scholar]
- 125.Maly T, Bryant J, Ruben D, Griffin R. J Magn Reson. 2006;183:303. doi: 10.1016/j.jmr.2006.09.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126.Jacquinot JF, Wenckebach WT, Goldman M, Abragam A. Phys Rev Lett. 1974;32:1096. [Google Scholar]
- 127.Afeworki M, Vega S, Schaefer J. Macromolecules. 1992;25:4100. [Google Scholar]
- 128.Iijima T. Cryobiology. 1998;36:165. doi: 10.1006/cryo.1998.2075. [DOI] [PubMed] [Google Scholar]
- 129.Rosay M, Zeri A, Astrof N, Opella S, Herzfeld J, Griffin R. J Am Chem Soc. 2001;123:1010. doi: 10.1021/ja005659j. [DOI] [PubMed] [Google Scholar]
- 130.Rosay M, Lansing J, Haddad K, Bachovchin W, Herzfeld J, Temkin R, Griffin R. J Am Chem Soc. 2003;125:13626. doi: 10.1021/ja036898k. [DOI] [PubMed] [Google Scholar]
- 131.Rosay M, Weis V, Kreischer K, Temkin R, Griffin R. J Am Chem Soc. 2002;124:3214. doi: 10.1021/ja0176752. [DOI] [PubMed] [Google Scholar]
- 132.Sawaya M, Sambashivan S, Nelson R, Ivanova M, Sievers S, Apostol M, Thompson M, Balbirnie M, Wiltzius J, McFarlane H, Madsen A, Riekel C, Eisenberg D. Nature (London) 2007;447:453. doi: 10.1038/nature05695. [DOI] [PubMed] [Google Scholar]
- 133.Nelson R, Sawaya M, Balbirnie M, Madsen A, Riekel C, Grothe R, Eisenberg D. Nature (London) 2005;435:773. doi: 10.1038/nature03680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 134.Maricq MM, Waugh JS. J Chem Phys. 1979;70:3300. [Google Scholar]
- 135.Stevenson S, Dorn HC. Anal Chem. 1994;66:2993. doi: 10.1021/ac971337v. [DOI] [PubMed] [Google Scholar]
- 136.Stevenson S, Glass T, Dorn HC. Anal Chem. 1998;70:2623. doi: 10.1021/ac971337v. [DOI] [PubMed] [Google Scholar]
- 137.Russ JL, Gu J, Tsai KH, Glass T, Duchamp JC, Dorn HC. J Am Chem Soc. 2007 doi: 10.1021/ja064632i. [DOI] [PubMed] [Google Scholar]
- 138.Granwehr J, Leggett J, Kockenberger W. J Magn Reson. 2007;187:266. doi: 10.1016/j.jmr.2007.05.011. [DOI] [PubMed] [Google Scholar]
- 139.Frydman L, Scherf T, Lupulescu A. Proc Natl Acad Sci USA. 2002;99:15858. doi: 10.1073/pnas.252644399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 140.Frydman L, Blazina D. Nat Phys. 2007;3:415. [Google Scholar]


