Abstract
It is now well known that altered hemodynamics can alter the genes that are expressed by diverse vascular cells, which in turn plays a critical role in the ability of a blood vessel to adapt to new biomechanical conditions and governs the natural history of the progression of many types of disease. Fortunately, when taken together, recent advances in molecular and cell biology, in vivo medical imaging, biomechanics, computational mechanics, and computing power provide an unprecedented opportunity to begin to understand such hemodynamic effects on vascular biology, physiology, and pathophysiology. Moreover, with increased understanding will come the promise of improved designs for medical devices and clinical interventions. The goal of this paper, therefore, is to present a new computational framework that brings together recent advances in computational biosolid and biofluid mechanics that can exploit new information on the biology of vascular growth and remodeling as well as in vivo patient-specific medical imaging so as to enable realistic simulations of vascular adaptations, disease progression, and clinical intervention.
1 Introduction
Since the 1970s, we as a research community have come to appreciate the fundamental importance of biomechanical factors in regulating normal vascular biology and physiology and similarly in impacting the progression of many diseases as well as their responses to clinical intervention. Although such factors clearly involve coupled effects between the flowing blood, vascular wall, and perivascular tissues, that is, fluid-solid-solute interactions, research in vascular biomechanics has traditionally advanced along separate lines - biofluid mechanics, biosolid mechanics, and biotransport phenomena. There is, therefore, a pressing need to move toward coupled problem formulations and solutions. Moreover, it is well known that most physiologic, pathophysiologic, and reparative processes in the vasculature manifest over periods of days to weeks, months, or even years. Yet, most attention in vascular biomechanics has focused on behaviors during a cardiac cycle or, at best, at select time points during the progression of a disease or response to a treatment or injury. Clearly, there is also a pressing need to understand better the underlying processes that are responsible for the conspicuous changes in structure and function that occur over long periods, changes that likewise depend strongly on the biomechanics.
This paper is motivated by these needs, indeed, the need for a new paradigm to address diverse biomechanical problems of the vasculature by accounting for coupled fluid-solid-transport over long periods of vascular adaptation and maladaptation [1]. Hence, in this paper we show how computations of complex fluid-solid interactions during a cardiac cycle can be linked to detailed analyses of the solid mechanics of the vascular wall as well as descriptions of the kinetics of biological growth and remodeling which can depend strongly on solute transport. We refer to this new approach as Fluid-Solid-Growth (FSG) modeling. Toward this end, we build primarily on four separate advances by our groups: biomechanics of growth and remodeling [2], a coupled momentum method for fluid-solid interactions during a cardiac cycle [3], a theory of small on large for coupling biosolid and biofluid mechanical models [4], and improved approaches for modeling fluid boundary conditions in complex vascular systems [5]. Because these developments progressed independently, and tended to follow different notational conventions used by the biosolids and biofluids communities, we introduce notational changes herein to meld better these prior developments; where possible, we follow Marsden and Hughes [6] for such notational conventions, including lightface italics for scalars, boldface italics for vectors and second-order tensors, and boldface block letters for higher-order tensors. Furthermore, where possible we use upper case characters to refer to material quantities and lower case for spatial quantities.
Although the formalism presented herein is meant to be sufficiently general to accommodate many different types of advances in modeling FSG problems, including 3-D patient-specific simulations, we necessarily restrict our illustrative numerical results to a simple situation - influence of pressure-induced intramural stress and flow-induced wall shear stress on the evolution of shape and properties of a basilar artery following an initial concentric loss of a portion of the elastin within the wall. Notwithstanding the complexity of the associated biomechanical and biochemical processes, which will certainly require further research to identify more complete constitutive relations for the growth and remodeling kinetics, we submit that the simple illustrative examples herein reveal both the need for and the great potential of Fluid-Solid-Growth modeling in basic research, industrial R&D, and clinical applications.
2 Methods
2.1 General Framework for Fluid-Solid-Growth (FSG) Simulations
The FSG framework consists of two computational analyses defined over different time scales. On one hand, we consider long-term (weeks to months) simulations of the evolution of vascular wall geometry, structure, and properties governed by stress-mediated growth and remodeling (G&R). On the other hand, we study short-term (seconds) fluid-solid interaction (FSI) processes that characterize the hemodynamic forces acting on the wall throughout the cardiac cycle.
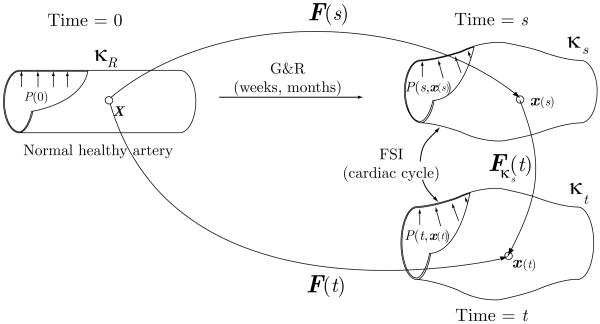
Each aspect of the framework uses different computational configurations. For the G&R simulation, we introduce a reference configuration κR and an intermediate configuration κs (see figure 1). The reference configuration κR is a computationally convenient fixed configuration from which the position of each particle in other configurations can be mapped. In this work, the healthy arterial segment at G&R time 0 is chosen to be the reference configuration. The intermediate configuration κs represents the mean geometry of the artery over the cardiac cycle at some later time s. Positions of a given particle in κR and κs are given by X and x(s), respectively. Evolution of a lesion is represented by a mapping between these two positions and the deformation gradient F(s).
Figure 1.
In vivo configurations for FSG simulations. In the growth and remodeling (G&R) part of the analysis we simulate the evolution of an artery over long time scales. This process is represented by a deformation gradient F(s) corresponding to the mapping from the reference configuration κR (a healthy configuration of the artery at time zero) to an intermediate configuration κs at G&R time s. This intermediate configuration represents the mean geometry of the artery over the cardiac cycle. The fluid-solid interaction (FSI) part of the analysis computes the hemodynamic forces acting on the vessel wall over the cardiac cycle. This analysis considers a small-deformation gradient Fκs(t) from the intermediate configuration κs to a current configuration κt, representing the position of the artery at any time t during the cycle. Hence, the variable s corresponds to long time scale G&R processes whereas the variable t is used for small time scale FSI processes.
On the other hand, the FSI simulations utilize the intermediate configuration κs as a reference configuration whereas the current configuration of the artery at any given time t during the cardiac cycle is given by κt. The deformation gradient corresponding to a mapping from κs to κt is denoted by Fκs(t), which is assumed to always be associated with a “small” deformation. Considering this, the deformation gradient F(t) corresponding to the mapping from κR to κt can be written as
| (1) |
Significant attention is given below in finding F(s) for G&R processes. Finally, we denote the Cauchy stress in the wall by σ; the first Piola-Kirchhoff stresses in the wall, defined per unit area in κR and κs, are denoted by PκR(t) and Pκs(t), respectively.
The FSG framework utilizes a loose coupling between the short-term FSI simulations and the long-term G&R simulations. This coupling is illustrated by the loop depicted in figure 2. In this loop, at a given time sn defined over long-time scales, the FSI analysis calculates hemodynamic loads acting on the arterial wall during the cardiac cycle, extracts the mechanical stimuli that affect vascular wall G&R, and then transfers the information to the G&R formulation. The G&R analysis then simulates the evolution of the arterial wall over multiple G&R time steps. When changes in vessel wall geometry and/or structure are significant, the loop returns to the FSI analysis with updated information about the geometry, pre-stresses, and material properties.
Figure 2.
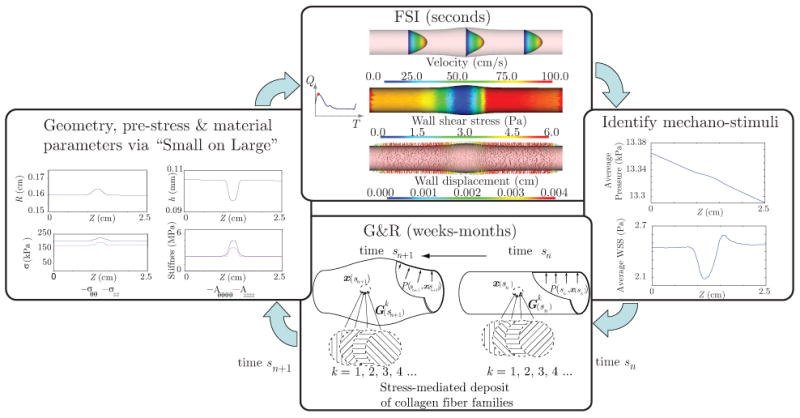
Iterative loop and information transferred in the coupling between the FSI and G&R parts of the FSG framework.
The transfer of material properties and pre-stresses between the G&R analysis and the FSI analysis is facilitated using the theory of small on large, which was reformulated in Baek et al. [4]. This theory provides a consistent linearization of the constitutive relation for the wall by considering the multiplicative decomposition of the total motion given by equation (1). That is, we assume that the enlargement of the lesion is represented by a “large” deformation characterized by F(s), while the “small” deformation during the cardiac cycle is characterized by Fκs(t).
For completeness, and to introduce a consistent notation, we now briefly describe the main aspects of the FSG framework, namely a constrained mixture theory for G&R of the wall, a coupled momentum method for FSI, and a theory of small deformations superimposed on large.
2.2 Biomechanics of Growth and Remodeling
2.2.1 Kinematics of an enlarging fusiform aneurysm
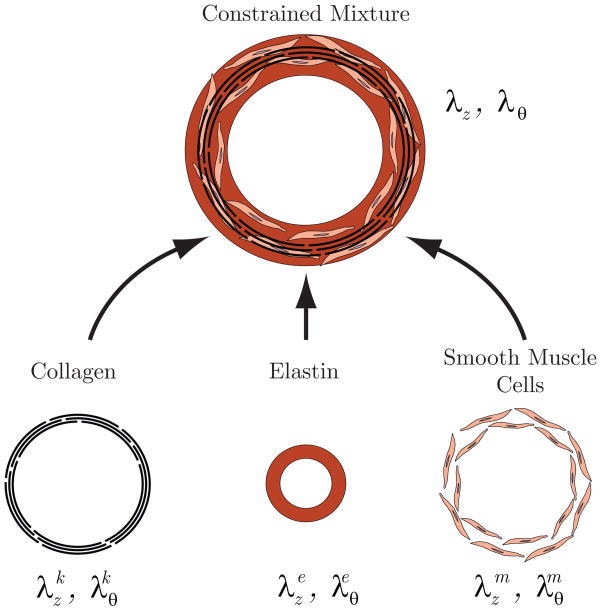
The G&R formulation is based on the framework presented by Baek and colleagues [2]. The arterial wall is assumed to consist of elastin, multiple families of collagen, and vasoactive smooth muscle cells (see figure 3). Collagen families with different preferred fiber orientations are treated as different co-existing constituents. In this section, we use the superscript ‘i’ to refer to each constituent (i.e., elastin, collagen, muscle) and the superscript ‘k’ to refer to the kth family of collagen with a common fiber orientation. Thus, i = e, 1, 2, …, k, m, where e denotes elastin and m denotes smooth muscle. Not only can different types of constituents co-exist at a point, constituents produced at different times can also co-exist.
Figure 3.
Arterial wall as a constrained mixture of amorphous elastin matrix, collagen fibers and smooth muscle.
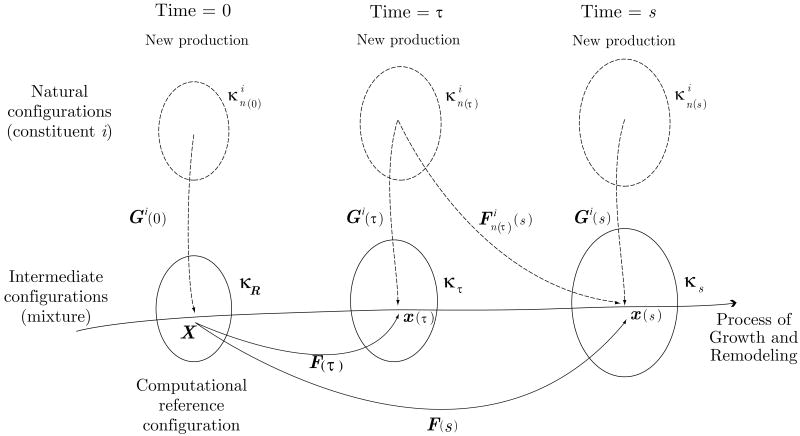
Important configurations for this G&R formulation are shown in figure 4. As we saw earlier, κR represents a fixed reference configuration for a healthy artery at time s = 0, which need not be stress-free even if traction free. That is, different constituents can have different pre-stresses at any G&R time s. Using ideas of constrained mixture theory, however, we assume that there exists a natural (stress-free) configuration for each constituent ‘i’ when produced at a time τ ∈ [0, s] [7] (see figure 4).
Figure 4.
Configurations for arterial G&R. The reference configuration κR is an initial configuration of a healthy artery under homeostatic and normal hemodynamic conditions. The growth and remodeling of the artery is tracked by F(τ) (τ = [0, s]) which maps κR to the intermediate configurations κτ. The natural configuration is prescribed for a constituent i that was produced at time τ. The tensor Gi(τ) represents the prescribed “deposition stretch” of constituent i.
Indeed, defining a stress-free or traction-free configuration in vivo is challenging since such configurations do not exist clinically. Rather, we must rely on biomedical images obtained under physiologic pressure; such images represent pre-stressed arterial configurations. Recently, two different approaches have been proposed to account for this pre-stress. The first approach enforces prescribed values of pre-stress (or pre-strain) [8] whereas the second approach uses an inverse elastostatic formulation to estimate the pre-stress [9, 10]. We emphasize, however, that in both cases the tissue is treated as a materially uniform continua. In this work, we employ an extension of the first approach: we assume that the pre-stress in each constituent produced is the same as a postulated homeostatic value in κR. In other words, we assume that cells incorporate newly produced constituents within extant tissue at a homeostatic (target) stress or strain. We describe how to enforce this homeostatic state in κR in section 3.2.
For each constituent, we must define the mapping from its individual natural configuration to the reference configuration κR. Let Gi(τ) be the deformation gradient corresponding to the deposition of the ith constituent at time τ. Then, the deformation gradient of constituent i from its natural configuration to the reference configuration κR is given by F−1(τ)Gi(τ). Therefore, the deformation gradient mapping constituent i with natural configurations defined at time τ to the current G&R time s can be defined as
| (2) |
New constituents are not only deposited at a particular pre-stretch or pre-stress, they are also oriented in an optimal mean. Let the orientation of collagen fiber family k produced at time τ be represented by the unit vector mk(τ) in the configuration κτ. The orientation of this fiber family in its natural configuration is thus given by the unit vector defined as
| (3) |
If we assume that the deposition stretch for collagen fibers has a homeostatic value for all k, the following relation between unit vectors in and κτ holds
| (4) |
Hence, we can calculate the stretch at the current time in a collagen fiber family produced at time τ considering the deformation gradient and the orientation in its natural configuration:
| (5) |
Whereas arterial collagen turns over continually throughout life (and at higher rates in disease and cases of altered loading), elastin has a very long half-life and thus does not turnover effectively [11]. The deposition of elastin is thus characterized differently given that the majority of cross-linked elastin layers are synthesized at some time τo < 0 during development [12], and it is difficult to trace the production time. We define a new tensor G̃e = F−1(τo)Ge representing the mapping from the natural configuration of elastin to the computational reference configuration κR [13], which relative to principal directions is assumed to be
| (6) |
Considering this, the deformation gradient for elastin at the current time is given by
| (7) |
Although figure 4 presents a general scheme for a G&R framework, in this work we specialize it to a two-dimensional (2D) model, treating the vessel wall as a membrane. Henceforth, F(s) denotes a 2D deformation gradient associated with a mapping from a membrane topology defined in the reference configuration κR to that in the intermediate configuration κs.
2.2.2 Constituent turnover and wall properties
Each constituent can be produced and removed over time. The areal mass density M(τ) denotes the total mass per unit area in the configuration κτ at time τ ∈ [0, s], and the areal mass density at time s, M(s), can be calculated by [2]
| (8) |
where J(τ) is the determinant of the 2D deformation gradient F(τ), Qi(s) is the fraction of the ith constituent that was present at time 0 and still remains at time s, mi(τ) is the true rate of production of the ith constituent at time τ per unit area in κτ, and qi(s − τ) is its survival function, that is, the fraction of constituent i produced at time τ that remains at time s. Note that equation (8) can be rewritten in terms of MR(τ) and (see [2]), where MR(τ) = M(τ)J(τ) and for τ ∈ [0, s]. Let the mass fractions φi(s) (i = e, k) be
| (9) |
Assuming that the overall mass density of the wall remains constant throughout G&R (i.e., ρ(s) = ρ; [14]), the current thickness of the wall is calculated by
| (10) |
In our previous work [2,15], we assumed that the production rate of collagen fibers depended solely on the intramural stress experienced by the cells interacting with the surrounding matrix. We know, however, that changes in wall shear stress affect the release of vasoactive substances by the endothelium that also affect the turnover of collagen and smooth muscle. In this work, by coupling the G&R and FSI formulations, we can incorporate this additional mechanical stimulus. Therefore, the rate of mass density production for a collagen family mk(s) is postulated to depend on both the deviation of a scalar measure of the intramural stress from its postulated homeostatic value (σk − σh) and the deviation of the wall shear stress from its homeostatic value . Let σk be given by:
| (11) |
where Tc(s) and hc(s) are the collagen Cauchy membrane stress determined by satisfying wall equilibrium and collagen thickness at time s, respectively. The mean value of wall shear stress τw is obtained directly from the FSI simulations (see figure 2). As an illustrative example, consider the following linearized form for the rate of mass production:
| (12) |
where kσ and kτ are scalar parameters that control the stress-mediated G&R and is a basal rate of mass production for the kth fiber family. At the homeostatic state, therefore, the production rate follows the basal rate. We define the survival function for the kth collagen family as
| (13) |
We should note that the basal rate of mass production for each constituent must be selected in a way such that production and removal are perfectly balanced in the absence of altered stresses from homeostatic values. Using this condition, and Qk(s) can be obtained as [15]
| (14) |
The alignment of newly deposited collagen fibers within the arterial wall is not clearly understood, but it has been suggested that it may depend on the deformation of existing collagen fibers or on their state of stress [16, 17]. Our previous work on G&R of fusiform aneurysms [2] suggests that unstable growth may occur if newly deposited collagen fibers align towards the direction of the larger principal stresses, whereas stable growth may occur if alignment is towards the direction of smaller principal stress. For illustrative purposes, however, we assume simply that the collagen deposition alignment during G&R depends only on the deformation of existing fibers. More specifically, we assume that
| (15) |
where αk(s) is the orientation of the collagen fiber family k at deposition time s and λ1 and λ2 are principal stretches during the G&R process.
Our treatment of the kinetics of elastin fibers is simpler since the isotropically deposited elastin is synthesized primarily during development and its half-life is much longer than that of collagen. Therefore, the following assumptions for mass production rate and survival function are made: me(s) = 0 and Qe(s) = 1. It is noted, however, that Qe(s) could be allowed to be a decreasing function of time s, as in true aneurysmal development, Marfan syndrome, aging, and so on. Herein, we simply consider consequences of an instantaneous loss of a portion of the elastin just prior to s = 0.
For an elastic body, the Cauchy membrane stress T for the mixture can be given by
| (16) |
where C = FTF. The strain energy of the mixture per unit reference area wR is defined as the sum of the energy stored in the elastin-dominated amorphous matrix and the multiple families of collagen, namely
| (17) |
To account for the constancy (or time-dependent loss) of elastin and collagen turnover, the strain energy function for these constituents can be written as [2]
| (18) |
| (19) |
where . Ψe and Ψk are the strain energy of the elastin-dominated amorphous matrix and the kth collagen fiber family per unit mass, respectively. The strain energy for the elastin-dominated matrix is typically assumed to be neo-Hookean:
| (20) |
where and are diagonal components of . For collagen, we postulate that the form of the strain energy function for the kth collagen fiber family Ψk is the same for all fiber families, i.e. Ψk ≡ Ψc. This energy is typically given by the exponential form [18]
| (21) |
where is the stretch of the fiber family k produced at time τ but currently in configuration κs.
The Cauchy membrane stress is given as the sum of passive and active membrane stresses, i.e., T = T(pass) + T(act). Substituting (20) and (21) into (16), T(pass) can be written for a state of biaxial deformation as
| (22) |
| (23) |
where .
The active membrane stress due to vascular smooth muscle T(act) is assumed to have the following form (similar to [19])
| (24) |
where h is the current thickness, T(Ca++) represents the contractility of smooth muscle cells, λ̃2 is the stretch of the smooth muscle cells relative to their preferred homeostatic state, and λ̃M and λ̃o are stretches corresponding to the maximum contraction and the active force generation limits, respectively. Considering equations (16) and (24), we can define an active potential Ψ(act) such that w(act) = M(s)J(s)Ψ(act). The first derivatives of this active potential energy are given by
| (25) |
The vasoactive response can be altered by either changing the contractility T(Ca++) or by shifting the preferred homeostatic state via rearrangement of smooth muscle cells [13]. In this work, however, we assume that T(Ca++) is constant. Furthermore, we assume that smooth muscle cells reorganize during the long-term G&R so that they are in a preferred homeostatic state at all intermediate configurations κs. The preferred state of smooth muscle cells, however, does not change during the cardiac cycle modeled by the FSI formulation in section 2.3. The stretch of smooth muscle during the cardiac cycle can be calculated by λ̃2 = λ2(t)/λ2(s).
2.2.3 Numerical simulations of G&R of an axisymmetric vessel
We consider a membrane formulation for the G&R simulations where the computational domain of the vessel wall is given by the surfaces ΓR and Γs defined in the reference and intermediate configurations, respectively:
| (26) |
We assume an axisymmetric geometry for the vessel at all times (which is appropriate given axisymmetric G&R in response to a concentric loss of elastin), whereby positions of a point in reference and intermediate configurations, X and x(s), can be expressed by two sets of cylindrical coordinates (Z, Θ, R) and (z, θ, r), with θ = Θ for all s, namely
| (27) |
| (28) |
We can further define the geometry of the artery in the reference configuration using a continuous function R = R(Z). Furthermore, using a set of two-dimensional curvilinear coordinates Ξa = {Z, Θ}, we can parameterize the current position of a point x in κs as
| (29) |
The associated bases for this curvilinear parametrization are
| (30) |
where A, a = 1, 2. Local orthonormal bases and outward normal vectors in the reference and intermediate configurations are thus given by
| (31) |
Consequently, the deformation experienced by the artery due to growth is defined by
| (32) |
and F(s) = FiJei ⊗ EJ where
| (33) |
where λ1 and λ2 are the two principal stretches and (·)′ = ∂(·)/∂Z.
G&R of the artery is simulated using a finite element method based on the principle of virtual work to satisfy equilibrium at each G&R time s. It is noted, therefore, that inertial forces are negligible in most arteries with respect to in vivo stress analyses [14]. The governing equation is given by
| (34) |
where P(x) is the transmural pressure and δx represents virtual changes in position, with a and A denoting surface areas in the current and reference configurations. A variation of equation (34) with respect to r and z yields two sets of nonlinear algebraic equations:
| (35) |
where ψj is a global quadratic interpolation function corresponding to the jth node. After obtaining the non-dimensional counterpart of equation (35), it is possible to define non-dimensionalized stress mediation parameters, k̂σ and k̂τ used in section 3 (see [2] for details).
| (36) |
The set of non-linear algebraic equations represented in (35) is solved using a Newton-Raphson procedure.
2.3 Method for Fluid-Solid Interaction
Solving the coupled problem of blood flow and vessel wall motion in an arbitrary geometry given by a patient-specific arterial tree is a computationally expensive task ([3, 20–22].). In the context of the FSG framework presented in this paper, where we must evaluate a large number of hypotheses regarding different mechanisms that may regulate vessel growth and remodeling, it is important that we perform the requisite fluid-solid interaction computations as efficiently as possible. Although arterial wall behavior is highly nonlinear under finite deformations, particularly during G&R, it appears that this behavior can be approximated well over the cardiac cycle using an appropriate linearization [4]. Hence, it is possible to use methods that take advantage of a linear wall behavior in these fluid-solid interaction problems. Figueroa et al. [3] recently developed one such method. Their “coupled momentum method” employs a monolithic scheme, conforming meshes at the vascular wall-fluid boundary interface, and a thin linearly elastic enhanced membrane model for the arterial wall. This set of features and simplifications make the formulation computationally efficient for problems where the deformation and thickness of the arterial wall are small (as in most cerebral aneurysms like the one considered in this work), thus enabling patient-specific fluid-structure computations with a modest increase in computing time compared to that of rigid wall analysis. In section 2.3.1, we briefly describe the basis of the coupled momentum method. For internal consistency, however, some of the notation has been changed from the original paper.
Another important aspect to consider when solving FSI problems in the cardiovascular system is the specification of boundary conditions on the fluid domain (both inlet and outlet). These boundary conditions should represent hemodynamic characteristics of the vasculature not included in the computational domain. Indeed, this is particularly important in FSG modeling for these boundary conditions set the “loads” that the vascular wall experiences through the cardiac cycle, that is, they determine the overall level of pressure and shear stress. Vignon-Clementel et al. [5] described a “coupled multi-domain” formulation based on the Dirichlet-to-Neumann [23] and variational multiscale methods [24] that embeds the effects of downstream vascular beds, using reduced-order models, into a three-dimensional finite element formulation for the computational domain. In this work, we include this “coupled multi-domain” approach for boundary condition specification and summarize this method in section 2.3.2.
2.3.1 A coupled momentum method for FSI
The coupled momentum method is based on a stabilized finite element formulation [20,25] applied to the incompressible Navier-Stokes equations in a fixed computational grid. The method formulates the degrees-of-freedom (i.e., displacements u) for the vascular wall as a function of the fluid velocities v at the fluid-solid interface, using an enhanced linear membrane formulation. To characterize the method, we first introduce the configurations, domains, and boundaries considered for blood flow and vascular wall motion.
As described in section 2.1, the FSI problem defined on the small time scales employs an intermediate configuration κs representing the average geometry of the arterial structure over the cardiac cycle. The position of any point x(s) on the fluid-solid interface at the intermediate configuration Γs ∈ κs will be mapped to a point x(t) on Γt ∈ κt via a “small” deformation and associated deformation gradient Fκs(t) introduced in equation (1) (see figure 5).
Figure 5.
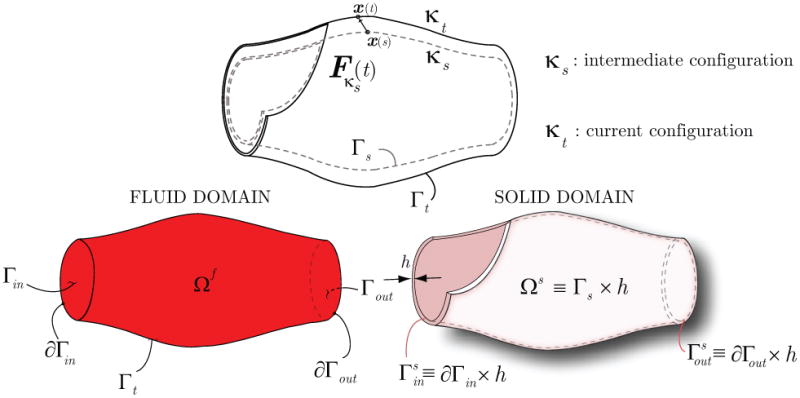
Schematic representation of arterial configurations used in the FSI formulation (top), and fluid-solid domains and their boundaries (bottom).
Blood flow equations
The blood flow problem is defined within a domain Ωf that represents the current configuration of the blood volume inside the artery at any time t during the cardiac cycle. The boundary of this blood flow domain Ωf is given by
| (37) |
where Γin represents the boundary where a velocity field v = vin is prescribed; this usually corresponds to the inflow face of the model. Γout represents the boundary where a traction field tout is prescribed; this usually corresponds to an outflow face of the model. This traction is prescribed weakly by considering a reduced-order model of the downstream vasculature via the “coupled multi-domain” method (see section 2.3.2). Lastly, Γt represents the interface between blood and vessel wall (i.e., the luminal surface). The traction tf acting on this boundary is determined using information coming from the weak form solution for the dynamics of the vascular wall.
Because the motion of the vessel wall is considered to be small, we assume for the FSI problem that the current configuration κt can be approximated by the intermediate configuration κs for all times: κt ≈ κs ∀t. Therefore, the Eulerian coordinates x(t) defining the boundaries of the flow domain will be given by the coordinates x(s) of the boundaries at the intermediate configuration. Considering this, the weak formulation of the blood flow problem in the fixed Eulerian frame is:
| (38) |
Here, p and v are the blood pressure and velocity, respectively, and T is the period for a cardiac cycle (∼ 1 sec. in humans). The test functions for mass and momentum balance are q and w, respectively; ρf is the mass density of the blood, b is a body force per unit volume (e.g. gravity), and τ is the viscous part of the stress response for the blood, where
| (39) |
and μ is the dynamic viscosity. The total response of the blood (considered Newtonian) is thus
| (40) |
where the Lagrange multiplier p that enforces incompressibility equals the blood pressure.
We refer the reader to the original paper [3] for the expression of the stabilization terms considered in equation (38).
Vessel wall equations
Assuming the wall to be a membrane, the problem is defined in a “volume” Ωs given by the interface between blood and the vascular wall in the intermediate configuration κs having some thickness h:
| (41) |
The boundaries of this domain are and (see figure 5), with a Dirichlet condition on the velocity prescribed on the former and a Neumann boundary with a traction hs prescribed on the latter. Lastly, a traction ts acts on the fluid-solid interface Γs. The Galerkin formulation for the vascular wall can then be given in Lagrangian form as
| (42) |
Here, v represents the velocity of the vascular wall, which is identical to the fluid velocity due to the conforming meshes at the interface Γs, w is the wall test function, ρ is the mass density of the vessel wall, 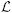 (Pκs) is the linearization via small on large of the first Piola-Kirchhoff stress tensor defined in the G&R formulation, and bs is a body force per unit volume. In this context, it is appropriate to characterize the vessel wall stress using a linearized first Piola-Kirchhoff tensor
(Pκs) is the linearization via small on large of the first Piola-Kirchhoff stress tensor defined in the G&R formulation, and bs is a body force per unit volume. In this context, it is appropriate to characterize the vessel wall stress using a linearized first Piola-Kirchhoff tensor 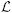 (Pκs), since we are relating forces in current time with a geometry given in a fixed configuration (i.e., intermediate configuration κs). This linearized first Piola-Kirchhoff tensor is a function of the vessel wall displacement u(x(s), t), which is calculated via integration of the vessel wall velocity using a Newmark scheme [26].
(Pκs), since we are relating forces in current time with a geometry given in a fixed configuration (i.e., intermediate configuration κs). This linearized first Piola-Kirchhoff tensor is a function of the vessel wall displacement u(x(s), t), which is calculated via integration of the vessel wall velocity using a Newmark scheme [26].
At the interface Γs, the deformation gradient Fκs is associated with a mapping from the position x(s) on Γs to the position x(t) on Γt (see figure 5). The traction vectors can be written as tf = σfnf on Γt and ts = 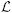 (Pκs)Ns on Γs, where nf and Ns are outward unit normals to the surfaces Γt and Γs, respectively. The mapping of the surface vector element is given by nf da = −JκsFκs−TNsdA (e.g., [27]). Therefore, the term (∫Γt w · tf da) in equation (38) can be rewritten as
(Pκs)Ns on Γs, where nf and Ns are outward unit normals to the surfaces Γt and Γs, respectively. The mapping of the surface vector element is given by nf da = −JκsFκs−TNsdA (e.g., [27]). Therefore, the term (∫Γt w · tf da) in equation (38) can be rewritten as
| (43) |
Using the traction condition σsns = −σfnf at the interface and 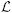 (Pκs) = JκsσsFκs−T, we obtain the condition at the interface
(Pκs) = JκsσsFκs−T, we obtain the condition at the interface
| (44) |
Neglecting the body force in the wall (e.g., [28]), using a membrane assumption, and combining equations (42) and (44), the fluid-solid interface condition can be written as
| (45) |
Combining equations (45) and (38), we obtain the variational formulation for the “coupled momentum” method in a fixed Eulerian frame (cf. [3]):
| (46) |
In order to complete the description of the method, we must describe the vessel wall stress term
| (47) |
according to the linear membrane adopted.
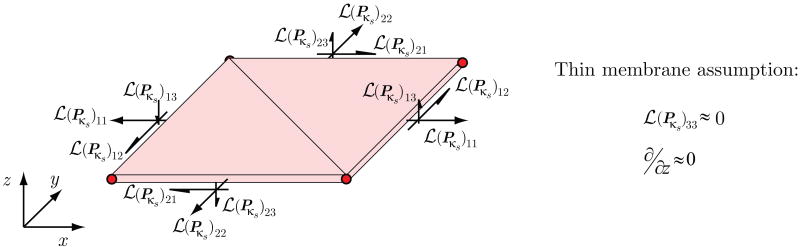
Linear enhanced membrane model
The membrane model used by the coupled momentum method utilizes a standard two-dimensional triangular linear membrane element, with additional out-of-plane shear components (see figure 6). As discussed earlier in section 2.1, we assume that the deformation gradient Fκs(t) characterizing the motion of the vessel wall over the cardiac cycle is defined by a small displacement gradient H:
Figure 6.
Schematic representation of the stresses and strains used in the linear enhanced membrane model of the fluid-solid interaction formulation described in section 2.3.
| (48) |
∀s fixed and t ∈ [0, T].
For the thin membrane considered here, we neglect the through-thickness components of the displacement gradient and define the following membrane strain tensor:
| (49) |
The membrane model utilizes a linearization of the first Piola-Kirchhoff tensor defined in the G&R analysis 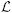 (Pκs) around F(t) ≈ F(s). This linearization is accomplished via the theory of small on large as summarized in section 2.4. The membrane stresses resulting from this linearization are depicted in figure 6. Note that, as justified by the thin membrane formulation, we assume that the
(Pκs) around F(t) ≈ F(s). This linearization is accomplished via the theory of small on large as summarized in section 2.4. The membrane stresses resulting from this linearization are depicted in figure 6. Note that, as justified by the thin membrane formulation, we assume that the 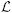 (Pκs)33 component of the linearized stress tensor is small compared to the other components.
(Pκs)33 component of the linearized stress tensor is small compared to the other components.
Equation (46) is spatially discretized using linear tetrahedral elements. The resulting semi-discrete system of equations is integrated over time using a Generalized-alpha method [29]. Details on the solution strategy are described in Figueroa et al. [3].
2.3.2 Boundary conditions for the FSI problem
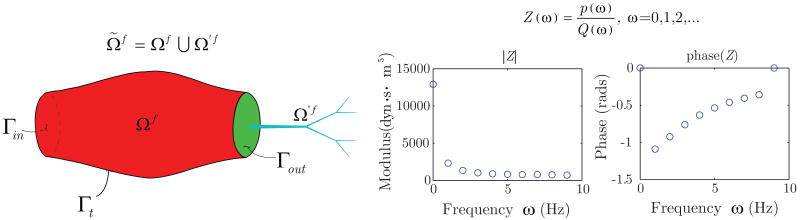
The “coupled-multidomain” formulation for specifying outlet boundary conditions [5] for the fluid domain employs a disjoint decomposition of the blood flow spatial domain Ω̃f into an upstream “numerical” domain Ωf and a downstream “analytical” domain Ω′f such that and Ωf ∩ Ω′f = Ø. These two domains are separated by the boundary Γout (see figure 7).
Figure 7.
The spatial fluid domain Ω̃f is separated into an upstream “numerical” domain Ωf and a downstream “analytical” domain Ω′f, demarcated by the interface Γout. The effect of the analytic domain on the numerical domain is incorporated in boundary operators that characterize the relationship between pressure and flow in the downstream vasculature. Note that distributed or lumped models can be used for the analytic domain. In this work, we have used a distributed model to generate a terminal impedance function Z(ω).
The method then applies a similar disjoint decomposition to the flow variables. If the solution vector is written as Ṽ = {ṽ, p̃}T, then this vector can be separated into a component that is defined within the numerical domain Ωf and a component defined within the analytical domain Ω′f, viz.
| (50) |
This decomposition further satisfies the condition V = V′ at the interface Γout, and is also applied to the weighting functions. The coupled-multidomain method produces a variational form for the numerical domain Ωf similar to the one given by equation (38), where the integral term defined on Γout is written in terms of operators 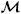 = {
= {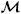 m,
m, 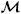 c}T|Γout and
c}T|Γout and 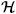 = {
= {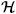 m,
m, 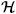 c}T|Γout
c}T|Γout
| (51) |
where subscripts m and c denote the fluid momentum and mass balance components of the operators, respectively. These operators are defined in the domain Ω′f based on the model chosen to represent blood flow and pressure in that domain. For instance, if we consider a linear wave propagation model as the analytical solution in Ω′f defined as a one-dimensional network, then it is possible to derive an input vascular impedance function Z(ω) for the inlet of the analytical domain (i.e., the boundary Γout) that is used as a terminal impedance of the numerical domain [30]. This impedance function Z(ω) relates flow and pressure modes for all frequencies ω considered in the analysis, and is used to define the operators 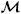 and
and  . More specifically, for the examples considered in this paper, we have
. More specifically, for the examples considered in this paper, we have
| (52) |
| (53) |
Equations (52) and (53) represent mass and momentum balance between the numerical and analytical domains. In equation (52), we can see the convolution of the impedance function in the time domain z(t) and flow Q(t) on Γout. This convolution integral sets the pressure p at the interface as a function of the flow characteristics in the downstream domain Ω′f.
2.4 Theory of Small on Large for FSG Simulations
We have previously suggested that the theory of small deformations superimposed on large can serve as a useful tool to obtain a linearized response of the wall during the cardiac cycle without compromising important characteristics such as anisotropy and smooth muscle tone [4]. Furthermore, we have shown that this linearized response can provide a good approximation for the wall constitutive behavior during the cardiac cycle and can be used in fluid-solid interaction computations. Here, we briefly describe how to obtain a linearized response from the constitutive relation used during arterial adaptation in section 2.2.2.
For an incompressible elastic material, the constitutive relation for Cauchy stress σ is given by
| (54) |
where p is a Lagrange multiplier and W is the strain energy per unit reference volume. During the cardiac cycle we assume that the G&R time s and the configuration κs are fixed and we utilize the configuration κs as a reference configuration for FSI simulations. Hence, although not specified explicitly, the kinematic quantities are functions of position x(s). The first Piola-Kirchhoff stress Pκs(t) with respect to an area of the intermediate configuration κs can be written as (see figure 1 and recall that F(t) = Fκs(t)F(s))
| (55) |
Note that, when Fκs(t) = I, Pκs(t) is the same as the Cauchy stress σ(t) and will be denoted as P(s). As introduced in section 2.3.1, Pκs can be linearized at Fκs(t) = I (or H(t) = 0) with respect to the small deformation gradient H(t) (see equation (48)), so that components of the linearized stress  (Pκs) can be written as (see [4])
(Pκs) can be written as (see [4])
| (56) |
where εkl(t) = (Hkl(t) + Hlk(t))/2 and ωkl(t) = (Hkl(t) − Hlk(t))/2. The fourth-order tensor coefficients Aijkl and Bijkl of equation (56) are given by:
| (57) |
| (58) |
Considering the elastin, collagen, and vasoactive components of the strain energy function defined in section 2.2.2, the total strain energy per unit reference volume can be written as
| (59) |
| (60) |
For a pressurized thin membrane, the radial component of stress P33(s) is small compared to P11(s) and P22(s) and can be assumed to be zero (see figure 6). Then, the Lagrange multiplier p can be replaced by the extra part of P33(s) as given by equation (55) (cf. [18]). This term is small, however, and negligible compared to the other terms of Aijkl. Equation (57) can be simplified to
| (61) |
As we saw in section 2.3.1, our FSI formulation considers a special definition for the strains (see equation (49)). Therefore, we use a vector of test function gradients ∇w = {w1,1, w2,2, w1,2 + w2,1, w3,1, w3,2}T in equation (47). Considering this, components of this equation can be written as:
| (62) |
Note that the dependency of wi,j, εkl, and ωkl with respect to time t is suppressed. The second term in the right hand side of equation (62) can be evaluated considering the following cases:
1) when i = j, k = l (no sum)
| (63) |
2) when i = j, k ≠ l (no sum)
| (64) |
3) when i ≠ j, k = l (no sum)
| (65) |
4) when i ≠ j, k ≠ l (no sum)
| (66) |
Considering equation (61), the following relations should be satisfied
| (67) |
| (68) |
| (69) |
Furthermore, we assume that multiplications involving the following components {P12(s), P22(s) − P11(s), P33(s), ω12, w1,2 − w2,1, H13, H23, w1,3, w2,3} generate second-order terms that are negligible based on the axisymmetric membrane assumption. Then, the term wi,j (Pκs)ij in (62) can be written in a matrix form
(Pκs)ij in (62) can be written in a matrix form
| (70) |
where P̃ = {P11(s), P22(s), P12(s), P31(s), P32(s)}T is a “pre-stress” tensor and K̃ is a “stiffness matrix” given by
| (71) |
The components of P̃ and K̃ are obtained from post-processing of the G&R simulation results at time s and given in the “membrane” polar coordinates defined in section 2.2.3. We must then transform these tensors to the “local” reference frame defined by the finite element mesh of the FSI membrane formulation (see figure 8).
Figure 8.
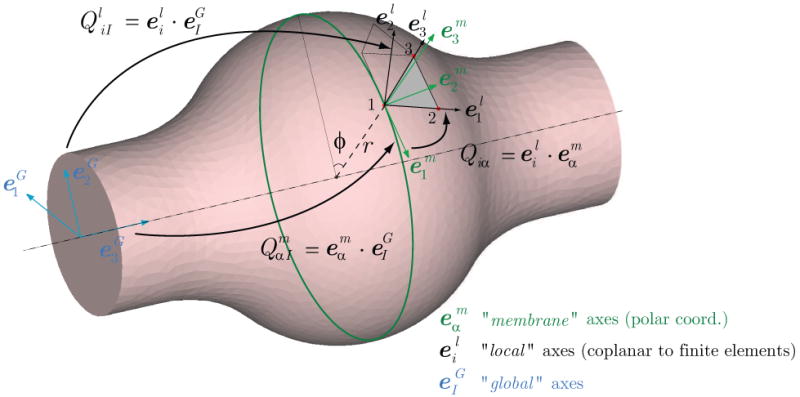
Definition of the transformation tensor Qiα between the reference systems used by the Nonlinear G&R formulation and the FSI formulation. (I = 1, 2, 3) are the bases of a global Cartesian coordinate system. (α = 1, 2, 3) are the orthonormal bases of membrane at a point, where is the basis vector in the circumferential direction and is the basis in the outward normal direction. (i = 1, 2, 3) is the orthonormal bases for a local triangular element used by the membrane formulation of the FSI code.
2.4.1 Mapping anisotropic material properties from the 2D G&R membrane frame to the 3D FSI local frame
The transformation of Aijkl and Pij(s) given in “membrane coordinates” to the FSI “local coordinates” is done by means of the rotation tensor Qiα according to the following expressions:
| (72) |
| (73) |
In order to characterize the components of the rotation tensor Qiα, we introduce the three sets of orthonormal bases represented in figure 8: (I = 1, 2, 3) are the bases of a “global” Cartesian coordinate system; (α = 1, 2, 3) are the “membrane” orthonormal bases used by the G&R formulation, where and are the bases in the circumferential and axial directions, respectively, and is the basis in the outward normal direction. (i = 1, 2, 3) is the “local” orthonormal bases for a triangular element of the FSI membrane formulation.
An orthogonal transformation Qm from the “global” frame to the “membrane” frame can be calculated by . Similarly, a transformation Ql from the “global” to the “local” frame is given by and the components of the tensor can be obtained from the three nodal points of the elements. Considering this, the orthogonal transformation Q from the “membrane” frame to the “local” frame becomes Q = Ql(Qm)−1 (or ).
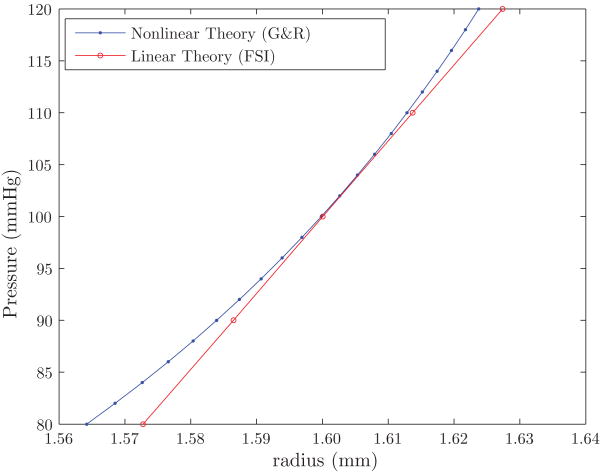
In order to validate the linearization proposed here, we performed a hydrostatic pressurization test of a cylindrical vessel of radius R = 1.6 mm and length L = 25 mm. In this problem, we constrained the longitudinal motion of both ends of the vessel. We compared deformations at the central cross section of the vessel (Z = 12.5 mm) obtained from the nonlinear constitutive theory used by the G&R formulation with the linearized theory used by the FSI formulation derived via small on large. The results of the pressurization test are shown in figure 9 and demonstrate a good agreement between the two formulations over the physiologic range of pressures (80 - 120 mmHg).
Figure 9.
Pressurization test comparing the radial deformation at the central cross section of the vessel obtained with the nonlinear G&R code and the linear FSI code.
3 Illustrative Simulation
3.1 Problem Definition
Consider a simple geometry given by an idealized cylindrical, axisymmetric representation of a basilar artery. We first study the evolution of the artery from an initial state (time 0) where the geometry is perfectly cylindrical (i.e., no taper) and the spatial distribution of material properties is uniform, to a postulated homeostatic state (time sN, see figure 10). This state exhibits a slight tapering in geometry and wall thickness and small longitudinal variations in material properties. We study this state in section 3.2. Once this homeostatic state is obtained, we introduce a concentric insult in the central section of the artery. This insult results in the removal of elastin, an associated change in intramural stress and geometry, and a consequent stress-mediated FSG process. Moreover, because intact elastin provides smooth muscle with many important biological cues (e.g., to not proliferate, to not migrate, to not synthesize matrix, and to not enter the cell death cycle prematurely; Karnik et al., [31]), loss of elastin within the aneurysmal segment necessarily changes the smooth muscle phenotype. For simplicity here, we assume that loss of elastin results in an associated loss of smooth muscle, as seen histologically in intracranial aneurysms [32], hence the primary growth and remodeling response is due to turnover of collagen (cf. Baek et al., [13]). Future models will need to include more gradual loss of elastin and changes in smooth muscle, however.
Figure 10.
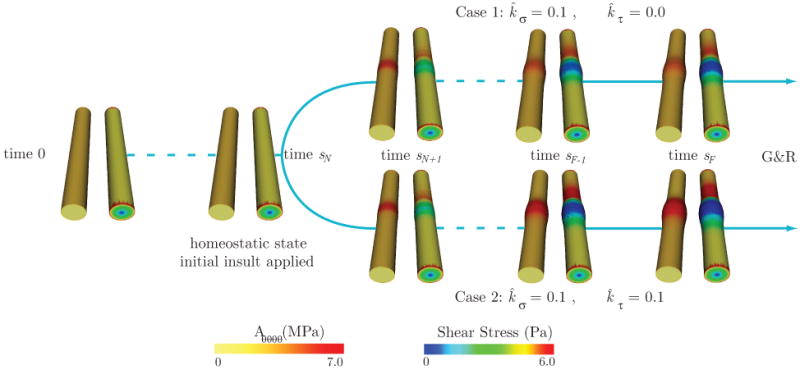
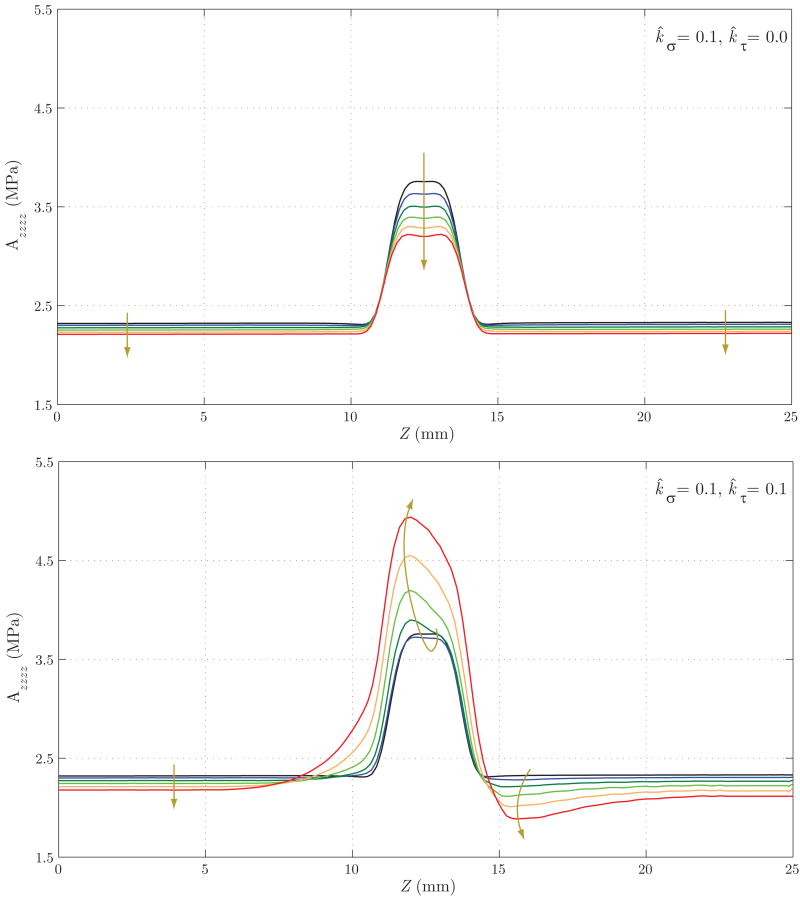
Schematic representation of the FSG problem considered. In the first stage of the analysis, we grow the artery until it reaches a homeostatic equilibrium at time sN. We then introduce an insult in the vessel wall that results in a local concentric loss of the elastin matrix, and perform two different FSG simulations: in Case 1, the arterial growth and remodeling is mediated by tensile stress only, whereas in Case 2, the growth is mediated by tensile and wall shear stress. For illustrative purposes, we show the evolution of the linearized circumferential component of the stiffness Aθθθθ (left) and the vessel wall shear stress (right) for each time step of the analysis.
We consider two different FSG cases (see figure 10): in Case 1, the growth and remodeling is mediated only via vessel wall tensile stress whereas in Case 2, this process is mediated by both tensile stress (via the effects of increased stretch on collagen production) and wall shear stress (via the effects of vasoactive molecules on collagen turnover).
We proceed to define the boundary conditions, vessel wall material parameters, and vasoactive parameters used in the analysis for both the fluid-solid interaction problem defined over the small time scales and the growth and remodeling problem defined over the large time scales.
FSI problem over the small time scales
Consider a typical volumetric flow wave mapped to a Womersley velocity profile at the inlet face of the basilar artery (see figure 11). The mean flow is Q̄ = 1.97 ml/s and the cardiac cycle has period T = 1.1 s. At the outlet face of the model we prescribe an impedance function Z(ω) that produces a typical range of pressures expected for this part of the vasculature: 85 mmHg diastolic pressure and 115 mmHg systolic pressure. The zero-frequency component of this impedance function (i.e., the vascular resistance ℜ) is Z(ω = 0) = ℜ = 6.75 × 104 dyn · cm−5 · s. The vessel is held in place by clamping the inlet and outlet sections of the wall. This set of boundary conditions for the small temporal scales remain constant during the modest growth and remodeling process defined herein over the large time scales, because we assume that the changes experienced by the artery are local and do not significantly affect the upstream and downstream hemodynamic conditions.
Figure 11.
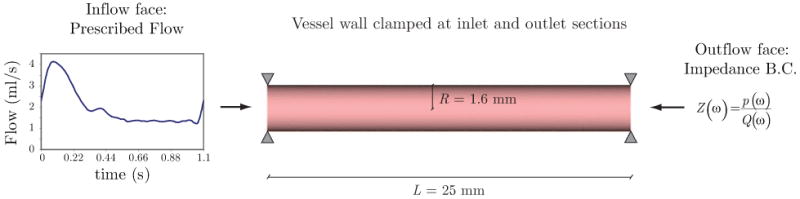
Geometry and boundary conditions considered in the FSI problem.
Vessel wall G&R problem over the large time scales
The boundary conditions for the G&R problem are such that the ends (Z = 0, L) of the arterial wall are fixed in the longitudinal direction but are free to move in the radial direction. The mass density of the vessel wall is assumed to remain constant at ρ = 1050 kg/m3. For the elastin fibers, the initial mass fraction is set to φe(0) = 0.1. The natural configuration mapping parameters (see equation (6)) are given by and . Lastly, the coefficient for the amorphous neo-Hookean function (see equation (20)) is c1 = 526.94 N · m/kg. As for the collagen fibers, for each family k we consider the following initial collagen mass fractions φk(0) and orientation angles αk(0):
The homeostatic deposition stretch for the collagen fiber families is and the coefficients in the exponential function for the material behavior (see equation (21)) are set to c2 = 746.97 N · m/kg, c3 = 29.16. The parameters for vasoactive behavior are T(Ca++) = 39.86 kPa, λ̃M = 1.2, and λ̃o = 0.7 (see equations (24-25)).
3.2 Identifying a Homeostatic State
At time 0, the length L, reference radius R, and thickness H of the artery are set to 25, 1.6, and 0.1047 mm, respectively. These are typical dimensions for a disease-free human basilar artery. In order to initialize the FSG computation, the fluid-solid interaction part of the analysis needs a distribution of material properties and geometry consistent with the known small pressure drop along the length of the vessel. We obtain these properties by arbitrarily defining a homeostatic state under a hydrostatic pressure of p(s = 0) = 13.332 kPa. This pressure is defined based on the mean flow Q̄ and resistance ℜ used in the subsequent pulsatile analysis. In this homeostatic state, the rates of mass production and removal of collagen fibers are balanced, and the vasoactive response of the smooth muscle is “normal”. Since this homeostatic state is defined by a hydrostatic loading, it has an associated uniform geometry and spatially uniform distribution of material parameters and pre-stresses. We can then apply the theory of small on large to compute the linearized material parameters and pre-stresses .
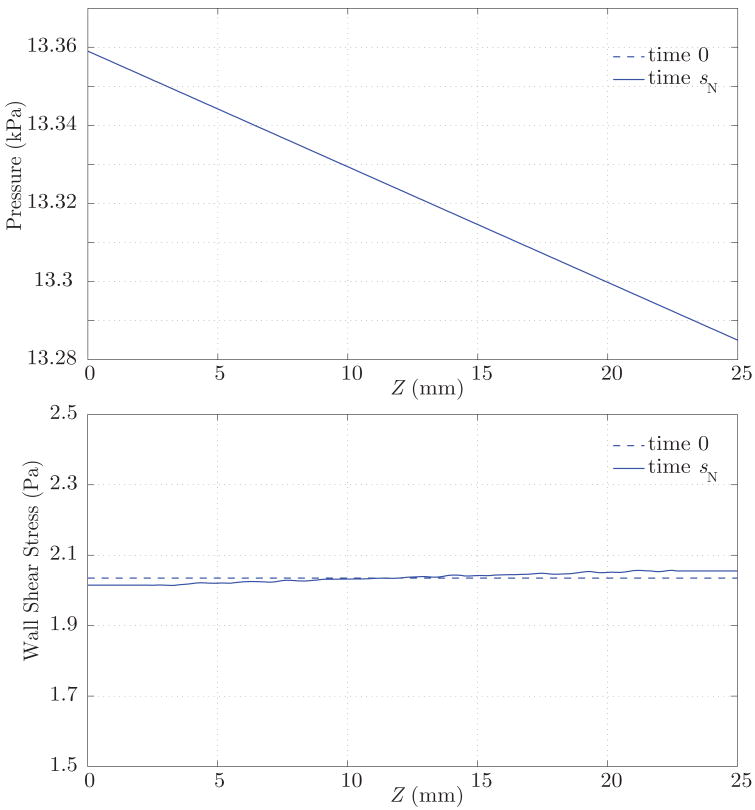
We then proceed to run the fluid-solid interaction analysis to obtain the mechanical stimuli experienced by the artery under pulsatile conditions. Identifying relevant stimuli is a challenge by itself, for many factors can regulate the biochemical processes defining growth and remodeling of the wall constituents. Here, we consider the simplest stimuli given by the time-average over the cardiac cycle of the blood pressure and the wall shear stress fields. We assume that these mechanical stimuli, acting on the small time scales, remain unchanged during the growth and remodeling process, acting on the large time scales, that defines the homeostatic state. These fields are presented in figure 12 (dashed lines). Observe the linear variation of the pressure along the vessel length and the spatially uniform wall shear stress field, as it corresponds to a vessel with uniform radius R. Using these mechanical stimuli, the G&R simulation grows the artery iteratively, exchanging information with the FSI formulation (see figure 2) until it reaches a new homeostatic equilibrium under such stimuli at some time tN. During this process, we consider the following non-dimensional stress mediation parameters k̂σ = 4.0 and k̂τ = 0.0, which induce a fast stable growth.
Figure 12.
Time-average pressure and wall shear stress at time 0 (dashed lines) and time sN (solid lines). This time sN defines the homeostatic state for the artery, wherein the growth and remodeling processes in the arterial wall are balanced with the hemodynamic environment.
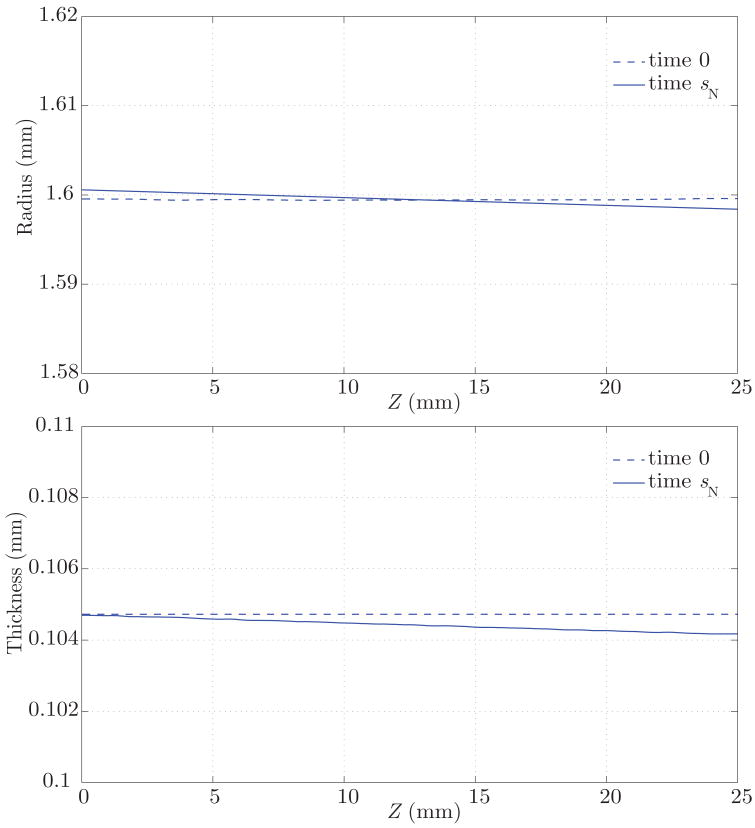
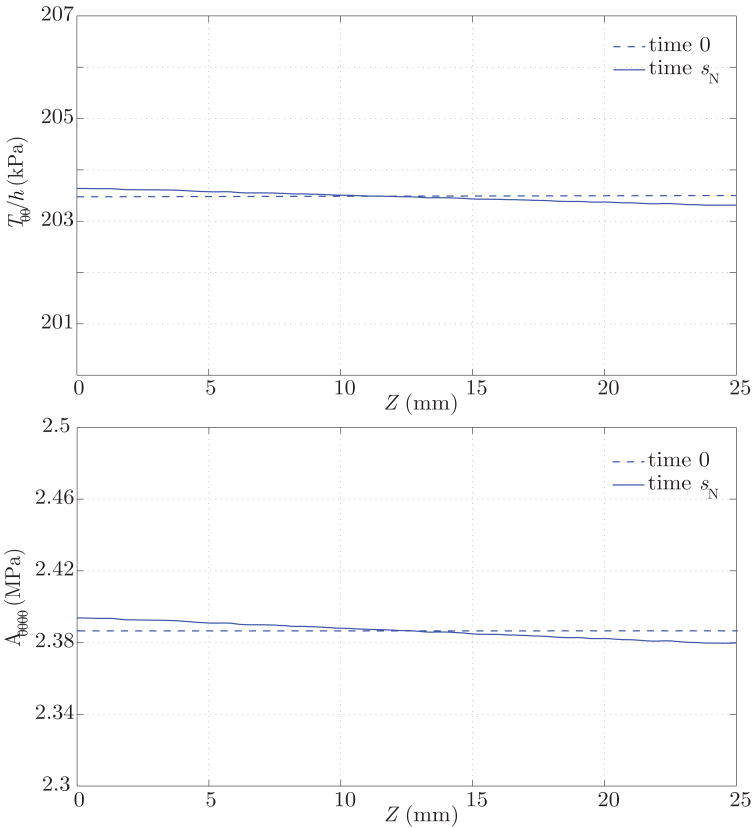
The result of this growth and remodeling is a new homeostatic configuration wherein the vessel is tapered. That is, the radius is slightly larger at the proximal end, where the average pressure is slightly larger. The wall thickness also decreases along the length of the artery, following the same linear trend of the radius and pressure (see figure 13). Figure 14 shows the corresponding changes in circumferential stress and stiffness. The artery at time sN is under a slightly larger circumferential stress in the proximal segment, and the circumferential stiffness is likewise higher proximally. These are manifestations of more collagen being turned over proximally due to the elevated tensile stress environment. These changes, although small, show a logical trend. In the homeostatic configuration we observe a linear variation in the time-averaged wall shear stress field, consistent with the observed variation in radius (see figure 12). Changes in the pressure field between the homeostatic configuration at time sN and the initial configuration at time 0 are negligible (i.e., less than a few dynes/cm2).
Figure 13.
Vessel wall inner radius and thickness at time 0 (dashed lines) and time sN (solid lines), where the vessel has adapted to a homeostatic configuration. In this configuration, the radius and thickness are larger on the proximal end due to a slightly elevated tensile stress.
Figure 14.
Circumferential tension and stiffness at time 0 (dashed lines) and time sN (solid lines), where the vessel has adapted to a homeostatic configuration. In this configuration, the circumferential tension and stiffness are larger in the proximal end due to a slightly elevated tensile stress.
3.3 Role of Pressure and Shear Forces after an Initial Circumferential Insult
Once we have obtained numerically a homeostatic state 1, we introduce an insult in the central section of the artery at time sN, resulting in the concentric loss of elastin in that position of the arterial wall. The mathematical representation of this insult is given by the following expression for the elastin mass density for all s, Z ∈ [0, L]:
| (74) |
This insult results in an instantaneous thinning of the vessel wall in the affected region, a new stress environment, and a consequent departure from homeostatic conditions. Therefore, the postulated rates of mass density production (see equation 12) for the different collagen families are altered from basal conditions. We study the stress-mediated growth and remodeling of the artery from this point on, considering two cases: Case 1 studies G&R mediated by tensile stress only, with k̂σ = 0.1 for the non-dimensionalized tensile stress mediation parameter; Case 2 considers G&R mediated by both tensile stress and wall shear stress, with tensile stress and wall shear stress mediation parameters k̂σ = 0.1 and k̂τ = 0.1, respectively.
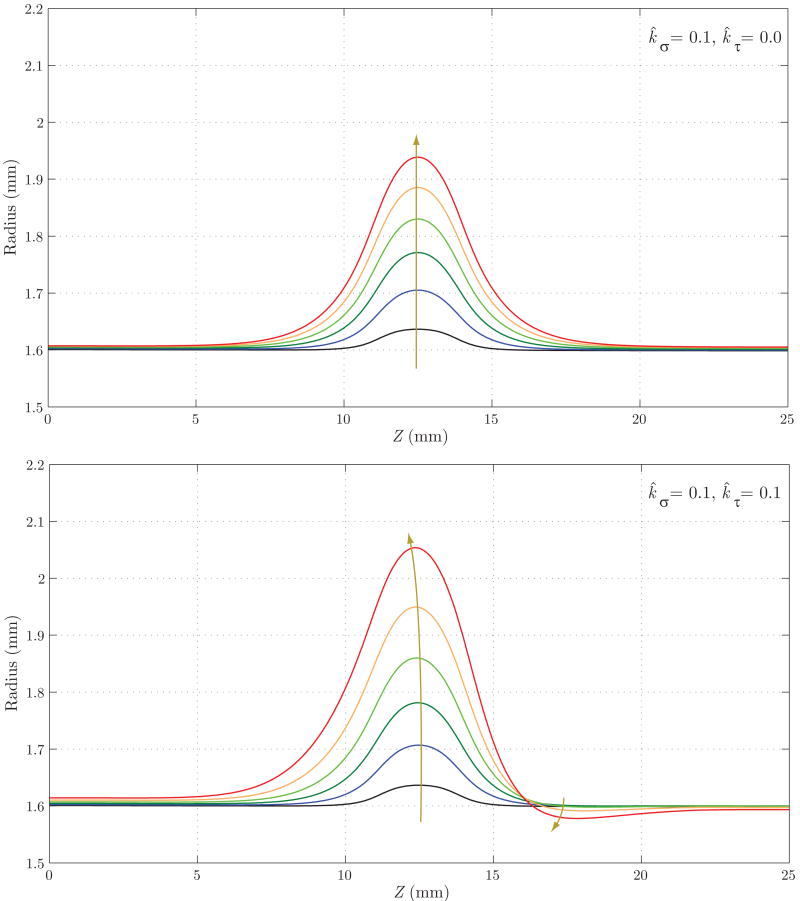
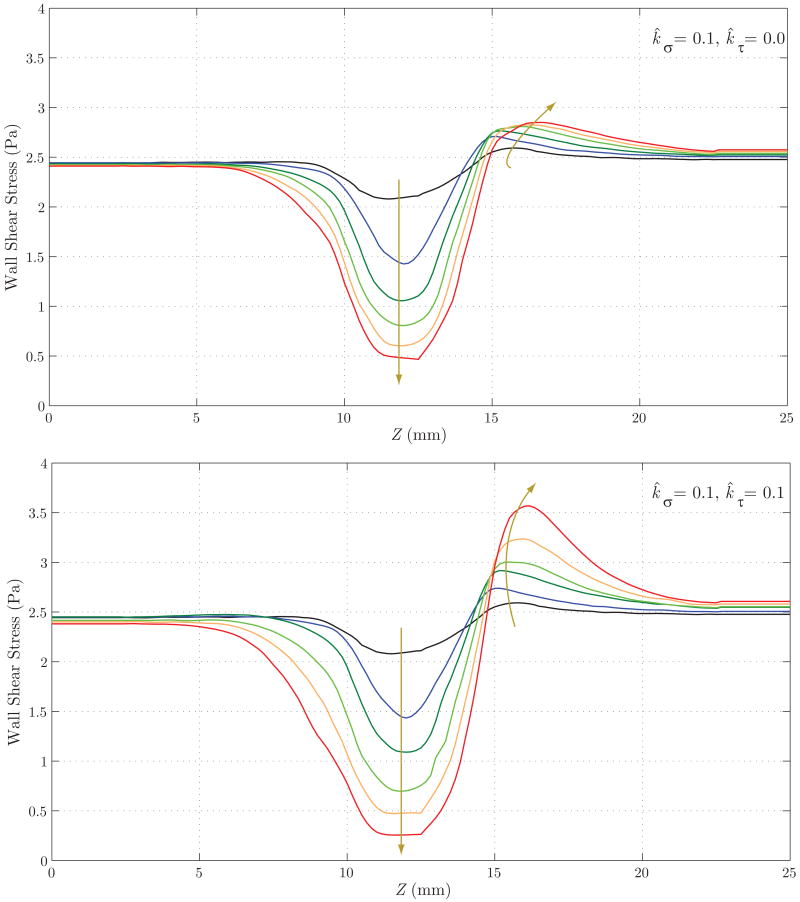
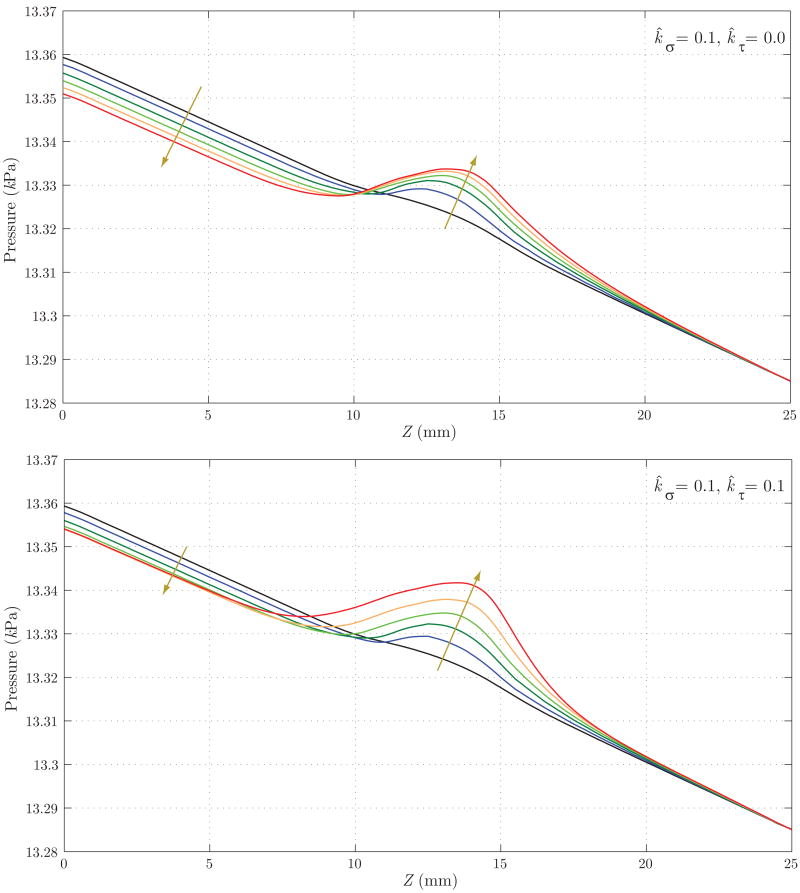
Figure 15 shows the evolution of the luminal radius for both cases. Case 2 yields a noticeably faster rate of enlargement in the center of the aneurysmal region, but a reduction in radius at the distal end of the aneurysm (Z ≈ 17 mm). This is probably due to the increase in wall shear stress in that region (see figure 17) and the specific rule adopted for mass production as a function of shear stress (see equation (12)). In figure 16, we observe a faster localized increase in pressure for Case 2 due to the corresponding faster increase in radius. The magnitude of this pressure increase is very modest in both cases, however, accounting for less than one mmHg. Figure 17 shows the evolution of time averaged wall shear stress. The shear stress decreases significantly over time within the aneurysmal region in both cases, but this reduction occurs faster in Case 2. This is consistent with the faster increase in radius seen in figure 15. In both cases, we observe an increase in wall shear stress at the distal end of the aneurysm (Z ≈ 15 mm). This increase is more pronounced in Case 2 due to the radius reduction seen in this region in figure 15.
Figure 15.
Evolution of the luminal radius for Case 1 (tensile stress mediated growth and remodeling, above) and Case 2 (a combination of tensile stress and wall shear stress mediated growth and remodeling, below). Case 2 shows a faster, non-symmetric enlargement. Note that the arrows denote changes with increasing time.
Figure 17.
Evolution of wall shear stress for Case 1 (above) and Case 2 (below). Note the faster reduction of shear stress in the aneurysmal region for Case 2, consistent with the faster enlargement seen in figure 15. In both cases, we observe an increase in wall shear stress at the distal end of the aneurysm (Z ≈ 15 mm). This increase is more pronounced in Case 2 due to the radius reduction seen in this region in figure 15.
Figure 16.
Evolution of blood pressure for Case 1 (above) and Case 2 (below). Case 2 shows a faster localized increase in pressure due to the faster increase in radius seen in figure 15. The magnitude of pressure variation in the aneurysmal region is very small (only a fraction of a millimeter of mercury) in both cases, however. The arrows denote changes with increasing time.
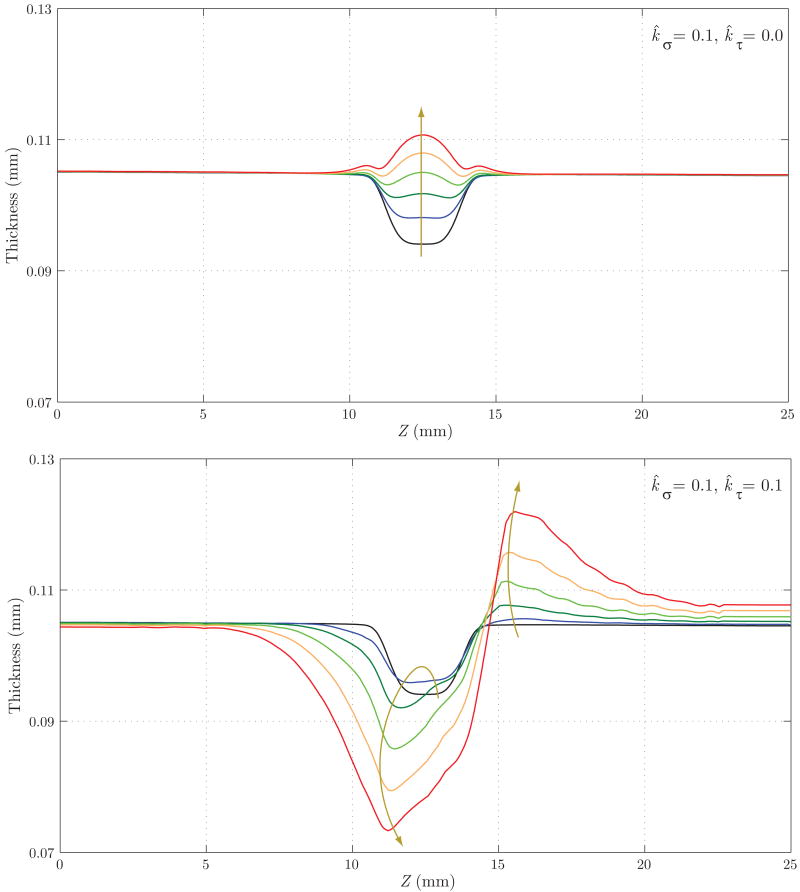
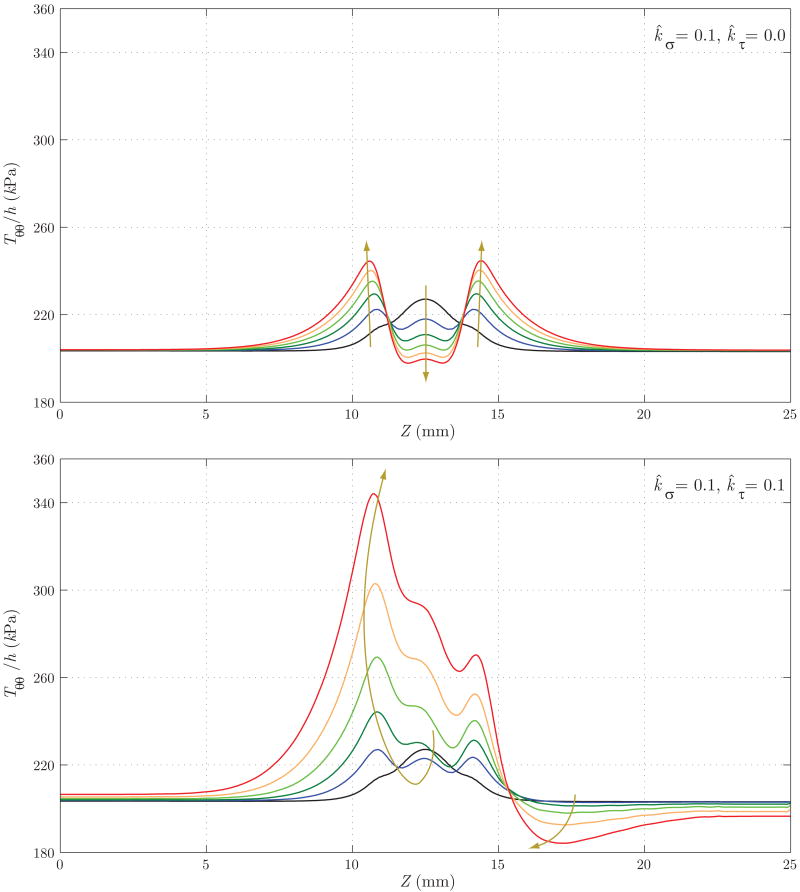
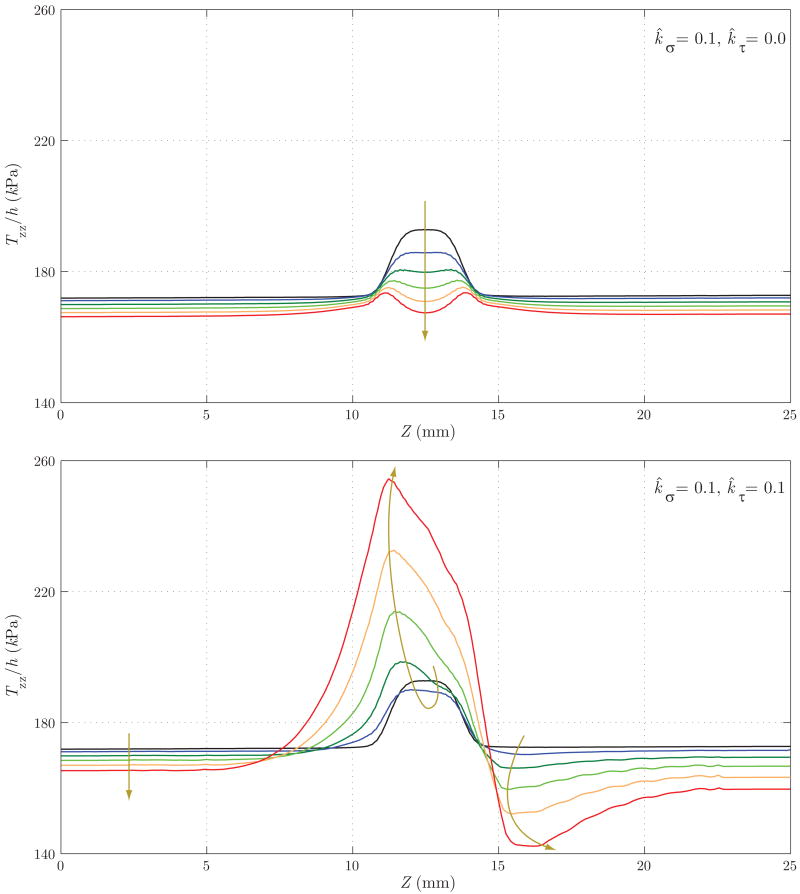
Figure 18 shows the evolution of the thickness h. Here, the differences between the two cases are remarkable: whereas in Case 1 we observe an eventual thickening due to the stress-mediated G&R confined to the region that suffered the original insult, in Case 2 the wall gets thinner not only in the aneurysmal region, but also at the proximal end of the aneurysm. On the other hand, the distal end thickens due to the higher wall shear stress concentration observed in figure 17. Figures 19 and 20 show the evolution of the circumferential and axial components of the wall stress Tθθ/h and Tzz/h, respectively. These trends also differ significantly. For Case 1, we observe a symmetric concentration of circumferential stresses at the proximal (Z ≈ 11 mm) and distal (Z ≈ 14 mm) ends of the aneurysm, whereas the axial stress reduces probably due to a combination of changes in fiber angle orientation (new collagen fibers are more aligned in the circumferential direction due to the radial growth) and wall thickening. For Case 2, however, the circumferential stress is highest at the proximal end of the aneurysm (Z ≈ 11 mm), corresponding to the thinnest portion of the wall. The evolution of the axial stress can also be explained by the changes in wall thickness and fiber orientation.
Figure 18.
Evolution of wall thickness for Case 1 (above) and Case 2 (below). These trends differ significantly: whereas in Case 1 we observe an eventual thickening due to the stress-mediated G&R confined to the region that suffered the original insult, in Case 2 the wall becomes thinner, not only in the aneurysmal region but also at the proximal end of the aneurysm. On the other hand, the distal end thickens due to the higher wall shear stress concentration seen in figure 17.
Figure 19.
Evolution of the circumferential component of the intramural stress for Case 1 (above) and Case 2 (below). Case 1 shows a symmetric concentration of stresses in the proximal (Z ≈ 11 mm) and distal (Z ≈ 14 mm) ends of the aneurysm. This character is reminiscent of that presented by Elger et al. [33] based on a static analysis of a developed axisymmetric lesion. On the other hand, Case 2 shows the highest stress concentration at Z ≈ 11 mm, corresponding to the thinnest portion of the wall (see figure 18).
Figure 20.
Evolution of the axial component of the intramural stress for Case 1 (above) and Case 2 (below). Case 1 shows a reduction in Tzz/h due to a combination of changes in fiber angle orientation (collagen fibers get more aligned in the circumferential direction) and wall thickening. The same changes in fiber orientation and especially wall thinning at Z ≈ 11 mm explain the trend for Case 2.
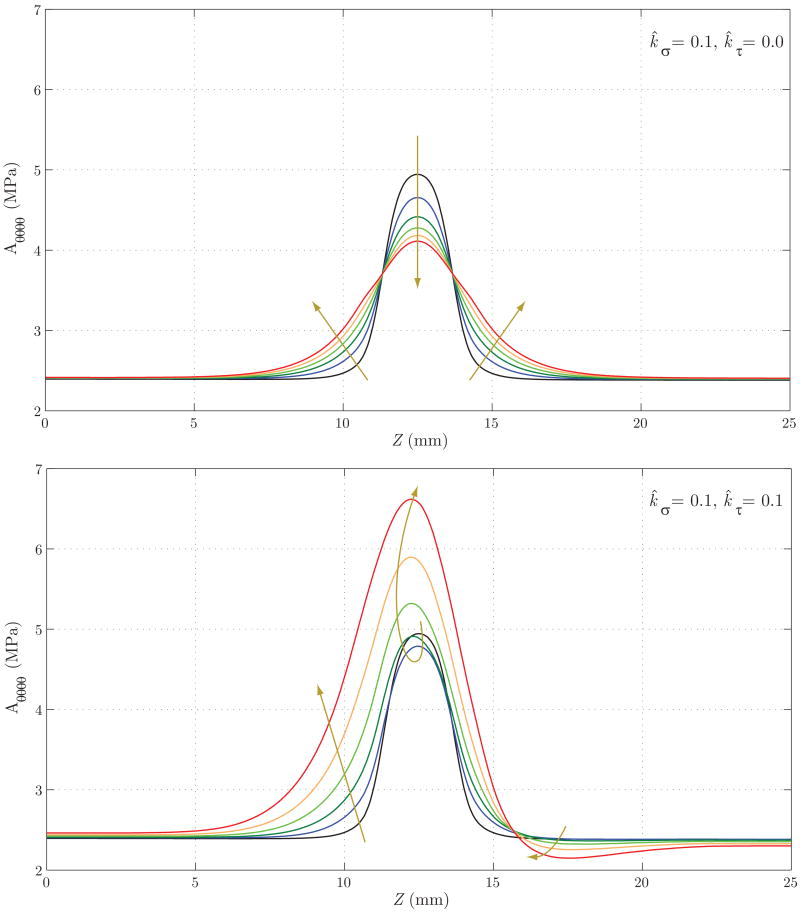
Lastly, figures 21 and 22 show the evolution of the main components of the linearized circumferential and longitudinal stiffness, Aθθθθ and Azzzz, respectively. In figure 21, we see that for Case 1 the concentration of stresses at Z ≈ 11 mm and Z ≈ 14 mm observed in figure 19 results in a faster turnover of collagen fibers and a consequent circumferential stiffening of the wall. This trend is the opposite in the central section of the vessel. For Case 2, the generalized increase in circumferential stress seen in figure 19 explains the stiffening of the wall. In figure 22 we observe a stiffness decrease in Case 1 consistent with the axial stress decrease seen in figure 20. On the other hand, the increase in longitudinal stress seen in figure 20 for Case 2 explains the increase in stiffness seen in this case.
Figure 21.
Evolution of the linearized circumferential stiffness for Case 1 (above) and Case 2 (below). In Case 1, the concentration of stresses at Z ≈ 11 mm and Z ≈ 14 mm observed in figure 19 results in a faster turnover of collagen fibers and consequent stiffening of the wall in the circumferential direction. This trend is opposite in the central section of the vessel. For Case 2, the generalized increase in circumferential stress seen in figure 19 explains the stiffening of the wall.
Figure 22.
Evolution of the linearized longitudinal stiffness for Case 1 (above) and Case 2 (below). Case 1 shows a stiffness decrease consistent with the decrease in axial stress seen in figure 20. The increase in axial stress seen in figure 20 (Case 2) also explains the increase in stiffness seen here.
4 Discussion
Cell culture experiments have been very important in elucidating the types and extents of responses by individual vascular cells to changes in mechanical loading [34]. For example, smooth muscle cells of the vascular wall increase their production of collagen in response to increased cyclic stretch (or stress). Such stress-mediated increases in collagen production are consistent with, indeed explain in part, clinically observed increases in collagen content in pathologies ranging from hypertension to aneurysms. Production is typically balanced by removal, however, thus it is not surprising that it has also been found that cyclic stretch (or stress) can also increase the production of matrix metalloproteinases (MMPs) by smooth muscle cells. These MMPs enable selective enzymatic degradation of matrix constituents, including collagen, and are thus fundamental to refashioning the vascular wall in cases of adaptation and disease [35]. Whereas these, and similar, changes in cell and matrix turnover clearly depend on changes in intramural wall stress, cell culture studies similarly reveal the importance of endothelial-derived vasoactive molecules in cell and matrix turnover.
It is well known that local increases in wall shear stress increase the production of nitric oxide (NO) by the endothelium whereas decreases in wall shear stress increase the production of endothelin-1 (ET-1). NO is a potent vasodilator whereas ET-1 is a potent vasoconstrictor, hence explaining the clinically observed dilation of the wall in response to increases in flow and contraction in response to decreases in flow, each of which tend to restore the wall shear stress toward its local baseline value. What has become known more recently, however, is that NO is also an inhibitor of both smooth muscle cell proliferation and its synthesis of collagen [36] whereas ET-1 is a promoter of smooth muscle proliferation and the synthesis of collagen [37]. Note, too, that decreased wall shear stress upregulates adhesion molecules such as ICAM-1 and VCAM-1, which promotes the recruitment of circulating blood cells to the endothelium that contribute to local degradation of underlying matrix [14]. In other words, not only do changes in local wall shear stress from baseline play important roles in controlling smooth muscle contractility, they also contribute to the rate and extent of cell and matrix turnover within the wall. Clearly, then, to understand hemodynamic-induced changes in vascular geometry, structure, and function, we must quantify the complexities of the flow field and the distribution of stress on and within the arterial wall.
Motivated by these and similar observations, we have brought together for the first time computational frameworks for solving the full 3-D hemodynamics problem in complex domains (e.g., patient-specific geometries) and the wall mechanics problem defined on complex domains and involving geometrically and materially nonlinear behaviors. Moreover, for the first time, this has been accomplished by incorporating within the mechanics a conceptual and mathematical framework that accounts for cell and matrix turnover in evolving configurations as observed in vivo. We emphasize, however, that our goal here was to focus on developing a general framework, not to solve specific biological or clinical problems. Specifically, our goal was to develop a framework general enough to enable new data on stress-mediated growth and remodeling processes to be incorporated mathematically as they become available. For example, there is a pressing need for more data on which to build more comprehensive constitutive models for mass production and removal as a function of the evolving state of stress (or strain). This may include the need to model turnover as a function of changes in cyclic stress or stress rates associated with changes in pulse pressure, but this will be straightforward because the current FSI solver accounts for such complexities. There may also be a need to relate growth and remodeling directly to changes in smooth muscle contractility, but again that should be straightforward to accomplish given our formulation of the wall mechanics.
For illustrative purposes, we focused on a simple yet important situation: altered hemodynamics within a nearly cylindrical section of an artery that experiences an axisymmetric loss of elastin within the central region. This situation is similar to that considered in Baek et al. [2] except that here we contrasted growth and remodeling responses that could occur in response to changes in both intramural stresses and wall shear stresses (cf. figure 10). One of the first observations is that because of the modest pressure drop along the vessel both before and after the loss of elastin (cf. figures 12a and 16a), subsequent growth and remodeling was nearly symmetric about the center-point (Z = 12.5 mm) in response to pressure-induced intramural stresses, as found by Baek et al. [2] (see their figure 3). Indeed, it is for this reason that the mechanical state that evolved reflected well the findings by Elger et al. [33] for a model lesion. One of the most notable changes that can occur with shear stress mediated growth and remodeling, therefore, is the breaking of this symmetry (i.e., differences in shear distally versus proximally). Indeed, clinical observation reveals time and again the myriad sizes and shapes of aneurysms, and the present simple simulation reveals the potential importance of complex shear stress fields in contributing to this biological diversity. Indeed, note that the growth and remodeling tended to be more localized to the region of the initial insult in the cases of intramural stress mediated turnover whereas the region of active growth and remodeling extended more in the case of shear stress mediation. Figure 18, in particular, shows the potentially dramatic influence of regional variations in wall shear stress (cf. figure 17) on wall thickness, a critical parameter in defining the enlargement and rupture-potential of an aneurysm for it contributes directly to the structural stiffness of the vascular wall (figures 19 to 22). This situation will only increase in complexity once contributions such as shear stress mediated monocyte localization or platelet activation are included in the analyses.
For this illustrative problem we have assumed a smooth geometry for the blood vessel (even after introducing the damage) and have used mean values for the mechano-stimuli to rule the long-term G&R. This results in a small local variation of the stimuli during the evolution (both in time and space). Therefore increasing the time step size would not change the results qualitatively. However, when applying this method to patient-specific geometries or using temporal change of stress as mechano-stimuli, we should investigate the robustness of the method by studying parameters such as frequency of ‘hand-shaking’ between codes, time step size, etc.
In summary, we emphasize that the simple case considered herein is intended to be for illustrative purposes only. Thus, although the results presented consider an axisymmetric geometry, the code has been written generally to address three-dimensional flows and complex wall geometries. Idealized stress-mediated growth and remodeling kinetics were used simply to show possible changes in the geometry, structure, and function of the wall in response to evolving changes in hemodynamic loading. Now that this framework has been completed and tested conceptually, there is pressing need to search for physiologically realistic models of stress-mediated turnover and to design new classes of experiments that enable the validation of such FSG modeling. Once validated in well designed experiments, we suggest that FSG modeling will become an essential tool in the understanding of diverse vascular pathologies, the design of improved clinical interventions (e.g., surgical planning), and the design of improved implantable medical devices.
Acknowledgments
This material is based upon work supported, in part, by grants from the National Science Foundation (ITR-0205741 CAT) and the National Institutes of Health (HL-64372, HL-80415 JDH; U54-GM072970, P50 HL083800 CAT).
Footnotes
To properly define a homeostatic state resulting from developmental biology is of great interest, but exceedingly complex and not needed for the present purposes.
References
- 1.Humphrey JD, Taylor CA. Intracranial and abdominal aortic aneurysms: Similarities, differences, and need for a new class of computational models. Annual Review of Biomedical Engineering. 2008;10:221–246. doi: 10.1146/annurev.bioeng.10.061807.160439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Baek S, Rajagopal KR, Humphrey JD. A theoretical model of enlarging intracranial fusiform aneurysms. ASME Journal of Biomedical Engineering. 2006;128:142–149. doi: 10.1115/1.2132374. [DOI] [PubMed] [Google Scholar]
- 3.Figueroa CA, Vignon-Clementel IE, Jansen KE, Hughes TJR, Taylor CA. A coupled momentum method for modeling blood flow in three-dimensional deformable arteries. Computer Methods in Applied Mechanics and Engineering. 2006;195:5685–5706. [Google Scholar]
- 4.Baek S, Gleason RL, Rajagopal KR, Humphrey JD. Theory of small on large: Possible utility for computations of fluid-solid interactions in arteries. Computer Methods in Applied Mechanics and Engineering. 2007;196:3070–3078. [Google Scholar]
- 5.Vignon-Clementel IE, Figueroa CA, Jansen KE, Taylor CA. Outflow boundary conditions for three-dimensional finite element modeling of blood flow and pressure in arteries. Computer Methods in Applied Mechanics and Engineering. 2006;195:3776–3796. [Google Scholar]
- 6.Marsden JE, Hughes TJR. Mathematical foundations of elasticity. Dover Publishers; Toronto: 1994. [Google Scholar]
- 7.Humphrey JD, Rajagopal KR. A constrained mixture model for growth and remodeling of soft tissues. Mathematical Models and Methods in Applied Science. 2002;12:407–430. [Google Scholar]
- 8.Alastrué V, Peña E, Martínez MA, Doblaré M. Assessing the use of the “opening angle method” to enforce residual stresses in patient-specific arteries. Annals of Biomedical Engineering. 2007;35:1821–1837. doi: 10.1007/s10439-007-9352-4. [DOI] [PubMed] [Google Scholar]
- 9.Govindjee S, Mihalic PA. Computational methods for inverse finite elastostatics. Computer Methods in Applied Mechanics and Engineering. 1994;136:47–57. [Google Scholar]
- 10.Lu J, Zhou X, Raghavan ML. Inverse elastostatic stress analysis in pre-deformed biological structures: Demonstration using abdominal aortic aneurysms. Journal of Biomechanics. 2007;40:693–696. doi: 10.1016/j.jbiomech.2006.01.015. [DOI] [PubMed] [Google Scholar]
- 11.Langille BL. Arterial remodeling: relation to hemodynamics. Can J Physiol Parmacol. 1996;74:834–841. [PubMed] [Google Scholar]
- 12.Langille BL. Remodeling of developing and mature arteries: endothelium, smooth muscle, and matrix. Journal of Cardiology and Pharmacology. 1993;21:S11–S17. doi: 10.1097/00005344-199321001-00003. [DOI] [PubMed] [Google Scholar]
- 13.Baek S, Valentín A, Humphrey JD. Biochemomechanics of cerebral vasospasm and its resolution: II. constitutive relations and model simulations. Annals of Biomedical Engineering. 2007;35:1498–1509. doi: 10.1007/s10439-007-9322-x. [DOI] [PubMed] [Google Scholar]
- 14.Humphrey JD. Cardiovascular Solid Mechanics: Cells, Tissues, and Organs. Springer-Verlag; New York: 2002. [Google Scholar]
- 15.Baek S, Rajagopal KR, Humphrey JD. Competition between radial expansion and thickening in the enlargement of an intracranial saccular aneurysm. Journal of Elasticity. 2005;80:13–31. [Google Scholar]
- 16.Driessen NJB, Wilson W, Bouten CVC, Baaijens FPT. A computational model for collagen fibre remodelling in the arterial wall. Journal of Theoretical Biology. 2004;226:53–64. doi: 10.1016/j.jtbi.2003.08.004. [DOI] [PubMed] [Google Scholar]
- 17.Hariton I, deBotton G, Gasser TC, Holzapfel GA. Stress-modulated collagen fiber remodeling in a human carotid bifurcation. Journal of Theoretical Biology. 2007;248:460–470. doi: 10.1016/j.jtbi.2007.05.037. [DOI] [PubMed] [Google Scholar]
- 18.Holzapfel GA, Gasser TG, Ogden RW. A new constitutive framework for arterial wall mechanics and a comparative study of material models. Journal of Elasticity. 2000;61:1–48. [Google Scholar]
- 19.Rachev A, Hayashi K. Theoretical study of the effects of vascular smooth muscle contraction on strain and stress distributions. Annals of Biomedical Engineering. 1999;27:459–468. doi: 10.1114/1.191. [DOI] [PubMed] [Google Scholar]
- 20.Taylor CA, Hughes TJR, Zarins CK. Finite element modeling of blood flow in arteries. Computer Methods in Applied Mechanics and Engineering. 1998;158:155–196. [Google Scholar]
- 21.Heil M. An efficient solver for the fully coupled solution of large-displacement fluid-structure interaction problems. Computer Methods in Applied Mechanics and Engineering. 2004;193:11–23. [Google Scholar]
- 22.Torii R, Oshima M, Kobayashi T, Takagi K, Tezduyar TE. Computer modeling of cardiovascular fluid-structure interactions with the deforming-spatial-domain/stabilized space-time formulation. Computer Methods in Applied Mechanics and Engineering. 2006;195:1885–1895. [Google Scholar]
- 23.Givoli D, Keller JB. A finite element method for large domains. Computer Methods in Applied Mechanics and Engineering. 1989;76(1):41–66. [Google Scholar]
- 24.Hughes TJR. Multiscale phenomena: Green's functions, the dirichlet-to-neumann formulation, subgrid scale models, bubbles and the origins of stabilized methods. Computer Methods in Applied Mechanics and Engineering. 1995;127:387–401. [Google Scholar]
- 25.Whiting CH, Jansen KE. A stabilized finite element method for the incompressible navier-stokes equations using a hierarchical basis. International Journal for Numerical Methods in Fluids. 2001;35:93–116. [Google Scholar]
- 26.Hughes TJR. The finite element method: Linear static and dynamic finite element analysis. Dover Publishers; New York: 2000. page. [Google Scholar]
- 27.Holzapfel GA. Nonlinear Solid Mechanics: A Continuum Approach for Engineering. John Wiley & Sons; Chichester: 2000. [Google Scholar]
- 28.Humphrey JD, Na S. Elastodynamics and arterial wall stress. Annals of Biomedical Engineering. 2002;30:509–523. doi: 10.1114/1.1467676. [DOI] [PubMed] [Google Scholar]
- 29.Jansen KE, Whiting CH, Hulbert GM. Generalized-alpha method for integrating the filtered navier-stokes equations with a stabilized finite element method. Computer Methods in Applied Mechanics and Engineering. 2000;190(34):305–319. [Google Scholar]
- 30.Olufsen MS. Structured tree outflow condition for blood flow in larger systemic arteries. American Journal of Physiology. 1999;276:H257–H268. doi: 10.1152/ajpheart.1999.276.1.H257. [DOI] [PubMed] [Google Scholar]
- 31.Karnik SK, Brooke BS, Bayes-Genis A, Sorensen L, Wythe JD, Schwartz RS, Keating MT, Li DY. A critical role for elastin signaling in vascular morphogenesis and disease. Development. 2003;130:411–423. doi: 10.1242/dev.00223. [DOI] [PubMed] [Google Scholar]
- 32.Humphrey JD, Canham PB. Structure, mechanical properties, and mechanics of intracranial saccular aneurysms. Journal of Elasticity. 2000;61:49–81. [Google Scholar]
- 33.Elger DF, Blackketter DM, Budwig RS, Johansen KH. The influence of shape on the stresses in model abdominal aortic aneurysms. Journal of Biomechanical Engineering. 1996;118(3):326–332. doi: 10.1115/1.2796014. [DOI] [PubMed] [Google Scholar]
- 34.Humphrey JD. Vascular adaptation and mechanical homeostasis at tissue, cellular, and sub-cellular levels. Cell Biochemistry and Biophysics. 2008;50:53–78. doi: 10.1007/s12013-007-9002-3. [DOI] [PubMed] [Google Scholar]
- 35.Newby AC. Matrix metalloproteinases regulate migration, proliferation, and death of smooth muscle cells by degrading matrix and non-matrix substrates. Cardiovascular Research. 2006;69:614–624. doi: 10.1016/j.cardiores.2005.08.002. [DOI] [PubMed] [Google Scholar]
- 36.Rizvi MAD, Myers PR. Nitric oxide modulates basal and endothelin-induced coronary artery vascular smooth muscle cell proliferation and collagen levels. Journal of Molecular and Cellular Cardiology. 1997;29:1779–1789. doi: 10.1006/jmcc.1996.0480. [DOI] [PubMed] [Google Scholar]
- 37.Rizvi MAD, Katwa L, Spadone DP, Myers PR. The effects of endothelin-1 on collagen type i and type iii synthesis in cultured porcine coronary artery vascular smooth muscle cells. Journal of Molecular and Cellular Cardiology. 1996;28:243–252. doi: 10.1006/jmcc.1996.0023. [DOI] [PubMed] [Google Scholar]