Intermolecular shielding contributions studied by modeling the ¹³C chemical-shift tensors of organic single crystals with plane waves

Abstract

In order to predict accurately the chemical shift of NMR-active nuclei in solid phase systems, magnetic shielding calculations must be capable of considering the complete lattice structure. Here we assess the accuracy of the density functional theory gauge-including projector augmented wave method, which uses pseudopotentials to approximate the nodal structure of the core electrons, to determine the magnetic properties of crystals by predicting the full chemical-shift tensors of all ¹³C nuclides in 14 organic single crystals from which experimental tensors have previously been reported. Plane-wave methods use periodic boundary conditions to incorporate the lattice structure, providing a substantial improvement for modeling the chemical shifts in hydrogen-bonded systems. Principal tensor components can now be predicted to an accuracy that approaches the typical experimental uncertainty. Moreover, methods that include the full solid-phase structure enable geometry optimizations to be performed on the input structures prior to calculation of the shielding. Improvement after optimization is noted here even when neutron diffraction data are used for determining the initial structures. After geometry optimization, the isotropic shift can be predicted to within 1 ppm.

INTRODUCTION

The prediction of magnetic properties by electronic structure methods provides valuable information to NMR spectroscopists.¹ Calculations of the chemical shift allow for the interpretation of spectral data in terms of structural parameters while assisting in spectral peak assignments. Moreover, theory and computation together play vital roles in the growing field of NMR crystallography.² There is consistent evidence that in order to properly investigate condensed phase properties, a periodic crystal structure must be employed. Numerous approximate methods, which are reviewed in Ref. 3, have been used previously,³ but only recently have methods been developed to perform NMR calculations using periodic boundary conditions.^{4, 5} It has been shown^{6, 7, 8} that comparing calculated shielding and experimental shift tensors from single-crystal measurements provides the most stringent test of theoretical and computational approaches. Moreover, the crystal tensor data allow exploration of lattice effects, a topic that has not previously been explored with both complete chemical-shift tensors and accurate shielding calculations that incorporate periodic boundary conditions. Here, we demonstrate the ability of the gauge-including projector augmented wave (GIPAW) method⁵ to accurately calculate the chemical-shift tensors of ¹³C nuclides located at all carbon atom positions in 14 organic single crystals.

Compared to all-electron correlated methods, the use of density functional theory (DFT) is relatively inexpensive with regard to computational resources and, in principle, accounts for electron correlation. Consequently DFT has become the electronic structure method of choice for NMR shielding calculations in large molecules.⁹ Results from DFT methods using all-electron wave functions to determine the magnetic properties via the gauge including atomic orbital (GIAO) method¹⁰ are commonly reported in the literature. The newer GIPAW method of Pickard and Mauri⁵ overcomes the challenge of gauge invariance in plane waves by the addition of a field-dependent phase factor to the projector operator, enabling computationally efficient NMR simulations from periodic crystal structures. This approach was proven very effective in accounting for intermolecular interactions and solid-phase distortions.¹¹

An experimental data set of ¹³C chemical-shift tensors from all carbon atom locations in 14 organic single crystals^{12, 13, 14, 15, 16, 17, 18, 19} has been compiled by Grant and co-worker; due to the high precision of these measurements, this data set is of great value for testing theoretical and computational approaches.^{6, 7, 8} Typically, new methodologies to predict the chemical shift focus on collections of shifts from small gas phase molecules.²⁰ These gas-phase databases provide a diversity of local environments to predict accurate ¹³C isotropic shift values where rotational and vibrational effects have been accounted for and include molecules with known electron correlation issues. While these databases are advantageous in these studies, the single-crystal database examined here offers additional benefits. The complete ¹³C chemical-shift tensor has been measured to a precision of 0.5 ppm or better for these molecules, and the 102 carbon atoms within these molecules supply 612 ¹³C tensor elements. These elements span a range of over 240 ppm, thus providing the quantity and quality of data necessary for a statistically significant set of regression parameters. In addition, these tensor data enable the assessment of the theory spatially. Since the orientational information of the tensor is mappable onto the molecular axis system, the discrepancies in the agreement that are decomposed into the tensor components identify the location of inadequacies of the electronic method. These organic compounds are ideal for the study of crystalline effects as their modest sizes lend themselves to modeling with sufficient theory, and they also represent a diversity of chemical bonding environments. The study of molecules in condensed phases rather than as gaseous species, while more challenging, moves toward applications in areas of ever-expanding scientific interest such as nanomaterials and solid-state (e.g., membrane bound) biomolecules.

The high sensitivity of the chemical shift renders it an attractive parameter for the characterization of materials. This sensitivity, however, requires that one take caution in interpreting the shift. The same is true when assessing models to predict the shift. Electronic structure methods have known limitations when predicting the magnetic shieldings.⁹ If one removes these systematic flaws, a powerful tool is realized for the analysis of spectral data. The current state-of-the-art for predicting chemical shifts, demonstrated here by incorporating the lattice structure, is at 3.0 ppm for aromatic tensors and 1.9 ppm for carbohydrates. This level is achieved only after removing the systematic flaws from the theory, as demonstrated in this work.

THEORY AND METHODS

Magnetic shielding and chemical shift tensors

Magnetic shielding refers to the physical phenomenon of a secondary magnetic field being generated by the induced motions of the electrons nearby to a nucleus when in the presence of an applied magnetic field. The degree to which current density is created in a molecular system will depend on the chemical bonding as well as the spatial arrangement of nuclei. Because the induced current density will generally have an orientational dependence, the magnetic shielding is a tensor quantity. Formally, the shielding tensor is defined as the second derivative of the energy with respect to the external field B and the magnetic moment of the nucleus μ,

$${\sigma }_{ij}=\frac{{\partial }^{2}E}{\partial {\mathbf{B}}_i\partial {\mathbf{\mu }}_j},$$ (1)

where i and j are components of the field and moment vectors. There exist nine tensor elements, in principle. However, only the six symmetric elements are observable in the NMR spectrum. The three antisymmetric elements contribute to the second order response in NMR, i.e., spin relaxation of the nuclei.²¹ Electronic structure calculations naturally predict all nine tensor elements. When comparing to experimental values, one must consider only the symmetric part obtained by averaging the two off-diagonal elements, σ_ij and σ_ji, in the 3×3 Cartesian matrix of the shielding tensor. For brevity here, the complete tensor refers to the six observable symmetric tensor elements. It is more convenient, when comparing two complete tensors, to use the icosahedral representation of the shielding tensor.²² In this basis, the tensor matrix is diagonal allowing one to compress the two indices into one. The six icosahedral shielding tensor components are represented by σ_j where j ranges from 1 to 6. The conversion of the symmetric Cartesian tensor to the icosahedral representation is described elsewhere.²²

In practice, one measures the shielding by observing the change in the resonance with respect to a reference compound, producing the well-known “chemical shift” scale. The symmetric magnetic shielding component σ_j is related to the corresponding chemical shift tensor component δ_j by

$${\sigma }_j=-1{\delta }_j+{\sigma }_{\text{ref}},$$ (2)

where the proportionality constant is −1 and σ_ref is the magnetic shielding of the reference compound. The shift-to-shielding conversion can be challenging for two reasons: The proportionality constant can deviate significantly from −1, and difficulties in the measurement of the shift in a bare nucleus prevent accurate prediction of shielding of the reference nucleus. An estimate of the ¹³C shielding of tetramethylsilane (TMS), 188 ppm, can be obtained from spin rotational measurements of carbon monoxide.²³ Both the proportionality constant and the shielding value of TMS are left as fitting parameters obtained from a linear regression analysis. The best estimate of the shielding from the chemical shifts is

$${\widehat{\sigma }}_j=\widehat{m}{\delta }_j+{\widehat{\sigma }}_{\text{ref}}.$$ (3)

The accuracy of the results can be assessed by the deviation of the least-squares regression parameters from their ideal value and by the root-mean-square deviation (RMSD)

$$\text{RMSD}=\sqrt{\frac{{\sum }_j{\left({\sigma }_j^c-{\widehat{\sigma }}_j\right)}^2}{\text{df}}}$$ (4)

between the calculated shielding σ^c and the best estimate of the shielding $\widehat{\sigma }$. The degrees of freedom (df) is the number of tensor elements minus 2. It may prove useful to consider the RMSD for predicting the isotropic shift without accounting for deviations of the regression parameters from their ideal values. The predicted isotropic shift

$${\delta }_{\text{iso}}^c=-{\sigma }_{\mathrm{iso}}^c+188\text{ppm}$$ (5)

will provide a measure of RMSD_iso given by

$${\text{RMSD}}_{\text{iso}}=\sqrt{\frac{{\sum }_j{\left({\delta }_{{\text{iso}}_j}^c-{\delta }_{{\text{iso}}_j}\right)}^2}{\text{df}},}$$ (6)

where δ_iso is the isotropic shift determined from the experimental tensor,

$${\delta }_{\text{iso}}=\frac{1}{6}\sum _j{\delta }_j,$$ (7)

and δ_j is the jth tensor element in the isocosahedral representation.

Calculation of NMR shifts by DFT

DFT is an attractive approach for predicting NMR shifts due to its relatively low scaling with regard to computational costs with the size of the molecule. While electron-correlated methods can scale to the seventh power, DFT scales with roughly the square of the number of electrons.²⁴ Recent DFT implementations even scale linearly with the number of atoms, but so far are not able to compute chemical shifts.²⁵ In the presence of a vector potential (e.g., a magnetic field), gauge invariance demands that the current density derived from the wave functions be conserved with respect to the selection of the vector origin. For calculations performed with an incomplete basis set, this gauge origin problem must be addressed. The GIAO method, which exploits London’s gauge invariant atomic orbitals, was proven to be robust when considering a small finite basis set. The GIAO method has been reviewed by Pulay and Hinton.²⁶

Most ab initio predictions of NMR chemical shifts have focused on obtaining accurate results for isolated molecules. When considering solid-state systems, however, such calculations ignore the effects of the crystal environment which can affect the shielding parameters.²⁷ This may be partially overcome through the use of large molecular clusters, but in many cases the computed chemical shifts converge poorly with cluster size.²⁸ Calculations performed on a true periodic system, i.e., one that includes translation symmetry, overcome this limitation. In the approach employed in the CASTEP program,²⁹ the basis consists of plane waves, which are more appropriate for modeling infinitely periodic systems. The wave function must be periodic with respect to translations along the lattice vectors R, hence,

$$\Psi \left(\mathbf{r}\right)=e^{i\mathbf{k}\mathbf{\cdot }\mathbf{R}}\Psi \left(\mathbf{r}\right).$$ (8)

The one-particle wave functions expanded in a basis of plane waves become

$${\phi }_i\left(\mathbf{r}\right)=\sum C_{i\mathbf{G}}{e}^{i\mathbf{G}\mathbf{\cdot }\mathbf{R}}.$$ (9)

This approach leads to a simplified expression for the Kohn–Sham equations in which the kinetic energy term is diagonal, and the various potentials (electron-ion, Hartree, exchange correlation) can be computed in terms of their Fourier transforms. Pseudopotentials replace core electrons, thereby significantly decreasing the computational effort. These simplifications make the method computationally efficient for studying problems with a large number of atoms.

While effective, the use of pseudopotentials introduces a complication when modeling NMR parameters: A reasonable valence wave function near the nucleus is lacking, although such a wave function is essential for computing accurate results.¹¹ The all-electron wave function can, fortunately, be reconstructed using the projector augmented wave (PAW) method.³⁰ Pickard and Mauri⁵ introduced an extension of PAW referred to as the GIPAW approach. The Hamiltonian constructed using GIPAW includes the required translational invariance in the presence of a magnetic field and is suitable for computing NMR shifts in a crystal.

A uniform external magnetic field B applied to a sample induces an electric current. In an insulating, nonmagnetic material, only the orbital motion of the electrons contributes to this current. In addition, for the field strengths typically used in NMR experiments, the induced electric current is proportional to the external field B. This first-order induced current j⁽¹⁾(r) produces a nonuniform magnetic field,

$${\mathbf{B}}_{\text{in}}^{\left(1\right)}\left(\mathbf{r}\right)=\frac{1}{c}\int d^3{r}^{\prime }{\mathbf{j}}^{\left(1\right)}\left({\mathbf{r}}^{\prime }\right)\frac{\mathbf{r}-{\mathbf{r}}^{\prime }}{{\mid \mathbf{r}-{\mathbf{r}}^{\prime }\mid }^3}.$$ (10)

The chemical shift tensor σ connects the first-order induced magnetic field and the applied field

$${\mathbf{B}}_{\text{in}}^{\left(1\right)}=-\sigma \mathbf{B}.$$ (11)

To compute the chemical shift tensor, the GIPAW method first obtains j⁽¹⁾(r) by perturbation theory and then evaluates the first-order induced field B⁽¹⁾. From those quantities it is simple to compute the tensor σ. The method has been applied successfully to a number of molecular organic crystals and metal oxide systems, and these results were recently reviewed.¹¹ The present work is intended to provide a systematic and quantitative comparison between results obtained on crystals and those obtained from isolated molecules.

Molecular systems

The crystal structures for the 14 molecules in the database considered here are accurately known from neutron diffraction data, and our calculations initially utilize these diffraction structures. Since the structures reflect the crystalline geometry, the solid-phase molecular structure has already been taken into account. The 14 crystals consist of two distinctly different classes of molecules, which fall into the general chemical classes of aromatic molecules and carbohydrates. Within this set there are 37 sp² carbon tensors from the aromatic molecules and the 65 oxygenated sp³ carbon tensors (i.e., representing alcohol, ether, methoxy, acetal, ketal, or hemiacetal carbons) from the carbohydrate molecules. The organic crystals correspond to the compounds naphthalene,^{12, 31} acenaphthene (both crystallographic forms),^{13, 32} triphenylene,^{14, 33} sucrose,^{15, 34} methyl α-D-galactopyranoside monohydrate,^{16, 35} methyl β-D-galactopyranoside,^{16, 35} methyl α-D-mannopyranoside,^{16, 36} methyl α-D-glucopyranoside,^{16, 36} methyl β-D-xylopyranoside,^{16, 37} methyl-D-fructopyranose,^{17, 38} α−L-xylopyranose monohydrate,^{17, 39} α-L-rhamnose monohydrate,^{18, 40} and pentaerythritol.^{19, 41} All coordinates for the atoms within these molecules were obtained from the Cambridge Crystallographic Database.⁴²

Functionals

Several DFT computational approaches, including calculations with and without periodic boundary conditions, were employed here. The GIAO method performed here used only isolated molecules in their experimentally determined crystal geometry. These calculations, therefore, exclude the direct effect of the intermolecular current density and charge distortions to the wave functions of the isolated molecule due to the lattice. GIPAW calculations with the Perdew-Burke-Ernzerhof (PBE) (Ref. ⁴³) exchange-correlation functional utilize the full lattice structures with periodic boundary conditions. Such calculations completely model the solid-phase structure, with the exception of temperature considerations and lattice motion.¹¹ The GIPAW calculations were also performed with DFT-optimized structures, allowing the exploration of structure refinement.

We have also included for comparison GIAO calculations on isolated molecules using B3LYP,⁴⁴ PBE1,⁴⁵ and KT3 (Ref. ⁴⁶) functionals. While it is known that a significantly large basis set is required for accurate shielding calculations,⁴⁷ the effect of finite basis is compensated for by the regression parameters and good agreement can be achieved with a modest basis.⁷ In this case, we used 6-31G(d) for the GIAO calculations, which previously provided good agreement with experiment. Basis sets as large as 6-311G(d,p) showed no further improvement in terms of RMSD. However, the 6-311G(d,p) basis in conjunction with PBE1 reproduces the ideal regression parameters.

Computational details

For isolated molecules, the GIAO method⁴⁸ was used for NMR shielding tensor calculations. Each calculation, conducted on a metacluster, was allocated up to 4 Gbytes of memory and the equivalent of 200 h of CPU time on a 1 GHz processor. Magnetic shielding calculations were performed using the GAUSSIAN03 quantum mechanical software package⁴⁹ using the B3LYP,⁴⁴ PBEPBE (PBE),⁴³ and PBE1PBE (PBE1) (Ref. ⁴⁵) functionals with the 6-31G(d) and 6-311G(d,p) basis sets. The DALTON quantum mechanical software package⁵⁰ was used for calculations utilizing the KT1, KT2, and KT3 (Ref. ⁴⁶) functionals with the 6-31G^*, 6-311G^**, and 6-31G(3df,3pd) basis sets. All Gaussian results are stored in databases as part of the Chem_XSeer system at Penn State University and are freely available to the research community. The Chem_XSeer system (http://chemxseer.ist.psu.edu) is a digital library and search engine for researchers in chemistry that integrates the scientific literature with experimental, analytical, and simulation data sets.

The GIPAW calculations were performed on a Dell Poweredge 1900 server with dual Xenon Quad-core processors and 8 Gbytes of random access memory. The GIPAW results were obtained using software programs from Accelrys Software, Inc.⁵¹ DFT calculations were performed with the CASTEP program,²⁹ and graphical displays generated withMATERIALS STUDIO 4.2. The full lattice structure was considered for all GIPAW calculations. The PBE functional was employed along with ultrasoft pseudopotentials. The so-called “fine” level was selected for the CASTEP parameters. No further improvement was observed at the “ultrafine” level when tested on two compounds (acenaphthene and sucrose). The fine level uses plane wave cutoff energies of 350 eV for hydrocarbons and 550 eV if O is present. The corresponding values for the ultrafine setting are 390 and 610 eV. A k-point spacing of 0.04 1∕Å is used in both cases. Geometry optimizations were performed until the maximum Cartesian force was less than 0.05 eV∕Å on all atoms. All atom positions were optimized, but unit cell parameters were not included in the optimizations.

The least-squares regression, shielding distance calculations, and the statistical analyses of the data were performed using programs written in the framework of the MathWorks MATLAB software package.⁵² The isosurface shown in Fig. 1 was created using GAUSSIAN03 and GAUSSVIEW software with calculations utilizing the B3LYP ∕3-21G model chemistry.

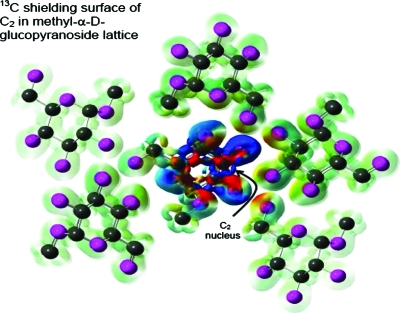
Figure 1.

The current density isosurface is shown for the lattice structure of methyl-D-glucopyranoside when the magnetic field is perpendicular to the plane of the paper. Carbon and oxygen are represented as black and magenta spheres, respectively. Hydrogen atoms are not shown in the image. The shielding contribution of the current density (isosurface set to 4×10⁻⁴ in GAUSSVIEW) to the C₂ nucleus is color mapped onto the isosurface. The magnitude of the shielding is indicated by color (blue deshielding and red shielding), which ranges from −0.05 to 0.05 ppm. While the intramolecular contributions dominate, it is visually evident that the oxygen atoms on neighboring molecules play a non-negligible role to the overall shielding.

DISCUSSION AND RESULTS

The solid-state crystal structure plays a significant role in the overall ¹³C chemical shift of organic materials.³ The influence of the lattice structure on magnetic shielding of a molecule can be ascribed as a direct effect of the lattice forces (i.e., electrostatic, hydrogen bonding, or magnetic effects) or an indirect effect as these forces distort the structure of the molecule. Since the chemical shift is dominated by local electronic structure, the subtle structural differences between condensed phase and isolated gas-phase molecules can be important. The lattice structure, therefore, must be included when performing geometry optimizations in order to obtain accurate agreement between measured shifts and calculated shieldings.

The lattice structure must also be included to correctly model the spatial charge distribution of the system to ensure the proper form of the wave function. The size of the distortion between gas phase and crystalline phases will depend on the type of intermolecular interactions dominant in the system. While this distortion may be modest for covalent systems, hydrogen bonding can cause significant perturbations. Induced current density on neighboring molecules can also directly contribute to the overall shift of the resonance frequency of the nucleus.⁵³ Although the chemical shift is dominated by current density in the vicinity of the nucleus, the intermolecular contribution can be measurable, which is significant when exploring crystallographic distortions or attempting to differentiate the sources of two spectral peaks separated by a few ppm. It can be expected that the importance of the intermolecular shielding will increase with the number of intermolecular atomic contacts that are smaller than the sum of the van der Waals radii. The presence of nearby atoms with a large electron density, such as oxygen, can further contribute to intermolecular shielding.

Magnetic shielding surface

Qualitatively, the magnitude of this intermolecular shielding contribution can be visually displayed on an isosurface of the magnetic current density in the solid system. The current density isosurface can be color mapped by the corresponding shielding it contributes to a particular nucleus. For example, consider the lattice structure of methyl-α D-glucopyranoside, as shown in Fig. 1. In this example, the nucleus selected for color mapping is the C₂ atom of the center molecule. Here, the magnetic field is selected to be perpendicular to the plane of the figure. The shape of the image represents the current density and the intensity indicates the degree of shielding that the current density contributes to the nucleus. The color describes the relative sign of the shielding, where blue represents deshielding and red corresponds to shielding. The level of theory used for this image (B3LYP∕3-21G) suffices for qualitative purposes. It is apparent from the image that for this example significant contributions to the overall shielding arise from neighboring oxygen atoms. While the intramolecular contributions dominate, oxygen atoms on neighboring molecules play a non-negligible role to the overall shielding.

Shielding and shift correlation

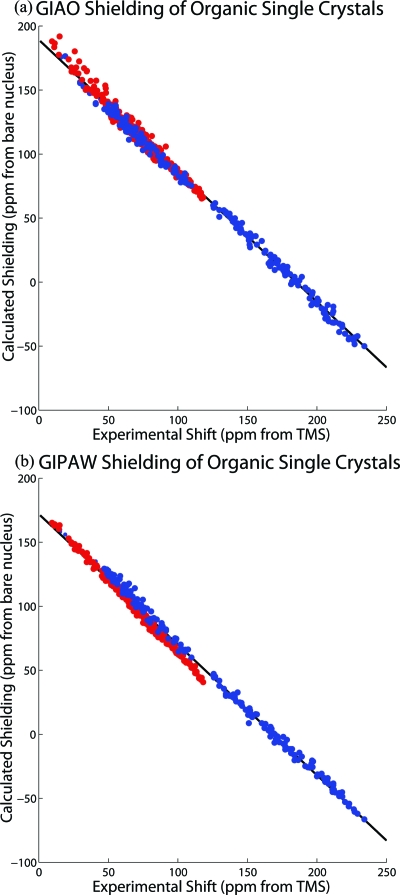
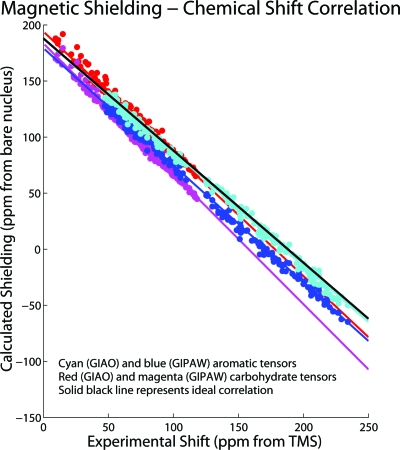
Linear least-squares regression is used to determine statistically the best relationship between the theory and experimental data; the proportionality constant and the shielding of the reference molecule (intercept of the fit) are the regression parameters. By fitting for the intercept, further uncertainties associated with the shielding of the reference molecule are avoided. The linear correlation between the ¹³C magnetic shielding and chemical shift tensors for all 14 organic compounds is shown in Fig. 2, where the marked improvement of GIPAW calculations is apparent. The GIAO results using PBE1∕6-311G(d,p) are shown in Fig. 2a, while the PBE∕Fine results utilizing GIPAW are displayed in Fig. 2b. The regression parameters, RMSD, slope, and intercept for the shielding-shift correlation for these calculations are reported in Table 1. The GIAO method using PBE1∕6-311G(d,p) nearly reproduces the ideal correlation with a slope of −1.023 and an absolute shielding for the reference TMS of 188.2 ppm. The plot scatter (RMSD) of 3.7 ppm demonstrates the accuracy of the theory to predict shieldings. This is less than 2% of the full shift range of 240 ppm. It is clear from Fig. 2 that DFT methods using plane waves are at the same level of excellence as all electron wave function approaches.

Figure 2.

The linear correlation between the ¹³C magnetic shielding and chemical shift tensors is plotted for all 14 organic compounds using the (a) GIAO PBE1∕6-311G(d,p) method and (b) the lattice-including GIPAW PBE∕Fine method. The atomic positions in the lattice are further refined for the GIPAW method while the geometries for the calculations were taken from neutron diffraction data without modification for the GIAO method. Color distinguishes the tensors associated with the carbohydrate molecules (red) and the aromatic molecules (blue). The plot scatter (RMSD) is reduced when including the lattice for GIPAW. Unexpectedly, the carbohydrate molecules follow a separate trend line from the aromatic molecules, which is clearly revealed by the structure of the residuals in (b).

Table 1.

RMSD and regression parameters for shielding-shift correlation.

Theory	RMSDa	Slopeb	σTMSc	Carbohydrates			Aromatic
				RMSDa	Slopeb	σTMSc	RMSDa	Slopeb	σTMSc
B3LYP∕6-31G(d)	3.96	−0.924	186.1	3.44	−1.039	193.6	3.05	−0.920	187.2
PBE∕6-31G(d)	4.80	−0.891	183.2	3.51	−1.072	194.9	2.98	−0.888	185.5
PBE1∕6-31G(d)	3.56	−0.940	191.9	3.07	−1.041	198.7	3.57	−0.939	191.5
PBE1∕6-311G(d,p)	3.73	−1.023	188.2	3.55	−1.090	193.0	3.50	−1.010	186.6
KT3∕6-31G(d)	5.15	−0.826	182.7	3.31	−1.032	195.8	2.85	−0.831	186.5
KT3∕6-311G(d,p)	5.23	−0.891	181.6	3.81	−1.080	193.8	3.62	−0.893	184.7
GIPAW PBE∕Fined	3.91	−1.034	174.5	2.59	−1.163	182.4	3.04	−1.045	178.3
GIPAW PBE∕Fined e, e	3.77	−1.020	171.0	1.88	−1.139	177.9	3.05	−1.041	176.5

^aThe RMSD is reported in ppm.

^b−1 is expected for perfect agreement.

^cShielding of TMS chemical-shift reference (ppm). 188 ppm is expected for perfect agreement.

^dSee text for definition of “Fine” settings.

^eGeometry optimization performed on neutron diffraction atomic coordinates. Unit cell parameters held constant.

The improvement in the model that is made by including the periodic boundary conditions, however, is not apparent when both the aromatic and carbohydrate tensors are considered together. Close examination of Fig. 2 reveals structure in the residuals of the correlation plot as the two types of carbon hybridization, sp² and sp³, of the aromatic and carbohydrate molecules display unique trends to the theory. The tensor elements are color coded (red from carbohydrates and blue from aromatic carbons) in Fig. 2, and a F-test differentiates the two groups in the GIPAW case where the lattice structure is included with the periodic boundary conditions. A probability of less than 0.1% is returned from the F-test for GIPAW for both the aromatic (F(610,210)=1.53,p<.001) and carbohydrate tensors (F(610,388)=4.04,p<.001), where the variances are obtained from squaring the RMSD. Since these two tensor populations are statistically distinct, the two molecular groups will be addressed separately in further discussions below. It is interesting to note that while PBE1∕6-311G(d,p) reproduces the ideal parameters for the linear correlation, it is the only model reported in Table 1 that does not differentiate the two populations (p<.001). The GIAO method using PBE1∕6-311G(d,p) returns probabilities greater than 10% for the aromatic (F(610,210)=1.10,p=0.149) and carbohydrate tensors (F(610,388)=1.14,p=0.135).

Inclusion of the lattice structure

The values obtained using the GIPAW method (bottom of Table 1) are consistent with the GIAO results in terms of the RMSD, thereby confirming that the use of the pseudopotential plane wave approach provides for efficient and precise calculations of the shielding in solid-phase structures. Not surprisingly, performing calculations utilizing crystal (rather than gas phase) structures improves the shielding-shift model. For the carbohydrate tensors where hydrogen bonding is present, a significant number of intermolecular contacts that are shorter than the sum of the van der Waals radii exist. The number of short contacts for these carbohydrate crystals ranges from 6 to 66, but on average the carbohydrate crystals have 40 short contacts. A significant decrease in the RMSD (2.59 ppm) is observed by applying the GIPAW method. The RMSD improvement is visually evident in the plot of the shielding-shift correlation shown in Fig. 2b and demonstrates that the models excluding the lattice structure for a hydrogen-bonded network are less accurate.

For the aromatic tensors studied here, the lattice structure plays less of a crucial role, as we note that improvement in the RMSD is less dramatic when the lattice structure is included. The geometry of these molecules already corresponds to the correct crystal structure. A decrease in scatter would signify the importance of intermolecular shielding and wave function distortions, which is not significant for these systems since these crystals have only 6–10 intermolecular contacts that are shorter than the sum of the van der Waals radii. With the exception of one aromatic molecule (acenaphthene), the lattice structures take on a herringbone configuration; thus, the π-stacking effects are reduced as well. While several of the GIAO calculations result in an RMSD below 3 ppm, they have significant deviations from the ideal slope of −1. The PBE1∕6-311G(d,p) calculations deliver an improved slope but a greater RMSD. By contrast, the GIPAW calculations provide a slope closer to ideal (−1.04) as well as a fairly low RMSD (3.05), and so may offer the best compromise.

The improvement in the fit with the use of GIPAW enables a thorough analysis of the numerical values within the single-crystal data set. When the lattice structure is included, the individual RMSD from many molecules fell to within three standard deviations of the estimated experimental uncertainty of 0.5 ppm. Sucrose, for example, provides a RMSD of 1.25 ppm when using GIPAW while values from GIAO models exceeded 2 ppm. This high quality fit made RMSD values above 3 ppm suspect and led us to discover a misalignment of the crystallographic reference frames of the experimental tensors for one molecule (methyl-D-fructopyranose). These corrections explain the difference between the regression parameters reported here using B3LYP∕6-31G(d) methods and those previously reported in the literature.^{6, 7}

Motion and structure refinement

The most useful consequence of modeling the full lattice structure lies in the ability to optimize the initial structures for their true lattice geometry. Naturally, this becomes a critical step when high quality diffraction structures are not available. However, it has also been shown that refinement of diffraction parameters is necessary in order to obtain an agreement between calculated shieldings and experimental shifts especially when solid-phase motion exists.^{54, 55} Here, the shielding-shift agreement significantly improved with the GIPAW optimized structure for six of the ten carbohydrate molecules. These refined structures drop the overall RMSD from 2.59 to 1.88 ppm, a reduction of 28%. In these cases, the dominant structural change from the original neutron structure was the lengthening of C–H bonds in the methyl groups (1.052–1.094 Å) and O–H bonds in the hydroxyl groups (0.962–0.987 A). The other four molecules, whose fits did not improve, already reveal individual RMSDs below 2 ppm prior to the optimization. Improvement was observed with the aromatic molecules as well, where one exhibited reduced RMSD from 2.7 to 2.1 ppm upon geometry optimization. Interestingly, this is the same aromatic molecule (acenaphthene form A) that possesses a lattice structure with stacked aromatic planes rather than a herringbone configuration.

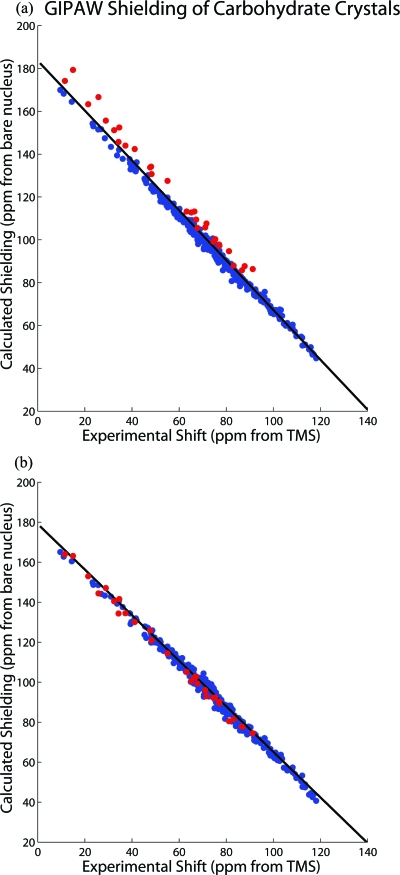
While the impressive agreement between theory and experimental data while utilizing the GIPAW method leaves little room for improvement, the shielding model used here still does not fully depict the experimental conditions under which the shift data were acquired. The calculations assume a static molecule ignoring both temperature effects and zero-point energy corrections, while the experimental shift data were all acquired at room temperature. Some attempts to account for these shortcomings in the theory have been reported in the literature⁵⁶ where they have been estimated to be significant. Moreover, it is suggested that these effects can directly contribute to the scaling issue.⁵⁶ Methyl rotation is one such important motion that is present in the carbohydrate molecules and will be reflected in their measured shielding tensors. In Fig. 3, the methyl tensor data points in the carbohydrate tensors are highlighted for GIPAW shieldings. All of these data points lie systematically above the trend line, thereby increasing the RMSD. Since these points also tend to lie on the left-hand side of the plot (i.e., at lower shift values), their deviation will increase the slope from the ideal value of −1. Full lattice optimization of the motionally averaged diffraction geometry reduces the slope deviation from −1.163 to −1.139 as well as the plot scatter. To further improve the agreement with experiment, temperature and vibrational effects need to be accounted for in shielding calculations.

Figure 3.

Refinement of the neutron diffraction structures can lead to an improved shielding-shift relationship. Geometry optimized structures when the lattice structure is included reduce the plot scatter and slope deviation from −1. The GIPAW∕PBE ¹³C magnetic shielding tensor components using (a) the neutron diffraction and (b) geometry-optimized structures are plotted here for carbon nuclides in the carbohydrate molecules within our test database. The methoxy groups (red), which have the most significant change in diffraction geometry upon GIPAW optimizations, show a systematic error in the trend line that is corrected by the optimization.

Tensor components

The shielding tensor can be represented as an ellipsoid where the six parameters of the tensor are expressed as three principal components (i.e., the magnitude) and three Euler angles describing the principal axis frame (i.e., the orientation). Often the experimental values of a complete chemical-shift tensor, which can only be obtained from a single crystal, are not available. It is, therefore, relevant to consider the ability of the model to predict the experimental isotropic shift and the principal components of the tensor, which can be measured in simpler experiments using powder samples and are usually determined in high-resolution magic-angle-spinning spectra of solids by the observation of spinning-sideband manifolds. Principal components are routinely reported along with the isotropic chemical shift in solid-state NMR studies.

The proper means, which was utilized here, to assess differences between complete tensors as a single scalar number is with the magnetic shielding distance.²² Differences between tensors can further be expressed for the individual principal components, the combined principal components, the isotropic value, and the orientation. Table 2 decomposes the averaged ¹³C shielding distances between the tensors predicted by theory and the experimental chemical shift tensors of this database. Further information about separating the total shielding distance into these separate components is described in Ref. 22. The shielding distance is equivalent to the plot scatter (RMSD) when tensors are presented in the icosahedral representation. Therefore the RMSD reported in Table 1 equals the shielding distance reported in Table 2 when all six tensor components are compared.

Table 2.

Magnetic-shielding distance for ¹³C organic crystals.

Carbohydrates
Theory	Fulla b, b	Principala c, c	Isotropicd	${\sigma }_{11}^{}$d	${\sigma }_{22}^{}$d	${\sigma }_{33}^{}$d	Orientationa e, e
B3LYP∕6-31G(d)	3.44	2.57	2.85	3.85	2.77	4.09	1.30
PBE∕6-31G(d)	3.51	2.67	2.85	4.03	2.98	4.11	1.36
PBE1∕6-31G(d)	3.14	2.34	2.54	3.66	2.48	3.56	1.29
PBE1∕6-311G	3.55	2.61	2.83	3.34	2.70	4.89	1.46
KT3∕6-31G(d)	3.31	2.52	2.67	4.00	2.69	3.66	1.35
KT3∕6-311G(d,p)	3.81	2.90	3.09	3.87	2.94	5.18	1.44
GIPAW PBE∕Finef	2.59	1.74	2.26	2.47	2.03	3.30	0.92
GIPAW PBE∕Finef g, g	1.88	1.24	0.91	2.04	1.59	1.67	1.33
Aromatic
Theory	Fulla b, b	Principala c, c	Isotropicd	${\sigma }_{11}^{}$d	${\sigma }_{22}^{}$d	${\sigma }_{33}^{}$d	Orientationa e, e
B3LYP∕6-31G(d)	3.05	2.22	1.56	2.99	3.33	3.56	1.87
PBE∕6-31G(d)	3.02	2.13	1.54	2.71	3.16	3.67	1.90
PBE1∕6-31G(d)	2.97	2.10	1.57	2.88	3.00	3.39	1.87
PBE1∕6-311G	3.62	2.96	1.58	5.12	4.37	3.80	1.92
KT3∕6-31G(d)	2.85	2.04	1.37	2.76	3.12	3.33	1.80
KT3∕6-311G(d,p)	3.62	2.88	1.21	4.58	5.45	3.59	1.93
GIPAW PBE∕Finef	3.04	2.27	1.25	3.03	4.27	3.49	1.73
GIPAW PBE∕Finef g, g	3.05	1.85	0.89	2.58	4.07	1.90	2.29

^aThe magnetic-shielding distance (Ref. ²²) is reported in ppm.

^bFull considers the distance for the complete six-parameter tensor.

^cPrincipal reports the distance for the three principal components by assuming identical orientation.

^dA RMSD reported in ppm.

^eThe orientation distance is estimated by taking the root of the squared difference between full and principal.

^fSee text for definition of Fine settings.

^gGeometry optimization performed on neutron diffraction atomic coordinates. Unit cell parameters held constant.

Examination of Table 2 further highlights the improvements provided by GIPAW methods. The incorporation of the lattice improves the ability of the theory to predict the magnitude of the shielding. The combined shielding distances of the three principal components drop significantly. A further improvement is gained when geometry optimizations are considered, which is even observed for the aromatic tensors. For all molecules, the agreement for the overall magnitude of the shielding (i.e., the principal components) is within 2 ppm, a value that is typical for the uncertainty in principal components measured in experiments using powdered samples. Since the isotropic value entails an averaging process, one expects an improvement through a cancellation of errors when the isotropic value is considered. The agreement drops to within 1 ppm for the isotropic shift after performing geometry optimizations.

Consideration of the complete experimental shift tensors allows one to identify spatially the inadequacy of the theory to predict the shielding. Visually one can consider the shielding tensor as an ellipsoid whose axes are the three principal components and which is oriented with respect to the molecule in the crystal lattice. Because the principal components can be negative, it is more convenient to represent the axes as the absolute value of the difference between the isotropic value and the jth individual component,

$${\text{axis}}_j=\mid {\sigma }_{\text{iso}}-{\sigma }_{jj}\mid .$$ (12)

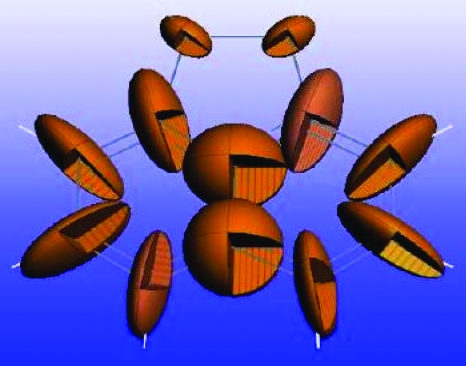
This creates a shielding anisotropy ellipsoid since the magnitude of the axes represents the differences. Figure 4 displays the ¹³C shielding anisotropy ellipsoids for each carbon nuclide in acenaphthene. Because σ₂₂ is closest to the isotropic value, this is the shortest axis for each ellipsoid. The ¹³C ellipsoids for acenaphthene confirm the general feature that σ₂₂ is oriented perpendicular to the carbon-hydrogen bond in aromatic rings. The 4 ppm discrepancy for σ₂₂ of aromatic molecules predicted by GIPAW stands out as it is a full ppm larger then the σ₁₁ and σ₃₃ distances reported in Table 2. Recalling that shielding is orthogonally sensitive to electronic distortions, the large deviation to this principal component may be explained by out-of-plane motion of the hydrogen. This motion may become anharmonic due to the lattice, and such motion would become a significant deviation for models assuming static molecules.⁵⁶

Figure 4.

Shielding anisotropy ellipsoids, where the axis length corresponds to the difference in principal components and the isotropic value graphically display the shielding tensors. The ellipsoids for acenaphthene demonstrate how the relative magnitude and orientation of the ¹³C shielding tensors appear in the molecule. For aromatic tensors, errors are largest in σ₂₂, which corresponds to the smallest axis and is oriented nearly perpendicular to the carbon-hydrogen bond.

Errors in predicting isotropic chemical shifts and the shielding-shift proportionality constant

One of the primary uses of theory by the experimentalist is to predict spectral values. In particular, the prediction of isotropic chemical shifts can be used to assign the peaks in a high-resolution solid-state NMR spectrum. To these ends, it is important to examine the errors in predicting the shift without properly accounting for deviations from linearity. Table 3 reports the RMSD of these isotropic values (RMSD_iso) as well as the maximum absolute value when assuming a slope of −1 and a shielding value of 188 ppm for TMS. It must be noted that such an analysis generates alarmingly high errors that obscure the true accuracy in the theory. RMSD_iso values reported in Table 3 are as high as 20 ppm and individual isotropic values can be off by as much as 25 ppm. Again these high deviations are largely systematic and can therefore be removed. We have demonstrated that the GIPAW method can predict the isotropic shifts to within 1 ppm. This excellent agreement comes only after removing the systematic flaws noted by the regression parameters deviating from their ideal values. The information in Table 3 serves to warn the experimentalist and they reiterate the deviations from ideal linearity reported in the correlation table. When the method is calibrated, the theory can accurately predict the isotropic shift.

Table 3.

Error in predicted isotropic shift (ppm).

Theory	RMSDisoa	Maxb	Carbohydrates		Aromatic
			RMSDisoa	Maxb	RMSDisoa	Maxb
B3LYP∕6-31G(d)	6.5	14.4	4.1	14.4	9.5	12.7
PBE∕6-31G(d)	7.5	15.4	3.5	13.5	11.8	15.4
PBE1∕6-31G(d)	9.9	18.0	8.2	18.0	12.5	15.8
PBE1∕6-311G(d,p)	3.4	10.8	3.6	10.8	3.1	5.6
KT3∕6-31G(d)	12.9	23.6	6.1	15.8	20.4	23.6
KT3∕6-311G(d,p)	6.7	12.9	3.3	12.5	10.5	12.9
GIPAW PBE∕Finec	16.9	21.5	17.7	21.5	15.5	18.7
GIPAW PBE∕Finec d, d	19.0	25.4	20.2	25.4	16.8	20.2

^aThe RMSD is reported in ppm.

^bThe absolute value of the maximum difference reported in ppm.

^cSee text for definition of Fine settings.

^dGeometry optimization performed on neutron diffraction atomic coordinates. Unit cell parameters held constant.

It is important to reflect upon the (often-large) deviation of the slope from the ideal value of −1. This systematic discrepancy is believed to stem from errors in occupied-virtual eigenvalue differences used in determining the paramagnetic component of the shielding, which can be associated with the well-known inability of existing exchange-correlation functionals to reproduce dynamic polarization in low electronic density regions.^{9, 57} The discrepancy in the theory has been shown to depend on both the basis set and functional employed.^{6, 7} Even the KT functionals, considered to be the most accurate for shielding calculations, show significant deviations from −1 for these organic molecules. With the level of precision obtained by GIPAW, the discrepancy is shown here to be also heavily dependent on the type of molecule. As dictated by the F-test above, it is no longer appropriate to describe the aromatic and carbohydrate tensors with a single trend line. This is evident by divergent trend lines in Fig. 5. As pointed out, the irregularities in the scaling may limit the ability to use shielding calculations as a means to provide spectral peak assignments. Even with the use of plane waves, the model describing the chemical shift is incomplete, as a static structure at a temperature of absolute zero is assumed. However, these GIPAW results do show that the scaling issue is not rectified by including the lattice structure or by geometry optimizations. Attempts incorporating motion of the molecules in the model still report a deviation from linearity,⁵⁶ suggesting that the linear deviation is caused by the electronic method itself.

Figure 5.

Different methods were employed to predict the shift result and result in unique trend lines for the ¹³C shielding-shift correlation plots. The linear fit parameters can deviate significantly from their ideal values (solid black line) of −1 for slope and 188 ppm for the ¹³C shielding of TMS reference for the different levels of theory and can be dependent on the bonding type of the molecules. While the ¹³C shielding-shift correlation for the lattice-including GIPAW PBE∕Fine (blue and magenta) method shows an improved scatter over the GIAO PBE1∕6-31G(d) method (cyan and red), the divergent trend lines for the carbohydrate and aromatic tensors are apparent.

CONCLUSION

In summary, this work has explored the value of using GIPAW for predicting ¹³C chemical shift values in organic crystals. The method offers the advantage of incorporating the environment of the entire crystal, demonstrating the contribution of intermolecular shielding from the lattice, which is significant in hydrogen-bonded systems. The ability to include the entire crystal environment leads not only to more accurate calculations, but opens the possibility for comparative calculations on crystalline polymorphs, polymers, and other solid-state materials.

Use of the GIPAW method provides the experimentalist with a computationally efficient tool to optimize the lattice structure of solid crystals. This ability is crucial for the refinement of structures in the field of NMR crystallography. The significant improvement over calculations on isolated molecules is vital for the assignment of spectral peaks in solid-state NMR spectra. The isotropic shift can be predicted to within 1 ppm and the level of precision for principal components rivals that of experiment. Yet the experimentalist must be warned that this precision comes only after removal of the systematic flaws when converting shielding values to the shift scale. Otherwise the prediction may be off by as much as 25 ppm, essentially rendering useless the results of these computational analyses.