Diotic and dichotic detection with reproducible chimeric stimuli

Abstract

Subject responses were measured for individual narrow-band reproducible stimuli in a low-frequency tone-in-noise detection task. Both N₀S₀ and N₀S_π conditions were examined. The goal of the experiment was to determine the relative importance of envelope and fine-structure cues. Therefore, chimeric stimuli were generated by recombining envelopes and fine structures from different reproducible stimuli. Detection judgments for noise-alone or tone-plus-noise stimuli that had common envelopes but different fine structures or common fine structures but different envelopes were compared. The results showed similar patterns of responses to stimuli that shared envelopes, indicating the importance of envelope cues; however, fine-structure cues were also shown to be important. The relative weight assigned to envelope and fine-structure cues varied across subjects and across interaural conditions. The results also indicated that envelope and fine-structure information are not processed independently. Implications for monaural and binaural models of masking are discussed.

INTRODUCTION

Fletcher (1940) suggested that tone-in-noise masking was directly related to the total stimulus energy in a narrow frequency region (the critical band) surrounding the tonal signal. Most subsequent research on diotic or monaural tone-in-noise masking also supports the idea that subjects base their decisions, at least in part, on the differences in energy between the stimulus on signal-plus-noise and noise-alone trials. Nevertheless, a wide variety of findings indicate that other stimulus cues also influence listeners’ detection judgments (e.g., Ahumada and Lovell, 1971; Hall et al., 1984; Neff and Callaghan, 1988; Richards, 1992; Colburn et al., 1997; Davidson et al., 2006). Specifically, several researchers have argued for the importance of fluctuations in the temporal envelope or the temporal fine structure of the wave form (e.g., Richards, 1992; Isabelle, 1995; Bernstein and Trahiotis, 1996; Carney et al., 2002). A variety of psychophysical models for detection have been developed that rely on envelope (e.g., Dau et al., 1996a, 1996b; Eddins and Barber, 1998) or on fine structure (e.g., Moore, 1975). Moreover, a number of researchers using a variety of approaches have provided evidence that envelope and fine structure are, or could be, separately processed in the auditory system (e.g., van de Par and Kohlrausch, 1997; van de Par and Kohlrausch, 1998; Kohlrausch et al., 1997; Eddins and Barber, 1998; Breebaart et al., 1999; Bernstein and Trahiotis, 2002; Smith et al., 2002; Joris, 2003; and Zeng et al., 2004). It has long been known that auditory-nerve responses phase lock to both individual cycles and to the envelopes of low-frequency stimuli (Kiang et al., 1965) and only to the envelopes of high-frequency stimuli (Joris and Yin, 1992; Kay, 1982).

The questions of whether envelope-based or fine-structure-based decision variables can really be processed separately at low frequencies, and if so which dominates the detection process, remain. Unfortunately, because energy, envelope, and fine structure tend to co-vary in randomly generated stimuli, it is difficult to evaluate separately their impact on detection judgments. That is, adding a tone to a narrow-band noise wave form tends to increase its energy, smooth its envelope, and reduce variation in the frequency of its fine structure.

One approach that has been successfully used to evaluate the role of envelope and fine-structure cues in other contexts involves the use of chimeras. Chimeras are stimuli formed by combining the envelope from one stimulus with the fine structure from another. Smith et al. (2002) tested speech recognition and sound localization using various chimeras and suggested that speech identification appeared to be based on envelope, whereas sound localization appeared to be based on fine structure. Zeng et al. (2004) refuted the latter result using chimeras with directionally conflicting interaural-time differences (ITDs, embedded in the fine structure) and interaural-level differences (ILDs, embedded in the envelope). The approach used in the study presented here differs from these efforts in that envelope and fine-structure cues were not systematically put in opposition. Instead, the envelopes and fine structures were chosen independently (within the bandwidth constraints discussed below), so that in any given wave form they could be in agreement or in disagreement in terms of their influence on a subject’s probability of responding “tone present,” and the subject could use either cue or both cues.

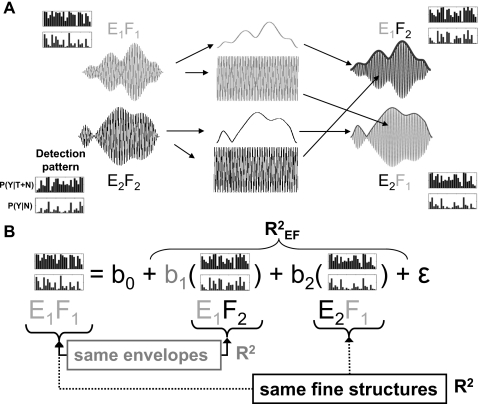
The goal of the study presented here was to evaluate the relative importance of envelope and fine-structure cues in detection judgments for both noise-alone and tone-plus-noise stimuli (i.e., for both hits and false alarms) for a task involving detection of low-frequency tones in narrow-band noise. The approach was straightforward and is described here in general terms, with reference to the N₀S₀ wave forms; a more explicit description is provided below in Sec. 2. The Hilbert transform was used to separate the envelope and fine structure of two reproducible wave forms [see Fig. 1a, left]. The envelopes and fine structures from the two different wave forms were then multiplied to yield two new wave forms, the chimeras [Fig. 1a, right]. If detection judgments were solely determined by envelope cues, then wave forms with the same envelopes should result in the same judgments even if their fine structures differed. Conversely, if detection judgments were solely determined by fine-structure cues, then wave forms with the same fine structures should result in the same detection judgments even if their envelopes differed.

Figure 1.

(A) Schematic illustration of the stimulus-construction procedure. Envelopes (e) and fine structures (f) were separated from the E₁F₁ and E₂F₂ stimulus sets using the Hilbert transform. The envelopes and fine structures were exchanged and recombined to create chimeric stimulus sets E₁F₂ and E₂F₁. Detection patterns are shown to remind the reader that each stimulus wave form illustrated is a single member of an entire set of wave forms. A more detailed description of the stimuli (including distortion-control procedures) is given in the text. (B) Illustration of the multiple regression procedure for the E₁F₁ stimulus sets. Chimeric detection patterns sharing envelopes (E₁ in the example above) and sharing fine structure (F₁ above) were used to predict the detection pattern residuals (see text) for the base line stimulus set (E₁F₁ above). The b coefficients represent the slopes of the regression lines used in the multiple regression statistical model and also indicate how strongly the subject weighted the information associated with that cue. The b₀ coefficient is always equal to zero because variability linearly associated with the base line stimulus set not in the model (E₂F₂ above) was removed (see text for details). The ε term represents error variance. R² values were computed for envelope (gray), fine structure (black), and a linear combination of envelope and fine structure $\left(R_{\text{EF}}^2\right)$. If envelope completely dominated the detection process, it was expected that the E₁F₁ and E₁F₂ detection patterns (and the related patterns of residuals) would be the same and the $R_{\text{envelope}}^2=1$. If fine structure completely dominated the detection process, it was expected that the E₁F₁ and E₂F₁ detection patterns (and residuals) would be the same and the $R_{\text{fine}\text{structure}}^2=1$.

Both N₀S₀ and N₀S_π cases were studied. In the N₀S₀ case, the noise-alone (N) and diotic tone-plus-noise (T–N) wave forms were adjusted to the same overall level, so that overall energy differences were not a viable cue for the N₀S₀ detection task. This experimental approach was intended to force listeners to rely on temporal information for the detection task, either in the form of the envelope or fine structure. Across-wave-form level equalization was not performed for the N₀S_π case because normalization of the energy of wave forms with tones added in different phases could have introduced overall level differences and thus potential ILD cues. However, in the N₀S_π case, very small energy differences between wave forms were created by adding threshold-level tones to the noise (see Sec. 2).

The same uncertainty about the roles of envelope and fine structure that exist for low-frequency diotic masking also exists for low-frequency dichotic masking. Models based on interaural differences (e.g., Hafter, 1971) can be viewed as recovering ITDs based on fine structure (or perhaps envelopes) and ILDs based on envelope, whereas noise-reduction (e.g., Durlach, 1963) and correlation (e.g., Osman, 1973) models compute energylike statistics based on the entire wave form. In the study presented here, experiments using chimera stimuli were also carried out using N₀S_π reproducible noise wave forms, again with the goal of determining the relative importance of envelope and fine-structure cues in determining detection judgments. Note that common envelopes imply similar ILD distributions in the signals and that common fine structures imply similar fine-structure ITD distributions. At the target frequency of 500 Hz used in this study, fine-structure ITDs tend to dominate detection results (Bernstein and Trahiotis, 1985), although envelope ITDs would still influence the ITD distribution. Models for dichotic detection based strictly on the statistics of ILD cues would predict similar detection judgments for reproducible wave forms that have the same envelope but different fine structures. In contrast, models based strictly on the statistics of fine-structure ITDs would predict similar detection results for wave forms that have matched fine structures. Thus, the detection results for these wave forms provide a useful test for these classes of models for dichotic detection.

METHODS

General design

Four related sets of reproducible stimuli were created as described below. Two of the sets contained “base line” stimuli, which were 25 random, narrow-band, noise-alone diotic wave forms, plus both diotic and dichotic tone-plus-noise stimuli created from these 25 noise wave forms using standard techniques (described in detail below).1 The other two sets contained “chimeras” that were created by combining individual wave form envelopes from one of the base line sets with the individual fine structures from the other base line set. Thus, each wave form in the chimera stimulus sets shared its envelope with a wave form in one of the base line sets and shared its fine structure with a corresponding wave form in the other base line set. The relative dominance of envelope vs fine structure in the detection task was then investigated by making detailed comparisons among the probabilities of “target present” or “yes” (Y) responses for N or T+N stimuli for the four sets of stimuli. Note that the potential influence on subject responses of spectral splatter introduced in the process of combining envelopes and fine structure from different wave forms (Amenta et al., 1987) was minimized by rejecting wave forms that resulted in chimeras with significantly increased bandwidth (see Appendix0). Details regarding the construction of the stimuli are discussed below.

Experimental procedures adapted from those of Davidson et al. (2006), Evilsizer et al. (2002), and Gilkey et al. (1985) were used to obtain detection patterns for each set of base line and chimeric stimuli. Detection patterns were defined as the hit rates and false-alarm rates estimated for each of the reproducible noise maskers in a particular group of wave forms; a detection pattern can be visualized as a bar graph of hit and false-alarm rates, plotted as a function of the masker identification numbers [shown in Fig. 1a]. Detection patterns were constructed for the probability of Y responses for T+N stimuli [P(Y∣T+N), i.e., hits] or for N stimuli [P(Y∣N), i.e., false alarms]. Thus, the first probability in each P(Y∣N) detection pattern shown in Fig. 1a is the probability of a Y response for N wave form 1 in that stimulus set. Similarly, the first probability in each P(Y∣T+N) detection pattern is the probability of a Y response for the T+N stimulus created with N wave form 1 in each set. The second probability in each detection pattern is for N or T+N stimuli created with N wave form 2 in each set, etc. Detection patterns for each subject were measured for each of the four sets of stimuli (two base line sets and two chimeric sets) for both N₀S₀ and N₀S_π conditions [note that Fig. 1a only shows the four detection patterns for the N₀S₀ condition for one subject]. Analyses of these detection patterns for stimulus sets that had matched envelopes or matched fine structures allowed quantification of the relative contributions of envelope and fine structure to the listeners’ decisions. For example, the ability to predict a subject’s detection pattern for one stimulus set using that subject’s detection pattern for another stimulus set that had the same envelopes (but different fine structures) would suggest that envelope cues dominated the detection results. Similarly, dominance of fine-structure cues would be indicated by the ability to predict the detection pattern based on results for another stimulus set with the same fine structures.

Six subjects, all of whom had previous listening experience, completed the experiment. S3 and S2 were the first and fourth authors of the present paper. Training and testing procedures were performed in a double-walled sound attenuating booth (Acoustic Systems, Austin, TX).

Stimuli

The goal of the experiment was to estimate the relative contribution of envelope and fine-structure cues in determining detection judgments when no detectable overall energy differences were present. The design also allowed the comparison of judgments across subjects and across interaural conditions (N₀S₀ vs N₀S_π). Generating the stimuli for the experiment is conceptually fairly simple: Create a group of narrow-band reproducible noises and interchange their envelopes and fine structures to produce chimeras. However, in practice, the need to avoid the introduction of unintended detection cues and to present comparable wave forms across subjects and under the two interaural conditions made the stimulus generation process more complicated. For example, combining envelopes and fine structures from different wave forms can produce chimeras that are wider in bandwidth than the original wave forms; therefore, stimulus selection was constrained to control this problem (see Appendix0 for details).

The same noise-alone (N) wave forms were used for each subject and under both interaural conditions. Tones (T) were added to these N wave forms to produce the T+N stimuli. However, because the tones were added at threshold level and threshold varied across subjects and across interaural conditions, the resulting wave forms differed somewhat across subjects and conditions.

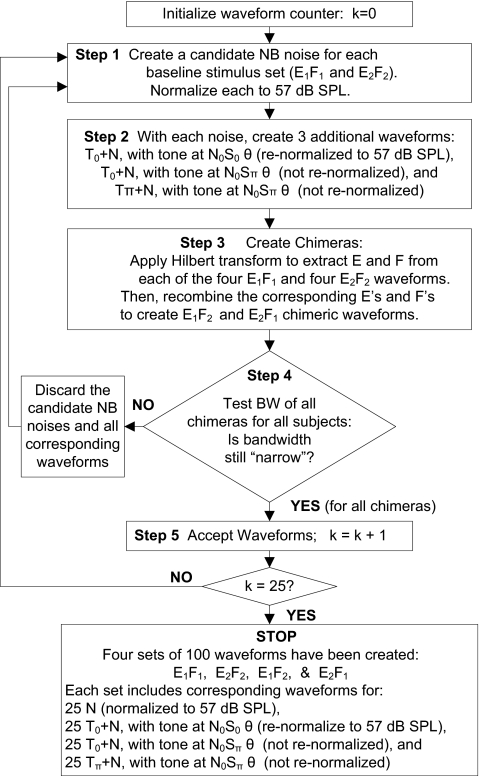
The four sets of reproducible wave forms were created for each subject, as follows (Fig. 2): A narrow-band (50 Hz) N wave form was created as a candidate for the ith reproducible stimulus in one of the base line stimulus sets (E₁F₁). Base line N wave forms were created in the frequency domain by adding five frequency components (480, 490, 500, 510, and 520 Hz). The magnitudes of the five components were randomly selected from a Rayleigh distribution, and the phases of the five components were selected from a uniform distribution on the interval [−pi, pi]. The inverse Fourier transform was used to generate the time-domain noise wave forms. All wave forms were 100 ms in duration, with 10-ms cos² on∕off ramps. Each of the N wave forms was normalized to an overall level of 57 dB SPL (sound pressure level), which corresponds to a 40-dB SPL spectrum level, N₀, for a bandwidth of 50 Hz.

Figure 2.

Flow chart illustrating procedure for stimulus generation. First, two random Gaussian narrow-band noises are created, one for the E₁F₁ base line stimulus set and one for the E₂F₂ set. The noises are normalized to 57 dB SPL, and then tones are added at the appropriate levels and phases for tests of detection in the N₀S₀ and N₀S_π interaural configurations. These wave forms are then used to create chimeras that have the envelopes from one wave form and the fine structure from another, and vice versa [see Fig. 1a]. Before accepting the original and chimera N and T+N wave forms into the four sets of wave forms to be used for testing, the bandwidths of the chimeras are checked (see Appendix0 for details). If all of the chimera wave forms are sufficiently narrow band, then all base line and chimera wave forms are accepted (N, T₀+N for N₀S₀, T₀+N for N₀S_π, and T_π+N for N₀S_π for each of the wave form sets: E₁F₁, E₂F₂, E₁F₂, and E₂F₁). For testing in the N₀S₀ condition, diotic N or T+N stimuli are used based on tone levels at the N₀S₀ thresholds, and all wave forms are normalized to 57 dB SPL. For N₀S_π testing, stimuli are diotic N stimuli on noise-alone trials (normalized to 57 dB SPL); on signal trials, T₀+N is presented to one ear and T_π+N is presented to the other ear (these are not normalized but differ only slightly from 57 dB SPL, see text). For N₀S_π stimuli, tone levels were based on N₀S_π thresholds during training. Abbreviations: NB, narrow band; E, envelope; F, fine structure; θ, detection threshold (during training for each subject); T₀, tone with zero phase re stimulus onset; T_π, tone with π phase re stimulus onset; BW, bandwidth.

Using the same procedure as above, another random noise was created as a candidate for the ith stimulus in the other base line stimulus set (E₂F₂). These ith N candidate wave forms in each of the base line stimulus sets were then used to create three other wave forms: (1) The ith T+N wave form for the N₀S₀ condition was created by adding a 500-Hz tone at 0 phase with respect to stimulus onset (T₀+N). The tone level was set to the listener’s N₀S₀ detection threshold, as determined during training. The stimulus was windowed with 10-ms cos² ramps and then re-normalized to 57 dB SPL to remove overall level differences as potential cues for discrimination between N and T+N wave forms in the N₀S₀ condition. (2) The ith T+N used for one of the ears in the N₀S_π condition was created by adding a 500-Hz tone at 0 phase and windowing with 10-ms cos² ramps. The tone level was matched to the subject’s N₀S_π detection threshold, determined during training. This T₀+N wave form was not re-normalized to avoid adding undesired interaural level cues in the N₀S_π condition (see below). (3) The ith T+N for the opposite ear in the N₀S_π condition was created by adding a 500-Hz tone at π phase (T_π+N) and by windowing with 10-ms cos² ramps. Again, the tone level was matched to the subject’s N₀S_π detection threshold. This wave form was also not re-normalized. In the N₀S_π condition, the un-normalized T₀+N was presented to one ear, and T_π+N was presented to the other ear. Because the T+N wave forms used for the N₀S_π condition were not normalized, level differences did exist across the stimuli used in the N₀S_π condition; however, the average level difference between N and T+N stimuli under the N₀S_π condition was 0.09 dB, and level varied across T+N wave forms with a standard deviation of 0.7 dB.

Next, each wave form in E₁F₁ base line set and the corresponding wave form in the E₂F₂ base line set (i.e., the ith N wave form in the E₁F₁ set with the ith N wave form in the E₂F₂ set, the ith T_π+N wave form in the E₁F₁ set with the ith T_π+N wave form in the E₂F₂ set, etc.) were used to create two chimeric wave forms (one for the E₁F₂ set and one for the E₂F₁ set) as follows: The Hilbert transform was used to compute the envelope and fine structure for each wave form in the base line set, and then the envelopes from the E₁F₁ wave form and fine structures from the E₂F₂ wave form were combined (multiplied) to create the corresponding E₁F₂ chimeric wave form [Fig. 1a, right]. Similarly, the fine structure from the E₁F₁ wave form and the envelope from the E₂F₂ wave form were combined to create the corresponding E₂F₁ chimeric wave form. The chimeric wave forms were then tested to ensure that they were still narrow band (see Appendix0 for details). If any of the chimeras failed the bandwidth test, then all of the associated wave forms (i.e., the ith N, T₀+N for N₀S₀, T₀+N for N₀S_π, and T_π+N for N₀S_π) in each of the four sets of reproducible stimuli (E₁F₁,E₂F₂,E₁F₂,E₂F₁) were discarded, and the process to create the ith wave forms in each set was re-initiated (Fig. 2). If all of the chimeras passed the bandwidth test, then the ith wave form of each stimulus type was accepted into each of the four stimulus sets, and the procedure moved on to the (i+1)th wave forms. The stimulus generation process was continued until there were 25 wave forms of each type (N, T₀+N for N₀S₀, T₀+N for N₀S_π, and T_π+N for N₀S_π) in each of the four sets (E₁F₁,E₂F₂,E₁F₂,E₂F₁).

Note that the ensemble of stimuli was specific to each subject because early in the stimulus generation procedure the tones were added to the base line N wave forms at threshold levels determined for each subject. However, the differences in the tone levels across subjects did not result in significant differences in the bandwidths of the chimeras. So, although the 25 E₁F₁ base line N wave forms and the 25 E₂F₂ base line N wave forms were identical for all subjects, the various T+N wave forms differed across subjects, as is true in any study with reproducible maskers (because subjects have different detection thresholds); however, these wave forms were “comparable” across subjects, as explored by cross-subject comparisons in the analyses of the detection results.

Stimuli were created using custom MATLAB software (Mathworks, Natick, MA) and were presented using a TDT System III (Tucker Davis Technologies, Gainesville, FL) RP2 digital-analog converter (48 828 Hz sampling rate, 24 bits∕sample) over TDH-39 headphones (Telephonics, Corp., Farmington, NY).

Training

Training stages were similar to those described in Davidson et al. (2006) and are summarized here. The extensive training paradigm was designed to encourage subjects to develop a consistent detection strategy at threshold-level performance that would remain constant over the duration of the experiment (threshold was defined here for each subject and each interaural condition as the E_S∕N₀ value in decibels, where the d^′ for yes∕no testing, $d_{\text{Y}∕\text{N}}^{\prime }$, was approximately equal to 1). The final testing procedure was a single-interval task without trial-by-trial feedback, but early in training other procedures were used to help subjects learn acoustic cues that could be used to determine the presence of the signal. Three separate training tasks were completed, and each task was progressively more similar to the final testing procedure. The training procedures used approximately 50-Hz bandwidth, 100-ms duration noise wave forms that were generated randomly on each trial (i.e., they were not reproducible stimuli as used in the testing procedure, and they were not chimeras). The training noises contained the same five frequency components as the testing noises. Randomly generated noises were used to prevent any possible learning of reproducible stimuli. Training stimuli were normalized with the same procedures as the testing stimuli; that is, all N₀S₀ N and T+N stimuli and N₀S_π N stimuli were normalized to 57 dB SPL, while N₀S_π T+N stimuli were not re-normalized after addition of the tone.

The following training and testing procedures were conducted under both the N₀S₀ and N₀S_π interaural conditions. In general, subjects received only one type of interaural stimulus condition per session (2–3 h). For S1, S3, and S4, the initial interaural condition was randomized across subjects, and the use of N₀S₀ or N₀S_π stimuli alternated by session. S1, S3, and S4 had relatively small differences between thresholds for the diotic and dichotic conditions, which raised the question as to whether the alternation of interaural stimulus conditions across sessions may have affected their results due to the possible confusion of the diotic and dichotic cues. Therefore, S2, S5, and S6, who were tested later, were trained and tested completely in one interaural condition before moving on to the other conditions. The initial interaural condition was also randomized across this subset of subjects. (As a further test, S3, who initially alternated interaural conditions by session, subsequently repeated the entire experiment but completed the N₀S_π interaural condition first, followed by the N₀S₀ condition. Detection patterns from the two training and testing orders for this subject were highly correlated.) In rare cases, stimuli from both interaural conditions were presented during the same session (e.g., to finish a particular training or testing paradigm). During those sessions, presentation of the individual blocks of stimuli never alternated between the two conditions.

During the first training stage, each subject completed 10–15 tracks in a two-interval two-alternative forced-choice, 2-down∕1-up tracking procedure with trial-by-trial feedback to estimate a level where $d_{2\text{AFC}}^{\prime }=0.77$. Each track had a fixed length of 100 trials. The step size was maintained at 4 dB for the first two reversals and dropped to 2 dB thereafter. Thresholds were estimated by averaging tone levels at all but the first four or five reversals in the track such that an even number of reversals was averaged. Subjects were instructed to “select the interval containing the tone” and learned the task based on trial-by-trial feedback.

During the second training stage, a single-interval, fixed-level task was used to familiarize the subject with the task that would be used during testing; however, trial-by-trial feedback was provided to help subjects stabilize their performance near threshold during this training stage. The instructions for the single-interval tasks were to “determine whether the tone was present” on each trial and to click on buttons labeled “tone” and “no tone.” Approximately ten blocks, containing 100 trials each, were completed at +3, +1, and −1 dB relative to the threshold established in the two-interval task. The d^′ values calculated from these blocks were used to estimate the tone level where d^′ was approximately equal to unity, rounded to 1-dB resolution. Approximately ten blocks were then run at that tone level. Throughout the single-interval training procedures (and the testing procedure described in Sec. 2D), d^′ and bias (β, Macmillan and Creelman, 1991) were monitored. (Note that d^′ with no subscript refers to d^′ for yes∕no testing, which was used throughout the rest of the study.) If a subject’s threshold changed, the tone level was adjusted again with 0.5 or 1-dB resolution until d^′ returned to unity.

After a stable tone level was established, the trial-by-trial feedback was removed, and subjects completed approximately ten 100-trial blocks without feedback in order to determine whether d^′ values remained near unity after feedback was removed. In rare cases, tone levels were further adjusted with 0.5- or 1-dB resolution such that d^′≈1. The block length was then increased to 400 trials, and subjects completed five more blocks.

If a listener was noticeably biased (i.e., β departed by more than 15% from unity, with unity indicating an equal probability of responding “tone” or “no tone”), the subject was given verbal feedback after the session to “try and make an equal number of tone and no tone responses.” Subjects were informed of the value of β after each block, and they were notified that β<1 indicated too many “tone” responses, and β>1 indicated too many “no tone” responses. The values of d^′ and β were computed using P(Y∣T+N) (the probability of a “yes” response conditional on a T+N trial, or hit rate) and P(Y∣N) (the probability of a “yes” response conditional on an N trial, or false-alarm rate).

Testing

The testing stage was identical to the final training stage except that the reproducible noises described in Sec. 2B were used as stimuli. Before each 400-trial block, 20 practice trials (that did not use reproducible stimuli or chimeras) were presented with feedback. The 20 practice trials were presented with tone levels 2 dB above the tone level used for testing. For each 400-trial block, which included only one interaural condition, the appropriate T+N (25 stimuli) and N (25 stimuli) from each of the four stimulus sets were presented twice each in a randomly interleaved order. A total of 50 blocks were presented to each listener under each interaural condition such that 100 presentations of each T+N and each N wave form were presented at the final tone level.

The narrow-band-noise wave forms used in training were random and did not include chimeric stimuli. As a result, the tone level determined from the training procedure did not necessarily represent the level where d^′≈1 for each subject when using the sets of reproducible noise wave forms. In these cases, the tone level was adjusted in 0.5- or 1-dB steps until d^′≈1 for each subject, and data collection was re-initiated for that subject. In practice, the tone level was adjusted at least once for each listener, which was most likely a consequence of the specific stimuli selected with the distortion-control algorithm (described in the Appendix0). Learning was unlikely to occur during this process because the long training procedure with feedback was designed to encourage subjects to establish a fixed decision strategy. Trial-by-trial feedback was never presented while testing with the reproducible noise wave forms. Values of d^′ and β were computed across the combination of all stimulus wave forms from the four stimulus sets (i.e., E₁F₁, E₁F₂, etc.), and were not monitored within each of the sets. No attempt was made to control for variations in values of d^′ and β computed for the individual envelope and fine-structure sets of stimuli (e.g., E₁F₁) during the course of the experiment.

RESULTS

The analyses of the experimental results are presented below in several sections. First, the reliability of the data is addressed. Next, detection patterns estimated with the base line and chimeric stimuli are compared within subjects to determine the relative contributions of envelope and fine-structure cues used in the detection task. Detection patterns are then compared between subjects to determine if the cues or detection strategies used by the different subjects were similar. Finally, detection patterns are compared between interaural conditions to determine if any similarities in detection cues occurred between the diotic and dichotic conditions. The analyses considered detection patterns constructed from the proportion of “yes” responses to N wave forms [P(Y∣N)] and to T+N stimuli [P(Y∣T+N)]. For each stimulus set and for each interaural condition, these two detection patterns (each having 25 elements) were also combined into one larger detection pattern (with 50 elements) to create P(Y∣W), where W refers to one of the 50 T+N or N stimuli. To compare detection patterns (i.e., P(Y∣N), P(Y∣T+N), or P(Y∣W)), they were first converted to z-scores (i.e., relative to the standard normal distribution),3 so that the predicted relation between detection patterns was linear. Detection patterns were then compared, both within and across subjects, using regression techniques, as further described below.

Two conflicting problems arise when using these techniques. On the one hand, when correlating z-scores based on P(Y∣W), the value of the correlation coefficient r is a function of d^′; that is, as d^′ goes to infinity (for both of the detection patterns being compared), r goes to 1.0. Thus, correlations of P(Y∣W), which include detection patterns for responses to both N and T+N stimuli, are influenced by the value of d^′, and high r values do not necessarily indicate that there is a relation between the two cases in terms of underlying processing. On the other hand, the approach of analyzing P(Y∣T+N) and P(Y∣N) results separately means that the range of observed proportions of “yes” responses is almost certainly truncated, forcing an artificial reduction in r. By analyzing all three detection patterns [i.e., P(Y∣W), P(Y∣N), and P(Y∣T+N))], it was possible to evaluate the relations between the full detection patterns (P(Y∣W) while safeguarding against artifactually high r values introduced by conditions with higher values of d^′.

Reliability of the data and detection performance

Tables 1, 2, 3, 4 show reliability and detection performance statistics for each individual subject and also the average across subjects (S_avg) under both the N₀S₀ (Tables 1, 2) and N₀S_π (Tables 3, 4) interaural conditions. These tables only include detailed results for one set of base line stimuli and one set of chimera stimuli; results for the other two sets of wave forms were comparable, as expected, and are available in Davidson (2007). Tables 1, 3 summarize data combined over both N and T+N wave forms [i.e., P(Y∣W)]; Tables 2, 4 separate the N and T+N data [i.e., P(Y∣N) and P(Y∣T+N)]. The threshold tone level used for the experiment (where d^′≈1) is given in terms of E_S∕N₀ for each subject and condition.n2 (Note that because the N₀S₀ stimuli were all normalized to 57 dB SPL, changes in E_S∕N₀ do not indicate changes in level between N and T+N stimuli. Also, note that because the level differences were eliminated from the N₀S₀ stimuli, the difference between N₀S₀ thresholds and N₀S_π thresholds is not necessarily comparable to masking level differences reported in other studies.) The actual d^′ and β values calculated across and within the four stimulus sets are also shown. The training procedure was relatively successful in finding overall d^′ values near 1 with the possible exception of S1 in the N₀S_π condition (d^′=0.78 in Table 3). For individual sets of N₀S₀ stimuli, d^′ values ranged from 0.51 to 1.14, and β values ranged from 0.70 to 1.32 (Table 1). For individual sets of N₀S_π stimuli, d^′ values ranged from 0.54 to 1.11, and β values ranged from 0.57 to 1.35 (Table 3).

Table 1.

Performance and reliability statistics for P(Y∣W) under the N₀S₀ interaural condition. One tone level (E_S∕N₀ in dBn2) was used for each subject. Overall d^′ and β were computed using responses to wave forms in all stimulus sets. Individual d^′ and β values are given for one base line stimulus set and for one chimera stimulus set. Values for the other stimulus sets are available in Davidson (2007). The coefficient of determination between responses from the first and the last half of the trials $\left(r_{12}^2\right)$ and the proportion of predictable variance $\left(r_{\text{max}}^2\right)$ are given for each condition. All r² values were significant (p<0.05).

S	Overall			Stimulus set	Per stimulus set		P(Y∣W)
	ES∕N0	d′	β		d′	β	$r_{12}^2$	$r_{\text{max}}^2$
S1	10	0.87	0.94	E1F1	0.95	0.70	0.93	0.97
				E1F2	0.76	1.05	0.95	0.98
S2	10	0.88	0.99	E1F1	1.01	0.87	0.93	0.97
				E1F2	0.63	1.03	0.95	0.97
S3	10	1.02	1.07	E1F1	0.86	1.02	0.88	0.94
				E1F2	1.01	1.10	0.89	0.94
S4	11	0.96	0.95	E1F1	0.85	0.85	0.93	0.96
				E1F2	0.95	0.93	0.93	0.97
S5	11	0.86	0.99	E1F1	0.51	0.88	0.95	0.97
				E1F2	0.68	0.97	0.95	0.97
S6	11.5	0.94	0.97	E1F1	0.79	0.81	0.89	0.94
				E1F2	1.05	1.04	0.89	0.94
Savg	10.58	0.92	0.98	E1F1	0.82	0.85	0.98	0.99
				E1F2	0.84	1.02	0.98	0.99

Table 2.

Reliability statistics for P(Y∣T+N) and P(Y∣N) under the N₀S₀ condition. The χ² statistic, coefficient of determination between responses from the first and the last half of the trials $\left(r_{12}^2\right)$, and the proportion of predictable variance $\left(r_{\text{max}}^2\right)$ are shown. All χ² values were significant (p<0.001), and all r² values were also significant (p<0.05).

S	Stimulus set	P(Y∣T+N)			P(Y∣N)
		χ2	$r_{12}^2$	$r_{\text{max}}^2$	χ2	$r_{12}^2$	$r_{\text{max}}^2$
S1	E1F1	1371	0.91	0.95	1829	0.91	0.95
	E1F2	2198	0.94	0.97	2078	0.95	0.97
S2	E1F1	1543	0.89	0.94	1856	0.92	0.96
	E1F2	1737	0.94	0.97	1779	0.94	0.97
S3	E1F1	669	0.73	0.85	1011	0.85	0.92
	E1F2	488	0.61	0.77	1431	0.89	0.94
S4	E1F1	1350	0.91	0.95	1340	0.89	0.94
	E1F2	940	0.86	0.93	1628	0.92	0.96
S5	E1F1	2352	0.95	0.97	3017	0.95	0.98
	E1F2	1645	0.90	0.95	2310	0.96	0.98
S6	E1F1	1258	0.75	0.86	1645	0.93	0.96
	E1F2	1113	0.77	0.87	1620	0.87	0.93
Savg	E1F1	4873	0.94	0.97	7659	0.98	0.99
	E1F2	3912	0.93	0.96	8530	0.98	0.99

Table 3.

Same as Table 1 but for the N₀S_π interaural condition. All r² values were significant (p<0.05).

S	Overall			Stimulus set	Per stimulus set		P(Y∣W)
	ES∕N0	d′	β		d′	β	$r_{12}^2$	$r_{\text{max}}^2$
S1	0	0.78	0.91	E1F1	1.10	0.57	0.93	0.97
				E1F2	0.66	0.97	0.93	0.96
S2	−10	0.97	1.10	E1F1	0.85	1.35	0.90	0.95
				E1F2	1.09	0.96	0.94	0.97
S3	−17	1.01	0.99	E1F1	0.94	1.11	0.89	0.94
				E1F2	1.06	0.92	0.86	0.92
S4	−1	0.93	1.00	E1F1	0.92	0.85	0.90	0.95
				E1F2	0.79	1.03	0.93	0.97
S5	−16.5	0.91	1.02	E1F1	0.90	1.24	0.92	0.96
				E1F2	1.09	1.11	0.92	0.96
S6	−10	0.96	1.06	E1F1	0.87	0.95	0.89	0.95
				E1F2	1.08	0.96	0.87	0.93
Savg	−9.08	0.92	1.01	E1F1	0.89	1.00	0.98	0.99
				E1F2	0.96	0.99	0.97	0.98

Table 4.

Same as Table 2 but for the N₀S_π interaural condition. All χ² values were significant (p<0.001), and all r² values were significant (p<0.05).

S	Stimulus set	P(Y∣T+N)			P(Y∣N)
		χ2	$r_{12}^2$	$r_{\text{max}}^2$	χ2	$r_{12}^2$	$r_{\text{max}}^2$
S1	E1F1	885	0.94	0.97	1621	0.89	0.94
	E1F2	1859	0.94	0.97	1938	0.90	0.95
S2	E1F1	1283	0.89	0.94	639	0.75	0.86
	E1F2	1188	0.91	0.95	970	0.85	0.92
S3	E1F1	844	0.81	0.90	530	0.75	0.86
	E1F2	909	0.72	0.84	366	0.63	0.78
S4	E1F1	921	0.90	0.95	1100	0.82	0.90
	E1F2	1390	0.91	0.95	1625	0.91	0.95
S5	E1F1	1388	0.89	0.95	623	0.87	0.93
	E1F2	1220	0.88	0.94	614	0.74	0.86
S6	E1F1	1438	0.87	0.93	490	0.73	0.85
	E1F2	1159	0.77	0.87	654	0.72	0.85
Savg	E1F1	3089	0.98	0.99	1287	0.87	0.93
	E1F2	1953	0.91	0.95	978	0.83	0.91

Tables 2, 4 include χ² statistics, with larger values indicating that variations in the subjects’ responses were tied to across-wave-form changes in the reproducible stimuli and not due to chance alone (Siegel and Colburn, 1989). All χ² values greatly exceeded the threshold for significance $\left({\chi }_{0.01}^2=43\right)$, demonstrating that the between-wave-form differences in hit rates and the between-wave-form differences in false-alarm rates were reliable. Note that the χ² values observed for S_avg under the N₀S_π condition (Table 4) were low relative to those under the N₀S₀ condition (Table 2), suggesting that although the detection patterns for individual subjects were reliable, there were individual differences that “diluted” the detection patterns when averaged across subjects, particularly under the N₀S_π condition.

Tables 1, 2, 3, 4 also include squared first-half, last-half correlation coefficients $\left(r_{12}^2\right)$. Again these values were high and significant, indicating that the subjects’ responses were driven by the stimulus in a manner that was consistent across time. The value of $r_{12}^2$ is directly related to $r_{\text{max}}^2$, the maximum proportion of predictable variance that can be expected when comparing detection patterns across stimulus sets, interaural conditions, or subjects (also shown in Tables 1, 2, 3, 4). The value of $r_{\text{max}}^2$ exceeds the value of $r_{12}^2$ because the first-half and last-half detection patterns are necessarily based on half as many trials as the overall (i.e., first half and last half combined) detection patterns (50 vs 100 trials).

Within-subject comparisons of detection patterns estimated with base line and chimeric stimuli

Recall that the overall logic of the experiment and analysis is fairly straightforward. If subjects used only envelope cues to make detection judgments, then stimulus sets that shared the same envelopes (e.g., E₁F₁ and E₁F₂) should have produced the same detection patterns. If fine structure were the only relevant cue, then stimulus sets with the same fine structures (e.g., E₁F₁ and E₂F₁) should have produced the same detection patterns. If a linear combination of envelope and fine structure was relevant, then it should be possible to combine two detection patterns to predict a third (e.g., E₁F₂ and E₂F₁ could be used to predict E₁F₁). The general strategy was then to predict each of the base line detection patterns (E₁F₁ or E₂F₂) with the chimeric detection patterns (E₂F₁ and E₁F₂) using multiple regression.5 The multiple regression method used for predicting the detection pattern for the E₁F₁ stimulus set [as shown schematically in Fig. 1b] is described here. The method for predicting the E₂F₂ detection pattern is equivalent, but the subscripts “1” and “2” would be exchanged in the description.

This correlation analysis assumes that the E₁F₁ and E₂F₂ stimulus sets are statistically independent of each other and that the detection patterns for these two stimulus sets are also statistically independent. Chance similarities, reflected in nonzero correlations, between the E₁F₁ and E₂F₂ detection patterns could cause misleading correlations between the detection patterns for E₁F₂ and E₂F₁. If this were true, there could be nonzero correlations between response patterns to E₁F₁ and E₂F₂, even in the case in which envelope manipulations had absolutely no effect on responses. Such misleading correlations are referred to as “false” correlations. These false correlations were avoided by considering only the components of the detection patterns that were uncorrelated with the original E₂F₂ pattern. This “partialing-out” approach, described below, automatically excludes correlations across response sets that arise from correlations in the original wave forms. These correlations could be based on similarities in the envelopes or fine structures of the original wave form sets but could also be due to any other response-determining components that are shared by the original wave form sets (i.e., the E₁F₁ and E₂F₂ sets). To avoid this potential problem, any such nonzero correlations were statistically “partialed out” by separately regressing the E₁F₁, E₁F₂, and E₂F₁z-score detection patterns on the E₂F₂ detection pattern and then using the residuals from each of these regressions in the subsequent analyses. The residuals of the regression of any detection pattern on the E₂F₂ detection pattern are by definition not correlated with the E₂F₂ pattern. Thus, by using these residual detection patterns in further analyses, any chance similarity in the variability of the detection patterns to that associated with the E₂F₂ pattern were “blocked” or “removed” from the other three patterns (i.e., the residual detection patterns for E₁F₁, E₁F₂, and E₂F₁ were uncorrelated with the detection pattern for E₂F₂). Note that the residuals were computed with separate regressions for the P(Y∣W), P(Y∣N), and P(Y∣T+N) data.

Next, two simple linear regressions were performed to predict the E₁F₁ detection pattern residuals using either the E₂F₁ or E₁F₂ detection pattern residuals as the predictor. These regressions indicated the proportion of variance explained (R²) by the fine structure (because F₁ was held constant) and by the envelope (because E₁ was held constant), respectively. Next, the E₁F₁ detection pattern residuals were simultaneously regressed on the E₂F₁ and E₁F₂ detection pattern residuals to compute the proportion of variance explained by the multiple regression or a linear combination of both envelope and fine structure. Incremental-F tests (Edwards, 1979) were performed to determine if the proportion of predicted variance in the E₁F₁ detection pattern residuals were significantly increased by incorporating fine-structure information (the E₂F₁ residuals) in addition to envelope alone (the E₁F₂ residuals) or by incorporating envelope information in addition to fine-structure information alone.

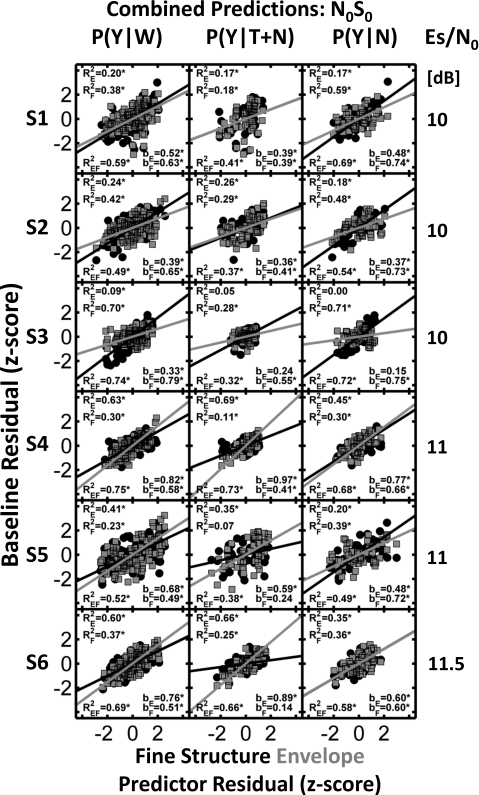
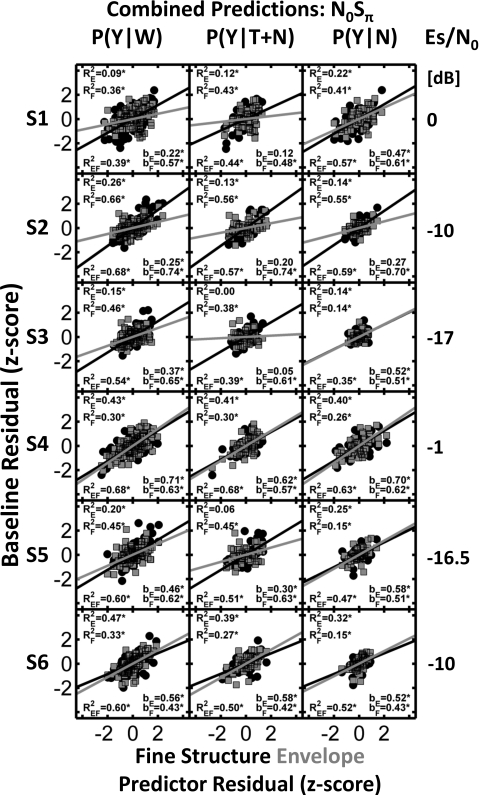
Because the findings when predicting E₁F₁ and when predicting E₂F₂ were comparable,6 the results were combined and are shown as scatter plots in Figs. 34. In each panel, the detection pattern residuals estimated from responses to chimeric stimuli were used to predict the detection pattern residuals estimated for the E₁F₁ or E₂F₂ stimulus sets. The predictors are plotted on the abscissa of each panel. Envelope-based predictions are always shown with gray squares, and fine-structure-based predictions are shown with black circles. The regression lines and the slopes of the linear regressions [b_E and b_F, see Fig. 1b] are shown in each panel. The slope values were computed using the multiple regression procedure (i.e., both envelope and fine structure were predictors) and thus differed slightly from the slopes that would be obtained using either envelope or fine structure individually (as discussed below). Slopes for the individual envelope-based and fine-structure-based predictions (corresponding to the individual envelope and fine structure R² values) are not shown. If the fine structure were a perfect predictor of the variance in the detection pattern residuals, the black circles would fall exactly along the diagonal and b_F would equal 1. Conversely, if the envelope were a perfect predictor of variance in the detection pattern residuals, the gray squares would fall exactly along the diagonal and b_E would equal 1.

Figure 3.

Combined predictions for E₁F₁ and E₂F₂ for the N₀S₀ conditions. Comparisons between cue conditions for P(Y∣W), P(Y∣T+N), and P(Y∣N) (columns) for six subjects (rows) using z-score residuals to characterize the probabilities. Envelope-based predictions are shown with gray squares, while fine-structure-based predictions are shown with black circles. Relative weights for each cue are shown by the b_E and b_F values, with asterisks indicating significant slopes (i.e., significant incremental-F-test results). $R_{\text{E}}^2$ and $R_{\text{F}}^2$ indicate the proportion of predictable variance based on the individual cues (asterisks indicate significant values). $R_{\text{EF}}^2$ corresponds to the proportion of predictable variance using a linear combination of both envelope and fine structure. Signal-to-noise ratio (E_S∕N₀ in dB) is shown to the right of each plot. See text for details.

Figure 4.

Same as Fig. 3 except that predictions were made for the N₀S_π conditions.

Three R² values are shown in each panel (Figs. 34). The $R_{\text{E}}^2$ corresponds to the prediction using only envelope information (i.e., using the detection pattern residuals for the stimulus set with the same envelopes as a predictor). $R_{\text{F}}^2$ corresponds to the prediction using only fine-structure information (i.e., using the detection pattern residuals for the stimulus set with the same fine structures as a predictor). $R_{\text{EF}}^2$ corresponds to the prediction using a linear combination of envelope and fine-structure information with weights given by b_E and b_F, respectively. Significant R² values are denoted with an asterisk. Incremental-F tests (p_incr) were used to determine if the addition of envelope as a predictor to a prediction based only on fine structure, or the addition of fine structure as a predictor to a prediction based only on envelope, significantly increased the amount of predictable variance in the detection pattern residuals. Note that the incremental-F test is equivalent to testing whether b_E or b_F is significantly different from zero; significant values are indicated by asterisks.

N₀S₀ stimuli

Inspection of Fig. 3 reveals that both envelope and fine structure show, in general, significant correlation with the responses of each listener under the N₀S₀ condition (in all but four cases). The large number of significant p_incr values (i.e., significant b values) indicates that for most subjects, both envelope and fine structure contributed unique information that was correlated with the listeners’ decision variables. However, there was some intersubject variability in the R² values observed in Fig. 3. In previous N₀S₀ detection experiments in which energy was not equalized, subjects’ detection patterns were highly correlated with one another (e.g., Evilsizer et al., 2002; and Davidson et al., 2006). These high correlations indicate that the same or very similar decision variables were used by each subject in those studies. Recall that in the N₀S₀ condition of this experiment, overall stimulus levels were equalized to remove the availability of energy as a decision variable. As a result, high intersubject correlations were not necessarily expected (Sec. 3C includes a more complete discussion of intersubject correlations), nor was the use of identical decision variables across subjects. In fact, the results shown in Fig. 3 (in addition to the relatively low intersubject correlations described in Sec. 3C) suggest the use of different detection strategies by different subjects. The b and R² values for subject 3 suggest the dominance of cues related to the fine structure of the stimulus wave forms rather than envelopes of the stimulus wave forms. The remaining subjects used a combination of fine-structure and envelope-related cues, as indicated by the b and R² values for envelope predictors with respect to the b and R² values for fine-structure predictors.

Although the majority of $R_{\text{EF}}^2$ values in Fig. 3 are significant, the values range from 0.32 to 0.75, and all are substantially lower than the estimates of the proportions of predictable variance shown in Tables 1, 2. That is, these linear multiple regression models do not provide a satisfactory description of these data. On the other hand, visual inspection of the scatter plots in Fig. 3 does not suggest that a nonlinear model would perform substantially better. Implications of these results for modeling are discussed in Sec. 3D.

N₀S_π stimuli

In the case of dichotic detection, the comparisons of detection results can be interpreted in terms of interaural differences. That is, the distributions of ILDs were similar for stimuli that had matched envelopes, and the distributions of fine-structure ITDs were similar for stimuli that had matched fine structures. Figure 4 shows the results of the same kind of regression analyses for the N₀S_π condition. Note that the threshold tone level under the N₀S_π condition varied widely across subjects. Subjects with similar thresholds also had more similar detection patterns, so the results are described for pairs of subjects with similar N₀S_π thresholds. Subjects S3 and S5 had the lowest threshold tone levels and showed similar trends in terms of envelope and fine-structure predictions. The linear combination of envelope and fine structure failed to predict the majority of the variance in the P(Y∣N) data. Predictions for the P(Y∣T+N) data indicated a stronger reliance on fine structure, but they failed to predict more than approximately half the variance in the base line detection pattern residuals. Predictions for P(Y∣W) indicate that fine-structure information dominated the detection process for these two subjects but also showed a significant contribution of cues based on the envelope. The multiple regression model predicted 54% and 60% of the variance in the base line detection pattern residuals for these subjects. Slightly larger weights (b values) were found in the best fits for cues derived from the fine structure as compared to the weights for fits derived from the envelope.

Subjects S2 and S6 were tested with threshold tone levels about 7 dB higher than subjects S3 and S5. Subject S2 showed consistent dominance of fine-structure-based cues over envelope-based cues. The multiple regression model explained 68% of the variance in the P(Y∣W) residuals for this subject. Results for subject S6 indicated a stronger contribution of envelope over fine structure with significant incremental-F tests for both envelope and fine structure. The multiple regression model explained about 60% of the variance in the P(Y∣W) residuals for this subject.

Subjects S1 and S4 were tested with the highest threshold tone levels. Subject S1 weighted cues derived from the fine structure more strongly than those derived from the envelope, but the predictions explained only 39% of the variance in the P(Y∣W) residuals. Subject S4 used cues derived from both envelope and fine structure, and the multiple regression model was able to explain up to 68% of the variance in the P(Y∣W) residuals.

In general, the results for the N₀S_π condition, as for the N₀S₀ condition, were not well described by the statistical model based on a linear combination of envelope and fine-structure information. The model seemed to fit best for the subjects with higher thresholds but, in general, predicted about 40%–70% of the variance in the base line detection pattern residuals, substantially lower than the estimates of predictable variance $\left(r_{\text{max}}^2\right)$ for the N₀S_π condition, which were 84% or higher.

Comparisons between subjects

To compare detection patterns across subjects, the square of Pearson’s correlation coefficient (r²) was computed. Table 5 shows between-subject r² values for the base line and chimeric detection patterns. The between-subject r² values were lower for the N₀S₀ condition in this study than in previous studies (Evilsizer et al., 2002; Davidson et al., 2006) and ranged from 0.34 to 0.69 for P(Y∣W). The lower between-subject correlations suggest the use of a more diverse set of decision variables across subjects in this experiment than in previous experiments with diotic stimuli, which was likely caused by the lack of a simple energy cue to rely on and by the narrow stimulus bandwidth. Pairs of subjects with the highest between-subject r² values did not necessarily share envelope or fine-structure dominance (e.g., S2 and S6 in Fig. 3 and Table 5).

Table 5.

Comparisons between subjects presented in terms of r². Correlations were based on responses to all four stimulus sets.

N0S0
	P(Y∣W)					P(Y∣T+N)					P(Y∣N)
	S2	S3	S4	S5	S6	S2	S3	S4	S5	S6	S2	S3	S4	S5	S6
S1	0.45a	0.52a	0.63a	0.34a	0.50a	0.28a	0.22a	0.36a	0.10a	0.27a	0.36a	0.49a	0.66a	0.34a	0.44a
S2		0.48a	0.57a	0.62a	0.69a		0.27a	0.30a	0.52a	0.60a		0.35a	0.56a	0.53a	0.56a
S3			0.49a	0.40a	0.51a			0.11a	0.21a	0.28a			0.36a	0.28a	0.31a
S4				0.43a	0.65a				0.15a	0.46a				0.44a	0.54a
S5					0.68a					0.44a					0.75a
N0Sπ
	P(Y∣W)					P(Y∣T+N)					P(Y∣N)
	S2	S3	S4	S5	S6	S2	S3	S4	S5	S6	S2	S3	S4	S5	S6
S1	0.00	0.14a	0.63a	0.05a	0.14a	0.13a	0.01	0.43a	0.01	0.00	0.37a	0.00	0.63a	0.02	0.05a
S2		0.40a	0.00	0.54a	0.39a		0.19a	0.18a	0.46a	0.24a		0.00	0.36a	0.10a	0.00
S3			0.19a	0.45a	0.50a			0.01	0.20a	0.24a			0.02	0.05a	0.05a
S4				0.06a	0.13a				0.02	0.03				0.09a	0.01
S5					0.36a					0.20a					0.00

^ap<0.05.

Under the N₀S_π condition, between-subject r² values were on average lower than those for N₀S₀ condition and ranged from 0.00 to 0.63 for P(Y∣W) (Table 5). Subject pairs with similar threshold tone levels had more similar detection patterns than those with differing threshold tone levels. Subject pair S1 and S4 had the highest intersubject correlations, and these subjects also had similar and relatively high thresholds, suggesting a dependence of threshold on detection strategy. However, comparing Fig. 4 to Table 5 for the pairs of subjects with the largest intersubject correlations (and the most similar thresholds) did not reveal any clear pattern of envelope or fine-structure dominance. Evidence for individual differences between subjects in the use of available cues for binaural detection has been described previously (e.g., McFadden et al., 1971).

Comparisons between interaural conditions

Table 6 shows correlations (in terms of r²) between N₀S₀ and N₀S_π interaural conditions for P(Y∣W) and for P(Y∣T+N) and P(Y∣N). The subjects with the highest thresholds (S1 and S4) had the highest correlations between detection patterns from the two interaural conditions. Closer inspection of Table 6 reveals that the sources of the correlations between the two interaural conditions for these subjects were largely from responses to noise-alone stimuli, P(Y∣N). Subjects S1 and S4 show substantial r² values (0.93 for both listeners) between P(Y∣N) values from the two interaural conditions. Recall that N stimuli in the N₀S_π condition were identical to those for the N₀S₀ condition (but not the T+N stimuli). Such high r² values suggest that S1 and S4 may have been attempting to use the same detection strategy for the two interaural conditions; if this strategy were more appropriate for N₀S₀ listening, that would explain their high thresholds for the N₀S_π stimuli. The fact that these subjects still had substantially lower dichotic thresholds suggests that they were not employing a strictly diotic strategy but may have instead been monitoring more than one cue for detection (e.g., one diotic cue and one dichotic cue). Because the dichotic cue would not be present on N trials, responses would be similar to those under the N₀S₀ condition. On T+N trials, both cues might be present, leading to the more modest correlations observed. The subjects with the lowest thresholds (S3 and S5) and intermediate thresholds (S2 and S6) had much lower correlations between detection patterns from the two interaural conditions. The noise-alone intersubject r² values have implications for the types of detection models used to explain the detection patterns, as outlined in Sec. 4.

Table 6.

Comparisons between interaural conditions presented in terms of r². Correlations were based on responses for all four stimulus sets.

Subject	P(Y∣W)	P(Y∣T+N)	P(Y∣N)
S1	0.60a	0.19a	0.93a
S2	0.02a	0.00	0.46a
S3	0.30a	0.00	0.02
S4	0.65a	0.15a	0.93a
S5	0.02a	0.00	0.33a
S6	0.13a	0.01	0.00

^ap<0.05.

DISCUSSION

Summary of results

As discussed in Sec. 1, there is an extensive literature indicating that monaural, diotic, and dichotic tone-in-noise detection can be partially, but not completely, predicted based on across-wave-form variations in energy. In order to better understand other cues that might also contribute to detection performance, this experiment investigated the roles of stimulus envelope and fine structure when energy differences among stimuli were eliminated. A simple multiple regression statistical model was unable to explain all of the predictable variance in the detection pattern residuals, yielding observed R² values between 0.32 and 0.75 for N₀S₀ stimuli and between 0.39 and 0.68 for N₀S_π stimuli. The predictable variance was estimated by $r_{\text{max}}^2$,n4 which ranged from 0.77 to 0.99 for both N₀S₀ and N₀S_π stimuli and was always substantially higher than the observed R².

The envelope and fine-structure provide a complete description of the energy-normalized stimuli used in this study. The fact that envelope and fine structure were unable to predict the subjects’ responses separately, or when combined linearly, suggests that this description is somehow inadequate or that this method of decomposing the stimuli is not consistent with underlying physiological and psychophysical processes. The implications of these results for future efforts to model detection are discussed below. Successful models must consider alternative descriptions of the stimuli and∕or must capture the impact of temporal interactions between the envelope and the fine structure of the stimuli.

Implications for computational models of detection

Comparisons between detection patterns estimated with base line and chimeric stimuli

With randomly generated tone-in-noise stimuli, many putative detection cues tend to co-vary. The approach in this experiment was to eliminate overall energy differences among the stimuli for both N and T+N wave forms under the N₀S₀ condition and for only N wave forms under the N₀S_π condition and thereby to force the subjects to base their detection judgments on envelope cues and∕or fine-structure cues. The assumption was that these two sets of temporal cues were separable and independent. The fact that a substantial portion of the variance in the responses to the base line stimulus sets was not predicted by the multiple regression statistical model suggests that this assumption is wrong, at least in part. Two broad possibilities are suggested: (1) Although the fine structure and the envelope are obvious visual features of the narrow-band noise wave form, and there is considerable physiological evidence that both fine-structure and envelope information are encoded at least somewhat independently in the firing patterns of auditory neurons (e.g., Joris and Yin, 1992), these cues may not be used to determine the presence or absence of the tone in the authors’ narrow-band detection task. Perhaps the subjects base their decisions on some other representation (e.g., spectral shape). (2) Short-time interactions between the wave form envelopes and the wave form fine structures are critical to understanding these data. That is, envelope and fine-structure cues may be used to detect the tone, but they are not independent. If so, for example, it is unwise for models to independently extract envelope and fine structure, unless some interaction between the two occurs before the decision variable is computed. Indeed, temporal interactions between envelope and fine structure occur in narrow-band Gaussian noise [Davenport and Root, 1958, pp. 159–160 (e.g., rapid changes in instantaneous frequency or phase often occur when the instantaneous amplitude is low)]. Moreover, the wave forms used in the present study may have under-represented this problem because the stimulus generation algorithm tended to reject wave form pairs for which the chimeric recombination would temporally align high envelope and rapid frequency fluctuations.

Some previous studies attempting to explain detection patterns for narrow-band stimuli with computational models have omitted peripheral filtering and nonlinearities under the assumption that these do not contribute to the detection process (e.g., Isabelle, 1995; Davidson et al., 2006). However, this type of processing may be critical to capture the interactions between envelope and fine structure that are suggested by the present data.

Several candidate models remain in contention for both diotic and dichotic signal detection, and each will be tested in detail in further studies of these experimental results. These models are worth briefly mentioning here. In general, these models either operate on a spectral representation of the stimulus or incorporate some sort of dynamic interaction of envelope and fine structure; that is, each computes the decision variable from the entire stimulus (rather than stripping the stimulus envelope or fine structure apart for separate analyses). An example of a diotic model that remains under consideration is the multiple-detector model (e.g., Ahumada and Lovell, 1971; Gilkey and Robinson, 1986), which uses monaural banks of filters that are weighted and combined linearly to produce a decision variable. With respect to binaural models, equalization-cancellation-style models with realistic peripheral processing stages (e.g., Breebaart et al., 2001) should remain under consideration. Cross-correlation-style models (e.g., Colburn, 1977) with realistic peripheral processing should also remain under consideration, given that these models operate on the entire stimulus wave form rather than on envelope or fine structure alone.

N₀S_π noise-alone data

This study, like numerous previous studies (e.g., Evilsizer et al., 2002; Gilkey et al., 1985; Isabelle, 1995; Siegel and Colburn, 1989), found reliable detection patterns (with significant across-wave-form variation in the probability of a “yes” response) under the N₀S_π condition for noise-alone stimuli. In the present study, these reliable differences in responding were found even though across-wave-form energy variations were eliminated from the noise-alone stimuli. This finding is particularly significant for modeling efforts because several hypothesized models (cf., Isabelle, 1995; Isabelle and Colburn, 2004; Goupell and Hartmann, 2007) rely only on interaural differences to compute decision variables and thus would require some sort of internal noise mechanism to generate decision variables for the diotic noise-alone stimuli. If independent internal noise processes dominated over external noise at each ear, any left-right-symmetric binaural processing would not result in a stable detection pattern for noise-alone stimuli (assuming additive internal noise). If the noise were additive, the response on each trial would simply be based on interaural differences that resulted from the internal noise processes. Over large numbers of trials, such noise-generated interaural differences would produce “flat” detection patterns with no reliable differences in detection probabilities from noise to noise. A multiplicative internal noise source may be able to produce a stable pattern, but a generally applicable model of such processing is not available [see Colburn et al. (1997) for a description of how multiplicative internal noise could lead to internal interaural differences that are dependent on the external diotic stimulus in the context of the equalization-cancellation model of Durlach (1963)].

Another mechanism that would generate reliable detection patterns for noise-alone stimuli is a static frequency mismatch (e.g., van der Heijden and Trahiotis, 1998), or a static internal interaural delay or internal interaural attenuation. These mechanisms would be stable over time and would generate specific detection patterns based on the processing asymmetry. The magnitudes and types of plausible processing asymmetries will be examined in future work.

APPENDIX: STIMULUS SELECTION PROCEDURE AND RELATED ISSUES

Because it is impossible to modify the temporal structure of the stimulus without also impacting the spectrum (e.g., Davenport and Root, 1958, pp. 159–160), the process of assembling chimeric stimuli in some cases resulted in wave forms with spectral splatter and associated temporal distortions. These distortions could interfere with the task and cause unintended interaural differences (in the N₀S_π condition), so the stimulus wave forms were examined for excessive spectral splatter and eliminated based on specific criteria. Note that if absolutely no spectral splatter were allowed, the stimulus-creation algorithm would have eventually created four sets of stimuli with identical corresponding wave forms. The spectrum of each chimeric stimulus (after applying the cos² ramps) was checked to ensure that the magnitude of each spectral component more than 50 Hz away from the target was at least 15 dB below the wave form’s spectral peak, and that each spectral component more than 90 Hz away from the target was at least 25 dB below the wave form’s spectral peak. When a wave form failed this test, it was eliminated, and the corresponding wave forms (N, T₀+N for N₀S₀, T₀+N for N₀S_π, and T_π+N for N₀S_π) in all four sets of stimuli were also eliminated for all six subjects.

Stimuli that were eliminated tended to have large frequency modulations in the fine structure that were temporally positioned at relatively high envelope values when recombined (see Amenta et al., 1987). Such a combination naturally increased the bandwidth of the wave form. When stimuli were eliminated, two new base line wave forms were created using random noise, and corresponding chimeric stimuli were created. The stimuli were scaled, tones were added, and the resulting wave forms were tested. The algorithm ran for approximately 12 h on a Pentium M computer (1.86 GHz) and eliminated thousands of candidate stimulus wave forms before obtaining the set used in the present study (the exact number of eliminated wave forms was not recorded). This process resulted in stimuli that had little distortions or spectral splatter.

One initial concern with limiting the amount of spectral splatter was that corresponding E₁F₁ and E₂F₂ wave forms could be too highly correlated (e.g., the only stimuli that could swap envelopes without generating any splatter would be identical stimuli), such that the detection patterns resulting from the E₁F₁ and E₂F₂ stimulus sets would be the same. Table 7 shows the mean r² values for correlations between corresponding wave forms in the E₁F₁ and E₂F₂ stimulus sets. For comparison, Table 7 also shows the mean of 10 000 r² values computed between pairs of randomly generated tone-plus-noise (T+N) stimuli, as well as between pairs of random noise-alone (N) stimuli. These statistics are also presented for the envelopes (computed as the absolute value of the complex analytic wave form, which adds the Hilbert transform of the original wave form as the imaginary part to the original real wave form) and the fine structure (computed as the cosine of the angle of the complex analytic function) of each wave form. Several Mann–Whitney U tests were performed comparing the r² values from the random stimuli to those of the reproducible stimuli. For N stimuli, the envelope correlation was significantly (p<0.01) larger for the reproducible stimuli with respect to the random stimuli, but the whole-wave-form and fine-structure-only correlations were not significantly different (p>0.5). For T+N stimuli, subjects S1–S5 showed significantly (p<0.01) larger correlations between the envelopes of the reproducible stimuli for corresponding wave forms in the E₁F₁ and E₂F₂ stimulus sets than those present for correlations between the envelopes of random stimuli (p>0.05). Whole-wave-form and fine-structure correlations were not significantly larger when computed between the E₁F₁ and E₂F₂ stimuli than when computed between randomly generated T+N stimuli.

Table 7.

Means and standard deviations for correlations (r²) between corresponding wave forms in the E₁F₁ and E₂F₂ stimulus sets for both T+N and N stimuli. The levels of the tone were set to each subject’s threshold (given as E_S∕N₀ in dB) for the N₀S₀ condition. The mean and standard deviations are also given for correlations between 10 000 pairs of randomly generated T+N and correlations between 10 000 pairs of randomly generated N wave forms (“Random”). Statistics are also given for the envelopes and fine structures of each wave form (see text for details).

Wave form	Subject	Es∕N0	Entire wave form		Envelopes only		Fine structure only
			Mean r2	SD r2	Mean r2	SD r2	Mean r2	SD r2
T+N	S1	10	0.44	0.18	0.31	0.23	0.47	0.19
	S2	10	0.44	0.18	0.31	0.23	0.47	0.19
	S3	10	0.44	0.18	0.31	0.23	0.47	0.19
	S4	11	0.52	0.16	0.33	0.24	0.56	0.17
	S5	11	0.52	0.16	0.33	0.24	0.56	0.17
	S6	11.5	0.55	0.15	0.34	0.24	0.60	0.16
	Random	10	0.45	0.12	0.24	0.23	0.49	0.22
	Random	11	0.50	0.18	0.26	0.24	0.56	0.21
	Random	11.5	0.54	0.18	0.27	0.24	0.60	0.20
N	All	⋯	0.14	0.18	0.35	0.28	0.12	0.15
	Random	⋯	0.11	0.13	0.16	0.12	0.08	0.11

The similarity of the resulting E₁F₁ and E₂F₂ detection patterns (i.e., the patterns of hit and false-alarm rates for a particular group of the reproducible wave forms) was also examined. If the detection patterns for the responses to E₁F₁ and E₂F₂ had been highly correlated, results from the regression analysis (Sec. 2D) would be questionable because of the perceptual similarity of the two groups (and likely similarity of the E₂F₁ and E₁F₂ wave forms). Table 8 shows correlations in terms of r² [the squared Pearson correlation coefficient of the z-scores (but not residuals) computed from the two detection patterns] between the E₁F₁ and E₂F₂ detection patterns for the subjects in this study. If both T+N and N responses are considered together [i.e., the detection pattern for the probability of saying “yes, the tone is present” across all reproducible wave forms, P(Y∣W)], detection patterns from the E₁F₁ and E₂F₂ stimulus sets were significantly, albeit weakly, correlated (as one would expect because on average P(Y∣T+N)>P(Y∣N), introducing correlation between any two sets of stimuli for which d^′>0). However, for N₀S₀ stimuli the detection patterns for the E₁F₁ and E₂F₂ stimulus sets that were based on only T+N trials, P(Y∣T+N), were not significantly correlated for any subjects except S2, and the detection patterns based only on N trials, P(Y∣N), were not significantly correlated except for S6. Thus, the similarity of the P(Y∣T+N) and P(Y∣N) detection patterns for the E₁F₁ and E₂F₂ stimulus sets was not of concern. Moreover, the correlations that did exist were removed by the statistical blocking procedure described in Sec. 2D).

Table 8.

Comparisons between detection patterns estimated with wave forms from the E₁F₁ and E₂F₂ stimulus sets. Presented in terms of r².

Interaural condition	Subject	P(Y∣W), r2	P(Y∣T+N), r2	P(Y∣N), r2
N0S0	S1	0.13a	0.01	0.05
	S2	0.14b	0.01	0.02
	S3	0.15b	0.22a	0.01
	S4	0.16b	0.00	0.03
	S5	0.05	0.03	0.10
	S6	0.18b	0.04	0.16a
N0Sπ	S1	0.26b	0.01	0.06
	S2	0.12a	0.00	0.00
	S3	0.24b	0.00	0.15
	S4	0.26b	0.03	0.07
	S5	0.22b	0.01	0.05
	S6	0.24b	0.03	0.02

^ap<0.05.

^bp<0.01.

Blauert (1981), Ghitza (2001), and Zeng et al. (2004) pointed out that an envelope may be recovered when relatively broadband stimuli are filtered in the auditory periphery with a filter narrower than the stimulus bandwidth. This was not likely to occur given the approximately 75-Hz critical bandwidth at 500 Hz and the fact that a 50-Hz noise bandwidth was used. Nevertheless, stimuli were diagnostically tested for possible envelope recovery by filtering all stimuli with a 50-Hz bandwidth, fourth-order gammatone filter at center frequencies from 400–600 Hz in 1-Hz steps. Envelopes were then recovered from the stimuli by half-wave rectification and filtering with a first-order low-pass filter with a 50-Hz cutoff frequency. First, envelopes from the filtered chimeric stimulus sets (E₁F₂ and E₂F₁) were compared to the envelopes from the filtered original stimulus sets (E₁F₁ and E₂F₂, respectively). The correlation value did not fall below 0.977 in any situation (i.e., at any filter center frequency or for any wave form). Then, the correlations between the envelopes extracted in the E₁F₁ and E₂F₂ stimulus sets were eliminated from the correlations between the envelopes extracted in the E₁F₂ and E₂F₂ stimulus sets and also from the correlations between the envelopes extracted from the E₂F₁ and E₁F₁ stimulus sets, all after filtering. This comparison examined whether the envelope of the base line stimulus sets (e.g., E₁) was recovered from the fine structures of the chimeric stimulus sets (e.g., E₂F₁), thereby potentially increasing the correlation of the envelopes of the base line and chimeric stimulus sets with respect to the two base line stimulus sets. The correlations never differed by more than 0.05, indicating that recovery of envelope information from stimulus fine structure by peripheral filtering was unlikely at these stimulus and filter bandwidths.