Abstract
Several psychophysical models for masked detection were evaluated using reproducible noises. The data were hit and false-alarm rates from three psychophysical studies of detection of 500-Hz tones in reproducible noise under diotic (N0S0) and dichotic (N0Sπ) conditions with four stimulus bandwidths (50, 100, 115, and 2900 Hz). Diotic data were best predicted by an energy-based multiple-detector model that linearly combined stimulus energies at the outputs of several critical-band filters. The tone-plus-noise trials in the dichotic data were best predicted by models that linearly combined either the average values or the standard deviations of interaural time and level differences; however, these models offered no predictions for noise-alone responses. The decision variables of more complicated temporal models, including the models of Dau et al. [(1996a). J. Acoust. Soc. Am. 99, 3615–3622] and Breebaart et al. [(2001a). J. Acoust. Soc. Am. 110, 1074–1088], were weakly correlated with subjects’ responses. Comparisons of the dependencies of each model on envelope and fine-structure cues to those in the data suggested that dependence upon both envelope and fine structure, as well as an interaction between them, is required to predict the detection results.
INTRODUCTION
The traditional goal of psychophysical experiments examining masked detection has been to characterize threshold signal-to-noise ratios (SNRs) as functions of physical parameters of the stimuli (e.g., signal frequency, noise bandwidth, and interaural phase difference of the signal). These threshold SNRs have been estimated using masker waveforms drawn on each trial without replacement from an effectively infinite set, such that no sample of masking noise is ever presented more than once. More recently, a number of studies have collected data using reproducible maskers (e.g., Pfafflin and Matthews, 1966; Ahumada and Lovell, 1971; Ahumada et al., 1975; Gilkey et al., 1985; Siegel and Colburn, 1989; Isabelle and Colburn, 1991; Isabelle, 1995; Isabelle and Colburn, 2004; Evilsizer et al., 2002; Davidson et al., 2006), allowing each sample of masking noise to be presented numerous times. These studies characterize detection responses for each individual stimulus waveform in a set of masking noise samples, rather than describing a single threshold estimated using maskers from an infinite set of noise waveforms. Such data present a more rigorous test for models of masked detection because, in addition to predicting average threshold, the models must predict detection statistics for individual waveforms. As shown here and in other works, models that accurately predict average thresholds may fail to predict responses to individual waveforms (e.g., Isabelle, 1995; Isabelle and Colburn, 2004).
The models tested in this study were selected because they have successfully predicted reproducible noise data in the past (e.g., Fletcher, 1940; Ahumada and Lovell, 1971; Ahumada et al., 1975; Gilkey and Robinson, 1986), because they have been used with some success to predict thresholds for a broad spectrum of psychophysical detection tasks (e.g., Dau et al., 1996a, 1996b; Breebaart et al., 2001a, 2001b, 2001c), because they are straightforward adaptations of observed physiological phenomena (e.g., McAlpine et al., 2001; Marquardt and McAlpine, 2001), or because they use a processing strategy that involves an interaction between stimulus envelope and fine structure (e.g., Goupell and Hartmann, 2007). The interaction of envelope and fine structure was of particular interest because such an interaction has been suggested by recent empirical studies of detection of low-frequency tones in reproducible maskers (Davidson, 2007; Davidson et al., 2009).
METHODS
Target data
Data sets from three psychophysical studies (Isabelle, 1995; Evilsizer et al., 2002; Isabelle and Colburn, 2004; Davidson, 2007; Davidson et al., 2009) that shared similar experimental methods are modeled in this work. In these studies, an approximate threshold was estimated, drawing from an infinite set of masker waveforms without replacement, first in a two-interval up∕down tracking experiment and subsequently verified in a single-interval experiment with fixed SNR. Then a fixed-SNR (i.e., at the estimated threshold), single-interval experiment was performed with a small (25–100) closed set of reproducible maskers. On each trial, the masker was randomly drawn, with replacement, from the closed set, with the constraint that all tone-plus-noise (T+N) and noise-alone (N) waveforms were presented an equal number of times during the course of the entire experiment (50–100 presentations, depending on the study). Upon completion of the experiment, the hit rate, or proportion of “yes” responses when the tone was present [P(Y∣T+N)], and the false-alarm rate, or proportion of yes response when the tone was not present [P(Y∣N)], were calculated separately for each individual masker waveform in the set. The resulting set of hit and false-alarm rates is termed the detection pattern. Note that although these hit and false-alarm rates could be used to calculate some performance metric [e.g., P(C), d′, etc.] on a per noise waveform basis, that was not the focus here. Instead, N and T+N trials were considered separately, and the hit and false-alarm rates were used to estimate the tendency of the subject to respond “tone present” (presumably, based on how much a particular waveform “sounded like” it contained the tone).
Hit and false-alarm rates from Isabelle (1995) (Study 1), Evilsizer et al. (2002) (Study 2), and Davidson et al. (2009) (see also Davidson, 2007) (Study 3) served as the data for the modeling presented in this study. These data were selected because collectively, they established a set of detection patterns estimated under diotic (N0S0) and dichotic (N0Sπ) interaural configurations, with several noise bandwidths [50 (Study 3), 100 (Study 2), 115 (Study 1), and 2900 Hz (Study 2)], at a single tone frequency of 500 Hz. Study 1 examined the N0Sπ configuration only, whereas the other studies examined N0S0 and N0Sπ configurations and used the same noise masker samples under both conditions.
In contrast to Studies 1 and 2, in which the sets of maskers were randomly generated, Study 3 examined four stimulus sets under each interaural configuration. These stimulus sets were denoted E1F1, E2F2, E1F2, and E2F1, with E denoting envelope and F denoting fine structure. Corresponding stimuli (N or T+N) within the E1F1 and E1F2 stimulus sets and within the E2F1 and E2F2 stimulus sets shared the same temporal envelopes. Similarly, corresponding stimuli within the E1F1 and E2F1 stimulus sets and within the E1F2 and E2F2 stimulus sets shared the same fine structures (i.e., had the same zero crossings). The energies of T+N and N waveforms were equalized for all N0S0 stimuli in Study 3, thus eliminating detection cues related to overall energy. Davidson et al. (2009) and Davidson (2007) provided details regarding stimulus construction for Study 3.
General modeling strategy
The models were implemented without internal noise and without a decision stage. The output of each model (i.e., the decision variable) was calculated and compared to the responses of each subject on a waveform-by-waveform basis. To do this, the value of P(Y∣T+N) or P(Y∣N) obtained for each subject in response to each waveform was converted to a z-score using the inverse cumulative normal distribution function1 as in Evilsizer et al. (2002). This conversion is equivalent to corrupting the model’s decision variable (DV) with normally-distributed, additive internal noise. That is, it was assumed that the subject’s DV was the sum of external and internal noise components, DV=DVext+DVint. The external component, DVext, was computed in response to the external stimulus and was assumed to be fixed across trials on which the same stimulus waveform was presented, but to vary across stimulus waveforms. The internal component, DVint, was assumed to be randomly drawn from a normal distribution with mean equal to zero and constant variance, independent of the trial or waveform presented. Under these assumptions, the z-score provides an estimate proportional to the distance from the subject’s criterion to DVext for a particular waveform and subject. (Criterion variation, if present, is one form of internal noise and is not separately considered here.) Thus, the computed (noise-free) DV of a correct model should be linearly related to these z-scores (i.e., both the subject z-scores and the model DV should be linearly related to DVext). The proportion of variance accounted for by each model was simply computed as the square of the Pearson product-moment correlation (r2) between the model DV and the subject z-score.2 Because it was assumed a priori that different subjects might employ different detection strategies (indeed, this appears to have been the case, at least in Study 3), each model was compared to each subject’s data individually (the analyses did not consider data that were averaged across subjects or attempt to predict the across-subject variance). Previous studies that modeled data that were averaged across subjects have been able to explain more of the variance in the data (e.g. Isabelle, 1995; Isabelle and Colburn, 2004; Davidson et al., 2006); however, in those studies there were energy differences across waveforms that were presumably a common source of variation in the detection patterns that could be enhanced by averaging.
Implementing the models and representing the data in this way has some important implications. First, this approach allowed an evaluation of models without developing a sophisticated internal noise model; however, many of the dichotic models considered require internal noise, or some other modification, to produce non-zero outputs on N trials. Therefore, those models were not applied on N trials. Second, in some cases it was advantageous to combine the outputs of two models in order to predict the subjects’ responses. Because a linear relationship between the decision variables of the models and the z-scores of the subjects was expected, linear multiple regression techniques could be applied.
Although the subjects’ thresholds were estimated using traditional psychophysical techniques before the experiment began, estimated thresholds were only used to set the SNR during the experiment. The analyses reported here do not attempt to predict thresholds (indeed, N and T+N trials were analyzed separately).3 The focus in this study was on the responses of subjects to individual reproducible stimulus waveforms (i.e., how likely the subjects were to say the target was present when that stimulus waveform was presented). The SNR for the models and the SNR for the subject were identical since both responded to identical stimulus waveforms.
When evaluating the success of these models it is important to establish an upper limit of expected performance for any given prediction.4Isabelle (1995) (see Isabelle and Colburn, 2004) described that the reasonable upper limit for predicting their N0Sπ data (Study 1) was an r2 of about 0.88. Evilsizer et al. (2002) (Study 2) reported first-half, last-half correlations that yield predictable variances (VP) (Ahumada and Lovell, 1971) from 0.80 to 0.97. Predictable variances for Study 3 (Davidson, 2007; Davidson et al., 2009) ranged from 0.85 to 0.99 for data averaged across the baseline stimulus sets in the N0S0 condition and from 0.92 to 0.99 for the N0Sπ data. Model results are presented here in terms of r2; qualitatively similar results presented in terms of an estimate of the proportion of predictable variance explained, computed as the ratio of r2 over VP, are available in Davidson (2007).
MODEL DESCRIPTIONS, RESULTS, AND DISCUSSION
A brief description of each diotic and dichotic model is provided below, along with the results for those models. Detailed descriptions of model implementations are provided in Appendixes A through H. Table 1 provides a list of the models studied here and includes a brief description of their decision variables. In the following discussion, the effect of stimulus energy on each model’s predictions is considered for both the diotic and dichotic stimulus conditions (i.e., to what extent is the performance of a model dependent on its correlation with energy). Finally, the extent to which each model relies on stimulus envelope or fine structure is compared to the empirical dependency observed for human subjects in Study 3.
Table 1.
List of models tested in this study.
| Model | Periphery | Decision variable |
|---|---|---|
| N0S0 | ||
| CBa | GT(4)b | Energy |
| MDc | GT(4), MFd | Linear combination of energy across channels |
| MDS | GT(4), MF | Linear combination of energy across channels |
| ESe | GT(4), Extract Envf | Average slope of the envelope |
| DAg | GT(4), Adapt. Loopsh | Similarity to peripherally transformed “noisy” tone template |
| BRi | GT(3), Adapt. Loops, MF | Difference from peripherally transformed noise-alone template |
| POj | GT(4), AN model,k MF | Monaural cross-frequency coincidence detection |
| N0Sπ | ||
| ENl | None | Energy |
| sTl | None | Standard deviation (Std) of ITDs |
| Sll | None | Std of ILDs |
| Wstl | None | Linear combination of Stds of ITD and ILD |
| Wavm | None | Linear combination of averages of ITD and ILD |
| Xstm | None | Std of linear combination of ITD and ILD |
| Xavm | None | Average of linear combination of ITD and ILD |
| Lpl n, n | None | Std of linear combination of ITD and ILD |
| FCco | GT(4), AN model | Linear combination of time-delayed binaural cross correlations and cancellations |
| FCno | GT(4), AN model | Linear combination of time-delayed normalized binaural cross correlations and cancellations |
| BRi | GT(3), Adapt. Loops, MF | Difference from peripherally transformed noise-alone template |
GT(N) indicates Nth-order gammatone filter.
MF indicates multiple frequency channels.
Envelope extraction performed using Hilbert transform.
Adaptation loops from Dau et al. (1996a).
Auditory-nerve model of Heinz et al. (2001).
Diotic models
There are six sets of models considered here for the diotic data. The first two are related: single critical-band (CB) models and multiple-detector (MD) models that linearly combine outputs of multiple critical bands. To date, detection patterns estimated under diotic conditions have been best predicted by a MD model (Ahumada and Lovell, 1971; Ahumada et al., 1975; Gilkey and Robinson, 1986; Davidson et al., 2006). The MD model accounted for up to 90% of the variance in one subject’s responses in Ahumada and Lovell (1971) and up to 72% of the variance in one subject’s responses in Gilkey and Robinson (1986). Davidson et al. (2006) used the MD model to predict the data of Study 2 and found that the model accounted for 78%–90% of the variance in the average subject’s responses, depending on bandwidth and interaural configuration [monaural (NmSm) or diotic]. The MD model’s DV is the weighted sum of energies at the outputs of several auditory filters surrounding the tone frequency. Thus, the MD model is an extension of Fletcher’s (1940) proposal that detection responses are determined by the energy at the output of a single CB centered at the tone frequency. Davidson et al. (2006) showed that the CB model predicted 64%–82% of the variance in their average subject’s responses.
Two simple models that depend on temporal cues were also considered here: a modified version of the Richards (1992) envelope-slope (ES) model (Zhang, 2004) and the phase-opponency (PO) model (Carney et al., 2002). Davidson et al. (2006) showed that the ES and PO models predicted about 60% of the variance in narrowband and wideband N0S0 and NmSm detection patterns. Neither model has previously been tested using detection patterns estimated from stimuli where energy was equalized across stimulus waveforms (as was the case in Study 3). Presumably, the likelihood that the subjects will use temporal cues, and thereby the success of these models, will increase when energy cues are not available.
Finally, two relatively more complex models were evaluated (Dau et al., 1996a; Breebaart et al., 2001a). These models combine temporal and energy information and also include a basic representation of both peripheral filtering and adaptation. Each of these models creates an internal-representation template through an iterative method, and decision variables for the detection task are derived based on comparisons to this template.
CB model
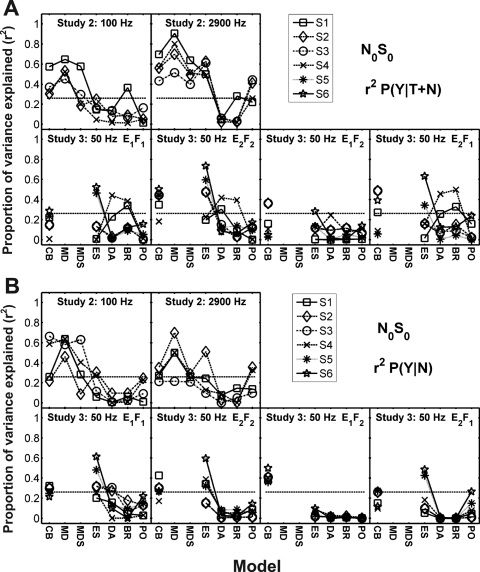
The DV for the CB model (Fig. 1) is the rms output of a fourth-order gamma-tone filter centered at 500 Hz. The equivalent rectangular bandwidth (ERB) of the filter was set at 75 Hz (Glasberg and Moore, 1990). The CB model was the simplest model tested in this study and, in general, was able to predict a significant and substantial proportion of the variance in the detection patterns for all subjects in Study 2 [Fig. 2A]. Recall that overall energies were equalized for all diotic stimuli in Study 3. The CB model made relatively poor predictions of the detection patterns in the equal-energy cases,5 as expected. In Study 3, where energy cues were not available, the predictions of the CB model were significantly correlated to the detection patterns for only 12 out of 24 cases for P(Y∣T+N) and for only 18 out of 24 cases for P(Y∣N). This finding is in agreement with the results of Richards (1992).
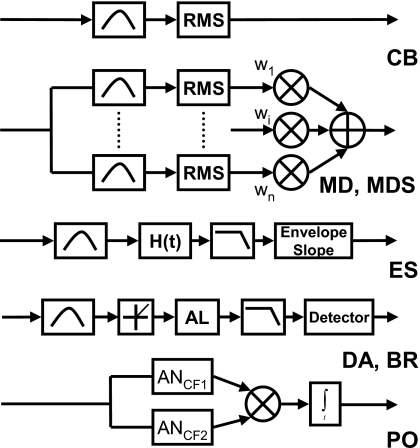
Figure 1.
Block diagrams of the models used to predict N0S0 detection patterns. The models listed from top to bottom are CB, critical band (Fletcher, 1940); MD, multiple detector with fit weights (Ahumada and Lovell, 1971; Ahumada et al., 1975; Gilkey and Robinson, 1986); MDS, multiple detector with suboptimal (independent channel) weights; ES, envelope slope (Richards, 1992; Zhang, 2004) DA, Dau model (Dau et al., 1996a); BR, Breebaart model (Breebaart et al., 2001a); PO, phase opponency (Carney et al., 2002). H(t) denotes the Hilbert transform used to recover the absolute value of the complex-analytic signal. AL denotes the adaptation loops as described in Dau et al. (1996a). AN denotes the auditory-nerve model of Heinz et al. (2001).
Figure 2.
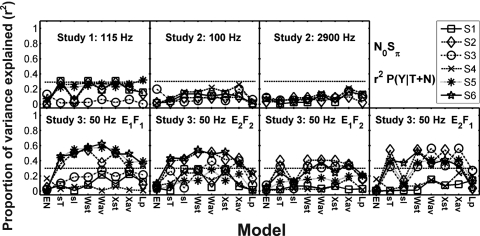
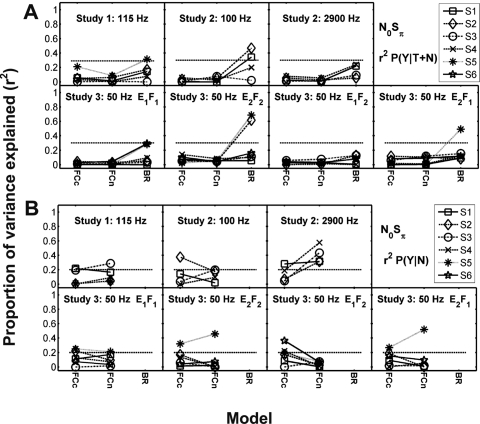
Proportion of variance explained (r2) in the z-scores of (A) P(Y∣T+N) and (B) P(Y∣N) by the N0S0 model predictions. Model abbreviations from left to right: CB, critical band; MD, multiple detector; MDS, multiple detector with suboptimal weights; ES envelope slope; DA, Dau; BR, Breebaart; and PO, phase opponency. Different subjects are indicated with different symbols connected with lines to facilitate intersubject and cross-model comparisons. Note that subject identification numbers do not correspond to the same subjects across studies. The critical r2 value for a significant prediction would be 0.16 for comparison of one model to the detection pattern for one subject. A Bonferroni correction was used to compensate for the comparison of each subject’s data to seven models in Study 2 resulting in a criterion of significance for r2 equal to 0.28 and for five models in Study 3 resulting in a criterion equal to 0.26 (horizontal-dashed lines).
MD models
As stated above, the DV of the MD model (Gilkey and Robinson, 1986) was a weighted sum of energies at the outputs of several auditory filters surrounding the tone frequency (Fig. 1). The MD model (as described in the literature) uses a fit to the subjects’ data, rather than a decision-theoretic weighting strategy. Here, we considered both this classic MD model and a multiple-detector model with suboptimal weights (MDS), which were computed using a decision-theoretic weighting scheme. This scheme is suboptimal in the sense that the chosen weights would maximize d′ for the model, not the fit (r2) between the detection patterns for the model and these specific data. Note that these models were only applied to Study 2, in which the stimulus bandwidth exceeded one critical band. Appendix A includes details of the MD and MDS implementations.
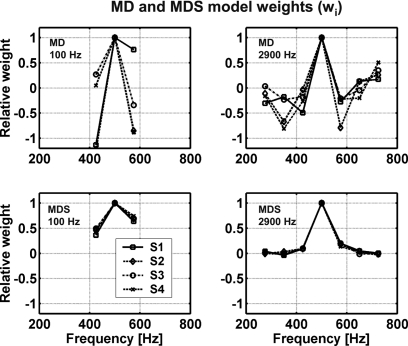
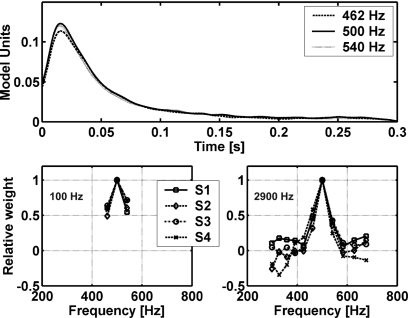
Plots showing the weights resulting from the fit to the data (MD model) and from the suboptimal computation (MDS model) provide insight into the differences between these models (Fig. 3). The negative weights for the MD model found above and below the target frequency were consistent with weighting patterns in previous MD model results (Ahumada and Lovell, 1971; Ahumada et al., 1975; Gilkey and Robinson, 1986), but only positive weights were possible in the suboptimal weighting scheme because these weights were derived from rms metrics. Note that the weights that fit to the responses of S3 for MD with the 100-Hz bandwidth were close to those fitted to the MDS model. Figure 2 shows that the proportions of variance accounted for by the MD and MDS models were also similar for that subject. The MDS model made poorer predictions for subjects that tended to have more negative MD weights, as expected. In fact, the MDS model predictions were even more poorly correlated to the data of S2 and S4 than the CB model predictions. For the MD model, significant and substantial predictions were made for all subjects’ detection patterns for P(Y∣T+N) and for 7 out of 8 cases for P(Y∣N), whereas while the MDS model prediction reached significance in 6 out of 8 cases for P(Y∣T+N) and in 5 out of 8 cases for P(Y∣N). The amount of variance predicted by the MDS model was lower than that predicted by the MD model in all but one case. It should be noted that the MD model includes a fit to the subject data, which partly explains the success of this model (see discussion of this issue in Davidson et al., 2006) relative to the models that have fixed parameter values, except for the mean and slope of the regression line. However, Davidson et al. (2006) showed that the weighting strategy of the MD model produced r2 values significantly greater than would be expected by simply adding free parameters to the CB model.6 Overall, the MD model accounted for more of the variance in the subjects’ detection patterns than any other model tested in this study. Davidson et al. (2006) found relatively little variation across subjects in the diotic results (e.g., as compared to the dichotic results, see below), which contributes to the success in fitting these data sets with a single model.
Figure 3.
Weights computed for MD and MDS models for the 100- and 2900-Hz data in Study 2. Weights are shown for the four subjects. Note that weights in each condition were normalized to the maximum weight (occurring at 500 Hz). These weights correspond to the wi for the MD and MDS models in Fig. 1 and Eq. A2.
ES model
A modified version of Richards’ (1992) ES model (Zhang, 2004) was evaluated. The ES model estimates the rate and magnitude of fluctuation in the stimulus envelope as a decision variable. Although, as will be shown later, envelope fluctuation co-varies with stimulus energy when energy variations are present, the ES model is not strictly dependent on energy, and this model can make meaningful predictions even when energy is normalized, as it was in Study 3. Implementation details for the ES model are described in Appendix B.
In general, the ES model predictions were no better than, and often poorer than, the predictions made with the CB, MD, and MDS models, with only 13 of the 32 predictions reaching significance for P(Y∣T+N) [Fig. 2A] and only 12 of the 32 predictions reaching significance for P(Y∣N) [Fig. 2B]. Model predictions were highly variable across subjects in all studies, except for P(Y∣T+N) for the wideband results of Study 2. Despite this model’s simplicity, it was able to account for more variance in some of the subject’s detection patterns than the more complicated temporal models (i.e., DA, BR, and PO; see below), particularly in the equal-energy cases of Study 3 for P(Y∣N) [Fig. 2B].7
Dau model
The Dau model (Dau et al., 1996a) has been used to predict thresholds in a number of monaural and diotic psychophysical tasks, including detection of tones in random and frozen noise as a function of the temporal position, duration, and frequency of the tone, as well as forward and backward masking tasks (Dau et al., 1996b). The model includes bandpass filters to represent peripheral filtering, plus rectification, a simplified model of adaptation, and a low-pass filter to extract the envelope (Fig. 1). This model’s DV is computed by comparing an “internal representation” of the response for each stimulus to a template. Details of the implementation of the Dau model are included in Appendix C.
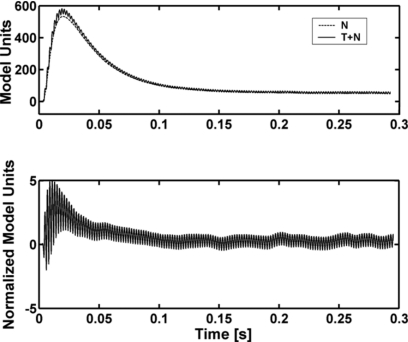
Like the ES model, the Dau model relies primarily on the temporal envelope of the stimulus waveform, but the Dau model allows some fine structure to pass onto the decision device (Fig. 4) because the low-pass filter used for envelope extraction is only first-order. This model uses a distinct template-matching strategy, where a previously computed N template is subtracted from the waveform on each trial, and the result is compared to a normalized version of the difference between previously computed T+N and N templates. Figure 4 shows representative T+N and N templates (top panel) and the normalized difference template (bottom panel) for the 100-Hz bandwidth stimuli of Study 2. Each trace in the top panel shows the output of the model’s adaptation loops (see Appendix C) averaged over 500 stimulus waveforms. It is clear that the averaging process brings out some fine-structure information related to the tone frequency in the T+N template. This information is effectively increased by the normalization with respect to the difference between the two templates (Fig. 4, bottom panel). The difference between templates is largest at the onset of the noise waveform because of the lack of compression in the adaptation loops for stimuli with fast changes in sound pressure level (whereas the latter portion of the difference is compressed). The covariation in time of the fine structure present in the stimulus waveform and in the internal template (requiring the detector to have knowledge of the phase of the target tone) also contributes to the decision variable.
Figure 4.
Templates used in the Dau model decision device. The T+N and N templates were computed as the mean of 500 internal representations of T+N and N stimuli, respectively. The templates (plotted in arbitrary model units) are the low-pass filtered outputs of the adaptation loops in the Dau model (see Appendix C). The lower panel shows the normalized difference between the two templates in the upper panel.
In general, the predictions of the Dau model were not significantly correlated to the subjects’ detection patterns. Only 5 of the 32 P(Y∣T+N) predictions [Fig. 2A] and only 2 of the 32 P(Y∣N) predictions [Fig. 2B] were significant. Note also that these results were obtained despite the fact that the Dau decision variables are at least partially correlated to overall energy, as discussed further below.
Breebaart model
The peripheral processing in the Breebaart model (Breebaart et al., 2001a) is similar to that of the Dau model. Differences between the predictions of the Breebaart and Dau models result from differences in the decision devices, including the template mechanisms. For example, in the Breebaart model, the N template is subtracted from the internal representation of each stimulus waveform as a measure of the “distance” from the N stimulus, which differs from the normalized difference strategy of the Dau model. Other features in the Breebaart model include temporal weighting using a double-sided exponential window and spectral weighting across multiple frequency channels. Details of the implementation are presented in Appendix D.
Representative templates of the Breebaart model are shown in Fig. 5 for the 100-Hz bandwidth stimuli of Study 2 for the three frequency channels used. The frequency weighting [see Appendix D, Eq. D1] is shown in Fig. 5. In this illustration, the time-varying weights are summed over time and normalized to facilitate comparison to the weights for the MD and MDS models. The weights for both narrowband and wideband results are similar to those in Fig. 3 for the MDS model. For our implementation of the Breebaart model, only 7 predictions of the 32 made for P(Y∣T+N) were significant [Fig. 2A], and none of the 32 made for P(Y∣N) were significant [Fig. 2B].
Figure 5.
Internal noise-alone templates (top panel) for the different frequency channels in the narrowband condition of Study 2 and frequency weighting (bottom two panels) imposed by the model of Breebaart et al. (2001a) on the internal representations of the stimulus waveforms. The internal representations (plotted in arbitrary model units) are the responses of Breebaart’s peripheral model, followed by half-wave rectification and low-pass filtering to represent transduction by the inner hair cells, and adaptation loops (see Appendix D). The frequency weights were summed over time and normalized to the peak value for the 100- and 2900-Hz conditions of Study 2 for the left and right panels, respectively.
PO model
The PO (Fig. 1) model (Carney et al., 2002) is a detection model that is based primarily on temporal cues in the stimulus fine structure. These cues are extracted using cross-frequency coincidence detection. This model successfully predicts that the detection threshold should be robust even in a roving-level paradigm (Carney et al., 2002); however, it has not been previously tested with detection patterns estimated from stimuli with energy equalized across stimulus waveforms (as was the case for Study 3). Details of the implementation of this model are presented in Appendix E.
The PO model’s ability to predict detection patterns was comparable to that of the DA model, with only 3 of the 32 P(Y∣T+N) predictions reaching significance [Fig. 2A] and 3 of the 32 P(Y∣N) predictions reaching significance [Fig. 2B]. This model performed no better for experiments in which energy was equalized (i.e., when fine structure might be expected to play more of a role) than for experiments with energy cues present.
Dichotic models
When out-of-phase tones are added to identical noise waveforms, as is done in the N0Sπ condition, the resulting tone-plus-noise stimulus waveforms have instantaneous interaural time differences (ITDs) and interaural level differences (ILDs) that vary over time due to interactions between the tones and the noise masker. Models for dichotic detection allow tests of hypotheses about the relations between these cues and the detection results and of hypotheses about the binaural mechanisms used to process these cues, such as cross correlation and equalization-cancellation. It should be noted that the ITDs and ILDs that are present in the tone-plus-noise stimuli are dynamic cues that vary throughout the time course of the stimuli, rather than the static interaural differences that are used in lateralization experiments. Some models for dichotic detection are based on the time averages of these interaural cues over the course of a stimulus waveform; others use the instantaneous, time-varying cues.
In general, dichotic models have been less successful at predicting the N0Sπ detection patterns than diotic models have been at predicting the N0S0 detection patterns. Isabelle (1995; i.e., Study 1) and Colburn et al. (1997) analyzed several decision variables for N0Sπ detection patterns. Colburn et al. (1997) considered the equalization-cancellation (EC) model and normalized cross correlation (NCC) and unnormalized cross correlation (UCC) models. They found that the EC DV was too strongly influenced by monaural stimulus energy, which did not correlate with subject performance, as compared to predictions based on non-linear combinations of interaural difference cues present in the acoustic stimuli, which showed significantly better correlation with performance in N0Sπ experiments (however, an internal noise model would be required for the interaural difference models to make predictions on N trials). They also found that the UCC model was too dependent on masker waveform, rather than on the addition of the tone to the masker waveform, for tone-plus-noise stimuli. Decision variables for the UCC model were almost identical regardless of signal presence (that is, hit and false-alarm rates were more similar for the model predictions than in the data). Finally, Colburn et al. (1997) found that the NCC model is equivalent to the EC model when using multiplicative time and amplitude jitter, such that the DV was again heavily dependent on the energy in each waveform. Isabelle (1995) showed that the variation in the NCC DV based on the addition of the tone was too weak compared to the dependence of the NCC DV on masker energy to predict his data. Isabelle (1995) (see Isabelle and Colburn, 2004) was able to explain at most about 50% of the variance in his N0Sπ data or in the Isabelle and Colburn (1991) data using stimulus energy (as a substitute for the EC and NCC models), standard deviations of ITDs and ILDs, and decision variables computed using various combinations of ITDs and ILDs. The highest model correlations to subject data in the Isabelle (1995) study were based on Webster’s (1951) time-deviation model, which included a subject-dependent (i.e., fitted) parameter related to the threshold of time-deviation detection. However, the correlation of this model to the data was not significantly better than those of the simpler model based on the standard deviation of ITD; the latter model was included in the results presented here.
In the current study, several decision variables (standard deviations of ITD, ILD, and combinations thereof) related to those used in Isabelle (1995) were re-examined using the data from Studies 2 and 3. In addition, the related decision variables from Goupell and Hartmann (2007) were also examined. The Goupell and Hartmann (2007) decision variables extended the Isabelle (1995) decision variables and included two distinct classes that make use of both ITD and ILD: “Independent-center” models, in which integration over time occurs separately for the decision variables based on ITD and ILD, and “auditory-image” models, in which ITDs and ILDs interact as a function of time, before integration across time. The results from Study 3 (Davidson, 2007; Davidson et al., 2009) suggest that the Isabelle (1995) decision variables could not predict the detection patterns because they do not allow envelope (ILDs) and fine structure (ITDs) to interact temporally. Thus, it was of interest to determine the effectiveness of the Goupell and Hartmann (2007) auditory-image decision variables that allow for this interaction. The lateral position model (Hafter, 1971; Isabelle, 1995; Isabelle and Colburn, 2004) was also evaluated because it includes an explicit interaction between envelope and fine-structure cues in the form of a trading ratio.
A variant of the Marquardt and McAlpine (2001) model for masked detection was also tested; this model has been shown to successfully predict masked-detection thresholds using only four binaural delay channels [henceforth referred to as the four-channel (FC) model]. This model was inspired by the findings of McAlpine et al. (2001), who reported that interaural phase tuning of delay-sensitive neurons in the guinea pig inferior colliculus was centered around 45°, regardless of the neurons’ best frequencies. The binaural counterpart of the Breebaart model was also tested; this model makes use of temporal fine structure in the binaural processor.
Independent-center and auditory-image models
As described above, Isabelle (1995) used several decision variables that were based either on fine structure (i.e., ITDs) or on envelope (i.e., ILDs). These included the standard deviations of ITD and ILD and a weighted linear combination of the variances of ITD and ILD. Goupell and Hartmann (2007) referred to these as independent-center models because the variances of ITD and ILD were computed before their weighted combination was computed. Goupell and Hartmann (2007) introduced what they referred to as auditory-image decision variables, in which ITD and ILD were combined before computing the variance or averaging over time. The auditory-image decision variables used here included the standard deviation of a temporal combination of ITD and ILD as well as the average absolute value of the temporal combination of ITD and ILD. Finally, Isabelle’s (1995) implementation of Hafter’s (1971) lateral position model was evaluated in the present study; this model was also one of the auditory-image models considered by Goupell and Hartmann (2007).
The Isabelle (1995) and Goupell and Hartmann (2007) decision variables are based on interaural differences calculated directly from the stimulus waveforms.8 Because internal noise was not used, the decision variables described in this section would have been identically zero for noise-alone stimuli; therefore, predictions were not computed for P(Y∣N). Details of the calculations of these decision variables are provided in Appendix F.
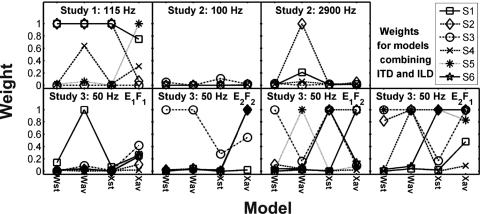
In order to provide a comparison and to confirm previous work, a simple energy-based model was also used to predict the detection patterns for the dichotic condition. The energy of the stimulus waveforms delivered to the two ears differed very slightly due to the addition of out-of-phase tones to the two waveforms, but on average this difference was very small for stimuli with tones added at N0Sπ threshold levels. Therefore, the energy (EN) based model used here was simply based on the rms energy of the right stimulus waveform. The EN model performed poorly, with none of the 37 predictions reaching significance (Fig. 6), consistent with Isabelle (1995) and indicating that the cue used by subjects to perform the detection task was not simply correlated to energy. Standard deviations of ITDs and ILDs (sT and sI) performed somewhat better, with 12 and 6 of the 37 predictions reaching significance, respectively (Fig. 6). Linear combinations of the standard deviations or of the average absolute values of ITD and ILD performed slightly better than the other models, suggesting that both envelope and fine-structure cues contribute to the detection process. Of the 37 predictions, 12 that used a weighted combination of the standard deviations of ITD and ILD as a DV (Wst) reached significance, and 13 that used an average of the absolute value of the weighted combination of ITD and ILD as a DV (Wav) reached significance. Note that the models that depended on weighted combinations of cues involved a fit to the subjects’ data. Predictions for models that computed separate decision variables before combining across ITD and ILD processors (Wst and Wav) accounted for about the same amount of variance in P(Y∣T+N) as those that first combined ITDs and ILDs as a function of time before computing decision variables. These variables were the standard deviation of the temporal combination of ITD and ILD (Xst), the average of the absolute value of the temporal combination of ITD and ILD (Xav), and the estimated lateral position (Lp) (see Appendix F for details). The Xst, Xav, and Lp decision variables made 12, 12, and 4 significant predictions, respectively, for the 37 comparisons performed (Fig. 6). In summary, the independent-center (Wst and Wav) and “auditory-image” (Xst and Xav) decision variables had about the same predictive power.
Figure 6.
Proportion of variance explained (r2) by the N0Sπ model predictions for selected Isabelle (1995) and Goupell (2005) decision variables for z-scores of P(Y∣T+N). EN is the rms energy of the right stimulus waveform, sT is the standard deviation of ITDs, sI is the standard deviation of ILDs, Wst is a linear combination of the standard deviations of ITDs and ILDs, Wav is a linear combination of the average absolute values of ITDs and ILDs, Xst is the standard deviation of a linear combination of ITDs and ILDs, Xav is the average value of a linear combination of ITDs and ILDs, and Lp is a lateral position model relating ITDs and ILDs with a trading ratio. Results for Studies 1 and 2 are shown on the first row, and Study 3 is shown on the second row. Each column represents a different bandwidth condition within Study 2 or a different stimulus set in Study 3. Different subjects are indicated with different symbols connected with lines to facilitate intersubject and cross-model comparisons. Note that subject identification numbers do not correspond to the same subjects across studies. The critical r2 value for reaching a significant prediction (p<0.05), including a Bonferroni correction for comparison of each data set to 11 models (across Figs. 69A), is 0.29 for Study 1 and 0.30 for Studies 2 and 3, as denoted by the horizontal dashed lines. Symbols are connected to facilitate comparisons across models.
The weights placed on ITD or ILD decision variables were also examined for possible trends across subjects and for relations to the threshold SNR. Figure 7 shows weights organized by model and subject for all three studies (see Appendix F for details of weight calculations). Weights were bounded by 0 and 1, with 1 indicating total reliance on ITD and 0 indicating total reliance on ILD. Figure 7 shows that the results of these models were largely due to their ability to exclusively select the DV that was better correlated with the individual subject’s responses from either sT or sI. Certain subjects, however, used a true weighted combination of the two decision variables (e.g., S4 in Study 1), and in almost all cases, these subjects had relatively low thresholds. Subjects with higher thresholds were fitted more reliably with weights of either 0 or 1, indicating that they relied solely on ITDs or ILDs.
Figure 7.
Model weights for decision variables based on both ITDs and ILDs. A weight approaching 1 indicates reliance on ITD and a weight approaching 0 indicates reliance on ILD. Note that subject identification numbers do not correspond to the same subjects across studies, but corresponding symbols are used in Figs. 67. Different subjects are indicated with different symbols connected with lines to facilitate intersubject and cross-model comparisons.
FC model
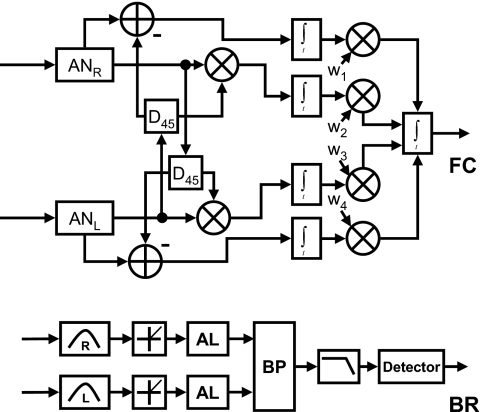
The general structure of the FC model (Marquardt and McAlpine, 2001) is shown in Fig. 8 (upper panel). The right and left stimulus waveforms were processed using the Heinz et al. (2001) auditory-nerve model. The output of each filter was passed to a delay line with a phase shift of 45° on each side, which corresponds to a delay of 250 μs for a 500-Hz stimulus. The delayed stimulus from the ipsilateral side and delayed stimulus from the contralateral side converged onto binaural coincidence detectors; both the UCC and the binaural cancellation (difference) were computed for each channel in order to approximate neurons that are excited by stimuli to both ears (EE) and neurons that are excited by stimulation of one ear and inhibited by the other (EI), respectively. The resulting FCs thus corresponded to cells tuned to ±45° and ±135°, spanning the entire range of possible interaural phase differences at 500 Hz in relative increments of 90°. Note that this model is a special case of the standard cross correlation model; it differs from the general model because it is restricted to a particular subset of channel correlations. The outputs of the four binaural channels were suboptimally weighted and summed using the same strategy as was used for the MDS model (see Appendix G for details).
Figure 8.
Block diagrams of the FC and binaural Breebaart (BR) models used to predict N0Sπ detection patterns. AN denotes the auditory-nerve model of Heinz et al. (2001). D denotes a delay block computed based on the center frequency of each model auditory-nerve fiber. AL denotes the adaptation loops as described in Dau et al. (1996a). BP denotes a binaural processor.
Two versions of this model were implemented; the common structure of both versions is shown in the upper part of Fig. 8 (FC). The first (FCc) used a cross correlation (product) of the inputs for the channels tuned to ±45° (weighted by w2 and w3 in Fig. 8), while the second (FCn) used a NCC (Colburn et al., 1997) for these channels. Neither version of the model made consistently significant predictions of the detection patterns (Fig. 9), with predictions reaching significance for none of the 74 comparisons (including both FCc and FCn) for P(Y∣T+N) [Fig. 9A], 9 of the 37 P(Y∣N) comparisons were significant for FCc, and 8 of the 37 P(Y∣N) comparisons were significant for FCn [Fig. 9B].
Figure 9.
Proportion of variance explained (r2) by N0Sπ model predictions for z-scores of (A) P(Y∣T+N) and (B) P(Y∣N). Model abbreviations are FCc, FC model using an UCC for simulated peaker channels (i.e., channels with ITD curves that are characterized by a central peak); FCn, FC model using a NCC for peaker channels; and BR, the binaural Breebaart model. Different subjects are indicated with different symbols connected across models to facilitate intersubject comparisons. Note that subjects sharing the same number do not correspond across studies, but corresponding symbols are used in Figs. 67. Symbols are connected to facilitate comparisons across models. The critical r2 value for reaching a significant prediction (p<0.05), including a Bonferroni correction for comparison of each data set to 11 models for P(Y∣T+N) (across Figs. 69A), is 0.29 for Study 1 and 0.30 for Studies 2 and 3, and including a correction for comparison to two models for P(Y∣N) (Fig. 9B) the critical r2 value is 0.20 for all three studies, as indicated by the horizontal dashed lines.
Binaural Breebaart model
The binaural version of the Breebaart model is an extension of the monaural model described above and is based on an interaural subtraction (EI) algorithm. A simplified block diagram is shown in Fig. 8 (BR). The output of the adaptation loops from the ipsilateral and contralateral sides passes to a binaural processor that simulates an excitatory-inhibitory interaction. As originally designed (Breebaart et al., 2001a), the model included a series of attenuation taps and delays with different values and selected the single delay and attenuation channel that showed the greatest change in output between T+N and N stimuli. However, because the zero delay and zero attenuation channel always has the greatest change in output for N0Sπ stimuli, the model was reduced to this single channel. Thus, this model has a structure that is generally similar to the EC model, but it differs in the details of the decision variable. Details of the implementation of this model are provided in Appendix H.
As with the Isabelle (1995) and Goupell and Hartmann (2007) decision variables, the binaural version of the Breebaart model produced decision variables that were identically 0 for N stimuli because of the subtraction mechanism [see Eq. H1]; thus, predictions for P(Y∣N) were not made. Figure 10 shows representative temporal and spectral weights for the binaural version of the model computed for the two bandwidths of Study 2. Note that the onset was weighted more heavily than the steady-state portion of the stimulus because of the action of the adaptation loops. This model produced significant predictions for only 6 of the 37 comparisons to P(Y∣T+N) (Fig. 9), performing more poorly than Wst or Wav despite its more complex and arguably more physiologically realistic structure. Note that although a few individual r2 values in Fig. 9 are high for the BR model, its predictions are not consistently significant across the stimulus sets used in Study 3, as was true for the Wst and Wav predictions (see Fig. 6).
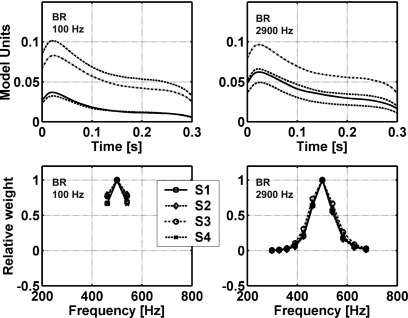
Figure 10.
Representative temporal weights (top) and spectral weights (bottom) for the binaural Breebaart model for two different masker bandwidths (100 and 2900 Hz). Note that the onset of the stimulus is weighted more heavily than the steady-state portion of the stimulus. The temporal weights (plotted in arbitrary model units) are the internal representations for the binaural model and thus include monaural peripheral processing (tuning, rectification, low-pass filtering, and adaptation loops) followed by binaural excitatory-inhibitory (EI) processing, a double-exponential filter, and logarithmic compression (see Appendix H).
Comparisons of diotic models
Although none of the models were able to predict a significant proportion of the variance in subjects’ detection patterns in every case, it was of interest to determine how similar or different each model’s DV was to those of the other models. Because the models operated at different SNRs for each subject, the models’ decision variables varied slightly across subjects. To simplify comparisons between diotic models, and because the threshold SNRs were within 3 dB under diotic condition for all subjects within each study, the SNR of the subject closest to the median threshold for each study (see Table 2) was selected. Correlations between model decision variables in response to the reproducible stimuli are presented in terms of r2 in Tables 2, 3 for P(Y∣T+N) and P(Y∣N), respectively, for the each of the models in Fig. 1. Blank values indicate study conditions for which a given model did not apply.
Table 2.
Correlations between model decision variables in response to reproducible T+N stimuli under the N0S0 condition are shown in terms of r2. Model abbreviations are the same as in Fig. 1. Note that the MD and MDS models were not applied to the 50-Hz bandwidth of Study 3. Each model was run at an ES∕N0 of 11.8 dB for the 100-Hz bandwidth condition of Study 2, 10.8 dB for the 2900-Hz bandwidth condition of Study 2, and 10 dB for all stimulus sets in Study 3.
| Model comparison | Study 2 | Study 3 | ||||
|---|---|---|---|---|---|---|
| 100 Hz | 2900 Hz | E1F1 | E2F2 | E2F1 | E1F2 | |
| CB-MD | 0.78a | 0.70a | ||||
| CB-MDS | 0.95a | 0.98a | ||||
| CB-ES | 0.33a | 0.56a | 0.22a | 0.51a | 0.07 | 0.12 |
| CB-DA | 0.00 | 0.09 | 0.04 | 0.00 | 0.17a | 0.01 |
| CB-BR | 0.10 | 0.28a | 0.01 | 0.00 | 0.11 | 0.09 |
| CB-PO | 0.01 | 0.20a | 0.23a | 0.30a | 0.14 | 0.10 |
| MD-MDS | 0.79a | 0.65a | ||||
| MD-ES | 0.34a | 0.55a | 0.22a | 0.51a | 0.07 | 0.12 |
| MD-DA | 0.00 | 0.07 | 0.04 | 0.00 | 0.17a | 0.01 |
| MD-BR | 0.07 | 0.30a | 0.01 | 0.00 | 0.11 | 0.09 |
| MD-PO | 0.00 | 0.21a | 0.23a | 0.30a | 0.14 | 0.10 |
| MDS-ES | 0.21a | 0.50a | 0.22a | 0.51a | 0.07 | 0.12 |
| MDS-DA | 0.00 | 0.08 | 0.04 | 0.00 | 0.17a | 0.01 |
| MDS-BR | 0.09 | 0.25a | 0.01 | 0.00 | 0.11 | 0.09 |
| MDS-PO | 0.00 | 0.19a | 0.23a | 0.30a | 0.14 | 0.10 |
| ES-DA | 0.00 | 0.05 | 0.11 | 0.00 | 0.16a | 0.00 |
| ES-BR | 0.01 | 0.33a | 0.03 | 0.00 | 0.03 | 0.03 |
| ES-PO | 0.34a | 0.51a | 0.49a | 0.41a | 0.46a | 0.55a |
| DA-BR | 0.31a | 0.38a | 0.86a | 0.81a | 0.74a | 0.89a |
| DA-PO | 0.00 | 0.13 | 0.26a | 0.24a | 0.36a | 0.22a |
| BR-PO | 0.05 | 0.20a | 0.18a | 0.26a | 0.22a | 0.09 |
p<0.05.
Table 3.
Correlations between model decision variables in response to reproducible N stimuli under the N0S0 condition are shown in terms of r2. Model abbreviations are the same as in Fig. 1. Note that the MD and MDS models were not applied to the 50-Hz bandwidth of Study 3. SNRs are the same as for Table 2.
| Model comparison | Study 2 | Study 3 | ||||
|---|---|---|---|---|---|---|
| 100 Hz | 2900 Hz | E1F1 | E2F2 | E2F1 | E1F2 | |
| CB-MD | 0.57a | 0.56a | ||||
| CB-MDS | 0.91a | 0.97a | ||||
| CB-ES | 0.20a | 0.44a | 0.30a | 0.23a | 0.06 | 0.01 |
| CB-DA | 0.40a | 0.34a | 0.00 | 0.02 | 0.05 | 0.05 |
| CB-BR | 0.41a | 0.08 | 0.01 | 0.03 | 0.10 | 0.13 |
| CB-PO | 0.11 | 0.37a | 0.03 | 0.03 | 0.00 | 0.00 |
| MD-MDS | 0.60a | 0.50a | ||||
| MD-ES | 0.22a | 0.35a | 0.30a | 0.23a | 0.06 | 0.01 |
| MD-DA | 0.35a | 0.35a | 0.00 | 0.02 | 0.05 | 0.05 |
| MD-BR | 0.20a | 0.20a | 0.01 | 0.03 | 0.10 | 0.13 |
| MD-PO | 0.05 | 0.33a | 0.03 | 0.03 | 0.00 | 0.00 |
| MDS-ES | 0.05 | 0.37a | 0.30a | 0.23a | 0.06 | 0.01 |
| MDS-DA | 0.33a | 0.27a | 0.00 | 0.02 | 0.05 | 0.05 |
| MDS-BR | 0.41a | 0.05 | 0.01 | 0.03 | 0.10 | 0.13 |
| MDS-PO | 0.01 | 0.31a | 0.03 | 0.03 | 0.00 | 0.00 |
| ES-DA | 0.20a | 0.22a | 0.01 | 0.00 | 0.00 | 0.03 |
| ES-BR | 0.03 | 0.32a | 0.04 | 0.03 | 0.01 | 0.02 |
| ES-PO | 0.78a | 0.58a | 0.58a | 0.29a | 0.56a | 0.39a |
| DA-BR | 0.35a | 0.47a | 0.81a | 0.78a | 0.69a | 0.88a |
| DA-PO | 0.12 | 0.35a | 0.23a | 0.01 | 0.05 | 0.02 |
| BR-PO | 0.02 | 0.34a | 0.34a | 0.02 | 0.11 | 0.06 |
p<0.05.
Tables 2, 3 show that the CB model was significantly correlated to each of the diotic models tested here. The most highly correlated models were the CB and MDS models, with r2 values from 0.95 to 0.98. Both of these models were also significantly correlated to the MD model, which is not surprising given that all three models use energy at the output of one or more critical bands as decision variables. The CB and ES models were also significantly, albeit weakly, correlated for the stimuli of Study 2 and for the non-chimeric stimulus sets in Study 3. The CB, MD, and MDS models were significantly correlated to the DA and the BR models for most noise-alone [P(Y∣N)] results for experiments that had differences in energy across stimulus waveforms (i.e., Study 2). These correlations were expected, given the Dau and BR models’ envelope dependences. Finally, the Dau and BR models were significantly correlated for every case tested, as were the PO and ES models. It is also interesting to note that nearly all of the models were significantly correlated for the wideband stimuli of Study 2.
The contribution of stimulus energy to each of the model decision variables was tested with a multiple regression approach: two models were used together to predict the subjects’ data, and the CB model was one of the two predictor models. An incremental F test (Edwards, 1979) was used to determine if the addition of the second model significantly increased the proportion of predicted variance. This procedure was equivalent to testing the significance of the partial correlation coefficient or the significance of the slope of a predictor variable in a multiple regression analysis. Results are briefly summarized in the text below in terms of the increase in R2 (the proportion of variance explained, with the upper-case R indicating a result of a multiple regression) achieved by adding the second model to the CB model for both P(Y∣T+N) and P(Y∣N).
Of all the diotic models tested in combination with the CB model [192 tests were run in total for P(Y∣T+N) and 192 for P(Y∣N); six models were tested for Study 2 with four subjects and two bandwidths and for Study 3 with six subjects and four stimulus sets], only regression analyses that included the MD, ES, or PO models as second predictors yielded significantly better predictions than the CB model alone. That is, the variance explained by the other models (MDS, DA, and BR) “overlaps” with the variance already explained by the CB model. Significant increases in R2 values by the addition of the MD model as a predictor were in the range of 0.10–0.33 for T+N stimuli and 0.10–0.36 for N stimuli, depending on the subject. Significant increases resulting from the addition of the ES model were in the range of 0.10–0.32 for T+N stimuli and of 0.10–0.52 for N stimuli. Significant increases resulting from adding the PO model were in the range of 0.08–0.46 for T+N stimuli and 0.16–0.21 for N stimuli.
These quantitative comparisons of the predictions of the diotic models illustrate the strong similarities between the CB, MD, MDS, DA, and BR models. The results suggest that a superior model might be constructed by combining the across-frequency structure of the MD model and the mechanisms in the ES and PO models. More detailed discussion of the diotic models is included below in Sec. 4.
Comparisons of dichotic models
Comparisons between EN, Wav, Xav, FCn, and BR models are shown in Tables 4, 5 for P(Y∣T+N) and for different levels. Recall that it appeared that subjects with substantially different thresholds were likely to be using distinct detection strategies. Therefore, Table 4 presents comparisons when the SNR was equal to the threshold of the best subjects in each study, and Table 5 presents comparisons when the SNR was equal to the threshold of the poorest subjects in each study.
Table 4.
Correlations between model decision variables in response to reproducible T+N stimuli under the N0Sπ condition are shown in terms of r2. Here, models were tested at the lowest subject threshold from each study; thus each model was run at an ES∕N0 of 1 dB for Study 1, −6.2 dB for the 100-Hz bandwidth condition of Study 2, −2.2 dB for the 2900-Hz bandwidth condition of Study 2, and −17 dB for all stimulus sets in Study 3. Model abbreviations are the same as in Fig. 8 and Sec. 3B1.
| Model comparison | Study 1 | Study 2 | Study 3 | ||||
|---|---|---|---|---|---|---|---|
| 115 Hz | 100 Hz | 2900 Hz | E1F1 | E2F2 | E2F1 | E1F2 | |
| EN-Wav | 0.30a | 0.43a | 0.30a | 0.05 | 0.15 | 0.08 | 0.01 |
| EN-Xav | 0.30a | 0.43a | 0.32a | 0.01 | 0.12 | 0.34a | 0.01 |
| EN-FCn | 0.23a | 0.12 | 0.08 | 0.00 | 0.04 | 0.04 | 0.00 |
| EN-BR | 0.06 | 0.20a | 0.10 | 0.04 | 0.01 | 0.01 | 0.01 |
| Wav-Xav | 1.00a | 1.00a | 0.78a | 0.93a | 1.00a | 0.83a | 1.00a |
| Wav-FCn | 0.07 | 0.01 | 0.03 | 0.01 | 0.14 | 0.03 | 0.15 |
| Wav-BR | 0.18a | 0.42a | 0.29a | 0.14 | 0.52a | 0.56a | 0.39a |
| Xav-FCn | 0.08 | 0.01 | 0.02 | 0.03 | 0.13 | 0.01 | 0.15 |
| Xav-BR | 0.16a | 0.42a | 0.18a | 0.11 | 0.52a | 0.35a | 0.39a |
| FCn-BR | 0.05 | 0.00 | 0.01 | 0.05 | 0.07 | 0.11 | 0.00 |
p<0.05.
Table 5.
Correlations between model decision variables in response to reproducible T+N stimuli under the N0Sπ condition are shown in terms of r2. Here, models were tested at the highest subject threshold from each study; thus each model was run at an ES∕N0 of 18 dB for Study 1, 3.8 dB for the 100-Hz bandwidth condition of Study 2, 4.8 dB for the 2900-Hz bandwidth condition of Study 2, and 0 dB for all stimulus sets in Study 3. Model abbreviations are the same as in Fig. 8 and Sec. 3B1.
| Model comparison | Study 1 | Study 2 | Study 3 | ||||
|---|---|---|---|---|---|---|---|
| 115 Hz | 100 Hz | 2900 Hz | E1F1 | E2F2 | E2F1 | E1F2 | |
| EN-Wav | 0.48a | 0.35a | 0.45a | 0.03 | 0.22a | 0.12 | 0.10 |
| EN-Xav | 0.25a | 0.43a | 0.39a | 0.00 | 0.56a | 0.21a | 0.06 |
| EN-FCn | 0.31a | 0.01 | 0.12 | 0.00 | 0.03 | 0.02 | 0.00 |
| EN-BR | 0.19a | 0.34a | 0.10 | 0.03 | 0.04 | 0.01 | 0.01 |
| Wav-Xav | 0.87a | 0.75a | 0.84a | 0.95a | 0.00 | 0.67a | 0.63a |
| Wav-FCn | 0.59a | 0.05 | 0.06 | 0.09 | 0.02 | 0.34a | 0.08 |
| Wav-BR | 0.37a | 0.46a | 0.37a | 0.17a | 0.34a | 0.17a | 0.14 |
| Xav-FCn | 0.39a | 0.04 | 0.09 | 0.10 | 0.09 | 0.14 | 0.00 |
| Xav-BR | 0.25a | 0.49a | 0.24a | 0.17a | 0.02 | 0.44a | 0.46a |
| FCn-BR | 0.47a | 0.07 | 0.10 | 0.11 | 0.02 | 0.19a | 0.04 |
p<0.05.
In Table 4, correlations between Wav and Xav, and Wav and BR are examined (Wst and Xst are not included because these models are highly correlated to Wav and Xav, respectively.) Stimulus energy (EN) was significantly, albeit modestly, correlated to Wav, Xav, and the BR models for some stimulus sets. The results of Table 5 are similar; however, as was expected for the responses of subjects with higher thresholds, the correlations of many of the model decision variables to energy were stronger at the higher SNR. Note also that Wav and Xav were slightly less correlated at the higher SNRs. [Also, note that the perfect correlations between Wav and Xav in some cases (Table 4) are due to the fact that Xav with weight a=0 or 1 reduces to Wav with weight a=0 or 1.]
Colburn et al. (1997) and Isabelle (1995) discounted models based on UCC, NCC, and EC mechanisms because of their dependence on stimulus energy. The comparisons in Tables 4, 5 showed only moderate correlations between energy and either the binaural BR or FC model, both of which include correlation and∕or cancellation mechanisms. (All stimulus sets of Study 3 had nearly equal energies; thus, correlations of the BR and FC models to energy would be expected to be near zero.) Because energy was not correlated to the subjects’ detection patterns, the failure of these models can be partially explained by their moderate correlations to stimulus energy.
Interactions between envelope and fine-structure cues
Some of the models tested in this work included interactions between cues derived from envelope and fine structure before computing decision variables. It was of interest to determine if the nature of these interactions was appropriate as compared to the interactions observed in the empirical data collected in Study 3 (Davidson, 2007; Davidson et al., 2009). This was examined by comparing the extent to which each of the models relied on envelope or fine structure and the extent to which each of the subjects relied on envelope or fine structure. The stimuli and analysis techniques used in the present study were the same as those used in Study 3.
The analysis procedure used by Davidson (2007) and Davidson et al. (2009) is briefly described here: Stimuli from four stimulus sets (E1F1, E2F2, E1F2, and E2F1) shared either envelopes (E) or fine structures (F); subscripts shared between stimulus sets indicate that the particular waveform component was shared between sets. Model detection patterns were computed, and subjects’ detection patterns were measured for each of the four stimulus sets. A multiple linear regression was performed that used model detection patterns from the “chimeric” stimulus sets (E1F2 and E2F1) to predict the baseline model detection patterns (E1F1 and E2F2). To simplify the analysis, the detection patterns that shared the predictor, either envelope or fine structure, were combined (i.e., concatenated). If the model (or subject) relied exclusively on envelope, the detection patterns for the baseline stimulus sets and those for the stimulus sets sharing the same envelopes should have been identical. If the model (or subject) relied exclusively on fine structure, the detection patterns from the baseline stimulus sets and the stimulus sets sharing the same fine structures should have been identical. The multiple regression procedure quantified the similarity of each detection pattern to the baseline detection patterns. Three R2 values were produced for each model and subject. was the proportion of variance accounted for when detection patterns with common envelopes were used as predictors; was the proportion of variance accounted for when detection patterns with common fine structures were used as predictors. was the proportion of variance accounted for when both detection patterns with common envelopes and detection patterns with common fine structures were used as predictors. The is underlined in Tables 6, 7 if the addition of envelope as a predictor along with fine structure significantly increased the proportion of variance explained (i.e., if was significantly greater than ), and is underlined if was significantly greater than (i.e., if addition of the fine structure as a predictor significantly increased the proportion of variance, as compared to that explained by the envelope alone). For a more detailed description of the methods used here and in Study 3, see Davidson (2007) and Davidson et al. (2009).
Table 6.
The contribution of cues based on envelope and fine structure to N0S0 model decision variables. Results for human subjects from Study 3 are presented along with results from each computational model. The entries and denote the proportion of variance in the baseline detection patterns explained by chimeric detection patterns measured using stimuli sharing the same envelopes or fine structures as the baseline stimuli, respectively. If the addition of envelope as a predictor to fine structure as a predictor significantly increased the proportion of variance explained (i.e., was significantly higher than ), then is underlined. If the addition of fine structure as a predictor to envelope as a predictor significantly increased the proportion of variance explained (i.e., was significantly higher than ), then is underlined. Note that the values are the proportion of variance explained by a multiple regression including both envelope and fine structure as predictors; all values were statistically significant (p<0.05). Model abbreviations are the same as in Fig. 1.
| N0S0 | ES∕N0 | P(Y∣T+N) | P(Y∣N) | |||||
|---|---|---|---|---|---|---|---|---|
| Subjects | S1 | 10 | 0.17 | 0.18 | 0.41 | 0.17 | 0.59 | 0.69 |
| S2 | 10 | 0.26 | 0.29 | 0.37 | 0.18 | 0.48 | 0.54 | |
| S3 | 10 | 0.05 | 0.28 | 0.32 | 0.00 | 0.71 | 0.72 | |
| S4 | 11 | 0.69 | 0.11 | 0.73 | 0.45 | 0.30 | 0.68 | |
| S5 | 11 | 0.35 | 0.07 | 0.38 | 0.20 | 0.39 | 0.49 | |
| S6 | 11.5 | 0.66 | 0.25 | 0.66 | 0.35 | 0.36 | 0.58 | |
| Models | DA | 10 | 0.97 | 0.16 | 0.98 | 0.91 | 0.30 | 0.94 |
| BR | 10 | 0.88 | 0.12 | 0.93 | 0.71 | 0.20 | 0.90 | |
| ES | 10 | 0.94 | 0.03 | 0.95 | 0.88 | 0.02 | 0.92 | |
| PO | 10 | 0.82 | 0.21 | 0.85 | 0.40 | 0.43 | 0.71 | |
Table 7.
Same as Table 6 except data are presented for the N0Sπ condition. Computational models were tested using stimuli with the lowest (−17 dB) and with the highest (0 dB) threshold observed for the subjects. All values were statistically significant (p<0.05). Note that significant values of 0.00 in this table represent very small but significant R2 values that were rounded to zero; these small but significant values were observed in cases when a single predictor explained nearly all of the variance in the data (e.g., values of 0.99–1.0), such that even a very small value of (<0.005) resulted in a significant increment in , as determined by the incremental F-test. Model abbreviations are the same as in Fig. 8 and Sec. 3B1.
| N0Sπ | ES∕N0 | P(Y∣T+N) | P(Y∣N) | |||||
|---|---|---|---|---|---|---|---|---|
| Subjects | S1 | 0 | 0.12 | 0.43 | 0.44 | 0.22 | 0.41 | 0.57 |
| S2 | −10 | 0.13 | 0.56 | 0.57 | 0.14 | 0.55 | 0.59 | |
| S3 | −17 | 0.00 | 0.38 | 0.39 | 0.14 | 0.14 | 0.35 | |
| S4 | −1 | 0.41 | 0.30 | 0.68 | 0.40 | 0.26 | 0.63 | |
| S5 | −16.5 | 0.06 | 0.45 | 0.51 | 0.25 | 0.15 | 0.47 | |
| S6 | −10 | 0.39 | 0.27 | 0.50 | 0.32 | 0.15 | 0.52 | |
| Models | sT | −17 | 0.04 | 0.95 | 0.95 | |||
| sI | −17 | 0.67 | 0.19 | 0.68 | ||||
| Wav | −17 | 0.06 | 0.99 | 0.99 | ||||
| Xav | −17 | 0.00 | 0.99 | 0.99 | ||||
| Lp | −17 | 0.01 | 0.30 | 0.32 | ||||
| FCc | −17 | 0.24 | 0.23 | 0.52 | 0.02 | 0.27 | 0.28 | |
| FCn | −17 | 0.25 | 0.25 | 0.46 | 0.62 | 0.01 | 0.66 | |
| BR | −17 | 0.02 | 0.55 | 0.56 | ||||
| sT | 0 | 0.00 | 1.00 | 1.00 | ||||
| sI | 0 | 0.99 | 0.16 | 0.99 | ||||
| Wav | 0 | 0.00 | 1.00 | 1.00 | ||||
| Xav | 0 | 0.22 | 0.90 | 0.91 | ||||
| Lp | 0 | 0.05 | 0.34 | 0.32 | ||||
| FCc | 0 | 0.30 | 0.26 | 0.38 | 0.27 | 0.85 | 0.98 | |
| FCn | 0 | 0.17 | 0.25 | 0.28 | 0.90 | 0.85 | 0.97 | |
| BR | 0 | 0.00 | 0.85 | 0.75 | ||||
Results are presented for simulations using a SNR of 10 dB ES∕N0 for the N0S0 condition (Table 6). Model abbreviations are as in Fig. 3. All of the N0S0 models relied more heavily on envelope than fine structure with the exception of the PO model, which made approximately equal use of envelope and fine-structure cues on noise-alone trials. In general, the patterns of model interactions between envelope and fine structure (i.e., R2 values) were in stark contrast to the results of the human subjects presented in the same table, which indicated that subjects relied roughly equally on envelope and fine-structure cues. The only notable exception was for the PO model, which predicted a more equal utilization of envelope and fine-structure cues than the other models [but recall that the PO model captured at most about 40% of the variance in subjects’ detection patterns (Fig. 2)].
Results are also presented for the N0Sπ condition (Table 7). Each model was evaluated twice: once with the SNRs set to the highest threshold observed for the human subjects in Study 3 and once at the lowest SNRs for the subjects. Every model except sI was dominated by the fine structure of the waveform, as would be expected for conventional ITD-based models of binaural detection at low frequencies. The interaction pattern for most models differs from the results of the subjects, which indicated a more equal reliance on envelope and fine structure. The Lp, FCc, FCn, and BR models produced R2 values that were most similar to the human subjects for T+N stimuli. For some of the linear regression analyses, R2 values are (much) higher than would be expected based on the subjects’ data (e.g., all but the PO model for N0S0 conditions, and the Wav and Xav models at low SNRs for N0Sπ conditions). This result suggests that the dependence of the model detection patterns on the envelope and fine-structure cues was more straightforward, and thus more predictable, than for the human subjects. The subject data from Study 3 indicate that a linear combination of average cues derived from the envelope and fine structure should not account for all of the predictable variance in the E1F1 and E2F2 detection patterns and suggest instead models may need some form of running temporal combination of envelope and fine-structure cues. Thus, the reliance on envelope and fine structure is likely a necessary, but insufficient, condition for predicting subjects’ detection patterns. Internal noise added at the decision stage would reduce the correlations between model results and the envelope or fine-structure cues, but addition of internal noise would not produce the patterns of correlations seen in the data.
CONCLUSIONS AND FUTURE WORK
The results of the present study show that several existing diotic models that have successfully predicted subjects’ thresholds for tone-in-noise detection tasks cannot explain diotic detection patterns for reproducible noise maskers. In particular, none of the temporal models examined in this work were able to predict significant proportions of variance in all subjects’ data; this was true even when energy cues were made unreliable, forcing subjects to rely on cues other than overall energy. A model based on a linear combination of energies at the output of several filters surrounding the target frequency (MD; Ahumada and Lovell, 1971; Ahumada et al., 1975; Gilkey and Robinson, 1986) best predicted the N0S0 data for stimuli with level variations between noises (Study 2). A model based on envelope fluctuation (ES; Richards, 1992; Zhang, 2004) predicted N0S0 detection patterns estimated using equal-energy stimuli (Study 3) more accurately than either the Dau et al. (1996a) or Breebaart et al. (2001a) models.
Implementations of several models of binaural detection were also tested. The models that made the most significant predictions used linear combinations of the average absolute values or of the standard deviations of ITDs and ILDs (Wst, Wav, Xst, and Xav; Isabelle, 1995; Isabelle and Colburn, 2004; Goupell and Hartmann, 2007). The binaural version of the model of Breebaart et al. (2001a) made fewer significant predictions than Xav and Wav, but seemed to more appropriately weight the use of stimulus envelope and fine structure in the computation of the model decision variable. As for the diotic condition, none of the models tested were comprehensive enough to make significant predictions for every subject in every stimulus condition.
Although the template-based models examined here (Dau et al., 1996a, 1996b; Breebaart et al., 2001a, 2001b, 2001c) did not predict a large portion of the variability in the subjects’ data, they are capable of predicting thresholds for a multitude of psychophysical tasks and will be examined more thoroughly in future work. Trial-by-trial responses were not simulated here, and a running template was not computed. Computation of a running template would be an interesting modeling exercise, which would more fully examine the potential of these specific models and would also provide an initial investigation of the general class of detection mechanisms that have the ability to change dynamically over time. Some of the subjects (including some of the authors) have reported being influenced by particular noise waveforms, or even feeling temporarily confused for brief periods (i.e., tens of trials) during an experiment. Individual responses and waveform identification numbers were recorded on each trial for the experiments presented here, providing data suitable for an interesting analysis of template-based models. Suppose that a template was constructed as the mean of several preceding trials of randomly generated noise. Suppose also that this memory was a buffer of a limited number of waveforms in a first-in, first-out configuration. Model predictions for the data in Studies 1–3 could be re-examined as a function of the buffer length (or the number of internal representations of the stimuli used to compute an average template). This analysis is possible because responses to each waveform can be used to sort waveforms into perceived tone-plus-noise and noise-alone groups, regardless of the stimuli used for each trial.
The models and analyses presented in this paper assume that normally-distributed internal noise is added at the decision stage. Implementing the models without complicated or model-specific internal noise had advantages for this particular study (as described in Sec. 2). This decision was not without consequences. Many of the dichotic models cannot make predictions for N trials without implementing a more complicated internal noise model or the introduction of some form of processing asymmetry. Thus, implementing these models without internal noise is incomplete but informative. The internal noise for the diotic models seems likely to make only marginal changes in their predictions for individual samples, at least as revealed by the correlation analyses used here.
A possible drawback of this modeling approach (and for that matter, a drawback of any of the models used in this study) is that the potential use of short-term cues is not captured by the template mechanisms employed in the above models. Subjects have reported that relatively brief segments of stimuli were often the basis for decisions during dichotic detection tasks. This fact compounds the modeling problem because the temporal locations of these stimulus segments are unknown and may differ among waveforms. Cues that occur in brief segments of the stimuli are not well suited for detection with the temporal weighting scheme of the Breebaart model, which averages across waveforms. Further, a strategy based on short-term cues would likely require a rethinking (i.e., shortening) of the time constant used for smoothing the output of the binaural processor in the Breebaart model. Recent evidence suggests that the relatively long estimates of binaural temporal windows, 60–200 ms (e.g., Grantham and Wightman, 1979; Kollmeier and Gilkey, 1990; Culling and Summerfield, 1998), may, in fact, be too long, and estimates on the order of 50 ms or shorter might be more suitable for modeling the current data (Bernstein et al., 2001; Kolarik and Culling, 2005). Researchers’ testing temporal aspects of binaural processing have reported time constants as short as 10 ms (e.g., Akeroyd and Bernstein, 2001). Note that the variances of the interaural differences depend on the distributions of short-time estimates of interaural differences, even though it is only the spread of values that is used for a decision.
Another possibility is that subjects may employ more than one type of (potentially short-term) template. This strategy could be investigated by grouping waveforms by their respective hit and false-alarm rates, and then investigating the templates that result from training the model with waveforms corresponding to high, moderate, and low hit rates.
Another class of models worth further investigation includes those based on the spectrum of the envelope of amplitude fluctuations, such as modulation filter bank models (e.g., Berg, 2004; Dau et al., 1997a, 1997b). These models have been successful at predicting average thresholds for low-frequency diotic tone-in-noise detection tasks, but were outside the scope of this paper. Future studies will test these models with the reproducible noise data.
Several of the models examined in this study incorporated information from multiple frequency channels (e.g., the MD model and MDS, the MD model with suboptimal weights) using linear weighting schemes that were either sub-optimal or fit to the subjects’ data. Preliminary simulations using optimal weighting strategies, such as linear discriminant analyses, produced improved model-data correlations with respect to sub-optimal weighting schemes. These results suggest that subjects may be exploiting correlations between frequency channels to perform the detection task. Future modeling efforts will investigate the use of optimal linear across-frequency weighting for the multi-channel models treated in this study.
Another suggestion for future modeling efforts is inspired by Hancock and Delgutte (2004). Results from the current study suggest that a single binaural delay∕attenuation model cannot explain detection of tones masked by reproducible noise stimuli. The Hancock and Delgutte (2004) model was originally designed to predict ITD discrimination data and is based on recordings from the inferior colliculus of cat. The model employs a neuronal pooling strategy that combines responses across a population of model neurons tuned in best frequency and ITD according to distributions measured in cat. It is possible that responses of a population of channels tuned to a number of different ITD values are necessary to account for the current data.
ACKNOWLEDGMENTS
This work was supported by NIDCD F31 077798 (S.A.D.), NIDCD 00100 (H.S.C.), and NIDCD 01641 (L.H.C. and S.A.D.). We thank Dr. Marty Sliwinski, Dr. Yan Gai, and Junwen Mao for helpful comments. We also thank Dr. Scott Isabelle for providing his data and stimulus waveforms. Dr. Torsten Dau and Dr. Jeroen Breebaart provided very helpful input regarding implementation strategies for their respective models. We also thank Susan Early for her editorial comments.
APPENDIX A: IMPLEMENTATION OF THE MD MODELS
The MD and MDS models were implemented using a linear combination of the rms output of three or seven fourth-order gammatone filters, depending on the masker bandwidth (Fig. 1). Davidson et al. (2006) showed that filters exceeding the bandwidth of the stimulus noise do not significantly increase the predictive power of the model. Therefore, the center frequencies were selected to span 275–725 Hz (in 75-Hz increments) for the 2900-Hz noise bandwidth condition of Study 2 and 425–575 Hz for the 100-Hz noise bandwidth condition of Study 2. The bandwidth of all of the filters was set to 75 Hz to match Davidson et al. (2006). The MD model was not used to predict the data from Study 3, as the masker bandwidth in that study was only 50 Hz.
The weights (wi) for the linear combination were established with two separate methods. For the first method (the standard MD model), the weights were fitted to the individual subjects’ detection patterns using the reproducible stimuli from each study (Fig. 3). The MATLAB function fminsearch was used to minimize the quantity of 1 minus the correlation coefficient between the linear combination of the rms filter outputs and the z-scores of P(Y∣T+N) or P(Y∣N) for each subject in each condition in Studies 1 and 2.
A second variant of the MD model was also tested. This model (the MDS model) used a decision-theoretic suboptimal weighting scheme to compute model weights (rather than fitting the weights to each subject’s data). Individual weights were computed for the MDS model using 1000 repetitions of randomly created (i.e., not reproducible) noise. Tones were added and weights were computed as
| (A1) |
where F is the root-mean-squared filter output for frequency channel i and random-noise repetition m for T+N or N stimuli, and the means and variances were computed across repetition m within frequency channel i. [Note that this method would be optimal if the covariance of each channel was accounted for in Eq. A1.] Both models’ decision variables were given by
| (A2) |
where j is the reproducible noise waveform index, using the weights computed with either method above.
APPENDIX B: IMPLEMENTATION OF THE ES MODEL
The implementation of the ES model (Fig. 1) was the same as that in Davidson et al. (2006). The ES model DV was computed as
| (B1) |
where x[t,j] is the Hilbert envelope of the output of a fourth-order gammatone filter centered at 500 Hz, with a 75-Hz ERB for stimulus waveform j, and Δt is the time resolution of the sampled waveform. To ensure that all fine structure was removed from the stimulus waveform, x[t,j] was filtered with a tenth-order maximally flat infinite impulse response (IIR) filter with a cut-off frequency of 250 Hz before being processed with Eq. B1. The statistic was normalized as suggested by Zhang (2004) to remove the effects of energy and duration. Upon addition of the tone to the noise waveform, the stimulus envelope flattens. As such, the DV decreases with increasing tone level.
APPENDIX C: IMPLEMENTATION OF THE DAU MODEL
The Dau model (DA, Fig. 1) consists of a third-order gammatone filter centered at the tone frequency (500 Hz) with a bandwidth of 1 ERB, approximately 75 Hz at a center frequency of 500 Hz (Glasberg and Moore, 1990). The output is half-wave rectified and passed to a series of adaptation loops (Dau et al., 1996a), designed to simulate adaptation in auditory-nerve responses by processing fast stimulus fluctuations almost linearly and compressing slowly fluctuating stimuli. The output of the adaptation loops is low-pass filtered with a time constant of 20 ms (8 Hz) to remove fine structure and leave envelope information. The output at this stage is referred to as the internal representation of the model.
The internal representation is passed to an optimal detector. The optimal detector uses a template derived from the normalized difference between the mean of 500 T+N internal representations and the mean of 500 N internal representations (Fig. 4). A large number of noises were used to simulate extensive subject training. The templates were computed using randomly generated noise with a signal added at 10 dB above each subject’s threshold. On each trial, the optimal detector first subtracts the noise-alone template from the internal representation computed from the reproducible stimulus on that trial. The mean scalar product of the normalized difference template and the difference between the noise-alone template and the internal representation of the reproducible stimulus is then computed as a function of time. The model was originally designed to pick the interval (from a two-interval task) with the larger scalar product as the one containing the tone. For the purposes of this study, which focuses on single-interval tasks, the scalar product itself was used as the decision variable. This process is summarized with the following equation:
| (C1) |
where D is the Dau decision variable, φj is the internal representation of the current stimulus waveform j, is the mean of 500 internal representations of T+N stimulus waveforms (the T+N template), is the mean of 500 internal representations of N stimuli (the N template), Td is the duration of the stimulus waveform, and rms is the root-mean-squared function.
The code used to implement this model is available at www.bme.rochester.edu/carney (last viewed August 19, 2009).
APPENDIX D: IMPLEMENTATION OF THE MONAURAL BREEBAART MODEL
The diotic version of the Breebaart model (Breebaart et al., 2001a) is shown in Fig. 1 (BR). This model is similar to the Dau model; however, the Breebaart model was implemented as a bank of processors with increasing center frequencies. Two filters per ERB were implemented over the same bandwidths as the MD and MDS models. The low-pass filter from the Dau model was replaced with a double-sided exponential window with time constants of 10 ms each. The structure of the decision device is described in detail in Breebaart et al. (2001a) and is composed of a suboptimally weighted combination of internal representations at different frequency channels, which are then summed as a function of time and frequency. Like the Dau model, the Breebart model also uses both T+N and N templates (Fig. 5). The templates were established as the means of 50 internal representations9 of randomly generated T+N and N waveforms at each subject’s threshold. The detector first computes the DV B according to the following equation:
| (D1) |
The quantity U(j,i,t) is the difference between the internal representation of the reproducible waveform j and the N template for each frequency (F) channel i. U(j,i,t) is weighted across frequency and time by the difference between the T+N and N templates (μ) normalized by the variance of the N templates (σ2).
The code used to implement this model is available at www.bme.rochester.edu/carney (last viewed August 19, 2008).
APPENDIX E: IMPLEMENTATION OF THE PO MODEL
The PO model was computed as described in Davidson et al. (2006) and was based on the model described by Carney et al. (2002) (PO, Fig. 1). Two model auditory-nerve fibers of Heinz et al. (2001) with spontaneous rates of 50 spikes/s converged upon a coincidence detector of the type described in Colburn (1977). The fibers’ center frequencies were selected such that their phase responses differed by 180° at the tone frequency (which occurred for the two center frequencies of 459 and 542 Hz). The count at the output of the coincidence detector was used for the model DV as described by
| (E1) |
where nfib is the number of auditory-nerve fiber inputs at each center frequency, TCW is the time window for coincidence detection, t is time, Td is the duration of the stimulus, and κ is the output of the auditory-nerve model of Heinz et al. (2001) at each of the two center frequencies.
The mechanism used by the PO model is as follows: as the level of the tone is increased, and the responses of the fibers become more phase locked to the tone. The count at the output of the coincidence detector decreases as tone level increases because the two model fibers progress to firing perfectly out of phase. The model detects the tone on the basis of a reduction in the coincidence detector’s average rate with respect to its response to the noise alone. The simulations presented here were performed at SNRs matched to the subjects’ thresholds; the model DV was the coincidence detector’s average rate. Ten model fibers were used with a coincidence window of 20 μs. As in Davidson et al. (2006), the onsets and offsets of the auditory-nerve fiber responses were truncated because they exceeded realistic levels and did not produce decision variables correlated to the psychophysical data. Due to the use of relatively short-duration stimuli in the present study, only the first and last 25 ms of the responses were truncated. The model DV (G) was computed for each reproducible stimulus j.
APPENDIX F: IMPLEMENTATION OF THE INDEPENDENT-CENTERS AND AUDITORY-IMAGE MODELS
Isabelle’s (1995) decision variables based on ITDs and ILDs for waveform j are given by
| (F1) |
and
| (F2) |
where ϕ(j,t) is the instantaneous phase computed from the complex analytic signal for the right (R) or left (L) stimulus waveforms, ωc is the center frequency of the noise band, A(j,t) is the envelope of the complex analytic signal for either the right or left stimulus waveform, and j is the index of each reproducible stimulus waveform. Note that T is only approximately equal to the ITD because the frequency of the masker stimulus varies as a function of time. The complex analytic signals were computed using the Hilbert transform. A selection of several decision variables related to those in Isabelle (1995) (see Isabelle and Colburn, 2004) and Goupell and Hartmann (2007) is shown below. These included the standard deviations10 of ITD and ILD computed for each reproducible stimulus as defined by
| (F3) |
and
| (F4) |
where Td is the duration of the stimulus, and T and I are as defined above in Eqs. F1, F2. A weighted combination of the standard deviations of ITD and ILD [Eq. F5] and a combination of the average absolute values of ITD and ILD [Eq. F6] were also explored, as defined by
| (F5) |
and
| (F6) |
respectively, where a is a weight determined by minimizing the sum of squared errors between W and z{P(Y∣T+N)} for each condition and subject in each study. Note that the decision variables described by Eqs. F5, F6 would fit into the class of independent-center models of Goupell and Hartmann (2007) because the standard deviations (or average absolute values) of ITD and ILD were computed before the weighted combination of ITD and ILD was computed. The four metrics described in Eqs. F3, F4, F5, F6 were compared to the standard deviation of a temporal combination of ITD and ILD [Eq. F7] as well as the average value of the absolute value of the temporal combination of ITD and ILD [Eq. F8] defined by
| (F7) |
and
| (F8) |
respectively, where b is a weight computed in the same manner as in Eqs. F5, F6, and T and I are as defined in Eqs. F1, F2. The decision variables in Eqs. F7, F8 would fit into the class of auditory-image models in Goupell and Hartmann (2007) because ITD and ILD were combined before computing the standard deviation or averaging over time.
Isabelle’s (1995) implementation of Hafter’s (1971) lateral position model was also considered. This model is based on a combination of ITD and ILD using a trading ratio of 20 μs∕dB defined by
| (F9) |
where Td is the duration of the stimulus, a is the trading ratio, and T and I are as defined in Eqs. F1, F2. The lateral position model is similar to Eqs. F7, F8, except that a constant trading ratio was used for all computations. These models [Eqs. F3, F4, F5, F6, F7, F8, F9] were of particular interest because they allow for the distinct interaction of statistics based on envelope and fine structure as a function of time. Such interactions are implied by the results of Study 3 (Davidson, 2007; Davidson et al., 2009).
APPENDIX G: IMPLEMENTATION OF THE FC MODEL
The DV of the FC model (Fig. 8) (Marquardt and McAlpine, 2001) was computed based on a linear combination of differences and cross correlations between channels with different delays:
| (G1) |
where FC(j) is the model DV for the reproducible stimulus j, κ(j,t−τ) is the output of the auditory-nerve model of Heinz et al. (2001) delayed by τ s (250 μs, corresponding to a phase delay of 45° at the 500-Hz signal frequency), and w is the suboptimal weight computed for each delay channel, as shown in Fig. 8. Weights were computed using a strategy similar to that used for the MDS model (see Appendix A). Weights derived for each of the four channels rarely took on a value of zero, as channels were tuned in increments of 90° of interaural phase. Two different types of weights were tested: FCc used an UCC (product) of the inputs for the channels tuned to ±45° (weighted by w2 and w3 in Fig. 8), while the FCn used a NCC (Colburn et al., 1997). For a more complete description of the FC model weights, see Davidson (2007) and Davidson et al. (2009).
APPENDIX H: IMPLEMENTATION OF THE BINAURAL BREEBAART MODEL
The binaural processor in the Breebaart model (Fig. 8) (Breebaart et al., 2001a) is described by
| (H1) |
for N0Sπ stimuli, where φ(j,i,t) describes the output of the adaptation loops for reproducible stimulus j, frequency channel i, at time t, for the left or right ear. (Only the 0.0 delay and 0.0 attenuation channel were included in these predictions, as explained in the main text.) The processor output E(j,i,t) is then filtered with a double-exponential window with a time constant of 30 ms per exponential. The filtered signal, E′(j,i,t), is then scaled, compressed with a logarithm, and then scaled again as follows:
| (H2) |
with a=0.1 and b=0.000 02. The two scale factors were calibrated by setting the model threshold to predict N0Sπ and NρSπ detection tasks, as described in Breebaart et al. (2001a). The detector stage for the binaural model is similar to that for the monaural models [Eq. D1]. However, for the binaural case, the temporally weighted internal representation of each waveform is integrated over both time and frequency to compute the decision variable. The templates used to compute the weights are computed using the compressed and filtered outputs of the binaural processor. This method differs from computing a difference between T+N and N templates and comparing to the double-exponential filtered output of the adaptation loops as in the monaural model; recall that the N template is identically zero for the binaural model.
Footnotes
The z-score was set to 0.005 for P(Y∣T+N) or P(Y∣N) values that were equal to 0 and to 0.995 for P(Y∣T+N) or P(Y∣N) values that were equal to 1 in order to avoid infinite z-score values.
Note that, although the parameters of most of the models examined here were set to fixed values suggested by the previous literature and were not fitted to each subject’s data (exceptions are specifically identified in the text), all of the fits had two free parameters, the slope and intercept of the line relating the values of the model’s DV to the z-scores of the subject. Note that the square of Pearson’s product-moment correlation is a measure of the variance predicted by this linear statistical model. As such, the reports of proportion of predicted variance assume a linear model with slope and intercept fit to the data.
When model d′s were large (because the SNR was set to the threshold of a poor subject or simply because the models did not include internal noise), r2 values for predictions of the detection patterns that included both hits and false alarms, referred to as P(Y∣W) (Davidson et al., 2006), were artificially high because of the separation between the distributions of P(Y∣T+N) and P(Y∣N). Thus, modeling analyses presented here were confined to predictions of P(Y∣T+N) and P(Y∣N). The net effect of analyzing hit and false-alarm rates separately was to lower the proportions of variance explained with respect to the variance that might be explained in P(Y∣W).
The values reported in this paragraph are based on the correlation between the first-half and last-half of the data in terms of P(Y∣N) and P(Y∣T+N), not z-scores. However, simulations indicate that similar values would be obtained if z-scores had been used.
Inspection of Fig. 2 shows some significant predictions for the energy model (CB) under these equal-energy conditions. These predictions appear significant because no internal noise was used in the simulations. One might suspect that the peripheral filter included in this model recovered energy differences across stimuli. The largest difference between levels at the output of the gammatone filter for the stimuli in Study 3 was about 1 dB. For the CB model to explain these results, given the variability of the hit and false-alarm rates in the detection patterns and also the variability of the energy-based decision statistic, the subjects would have had to reliably measure the output of a CB filter with a resolution of about 0.04 dB (to correctly order 25 T+N or N stimulus waveforms in terms of level) in the presence of internal noise with an effective variance of approximately 1 dB across noises (estimated assuming the internal-to-external noise ratio is approximately 1 for the data from Study 2 in the conditions where the data are correlated to the CB model; see Evilsizer et al., 2002).
It was also of interest to determine whether the MD model predictions were significantly better than the MDS model predictions. For all subjects but S3 [see Fig. 2B, P(Y∣N)], the MD model made better predictions than the MDS model. Tests of significant differences between non-independent correlations were computed for each subject with each stimulus bandwidth to test the hypothesis that the MD model was significantly better at predicting detection patterns than the MDS model. Results indicated that the MD model predicted significantly (p<0.05) more variance in P(Y∣T+N) for S2, S3, and S4 in the 100-Hz bandwidth condition and for S1 and S4 in the 2900-Hz bandwidth condition, and more variance in P(Y∣N) for S1 and S2 in the 100-Hz bandwidth condition and for S2 in the 2900-Hz bandwidth condition. Thus, the MD weighting strategy did, for some subjects, make significantly better predictions than the MDS weighting strategy.
Note that the ES model predictions shown here explain less variance than those in Davidson et al. (2006) because predictions were made separately for P(Y∣T+N) and P(Y∣N) in the present study, whereas Davidson et al. (2006) made predictions for the combined detection pattern, P(Y∣W).
These decision variables were also computed using fourth-order gammatone filters centered at 500 Hz. However, in all but the 2900-Hz case, predictions were poorer when peripheral filtering was used, and therefore, those results were not included in this document. These decision variables were also tested using the auditory-nerve models of Heinz et al. (2001) and Zilany et al. (2006). Poor results (i.e., worse than those achieved with no peripheral processing) were also encountered using the auditory-nerve models as a peripheral processing stage, but this was likely due to the fact that these decision variables rely on the complex-analytic signal, which is not well defined for the output of the auditory-nerve models (the outputs of which have nonzero dc components). Therefore, the predictions that used the peripheral model of Heinz et al. (2001) are not shown.
This number was reduced from 500 for practical considerations. The sensitivity of model decision variables to the number of internal representations was not great; results were stable for 20 or more repetitions.
Standard deviations were used in this study as they resulted in slightly, but not significantly, better predictions than did variances. Isabelle (1995) also mentioned that results based on standard deviation and variance were not significantly different.
References
- Ahumada, A., and Lovell, J. (1971). “Stimulus features in signal detection,” J. Acoust. Soc. Am. 49, 1751–1756. 10.1121/1.1912577 [DOI] [Google Scholar]
- Ahumada, A., Marken, R., and Sandusky, A. (1975). “Time frequency analyses of auditory signal detection,” J. Acoust. Soc. Am. 57, 385–390. 10.1121/1.380453 [DOI] [PubMed] [Google Scholar]
- Akeroyd, M. A., and Bernstein, L. R. (2001). “The variation across time of sensitivity to interaural disparities: Behavioral measurements and quantitative analyses,” J. Acoust. Soc. Am. 110, 2516–2526. 10.1121/1.1412442 [DOI] [PubMed] [Google Scholar]
- Berg, B. G. (2004). “A temporal model of level-invariant tone-in-noise detection,” Psychol. Rev. 111, 914–930. 10.1037/0033-295X.111.4.914 [DOI] [PubMed] [Google Scholar]
- Bernstein, L. R., Trahiotis, C., Akeroyd, M. A., and Hartung, K. (2001). “Sensitivity to brief changes of interaural time and interaural intensity,” J. Acoust. Soc. Am. 109, 1604–1615. 10.1121/1.1354203 [DOI] [PubMed] [Google Scholar]
- Breebaart, J., van der Par, S., and Kohlrausch, A. (2001a). “Binaural processing model based on contralateral inhibition I. Model structure,” J. Acoust. Soc. Am. 110, 1074–1088. 10.1121/1.1383297 [DOI] [PubMed] [Google Scholar]
- Breebaart, J., van der Par, S., and Kohlrausch, A. (2001b). “Binaural processing model based on contralateral inhibition II. Dependence on spectral parameters,” J. Acoust. Soc. Am. 110, 1089–1104. 10.1121/1.1383298 [DOI] [PubMed] [Google Scholar]
- Breebaart, J., van der Par, S., and Kohlrausch, A. (2001c). “Binaural processing model based on contralateral inhibition III. Dependence on temporal parameters,” J. Acoust. Soc. Am. 110, 1105–1117. 10.1121/1.1383299 [DOI] [PubMed] [Google Scholar]
- Carney, L. H., Heinz, M. G., Evilsizer, M. E., Gilkey, R. H., and Colburn, H. S. (2002). “Auditory phase opponency: A temporal model for masked detection at low frequencies,” Acta. Acust. Acust. 88, 334–347. [Google Scholar]
- Colburn, H. S. (1977). “Theory of binaural interaction based on auditory-nerve data. II. Detection of tones in noise,” J. Acoust. Soc. Am. 61, 525–533. 10.1121/1.381294 [DOI] [PubMed] [Google Scholar]
- Colburn, H. S., Isabelle, S. K., and Tollin, D. J., 1997, in Binaural and Spatial Hearing in Real and Virtual Environments, edited by Gilkey R. and Anderson T. (Erlbaum, New York: ), pp. 533–556. [Google Scholar]
- Culling, J. F., and Summerfield, Q. (1998). “Measurements of the binaural temporal window using a detection task,” J. Acoust. Soc. Am. 103, 3540–3553. 10.1121/1.423061 [DOI] [Google Scholar]
- Dau, T., Kollmeier, B., and Kohlrausch, A. (1997b). “Modeling auditory processing of amplitude modulation. II. Spectral and temporal integration in modulation detection,” J. Acoust. Soc. Am. 102, 2906–2919. 10.1121/1.420345 [DOI] [PubMed] [Google Scholar]
- Dau, T., Kollmeier, D., and Kohlrausch, A. (1997a). “Modeling auditory processing of amplitude modulation: I. Detection and masking with narrowband carriers,” J. Acoust. Soc. Am. 102, 2892–2905. 10.1121/1.420344 [DOI] [PubMed] [Google Scholar]
- Dau, T., Püschel, D., and Kohlrausch, A. (1996a). “A quantitative model of the “effective” signal processing in the auditory system. I. Model structure,” J. Acoust. Soc. Am. 99, 3615–3622. 10.1121/1.414959 [DOI] [PubMed] [Google Scholar]
- Dau, T., Püschel, D., and Kohlrausch, A. (1996b). “A quantitative model of the “effective” signal processing in the auditory system. II. Simulations and measurements,” J. Acoust. Soc. Am. 99, 3623–3631. 10.1121/1.414960 [DOI] [PubMed] [Google Scholar]
- Davidson, S. A. (2007). “Detection of tones in reproducible noise: Psychophysical and computational studies of stimulus features and processing mechanisms,” Ph.D. thesis, Syracuse University, Syracuse, NY. [Google Scholar]
- Davidson, S. A., Gilkey, R. H., Colburn, H. S., and Carney, L. H. (2006). “Binaural detection with narrowband and wideband reproducible noise maskers. III. Monaural and diotic detection and model results,” J. Acoust. Soc. Am. 119, 2258–2275. 10.1121/1.2177583 [DOI] [PubMed] [Google Scholar]
- Davidson, S. A., Gilkey, R. H., Colburn, H. S., and Carney, L. H. 2009. “Diotic and dichotic detection with reproducible chimeric stimuli,” J. Acoust. Soc. Am. 10.1121/1.3203996 126, 1889–1905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edwards, A. L., 1979, Multiple Regression and the Analysis of Covariance (Freeman, New York: ). [Google Scholar]
- Evilsizer, M. E., Gilkey, R. H., Mason, C. R., Colburn, H. S., and Carney, L. H. (2002). “Binaural detection with narrowband and wideband reproducible noise maskers: I. Results for human,” J. Acoust. Soc. Am. 111, 336–345. 10.1121/1.1423929 [DOI] [PubMed] [Google Scholar]
- Fletcher, H. (1940). “Auditory patterns,” Rev. Mod. Phys. 12, 47–65. 10.1103/RevModPhys.12.47 [DOI] [Google Scholar]
- Gilkey, R. H., and Robinson, D. E. (1986). “Models of auditory masking: A molecular psychophysical approach,” J. Acoust. Soc. Am. 79, 1499–1510. 10.1121/1.393676 [DOI] [PubMed] [Google Scholar]
- Gilkey, R. H., Robinson, D. E., and Hanna, T. E. (1985). “Effects of masker waveform and signal-to-masker phase relation on diotic and dichotic masking by reproducible noise,” J. Acoust. Soc. Am. 78, 1207–1219. 10.1121/1.392889 [DOI] [PubMed] [Google Scholar]
- Glasberg, B. R., and Moore, B. J. C. (1990). “Derivation of auditory filter shapes from notched-noise data,” Hear. Res. 47, 103–138. 10.1016/0378-5955(90)90170-T [DOI] [PubMed] [Google Scholar]
- Goupell, M. J. (2005). “The use of interaural parameters during incoherence detection in reproducible noise,” Ph.D. thesis, Michigan State University, East Lansing, MI. [Google Scholar]
- Goupell, M. J., and Hartmann, W. H. (2007). “Binaural models for the detection of interaural coherence III. Narrowband experiments and binaural models,” J. Acoust. Soc. Am. 122, 1029–1045. 10.1121/1.2734489 [DOI] [PubMed] [Google Scholar]
- Grantham, D. W., and Wightman, F. L. (1979). “Detectability of time-varying interaural correlation in narrow-band noise stimuli,” J. Acoust. Soc. Am. 65, 1509–1517. 10.1121/1.382915 [DOI] [PubMed] [Google Scholar]
- Hafter, E. R. (1971). “Quantitative evaluation of a lateralization model of masking-level differences,” J. Acoust. Soc. Am. 50, 1116–1122. 10.1121/1.1912743 [DOI] [Google Scholar]
- Hancock, K., and Delgutte, B. (2004). “A physiologically based model of interaural time difference discrimination,” J. Neurosci. 24, 7110–7117. 10.1523/JNEUROSCI.0762-04.2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heinz, M. G., Zhang, X., Bruce, I. C., and Carney, L. H. (2001). “Auditory-nerve model for predicting performance limits of normal and impaired listeners,” ARLO 2, 91–96. 10.1121/1.1387155 [DOI] [Google Scholar]
- Isabelle, S. K. (1995). “Binaural detection performance using reproducible stimuli,” Ph.D. thesis, Boston University, Boston, MA. [Google Scholar]
- Isabelle, S. K., and Colburn, H. S. (1991). “Detection of tones in reproducible narrow-band Noise,” J. Acoust. Soc. Am. 89, 352–359. 10.1121/1.400470 [DOI] [PubMed] [Google Scholar]
- Isabelle, S. K., and Colburn, H. S. (2004). “Binaural detection of tones masked by reproducible noise: Experiment and models,” BU-HRC Report No. 04:01, Boston University, Boston, MA.
- Kolarik, A. J., and Culling, J. (2005). “Measuring the binaural temporal window,” J. Acoust. Soc. Am. 117, 2563. [Google Scholar]
- Kollmeier, B., and Gilkey, R. H. (1990). “Binaural forward and backward masking: Evidence for sluggishness in binaural detection,” J. Acoust. Soc. Am. 87, 1709–1719. 10.1121/1.399419 [DOI] [PubMed] [Google Scholar]
- Marquardt, T., and McAlpine, D. (2001). “Simulation of binaural unmasking using just four binaural channels,” Assoc. Res. Otolaryngol. Abstr. 24, 87. [Google Scholar]
- McAlpine, D., Jiang, D., and Palmer, A. R. (2001). “A neural code for low-frequency sound localization in mammals,” Nat. Neurosci. 4, 396–401. 10.1038/86049 [DOI] [PubMed] [Google Scholar]
- Pfafflin, S. M., and Mathews, M. V. (1966). “Detection of auditory signals in reproducible noise,” J. Acoust. Soc. Am. 39, 340–345. 10.1121/1.1909895 [DOI] [PubMed] [Google Scholar]
- Richards, V. M. (1992). “The detectability of a tone added to narrow bands of equal energy noise,” J. Acoust. Soc. Am. 91, 3424–3425. 10.1121/1.402831 [DOI] [PubMed] [Google Scholar]
- Siegel, R. A., and Colburn, H. S. (1989). “Binaural processing of noisy stimuli: Internal∕external noise ratios under diotic and dichotic stimulus conditions,” J. Acoust. Soc. Am. 86, 2122–2128. 10.1121/1.398472 [DOI] [PubMed] [Google Scholar]
- Webster, F. A. (1951). “The influence of interaural phase on masked thresholds, I. The role of interaural time-deviation,” J. Acoust. Soc. Am. 23, 452–462. 10.1121/1.1906787 [DOI] [Google Scholar]
- Zhang, X. (2004). “Cross-frequency coincidence detection in the processing of complex sounds,” Ph.D. thesis, Boston University, Boston, MA. [Google Scholar]
- Zilany, M. S. A., and Bruce, I. C. (2006). “Modeling auditory-nerve responses for high sound pressure levels in the normal and impaired auditory periphery,” J. Acoust. Soc. Am. 120, 1446–1466. 10.1121/1.2225512 [DOI] [PubMed] [Google Scholar]