Choosing an Optimal Method to Combine P-values

Abstract

Fisher [1925] was the first to suggest a method of combining the p-values obtained from several statistics and many other methods have been proposed since then. However, there is no agreement about what is the best method. Motivated by a situation that now often arises in genetic epidemiology, we consider the problem when it is possible to define a simple alternative hypothesis of interest for which the expected effect size of each test statistic is known and we determine the most powerful test for this simple alternative hypothesis. Based on the proposed method, we show that information about the effect sizes can be used to obtain the best weights for Liptak’s method of combining p-values. We present extensive simulation results comparing methods of combining p-values and illustrate for a real example in genetic epidemiology how information about effect sizes can be deduced.

1. INTRODUCTION

Since the first approach proposed by Fisher¹, several other approaches^2–5 have been suggested for combining p-values. Combining p-values is usually required in one of two situations: (1) when either the values of the actual statistics that need to be combined or the forms of their distributions are unknown, or (2) this information is available, but the distributions are such that there is no known or reasonably convenient method available for constructing a single overall test⁶. In addition, in practical situations, combining p-values gives the statistician flexibility to weight the individual statistics according to how informative they are and allows the designs of complex experiments to be determined independently of each other.

Combining p-values has usually been used for multi-stage analyses, in which inferences are pooled using the same statistic from different samples. However, another situation has recently arisen in genetic epidemiology, which we here call multi-phase analysis. Multi-phase analysis is the process of drawing similar inferences using different statistics calculated from the same sample^7–9. The null hypothesis, stated in genetic terms, is simply that a particular genomic region is not associated with the presence of disease. If this hypothesis is rejected, there is reason to seek a causal mechanism experimentally, for example using cell lines or an animal model. There are two different types of multi-phase analysis: the independent (or predictor) variables can be biologically either the same or different, and correspondingly the statistical tests will be quite different or of the same form. For example, in genetic epidemiology, association between a marker locus and a disease can be confirmed by differences between cases and controls either in marker allele frequencies or in parameters for Hardy-Weinberg disequilibrium^{7, 9}; in this case the same genetic marker can be the biological predictor, but the two statistics that test for association are different in form, each testing a different aspect of the distribution of marker genotypes (i.e. we have different statistics for the same biological predictor marker). Alternatively, several different genetic markers near a disease locus may be associated with the disease of interest and we perform tests of allele frequency difference between cases and controls for the alleles at each of the marker loci^{7, 10–14}; in this case each marker locus is a different biological predictor (i.e. we use the same type of statistic to test for association with each of the marker loci). The importance of both kinds of multi-phase analysis is related to power, because power can be improved by combining the p-values of the different tests. The methods for multi-phase analysis in genetic epidemiology, for example, have so far not considered the expected genetic effects, ^{7–9, 13, 14} even though the optimal method of combining p-values depends on the magnitude of the genetic effects to be expected, and theoretical investigations on detecting genetic association has shed light on the genetic effect size expected under alternative hypotheses ^{15, 16}. Thus multi-phase analysis should be performed using this information which, because it can be determined a priori, allows us to choose the most powerful method for combining the p-values that these tests produce.

fter Fisher introduced his χ²-based method, Pearson suggested an approach that has a similar, but different, rejection function. Let U_j be the p-value resulting from the j-th of P independent statistics. Whereas Fisher’s method rejects the null hypothesis if and only if U₁·U₂· ⋯ U_P ≤ c, Pearson’s method rejects it if and only if (1 – U₁)·(1 – U₂)⋯(1 – U_P) ≥ c, where in each case c is a predetermined constant corresponding to the desired overall significance level. Wilkinson⁵ suggested a method in which the null hypothesis is rejected if and only if U _j ≤ c for r or more of the U_j, where r is a predetermined integer, 1 ≤ r ≤ P. The approaches of Fisher and Pearson were also generalized by using the inverse of a cumulative normal distribution, and extended by Liptak to allow each test to have different weights w_j, where ${\displaystyle {\sum }_{j=1}^P{w}_j^2}=1$, using the combined statistic ${\displaystyle {\sum }_{j=1}^P{w}_j{\mathrm{\Phi }}^{-1}(U_j)}$. This, if Φ is the cumulative standard normal distribution, follows the standard normal distribution under the null hypothesis^{3, 17}. Either the inverse of the standard error or the square root of the sample size has been suggested for the weight w_j, but we shall see that neither of these may be appropriate. Goods¹⁸ suggested another function for weighting p-values, $U_1^{w_1}{U}_2^{w_2}\dots U_P^{w_P},\text{where}{({\chi }_{k_j}^2)}^{-1}$ (1 – U_j) is the (1 – U_j)-th quantile of the chi-square distribution with k_j degrees of freedom (DF). Lancaster¹⁹ suggested ${\displaystyle {\sum }_{j=1}^P{({\chi }_{k_j}^2)}^{-1}}(1-U_j)$ for when the k-th test has k_j DF. Koziol²⁰ showed the asymptotic equivalence of Lancaster’s and Liptak’s tests when $w_j=\sqrt{2k_j}$. Furthermore, there have been extensions to allow for the statistics to be correlated ^{13, 21–23}. However, so far little work has been done to find the most powerful (MP) way of combining p-values and this is now becoming of increasing interest.

For a method of combining p-values to be optimal, the method needs to be uniformly MP (UMP). However, it has been shown that a UMP test does not exist because the MP test is different according to the situation⁶. In view of this, admissibility – which is satisfied by many of the methods and is always preserved in the UMP method – can be considered as a minimum requirement for the method to be valid. For a method of combining p-values to be admissible, if the null hypothesis is rejected for any given set of p-values u_j, then it must also be rejected for all sets of ν_j such that ν_j ≤ u_j⁶. Also, even though Fisher’s method was shown to be approximately most efficient in terms of Bahadur relative efficiency²⁴, Naik²⁵ and Zaykin et al.^{13, 14} found that Wilkinson’s⁵ method can be better than Fisher’s. Here we shall show that an admissible MP test can be found for a particular situation that occurs in practice, even though there is no UMP test.

In many practical situations, the parameter spaces for both the null (H₀) and alternative (H₁) hypotheses can be considered simple, because the effect size is naturally assumed to be zero under the null hypothesis and there is an expected effect, or at least a minimum magnitude of effect that we would wish to detect, under the alternative hypothesis. In this situation, when the alternative hypothesis is simple, it can be shown that there is a MP test. Here we derive the MP test for a simple alternative hypothesis when we can specify this expected effect size for each alternative, and also an approximation to this test if only their ratios are available. We compare the method we derive for this situation with the previously suggested methods and show that it has optimal power as long as the prerequisites are satisfied. In section 2 we show theoretically that the most powerful method for combining p-values can be approximately achieved with information about the effect sizes; and that the parameters that are needed for existing methods of combining p-values, such as the weights in Liptak’s method, should be chosen using the expected effect sizes. In section 3 we give detailed simulation results comparing the various methods in different situations, and illustrate how the information about effect sizes can be deduced for a particular type of genetic association analysis. Finally, in Section 4, we discuss extensions, including the case of correlated tests, and suggest a general strategy for combining p-values.

2. MOST POWERFUL REJECTION REGION

Suppose we want to combine the p-values from P tests. Let $H_0^1:{\theta }_{1\in }{\mathrm{\Omega }}_1^N\text{VS}{H}_1^1:{\theta }_{1\in }{\mathrm{\Omega }}_1^A,H_0^2:{\theta }_{2\in }{\mathrm{\Omega }}_2^N\text{VS}{H}_1^2:{\theta }_{2\in }{\mathrm{\Omega }}_2^A,\dots ,\text{and}{H}_0^P:{\theta }_{P\in }{\mathrm{\Omega }}_P^N\text{VS}{H}_1^P:{\theta }_{P\in }{\mathrm{\Omega }}_P^A$ be the null and alternative hypotheses for each test, respectively. The null and alternative hypotheses for combining the p-values are

$$H_0:{\theta }_1\in {\mathrm{\Omega }}_1^N,{\theta }_2\in {\mathrm{\Omega }}_2^N,\dots ,\text{and}{\theta }_P\in {\mathrm{\Omega }}_P^{N}vs{H}_1:\text{not}{H}_0.$$

If we restrict the parameter space for the alternative hypothesis to the simple case, then the alternative is

$$H_1:{\theta }_1={\theta }_1^A,{\theta }_2={\theta }_2^A,\dots ,\text{and}{\theta }_P={\theta }_P^A,$$

where it should be noted that some of the ${\theta }_j^A$ can be in ${\mathrm{\Omega }}_j^A$ because the alternative hypothesis is that at least one of the $H_0^j$ is rejected. As usual, the rejection region for any test, ϕ, for combining p-values should be admissible, i.e. if H₀ is rejected for any given set of U_j = u_j, then it will also be rejected for all sets of ν_j such that ν_j ≤ u_j for each j⁶ However, ϕ is different from the usual hypothesis testing paradigm for a single parameter because, if we let the p-values from each test be U₁, U₂, … and U_P and they are independent, the density function of U₁, U₂, … and U_P under H₀ must be 1. Then the Neyman-Pearson lemma results in the following, if we let ϕ = 1 when H₀ is rejected and ϕ = 0 otherwise, and let f_A(U₁, … , U_P), T_j and A_j(U_j) be respectively the density function of U₁, U₂, … and U_P under H₁ , the statistics for U_j, and a region that results in the p-value U_j for T_j:

Given α, where 0 ≤ α ≤ 1, there exists k such that

$$\varphi (U_1,\dots ,U_P)=\{\begin{array}{c}1\text{if}1\le k{f}_A(U_1,\dots ,U_P)\hfill \\ 0\text{if}1>k{f}_A(U_1,\dots ,U_P)\hfill \end{array}\text{\hspace{1em}and}{E}_{H_0}\left(\varphi (U_1,\dots ,U_P)\right)=\alpha ,$$

where independence of the statistics implies that $f_A(U_1,\dots ,U_P)={\displaystyle {\prod }_{j=1}^P{f}_{A,j}(U_j)}$ and f_A,j(U_j) is $\frac{\partial }{\partial U_j}\mathrm{P}(T_j\in A_j(U_j);{\theta }_j={\theta }_j^A)$. It should be noted that f_A,j(U_j) is 1 if ${\theta }_j^A\in {\mathrm{\Omega }}_P^N$. Admissibility requires that f_A,j(U_j) be a monotonic decreasing function of U_j for all j, by the following lemma:

If we let $A_{\alpha }^{\varphi }$ be the rejection region of ϕ at the significance level α, $A_{\alpha }^{\varphi }$ is admissible if all the f_A,j(U_j) are positive monotonic decreasing functions of U_j. The proof of this lemma is trivial. As a result, by the Neyman-Pearson lemma, as long as f_A,j(U_j) is a monotonic decreasing function of U_j we can find an optimal test.

In general, we can define the functions P(T_j ∈ A_j(U_j); θ_j) and f_A,j(U_j) as functions of the quantiles of the distribution of p-values. For example, if T_j is a statistic for a two-tail test that estimates a difference in means, se_j is its standard error, and the sample size is large enough, then, for some positive real constant c and denoting the cumulative standard normal distribution Φ,

$$\begin{array}{c}{P}_A(T_j\in A_j(U_j);{\theta }_j)=\mathrm{\Phi }\left(S_j-Z_{1-U_j/2}\right)+\mathrm{\Phi }\left(-S_j-Z_{1-U_j/2}\right)\hfill \\ f_{A,j}(U_j)=\frac{\partial }{\partial U_j}{P}_A(T_j\in A_j(U_j);{\theta }_j)=c\left[\text{exp}\left(Z_{1-U_j/2}{S}_j\right)+\text{exp}\left(-Z_{1-U_j/2}{S}_j\right)\right],\hfill \end{array}$$

where S_j is the standardized expected difference in means (i.e. the expected difference in means under H₁, divided by se_j - or sê_j if se_j is unknown), and Z_U is the U- th quantile of the standard normal distribution. For a one-tail test, f_A,j(U_j)=c′exp(t_jZ_1-UjS_j), where t_j is 1 for testing positive effects and −1 for testing negative effects. Thus, the test ϕ for two-tail tests becomes, by the Neyman-Pearson lemma,

$$\varphi (U_1,\dots ,U_P)=\{\begin{array}{c}1\text{if}1\le c\text{'}{\displaystyle \prod _{j=1}^P\left[\text{exp}\left(Z_{1-U_j/2}{S}_j\right)+\text{exp}\left(-Z_{1-U_j/2}{S}_j\right)\right]}\hfill \\ 0\text{if}1>c\text{'}{\displaystyle \prod _{j=1}^P\left[\text{exp}\left(Z_{1-U_j/2}{S}_j\right)+\text{exp}\left(-Z_{1-U_j/2}{S}_j\right)\right]}.\hfill \end{array}$$

If the T_j include both one-tail and two-tail tests, ϕ is a product of both types of f_A,j(U_j). These results can be applied in a practical situation using the following Monte-Carlo algorithm, provided we have information about the expected effect sizes.

algorithm 1:

1. Generate z ₁, … , and z _p from a standardized normal distribution.

2. Confirm whether g_A(z₁, … , z_p) is larger than g_A(Z_1-U1/2, … , Z_1-Up/2)(g_A(Z_1-U1, … , Z_1-Up) if the T_j are one-side tests) and, if it is larger, add 1 to C.

After N iterations, the p-value C/N, where g_A(z₁, … , z_P) = Π_j g_A,j(z_j), g_A,j(z_j) = exp(z_j·S_j) + exp(−z_j·S_j) for a two-tail test and g_A,j(z_j) = exp(z_j·S_j) (g_A,j(z_j) = exp(−z_j·S_j)) for a one-tail test of positive (negative) effect. This approach can be shown to be the same as Liptak’s method when p-values from one-tail tests are combined if S_j is used for w_j, because

$$\begin{array}{c}{g}_A(z_1,z_2,\dots ,z_P)\le g_A(Z_{1-U_1},Z_{1-U_2},\dots ,Z_{1-U_P})\hfill \\ \iff {\displaystyle \prod _{j=1}^P\text{exp}(t_j{z}_j{S}_j)}\le g_A(Z_{1-U_1},Z_{1-U_2},\dots ,Z_{1-U_P})\hfill \\ \iff {\displaystyle \sum _{j=1}^P{t}_j{z}_j{w}_j}\le c"\iff {\displaystyle \sum _{j=1}^P{w}_j{z\prime }_j}\le c",\hfill \end{array}$$

where $w_j=S_j/\sqrt{{\displaystyle {\sum }_j^P{S}_j^2}}$, t_j is 1 for testing a positive effect and −1 for testing a negative effect, and z′ ~ N(0,1). In addition, if only ratios of the expected differences are available, we have the following approximation:

$$\begin{array}{c}{g}_A(z_1,z_2,\dots ,z_P)\le g_A(Z_{1-U_1/2},Z_{1-U_2/2},\dots ,Z_{1-U_P/2})\hfill \\ \iff {\displaystyle \prod _{j=1}^P\left[\text{exp}(|z_j{S}_j|)+\text{exp}(-|z_j{S}_j|)\right]}\le {\displaystyle \prod _{j=1}^P\left[\text{exp}(|Z_{1-U_j/2}{S}_j|)+\text{exp}(-|Z_{1-U_j/2}{S}_j|)\right]}\hfill \\ \Rightarrow {\displaystyle \prod _{j=1}^P\left[\text{exp}(|z_j{S}_j|)\right]}\le c"\iff {\displaystyle \sum _{j=1}^P|z_j{w}_j|}\le c"\text{'}.\hfill \end{array}$$

This can also be implemented using a Monte-Carlo algorithm, as follows.

algorithm 2:

1. Generate z ₁, … , and z _p from a standardized normal distribution.

2. Confirm whether ${\displaystyle \sum _{j=1}^P|w_j{z}_j|}\text{is larger than}{\displaystyle \sum _{j=1}^P|w_j{Z}_{1-U_j/2}|}$ and, if it is larger, add 1 to C.

After N iterations, the p-value C/N, Thus, the rejection region that results in the predefined significance level is similar to that of Liptak’s method if Liptak’s method uses as weight the standardized effect size instead of the square root of the sample size or the inverse of the standard error.

Also, with a slight modification, the method can be applied to statistics with other distributions, such as chi-square or F distributions. For example, if T_j follows a chi-square distribution with k_j DF, then

$$\begin{array}{c}{f}_{A,j}(u_j)={\left({\chi }_{1-U_j}^2(k_j)\right)}^{-k_j/4+1/2}{I}_{k_j/2-1}\left(\sqrt{{\left({\chi }_{k_j}^2\right)}^{-1}(1-U_j)S_j}\right),\hfill \\ I_a(x)={\left(\frac{x}{2}\right)}^a{\displaystyle \sum _{i=0}^{\infty }\frac{{(x^2/4)}^i}{i!\mathrm{\Gamma }(a+i+1)}},\hfill \end{array}$$

where S_j is the non-centrality parameter for T_j, and I_a(·) and Γ(·) are respectively a modified Bessel function of the first kind and a gamma function.

However, the Monte-Carlo algorithm usually requires intensive computation, which can be alleviated as follows when all the statistics are normally distributed. The combined p-value for the p-values (U₁, …, U_P) is the hyper-volume of the region where g_A(z₁,…z_p) is larger than g_A(Z_1-U1/2,…,Z_1-Up/2) and, for any z₂,…,z_P that are between 0 and 1, if ν₁ satisfies the following inequality, then g_A(z₁,…z_p) > g_A(Z_1-U1/2,…,Z_1-Up/2):

$$\begin{array}{cc}{z}_1\le \frac{1}{S_1}\text{log}\frac{1}{2}\left[k-\sqrt{k^2-4}\right]\text{or}{z}_1\ge \frac{1}{S_1}\text{log}\frac{1}{2}\left[k+\sqrt{k^2-4}\right]\hfill & \text{for algorithm}1,\hfill \\ |z_1|\le \frac{1}{w_1}\left[|w_1{Z}_{1-U_1}|+|w_2{Z}_{2-U_2}|-|w_2{z}_2|\right]\hfill & \text{for algorithm}2,\hfill \end{array}$$

where $k={\displaystyle {\prod }_{j=1}^P{g}_{A,j}(Z_{1-U_j/2})/}{\displaystyle {\prod }_{j=2}^P{g}_{A,j}(z_j)}$. Thus, the calculation only involves being able to calculate the cumulative normal distribution and numerical integration over the above region.

3. COMPARISON WITH PREVIOUS METHODS

3.1. Rejection regions

Several approaches to combine p-values from independent tests have been suggested but their power has not been compared. Because algorithm 1 always results in the most powerful rejection region, we compare it with the following previously suggested approaches for P = 2 only:

1. Minimum p-value method: reject H ₀ if and only if min (U ₁,U ₂)<c

2. Cutoff-based method: reject H ₀ if and only if U ₁ < c ₁ and U ₂ < c ₂

3. Pearson's method : reject H ₀ if and only if (1–U ₁)(1–U ₂)≥c

4. Fisher's Method : reject H ₀ if and only if U ₁ U ₂≤c

5. Liptak's method : reject H ₀ if and only if $Z^w=(w_1{Z}_{1-U_1}+w_2{Z}_{1-U_2})/\sqrt{w_1^2+w_2^2}\ge c$ where Z^w~N(0,1).

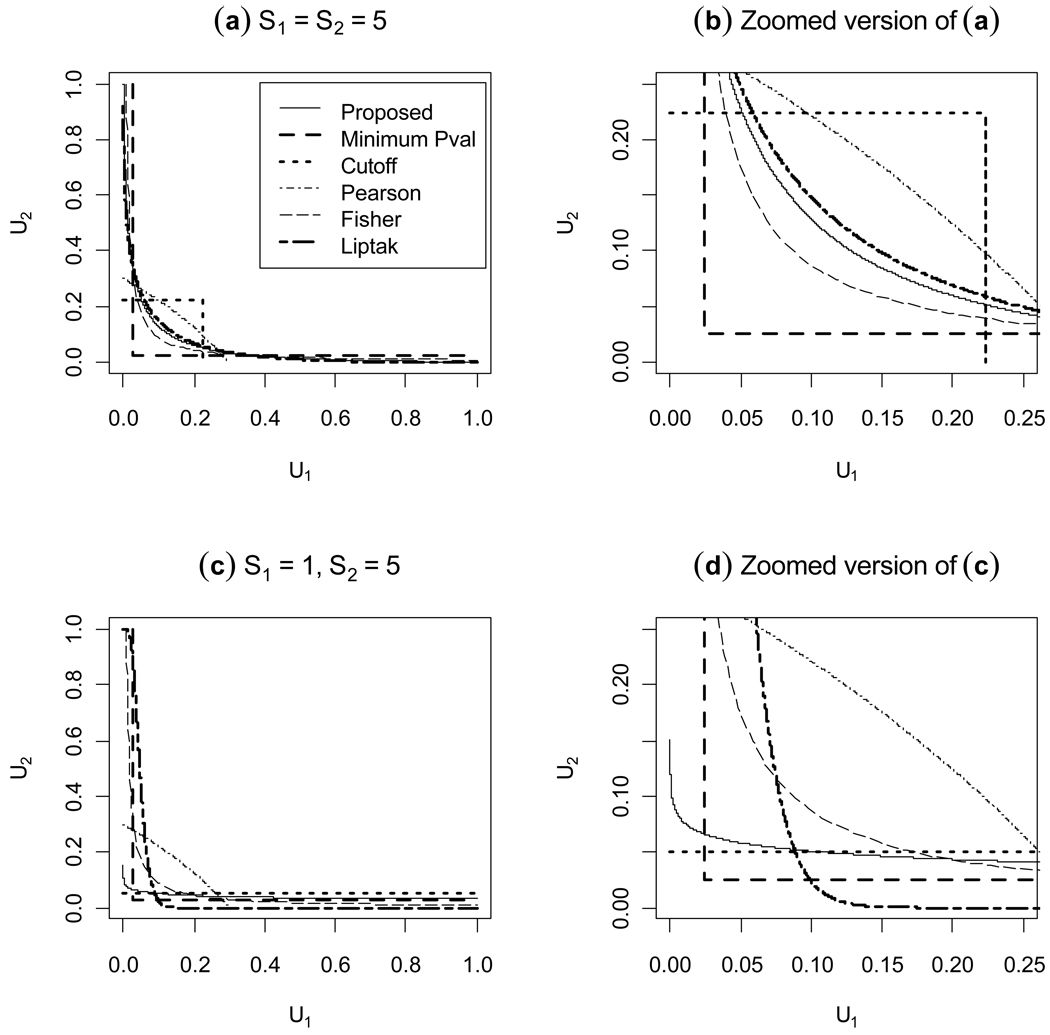
In each case c is determined by the desired value of α. Figure 1 shows results for two different cases: S₁ = S₂ = 5 for (a) and (b), and S₁ = 1, S₂= 5 for (c) and (d). First, when S₁ and S₂ are equal, the MP region is expected to be symmetric and this is seen to be the case for the rejection region of our proposed method. Also, the MP region is fairly similar to the region given by Liptak’s method using S₁ and S₂ as weights in this case, and Liptak’s approach is second best. Investigation shows that which method is second best depends on the size of S₁ and S₂; if it is less than about 3, Fisher’s method is better than Liptak’s method, but otherwise Liptak’s is better. Second, when S₁ and S₂ are unequal, the MP region is expected to be asymmetric and our results confirm this. For Liptak’s method, we used the weights $1/\sqrt{26}\text{and}5/\sqrt{26}$ because the ratio between S₁ and S₂ is 1:5. The plot (c) and (d) in Figure 1 shows that the cutoff-based approach with c₁=1 and c₂=0.05 is the closest to the MP region, though Liptak’s rejection region is very close to the MP region. Here the results indicate that using a more powerful statistic alone, T₂ in this case, is better than combining the two together using Liptak’s method.

Figure 1. Rejection regions for five methods of combining two P-values at the 0.05 significance level.

Two different cases are considered: the standardized effect sizes under H₁ are equal (a) and unequal (c). Because the proposed method is the most powerful, we can compare the methods that have been suggested by comparing the closeness of their rejection regions to that of our proposed method.

3.2. Simulation when the standardized expected difference is known

We applied our approach to the mean difference test of two samples when the standardized expected difference is known. For two different test statistics, we generated X_i1, X_i2, Y_k1 and Y_k2 (i = 1, 2, … , N₁ and k = 1, … , N₂) as follows:

$$\begin{array}{c}{X}_{i1}={\epsilon }_{i1},X_{i2}={\mu }_X+{\epsilon }_{i2},\hfill \\ Y_{k1}={\epsilon }_{k1}\text{'},Y_{k2}={\mu }_Y+{\epsilon }_{k2}\text{'},\hfill \end{array}$$

where μ_X and μ_Y are either 0.1 or 0.02, ε_il and ε_il′ (l = 1, 2) independently follow normal distribution with mean 0 and variance 0.5. The t-statistic approximately follows a normal distribution if the sample size is large enough. Thus, we obtain the following function for our suggested approach:

$$g_A(z_1,z_2)={\displaystyle \prod _{j=1}^2\left[\text{exp}\left(z_j{S}_j\right)+\text{exp}\left(-z_j{S}_j\right)\right]}$$

where $S_1={\mu }_X\sqrt{N_1}\text{and}{S}_2={\mu }_Y\sqrt{N_2}$.

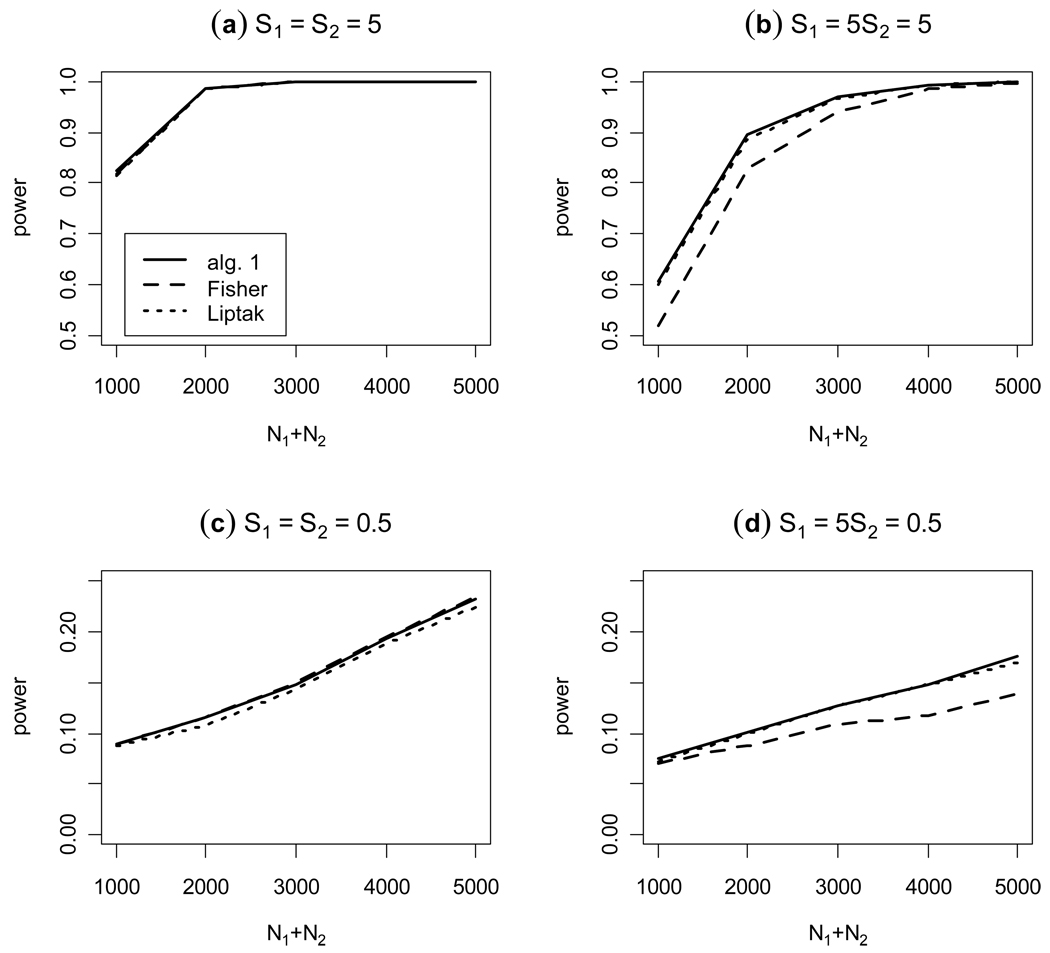
Figure 2 shows the power results of a simulation with various sample sizes for four different cases and they are calculated from 5000 replicate samples: (a) μ_X = μ_Y = 0.1 and N₁ = N₂, (b) μ_X = μ_Y = 0.1 and N₁ = 5N₂, (c) μ_X = μ_Y = 0.02 and N₁ = N₂ and (d) μ_X = μ_Y = 0.02 and N₁ = 5N₂. In each case we compare our proposed method with Fisher’s and Liptak’s methods. First, even though the three approaches have similar power when S₁ = S₂, the proposed method has the best empirical power, followed by Liptak’s method and then by Fisher’s for case (a), but followed by Fisher’s method and then by Liptak’s for case (c). As we mentioned before, Liptak’s method is better than Fisher’s if the standardized expected effect size is larger than about 3, and otherwise Fisher’s is better; the range of S_j considered for the simulation is from 2.2 to 5 for case (a) and from 0.4 to 1 for case (c). Second, if S₁ and S₂ are different (we considered the ratio 5:1), Fisher’s is the worst method and Liptak’s method using S₁ and S₂ as weights is approximately equal to our proposed method.

Figure 2. Empirical power as a function of the sum of the sample sizes for two p-values.

The empirical power at the 0.01 significance level is calculated, in each case for total sample sizes 1000, 2000, 3000, 4000, and 5000, obtained from a simulation of 5000 replicate samples, as a function of the sum of the sample sizes; for algorithm 1, 100,000 Monte Carlo replicates were used. Two different cases are considered: the standardized effect sizes under H₁ are equal, (a) and (c), and unequal (b) and (d).

3.3. Simulation for a multi-stage analysis with estimated standard error

As mentioned above, methods for combining p-values can be used for both multi-stage analysis and multi-phase analysis. We applied our approach to testing the mean difference between two samples for multi-stage analysis, i.e. pooling the results of using the same statistic from different samples, when the standard deviation is unknown. In general, because multi-stage analyses (including meta-analysis) are usually for the same hypothesis, we can assume the same expected difference under the alternative hypothesis but the sample sizes or variances could be different. We therefore applied our approach to test a mean difference from simulated samples with different sample sizes and with different variances, using numerical integration for the proposed method of combing the p-values. For two different test statistics, we generated X_i1, X_i2, Y_k1 and Y_k2 (i = 1, 2, … , N₁ and k = 1, … , N₂) as follows:

$$\begin{array}{c}{X}_{i1}={\epsilon }_{i1},X_{i2}=\mu +{\epsilon }_{i2},{\epsilon }_{il}~N(0,{\sigma }_1^2)\hfill \\ Y_{k1}={\epsilon }_{k1}\text{'},Y_{k2}=\mu +{\epsilon }_{k2}\text{'},{\epsilon }_{kl}~N(0,{\sigma }_2^2),\hfill \end{array}$$

where ε_il and ε_il′ (l = 1, 2) are independent. Because the t-statistic approximately follows a normal distribution if the sample size is large enough, we obtain the following functions:

$$\begin{array}{cc}{g}_A(z_1,z_2)={\displaystyle \prod _{j=1}^2\left[\text{exp}\left(z_j{S}_j\right)+\text{exp}\left(-z_j{S}_j\right)\right]}\hfill & \text{for algorithm}1\hfill \\ g_A(z_1,z_2)=\raisebox{1ex}{${\displaystyle \prod _{j=1}^2\left|z_j{w}_j\right|}$}\!\left/ \!\raisebox{-1ex}{$\sqrt{w_1^2+w_2^2}$}\right.\hfill & \text{for algorithm}2,\hfill \end{array}$$

where S₁ = μ′ /sê₁, S₂ = μ′/sê₂, $w_j=s{\widehat{e}}_j^{-1}$ and μ′ is the expected difference under the alternative hypothesis. It should be noted that in this case w_j depends only on the standard error. We also applied Fisher’s method and Liptak’s method using as weights the inverse of the standard error (Liptak1) and the square root of the sample size (Liptak2).

Table 1 shows the empirical type I error from 10,000 replicate samples as a function of N₂ when we assume ${\mathrm{\sigma }}_1^2={\mathrm{\sigma }}_2^2=1$ and N₁ is 1000. μ and μ′ are assumed to be 0 and 0.05 respectively. The results show that all methods preserve type I error well at the significance level 0.05. Table 2 and Table 3 show the empirical power based on 5,000 replicate samples when equal variances but different sample sizes are assumed, and when equal sample sizes but different variances are assumed. In both cases, μ and μ′ are equal to 0.05. For Table 2, we assume that ${\mathrm{\sigma }}_1^2={\mathrm{\sigma }}_2^2=1$ and N₂ = 600, 700, 800, …, 1900 and 2000 while N₁ is fixed at 1000, and for Table 3, N₁=N₂=1000 and ${\mathrm{\sigma }}_2^2=1,2,\dots ,10\text{while}{\mathrm{\sigma }}_1^2$ is 1. In Table 2, algorithm 1 shows the best result, followed by algorithm 2. Fisher’s method is better than the Liptak methods when N₂ is similar to N₁ but otherwise the Liptak methods are better. Liptak 1 and Litpak 2 have similar empirical power because the weights for both are similar. In Table 3, we find similar results except that Liptak 1 is much better than Liptak 2 because the weights for Liptak 2 are not close to the standardized expected differences. Thus, we conclude that algorithm 1 is always the most powerful when we have information about the expected differences, but no information about the variances, and the same power can be approximately achieved with only their ratios using algorithm 2.

Table 1. Empirical type I error for multi-stage analysis.

The empirical type I error at the significance level 0.05 is calculated from 10,000 replicate samples, in each case for N₂=600, 200, 300, … , 1900 and 2000. For algorithm 1, μ′ is assumed to be 0.05 for S_j, and for simulating X_il and Y_kl μ is assumed to be 0. Liptak’s method uses as weights the inverse of the standard error (Liptak1) and the square root of the sample size (Liptak2); for algorithms 1 and 2, numerical integration was used.

N2	Fisher	Liptak1	Liptak2	alg. 1	alg. 2
600	0.052	0.0524	0.0524	0.0526	0.0532
700	0.0531	0.0479	0.0502	0.0513	0.0518
800	0.0471	0.0507	0.0479	0.0472	0.0471
900	0.0512	0.0501	0.0502	0.0499	0.05
1000	0.0505	0.052	0.0522	0.0499	0.0498
1100	0.0528	0.0503	0.0522	0.0532	0.0526
1200	0.0508	0.0521	0.0502	0.0505	0.0499
1300	0.053	0.049	0.0518	0.0534	0.0529
1400	0.0507	0.0499	0.049	0.0498	0.0503
1500	0.0505	0.0521	0.0503	0.051	0.0497
1600	0.0542	0.05	0.052	0.0523	0.0519
1700	0.496	0.0501	0.0501	0.0514	0.0504
1800	0.473	0.05	0.0499	0.497	0.0489
1900	0.497	0.0485	0.0482	0.474	0.478
2000	0.502	0.0505	0.0508	0.0488	0.495

Table 2. Empirical power for multi-stage analysis for different sample sizes.

The empirical power at the significance level 0.05 is calculated from 5,000 replicate samples, for N₂=600, 200, 300, … , 1900 and 2000. For algorithm 1, both μ and μ′ are assumed to be 0.05 for simulating X_il and Y_kl, and S_j in algorithm 1; for algorithms 1 and 2, numerical integration was used. Liptak’s method uses as weights the inverse of the standard error (Liptak1) and the square root of the sample size (Liptak2).

N2	Fisher	Liptak1	Liptak2	alg. 1	alg. 2
600	0.2338	0.2332	0.2316	0.2376	0.234
700	0.2392	0.235	0.2356	0.2412	0.2402
800	0.2454	0.2414	0.2418	0.2488	0.2464
900	0.2574	0.2474	0.2468	0.2574	0.2522
1000	0.2834	0.2792	0.2796	0.283	0.2822
1100	0.291	0.2872	0.287	0.2946	0.29
1200	0.3042	0.302	0.303	0.3078	0.3074
1300	0.3158	0.3146	0.3158	0.3234	0.3214
1400	0.3266	0.326	0.3262	0.329	0.328
1500	0.3362	0.3354	0.3354	0.343	0.3428
1600	0.3356	0.3334	0.3328	0.3468	0.3434
1700	0.3598	0.3592	0.3592	0.3662	0.3652
1800	0.3694	0.3688	0.3688	0.3824	0.3804
1900	0.3842	0.3876	0.3862	0.3954	0.3976
2000	0.3998	0.4074	0.4064	0.4144	0.415

Table 3. Empirical power for multi-stage analysis with different variances.

The empirical power at the significance level 0.05 is calculated from 5,000 replicate samples, for ${\sigma }_2^2=1,2,3,\dots ,9$ and 10. For algorithm 1, both μ and μ′ are assumed to be 0.05 for simulating X_il and Y_kl, and S_j in algorithm 1; for algorithms 1 and 2, numerical integration was used. Liptak’s method uses as weights the inverse of the standard error (Liptak1) and the square root of the sample size (Liptak2).

${\sigma }_2^2$	Fisher	Liptak1	Liptak2	alg. 1	alg. 2
1	0.2846	0.2716	0.2726	0.283	0.2798
2	0.1966	0.195	0.186	0.2088	0.2016
3	0.1848	0.1974	0.1824	0.2046	0.2018
4	0.1778	0.1876	0.1644	0.2006	0.1924
5	0.1818	0.2016	0.1676	0.2126	0.2066
6	0.174	0.2004	0.1604	0.2058	0.2054
7	0.1628	0.19	0.1486	0.1988	0.1926
8	0.1702	0.189	0.152	0.1932	0.192
9	0.1716	0.201	0.1584	0.2092	0.2068
10	0.1738	0.2062	0.154	0.2134	0.2096

3.4. Simulation for multi-phase analysis with estimated standard error

We also applied our approach to the mean difference test of two samples for multi-phase analysis when the standard deviation is unknown. Here we assume that the expected differences are known either from previous studies or on the basis of theoretical results that allow us to know their ratios, as can occur in genetic epidemiology ^15,16 . Again for two different test statistics, we generated X_i1, X_i2, Y_k1 and Y_k2 (i = 1, 2, … , N₁ and k = 1, … , N₂) as follows:

$$\begin{array}{c}{X}_{i1}={\epsilon }_{i1},X_{i2}={\mu }_X+{\epsilon }_{i2},\hfill \\ Y_{k1}={\epsilon }_{k1}\text{'},Y_{k2}={\mu }_Y+{\epsilon }_{k2}\text{'},\hfill \end{array}$$

where ε_il and ε_il′ (l = 1, 2) independently follow normal distributions with mean 0 and variance 1. For large sample sizes, we obtain the following function for our proposed approach:

$$\begin{array}{cc}{g}_A(z_1,z_2)={\displaystyle \prod _{j=1}^2\left[\text{exp}\left(z_j{S}_j\right)+\text{exp}\left(-z_j{S}_j\right)\right]}\hfill & \text{for algorithm}1\hfill \\ g_A(z_1,z_2)=\raisebox{1ex}{${\displaystyle \prod _{j=1}^2\left|z_j{w}_j\right|}$}\!\left/ \!\raisebox{-1ex}{$\sqrt{w_1^2+w_2^2}$}\right.\hfill & \text{for algorithm}2,\hfill \end{array}$$

where S₁ = μ_X′/sê₁, S₂ = μ_Y′/sê₂, w_j = S_j, and μ_X′ and μ_Y′ are the expected differences under the alternative hypothesis. For Liptak’s method, we again used as weights these w_j (Liptak1) and the inverse of the standard error (Liptak2). For both algorithms, the combined p-values were calculated using numerical integration.

Table 4 shows the results of a simulation with 10,000 replicate samples when N₁=N₂=1,000 and ${\sigma }_1^2={\sigma }_2^2=1$. For empirical type I error, μ_X and μ_Y are assumed to be 0 for simulating X_il and Y_k, and the empirical type I errors calculated at the nominal 0.05 significance level. For S₁ and S₂, μ_X′ is assumed to be 0.05 and we consider 0.01, 0.02, … and 0.15 for μ_Y′. The results show that both algorithm 1 and algorithm 2 preserve the type I error well, as in multi-stage analysis. Table 5 shows the results of a simulation with 5,000 replicate samples at the 0.05 significance level when N₁=N₂=1,000 and ${\sigma }_1^2={\sigma }_2^2=1$. For empirical power, μ_X and μ_Y were assumed equal to μ_X′ and μ_Y′, respectively, μ_X was assumed to be 0.05 and we considered 0.01, 0.02, …, 0.15 for μ_Y. The results show that algorithm 1 generally has the best power, followed by algorithm 2. Also, the proposed algorithms are always better than the Liptak methods and Fisher’s method, though the difference is not large. Finally, Liptak’s method is better than Fisher’s method if the S_j are used as weights and μ_X and μ_Y are not similar, which confirms first that Fisher’s method is usually good when the standardized expected differences are similar and small, and second that Liptak’s method should use the standardized expected differences as weights, as in algorithm 2.

Table 4. Empirical type I error for multi-phase analysis.

The empirical type I error at the significance level 0.05 is calculated from 10,000 replicate samples for multi-phase analysis, for μ_Y′ = 0.01, 0.02, 0.03, … , 0.14 and 0.15. Both μ_X and μ_Y are assumed to be 0 for simulating X_il and Y_kl, and μ_X′ is equal to 0.05 for algorithm 1. Liptak’s method uses as weights the standardized expected difference with the standard error estimated (Liptak1) and the inverse of the standard error (Liptak2); for algorithms 1 and 2, numerical integration was used.

μY′	Fisher	Liptak1	Liptak2	alg. 1	alg. 2
0.01	0.0512	0.0515	0.052	0.0514	0.0531
0.02	0.0489	0.0497	0.0481	0.0496	0.0508
0.03	0.0505	0.0501	0.0512	0.0498	0.0496
0.04	0.0541	0.0545	0.0551	0.0555	0.0539
0.05	0.0495	0.0485	0.0483	0.0483	0.0479
0.06	0.0483	0.0477	0.0481	0.0476	0.0483
0.07	0.047	0.0461	0.046	0.0469	0.0466
0.08	0.0483	0.0494	0.0502	0.0495	0.0501
0.09	0.0504	0.0473	0.0503	0.0483	0.048
0.10	0.0477	0.048	0.0492	0.0481	0.0476
0.11	0.0498	0.0516	0.0512	0.0513	0.0524
0.12	0.0482	0.0471	0.0466	0.049	0.0467
0.13	0.0467	0.0462	0.0486	0.0481	0.0476
0.14	0.0543	0.0522	0.0534	0.0518	0.0519
0.15	0.0524	0.0523	0.0508	0.0516	0.0521

Table 5. Empirical power for multi-phase analysis.

The empirical power at the significance level 0.05 is calculated from 5,000 replicate samples for μ_Y′=0.01, 0.02, 0.03, … , 0.14 and 0.15. Both μ_X and μ_X′ are assumed to be 0.05 and μ_Y′ is equal to μ_Y for algorithm 1; for algorithme 1 and 2, numerical integration was used. Liptak’s method uses as weights the standardized expected differences with the standard error estimated (Liptak1) and the inverse of the standard error (Liptak2).

μY′	Fisher	Liptak1	Liptak2	alg. 1	alg. 2
0.01	0.157	0.201	0.141	0.202	0.203
0.02	0.166	0.187	0.158	0.198	0.189
0.03	0.203	0.207	0.200	0.211	0.209
0.04	0.233	0.230	0.227	0.242	0.236
0.05	0.275	0.264	0.266	0.273	0.270
0.06	0.331	0.328	0.322	0.340	0.334
0.07	0.384	0.386	0.372	0.395	0.390
0.08	0.469	0.475	0.444	0.493	0.489
0.09	0.535	0.559	0.506	0.575	0.570
0.10	0.602	0.637	0.565	0.648	0.646
0.11	0.671	0.703	0.612	0.719	0.717
0.12	0.736	0.772	0.673	0.786	0.781
0.13	0.796	0.838	0.717	0.847	0.846
0.14	0.841	0.876	0.768	0.882	0.881
0.15	0.893	0.920	0.817	0.923	0.951

3.5 A genetic multi-phase example

The simulation results in sections 3.3 and 3.4 demonstrate the increase in power possible, but do not illustrate exactly how the effect sizes could be obtained in practice, nor do they examine the sensitivity of the method to assumptions made about those effect sizes. We illustrate this here for one particular genetic example of multi-phase analysis.

In genetic epidemiology, the Cochran-Armitage (CA) trend is usually used for association analysis in a case-control design assuming the two alleles of a diallelic marker act in an additive manner on disease susceptibility²⁶. The test for Hardy Weinberg proportions (HWP) in cases has been combined with the CA test in an attempt to improve the statistical power for association analysis by using either Fisher’s method⁷ or a cutoff-based method⁹, which was called self-replication. However, combining these two tests sometimes leads to a reduction in power¹¹. We now show that if we use the expected effect size information the power is improved with either algorithm 2 or Liptak’s method, and explain why, without using this information, combining these two tests sometimes fails to increase power.

For a disease locus D with disease allele D₁ and normal allele D₂, let P_Dk|case and P_Dk|cont be the frequencies of allele D_k in the case group and control group, respectively, and let P_DkDk'|case and P_DkDk'|cont be the analogous frequencies of the genotype D_kD_k'. As a measure of Hardy Weinberg disequilibrium (HWD) in cases, let d_A|case ≡ P_A1A1|case – (P_A1|case)². If we let ϕ and ϕ_l be the disease prevalence and the penetrance of disease genotype l at the disease location, the expected sizes of these quantities are^{16, 27}:

$$\begin{array}{c}{p}_{A_1|\text{case}}-p_{A_1|\text{cont}}=p_{D_1}{p}_{D_2}\left[\frac{1}{\varphi }-\frac{1}{1-\varphi }\right]\left[p_{D_1}({\varphi }_{D_1{D}_1}-{\varphi }_{D_1{D}_2})+p_{D_2}({\varphi }_{D_1{D}_2}-{\varphi }_{D_2{D}_2})\right]\text{and}\hfill \\ d_{A|\text{case}}=p_{A_1{A}_1|\text{case}}-p_{A_1|\text{case}}^2=\frac{({\varphi }_{D_1{D}_1}{\varphi }_{D_2{D}_2}-{\varphi }_{D_1{D}_2}^2)p_{D_1}^2{p}_{D_2}^2}{{\varphi }^2}.\hfill \end{array}$$

If the disease genotype effect is small, we can assume that ϕ_D2D2/ϕ ≈ 1 and then, for a rare disease with known mode of inheritance we have

$$\begin{array}{c}{p}_{D_1|\text{case}}-p_{D_1|\text{cont}}=p_{D_1}{p}_{D_2}\left[\frac{1}{\varphi }-\frac{1}{1-\varphi }\right]\left[p_{D_1}({\varphi }_{D_1{D}_1}-{\varphi }_{D_1{D}_2})+p_{D_2}({\varphi }_{D_1{D}_2}-{\varphi }_{D_2{D}_2})\right]\hfill \\ \approx \frac{p_{D_1}{p}_{D_2}}{\varphi }\left[p_{D_1}({\varphi }_{D_1{D}_1}-{\varphi }_{D_1{D}_2})+p_{D_2}({\varphi }_{D_1{D}_2}-{\varphi }_{D_2{D}_2})\right]\hfill \\ \approx p_{D_1}{p}_{D_2}\left[p_{D_1}({\lambda }_2-{\lambda }_1)+p_{D_2}({\lambda }_1-1)\right],\hfill \end{array}$$

and $d_{D\text{|case}}\approx p_{D_1}^2{p}_{D_2}^2\left({\lambda }_2-{\lambda }_1^2\right)$, where λ₁ is the heterozygous disease genotype relative risk and λ₂ is the homozygous disease genotype relative risk (i.e. relative to the homozygous genotype containing no disease predisposing allele). Thus, for a recessive disease we have

$$(p_{D_1|\text{case}}-p_{D_1|\text{cont}}):d_{D|\text{case}}\approx 1:p_{D_2}.$$

Also, we have (P_D1|case – P_D1|cont):d_D|case ≈ 1: λ₂P_D1 ≈ 1:P_D1 and d_D|case = 0 respectively, for dominant and multiplicative modes of inheritance. Because additive and multiplicative disease inheritance have similar λ₁, we can conclude that the HWP test in cases is non-informative for additive and multiplicative diseases, but can improve the CA test for dominant and recessive diseases, with the above expected ratios of effect sizes.

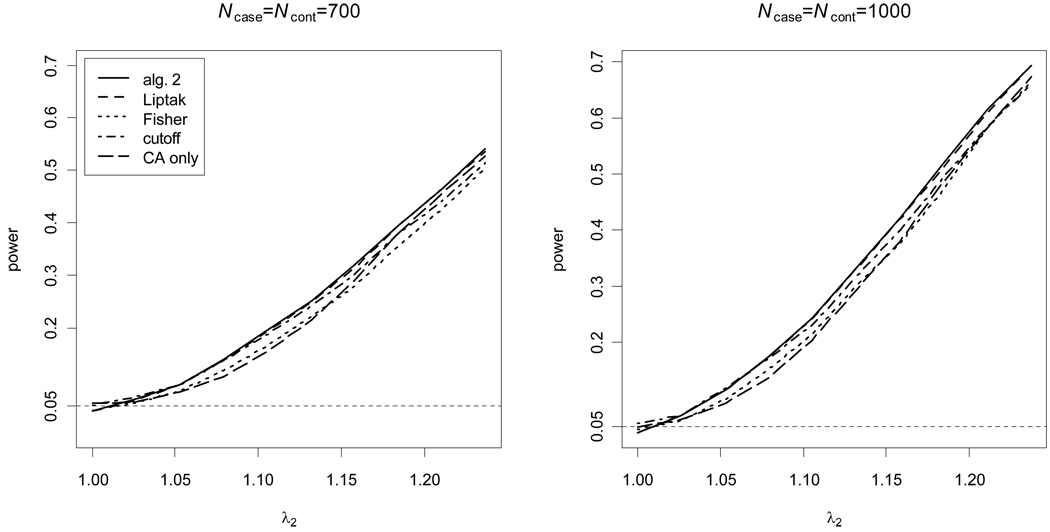
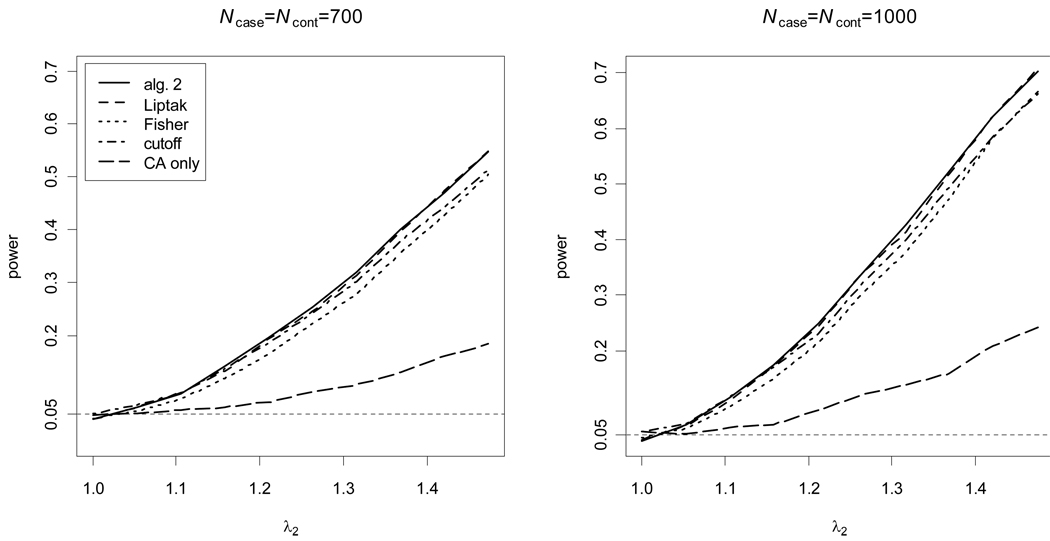
Figure 3 and Figure 4 show the empirical power from 10,000 replicate samples at the significance level 0.05 when the disease modes of inheritance are dominant and recessive, respectively. We assume the disease allele frequency is 0.2, and the numbers of cases and controls are equal. For the weights, w₁ and w₂, in algorithm 2 and Liptak’s method, we used

$$\begin{array}{c}1/({\widehat{p}}_{D_1|\text{case}}-{\widehat{p}}_{D_1|\text{cont}})\text{and}({\widehat{p}}_{D_2|\text{case}}+{\widehat{p}}_{D_2|\text{cont}})/{\widehat{d}}_{D|\text{case}}\text{for the recessive disease}\\ 1/({\widehat{p}}_{D_1|\text{case}}-{\widehat{p}}_{D_1|\text{cont}})\text{and}({\widehat{p}}_{D_1|\text{case}}+{\widehat{p}}_{D_1|\text{cont}})/{\widehat{d}}_{D|\text{case}}\text{for the dominant disease}\end{array}$$

divided by their estimated standard errors; and algorithm 1 is not considered because only ratios of the effect sizes are available. For the cutoff-based method, the value of c₁ that results in the maximal empirical power (among the values 0.05, 0.1, … , 0.95) was used. A one-tail test was applied for the HWP test because it is known, if the disease-predisposing allele is the less common allele, that d_D|case > 0 for a recessive disease and d_D|case < 0 for a dominant disease²⁸. The results show that algorithm 2 and Liptak’s method are similar, because algorithm 2 is equal to Liptak’s method in the case of a one-tail test. However, the results also confirm that the other methods that have been used to combine the CA and HWP tests are not as powerful as the proposed methods. Also, it should be noted that algorithm 2 and Liptak’s method using the proposed weights work well even though the proposed weights are not the true effect sizes, and the CA and HWP tests are not strictly independent under the alternative hypothesis. In particular, the empirical power at λ₂ = 1 is equivalent to the empirical type I error at significance level 0.05, and it is seen that both algorithm 2 and Liptak’s method using the proposed weights preserve this type I error.

Figure 3. Empirical power for a dominant disease.

The CA and HWP test p-values are combined using algorithm 2, Fisher’s method, Liptak’s method, and the best cutoff-based method, compared to the CA test alone. The empirical power at the significance level 0.05 is calculated from 10,000 replicate samples; for algorithm 2, 50,000 Monte Carlo replicates were used.

Figure 4. Empirical power for a recessive disease.

The CA and HWP test p-values are combined using algorithm 2, Fisher’s method, Liptak’s method, and the best cutoff-based method, compared to the CA test alone. The empirical power at the significance level 0.05 is calculated from 10,000 replicate samples; for algorithm 2, 50,000 Monte Carlo replicates were used.

4. DISCUSSION

Over the last few decades, the UMP region for combining p-values has been sought and it has been proved that there is no UMP test. Because of this, the various combination methods were compared empirically instead of by further theoretical investigation. However, all these investigations failed to find any practically MP region. Here we have shown that a MP test can be found if we specify the expected effect sizes, or it can be approximated if we only know their ratios. Also, our results show that this proposed method always has the best power, though the power may not be substantially larger than that of other methods. We have illustrated the method with a genetic example that demonstrated moderately increased power, even when the ratio of effect sizes was misspecified.

Although the proposed algorithms described here are for independent tests with underlying normal distributions, they can also be extended to other cases, such as the T_j follow different distributions or, for example, a multivariate normal distribution with correlations. If the statistic T_j for each p-value follows a different distribution, a factor g_Aj(·) appropriate for each T_j should be used in the Monte-Carlo algorithm, instead of only factors of the form exp(z_j·S_j) + exp(−z_j·S_j). In addition, when the statistics T_j for each p-value follow a multivariate normal distribution (MVN), the g_A(·) for the MVN density should be used in step (2) after sampling from the standard MVN distribution with appropriate correlations between the T_j under the null hypothesis. Thus, with some slight modification the same approach can be extended to complex cases.

Though the proposed method improves power, the need to have information about the expected effect sizes could limit its application. However, hypothesis testing for combining p-values should not be understood in the same way as for testing parameters because there is no uniformly most powerful method and the statistical power can be substantially different according to the situation. Instead, it would be better to use information about effect sizes, something that is often available, especially – as we have shown – in genetic epidemiology. The proposed method suggests the following general strategy for its application in practice:

1. If the effect sizes are known, the proposed method using the expected differences (algorithm 1) will give the best power.

2. If only the ratios between the effect sizes are available, the proposed method using their ratios (algorithm 2) should be considered. To avoid excess computation, Liptak’s method using as weights ratios of the standardized effect sizes can be used when the expected differences are different.

3. If precise information is not available but the effect sizes are expected to be small (large), Fisher method (Liptak’s method using equal weights) should be used.

Alternatively, if we consider other methods, such as a cutoff-based method (which is sometimes called self-replication or screening ^{8, 9}), instead of Liptak’s method or the proposed method, c₁ and c₂ should be determined by the ratios of the standardized effect sizes. Sometimes nothing is available about effect sizes, but the effect sizes can nevertheless be expected to be equal. For example, in a meta-analysis, we usually want to combine results from several studies for the same hypothesis. Then we suggest using inferences based on ratios between the standard errors because S₁:S₂=1/σ̂₁:1/σ̂₂. Finally, it should be remembered that Liptak’s method with appropriate weights is the same as our proposed method if the p-values are from one-tail tests.