The remapping of space in motor learning and human-machine interfaces

Abstract

Studies of motor adaptation to patterns of deterministic forces have revealed the ability of the motor control system to form and use predictive representations of the environment. One of the most fundamental elements of our environment is space itself. This article focuses on the notion of Euclidean space as it applies to common sensory motor experiences. Starting from the assumption that we interact with the world through a system of neural signals, we observe that these signals are not inherently endowed with metric properties of the ordinary Euclidean space. The ability of the nervous system to represent these properties depends on adaptive mechanisms that reconstruct the Euclidean metric from signals that are not Euclidean. Gaining access to these mechanisms will reveal the process by which the nervous system handles novel sophisticated coordinate transformation tasks, thus highlighting possible avenues to create functional human-machine interfaces that can make that task much easier. A set of experiments is presented that demonstrate the ability of the sensory-motor system to reorganize coordination in novel geometrical environments. In these environments multiple degrees of freedom of body motions are used to control the coordinates of a point in a two-dimensional Euclidean space. We discuss how practice leads to the acquisition of the metric properties of the controlled space. Methods of machine learning based on the reduction of reaching errors are tested as a means to facilitate learning by adaptively changing he map from body motions to controlled device. We discuss the relevance of the results to the development of adaptive human machine interfaces and optimal control.

1. Introduction

In the last two decades a growing number of studies have addressed three related issues: learning, plasticity and internal representations – also referred to as “internal models”. This new focus constitutes a paradigm shift in our approach to brain functions and, in particular, to sensory motor functions. For example, motor learning was largely studied and understood as a way to obtain stable performance improvements on particular tasks (Schmidt, 1988). Today, motor learning is widely regarded as a means to acquire knowledge about the environment (Kawato & Wolpert, 1998; Krakauer, Ghilardi, & Ghez, 1999; McIntyre, Berthoz, & Lacquaniti, 1998; Mussa-Ivaldi & Bizzi, 2000; Shadmehr & Holcomb, 1997; Wolpert, Miall, & Kawato, 1998). An acquired skill is the expert performance of a specific task due to practice or aptitude, yet the motor system can express knowledge by transforming experience acquired through practice of particular actions into the ability to perform novel actions in untrained contexts. In learning theory this distinct ability is often referred to as “generalization”.

In one experiment (Conditt, Gandolfo, & Mussa-Ivaldi, 1997), subjects practiced target-reaching movements of the hand against a deterministic field of perturbing forces, i.e., forces that depended upon the state of motion (position and velocity) of the hand. These were simple center-out movements. At first, the unexpected forces caused the hand to deviate from the straight motion pattern that is typical of reaching. With practice however, the hand trajectories returned to their original rectilinear shape. After training, a group of subjects were asked to draw shapes in the force field instead of making reaches, which is a version of generalization. Remarkably, subjects were able to compensate for the perturbing forces to produce these shapes accurately. Moreover, it was statistically impossible to distinguish their shapes and after-effects from those made by a group of subjects who spent their training time explicitly drawing these same shapes within the perturbing field. This is an example of learning generalization and shows that subjects did more than merely improve their performance when reaching against the disturbing forces. They effectively developed the ability to predict and compensate for the disturbing forces while producing new movements in new regions of “state space” that had not yet been explored in the presence of these forces. This ability to generalize is computationally equivalent to forming a model of the perturbing force field, that is, a prediction of the relation connecting the planned movement positions and velocities with the external forces.

In this article we consider a more fundamental representation than that of a perturbing field: the representation of space itself. We focus on the ability of our brain to reorganize motor coordination in a manner consistent with the geometrical properties of the physical space in which movements take place. To this end, we need to consider that purposeful motor actions may be described in two ways. First, they may be described in terms of motions of different body parts or articulations, for example, the joints of the arm in a reaching movement. Or, second, the same actions can be described in terms of specific control points “or endpoints”, for example, the hand in a reaching movement or a finger tip in a pointing movement. The endpoint is the entity that defines the motor task in terms of its effects and relevance in the environment. Consistent with these two descriptions, we can talk about an “articulation space” and an “endpoint space”. The geometrical properties of these two spaces are profoundly different. The articulation space typically has many more elements, or “dimensions”, than the endpoint space. But an even starker contrast between the two spaces is that they may have different metric properties. A movement of the fingertip can be measured in centimeters whereas movements of joint angles are measured in degrees or radians. The relation between articulation and endpoint spaces may be quite complex, yet, the nervous system is evidently capable of dealing with such complexity when planning and learning new actions.

In a now classical study, Morasso (Morasso, 1981) made the simple and critical observation that when asked to move the hand between two locations, without any specification for the trajectory, subjects moved the hand in a quasi-rectilinear path with a simple bell-shaped speed profile. This description is invariant across space, i.e., for different start and end positions. In contrast, if one describes the angular motions of the shoulder and elbow joints during the same movements the invariance disappears and qualitatively different patterns appear from place to place. In other words, for a single movement one sees smooth and straight trajectories in task space and correspondingly complex and variable trajectories in articulation space. From this, Morasso and others (Flash & Hogan, 1985; Hogan, 1984; Soechting & Lacquaniti, 1981) derived a simple conclusion: movement trajectories are planned as smooth straight lines in endpoint coordinates and executed by the appropriate commands depending upon the mechanical properties of the arm, which vary in different regions of endpoint space. Because the brain has imperfect knowledge of the mechanical properties of the arm, for example, its inertia, the resulting trajectories are generally not identical to the planned smooth motions (Flash, 1987; Hollerbach & Flash, 1982), they are only approximations (Mussa-Ivaldi, 1997; Mussa-Ivaldi & Bizzi, 2000). This straightforward and adequate explanation of experimental data is, however, not a generally accepted view.

Kawato and coworkers (Uno, Kawato, & Suzuki, 1989), and later others (Todorov & Jordan, 2002), have proposed that movement trajectories result from the nervous system optimizing some dynamical criteria. For example, Uno, Kawato and Suzuki (1989) found that data collected from subjects’ movements can be well approximated by a model that minimizes the square of the rate of change of the shoulder and elbow torques. This “minimum-torque change” model expressed a dynamical criterion that is alternative to the view that the brain plans movement trajectories in an explicit way. Based on this model, a change in dynamical conditions in which movements take place would be expected to result in changes of trajectories. In particular, the recovery of a smooth, rectilinear movement of the hand in the presence of a perturbing force field would require the generation of compensatory joint torques that may well be incompatible with the requirement of minimum torque change. Accordingly, an adaptive controller that seeks to minimize this dynamical cost function would compensate for the disturbance by establishing a new trajectory. Instead, it has been consistently observed that after adapting to a variety of force fields subjects tend to recover the original spatial and temporal features of unperturbed hand trajectories (Shadmehr & Mussa-Ivaldi, 1994). These same features (straight motions with smooth speed profiles) have also been observed when the controlled endpoint is a virtual mass connected to the hand via a simulated spring/damper system (Dingwell, Mah, & Mussa-Ivaldi, 2004). These findings support the view of Morasso (1981), Hogan (1984) and Flash and Hogan (1985) that the shape of trajectories is a deliberately planned property of motions. This paper goes beyond that statement and suggests that the trajectory of a controlled endpoint is consistent with the Euclidean properties of the space in which it moves. In particular, in the geometry of physical space the shortest path between two points is a straight line and the smoothest motion along this path is obtained by following a bell-shaped speed profile. The general form of smoothness optimization involves minimizing a functional containing all the derivatives – up to infinite order – of some cost function. In the particular form suggested by Hogan (1984) and Flash and Hogan (1985) smoothness is described by the “jerk” – the third time derivative of the position – and maximum smoothness is obtained by minimizing the jerk functional over all trajectories that share the same boundary conditions. We describe some evidence supporting that this simple geometrical principle applies to a greater variety of behaviors and guides the reorganization of movement when adapting to a novel geometrical map between motions of the body and their effect on a controlled endpoint.

Early studies by Fels and Hinton (1998) demonstrated the ability of subjects to learn new movements of the arms and hands to generate speech through the operation of an analog model of the vocal tract. In their study an artificial neural network was trained by the subject to associate particular gestures to vocal sounds. Then the subject needed to learn how to interpolate among the training examples. After some dual training, the interface developed a stable map between gestures and vocal sounds and the human learner was able to engage in conversations, poem recitation and even singing by producing coordinated sequences of gestures. In other words, subjects learned a “remapping” from the space of sounds normally produced by the vocal tract to a space of hand motions and postures that encoded voice formant parameters. In this article we consider how a similar form of behavioral remapping is induced by the interaction with an adaptive interface that transforms body motions into movements of a low-dimensional controlled endpoint and by the properties of the space in which the endpoint moves.

2. What is space?

The term “space” has a multiplicity of meanings, many of which are associated with a vast context of signals and systems. When we deal with a collection of signals, for example, from a population of neurons, we may associate each signal to an axis of a multi-dimensional signal space. The activity of the whole population is described as a moving point in this abstract space. At the origin of this mathematical concept lies the notion of ordinary physical space, the three-dimensional space in which we live. Physical space, the space we are most accustomed to, has some distinctive features that are not always shared by abstract signal spaces. Perhaps the most salient ones are the properties associated with Euclid’s postulates.

Euclid’s postulates state the notion that physical space is homogenous and that translations and rotations cannot affect the form of a body, an essential characteristic that fundamentally shapes our description of motion (Goldstien, 1981). In fact, Newtonian mechanics assumes the structure of physical space to be Euclidean. A key concept in mechanics is that of a rigid body, that is, an object whose size and shape are not affected by Euclidean transformations of space (e.g., rotations, translations and reflections). The most common of these transformations are those that are associated with our own motions. While it is self-evident that the objects in a room are not affected by our moving around the room, the same cannot be stated about the signals that are elaborated by our visual system, starting from earliest stage in the retina. The retina has a complex arrangement of photoreceptors with variable density. The spatial arrangement of these receptors is mapped non-linearly into the visual areas of the cortex. One of these maps, for example, has been modeled as a log-polar transformation (Schwartz, Greve, & Bonmassar, 1995; Tistarelli & Sandini, 1991). As a result, when we move in a room the neural signals that convey the information about a cup on a table continuously change in complex ways. Within these neural transformations, it is difficult to identify signal encoding for the size of the cup, which remains invariant not only in the physical world, but also in our own visual perception (Sutherland, 1968).

Euclid’s fifth postulate can be restated in the form of the “parallel postulate”: given a line and a point, one and only one line passes though that point and is parallel to the first given line. Quite remarkably, this postulate is completely equivalent to the well-known Pythagoras’ theorem, stating that in a right triangle the square on the hypotenuse is equal to the sum of the squares on the other two sides (Hilbert, 1971). This is a subtle but exceedingly important equivalence, because the Pythagorean theorem establishes a particular way to define and measure length, as a sum of squares of Cartesian coordinates. In fact, the mathematical concept of size or “norm” is very broad, with many ways to calculate the length of a line or the distance between two points in a given space (Courant & Hilbert, 1953); however, the L₂norm, based on sum of squares as per Pythagoras’ theorem, is the only norm whose value is invariant under the Euclidean group of transformations, which includes rotations and translations. It is, therefore, extremely likely that the ability to represent the invariance of distances between fixed points in space and of objects’ sizes is contingent upon the computation of something equivalent to the L₂norm starting from articulation spaces that are not inherently endowed with Euclidean properties.

We have briefly considered the way signals in the retina and in the visual cortex do not display Euclidean invariance. The same can be concluded for motor signals emanating from the motor cortex and descending all the way to muscle activations. The act of moving one’s index finger tip along a 10 cm path involves different activations of muscles and different patterns of motor cortical signals depending upon the starting position and the direction of the movement. While a neural correlate for the size of movement – independent of movement location and direction - has not yet been found, it is self-evident that such correlate must exist somewhere in the nervous system. This is demonstrated by our very ability to plan and execute movements, with approximately equal lengths, starting from different locations and in different directions. How these sensory and motor forms of Euclidean invariance, which are so central to our understanding of space, may be encoded in our brains remains largely an unsolved mystery. Nevertheless, it seems plausible to argue that Euclidean structure, as it emerges from perception and movement, is a learned property arising from the interaction between sensory experiences and motor activities. As we move around a room the sizes and shapes of the surrounding objects, as they are projected onto the retina and then onto the visual cortex, change in a correlated fashion to our motions. As our brains are aware of our own motions, and as it would be extremely unlikely for the environment to fluctuate “in sync” with us, these correlated changes can be removed. The ability to extract metric properties of a space from experience also needs to be maintained in the face of continuous physical changes of our sensory organs and motor apparatus. Contrary to casual speculations that the Euclidean properties of our movements – their natural smoothness and straightness - may derive from visual perception of physical space, one may argue that the latter derives from the constant interaction of visual information with motor activities.

Since the Euclidean properties of physical space are adequately represented by the sensory motor system that guides the motion of our hands and bodies, we can plausibly assume – as a working hypothesis – that these geometrical properties are transferred or “remapped” in novel situations. For example, these situations arise when one learns to control a device by coordinated body motions or in a brain-machine interface, where signals from a cortical population must be shaped to guide a robotic arm. A commonly experienced form of remapping takes places when one learns to drive a car. At first, the student driver must be fully aware of the movements of the hands on the wheel and of the feet on the pedals. But after some time these body motions become instinctively attached to the motion of the car. Here we discuss some recent results that demonstrate how new coordinated movements are created in a controlled remapping experiment.

3. Reorganizing the motor map

In the world of human practical experience, physical space is everywhere homogenous, but in general, the space of the motor system is not. As discussed above, the joint angle space of the arm is not Euclidean: a translation of the hand requires different angular motions of the joints depending on the hand’s initial location. However, the hand itself moves in ordinary physical space, which is Euclidean. The motor system is so adept at dealing with this joint-to-hand space mapping that most unimpaired people perform straight motions of the hand with almost no cognitive load. These types of movements, however, have the benefit of millions of iterations of experience. It may behoove motor control scientists to discover how the plastic motor system develops a novel transformation between articulation and endpoint spaces. Such information would not only reveal the mechanisms that allow the formation of internal models by the central nervous system, but it would also be likely to prove worthy in the development of rehabilitation techniques for those suffering from neurological damage who need to learn new ways to control their muscles. Last, but not least, remapping of coordination is of fundamental importance to the operation of assistive devices via human-machine or brain-machine interfaces (HMIs). Intrinsic to the nature of assistive devices and HMIs is that their articulation space is always of higher dimensionality than their endpoint space. Many control signals are manipulated by the user to operate an external device that can be completely described by a much lower number of variables. The dimensionality imbalance, like that of the many joint angles of the arm to the 3 spatial dimensions of a fingertip, engenders an interesting problem of redundancy where one solution among many must be chosen in a principled way.

The motor remapping of a space with this redundant characteristic was investigated in a study by Mosier et al. (2005), using a task similar to the glove-talk of Fels and Hinton (1998). Subjects wore a data glove that generated K = 19 signals encoding hand gestures. These signals formed a vector, h = [h₁,h₂,……h_K]^T, that was mapped linearly onto the two coordinates, p = [x,y]^T of a cursor on a computer screen:

$$\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{cccc}{a}_{x,1}& a_{x,2}& \cdots & a_{x,K}\\ a_{y,1}& a_{y,2}& \cdots & a_{y,K}\end{array}\right]\cdot \left[\begin{array}{c}{h}_1\\ h_2\\ \cdots \\ h_K\end{array}\right]$$

or, more concisely

$$p=A\cdot h$$ (1)

The mapping was calibrated prior to the start of each experiment by having the subjects position the hand in four different configurations and by establishing a correspondence between these configurations and the four vertices of a rectangular workspace on the computer screens (Figure 1). The mapping matrix, A, was derived from the calibration data as, A = P_cH_c⁺, where P_c is the 2×4 matrix of vectors representing the corners of the monitor, H_c is the corresponding 19×4 matrix of h-vectors obtained from the calibration postures in Figure 1 and the “+” superscript indicates the Moore-Penrose pseudoinverse, H_c⁺ = (H_c^TH)⁻¹H_c^T. This procedure corresponds to solving – with a minimum norm constraint - an underdetermined system of equations for the 2×19 elements of A. The calibration postures were chosen so that subjects could guide the cursor across the workspace bounded by P_c using comfortable hand configurations.

Figure 1.

The four hand postures used to create the transformation matrix, A, which linearly maps finger articulation to cursor location on a computer monitor. The transformation matrix was constructed such that each hand posture corresponded to a corner of the rectangular workspace on the monitor. (Modified from Mosier et al. 2005)

Subjects were asked to control movement of a cursor by changing the configuration of hand and fingers. They were required to make a first rapid movement to get as close as possible to the target and then stop. Then, they were allowed to take all time they needed for placing the cursor inside the target region. This second correction phase was discarded from the analysis but was necessary for placing the cursor in the starting position for the next reach. The focus of the experiment was in the first rapid movement that – when carried out without vision of the cursor – was directed toward the hand configuration corresponding to the “internal model of the target location”.

Movements were executed under one of two training protocols: in the No-Vision Protocol (NV) the cursor was suppressed during the fast reaching movements. The cursor was only presented at the end of reaching to allow for a correction (not analyzed). In the Vision (V) protocol, the cursor was always visible. Twelve subjects were divided into two groups. All subjects practiced reaching in several training trials and were evaluated on fewer test trials, interspersed with the training trials. Subjects in group 1 were trained and tested under the NV protocol. Subjects in group 2 were trained under the V protocol and tested under the NV protocol. Data analysis for both groups was carried out only on test trials, allowing for comparison of how subjects executed reaching movements without visual guidance after having trained without and with visual guidance. Thus, both groups were tested under identical conditions, the only difference being the training modalities. Some examples of cursor trajectories recorded from a subject in the first group during the initial training period are shown in Figure 2. These segments of the trajectories are limited to the initial movement and do not include the correction, which was also excluded from the subsequent analysis.

Figure 2.

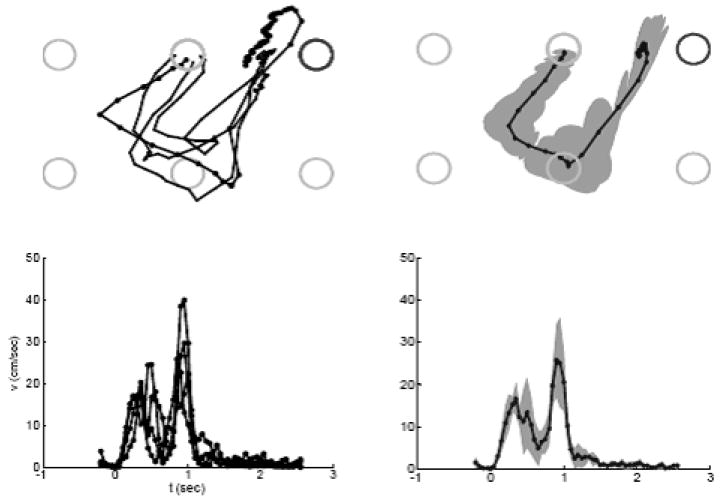
Example trajectories of a subject training in the no-vision (NV) condition. Top: movements of the cursor originating from the top-center target and directed toward the right-center (darker) target are shown individually and averaged. The grey cloud represents a 95% confidence region of cursor location. Bottom: individual and averaged speed profiles of the example movements shown in the top of the figure. Note that the trajectories display a significant curvature. At this early stage of training the subject passed by one of the lower position before heading toward the target. (From Mosier et al. 2005)

The experimental protocol has four notable features:

1. It is an extremely unusual motor task. It is virtually impossible that subjects had been exposed to anything similar before participating in the experiment. This is important as it allow us to assume that learning of the task starts from scratch.

2. The hand and the controlled object are physically uncoupled. There is no exchange of mechanical forces between the subject and the cursor. The only connection is established by a computer interface. Therefore, the only available feedback pathway for the performance of the task is provided by vision. Subjects have, of course, proprioceptive information about their hand. However, this cannot be related to the position of the cursor without knowledge of the map, A. Accordingly, when the visual feedback is suppressed, the control of the cursor can be considered to be “open loop”.

3. There is a relatively large dimensionality imbalance between the articulation space or the hand and the cursor space. This allowed us to address empirically some issues of redundancy control and its relevance to learning.

4. Most importantly, there is a sharp metric imbalance between articulation space of the fingers and cursor space. The cursor moves on a flat computer monitor that, in spite of minor irregularities of commercial monitors, is endowed with Euclidean properties. The theorem of Pythagoras can be safely applied to calculate the distance between any two points. In contrast, there is no natural and unique way to define the concept of distance between two gestures. One could use the joint angles of the fingers, or the distances of the finger tips, or the strain energies of the finger muscles and so on. Therefore, we can argue that, unlike the points on the monitor, the hand gestures do not possess intrinsic Euclidean properties. This metric difference allows us to investigate how the geometrical properties of space are “imported” into the coordination of movements.

Subjects in both groups learned to perform the task, as evidenced by the monotonically decreasing reaching errors. Reaching error was calculated as the Euclidean distance between target and cursor at the end of the initial movement (Figure 3 - Top). Note that group 1 subjects that trained with continuous visual feedback of the cursor had slightly larger errors than group 2 subjects that trained without visual feedback. This is only an apparent paradox, which is easily explained by considering that the data displayed in the figures were obtained from both groups in the absence of visual feedback. Therefore, the testing condition appeared to be slightly more challenging for the subjects trained with visual feedback because they needed to switch to the no-feedback condition in the test trials. This change of operating condition seemed to have caused a mild but statistically significant (p<0.01) degradation of performance, compared to the group that was trained and tested in the same no-feedback condition.

Figure 3.

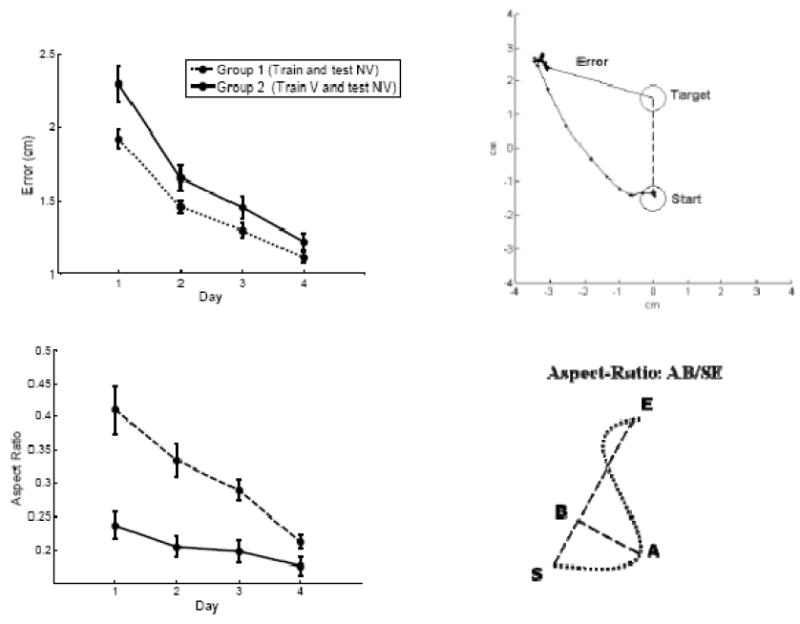
Performance results over training for subjects in both the no-vision (NV) and the vision (V) groups. Top-right: Definition of the error metric. When the cursor came to rest during a movement (the black trajectory), error was calculated as the Euclidean distance from the cursor to the target. Top-left: Ensemble average of reaching errors in both groups over four days of training. Bottom-right: A measure of rectilinearity. The aspect-ratio is the maximum lateral excursion over the distance between the start and end of a trajectory. Bottom-Left: Ensemble averages of the aspect ratio over four days of training. Decrease in aspect ratio indicates straighter motions. Error bars are 99% confidence intervals on the data. (Modified from Mosier et al. 2005)

The fact that with training subjects reduced the reaching error is important because it demonstrates that this was a feasible task. However, this is not - by itself – a surprising result: subjects learned to do what they were asked. The most important outcomes in motor learning experiments are those concerning movement parameters that are not explicitly specified by the task. One such parameter is the linearity of cursor motion. The task of this experiment did not specify any particular trajectory for the endpoint. The only requirement was to reach as close as possible to the target – i.e., to reduce the reaching error. Nevertheless, subjects in both training groups displayed a progressive trend toward straighter paths of the controlled cursor. This was illustrated by the steady decrease of “aspect ratio”, defined as the ratio of the maximum lateral excursion to the movement extent (Figure 3-Bottom). The maximum aspect ratio is – among all possible measures of straightness – an “infinity” norm. It is the simplest to calculate and is zero if and only if the movement occurs on a straight line. Mosier et al. (2005) subjects that trained with visual feedback produced straighter motion beginning at early training. Most importantly, the trend toward path linearity and the reduction of errors followed different time courses. The straightening of cursor motion was strongly facilitated by the presence of visual feedback concurrently with movement execution.

The task in the experiment of Mosier et al. (2005) was characterized by a high degree of kinematic redundancy, with 19 signals “contracted” into 2 cursor coordinates. Geometrically, this situation is sketched in Figure 4A and B, where the space of glove signals, ℋ, is simplified as a 3-dimensional Cartesian diagram, with a glove signal associated with each axis (h₁, h₂ and h₃). A configuration of the hand is a point, B, in this diagram and the subject is presented with the 2-dimensional image of this point - the cursor location P on the monitor – under the linear map A. This map A is, in fact, a rectangular matrix with two rows and 19 columns, and therefore, it does not have an inverse. Stated another way, the inverse image of P is not a point in the space of hand configurations, but an entire subspace – the null space of A at P - with 19-2=17 dimensions. In the figure, since the hand is represented with only 3 dimensions, this null space is the line (3-2=1) L_P. What this means is that the “null space” is all of the finger motion that has no effect on the movement of the cursor on the screen. All movement in the articulation space (space of hand gestures) that is not in the null space contributes directly to the movement of the cursor on the screen. One can say that the map A that was established by the experiment creates an Euclidean structure for the articulation space that is a counterpart for the natural Euclidean properties of the endpoint space – the computer monitor. In this structure, the articulation space is organized into a set of parallel 2D (affine) planes (Figure 3A). Each plane is an equivalent image of the endpoint space, and all planes are orthogonal to the null subspaces passing through each of them. Thus, the articulation space is organized by the map A into two types of subspaces: task space and null space. A task space is an inverse image of the endpoint space. It should not be confused with the endpoint space itself: a point in endpoint space, in this example, is identified by 2 coordinates over the computer monitor, whereas a point in task space is identified by the 19 glove signals. Task spaces are Euclidean because on each of them, as well as over the monitor, the theorem of Pythagoras can be used to measure distances. Furthermore, the line segments on each task subspace of ℋ satisfy a condition of minimum Euclidean length. This is illustrated in Figure 4B where, again, the point P on the monitor is the image of the configuration point B in ℋ. A subject, when asked to reach from this starting configuration B to the point Q on the monitor, can shape the hand so as to assume any configuration along the line L_Q. The segments BC, BD, BE, BF etc. in ℋ map equivalently to the segment PQ on the monitor. However, among these segments, the one that lies on the same image plane of B, the segment BC, has the minimum Euclidean norm,

$$\sum _i{(h_{\mathit{Ci}}-h_{\mathit{Bi}})}^2$$

Figure 4.

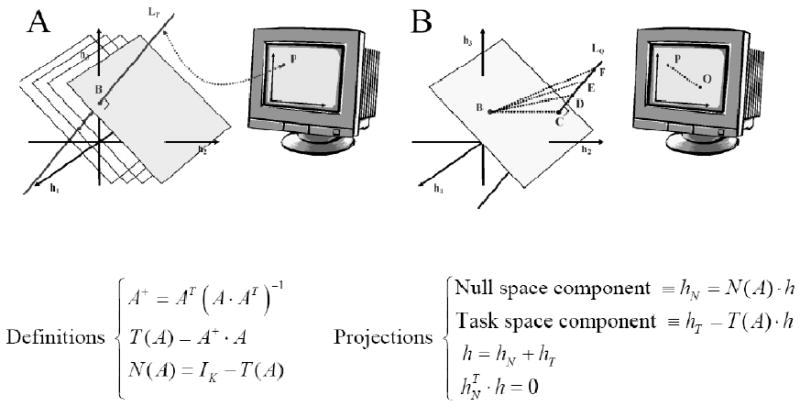
Geometrical representation. A) The articulation space, ℋ, is represented in reduced dimension as a 3D space. The calibration, A, establishes a linear map from three glove signals - h1, h2 and h3 - to a 2D computer monitor. The red line, LP, contains all the points in ℋ that map into the same screen point P. This line is the “null space” of A at the point P. A continuous family of parallel planes, all perpendicular to the null space “fills” the entire signal space, ℋ. Each plane is effectively a replica of the screen embedded in ℋ. B) The shortest path between two points, P and Q is a straight segment. The starting hand configuration, B, lies on a particular plane (a task subspace) and maps to the cursor position, P. All the dotted lines in ℋ leading from B to L_Q produce the line shown on the monitor. The “null space component” of a movement guiding the cursor from from P to Q is its projection along L_Q. The “task space component” is the projection on the plane passing by B (that is the segment BC̅) Bottom: The mathematical derivation of the null space and task-sace components generated by the transformation matrix A.

In other words, because there is a null space in the articulation space there is more than one way to move the cursor from point P to Q in the task space. But of all the paths in ℋ that take the cursor from P to Q, there is only one that has a minimum length in Euclidean sense. In summary, by partitioning the articulation space into null and task subspaces one has implicitly imported into the articulation space the Euclidean properties of the endpoint space. This, however, is only a mathematical statement. The relevant question remains whether or not the brain is building – through practice – an internal representation of the articulation space consistent with such structure.

On the bottom of Figure 4 one can find the algebraic formulas that allowed Mosier et al. (2005) to derive, for each measured movement, h, the component of the glove signal vector over a task space, h_T and the component in the null space, h_N. When applied to the subjects’ data, this decomposition revealed that, with practice, subjects reduced the amount of null space motion (Figure 5). One should observe that the extent of motion decreased with practice, both along the task space and in the null space. The reduction of the task space component corresponded to the tendency of the subjects to generate straighter, and therefore shorter, motions. However, the data revealed a generally stronger decrease of null space excursion. This means that the movements became increasingly confined to the image planes, as the segment BC in Figure 4B. Accordingly, it was possible to conclude that through practice subjects learned to partition the articulation space of the fingers (the space ℋ) into the null subspace and its orthogonal counterpart, containing the inverse images of the monitor. Performing this partition, as discussed above, is effectively equivalent to importing into the articulation space the natural Euclidean structure of the endpoint space. Mosier et al (2005) demonstrated that the partition of the articulation space in task and null subspaces results from a learned process of remapping that applies to the coordinated control of an external device. The ability of the motor learning system to perform such remapping operations is of fundamental importance to the development of effective human-machine and brain-machine interfaces. A similar approach was recently applied with success to the remapping of EMG signals (Radhakrishnan, Baker, & Jackson, 2008).

Figure 5.

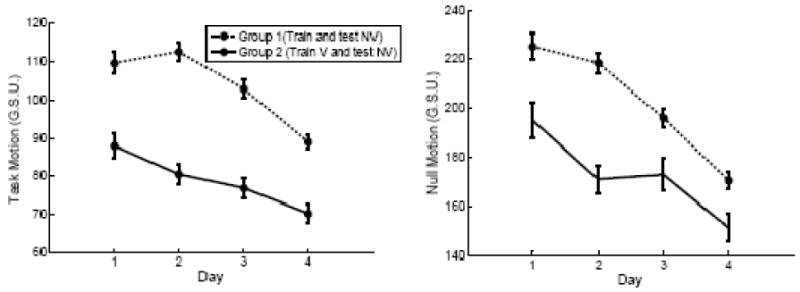
Task space (left) and null space (right) components of subjects’ trajectories in hand space, H, across four days of training. G.S.U.: Glove Signal Units. Subjects in both the vision and no-vision groups reduced task space motion (shorter cursor trajectories on the screen) and null space motion (movement of the fingers that does not contribute to the motion of the cursor). More marked decreases were observed in null space excursion. Error bars are 99% confidence intervals. (Modified from Mosier et al. 2005)

4. The engineering of learning in human-machine interfaces (HMIs)

4.1 Wheelchair control

Persons suffering from tetraplegia or other severe physical disabilities need to rely on assistive devices for mobility. The extensive scope and variability of motor impairment leaves scientists and clinicians with the daunting task of developing assistive systems that are both “custom made” and capable of adapting to the evolving degree of impairment in each user. This requires the adaptive remapping of the movements and/or the signals that remain available to the user into a new vocabulary of tasks. The essence of this problem is a sophisticated coordinate transformation from articulation space to the workspace of the assistive device. A research project currently underway in our laboratory (Fishbach & Mussa-Ivaldi, 2007; Gulrez et al., 2009) aims at developing an adaptive interface that maps upper body motions into control signals for powered wheelchairs (Figure 6). In this project, body motions are captured by wearable sensors applied to the torso. These could either be piezoresistive lines embedded in a shirt, as shown in the figure and described in (Gulrez et al., 2009), or other sensors, such as optical markers, accelerometers and EMG electrodes. The body motions are translated into control signals specifying the speed and the heading of the wheelchair. This operation involves two geometrical spaces: a) the space of body-generated signals and b) the space of wheelchair motion control. Both geometrical spaces offer multiple alternative choices of coordinates.

Figure 6.

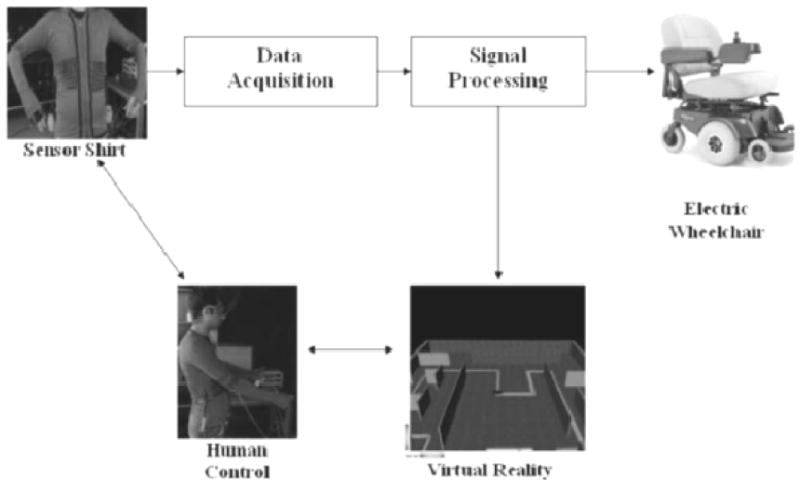
Body-wheelchair interface system concept. The virtual environment provides a safe training platform where the control parameters are set according to the motor skills of the users. Once a satisfactory behavior is reached, the control parameters will be applied to an actual powered wheelchair. (From Gulrez et al. 2009)

On one hand, body signals can be represented by a parsimonious system of natural coordinates expressing, for example, the distribution of movement variance among the body segments. These coordinates are derived empirically by the statistical technique of principal component analysis (PCA) (Jolliffe, 2002). Alternative methods of dimensionality reduction include independent component analysis (ICA) (Hyvärinen, Karhunen, & Oja, 2001) or nonlinear methods such as Isomap (Tenenbaum, deSilva, & Langford, 2000). All these methods provide a representation of natural movements as a superposition – or nonlinear combination – of few simpler components, or “primitives”.

On the other hand, the motion of a wheelchair can also be represented by different systems of control coordinates. For example, one may control the spinning rates of the two wheels or, alternatively a variety of combinations of forward speed and turning rate. Any control system for the wheelchair is inherently two-dimensional whereas body motions may have different dimensionality depending, among other factors, on the degree of disability of the user. However, with the exception of the most severe cases, the space of residual body motions is expected to have more than two dimensions. Therefore, from a geometrical point of view, the first task for an intelligent interface is to extract, in some optimal way, two controllable dimensions from the residual degrees of freedom of the user’s body.

The wheelchair interface was initially tuned and evaluated in a safe virtual reality environment. An example of performance from a spinal cord injured subject is shown in Figures 7 and 8. The subject was a 29 year-old male with a spinal cord injury at the C5-C6 level, with some residual movements in the arm. The experiment (Fishbach and Mussa-Ivaldi, 2007) was conducted following a protocol approved by the Institutional Review Board (IRB) at Northwestern University. After an initial calibration, in which the parameters for the virtual wheelchair were established (Figure 7), the subject performed a set of trials where he maneuvered the simulated wheelchair with body motions over a virtual path marked by a line on the floor (Figures 7 and 8). The subject begun by a sequence of short straight segments interspersed with adjustments of the heading direction (Figure 8, Trial 1). The speed profile of the simulated chair was a stop-and-go sequence, as the subject needed to stop before making a heading correction. As training progressed toward trial 4 the movements of the simulated wheelchair became smoother. The trajectory followed more closely the marked track and the steering motions were performed without stopping. In other words, the movement of the controlled device, through training, became smoother, following a trend that is common to the reaching motion of the hand and to the recovery of reaching performance following stroke (Krebs, Hogan, Aisen, & Volpe, 1998; Morasso, 1981). The goal of our work is to develop learning interfaces that can facilitate this progress by monitoring the evolution of performance errors.

Figure 7.

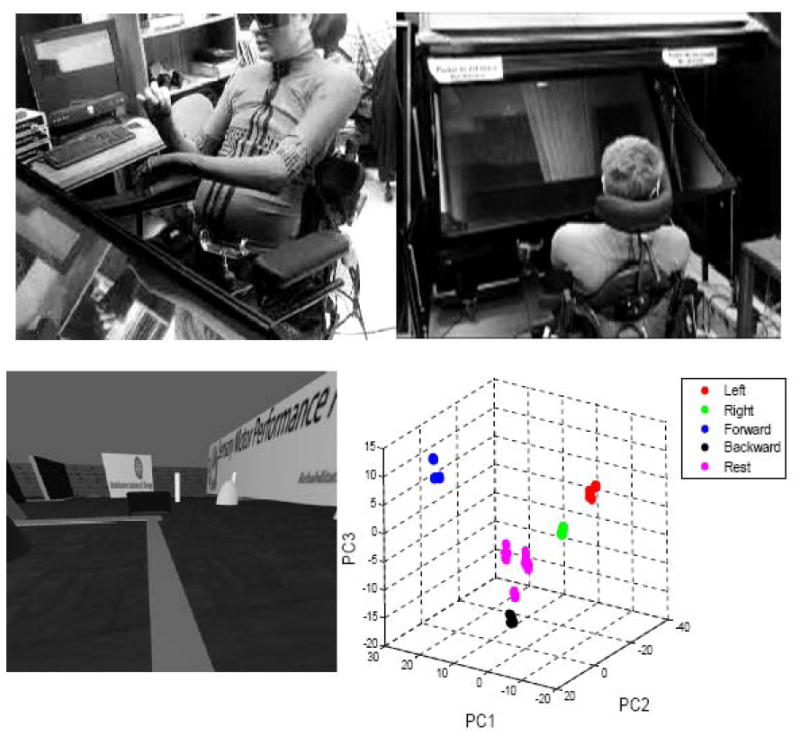
The subject, wearing the upper-body sensing garment, was asked to repeat a set of body motions (Top left) that were easy and comfortable for him to execute. Then, he was able to control the movements of the simulated wheelchair (Top right) by body motions, while immersed in the virtual environment (Bottom left). The signals collected during the calibration phase are shown in the reduced space of the 3 top principal components (Bottom right). Points with different colors represent body postures corresponding to selected control variables (Red: turn left – Green: Turn right – Blue: move forward – Black: move backward – Magenta: stop).

Figure 8.

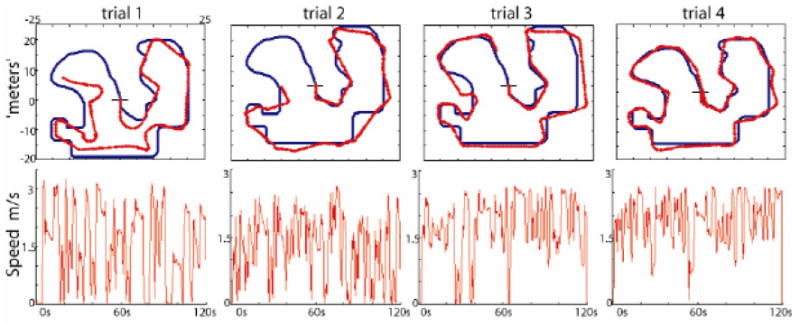
Trajectories of the simulated wheelchair and speed profiles as a spinal cord injured subject practiced controlling a simulated wheelchair in virtual reality, by motion of the upper body. The subject wore a sensorized shirt that generated over 50 electric signals modulated by movements of the arms and trunk. Top: The blue line indicates the virtual pathway that the subject was asked to follow. The red trace shows the motion of the simulated wheelchair, starting from the cross. Bottom: Speed of the simulated wheelchair vs. time. The four panels show four consecutive runs of the experiment. Initially, the subject needed to stop very frequently, particularly when he needed to change heading direction. With practice the stops and speed oscillations were reduced and the traversed path became smoother. (From Fishbach and Mussa-Ivaldi, 2007)

4.2 The human-machine interface: a dual learning system

Systems that transform residual movements or any volitional signal produced by the body into commands for an external device belong to the general class of human-machine interfaces (HMIs). While these systems are critical for improving quality of life for severely disabled users, they are currently performing below users’ expectations. The significant dissatisfaction expressed by users of these systems is not limited to power wheelchair control; many systems for controlling external devices such as computer cursors, prosthetics and communication systems are exceedingly difficult to operate (Fehr, Langbein, & Skaar, 2000; Lotte, Congedo, Lecuyer, & Arnaldi, 2007; Wolpaw & McFarland, 2004). To establish effective systems it seems necessary to deflect some of the burden of learning away from the user and toward the interface.

A fundamental tenet of computational learning theory is that a learning system must be trained by examples and synthesize an appropriate mapping when the desired mapping is not known a priori (Haykin, 2002; Poggio & Smale, 2003). The adaptive element of an HMI must, therefore, “learn” what the user’s representation of the mapping may be from a vocabulary of example-movements that the subject makes. Then, it must modify accordingly the actual mapping to match the users’ expectations. This creates a dual learning system, in which the user and the system are learning each other concurrently, as in (Fels & Hinton, 1998). The adaptive element must track the user performance and readily enact substantive changes to the HMI mapping for improving performance. Yet, if the system undergoes large, unchecked reorganizations, the unfamiliar environment will jeopardize the user’s ability to generalize their performance and impair their ability to control the HMI.

Danziger et al. (Danziger, Fishbach, & Mussa-Ivaldi, 2009) examined the performance of two adaptive algorithms in a paradigm analogous to the one developed by Mosier et al. (2005). Subjects controlled a 2-link simulated planar arm displayed to them on a computer monitor. The configuration of the simulated arm was controlled by coordinated motion of the subjects’ fingers (Figure 9), which were recorded by an instrumented data glove (the CyberGlove by Immersion Co.). Subjects were asked to position the simulated arm’s free moving tip, or “end-effector,” into targets that were displayed on the screen. The map in Danziger et al (2009) differed from that used by Mosier et al. (2005) in that the hand vector was first mapped linearly onto a pair of joint angles (an in Equation 1),

$$\theta =\left[\begin{array}{c}{\theta }_1\\ {\theta }_2\end{array}\right]=\mathit{Ah}$$

and then the joint angles were mapped into the screen cursor coordinates at,

$$p=\left[\begin{array}{c}{\stackrel{⌢}{s}}_1\cos ({\theta }_1)+{\stackrel{⌢}{s}}_2\cos ({\theta }_1+{\theta }_2)\\ {\stackrel{⌢}{s}}_1\sin ({\theta }_1)+{\stackrel{⌢}{s}}_2\sin ({\theta }_1+{\theta }_2)\end{array}\right].$$

where s̑ is a parameter vector containing link lengths and origin location. The error in subjects’ performance was calculated 800ms after movement onset as the distance between the target and the end effector. Over three days, subjects performed movements in 11 epochs per day, 8 of training and 3 of generalization.

Figure 9.

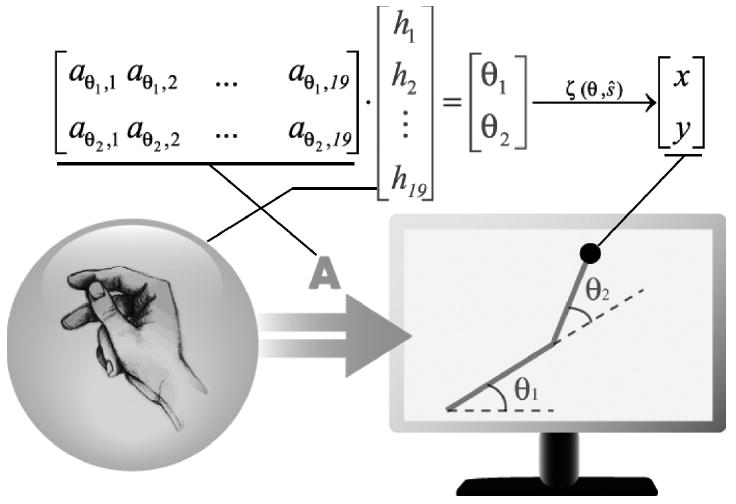
Schematic and mathematical description of the non-linear hand-cursor mapping. A hand posture was represented as a vector, h, and linearly mapped to the joint angles, Ө, of a planar arm. The cursor location is then determined by the forward kinematics of the 2-link mechanism ζ (θ,ŝ), where s is a vector of link lengths and shoulder location. The transformation matrix, A, was updated during batch machine learning to assist subjects in training. (From Danziger et al. 2009)

Three groups of subjects participated in the experiment, which tested two learning algorithms. Both algorithms updated the mapping matrix, A (Figure 9) so as to eliminate the reaching error in the training movements performed by the subjects. The algorithms were, for group 1, a Least Mean Squares (LMS) gradient descent algorithm (Kwong & Johnston, 1992; Widrow & Hoff, 1988) which takes steps in the direction of the negative gradient of the configuration error function, and for group 2, the Moore-Penrose pseudoinverse (MPP) which offers an analytical solution for error elimination while minimizing the norm of the mapping matrix as an additional constraint. The 3^rd group was a control group and performed the experiment without adaptive adjustments of the map.

1) LMS is a procedure that updates the mapping from hand posture to end-effector by following the gradient of the reaching error expressed as a function of each element in the A matrix, a_ij. We begin by establishing a sequence of target locations, {θ̑⁽¹⁾,θ̑⁽²⁾,⋯,θ̑^(N)}. Here, the superscript in parentheses is a label for the vector number in the sequence, whereas subscripts indicate vector components. The corresponding sequence of reaching error vectors is {e⁽¹⁾,e⁽²⁾,⋯,e^(N)} with

$$e^{(i)}\equiv {\theta }^{(i)}-{\stackrel{⌢}{\theta }}^{(i)}=A\cdot h^{(i)}-{\stackrel{⌢}{\theta }}^{(i)}$$ (2)

where (see Figure 9) θ⁽ⁱ⁾ and h⁽ⁱ⁾ represent, respectively, the two-dimensional configuration of the simulated arm and the 19-dimensional glove-signal vector at the end of the i-th reaching movement. With this notation the cumulative squared error is

$$E^2=\sum _{i=1}^N{e}^{(i)T}\cdot e^{(i)}={\sum _{i=1}^N\left(A\cdot h^{(i)}-{\stackrel{⌢}{\theta }}^{(i)}\right)}^T\left(A\cdot h^{(i)}-{\stackrel{⌢}{\theta }}^{(i)}\right)$$ (3)

The gradient of this squared error is

$$\frac{\partial E^2}{\partial A}=2\sum _{i=1}^N{e}^{(i)}\cdot h^{(i)T}$$ (4)

Therefore, the LMS algorithm iterates the matrix update

$$A\leftarrow A-\mu \sum _{i=1}^N{e}^{(i)}\cdot h^{(i)T}$$ (5)

until convergence. The “step size” parameter μ determines the convergence rate of the algorithm.

A batch learning process was performed offline on the average of movements to each target and the algorithm was allowed to converge to a solution before training continued. The resulting mapping displayed negligible average error on the training set.

2) The MPP algorithm is a method that recalibrates the hand-device map, A, by direct application of the (unique) Moore-Penrose pseudoinverse of the calibration-data matrix. Let

$$\stackrel{⌢}{\mathrm{\Theta }}\equiv \left[\begin{array}{cccc}{\stackrel{⌢}{\theta }}_1^{(1)}& {\stackrel{⌢}{\theta }}_1^{(2)}& \cdots & {\stackrel{⌢}{\theta }}_1^{(N)}\\ {\stackrel{⌢}{\theta }}_2^{(1)}& {\stackrel{⌢}{\theta }}_2^{(2)}& \cdots & {\stackrel{⌢}{\theta }}_1^{(N)}\end{array}\right]$$ (6)

be the 2×N matrix of target joint configurations of the simulated arm and

$$H\equiv \left[\begin{array}{cccc}{h}_1^{(1)}& h_1^{(1)}& \cdots & h_1^{(N)}\\ h_2^{(1)}& h_2^{(1)}& \cdots & h_2^{(N)}\\ ⋮& ⋮& \ddots & ⋮\\ h_K^{(1)}& h_K^{(1)}& \cdots & h_K^{(N)}\end{array}\right]$$ (7)

the K×N matrix of K average glove signals at each of the N targets. In the experiments of Danziger et al. it was K=19. With this notation, the calibration only requires that

$$A\cdot H=\widehat{\mathrm{\Theta }}$$ (8)

The problem of deriving A from H and Θ̂ is generally ill posed, unless there are exactly K calibration points. The Moore-Penrose inverse of H, H⁺, provides a unique solution and comes in two forms (Ben-Israel & Greville, 1980):

1. If N < K there are potentially infinite (actually ∞^K−N) solutions compatible with the data. In this case, the Moore-Penrose inverse is H⁺ = (H^T·H)⁻¹·H^T. The solution, A = Θ̂·H⁺, is the matrix that has the smallest L₂ (Euclidean) norm among those that satisfy identically the calibration equation (8).

2. If N > K then there are more equations than unknowns and, accordingly, it is not possible to fit all the data but only to approximate. The Moore-Penrose pseudoinverse, H⁺ = H^T·(H·H^T)⁻¹ in this case yields the least-squares approximant A = Θ̂·H⁺

In the experiments of Danziger et al. (Danziger et al., 2009) the number of targets was less than the number of glove signals, therefore the MPP algorithm provided a solution of the first kind.

The results of the training are shown for all 3 groups in Figure 10A. The LMS group outperformed the control group significantly during training. This suggests that the adaptive algorithm, based on canceling subjects’ endpoint errors, facilitated faster learning than the control. However, the MPP, which also cancels the average reaching errors, failed to generate better performance than control. Actually, MPP subjects performed worse than control subjects and failed to demonstrate any learning whatsoever. The curious aspect of this result lies in the fact that both the MPP and LMS algorithms are structured to minimize the same cost, the endpoint error of the subject’s movements.

Figure 10.

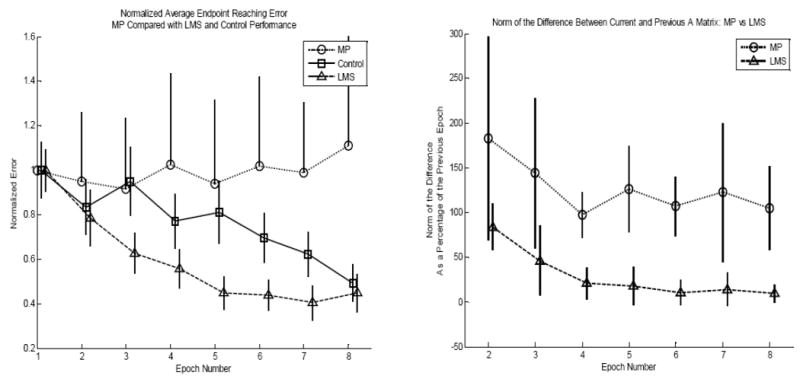
Subject performance over 8 training epochs (1 day). Left: Comparison of subject performance under the Moore-Penrose pseudoinverse (MP) machine learning condition, the least mean squares (LMS) machine learning condition, and the no machine learning (control) condition. Endpoint error is normalized to each subject’s error on the 1^st training epoch. LMS subjects reduce error significantly faster than controls; MP subjects demonstrate no average improvement at all. Right: The norm of the difference between two successive mapping matrices, A, is a measure of how much a machine learning method is changing the structure of A to complete its goal of eliminating error in a set of the subject’s movements. The LMS method makes less marked changes to A, which may explain why subjects in the LMS condition improve performance while those in the MPP condition fail to. Error bars are 95% confidence intervals. (From Danziger et al. 2009)

How can it be that two solutions, which equally compensate for errors, result in such drastically different performances? A plausible explanation for the lack of improvement seen when using the MPP method is that after each update the variation of the map matrix A is unconstrained. When the MPP method solves the underdetermined system it places no restriction on how far, in the space of allowable mappings, the updated matrix is from the previous one. In contrast, the LMS algorithm, while not imposing explicit constraints on the change of A, searches for local minima in the vicinity of its initial conditions (set to be the previous mapping), as all gradient algorithms do. This result can be seen in Figure 10B. The norm of the difference between two successive A matrices is essentially a measure of the magnitude of the change in the mapping caused by an algorithm’s update. The LMS algorithm changed the mappings approximately 50% less than the pseudoinverse solution.

A striking result is that setting the cost function as endpoint error alone - the standard for nearly all adaptive algorithms in HMIs (Hochberg et al., 2006; Pfurtscheller et al., 2000; Taylor, Tillery, & Schwartz, 2002) – yielded only a moderate facilitation of learning rate, and if chosen without limiting the changes from one epoch to the next it became detrimental. Figures 10A and B illustrate clearly that upsetting the balance of the dual learning system, allowing the adaptive algorithm to choose any solution, can be counterproductive. Results for the successful LMS and control groups (Figure 11) indicate that exposure to the adaptive component did not facilitate rapid or superior performance in generalization over controls. This failure to outperform controls on novel areas of the workspace further suggests that an adaptive algorithm blind to factors other than final position error (as is the case for the LMS algorithm) is not adequate to improve performance beyond the trained examples. The LMS algorithm did not demonstrate any benefit in generalization compared to the control. Subjects in the LMS group did not form a more general internal representation of the inverse transformation from target location to hand gestures.

Figure 11.

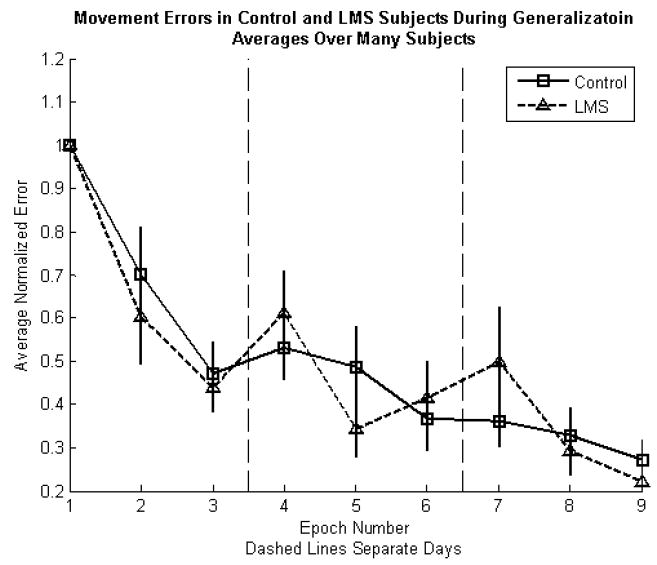
Endpoint errors for generalization targets illustrate that the control and LMS groups perform successfully on tasks for which they have received minimal training. The fact that both groups perform comparably indicates a failure on the part of the LMS algorithm to induce a richer representation of the hand-to-cursor mapping in subjects using the algorithm over subjects without the benefit of a machine learning algorithm. Error bars are 95% confidence intervals. (From Danziger et al. 2008)

Despite these shortcomings, the need for an adaptive element focusing on task-level user performance is apparent. The task was intentionally constructed to be difficult to mimic the challenges faced by users in common HMI applications. Anecdotally, initial subject frustration levels were often unmanageable, and their lack of success and aptitude in early training could cause them to speculate that the experiment was designed to thwart them by constantly shifting mappings. This sentiment was felt by both the controls, where the mapping was fixed, and in the LMS group where the mapping was changing, but in a way designed to assist performance. However, frustration abated much sooner in LMS subjects. This appeared to be a considerable advantage offered by the adaptive algorithm.

5. Conclusions

We began this article by reviewing evidence suggesting that the motor system is deliberately planning the shape of trajectories. This is not an uncontroversial statement. In a recent influential paper, Todorov and Jordan (2002) argued against explicit trajectory planning and affirmed that “deviations from the average trajectory are corrected only when they interfere with task performance.” While this encompasses the entire domain of what one may define as task performance, here we consider a more restrictive view. Movements have immediate goals. For example, reaching an object or hitting a target with a stone. Todorov and Jordan’s approach prescribes that trajectories derive from these explicit terminal goals. Therefore, trajectories are no longer pre-planned, but follow implicitly from optimally aiming to the final goal. An important conclusion from this model is that “the optimal strategy, in the face of uncertainty is to allow variability in redundant (task-irrelevant) dimensions.” This conclusion is not just a speculation but matches a variety of observations (Latash, Scholz, & Schoner, 2002; Scholz & Schoner, 1999). However, the results of the remapping experiments suggest otherwise.

When subjects were faced with task of reorganizing the movements of the fingers to control a simple two-dimensional cursor, they consistently reduced the variance and the amount of motion in those “task- irrelevant” dimensions. We must stress that this is no easy feat. To accomplish this, subjects effectively discovered how the multiplicity of degrees of freedom available from their finger movements collapsed into the motion of the cursor. The motions of the fingers that do not contribute to the motion of the cursor – the “null space” motions – are indeed obtained by particular combinations of individual degrees of freedom. Finding these combinations is computationally expensive, yet, it is fundamental because it allows us to solve an important ill-posed problem (Tikhonov & Arsenin, 1977). This is the problem of deriving in a repeatable manner the gesture of the hand corresponding to a target on the monitor. Furthermore, the movements of the cursor became straighter and smoother with practice, although there is no obvious reason for subjects to do this based on the reaching task itself or the nature of distance in “hand space”. The improvement in attaining the goal followed a time-course independent of the straightening of motions. Thus, it appears that the formation of straighter motions of the controlled endpoint is not a byproduct of optimal reaching.

To put all this succinctly, the remapping experiments suggest that optimizing performance in a specific task is only one component of learning. The other component is about learning the properties of space. These are properties that affect the execution of different motor tasks and that concern the relations among objects in the environment and between these objects and us. How do we reconcile our evidence from remapping with the evidence supporting optimal control? Consider the classic observation by Nicolai Bernstein who pointed out the great variability of arm movements when one performs the simple task of hitting a nail with a hammer (Bernstein, 1967) and that despite this variability, the hammer, i.e., the endpoint of this particular task, always hits the same spot. Here, we suggest that the apparent divergence between these observations and our remapping results may be reconciled by considering the difference between tasks that take place in a well-known geometry (e.g., hitting nails) and tasks that take place in a new geometry (e.g., remapping finger movements or learning to operate a brain-machine interface). An inexperienced subject must first learn to produce a stable map from desired behaviors to motor commands. This is necessary for partitioning the degrees of freedom into task-relevant and task-irrelevant combinations. Once a stable model of this spatial map is acquired, variability can be redirected toward the task-irrelevant subspaces. A piano teacher once said that before trying to improvise variations on a classical theme one needs to master the theme itself. The same wisdom may apply to establishing a tradeoff between planning well-defined trajectories that reflect the geometry of space and allowing for variability to optimize the reaching of particular goals.

The studies that we have presented here support the idea that the first and perhaps most important learning goal in a remapping task is to learn how to embed the controlled space within the articulation space. We suggest that this insight is fundamental for the design of efficient and adaptable human-machine interfaces. The specific engineering problem is to build a system that can continuously optimize the placement of few control axes (e.g. the speed and rotation of a wheelchair) within a high dimensional and variable space of residual motions. At this time, we cannot claim to have solved this problem. We have tested two learning algorithms that adapt the transformation from many degrees of freedom to two cursor coordinates based on the history of reaching errors. Our findings suggest that this approach may lead to faster learning, but not to better learning. In the end, our best algorithm produced the same amount of generalization and the same final performance as a fixed interface that does not change its mapping. This finding reinforces the overall concept of this paper, namely, that the removal of final errors does not seem to be the main component of learning. The framework of optimal control may still help us to understand learning and to design adaptive interfaces. However, one must base the optimization on cost functions that include explicitly not only the reaching of final goals and targets, but also the shaping of trajectories that are consistent with the metric properties of the space in which they take place.