The use of nonregular fractional factorial designs in combination toxicity studies

Abstract

When there is interest to study n chemicals using x dose levels each, factorial designs that require xⁿ treatment groups have been put forward as one of the valuable statistical approaches for hazard assessment of chemical mixtures. Exemplary applications and cost-efficiency comparisons of full factorial designs and regular fractional factorial designs in toxicity studies can be found in Nesnow et al. (1995), Narotsky et al. (1995), and Groten et al. (1996,1997). We introduce nonregular fractional factorial designs and show their benefits using two studies reported in Groten et al. (1996). Study 1 shows nonregular designs can provide the same amount of information using 75% of the experimental costs required in a regular design. Study 2 demonstrates nonregular designs can additionally estimate some partially aliased effects, which cannot be done using regular designs. We also provide a statistical method to evaluate the quality of an assumption made by experts in Study 2 of Groten et al. (1996).

1 Introduction

There is considerable scope for reducing resources used in research by designing more efficient studies. Giles (2006) in a foreword in a recent issue in the journal Nature observed that some toxicology studies seemed to lack so-phisticated thinking in their designs and wondered whether that had led to many inconclusive studies. The importance of a well designed study cannot be over-emphasized. Experiments are increasingly complex, in addition to rising experimental cost and competing resources. In the extreme case, a poorly-designed study may not be able to answer the posited scientific hypotheses. Careful design considerations even with only minor variation in traditional designs can lead to a more efficient study in terms of more precise estimates or able to estimate more effects in the study at the same cost.

A problem in the risk assessment of chemical mixtures is that the chemical interactions hamper prediction of the toxicity of the mixture. It is impossible to test each possible chemical interaction individually because of the multitude of potential interactions. One way to overcome this problem is to treat the mixture as a single compound and to test it as a whole. In this type of study, the net combined effects of all components in the mixture are reflected. Factorial designs are used to detect interactions between two or more chemicals in a chemical mixture. Such designs were suggested by the US Environmental Protection Agency as one valuable statistical approach for risk assessment of chemical mixtures (Svensgaard and Hertzberg 1994). A full factorial experiment allows all factorial effects to be estimated independently and s commonly used in practice (Nesnow et al. 1995, Narotsky et al. 1995). However, it is often too costly to perform a full factorial experiment. For example, if we have 8 factors to investigate and each factor has two levels, we need to have 2⁸ = 256 runs. Instead, a fractional factorial design, which is a subset or fraction of a full factorial design, is often preferred because much fewer runs are required. When this fraction is properly selected, the resulting design can estimate the maximum number of factorial effects of interest with maximum precision.

Fractional factorial designs are classified into two broad types: regular designs and nonregular designs. Regular designs are constructed through defining relations among factors and are described in many textbooks such as Wu and Hamada (2000), Box, Hunter and Hunter (2005) and Montgomery (2009). These designs are widely used in toxicity studies and other biochemical areas because they are simple to construct and to analyze. The run sizes are always a power of 2, 3 or the number of dose levels, and thus the “gaps” between possible run sizes are getting wider as the power increases. Nonregular designs such as Plackett-Burman (1946) designs and other orthogonal arrays are often used in various screening experiments for their run size economy and flexibility (Wu and Hamada 2000). They fill the gaps between regular designs in terms of various run sizes and are flexible in accommodating various combinations of factors with different numbers of levels. Compared to regular designs, nonregular designs have a more complex aliasing structure and thus is more difficult to analyze because main effects may be partially aliased with some interactions. Nevertheless, as we will demonstrate, the complex aliasing structure is a benefit because partially aliased effects can be estimated together. A key step is to disentangle the interactions from the estimates of the main effects. As Hamada and Wu (1992) pointed out, ignoring non-negligble interactions can lead to (i) important effects being missed, (ii) spurious effects being detected, and (iii) estimated effects having reversed signs resulting in incorrectly recommended factor levels.

This paper aims at demonstrating the advantages of nonregular designs over regular designs in two subacute toxicity studies reported in the literature. In particular, we use a 12-run Plackett-Burman design in the first study and a 16-run quaternary-code design in the second study. Both Plackett-Burman and quaternary-code designs are special classes of nonregular designs. These demonstrations show that nonregular designs are able to (i) further reduce the cost of regular designs, (ii) estimate additional interactions besides those that can be done with regular designs, and (iii) further reduce the biases in the effect estimates.

2 Methods

We first use two studies to demonstrate the differences in analyzing data from regular designs and nonregular designs. In particular, we use Groten et al. (1991, 1996) to demonstrate how nonregular designs can be more cost efficient than regular designs. Our second study is taken from Groten et al. (1996, 1997) and we show that nonregular designs can provide additional information on the estimates of some effects that regular designs are unable to do.

Example 1 Interaction of eight minerals with the oral toxicity of cadmium in rats: application of a 12-run Plackett-Burman design

Groten et al. (1991, 1996) performed an 8-week toxicity study in Wistar rats to investigate the effect of several mineral supplements, all of which had been suggested to interact with the accumulation and toxicity of cadmium chloride (CC). The 8 minerals to be tested were calcium (Ca), phosphorus (P), manganese (Mn), magnesium (Mg), selenium (Se), copper (Cn), zinc (Zn) and iron (Fe). In their study, the researchers kept the ratio between Ca and P constant to avoid the interactive effects of each other’s bioavailability. Accordingly, the two minerals Ca and P were always treated as one supplement resulting in a total of 7 mineral supplements under investigation. The experiment used a regular fractional factorial design with 8 test groups. The chemical Cadmium (Cd) was present in all test groups and so we may ignore its contribution to all statistical analyses. The responses included clinical chemistry parameters and mineral content in liver and kidneys. Groten et al. (1996) analyzed the main effects first and then further tested the significant main effects and their aliased two-factor interactions in a subsequent experiment. Further details of the experimental setting and conditions were given in Groten et al. (1996).

Although combining Ca and P as a single mineral supplement enabled the researchers to study eight minerals in eight test groups, their design has two major drawbacks. First, Ca and P were fully aliased and their effects could not be separated. Two effects are fully aliasing if the correlation between them is either −1 or +1. When the ratio of Ca and P was kept constant, one could neither distinguish the effects between them nor discover how they would interact with each other. This might not be a concern for Groten et al. (1996), but this is not desirable in general. Second, the design with 8 test groups for testing 7 mineral supplements is saturated, so there is no degree of freedom left for estimating the error variance or interactions. In their design each main effect is aliased with 3 two-factor interactions. The estimate of the main effect was biased and could be misleading if any of the interactions were significant. As a result, the researchers had to use follow-up experiments to resolve the ambiguity of the interpretation of significant effects, adding the overall cost. To overcome these drawbacks, one has to use a larger design with more test groups.

One possible design would consist of 16 test groups shown in Table 1(a). For instance, the first test group involves four mineral supplements Ca, P, Mg, Cu, in addition to the common mineral Cd. In statistical design terminology, this is a regular 1/16^th fraction of a 2⁸ design or a 2^{8− 4} design. In this design none of the main effects is aliased with two-factor interactions; therefore, all of the eight main effects can be estimated even if some two-factor interactions are non-negligible. Furthermore, there are 7 degrees of freedom left for estimating the error variance or potential significant interactions. One disadvantage of this design is that it doubles the number of test groups. However, to study 8 minerals together (i.e. treat Ca and P separately) , a regular design requires a minimum of 16 test groups.

Table 1.

Test groups in Study 1: Interaction of mineral supplements with the toxicity of CC (a) Test groups of a regular design and (b) Test groups of a nonregular design.

Table (a): 1/16th fraction of a 28 design (Regular Design)
1. + Cd + Ca, P, Mg, Cu	2. + Cd + Ca, P, Fe, Zn
3. + Cd + Ca, P, Se, Mn	4. + Cd + Ca, Mg, Fe, Se
5. + Cd + Ca, Mg, Zn, Mn	6. + Cd + Ca, Fe, Cu, Mn
7. + Cd + Ca, Cu, Zn, Se	8. + Cd + all minerals at a high level
9. + Cd + Mn, Se, Zn, Fe	10. + Cd + Mn, Mg, Se, Cu
11. + Cd + Mg, Cu, Zn, Fe	12. + Cd + P, Mn, Cu, Zn
13. + Cd + P, Se, Cu, Fe	14. + Cd + P, Mg, Se, Zn
15. + Cd + P, Mn, Mg, Cu	16. + Cd + all minerals at a low level
Table (b): 12-run Plackett-Burman design (Nonregular Design)
1. + Cd + Mn, Zn, Fe	2. + Cd + P, Cu, Zn, Fe
3. + Cd + Ca, Se, Cu, Zn	4. + Cd + Mg, Se, Cu, Fe
5. + Cd + Mn, Mg, Se, Zn	6. + Cd + P, Mn, Mg, Cu
7. + Cd + Ca, P, Mn, Se, Fe	8. + Cd + Ca, P, Mg, Zn
9. + Cd + Ca, Mn, Cu	10.+ Cd + P, Se
11.+ Cd + Ca, Mg, Fe	12.+ Cd + all minerals at a high level

To reduce the number of test groups, we suggest to use a nonregular design with 12 test groups shown in Table 1(b). This design is an example of the Plackett-Burman designs available from the large collection of orthogonal arrays given by Plackett and Burman (1946). Since there are only 8 mineral supplements in the study, we choose the first 8 columns in the design, and treat the remaining 3 columns as dummy variables that are negligible. Table 2 gives the units, levels and level assignments of each factor.

Table 2.

Study 1: (a) Factors and levels; (b) Test groups and exposure levels (D1, D2, D3 ae dummy).

(a)
Factor	Unit	Low (−)	High (+)
Ca	%	0.64 – 0.66	1.28 – 1.30
P	%	0.59 – 0.60	1.30 – 1.35
Zn	mg/kg	28 – 29	125 – 140
Cu	mg/kg	7 – 11	46 – 70
Fe	mg/kg	35 – 46	185 – 245
Mg	%	0.046 – 0.047	0.24 – 0.26
Mn	mg/kg	45 – 60	235 – 270
Se	mg/kg	0.09 – 0.11	0.62 – 0.88

(b)
Compounds	Ca	P	Mn	Mg	Se	Cu	Zn	Fe	D1	D2	D3
+Cd+Mn, Zn, Fe	−	−	+	−	−	−	+	+	+	−	+
+Cd+P, Cu, Zn, Fe	−	+	−	−	−	+	+	+	−	+	−
+Cd+Ca, Se, Cu, Zn	+	−	−	−	+	+	+	−	+	−	−
+Cd+Mg, Se, Cu, Fe	−	−	−	+	+	+	−	+	−	−	+
+Cd+Mn, Mg, Se, Zn	−	−	+	+	+	−	+	−	−	+	−
+Cd+P, Mn, Mg, Cu	−	+	+	+	−	+	−	−	+	−	−
+Cd+Ca, P, Mn, Se, Fe	+	+	+	−	+	−	−	+	−	−	−
+Cd+Ca, P, Mg, Zn	+	+	−	+	−	−	+	−	−	−	+
+Cd+Ca, Mn, Cu	+	−	+	−	−	+	−	−	−	+	+
+Cd+P, Se	−	+	−	−	+	−	−	−	+	+	+
+Cd+Ca, Mg, Fe	+	−	−	+	−	−	−	+	+	+	−
+all minerals at a high level	+	+	+	+	+	+	+	+	+	+	+

An obvious advantage of the new plan is the cost efficiency. The Plackett-Burman design uses only 12 test groups, a 25% saving over the regular design with 16 test groups given in Table 1(a). Like the regular design, the Plackett-Burman design allows all eight main effects to be separately estimated. It also provides 3 degrees of freedom to estimate the error variance or potential interactions.

Example 2 Interactive effects of nine chemicals in a 4-week toxicity study: application of a 16-run quarternary-code design

Groten et al. (1996, 1997) performed a 4-week oral/inhalatory study in which the toxicity of combinations of nine compounds was examined in male Wistar rats. The nine chemicals tested were dichloromethane (MC), formaldehyde (For), aspirin (Asp), di-(ethylhexyl) phthalate (DEHP), cadmium chloride (CC), stannous chloride (Sn), butylated hydroxyanisole (BHA), lop-eramide (Lop) and spermine (Sper) at a concentration equal to the “minimum-observed-adverse-effect level” (MOAEL). Their experiment had 16 test groups (Table 3(a)), which is 1/32^nd fraction of a 2⁹ design. Besides assuming that three-factor or higher-order interactions were negligible, Groten et al. (1996, 1997) further assumed that there were no interactions between formaldehyde and other compounds in the study and so they deliberately chose a design such that the main effect of formaldehyde was fully aliased with four two-factor interactions. The aliasing pattern, experimental setting and conditions were reported in Groten et al. (1997).

Table 3.

Test groups in Study 2: Interactive effects between nine chemicals in 4-week toxicity study with the response ASAT: (a) Test groups of a regular design and (b) Test groups of a nonregular design.

Table (a): 1/32nd fraction of a 29 design (Regular Design)
Mixture Components	ASAT	Mixture Components	ASAT
1. +For	70	2. +Sn, MC, Lop, Asp	71
3. +CC, MC, Sper, Asp	86	4. +Sn, CC, Sper, Lop, For	75
5. +BHA, MC, Sper, Lop	65	6. +Sn, BHA, Sper, Asp, For	70
7. +CC, BHA, Lop, Asp, For	96	8. +Sn, CC, BHA, MC	65
9. +DEHP, Sper, Lop, Asp	77	10. +Sn, DEHP, MC, Sper, For	71
11. +CC, DEHP, MC, Lop, For	88	12. +Sn, CC, DEHP, Asp	80
13. +BHA, DEHP, MC, Asp, For	68	14. +Sn, BHA, DEHP, Lop	69
15. +CC, BHA, DEHP, Sper	72	16. +All nine compounds at MOAEL	82
Table (b): 1/32nd fraction of a 29 design (Nonregular Design)
Mixture Components	ASAT	Mixture Components	ASAT
1. +For	70	2. +Sn, MC, Lop, Asp, For	71 + a
3. +CC, MC, Sper, Asp	86	4. +Sn, CC, Sper, Lop, For	75
5. +BHA, MC, Sper, Lop	65	6. +Sn, BHA, Sper, Asp, For	70
7. +CC, BHA, Lop, Asp	96 − a	8. +Sn, CC, BHA, MC	65
9. +DEHP, Sper, Lop, Asp	77	10. +Sn, DEHP, MC, Sper	71 − a
11. +CC, DEHP, MC, Lop, For	88	12. +Sn, CC, DEHP, Asp	80
13. +BHA, DEHP, MC, Asp, For	68	14. +Sn, BHA, DEHP, Lop	69
15. +CC, BHA, DEHP, Sper, For	72 + a	16. +All nine compounds at MOAEL	82

The responses in their study included body weights, organ weights, hematology, clinical chemistry and biochemistry values. They first analyzed the main effects, and then analyzed the significant main effects together with their two-factor interactions in a subsequent analysis. These analyses resulted in equations that describe all hematological and clinical responses in terms of the variables tested. For example, using the aspartate aminotransferase (ASAT) activity (in Table 3(a)) as a response, the fitted regression equation is:

$$\begin{array}{c}\hfill \mathit{\text{ASAT}}(\text{units}/\text{liter})=75.31+3.44*\mathit{\text{Asp}}+5.19*\mathit{\text{CC}}-2.44*\mathit{\text{Sn}}\\ \hfill +2.56*\mathit{\text{Lop}}+2.19*(\mathit{\text{For}}+\mathit{\text{CC}}\times \mathit{\text{Lop}})-2.56*\mathit{\text{CC}}\times \mathit{\text{Sn}}\end{array}$$

where CC × Lop is the interaction between CC and Lop and CC × Sn is the interaction between CC and Sn. Note that we have substituted the two-factor interaction CC × Lop in the original equation in Groten et al. (1996) by a term denoted by (For + CC × Lop) in the above equation, because the coefficient +2.19 is a mixed estimate from two fully aliased effects For and CC × Lop. Because For and CC × Lop are fully aliased, it is impossible to distinguish between them in the analyisis. Groten et al. (1996, 1997) ignored the main effect of For in this aliased pattern mainly because they assumed For was not active based on their expert opinion. However, as we will show below, by using a nonregular design, we can estimate For and CC × Lop together and question the validity of the expert opinion on statistical grounds.

For this study, we propose a nonregular design with 16 test groups displayed in Table 3(b). This design is one of the quaternary-code designs constructed by Xu and Wong (2007, design 9-5.ac in Table 2). The mixtures in all test groups of the nonregular design are the same as those in the regular design, except for test groups #2, #7, #10 and #15. In test groups #2 and #15, we have added For into the original mixture, while in test groups #7 and #10, we have deleted For from the original mixture. Table 4 gives the units, levels and level assignments of each factor.

Table 4.

Study 2: (a) Factors and levels; (b) Test groups and exposure levels.

(a)
Factor (Symbol)	Unit	Low (−)	High (+)
Aspirin (Asp)	mg/kg	0	5000
Cadmium Chloride (CC)	mg/kg	0	50
Stannous Chloride (Sn)	mg/kg	0	3000
Loperamine (Lop)	mg/kg	0	30
Spermine (Sper)	mg/kg	0	2000
Butyl hydroxyanisol (BHA)	mg/kg	0	3000
di(2-ethylhexyl)phthalate (DEHP)	mg/kg	0	1000
Dichloromethane (MC)	ppm	0	500
Formaldehyde (For)	ppm	0	3

(b)
Compounds	For	MC	Asp	CC	Sn	Lop	Sper B	BHA	DEHP	ASAT
+For	+	−	−	−	−	−	−	−	−	70
+Sn,MC,Lop,Asp,For	+	+	+	−	+	+	−	−	−	71 + a
+CC,MC,Sper,Asp	−	+	+	+	−	−	+	−	−	86
+Sn,CC,Sper,Lop,For	+	−	−	+	+	+	+	−	−	75
+BHA,MC,Sper,Lop	−	+	−	−	−	+	+	+	−	65
+Sn,BHA,Sper,Asp,For	+	−	+	−	+	−	+	+	−	70
+CC,BHA,Lop,Asp	−	−	+	+	−	+	−	+	−	96 − a
+Sn,CC,BHA,MC	−	+	−	+	+	−	−	+	−	65
+DEHP,Sper,Lop,Asp	−	−	+	−	−	+	+	−	+	77
+Sn,DEHP,MC,Sper	−	+	−	−	+	−	+	−	+	71 − a
+CC,DEHP,MC,Lop,For	+	+	−	+	−	+	−	−	+	88
+Sn,CC,DEHP,Asp	−	−	+	+	+	−	−	−	+	80
+BHA,DEHP,MC,Asp,For	+	+	+	−	−	−	−	+	+	68
+Sn,BHA,DEHP,Lop	−	−	−	−	+	+	−	+	+	69
+CC,BHA,DEHP,Sper,For	+	−	−	+	−	−	+	+	+	72 + a
+all compounds at MOAEL	+	+	+	+	+	+	+	+	+	82

For illustrative purposes, we focus on the ASAT activity as the only response in this study. Data from Groten et al. (1996) for the study are shown in Table 3(a). To compare our proposed design with the design used in Groten et al. (1996), we have to generate reasonable responses from runs in our design but were not used in Groten’s design. Fortunately by construction, we can predict how the set of responses will be for our design. Specifically, the only changes we expect are shown in the column of ASAT in Table 3(b), where there are now “±a” in test groups #2, #7, #10 and #15. Here the value of “a” represents the hypothetical effect of For on the response ASAT when we add For into the original mixture.

Clearly the value of a is unknown without running a real study using our design. We can however provide realistic guesses of likely values for a. In this case, we consider likely values of a to be −4, −2, 0, 2 and 4. The rationale for picking these values of a is consistent with the magnitude of the observed effects from the real experiment. The values of a may be interpreted as follows: for example, if a = −2, this reflects a significant negative effect, meaning that when we add For into the mixture, the ASAT is expected to decrease significantly, other things being equal. Likewise, a value of a = 2 implies that we can expect a significant increase in the mean ASAT level when For is included in the mixture. As an illustration, suppose a = −2. Our responses in test groups #2, #7, #10 and #15 will change from 71, 96, 71, 72 to 69, 98, 73, 70 respectively, and other responses remain unchanged. Note that the added effect “±a” only changes the estimate of the main effect of For and its aliased interactions including CC × Lop, but it will not affect the estimates of other main effects and interactions. For example, one can verify that the estimate of Sn is always −2.44 for any choice of a.

The main reason that regular designs are incapable of estimating some interactions is that these interactions are fully aliased with the main effects or other interactions. This is a property of the regular design where fully aliasing is the only possible kind of aliasing. In nonregular designs, partial aliasing is possible, that is, the correlation between two effects is strictly between −1 and 0 or between 0 and +1. For example, the correlation between For and CC × Lop is 0.5 and they are partially aliased in the nonregular design. Since For is only partially aliased with other interactions including CC × Lop, it is not necessary to assume that For is not active as Groten et al. (1996, 1997) did. In addition, partial aliasing reduces the bias of the estimation of main effects from non-negligible two-factor interactions.

3 Results

Groten et al. (1996) did a 4-week toxicity study with nine chemicals and showed that combined exposure to nine compounds at the “minimum-observed-adverse-effect level”(MOAEL) of the individual compounds resulted in a wide range of adverse effects. Their factorial analysis suggested that the main effects of Sn, CC, Lop, Asp and the interactions between CC and Lop and between CC and Sn were significant to the response aminotransferase (ASAT) activity. If the significant level were increased to 15%, the main effect of buty-lated hydroxyanisole (BHA) would also be significant to the response. They purposely designed their experiment such that formaldehyde (For) was fully aliased with four two-factor interactions, including the significant interaction between CC and Lop. Then they suggested choosing the interaction, rather than the main effect, as one of the significant effects based on their expert knowledge, even though the analysis failed to distinguish between them.

The nonregular design has a distinct advantage over the regular design because it allows the estimation of all of the main effects, even when they are partially aliased with some two-factor interactions. In our case, we were able to identify the significance of For and its partially aliased two-factor interactions together. For example, six compounds were found to affect the ASAT activity when we generated the response with a = −2: there was a decrease in ASAT activity due to Sn or BHA or For, and an increase in ASAT activity caused by CC, Asp or Lop. Two interactions (CC × Lop and CC × Sn) included in the original analysis of the regular design were also found to be significant in our analysis.

Following Groten et al. (1996), we have a final equation to describe the value of the response in any particular mixture in terms of the compounds tested. The final equation for the ASAT activity with a = −2 is:

$$\begin{array}{cc}\hfill \mathit{\text{ASAT}}(\text{units}/\text{liter})& \hfill =75.31+3.44*\mathit{\text{Asp}}+5.19*\mathit{\text{CC}}-2.44*\mathit{\text{Sn}}\\ \hfill & \hfill +2.56*\mathit{\text{Lop}}-1.94*\mathit{\text{BHA}}-3.54*\mathit{\text{For}}\\ \hfill & \hfill +4.46*\mathit{\text{CC}}\times \mathit{\text{Lop}}-2.56*\mathit{\text{CC}}\times \mathit{\text{Sn}}\end{array}$$

where Asp, CC, Sn, Lop, BHA and For are the level assignments of the corresponding compounds in the mixture, having a value of either +1 (presence) or −1 (absence). For every random selection of mixtures from the nine compounds tested, it is possible to predict the overall effect for the ASAT activity with the final equation.

This equation can be interpreted as follows. When 5000mg acetyl salicylic acid per 1kg diet is added and the exposure levels of other chemicals are fixed, the ASAT activity increases by 6.88(= 3.44×2) units/liter. The interpretations for For and BHA are similar. However, the interpretations for Sn, Lop and CC are more complicated because of the existence of two-factor interactions. When 3000mg stannous chloride per 1kg diet without cadmium chloride is added and the exposure levels of other chemicals are fixed, the ASAT activity increases by 0.24(= (−2.44+(−2.56)(−1))×2) units/liter. If cadmium chloride exists in the diet, then the addition of stannous chloride leads to a decrease in the ASAT activity by 10.00 units/liter because (−2.44 + (−2.56)(+1)) × 2 = −10.00. Similarly, the interpretation for Lop depends the presence of CC while the interpretation for CC depends the presence or absence of both Sn and Lop.

4 Discussion

Our first study illustrates the run size economy of nonregular designs without sacrificing the estimation abilities of the designs. The number of test groups or trials in an experiment using regular designs is always a power of the number of dose levels. To study 8 mineral supplements, each with two dose levels, a regular design requires at least 16 test groups while a nonregular design uses only 12 test groups. Nonregular designs are also flexible in accommodating various combinations of factors with different numbers of dose levels.

Our second study illustrates how a nonregular design provides additional information of the interactions through their partially aliasing with the main effects. Groten et al. (1996) noticed that the combined effects of two compounds were not a simple summation of responses of the individual compounds. In a regular design, independent estimates of a fully aliased pair of factorial effects are impossible without additional assumptions on the significance of the aliased factorial effects. However, by proper choice of a nonregular design, we were able to decouple the partial aliasing between main effects and two-factor interactions and so able to estimate both effects simultaneously. This is possible as long as there are enough degrees of freedom left in the model.

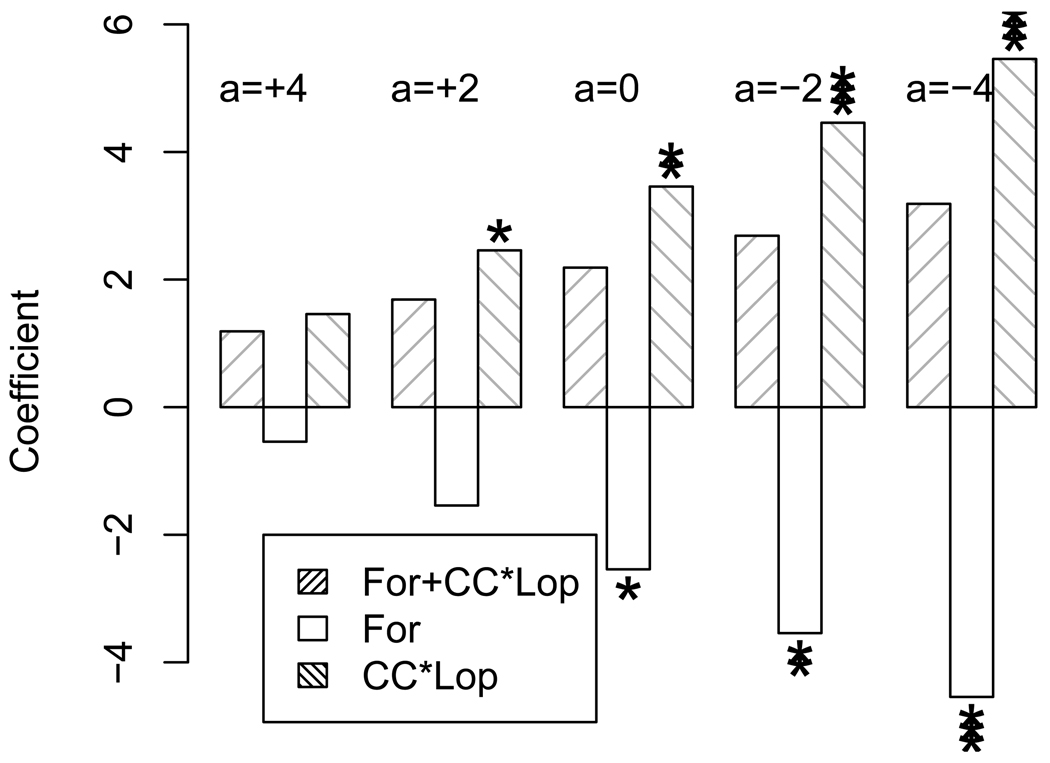
We demonstrate this advantage via Study 2. The analysis of Groten et al. (1996) showed the significance of the CC × Lop interaction under the assumption that For were negligible due to their expert knowledge. Figure 1 provides a test on the significance of the estimates of the main effect of For and the CC × Lop interaction. We use the original equation from Groten et al. (1996) and vary different values of a. In Figure 1, For and CC × Lop represent the estimates of the individual effects using the nonregular design, while (For + CC × Lop) represents the estimates of the fully aliased effects of For and CC × Lop using the regular design.

Figure 1.

A comparison of the magnitudes and the significance of the estimated coefficients of, (For + CC × Lop) in the final equation of ASAT using the regular design with the corresponding magnitudes and coefficients for For and CC × Lop in the final equation of ASAT using the nonregular design when the value of “a” varies from +4, +2, 0, −2 to −4. The height of a bar represents the magnitude of the estimate and the number of asterisks represents the significance level (0:01 <* P < 0.05, 0.001 <** P < 0:01 and ***P < 0:001).

One of the most surprising results is that when a = 0, For has a negative effect, CC × Lop has a positive effect, and both For and CC × Lop are significant at 5% level while (For + CC × Lop) is not. Recall that the value of “a” is the additional hypothetical effect of For on the response ASAT when we add For into the original mixture. Groten et al. (1996) assumed that the main effect of For was negligible in their analysis. If their assumption was correct, we would expect that For is not significant when a = 0. The contradiction provides statistical evidence to question their expert opinion on the insignificance of For. Our finding further suggests that the interaction CC × Lop could be underestimated by Groten et al. (1996) because For had a negative effect.

When we deliberately add a negative effect (like a = −2 or a = −4) to For, both For and CC × Lop are significant at 1% significance level while (For + CC × Lop) is not significant at 10% significance level. This shows how the nonregular design correctly identifies the significance of both For and CC ×Lop individually but the regular design fails to do so. On the other hand, when we add a positive effect a = 2 to For, CC × Lop is significant at 5% level but For and For + CC × Lop are not. This is not surprising because the additional positive effect cancels the original negative effect of For.

Furthermore, the nonregular design can reduce the bias in the estimates of the main effects when not all two-factor interactions are negligible. If it is not known in advance which interactions can be considered as negligible, a conservative approach is to minimize the maximum possible bias arising from the existence of two-factor interactions in the true model. Because main effects are partially aliased with two-factor interactions in nonregular designs but not in regular designs, it follows that the maximum value of the bias could be relatively small in nonregular designs. This implies that the estimates of the main effects suffer a smaller bias in nonregular designs than in regular designs.

To fix ideas, consider the bias of the estimate of a main effect from both the regular design and the nonregular design. In the regular design, the expected value of the estimate of the main effect of For is

$$E({\hat{\beta }}_{\mathit{\text{For}}})={\beta }_{\mathit{\text{For}}}+{\beta }_{\mathit{\text{MC}}\times \mathit{\text{DEHP}}}+{\beta }_{\mathit{\text{Asp}}\times \mathit{\text{BHA}}}+{\beta }_{\mathit{\text{CC}}\times \mathit{\text{Lop}}}+{\beta }_{\mathit{\text{Sn}}\times \mathit{\text{Sper}}}$$

This expression includes the main effect of For and four two-factor interactions with coefficients all equal to 1. The aliasing structure of the nonregular design is more complicated than that of the regular design. Table 5 gives the expected value of the estimate of each main effect when two-factor interactions are present. All the expressions include some two-factor interactions with coefficients all equal to ±1/2. Therefore, if there is no prior information on which interactions can be considered as negligible, a conservative approach in minimizing the coefficients is to minimize their maximum value, which is 1 in the case of the regular design and 1/2 in the case of the nonregular design. This shows that there is a larger bias in the regular design than in the non-regular design. Further details on bias reduction are given in Wu and Hamada (2000) and Deng and Tang (2002).

Table 5.

Aliasing structure between each main effect and two-factor interactions in the quaternary-code design used in Study 2.

$\begin{array}{cc}\hfill E({\hat{\beta }}_{\mathit{\text{For}}})=& \hfill {\beta }_{\mathit{\text{For}}}+\frac{1}{2}({\beta }_{\mathit{\text{MC}}\times \mathit{\text{Asp}}}+{\beta }_{\mathit{\text{MC}}\times \mathit{\text{Lop}}}-{\beta }_{\mathit{\text{MC}}\times \mathit{\text{Sper}}}+{\beta }_{\mathit{\text{MC}}\times \mathit{\text{DEHP}}}\\ & \hfill -{\beta }_{\mathit{\text{Asp}}\times \mathit{\text{CC}}}+{\beta }_{\mathit{\text{Asp}}\times \mathit{\text{Sn}}}+{\beta }_{\mathit{\text{Asp}}\times \mathit{\text{BHA}}}+{\beta }_{\mathit{\text{CC}}\times \mathit{\text{Lop}}}\\ & \hfill +{\beta }_{\mathit{\text{CC}}\times \mathit{\text{Sper}}}+{\beta }_{\mathit{\text{CC}}\times \mathit{\text{DEHP}}}+{\beta }_{\mathit{\text{Sn}}\times \mathit{\text{Lop}}}+{\beta }_{\mathit{\text{Sn}}\times \mathit{\text{Sper}}}\\ & \hfill -{\beta }_{\mathit{\text{Sn}}\times \mathit{\text{DEHP}}}-{\beta }_{\mathit{\text{Lop}}\times \mathit{\text{BHA}}}+{\beta }_{\mathit{\text{Sper}}\times \mathit{\text{BHA}}}+{\beta }_{\mathit{\text{BHA}}\times \mathit{\text{DEHA}}})\end{array}$

$E({\hat{\beta }}_{\mathit{\text{MC}}})={\beta }_{\mathit{\text{MC}}}+\frac{1}{2}({\beta }_{\mathit{\text{For}}\times \mathit{\text{Asp}}}+{\beta }_{\mathit{\text{For}}\times \mathit{\text{Lop}}}-{\beta }_{\mathit{\text{For}}\times \mathit{\text{Sper}}}+{\beta }_{\text{For}\times \mathit{\text{DEHP}}})$

$E({\hat{\beta }}_{\mathit{\text{Asp}}})={\beta }_{\mathit{\text{Asp}}}+\frac{1}{2}({\beta }_{\mathit{\text{For}}\times \mathit{\text{MC}}}-{\beta }_{\mathit{\text{For}}\times \mathit{\text{CC}}}+{\beta }_{\mathit{\text{For}}\times \mathit{\text{Sn}}}+{\beta }_{\mathit{\text{For}}\times \mathit{\text{BHA}}})$

$E({\hat{\beta }}_{\mathit{\text{CC}}})={\beta }_{\mathit{\text{CC}}}+\frac{1}{2}(-{\beta }_{\mathit{\text{For}}\times \mathit{\text{Asp}}}+{\beta }_{\mathit{\text{For}}\times \mathit{\text{Lop}}}+{\beta }_{\mathit{\text{For}}\times \mathit{\text{Sper}}}+{\beta }_{\mathit{\text{For}}\times \mathit{\text{DEHP}}})$

$E({\hat{\beta }}_{\mathit{\text{Sn}}})={\beta }_{\mathit{\text{Sn}}}+\frac{1}{2}({\beta }_{\mathit{\text{For}}\times \mathit{\text{Asp}}}+{\beta }_{\mathit{\text{For}}\times \mathit{\text{Lop}}}+{\beta }_{\mathit{\text{For}}\times \mathit{\text{Sper}}}-{\beta }_{\mathit{\text{For}}\times \mathit{\text{DEHP}}})$

$E({\hat{\beta }}_{\mathit{\text{Lop}}})={\beta }_{\mathit{\text{Lop}}}+\frac{1}{2}({\beta }_{\mathit{\text{For}}\times \mathit{\text{MC}}}+{\beta }_{\mathit{\text{For}}\times \mathit{\text{CC}}}+{\beta }_{\mathit{\text{For}}\times \mathit{\text{Sn}}}-{\beta }_{\mathit{\text{For}}\times \mathit{\text{BHA}}})$

$E({\hat{\beta }}_{\mathit{\text{Sper}}})={\beta }_{\mathit{\text{Sper}}}+\frac{1}{2}(-{\beta }_{\mathit{\text{For}}\times \mathit{\text{MC}}}+{\beta }_{\mathit{\text{For}}\times \mathit{\text{CC}}}+{\beta }_{\mathit{\text{For}}\times \mathit{\text{Sn}}}+{\beta }_{\mathit{\text{For}}\times \mathit{\text{BHA}}})$

$E({\hat{\beta }}_{\mathit{\text{BHA}}})={\beta }_{\mathit{\text{BHA}}}+\frac{1}{2}({\beta }_{\mathit{\text{For}}\times \mathit{\text{Asp}}}-{\beta }_{\mathit{\text{For}}\times \mathit{\text{Lop}}}+{\beta }_{\mathit{\text{For}}\times \mathit{\text{Sper}}}+{\beta }_{\mathit{\text{For}}\times \mathit{\text{DEHP}}})$

$E({\hat{\beta }}_{\mathit{\text{DEHP}}})={\beta }_{\mathit{\text{DEHP}}}+\frac{1}{2}({\beta }_{\mathit{\text{For}}\times \mathit{\text{MC}}}+{\beta }_{\mathit{\text{For}}\times \mathit{\text{CC}}}-{\beta }_{\mathit{\text{For}}\times \mathit{\text{Sn}}}+{\beta }_{\mathit{\text{For}}\times \mathit{\text{BHA}}})$

The second study shows a potential drawback of a nonregular design is that its aliasing pattern can be more complicated than that from a regular design. However, we feel that the advantages of nonregular designs outweigh their disadvantages.

As a final note, all the designs discussed here are two-level designs. While two-level designs are cost-effective in screening variables, they cannot identify nonlinear relationship between the response and factors. A linear relationship is good approximation when the high and low dose levels are close enough. The approximation becomes worse when the distance between two levels increases. One way to cope with this concern is to add a few (3–5) runs at the center. Adding center points to a two-level design can not only provide a check on a curvature effect but also provide an unbiased estimate of the error variance. If a curvature effect is present, the researchers should conduct further experiments to investigate the nonlinear relationship.

Aberration

ASAT

aspartate aminotransferase

Asp

aspirin

BHA

butylated hydroxyanisole

Cd

cadmium

CC

cadmium chloride

Ca

calcium

Cu

copper

MC

dichloromethane

DEHP

di-(ethylhexyl; phthalate

For

formaldehyde

Fe

iron

Lop

loperamide

Mn

manganese

Mg

magnesium

MOAEL

minimum-observed-adverse-effect level

P

phosphorus

Se

selenium

Sper

spermine

Sn

stannous chloride

Zn

zinc

Appendix: Statistical Analysis Strategy

We provide more details on how we perform analysis in study 2. We adopt one of the analysis strategies suggested by Hamada and Wu (2000, p. 356). The procedure is as follows.

Step 1 For each factor X, consider X and all its two-factor interactions XY with other factors. Use a stepwise regression procedure to identify significant effects from the candidate variables and denote the selected model by M_X. Repeat this for each of the factors and then choose the best model.

Step 2 Use a stepwise regression procedure to identify significant effects among the effects identified in the previous step as well as all the main effects.

Step 3 Consider (i) the effects identified in step 2 and (ii) the two-factor interactions that have at least one component factor appearing among the main effects in (i). Use a stepwise regression procedure to identify significant effects among effects in (i) and (ii).

We iterate between steps 2 and 3 until the selected model does not change. We may have an over-parameterized model, i.e., more variables than the number of runs, in steps 2 and 3. In such a case we replace stepwise regression with forward selection.

In step 1 we compare nine different models, each consisting of a main effect and some two-factor interactions selected via stepwise regression. Guided by the prior information that For does not interact with other compounds, we choose a model consisting of the main effect of CC and three two-factor interactions CC × Lop, CC × Sn and CC × Asp. In step 2 we consider all main effects and the three interactions suggested in step 1. When stepwise regression is applied, there are eight significant effects at the 5% significance level. They are Asp, CC, Sn, Lop, BHA, For, CC × Lop and CC × Sn. Note that CC × Asp is no longer significant. In step 3 we consider the eight significant effects identified in step 2 together with two-factor interactions that have at least one component factor appearing among the six main effects in step 2. Forward selection does not find any additional significant effects and thus there is no need to iterate between steps 2 and 3. The final model consisting of the eight effects has a multiple R-squared of 0.97, indicating a good fit.

The analysis strategy works well under the following two conditions: (1) only a few effects are statistically significant and (2) when a two-factor interaction is significant, at least one of the corresponding factor main effects is also significant. In practice it is possible to obtain uninterpretable models that consist of an interaction term without any of its parent main effects. It is also possible that the analysis procedure finds several incompatible models that are equally plausible. When these happen, it is a strong indication that the information provided in the data and design is limited and no analysis method can rescue. One solution is to conduct follow-up experiments using additional runs. See Wu and Hadamard (2000, Section 4.4) and Box, Hunter and Hunter (2005, Section 7.2) for choosing follow-up runs.