Contribution of individual histidines to the global stability of human prolactin

Abstract

A member of the family of hematopoietic cytokines human prolactin (hPRL) is a 23k kDa polypeptide hormone, which displays pH dependence in its structural and functional properties. The binding affinity of hPRL for the extracellular domain of its receptor decreases 500-fold over the relatively narrow, physiologic pH range from 8 to 6; whereas, the affinity of human growth hormone (hGH), its closest evolutionary cousin, does not. Similarly, the structural stability of hPRL decreases from 7.6 to 5.6 kcal/mol from pH 8 to 6, respectively, whereas the stability of hGH is slightly increased over this same pH range. hPRL contains nine histidines, compared with hGH's three, and they are likely responsible for hPRL's pH-dependent behavior. We have systematically mutated each of hPRL's histidines to alanine and measured the effect on pH-dependent global stability. Surprisingly, a vast majority of these mutations stabilize the native protein, by as much as 2–3 kcal/mol. Changes in the overall pH dependence to hPRL global stability can be rationalized according to the predominant structural interactions of individual histidines in the hPRL tertiary structure. Using double mutant cycles, we detect large interaction free energies within a cluster of nearby histidines, which are both stabilizing and destabilizing to the native state. Finally, by comparing the structural locations of hPRL's nine histidines with their homologous residues in hGH, we speculate on the evolutionary role of replacing structurally stabilizing residues with histidine to introduce pH dependence to cytokine function.

Introduction

Many molecular processes in human biology depend on the effective hydrogen ion concentration, or pH, within the local microenvironment. In particular, protein cytokines are likely exposed to solution acidities ranging from pH 5 to 8 during their functional lifetimes. Although the pH of both blood and the intracellular cytosol are tightly regulated within a few tenths of a unit near 7.3, the acidity of interstitial fluid displays much greater variety, generally ranging from pH 6.5 to 7.7.¹ Malignant tissues consistently demonstrate more acidic interstitial fluid by as much as 0.5 pH units lower than their surrounding stroma. Another source of pH variation occurs after cytokines bind and activate their cell surface receptors, when they are internalized by endocytosis. As the resulting intracellular endosomes mature, their internal pH lowers from an initial value determined by extracellular fluid to a low value around 5.5–6.0. Frequently, this increase in solution acidity causes dissociation of receptor-bound ligands and the cessation of cytoplasmic signaling.² The decreased pH also activates endosomal proteases, which cleave and inactivate internalized ligands.³ In many cases, the structural and biophysical consequences of physiological variations in pH on protein cytokines are not well understood. Biochemically, the most likely “sensor” across the pH range of 6–8 is the imidazole ring of histidine side chains. With typical pK_a values between 6 and 7, it represents the only amino acid whose protonation is generally responsive to pH changes in this physiologic range. Human prolactin (hPRL) contains nine histidines on its surface, more than expected for its size, and we previously reported a dependence of its structural and functional properties on solution acidity across a physiologic pH range.⁴ Specifically, the structural stability of the recombinant protein decreases from 7.6 kcal/mol at pH 8 to 5.6 kcal/mol at pH 6. More striking is the greater than 500-fold decrease in the equilibrium association constant for the extracellular domain of the hPRL receptor over this same relatively narrow pH range.

Using hPRL as a case study, we are currently systematically investigating the molecular consequences of histidine protonation. We recently reported the site-specific pK_a values for eight of the nine His imidazoles in hPRL,⁵ as determined using NMR spectroscopy. Individual protonation constants ranged from 5.0 to 6.6, a distribution that appears shifted toward lower pK_a values. Interestingly, the localized triplet of H27, H30, and H180, found within the high affinity receptor-binding site, displayed strong negative cooperativity in their protonation reactions. Here, we present the effect of systematic, single-site mutation of each of hPRL's histidines on the global stability of the protein. We also utilize double-mutant cycles to analyze the energetic interactions between selected histidines. As human growth hormone (hGH) is its closest homologue yet does not display the same pH-dependent properties, we compare the structural locations of histidines in hPRL with homologous residues in hGH, during which we identify a conserved, secondary hydrophobic bundle in both proteins differing only in its pH dependence. Finally, we speculate on the evolutionary importance of histidines in the language of polypeptides, wondering if their importance lies not in their contributions to stabilization of protein structure but, instead, in regulating their responsiveness to variation in acidity across the range from pH 6 to 8, experienced by a majority of secreted, eukaryotic proteins throughout their functional lifetimes.

Results and Discussion

Effect of single His to Ala mutations on hPRL stability

The fluorescence-detected urea denaturation data for wild-type (WT) hPRL and each of the single histidine to alanine mutants are shown in Figure 1. Each dataset is matched by its corresponding least-squared curve fit, as described by Eq. (1) later, along with the results for the WT protein for visual comparison. Best-fit parameters (ΔG_unf, m, and [urea]_1/2) from each curve fit are listed in Table I. The pH dependence to hPRL's global stability is evidenced by changes in both the slope and midpoint of its denaturation curves between pH 5.8 and 7.8. These pH values were chosen for their physiologic significance and because they are well separate from the likely range of pK_a values for non-His titratable residues. With the exception of H173, all histidines in hPRL should have pK_a values at 25°C within this range. However, interpretation of the significance of H173 mutation on the pH dependence of hPRL global stability will be somewhat limited. The single-site His to Ala mutants of hPRL generally display similar pH dependences in their denaturation profiles, albeit with variable changes in both the midpoints and slopes of their global unfolding transitions. In general, there is a good agreement between the changes in global stability implied by visual inspection of the denaturation curves and the best-fit ΔG_unf values presented in Table I. Finally, we note that the denaturation profile of the H59A mutant differs from all other hPRL variants. At low urea concentrations, a steep slope is found in the “pretransition” baseline at both pH values. Typically, nonzero slopes in either the pre- or posttransition baselines of denaturation curves are modeled as a linear dependence of the intrinsic fluorescence of the native or denatured states, respectively, on urea concentration. However, an alternative interpretation involves a two-step unfolding reaction, including native, intermediate, and denatured state conformations. Although we do not exclude this possibility for hPRL, the current data do not warrant quantitative characterization of such more complex models.

Figure 1.

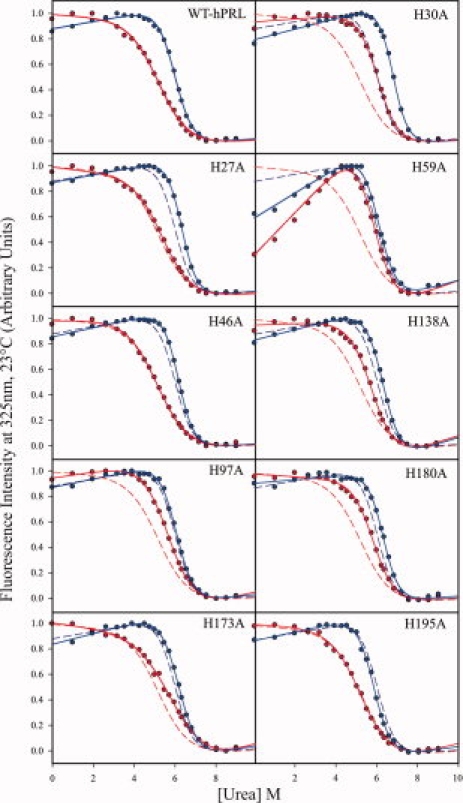
Fluorescence-detected urea denaturation data and curve fits for WT-PRL and each of its single-site histidine to alanine mutants at pH 5.8 (mauve) and 7.8 (dark blue). Curve fits for wild-type hPRL are shown in each plot for visual comparison, illuminated by dashed lines.

Table I.

Summary of Denaturation Data Curve-Fitted Parameters

	pH 5.8 KPO4			pH 7.8 KPO4
Protein	m	[D]1/2	ΔGunf	m	[D]1/2	ΔGunf
WT-PRL	0.79	5.48	4.30	1.35	6.08	8.20
H27A-PRL	0.77	5.71	4.39	1.49	6.35	9.49
H30A-PRL	1.20	6.18	7.40	1.51	6.79	10.25
H46A-PRL	0.81	5.14	4.19	1.58	6.19	9.75
H59A-PRL	1.13	5.81	6.56	1.35	6.08	8.18
H97A-PRL	0.94	5.72	5.37	1.40	6.10	8.53
H138A-PRL	1.08	5.87	6.34	1.38	6.38	8.78
H173A-PRL	0.76	5.98	4.54	1.26	6.22	7.85
H180A-PRL	0.96	5.94	5.69	1.28	6.36	8.16
H195A-PRL	0.81	5.29	4.27	1.42	5.85	8.32
H27A/H30A-PRL	1.24	6.27	7.76	1.39	6.94	9.62
H27A/H180A-PRL	1.05	6.08	6.36	1.62	6.64	10.77
H30A/H173A-PRL	1.19	6.70	8.00	1.49	6.53	9.73
H30A/H180A-PRL	1.17	6.31	7.36	1.37	6.71	9.20
H173A/H180A-PRL	0.93	6.49	6.01	1.17	6.66	7.79
H27A/H30A/H180A-PRL	1.16	6.67	7.71	1.59	7.10	11.31
H30A/H173A/H180A-PRL	1.22	6.81	8.28	1.31	6.94	9.07

To better visualize changes in the pH dependence of global stability due to mutation of individual His residues, Figure 2(A) plots the best-fit free energy of unfolding (ΔG_unf) for each hPRL variant. It is immediately evident that mutation of any His residue in hPRL to Ala generally stabilizes the folded protein at either or both pH values. Interestingly, the greatest stabilization results from mutation of H30, which is in close proximity to H27 and H180 in the tertiary structure and whose protonation reactions are strongly linked thermodynamically.⁵ As stabilization is equivalent at both pH values, the overall pH dependence of H30A is similar to WT hPRL, and thus protonation of this residue does not appear to contribute significantly to the overall pH-dependent stability of the native protein. Equivalent conclusions can be reached for residues H97, H138, H173, H180, and H195 based on the trends seen in Figure 2(A). However, mutation of the three remaining residues (H27, H46, and H59) does alter the pH dependence of hPRL global stability. H27A and H46A are selectively stabilized at pH 7.8, resulting in an overall increase in slope. In contrast, a reduction in the pH dependence of stability is observed for H59A-hPRL, because of selective stabilization of the native conformation at lower pH.

Figure 2.

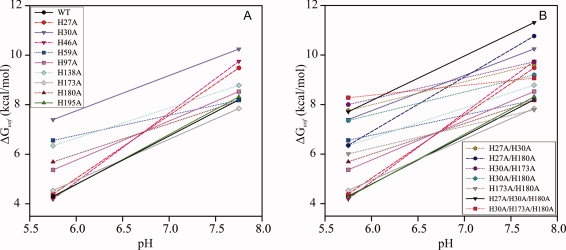
Summary of ΔG_unf results from fluorescence-detected urea denaturation experiments for WT-hPRL and its (A) single-site histidine mutants and (B) multisite histidine mutants. General pH-dependent trends are highlighted by traces, with decreases in pH dependence relative to WT-PRL highlighted by dotted lines, and increased pH dependence denoted by dashed lines. The traces are shown to emphasize the apparent pH-dependent trend of two data points and should not be interpreted to represent a complete theoretical or empirical-based pH-dependent model over the pH range of the two data points.

A number of double and triple His to Ala mutants, involving residues H27, H30, H173, and H180, were constructed for the analysis of interaction free energies,^6–8 described later. The pH dependences of their individual global stabilities are displayed in Figure 2(B). All the combination mutants demonstrate an increase in ΔG_unf relative to WT hPRL at both pH values, with the sole exception of H173A/H180A, which shows no increase in stability at high pH. Interestingly, all of the hPRL variants including the H173A mutation display an overall decrease in pH-dependent stability compared with WT. In contrast, the only combination to show increased pH dependence is H27A/H180A, which is consistent with the increased pH dependence seen for H27A alone. The observation that the H27A/H30A does not similarly show increased pH dependence suggests a compensatory change in one or more additional titratable residues, potentially H180. Finally, the triple mutant H27A/H30A/H180A shows the highest stability of all the hPRL variants (at pH 7.8) with pH dependence similar to WT; whereas, the H30A/H173/H180A mutant has the flattest pH dependence.

Structural rationalization for pH-dependent changes to ΔG_unf

Table II summarizes the experimentally derived pK_a values, calculated solvent accessibilities, tautomeric states, intramolecular structural contacts, and general ΔG_unf trends for each of the His imidazoles in hPRL. All pK_a and tautomeric state data were empirically measured at 35°C as described elsewhere.⁵ Our urea denaturation studies have been performed at 23°C; however, a preliminary analysis of His protonation in hPRL by NMR at that temperature reveals only minor shifts in pK_a values, on an average 0.13 U higher, compared with the previous analysis at 35°C. We attempted urea denaturation studies at the higher temperature, but the quality of the data was poor. Therefore, we have chosen to use temperature mismatched data in this analysis, as it should not affect our essentially qualitative conclusions. Imidazole ring contacts were generated from analysis of the crystal structure of Δ(1-10)G129R-hPRL (PDB: 2q98)¹² using the program STING,¹¹ with solvent accessibility calculated from ASAView⁹ and GetArea.¹⁰ Using this accumulated information, we have attempted to structurally rationalize changes in the pH dependence of global stability because of individual His to Ala mutations. In this analysis, we begin with the basic assumption, supported by the surprising stabilizing effect of a majority of His to Ala mutations, that His imidazole rings in hPRL are generally able to make more favorable interactions in the denatured state compared with the folded protein. Therefore, removal of any imidazole ring by mutation to Ala results in a generic stabilization of folded hPRL, regardless of pH. This finding appears consistent with the group transfer free energy model of osmolyte-induced protein unfolding, where updated transfer free energies (ΔΔG_tr) as a function of surface area predict, in 1M urea, a positive change in ΔΔG_tr (i.e., stabilizing contribution) when mutating from His to Ala in proteins.^13,14 Although this Transfer Model has proven useful for predicting the efficacy of an osmolyte-induced protein folding or unfolding reaction, to date, the transfer free energies have been determined for histidine only at neutral pH, presumably where most histidines are not charged. This limits the utility of this model in describing the pH-dependent changes observed for hPRL. Thus, the specific structural interactions identified for each individual His residue and the corresponding effect of their mutation on the pH dependence of global stability will be interpreted qualitatively relative to the generic stabilization of a His to Ala mutation in hPRL.

Table II.

Summary of Histidine Imidazole pK_a Values, Tautomeric States, Calculated Solvent Accessibility, and Key Structural Interactions in WT-hPR

Res	Solvent exposurea	pKab	Tautomeric state	Effect of mutation on pH-dependence of ΔGunf	Imidazole ring structural interactions (pH > 7)c
H27	0.51/0.63	6.6	NE2-H	Increased	Salt bridge with D183
					H-bond donor with N31(sc)
H46	0.69/0.61	6.6	NE2-H	Increased	Salt bridge with D41
					Aromatic-cation stacking with K42
					H-bond donor with K42(bb)
H59	0.15/0.08	5.8	NE2-H	Decreased	H-bond acceptor with S90(sc)
					Aromatic stacking with W91/W150
H30	0.15/0.20	6.0	ND1-H	Similar	Aromatic stacking with H180
					H-bond donor with S179(sc)
H180	0.46/0.55	6.0	NE2-H	Similar	Aromatic stacking with H30(sc)
					Polar contacts with N184(sc)
H97	0.23/0.25	6.2	ND1-H	Similar	Aromatic stacking with W150/Y96
					Hydrophobic stacking with L153
					H-bond donor with E93(bb)
H138	0.15/0.16	5.8	NE2-H	Similar	Hydrophobic packing with V137 and
					Aliphatic portion of K78
					H-bond donor with Q77(sc)
H173	0.13/0.17	5.0	NE2-H	Similar	Aromatic stacking with F37
					Aromatic-cation stacking with R176
H195	0.43/0.47	5.9	NE2-H	Similar	Hydrophobic packing with I194 and
					Aliphatic portion of K190
					Aromatic-cation stacking with K190

^aSolvent accessibility calculated from Asaview, left value⁹ and GETAREA, right value¹⁰ programs.

^bpK_a values determined at 35°C.⁵ Titration of H27, H30, and H180 is thermodynamically coupled; pK_a values shown assume the other two residues are not protonated. Preliminary analysis of hPRL protonation at 25°C by NMR reveals only small shifts in pK_a values, which are on an of average 0.13 U greater.

^cThe predominant structural interactions were manually identified with the assistance of STING,¹¹ as described in the text.

Individual mutation of both H27 and H46 to Ala leads to an hPRL variant with significantly increased pH dependence of ΔG_unf, which in both cases is the result of selective stabilization of the protein at high pH. These two residues have the highest measured imidazole pK_a values in hPRL at 6.6. On inspection of the hPRL tertiary structure, the imidazole ND1 nitrogens of H27 and H46 appear to participate in salt bridges with the side chains of D183 and D41, respectively. This is also reflected in their low ¹⁵N-ND1 NMR chemical shifts measured at pH 7.5, an indication of a highly polar local environment. His salt bridges can only exist when their imidazole rings are positively charged, which occurs at a solution pH below their pK_a values. The relative stabilization of their protonated states from these favorable electrostatic interactions is likely responsible for their high pK_a values. Therefore, similar to a majority of the other His mutants, H27A and H46A display increased stability at high pH (when their imidazole rings are unprotonated and neutral) because of the same generic destabilizing effect of the imidazole ring, as described earlier. However, at low pH, this generic destabilization should be counterbalanced by the favorable formation of salt bridges, resulting in no net change in global stability and the apparent increase in the overall pH dependence to ΔG_unf.

Another residue whose mutation results in a significant change to the pH dependence of global stability compared to WT hPRL is H59. Reversed compared to H27A and H46A, the decreased pH dependence of H59A's ΔG_unf is due to selective stabilization of the mutant protein at low pH. Again, this effect can be rationalized based on its structural interactions. Although many imidazoles in hPRL function as hydrogen bond donors, the imidazole of H59 is unique in its role as a hydrogen bond acceptor. The side chain hydroxyl of S90 donates its hydrogen to bond with the unprotonated NE2 atom in the neutral state imidazole ring of H59, a favorable interaction that can only exist at high pH. Again, in reverse fashion to H27 and H46, mutation of H59 to Ala stabilizes the hPRL at low pH, where the hydrogen bond with S90 is broken, because of the generic destabilizing effect of His imidazoles on hPRL global stability. However, at high pH, the favorable formation of the hydrogen bond counterbalances this generic destabilization, and thus flattening the overall pH dependence to ΔG_unf.

Mutation of the remaining His residues to Ala does not significantly change the pH dependence of hPRL global stability compared with WT, which is consistent with our assessment of their dominant intramolecular structural interactions. Consisting primarily of hydrophobic/aromatic stacking and hydrogen bonding (always serving as the hydrogen donor), these structural interactions are not automatically dependent on the protonation status of the imidazole. Thus, unlike the role of H59 as a hydrogen bond acceptor and unlike the salt bridges seen for H27 and H46, the native structural interactions for the remaining histidines should remain largely unchanged over the entire pH range investigated, with no net contribution to the pH dependence of hPRL global stability.

An alternate approach to rationalization of the effects of His mutation on the pH dependence of global stability is to consider more directly their experimentally measured pK_a values. If all the individual pK_a values are known for each ionizable group in the appropriate folded and unfolded states, the pH dependence to global stability could be described. In this regard, we are limited by a lack of experimentally determined site-specific pK_a values for unfolded hPRL in aqueous solution. It is important to note that measurements of histidine titrations by NMR of the chemically denatured protein, for example by preparation of an NMR sample with 7M urea, would not provide the relevant thermodynamic parameters, as the high urea concentration would perturb individual imidazole ring affinities for protonation because of alteration of the bulk solution properties.^15,16 Instead, what we require are knowledge of the unfolded-state pK_a values under native conditions or, alternatively, the pK_a values for chemically denatured protein along with residue-specific transfer free energies of the protonated and unprotonated imidazoles from 7M urea to aqueous solution. Direct measurement of either of these possibilities is technically problematic and not currently available. Nevertheless, a number of general conclusions can be drawn from our current results, based on the general patterns seen in native-state pK_a values and the effect of mutations on the pH dependence to hPRL global stability.

Measurements on model compounds support a typical pK_a around 6.3 for a nonbonded His imidazole in a short peptide chain.¹⁷ However, we do note that the precise nature of the denatured state is not well understood and is not likely to resemble a truly, randomly orienting polypeptide chain. In fact, unfolded-state pK_a values are often found to be significantly perturbed from typical values.^18,19 This may be especially true for hPRL as it contains three disulfide bridges, which have not been reduced in our unfolding studies and should constrain the unfolded protein to a more compact and, potentially, native-like state. Many of the His residues in hPRL do not alter the pH dependence of global stability when the imidazole ring is removed by mutation. The simplest explanation for this effect is for their denatured-state pK_a values (under aqueous conditions) to be very similar to what we have measured for the native protein. In fact, mutation of the four histidines in hPRL with pK_a values closest to the median of our measured values (H30, H97, H180, and H195) has minimal effect on the net pH dependence to hPRL global stability. In contrast, mutation of either H27 or H46, the two residues with the highest pK_a values in hPRL, greatly increases the measured pH dependence. Their pK_a values would be expected to most likely decrease upon denaturation, because of the loss of the structural salt bridges responsible for their atypically high values in the native state. Thus, the higher affinity for protonation of these residues in their native conformation would favor the folded protein with increasing acidity (lower pH), and, correspondingly, mutation to Ala would have the opposite effect of raising protein stability at high relative to low pH. This is precisely what was observed experimentally.

In contrast to the effect described earlier for H27 and H46, mutation of any histidine with an atypically low pK_a value in the native state would be expected to decrease the net pH dependence to hPRL's global stability. However, the three histidines with pK_a values significantly below 6.0 (H59, H138, and H173) do not consistently follow this pattern. Of these, only mutation of H59, with an experimental pK_a of 5.8, decreases the net pH dependence of global stability. For the other two histidines, the most likely explanation for the lack of a change in pH dependence is that their imidazole ring pK_a values are similarly perturbed in the unfolded state (under aqueous conditions), presumably because of residual structural interactions. We find the lack of change in pH dependence upon mutation of H173 most surprising given its low native-state pK_a of 5.0. However, a possible explanation resides in its close proximity to the C58–C174 disulfide linkage. We must presume that in the unfolded state, this long-range structural restraint retains a significant degree of local, native-like molecular interactions surrounding H173. On the other hand, an alternative explanation is that mutation of H173 perturbs the pK_a of other titratable residues in hPRL, such that the altered affinity for protonation of these other residues counterbalances the large change in H173's pK_a upon unfolding. Attempts to computationally model this second possibility (unpublished results) reveal that rather large changes in pK_a values of linked residues would be required to explain the lack of pH dependence. Additionally, the previously measured pH titration curves using NMR spectroscopy for the H173A mutant did not find any significant changes for any other histidine in hPRL. Hence, we currently favor the former possibility of an unusually low unfolded-state pK_a for H173.

Finally, H59 is the only histidine whose mutation significantly decreases the net pH dependence to hPRL's global stability, despite similar neighboring of the C58–C174 disulfide as H173, discussed earlier. As mentioned previously, the imidazole ring of H59 serves as the hydrogen bond acceptor for S90 in the hPRL tertiary structure, which is likely responsible for suppression of its native-state pK_a. Loss of this interaction in the unfolded state would be expected to increase H59's pK_a to more typical values, and this difference would contribute to destabilization of hPRL's native state with decreasing pH. Correspondingly, removal of the H59 imidazole by mutation to alanine would decrease the overall pH dependence of hPRL global stability, as was seen experimentally.

Double mutant cycle analysis of interactions between histidines

Histidines 27, 30, and 180 form a thermodynamically coupled structural unit in hPRL. Chemical denaturation data presented earlier for single-site mutants of these residues reveal their net destabilizing influence on the structural stability of the protein. To ascertain the molecular origins of this structural destabilization, we have performed double-mutant cycle analyses of their energetic interactions, as originally described by Fersht and coworkers.^6–8 Figure 3 compares the results of the double-mutant cycle analysis for the coupled triplet (H27, H30, and H180) along with nearby H173, for comparison. Their interaction free energies have been calculated such that negative values reflect net destabilizing interactions. Because the interaction free energies are derived from four independently measured unfolding free energies, each with their own independent experimental errors, understanding of the total statistical uncertainty in the final result is critical. Instead of attempting to propagate the uncertainty in each independent free energy into the double-mutant cycle calculation, we have compiled all the raw denaturation data for all four relevant proteins into a single data set for global fitting. For each double-mutant cycle, the interaction free energy has been expressed as a single equation based on the fluorescence of each protein as a function of urea concentration. After optimization to derive the best-fit value, the uncertainty in the interaction free energy has been determined by systematic variation of the fitted value and application of the F-test, as detailed in Materials and Methods section. The significance of adding an additional residue to the double-mutant cycle calculations, as a test for synergism among select trios of histidine residues, was determined with paired t-tests, and the results of which are shown in Table III.

Figure 3.

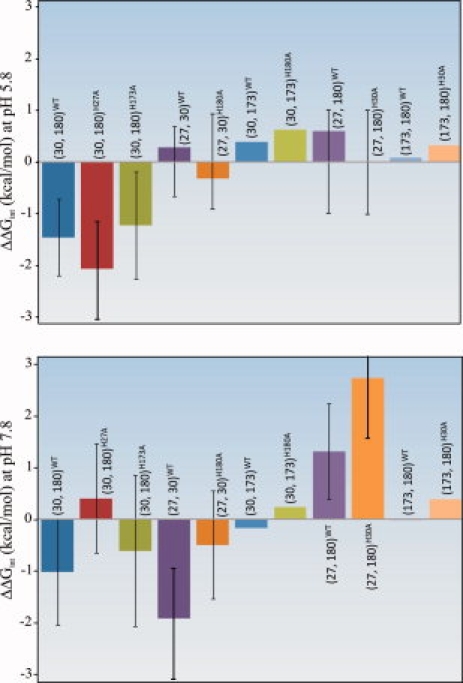
Bar graph summary of ΔΔG_int and corresponding F-statistic-derived 95% confidence intervals for select interaction energies. The residue pair under consideration is denoted by residue numbers within parentheses, with the hPRL variant (WT versus single site mutant) identified in the accompanying superscript.

Table III.

Paired t-Tests for the Significance of Additional Mutations to Double-Mutant Cycle Interaction Free Energies

		P (one tail)	P (two tail)
Paired t-test pH 5.8
ΔΔGint (30, 180)WT	ΔΔGint (30, 180)H27A	0.016	0.031
ΔΔGint (30, 180)WT	ΔΔGint (30, 180)H173A	0.149	0.297
ΔΔGint (27, 30)WT	ΔΔGint (27, 30)H180A	0.033	0.065
ΔΔGint (27, 180)WT	ΔΔGint (27, 180)H30A	0.060	0.120
Paired t-test pH 7.8
ΔΔGint (30, 180)WT	ΔΔGint (30, 180)H27A	<0.001	<0.001
ΔΔGint (30, 180)WT	ΔΔGint (30, 180)H173A	0.124	0.248
ΔΔGint (27, 30)WT	ΔΔGint (27, 30)H180A	<0.001	<0.001
ΔΔGint (27, 180)WT	ΔΔGint (27, 180)H30A	0.008	0.092

The interaction free energies of H27, H30, H173, and H180 depicted in Figure 3 depend strongly on both solution pH and mutation of individual residues. We note that none of the interaction free energies involving H173 is statistically significant, indicating that H173 is energetically isolated from the remaining trio of histidines. However, focusing initially on WT hPRL (blue bars in Fig. 3), the interaction free energy between H30 and H180 is statistically significant and net destabilizing to the folded protein at both low and high pH. Similarly, a net destabilizing interaction between H27 and H30 is seen at pH 7.8, but this disappears when the pH is lowered. In contrast, H27 and H180 have a net stabilizing interaction free energy at pH 7.8, which is also lost at lower pH. We conclude that at basic pH the close proximities between two important pairs of residues, H27-H30 and H30-H180, have a net destabilizing effect on the structural stability of hPRL. Furthermore, these destabilizing interactions are focused on H30 as the central point in the triad, consistent with the high structural stability of H30A compared with all other single-site His to Ala mutants. In contrast, H27 and H180 are not in direct contact and their energetic interaction is net stabilizing to the hPRL native structure. A likely explanation is that mutation of either H27 or H180 allows relaxation of the net destabilizing interactions between either H30–H180 or H27–H30, respectively. Finally, we note that many of the measured interaction free energies between pairs of histidines diminish in absolute value at lower pH. This is most likely related to global destabilization of hPRL as solution pH is lowered. We envision a general spreading of destabilizing interactions in hPRL as surface ionizable groups become protonated. The expected increase in protein dynamics and broader sampling of conformational space would reduce the direct energetic interactions between single, isolated pairs of residues.

In addition to the double-mutant cycle analysis discussed earlier, the inclusion of two triple mutants, H27A/H30A/H180A and H30A/H173A/H180A, allows consideration of higher order interactions between residues. One way to visualize the linkages between double-mutant cycles is to compare the interaction free energies between two histidines with and without mutation of a third residue. Changes in net ΔΔG_ints, because of mutation of a third, potentially interacting residue, are visualized in Figure 3, and their statistical significance assessed using paired t-tests (Table III). For example, the interaction between H30 and H180 changes significantly when H27, but not H173, is mutated to alanine. Similarly, the interactions between H27 and H30 and between H27 and H180 are dependent on the imidazole ring of the third residue in the linked triplet. At basic pH, the direction of the change is always toward increased stability (i.e., less destabilizing or more stabilizing), consistent with the idea that the histidine triplet represents a locus of structural strain that relaxes upon removal of any one of the linked imidazoles. At more acidic pH, a majority of the higher order interaction free energies are lost, again presumably because of a more dynamic conformational state and more widely distributed energies of interaction. The only exception is the ΔΔG_int between H30 and H180, which becomes more destabilizing upon mutation of H27 at acidic pH. One potential explanation is that mutation of H27 increases site-specific pK_a values for protonation of H30 and H180, resulting in a greater tendency to protonate these residues and create electrostatic repulsion.

Identification of a secondary hydrophobic cluster in hPRL and hGH

Figure 4 compares the structural locations of hPRL's nine histidines with their homologous residues in hGH (colored blue), who share 23% identity in their overall protein sequence. The primary hydrophobic cores of both proteins are found within the interiors of their four-helical bundles, shifted slightly more toward their lower halves (as situated in the figure) because of slight splaying of the helices at their upper ends. However, we note the presence of a secondary hydrophobic/aromatic bundle located between the upper halves of the two long loops and the underlying surfaces of the 2nd and 4th long helices (colored red). In hPRL, H59 and H97 are integral components of this cluster, most likely imparting a degree of pH dependence to the stability of this secondary core. In contrast, within the homologous region of hGH, H59 and H97 are replaced with phenylalanine, which would be expected to remove any analogous pH dependence while maintaining local hydrophobic packing. We also note that in both proteins the tryptophan side chains responsible for our measured fluorescence are also found here. Therefore, the local structural stability of this secondary hydrophobic bundle could impact the native-state fluorescence of hPRL and hGH. Consistent with this hypothesis, mutation of H59 in hPRL, which is highly buried within this cluster and involved in a stabilizing hydrogen bond with S90, generates a steep slope in the preunfolding baseline of its fluorescence-detected chemical denaturation curve. It is likely that this low urea-induced transition and the associated decrease in hPRL's native state fluorescence results from a local destabilization of this region. Although the secondary hydrophobic core is distal to the known receptor-binding interface for hPRL,²⁰ it may still impact the biologic function of the hormone. The molecular mechanism for low pH-induced dissociation of hPRL from its receptor has yet to be described. One possibility is pH-dependent destabilization of the secondary hydrophobic bundle at the upper ends of the long loops indirectly alters the structure or stability of the short helix at the other end of the loops, known to play a critical role in receptor recognition. In fact, we feel that such a mechanism appears likely for the lowering of receptor-binding affinity for bovine PRL phosphorylated at S90,^21,22 given its buried position within this secondary hydrophobic core and its intimate relationship with H59 (assuming the bovine and human PRL tertiary structures are sufficiently similar). Alternatively, local destabilization and the associated increased mobility of the long loops in hPRL may increase susceptibility to enzymatic proteolysis, either as part of the mechanism for generation of the potently antiangiogenic 16 kDa N-terminal fragment of hPRL^23,24 or during lysosomal degradation of the hormone after endocytosis.²⁵

Figure 4.

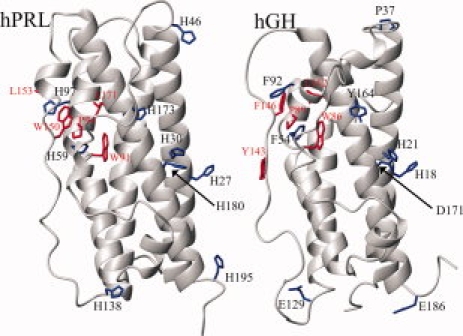
Backbone ribbon diagrams of hPRL-1-14-G129R (PDB: 2Q98) (left) and hGH (PDB: 1HGU) (right) with key side chains highlighted. Histidine side chains in the hPRL structure (H27, H30, H46, H59, H97, H138, H173, H180, and H195) and the homologous residues in hGH (H18, H21, P37, F54, F92, E129, Y164, D171, and E186) are shown in blue. Side chains involved in a hydrophobic cluster in hPRL (W91, P94, W150, L153, and L171) and their homologous counterparts in hGH (W86, P89, Y143, F146, and L162) are highlighted in red.

Conservation of histidines in PRL

Sequence-function relationships and the alignment of hPRL with orthologous proteins have been nicely reviewed,²⁶ and a similar, abbreviated alignment is available in Supporting Information. Remarkably, H27 and H30 are essentially 100% identical across species, supporting their likely functional importance. Residues H59, H97, H173, and H180 are better than 50% identical, whereas H46, H138, and H195 are less well conserved. This agrees well with our hypotheses in that all His residues within the high-affinity binding site, the two histidines in the secondary hydrophobic bundle, and H173 with its highly perturbed pK_a show a high degree of conservation.

Significance and conclusions

Surprisingly, mutation of a majority of histidines in hPRL stabilizes the native protein structure relative to its unfolded state. Generally, the highly cooperative nature of protein folding and evolution toward optimal global stability guarantees that a majority of single-site mutations destabilize protein native states. Notable exceptions are frequently found at enzymatic active sites, where structurally destabilizing residues are retained for their functional importance. However, we are not aware of any systematic evaluation of histidine's contributions to protein stability, and we accept that the above generalization regarding evolutionary optimization may not apply equally to all amino acid types. Nevertheless, the results presented here lead us to the general speculation that histidines may not commonly promote protein folding by stabilization of native structural states similarly to other amino acids. Instead, their inclusion in the language of polypeptides may be to serve primarily as physiologic pH sensors. Histidines are the only amino acid sensitive to changes in protonation over a physiologic pH range between 6 and 8. Their frequency of roughly 2% of amino acids in modern proteins is lower than most other amino acid types²⁷; whereas, 4.5% of amino acids in hPRL are histidine. By comparing the primary sequence and tertiary structures of hPRL and hGH, it is clear how substitution of pH-insensitive aromatic residues, such as Phe or Tyr, with His introduces potential pH dependence while conserving local structural interactions. We expect that upon proper scrutiny, the emergence of physiologic pH-dependent properties within protein families or subfamilies will be frequently associated with similar histidine substitutions.

We began the investigation reported here to identify the individual histidines responsible for pH-dependent destabilization of hPRL between pH 8 and 6.⁴ However, we find that the overall pH dependence to hPRL global stability is not focused in any single residue or even within the coupled His 27/30/180 triad, but is simply the net result of the pH-dependent contributions from multiple residues, each with their own, individual pH-dependent effects. Therefore, a variety of mutation strategies exist to flatten the pH dependence of global stability. The most effective combination of mutations reported here is the H30A/H173A/H180A triplet, with less than a 1 kcal/mol difference in stability between pH 5.8 and 7.8. Independent combinations of mutations involving H59 should also serve to similarly flatten pH dependence (unpublished results). In general, many of the reported changes in pH dependence to ΔG_unf could be generally rationalized based on observed structural interactions within the hPRL tertiary structure. However, for some residues, perturbed unfolded-state pK_a values must also be hypothesized. This is particularly true for H173 whose mutation had little impact on the stability of hPRL, despite its unusually low native-state pK_a of 5.0.

Materials and Methods

Mutagenesis, expression, and purification of proteins

Both WT and mutant hPRL variants were recombinantly expressed in BL21 DE3 Escherichia coli, purified from inclusion bodies, and refolded using a previously described hPRL bacterial expression vector and protocol.²⁸ Single-site His to Ala mutations were introduced using the Quickchange Site-Directed Mutagenesis Kit from Stratagene (La Jolla, CA) and appropriate oligonucleotide primers (available as Supporting Information), with the exception of those already available.⁵ Double- and triple-site His mutants were produced using sequential mutagenesis, with the exception of any variant including mutation of both H27 and H30, which required a unique primer. All the mutated coding sequences were verified by DNA sequencing at the W.M. Keck Foundation Biotechnology Resource Laboratory at Yale University.

Urea denaturation monitored by fluorescence spectroscopy

Fresh 9.8M urea stock solutions were prepared from stirring urea crystals (American Bioanalytical, Natick, MA, ultra-pure urea) in hot distilled water. The solution was allowed to cool to room temperature and filtered through a 0.2-μm filter and its concentration confirmed from refractive index measurements using a hand-held refractometer (Atago U.S.A., Bellevue, WA, model R5000). Fresh urea stocks were prepared and used within a few days of each experiment. One molar potassium phosphate buffer stocks at pHs 6.0 and 8.0 were prepared along with a separate stock of 4M NaCl. These stock solutions, along with water and the aforementioned 9.8M urea stock solution were used to generate a series of 24 1.6 mL buffered urea solutions (in quadruplicate) in a 96 deep-well tray.

The 24 buffered urea solutions were prepared in quadruplicate in a 96 deep-well tray using four channels of an eight-channel automated reagent dispenser (Thermo Electron Corporation, Waltham, MA, model Multidrop DW) controlled via the serial port of a personal computer. A simple program was written to utilize four of the eight reagent lines on the reagent dispenser to aliquot the water, buffer, and urea stock. Final solution conditions contained 25 mM NaCl and 25 mM potassium phosphate buffer. All pH measurements were taken with an Accumet AP61 hand-held pH meter (Fisher Scientific, Pittsburgh, PA) and Orion glass micro pH combination electrode (Ag/AgCl) (Thermo Electron Corporation, Waltham, MA, model 9826BN).

Protein stock solutions were typically prepared in water to a minimum concentration of 50 μM and transferred to populated 96 deep-well trays suing a multichannel pipette to generate a minimum final protein concentration of 1.5 μM. Protein/urea solutions were manually transferred from the sealed 96 deep-well plates to quartz cuvettes in a Cary Eclipse fluorescence spectrophotometer, (Varian Instruments, Walnut Creek, CA) employing a four-cell temperature-controlled and stir-bar capable carriage. Fluorometric measurements were taken in 1 cm by 1 cm matched quartz cuvettes. All fluorescence measurements were carried out with active stirring and temperature control at 23°C with an excitation wavelength of 280 nm with a 20 nm slit width and detection at 325 nm with a 5 nm slit width.

For each of the protein denaturation curves, each data point represents the average of the fluorescence intensity readings from two separate cuvettes. Each cuvette was filled with the contents from two independently prepared wells with identical solution conditions to a final volume of 3.2 mL, allowing adequate volume to accommodate stirring and the light beam. Typically, a single populated 96 deep-well tray would yield a single 24-point urea denaturation curve under a particular buffer and temperature condition. All readings were taken in order of increasing urea concentration. For all the hPRL variants involved in higher order interaction free-energy calculations, the aforementioned denaturation experiment would be conducted in triplicate (i.e., three separate and identical runs) to better define experimental variability for calculation of F-statistics.

Samples transferred to the quartz cuvettes for room temperature measurements were allowed to temperature equilibrate for 1 min with stirring prior to the fluorescence measurement. Fluorescence data were collected from the Cary Eclipse “Advanced Reads” program running under the Windows XP operating system. Data were organized and prepared for regression analysis using the Microsoft Excel spreadsheet program. Final regression and error analysis was achieved using Scientist 3.0 (Micromath Research, St. Louis, MO).

Reversibility of the urea denaturation of hPRL and hPRL His to Ala mutants was tested at pH 5.8 and 7.8 using fluorescence methods similar to those employed in the denaturation experiments described earlier. Protein was diluted into four aliquots of 9.8M urea and into an additional four aliquots of 1.2, 2.4, 6.1, and 9.0M urea, which were all allowed to equilibrate for several hours at room temperature. The four protein samples at 10M urea were then correspondingly diluted to 1.2, 2.4, 6.1, and 9.0M urea and given additional time to (potentially) refold. Reversibility was gauged by the difference in fluorescence response between the two sets of protein solutions. In all cases, the protein samples diluted from 10M urea had nearly identical fluorescence to the simultaneously prepared control samples, confirming reversible folding during the denaturation experiments.

Calculation of ΔG_unf from the denaturation data

Fluorescence-detected denaturation curves, many with significant initial and final slopes in the sigmodal response, were fit to the following equation:

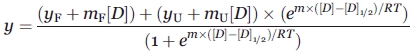(1)

where y_F and m_F are the fluorescence intercept and signal dependence on denaturant concentration [D] for the initial portion of the denaturation curve and, similarly, y_U and m_U are representative of the unfolded portion with R being the ideal gas constant, for experiment conducted at temperature T. Under the assumption that the change in Gibbs free energy as a function of denaturant concentration continues its linear dependence to 0M urea, the change in Gibbs free energy of unfolding in water is given by:

(2)

where [D]_1/2 is the concentration of denaturant at the unfolding midpoint with slope m for protein Z. The reported values of [D]_1/2 and m for prolactin and each prolactin variant were calculated from fitting the nonlinear Eq. (1) to the fluorometric denaturation data using the program Scientist 3.0.

Double-mutant cycle analysis

The double-mutant cycle is used to predict the interaction energy between two side chains in a protein, achieved by comparing the Gibbs energy of unfolding, extrapolated to 0M urea, for WT protein, the component single site mutations, and the double side-chain mutant. The difference between the predicted and experimentally derived values is regarded as the interaction free energy:

(3)

where X and Y represent each of the amino acid side chains studied (denoted by their single-letter amino acid representation, numerical position in the protein, and single letter mutation) in protein Z (in this case, the WT protein). The validity of the result from the above formulation is dependent on the extent to which noncovalent secondary side chain contacts of the double-mutant cycle cancel out. It is also dependent on the extent of the interaction energy between the mutant substitutions, as this interaction serves as a reference state for the double-mutant cycle energy calculation. Based on the construct described herein, the double-mutant cycle will show a net negative result if the two side chains studied share a destabilizing interaction in the folded protein.

The basic principles of the double-mutant cycle have been extrapolated to higher order constructs with the goal of predicting the energetic synergism of multiple side chain interactions in a protein.⁶ Of particular interest here is to determine if energetic interactions described in the double-mutant cycle analysis extend to a third side chain. This is achieved by experimentally conducting a second mutant cycle on a protein with the third side-chain mutation 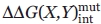and comparing this result to that from the double-mutant cycle 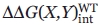in the WT protein.

Statistical analysis of errors in interaction free energies

The 95% confidence intervals for interaction free energies were determined by matching the critical F distribution to the computed F for least-squared fits of the data with the single parameter (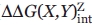) fixed and systematically varied. Typically, an F distribution was calculated over a range of interaction free energies at least 2 kcal/mol beyond the critical F using sum square error values reported from the curve fitting program Scientist 3.0. The F distribution was determined from:

(4)

where SSE_BestFit is the calculated sum square error for the best nonlinear regression fit of the fluorescence data (not normalized), SSE_ΔΔGfixed is the sum square error for the best nonlinear regression fit with the single parameter for the interaction free energy fixed, N is the number of data points in the nonlinear regression, and P is the number of parameters. The calculated F-statistic distributions and all relevant statistical parameters are shown in tabular format in Supporting Information along with propagated errors derived from standard deviations reported by the Scientist 3.0 program. In all cases, the propagated errors for each interaction free energy value were significantly smaller than those computed from an F-test with a 95% confidence interval. A paired t-test was used with the F-statistic-derived confidence interval to determine the significance of adding a particular mutation to the interaction energy from the double-mutant cycle result.