Building a foundation for structure-based cellulosome design for cellulosic ethanol: Insight into cohesin-dockerin complexation from computer simulation

Abstract

The organization and assembly of the cellulosome, an extracellular multienzyme complex produced by anaerobic bacteria, is mediated by the high-affinity interaction of cohesin domains from scaffolding proteins with dockerins of cellulosomal enzymes. We have performed molecular dynamics simulations and free energy calculations on both the wild type (WT) and D39N mutant of the C. thermocellum Type I cohesin-dockerin complex in aqueous solution. The D39N mutation has been experimentally demonstrated to disrupt cohesin-dockerin binding. The present MD simulations indicate that the substitution triggers significant protein flexibility and causes a major change of the hydrogen-bonding network in the recognition strips—the conserved loop regions previously proposed to be involved in binding—through electrostatic and salt-bridge interactions between β-strands 3 and 5 of the cohesin and α-helix 3 of the dockerin. The mutation-induced subtle disturbance in the local hydrogen-bond network is accompanied by conformational rearrangements of the protein side chains and bound water molecules. Additional free energy perturbation calculations of the D39N mutation provide differences in the cohesin-dockerin binding energy, thus offering a direct, quantitative comparison with experiments. The underlying molecular mechanism of cohesin-dockerin complexation is further investigated through the free energy profile, that is, potential of mean force (PMF) calculations of WT cohesin-dockerin complex. The PMF shows a high-free energy barrier against the dissociation and reveals a stepwise pattern involving both the central β-sheet interface and its adjacent solvent-exposed loop/turn regions clustered at both ends of the β-barrel structure.

Introduction

The recalcitrance of lignocellulosic biomass to enzymatic hydrolysis is a bottleneck in cellulosic ethanol production.¹ One promising avenue for overcoming biomass recalcitrance is to understand and modify the properties of bacterial cellulosomes.² Cellulosomes are large extracellular enzyme complexes that are produced by anaerobic bacteria and can efficiently break down plant cell wall polysaccharides, such as cellulose, hemicellulose, and pectin into sugars.^3–5 The cellulosome complex consists of various kinds of enzymes arranged around a scaffolding protein that does not exhibit catalytic activity but enables the complex to adhere to cellulose.

The organization of the cellulosome is mediated by high-affinity protein–protein interactions between Type I cohesin domains within the scaffolding proteins and complementary Type I dockerin domains carried by cellulosomal enzymes. Early studies on cellulosomes demonstrated that, although cohesin and dockerin exhibit relatively high-sequence homology, the interaction between cohesins and dockerins is generally species specific, that is, cohesins from one species do not recognize and interact with dockerins present in other species.⁶

A crystal structure for the Type I cohesin-dockerin complex from C. thermocellum has been determined⁷ (Fig. 1), providing insight into the structure and mechanism of cohesin-dockerin assembly. The cohesin domain forms a nine-stranded β-barrel with an overall jelly-roll topology. The two sheets of the β-barrel are composed of strands 5, 6, 3, and 8 on the contact face with the dockerin, and strands 4, 7, 2, 1, and 9 on the opposite face. The entire structure is stabilized by a tightly packed aromatic/hydrophobic core. The compact nature of the cohesin structure, together with the fact that the contact surface features no obvious binding pocket or cleft, suggests that binding between cohesins and dockerins occurs through the exposed surface residues. The dockerin partner of the cohesin-dockerin complex forms three α-helices, in a conformation defined by two-calcium-binding loop-helix motifs. Indeed, it has been found that Ca²⁺ plays a key role in maintaining the structural integrity of the cohesin-dockerin complex.^8,9

Figure 1.

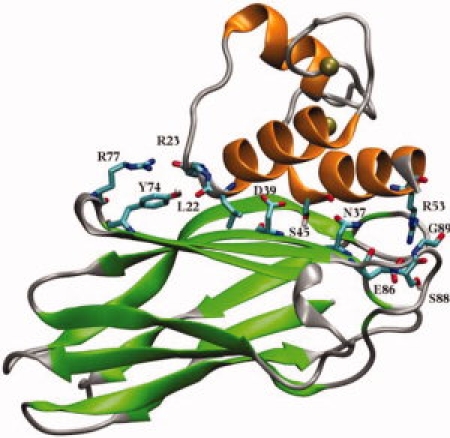
Crystal structure of the cohesin-dockerin complex in cartoon representation with β-sheets (cohesin) in green, α-helices (dockerin) in orange, and loop regions in silver. Key residues involved in interdomain interaction are highlighted in licorice mode and colored by atom names.

Inspection of available crystal structures^7,10–12 and site-directed mutagenesis experiments^13,14 suggest that the cohesin-dockerin association is maintained by hydrophobic interactions promoted through an extensive hydrogen-bonding network between one face of the cohesin and the dockerin. A number of hydrophilic residues play an essential role in the recognition and formation of the complex as follows: Arg77, Tyr74, Asp39, Glu86, and Ser88 of the cohesin domain, and Leu22, Arg23, Ser45, Thr46, and Arg53 from α-helices 1 and 3 of the dockerin domain (Fig. 1). In addition to structural information, the effect of single mutations of key residues on the affinity of the interaction has been probed,^13,15 and the binding affinity of WT cohesin-dockerin complex has also been measured.¹²

Although the crystallographic structure and experimental measurements have provided essential information about the association of cohesins and dockerins, the underlying microscopic dynamic and energetic processes are not directly accessible to experiments. Consequently, aspects of the mechanism governing the assembly of cohesins and dockerins remain uncertain. To deepen our understanding and gain further insight into the assembly mechanism, we have performed molecular dynamics (MD) simulations of the cohesin-dockerin complex. Simulations were also performed of the D39N mutant that has been demonstrated experimentally to dramatically reduce the binding affinity.¹⁵ Global dynamics of the complexes and local hydrogen bonding networks formed by several highly conserved residues are examined; the change in free energy of binding accompanying the mutation of Asp39 are also calculated. Furthermore, the free energy landscape for the dissociation of the cohesin and dockerin domains in aqueous solution is explored. The specific domains and amino acid residues that may be involved in this interaction are discussed. The results reveal a detailed view on how the two domains interact.

Results

Structural flexibility and involved regions in the WT and D39N mutant

Before proceeding with more detailed analysis, it is important to assess the dynamical stability of the systems. For this purpose, we analyzed the root-mean-square deviation (RMSD) of the C_α atoms with respect to the initial structure as a function of time for both the WT and the D39N mutant. The average RMSDs of both structures (not shown) are relatively modest: for the WT simulation, the RMSD grew slowly and remained smaller than 1.4 Å over the entire 10 ns simulation trajectories, indicating structural stability. The D39N structure was also stable, although its RMSD (∼1.7 Å) was slightly higher than that of the WT. No large global deformation of the protein was observed during the D39N simulation. Secondary structure analysis of both the WT and D39N mutant indicated that the β-sheet of the cohesin domain and α-helices of the dockerin domain were well conserved throughout the trajectory, again suggesting that the complex is a stable entity in the simulation. In the crystal structure, one of the bound calcium ions, located close to the N-terminus of the first α-helix in the dockerin, is coordinated by five residues as follows: Asp2 (OD1), Asp6 (OD1), Asp13 (both OD1 and OD2), Asn4 (OD1), the carboxylic oxygen atom of Thr8, and a water molecule. The second Ca²⁺ is coordinated by the side chains of Asp36 (OD1), Asp38 (OD1), Asp47 (both OD1 and OD2), Asn40 (OD1), and Ser42 (O), as well as by a water molecule. In both the WT and D39N mutant simulations, all the interactions are very stable (i.e., relatively small fluctuations in the distances), and the distances are maintained with ∼2.1–2.3 Å.

The picture changes, however, when dynamic properties are considered. Figure 2 shows the time-averaged structures of the WT and D39N with residues colored by B-factors calculated from the atomic root-mean-square fluctuations (RMSF) (Figure caption for details). It is apparent that, although the mobility of most of the parts of the proteins is similar, certain regions differ greatly between the WT and D39N mutant. Differences are particularly apparent in the β-strand 4/5 loop and β-strand 6/7 loop (Fig. 2) that are contiguous and run approximately along the edge between the two faces of the cohesin domain. The structural protrusion formed by these two loops, also known as the “recognition strip,” is found in all cohesin domains and contains some of the most highly conserved sequence segments, and this region has been suggested to be important in the cohesin-dockerin contacts.^16,17

Figure 2.

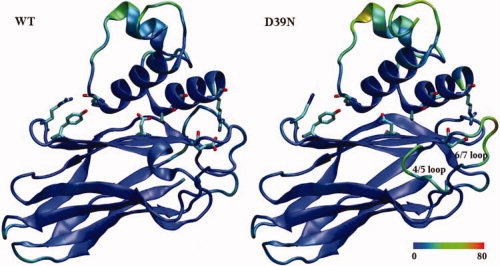
Time-averaged structures of the WT Cohesin-Dockerin complex and the D39N mutant resulting from MD simulations. Colors are assigned by B-factor from low-mobility (blue) to high-mobility (red), with the color scale in Å shown at the bottom. Carton representations are shown for both the WT and D39N mutant. Key residues are highlighted in licorice mode and colored by atom name.

Examination of the crystallographic structure shows that the recognition strip loops have a well-defined conformation stabilized by several intramolecular hydrogen-bonding interactions, such as between the backbone and side-chain atoms of Glu86, Ser88, Ala92, and Tyr93 (Fig. S1a in the Supporting Information). Simultaneously, Glu86 also forms an intermolecular salt bridge with Arg53 from the dockerin, which presumably contributes to the stability of the complex. These interactions were strongly maintained throughout the simulations in the WT, but undergo substantial changes in the D39N mutant. Inspection of the D39N simulation trajectory revealed that the above hydrogen-bonding interactions form only occasionally, the connections among Glu86, Ser88, Ala92, Tyr93, and Arg53 being either broken or maintained through relatively weak hydrogen bonds of N-H groups with backbone C=O groups. Interatomic distances are found to vary dramatically in the mutant and are accompanied by rotation of the Glu86 carboxylate group (Fig. S1 and additional text in the Supporting Information). This observation is consistent with the network of hydrogen bonds playing an important role in maintaining the stability of the residues forming the WT recognition strips. Multiple simulations with different initial configurations and momenta were also performed, and the resulting analysis confirmed that the above observed behavior is not an artifact of the initial conditions (Fig. S2 in the Supporting Information).

To further identify the essential modes of motions in the cohesin-dockerin complexes captured by the MD simulations, a principal component analysis (PCA)^18–20 was performed on the C_α atoms, using both the WT and D39N mutant trajectories, over the time interval of 5–10 ns. PCA identifies collective dynamic modes and their amplitudes from a MD trajectory based on eigenvectors and eigenvalues of the covariance matrix of interatomic fluctuations. This enables separation of large-scale concerted motions from random thermal fluctuations.

The modes corresponding to the two largest eigenvalues for both simulations are presented in Figure 3. The amplitudes of the two largest PCA modes are remarkably different in the WT complex and D39N mutant (Fig. S3 in the Supporting Information). Whereas in the WT complex, the two largest modes do not exhibit substantial amplitudes, apart from a moderate twisting motion in the loop-helix-loop region of the dockerin [Fig. 3(a)], the motions corresponding to the two leading modes in the D39N mutant are pronounced and concentrated in those regions that also show the largest RMSF. The most remarkable motion of the D39N mutant [blue arrow in Fig. 3(b)] corresponds to a translation-like mode in the recognition strips, with one loop containing Glu86 and Ser88 moving away from the dockerin domain and its neighbor loop moving in the opposite direction. The second most significant internal motion is a mixture of rotation and twisting concentrated in the loop-helix-loop segment of the dockerin domain that is not in direct contact with its cohesin partner, as shown in Figure 3(b), and therefore this motion may not impact the interdomain packing. The two large α-helices, the β-sheets, and other loop regions from the cohesin all show no large-amplitude concerted motion. In summary, the PCA results indicate that replacement of Asp39 not only directly disrupts part of the hydrogen-bonding network between the cohesin and dockerin domains but also substantially affects the internal protein dynamics. These results correlate closely with the essential role of the conserved Asp39 suggested by site-directed mutagenesis.¹⁵

Figure 3.

Porcupine plots of the two largest PCA modes for both the WT and D39N mutant. The modes are colored blue and green in order of decreasing amplitudes. The recognition strips are colored in yellow.

Polar interactions at the interface

Although the association between cohesin and dockerins is largely driven by hydrophobic interaction, the proteins also interact via a series of hydrogen bonds,⁷ some of which play essential roles in enhancing the binding and defining the specificity of the cohesin-dockerin interaction.^13–15

Asp39 in the cohesin domain is located at a site exposed to both solvent and the protein interior, with its side chain participating in a hydrogen-bonded network that includes several conserved residues as follows: Ser45, Asn37, Ile43, and Val21. Local structural changes induced by the D39N point mutation are hereby assessed by comparing two representative structures of the local environment taken from the end of the MD simulations (Fig. 4). The effects of the mutation include a moderate scale conformational rearrangement of the Asn39 side chain and the residues in its close vicinity. In the WT complex [Fig. 4(a)], one of the carboxylic oxygens in the Asp39 side chain exhibits persistent H-bonding interactions with the OH and NH groups of Ser45 in the dockerin counterpart, one of the key residues serving as recognition codes for binding to the cohesin^6,12,14,21; whereas the other carboxylic oxygen establishes water-mediated hydrogen bonds with two carbonyl oxygens of Val21 and Ile43. The former is strongly maintained throughout the simulations, whereas the latter appears to be weaker, with higher fluctuations. The neighboring Asn44 also occasionally participates in the H-bond interaction with Asp39. It is interesting to note that, in contrast to the crystal structure, the terminal polar groups NH₂ and CO of Asn37 quickly switch positions at the beginning of the simulation, with the amino group forming a H-bond with the hydroxyl group of Ser45. Evidently, the position of Asn39 is locked in this structure, and the extensive polar network at the interface would presumably contribute to the stability of the WT cohesin-dockerin complex.

Figure 4.

The hydrogen-bonded structures near Asp39 in the (a) WT and (b) D39N mutant. The residues are represented in licorice mode and colored by atom names.

In the case of the D39N mutant [Fig. 4(b)], at the early stage of the simulation, the Asn39 side chain rotates slightly out of its original position, followed by a quick flip of the Ser45 hydroxyl group serving as a hydrogen donor to Asn37. As a result, the interaction between Asn39 and Ser45 is only weakly maintained through CO···HN hydrogen bond; the water-mediated hydrogen bonds Asn39-Ile43 and Asn39-Val21 being mostly still preserved at this moment. As the simulation proceeds, Asn39 gradually drifts away from its original crystal position, reorientating its side chain by pointing down toward the cohesin and forming new highly occupied hydrogen bonds with Phe82. Structural dynamics monitored by the distance between Asn39-OD1 and the hydroxyl oxygen atom of Ser45 can be found in the Supporting Information, together with results from the WT simulation for a comparison (Fig. S4). These conformational rearrangements lead to a situation in which the direct H-bond Asn39-Ser45 and the water-bridged H-bond connection between Asn39 and Ile43 can no longer be established; the interaction between Asn39 and Val21 is, however, retained via a bridging water molecule. The local structural fluctuations of the protein side chains and bound water molecules and the resultant breaking of hydrogen bonds may loosen the structure of the complex and are likely to be relevant to the reduced binding affinity in the mutant.

Several bound water molecules were identified at the edge of the cohesin-dockerin interface in the crystal structure (Fig. 4). These water molecules mediate the polar interactions between the two protein surfaces. During the simulations of the WT complex, some of the interface solvent molecules jump diffusively and exchange with the bulk solvent, but the interface sites remain occupied and water-mediated H-bond interactions ensure that the interface remains close-packed. In contrast, in the D39N mutant, the conformational change of the Asn39 side chain is accompanied by several bound water molecules diffusing irreversibly away from the binding sites, leaving an empty cavity between Asn39 and Ile43. Thus, the interface water molecules play a major role in bridging hydrogen bonds. Dense packing of buried water molecules also provides better van der Waals interactions than an empty cavity.

Nevertheless, due in part to the similar volume and shape Asp and Asn share, the overall structure near the contact surface at which Asn39 is situated remains essentially unchanged, without considerable perturbation of the backbone structure. Also, the D39N point mutation was found not to disrupt other interdomain contacts on the β-sheet surface formed by those residues responsible for binding.

Effect of D39N mutation on the binding free energy

Free energy calculations are an important tool for providing a link between the microscopic interactions that are changed by a mutation and macroscopic experimentally accessible quantities such as the binding affinity.^22,23 Hence, simulations were carried out one step further to quantify the thermodynamic effects of the D39N point mutation using the free energy perturbation (FEP) method outlined in the Methods section. Three independent FEP runs, each consisting of two legs, following the Asp to Asn path (λ = 0 → 1), were computed using different initial sets of coordinates and momenta. Replacement of Asp39 by Asn led to an average binding free energy change (ΔΔG) of 4.8 kcal/mol, with a standard deviation of 0.4 kcal/mol. A reverse FEP calculation was also carried out in which the D39N variant structure was used as the initial state for modeling the final WT state, yielding ΔΔG of 5.2 kcal/mol, which also falls within the above-estimated error bar. Analysis of the convergence properties of the simulations indicated a smooth behavior of the free energy as a function of λ. The calculated change in free energy of binding is consistent with the experimental result that shows more than a 1000-fold reduction in the affinity, corresponding to a ΔΔG of more than 4 kcal/mol.¹⁵ Possible effects of the side-chain replacement include changes in the electrostatic interaction with other side chains, in the side chain packing, and in solvent accessibility as presented in the previous sections.

Free energy landscape of WT cohesin-dockerin dissociation

Our primary goals in computing the cohesin-dockerin dissociation free energy profile are to determine the relative difference in free energy between the free state and the bound state and to examine microscopic factors controlling the energetics of dockerin binding to cohesins. The free energy of cohesin-dockerin association was estimated from a total of 100 ns MD simulation in bulk solution, during which the free energy profile was obtained by allowing the two domains to diffuse reversibly along the relative center-of-mass reaction coordinate. The results are shown in Figure 5a.

Figure 5.

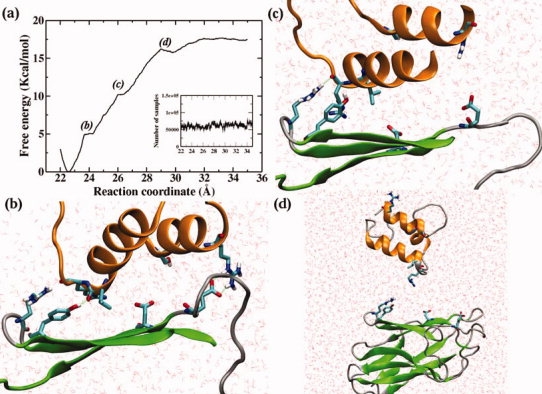
(a) Free energy profile for the dissociation of cohesin and dockerin domains. The sampling distribution is included in the inset. (b) Snapshot of the cohesin-dockerin complex at ξ = 24 Å; (c) Snapshot at ξ = 27 Å; and (d) Snapshot of cohesin-dockerin complex in the dissociated state, that is, ξ > 30 Å. The two α-helices, β-strands 3, 5, 6, and loop/turn regions are represented in cartoon mode, colored orange, green, and gray, respectively. The rest of the protein structure was omitted for clarity.

The overall shape of the free energy profile along the reaction coordinate exhibits a general uphill trend, illustrating quantitatively that the cohesin-dockerin complex exhibits a resistance against external forces and that there is a high-affinity for the two domains to remain bound. This high-affinity may arise from the favorable hydrophobic effect involving the removal of nonpolar surface from water¹⁴ and from the extensive hydrogen-bonding network formed by hydrophilic/charged residues across the contact surface. The global free-energy minimum in the profile appears at a distance separating the centers of mass equal to 22.5 Å, corresponding to the stable bound state with the key residues directly in contact.

As the two domains move away from each other, the cohesin-dockerin interactions are progressively disrupted. First, this leads to a steep increase of the free energy before reaching the first shoulder at ∼24 Å, at which point the hydrogen bond Asp39 (OD)-Ser45 (HG) has been dissociated and residues Asp39 and Ser45 at the interface of the protein complex are no longer in contact [Fig. 5(b)]. Another characteristic of the initial dissociation is flow of water into the binding area, substituting protein residues, and forming new hydrogen bonds. The first dissociation step therefore corresponds to disrupting the hydrophobic core and overcoming the resistance imposed by the Asp39-Ser45 hydrogen bond. However, the other hydrogen bonds, between the loop/turn regions at the ends of the β-barrel and the α-helices terminals, are preserved, initially resisting separation.

As the two domains move further apart, the free energy profile reaches the second slight shoulder at ∼26 Å. Inspection of the simulation trajectory indicated that the second shoulder corresponds to the disruption of the recognition strip interaction with the C-terminal region of α-helix 3, accompanied by the rupture of hydrogen bonds/salt bridges between Arg53 and Glu86 [Fig. 5(c)]. The presence of the second disruption is consistent with previous suggestions of the critical functional role of the recognition strips and their nearby region in the cohesin-dockerin interaction in C. thermocellum.^16,17 In contrast, at this point of the dissociation, the C-terminal of the first α-helix of the dockerin, and especially the backbone carbon atom of residue Arg23, is still repeatedly in contact with the side chains of the solvent-exposed Arg74 and Tyr77 in the β-strand 5/6 loop at the other end of the β-barrel, with large fluctuations of interatomic distances.

The ultimate dissociation of the interactions corresponds to the shallow well emerging at ∼30 Å before the PMF eventually becomes nearly flat at >35 Å. Thus, it can be seen that, although the cohesin binds predominantly to the second segment of the dockerin, a few residues on the first segment also participate in the complex formation, through either hydrophobic interactions or hydrogen bonding. The above results agree with a previous report demonstrating that the two segments of the CelS dockerin are both required for interaction with a cohesin.²⁴

Conformational change upon dissociation

During the dissociation process, the core structure of the cohesin remains essentially unchanged, but the solvent-exposed loop regions, and especially the recognition strips, undergo considerable conformational change, consistent with the notion that in the bound state the C-terminal region of α-helix 3 aids in stabilizing the well-defined conformations of the recognition strips. Overlaying the time-averaged free and complexed structures (not shown) also shows relatively large displacements of the loop regions, which include shifts in the recognition strips and movements of other short segments of polypeptide chain by up to 3 Å.

In the case of the dockerin, due to the absence of structural restraints imposed by cohesin-dockerin interactions, the dockerin adopts a flexible conformation in solution after dissociation from its cohesin partner, consistent with inspection of the crystal structures.^7,11 Particularly notable is the coil connecting helix 1 and 2, which is locked in the complex, but highly flexible and disordered in the isolated form. The ordered-to-disordered transition is reflected in the difference in the RMSF values of the backbone atoms: <1 Å in the bound structure, but ∼2 Å in the free structure. The C-terminal end of helix 1 also contributes to the structural change, with the most fluctuations at residues Arg23 and Leu22, alternating between helix and random coil structures over the course of the simulation. As suggested by the PMF calculations, this part of the dockerin domain is one of the crucial interaction sites involved in the cohesin-dockerin binding. The rest of the helix structure behaves, however, very similarly in the isolated and complexed structures. The interhelix distances in these two structures, calculated from the center of masses of helix 1 and 3, are both within the range of 9.5–10.5 Å. The two bound calcium ions are also found to remain intimately associated with the corresponding helices over the time scale explored by the present simulations. The dissociation does not affect the coordination number of the calcium ions.

Discussion

Recognition of Type I cohesins by dockerins is the determining event in assembly of individual enzymatic subunits into the cellulosome complex. To our knowledge, however, protein–protein interactions between cohesin and dockerins have not been examined using computational tools. It is therefore particularly informative to elucidate the detailed molecular principles upon which the cohesin-dockerin interaction is based at the atomistic level. The present MD simulations on the Type I cohesin-dockerin complexes in aqueous solution provide information on static stability of the model structures and dynamic details of the cohesin-dockerin interaction, such as degrees of fluctuations and local conformational changes induced by mutations, thus complementing experimental studies.

Biochemical mutagenesis studies have provided critical clues as to the mode of cohesin-dockerin interaction. One of the striking mutations, known to cause recognition failure, is D39N. Asp39 of the cohesin, one of the most conserved residues, is located at the protein–protein interface of the complex. This residue forms direct hydrogen bonds with Ser45 of the dockerin, the most critical residue for domain recognition,^12,14,21 and water-mediated hydrogen bonds with Val21 and Ile43. It has been demonstrated by mutagenesis that the single substitution of Asp39 by a neutrally charged Asn reduces the affinity of the interaction by more than three orders of magnitude and disrupts the normal recognition of the dockerin.¹⁵ Thus, this residue is a hot-spot for the cohesin-dockerin interaction.

Although experimental studies have revealed the importance of Asp39, in the absence of high-resolution structures, the detailed mechanism of how the mutation causes the malfunction remains largely unclear. Extensive MD studies of both the WT cohesin-dockerin complex and D39N mutant were carried out in this study to examine the contribution of this residue to the protein–protein binding. The results indicate that the substitution of the key residue Asp39 by Asn leads to conformational rearrangements of the local structure, such as the geometric reorientation of Asn39 side chain and the loss of hydrogen bonds with Ser45 and Ile43, which may have an impact on the destabilization of the complex and the experimentally observed decrease in affinity. The mutation does not result in significant modification of the dynamic properties of the principal β-sheet contact surface or the α-helices 1 and 3, but does dramatically increase the degree of mobility in the recognition strips, the conserved loops connecting β-strands 4 and 5, 6, and 7 of the cohesin domain.

It is evident that the site of the mutation is spatially far from the recognition strip regions that show increased structural instabilities. Therefore, direct contacts may not be primarily responsible for these fluctuations; instead, conformational fluctuations might be due to alterations in the global modulating forces. It is well-known that long-range electrostatic interaction plays a crucial role in protein stability and protein–protein binding. One of the important electrostatic elements could be the dipole originating from the aligned peptide units of an α-helix, which can contribute to the stabilization of protein structure by interacting with charged side chains.^25,26 In the cohesin-dockerin complex, Ser45 and Arg53 are two key dockerin residues in close contact with Asp39 and Glu86 of the cohesin domain. Ser45 at the N-terminal positive end of α-helix 3 points toward Asp39, whereas Arg53 at the C-terminus forms salt bridges with Glu86 (Fig. S5 in the Supporting Information). This suggests that electrostatic interactions, possibly involving the helix 3 dipole,²⁷ may play a role in the behavior of the recognition strips. Furthermore, calculation of the electrostatic interaction energy between the peptide atoms in the α-helix 3 and the peptide atoms in the two β-strands-3, 5 indicates that there is indeed a favorable interaction between the α-helix and the β-strands that stabilizes the native structure by 9 kcal/mol over D39N. Thus, neutralization of the key residue Asp39 may promote a global conformational effect by altering the electrostatic interaction in the helix-sheet packing, and this interaction may play an essential role in the formation of cohesin-dockerin complexes. On the other hand, the rupture of the hydrogen bond between Asp39 and Ser45 by the D39N mutation may loosen the cohesin-dockerin structure and cause helix 3 to move more freely, thus further promoting structural fluctuations in the recognition strips by weakening the hydrogen bonds and salt bridges between key residues, such as Arg53 and Glu86. Overall, the molecular basis underlying the cause of the observed large protein flexibility in the recognition strips may arise from the decrease in the stability of the interaction of the secondary structure elements, presumably through a less-favorable electrostatic interaction, and from the consequent disruption of the hydrogen-bond network.

The understanding of the underlying molecular association/dissociation mechanism in terms of structure and dynamical events is further facilitated by the knowledge of the free energy profile for the WT cohesin-dockerin dissociation. Specific protein–protein interactions in the cohesin-dockerin complex give rise to the features in the free energy landscape of dissociation. The sequential events of interdomain hydrogen-bond rupture and the step-by-step pattern of the cohesin-dockerin dissociation revealed by the present free energy calculations identify the dominant protein–protein interactions contributing to the overall binding free energy, and indicate that a set of residues lying on the flattened β-sheet surface and in the peripheral loop regions is the main obstacle to dockerin unbinding. Although examination of the crystal structure alone suggests that the formation of the cohesin-dockerin complex involves relatively large surface areas on both partners, the present results show that specific surface regions play more critical roles than others in forming and maintaining the integrity of the cellulosome complex. The results also provide evidence for a mode of binding involving both α-helices in the dockerin and the corresponding surface region from its cohesin partner: the C-terminal end of dockerin helix 1 interacting with the β-strand 5/6 loop, whereas the N-terminus diverted away from the cohesin surface; the N-terminus of helix 2 covering the core fragment of the β-sheet interface and the C-terminus interacting with the recognition strips. The cohesin-dockerin binding may therefore take place in a cooperative manner.

The experimental estimate of the overall equilibrium binding constant for the present cohesin/dockerin complex is 8 × 10⁷M⁻¹,¹² corresponding to a free energy change of about 12 kcal/mol (ΔG = −RTlnK_a, where R is the gas constant and T = 65°C). In the simulations, the overall difference in the calculated free energy between the minimum of the bound state and the barrier is ∼17 kcal/mol. This agreement is reasonable, given that the direct comparison of the dissociation free energy with the experimentally determined absolute binding energy would require a knowledge of the contribution to the free energy difference of the change in the free energy associated in the translational and rotational degrees of freedom on complexation,^28–30 and given the inherent errors stemming from the implementation of free energy algorithms and the sampling errors that may arise from the conformational flexibility of the unbound dockerin domain in solution. Furthermore, this study is focused on a detailed view of the underlying mechanism of association and interaction in the cohesin-dockerin complex rather than calculating the absolute binding free energy.

The present simulation results provide insight into the molecular principles that govern cohesin-dockerin domain recognition. These principles could in turn be used to guide protein engineering modifications so as to alter cohesin-dockerin binding. Efforts are underway to design engineered cellulosomal modules, which can conduct more efficient biomass degradation than the corresponding wild-type protein complexes. Both atomic-detail and coarse-grained computer simulations are expected, in conjunction with appropriate biochemical and biophysical experiments,³¹ to provide a foundation for understanding the principles of domain synergy and cellulosomal activity, thus allowing the rational, structure-based design of improved cellulosomal assemblies for cellulosic ethanol production.

Materials and Methods

System preparation and MD simulations

All MD calculations were carried out using the NAMD software package³² with the CHARMM27 force field³³ and TIP3P water model.³⁴ CMAP dihedral cross-term corrections for the protein³⁵ were not used. The simulation trajectories were analyzed with tools either from the GROMACS package³⁶ or local code. Computer-aided structure analysis was performed using the VMD software.³⁷

The initial structures of the complexes were generated by solvation of the X-ray structure of the Type I cohesin-dockerin complex from C. thermocellum (PDB ID: 1QHZ).⁷ The model comprises the cohesin-dockerin complex (two domains of 196 amino acids for a total of 2954 atoms), two dockerin-bound Ca²⁺ ions, and 18,940 water molecules. The total number of atoms in the system is about 60,000. The D39N mutant was constructed by replacing Asp39 with neutrally charged Asn. Appropriate Na⁺ ions were added into the bulk water region to maintain charge neutrality of the systems. These Na⁺ ions did not approach the protein complex in any of our simulations. The starting structures were then subjected to energy minimization using 500 steps of the steepest descent and 2000 steps of the conjugate gradient method.

After minimization, the structures were equilibrated by performing a 30 ps MD simulation with a weak harmonic restraint of 0.5 kcal/mol/Ų on all C_α atoms. After releasing the constraints, NPT ensemble simulations were subsequently conducted for 10 ns. The temperature and the normal pressure were maintained at 300 K and 1 bar, respectively, using Langevin dynamics and the Langevin piston method.^38,39 The Particle-Mesh Ewald approach was used for computation of electrostatic forces.⁴⁰ Periodic boundary conditions were assumed in all directions. The box size was adjusted to make sure that the periodic images of the protein do not overlap with the protein in the primary cell during the simulation.

Principal component analysis

For the PCA, the g-anaeig and g_covar programs in GROMACS 3.3³⁶ were employed to calculate covariance matrix elements, and porcupine plots⁴¹ were used to visualize the collective dynamic modes. In our analysis, the first three residues in the MD simulation and the last three residues were omitted before the PCA to avoid excessive terminal motions.

FEP calculations

The change in free energy of binding due to D39N point mutation of the cohesin domain was obtained from a thermodynamic cycle in which the free energy was computed between two distinct cohesin domains: the WT and the D39N mutant, both in the free state and bound to the dockerin domain. The coordinates for cohesin free in solution were generated by removal of the dockerin, that is, the bound conformation was used for the calculations of the free cohesin. This treatment is based on the rationale that the structures of the cohesin free in solution and in complex with its complimentary dockerin domain are extremely similar (0.43 Å RMSD for 138 C_α atoms),⁷ indicating the cohesin does not undergo a significant conformational change upon binding to the dockerin. Point mutations in both states were performed employing the FEP method^42–44 implemented in NAMD. The alchemical transformations involved both the negatively charged Asp39 side chain and a sodium counterion, so that the overall charge of the system was zero throughout the transformation. For each transformation, either in bulk water or in the bound complex, the reaction path was divided into 30 states of uneven widths, each corresponding to a different λ value. Narrow intermediate states were defined toward the end points of the transformation. For every λ point, 50 ps of equilibration was followed by 150 ps of data collection, corresponding to a total simulation length of 6 ns for each transformation. Counterions in the simulation box were restrained by harmonic potentials so as to avoid interference with the dynamics of protein, which may cause severe convergence issues in free energy calculations.⁴⁵

PMF calculations

The free energy profile for the dissociation of the WT cohesin-dockerin complex was computed using the adaptive biasing force (ABF) method,^46–48 which relies upon the integration of the average force acting on the reaction coordinate (ξ) obtained from unconstrained MD simulations. In the course of the simulation, a biasing force is estimated such that, once applied to the system, a Hamiltonian is yielded in which no average force acts along ξ. As a result, all values of ξ are sampled with equal probability, thus greatly improving the accuracy of the calculated free energies. For a complete description of this method, as well as an assessment of its efficiency compared with other related approaches for calculating free energy changes, see Refs.^47,48.

Here, the reaction coordinate, ξ, was chosen as the distance separating the centers of mass of these two domains. To achieve additional efficiency, the pathway joining the bound complex and the dissociated domains, 22 < ξ < 35 Å, was divided into 18 nonoverlapping windows, with uneven window sizes from 0.5 to 1 Å. For each window, up to 5 ns of MD was generated, resulting in a total of ∼90 ns of trajectory. Finally, another 10 ns ABF simulation was performed using a single 14 Å wide window embracing the entire free energy barrier that arises separating these two domains. Instantaneous values of the force were accrued in bins 0.02 Å wide.

The trajectories were generated using the same protocol as described in the System Preparation and MD Simulations section except that the temperature was maintained at 338 K (65°C), to be consistent with the experimental conditions.¹²