Conformational preferences of 1-amino-2-phenylcyclohexanecarboxylic acid, a phenylalanine cyclohexane analogue

Abstract

The intrinsic conformational preferences of the restricted phenylalanine analogue generated by including the α and β carbon atoms into a cyclohexane ring (1-amino-2-phenylcyclohexanecarboxylic acid, c₆Phe) have been determined using quantum mechanical calculations. Specifically, the conformational profile of the N-acetyl-N’-methylamide derivative of the c₆Phe stereoisomers exhibiting either a cis or a trans relative orientation between the amino and phenyl substituents has been analyzed in different environments (gas phase, chloroform and aqueous solutions). Calculations were performed using B3LYP, MP2 and HF methods combined with the 6-31+G(d,p) and 6-311++G(d,p) basis sets, and a self-consistent reaction-field (SCRF) method was applied to analyze the influence of the solvent. The amino acids investigated can be viewed as constrained phenylalanine analogues with a rigidly oriented aromatic side chain that may interact with the peptide backbone not only sterically but also electronically through the aromatic π orbitals. Their conformational propensities have been found to be strongly influenced by the specific orientation of the aromatic substituent in each stereoisomer and the conformation adopted by the cyclohexane ring, as well as by the environment.

Introduction

The incorporation of restricted amino acids into peptide chains is a powerful tool for the construction of peptide analogues with well-defined three-dimensional arrangements. α,α-Dialkylated residues are particularly useful because tetrasubstitution at the α carbon severely restricts the conformational space available to the peptide backbone and this leads to the stabilization of certain elements of secondary structure.¹ Thus, the simplest α,α-dialkylated amino acid, (α-methyl)alanine (also known as α-aminoisobutyric acid, Aib) is found almost exclusively in the 3₁₀-/α-helical region of the Ramachandran map.¹ In comparison, higher homologues of Aib with linear side chains prefer the fully-extended conformation, whereas their cyclic counterparts, 1-aminocycloalkanecarboxylic acids (Ac_nc), strictly parallel the behavior of Aib, with some distortion in the case of the highly strained cyclopropane derivative (n = 3).¹

The repertoire of non-natural amino acids useful in peptide design may be expanded by attaching a substituent to the cycloalkane moiety of Ac_nc. This combines the presence of side-chain functionality, which may be essential for peptide-receptor recognition when dealing with a bioactive peptide, with the well-defined conformational properties of the Ac_nc residues. The new side-chain functionality incorporated may be selectively oriented by selecting a certain cycloalkane size and stereochemistry. Given that side chains are directly involved in molecular recognition processes, their three-dimensional arrangement is crucial for adequate peptide-receptor interaction. Moreover, side chains may play a role in directing the conformational preferences of the peptide backbone.²

In recent years, we have been working on the synthesis³ and structural study⁴ –both theoretically and experimentally– of the amino acids obtained by incorporating a phenyl substituent at one of the β carbons of Ac_nc for n = 3–6. The compounds thus generated are phenylalanine (Phe) analogues and we designate them as c_nPhe, where n refers to the ring size, as in Ac_nc. The cyclic nature of the c_nPhe residues precludes rotation about the C^α—C^β bond and the orientation of the aromatic side chain is therefore dictated by the size (n value) and stereochemistry of the cycloalkane ring. It should be noted that the phenyl substituent incorporated at the β position may exhibit either a cis or a trans relative orientation with respect to the amino function, respectively giving rise to cis- or trans-c_nPhe derivatives. The c_nPhe residues with diverse ring size and stereochemistry constitute a set of phenylalanine analogues with distinct well-defined side-chain arrangements. They are excellent tools to investigate the ability of the side chain to influence the peptide backbone conformation⁴ since the tightly held aromatic substituent may interact with the backbone not only sterically but also electronically through the aromatic π orbitals. Indeed, the different spatial orientation attained by the aromatic substituent in the c_nPhe residues has proven useful in several applications related to the stabilization of particular peptide backbone conformations.^4,5

In particular, we have shown that the cyclohexane members (c₆Phe) are able to stabilize different types of β-turns depending on the phenyl side-chain orientation,4b,e at variance with the behavior exhibited by the natural amino acid.4e,f These experimental results prove that the phenylalanine cyclohexane analogues (c₆Phe) are able to modulate the peptide backbone conformation, and show therefore great promise as phenylalanine substitutes in the design of peptides with controlled fold in the backbone. In early studies, molecular mechanics (MM) simulations were used to explore the conformational propensities of c₆Phe.^4d The minimum energy conformations located were subsequently used as starting points for energy minimizations at the HF/6-31G(d) quantum mechanical level. However, such a study cannot be considered as a complete description of the conformational propensities of c₆Phe due to the intrinsic limitations associated with MM methods. As a matter of fact, only 7 and 8 minima were characterized for the N-acetyl-N’-methylamide derivatives of cis-c₆Phe and trans-c₆Phe, respectively, in that MM study,^4d whereas the number of minima expected for these compounds is significantly higher. The reason for this is that quantum mechanical calculations provided as many as 11 different minima for the analogous unsubstituted Ac₆c derivative.⁶ Incorporation of a phenyl substituent into Ac₆c to generate cis- or trans-c₆Phe is expected to increase the number of minima because the symmetry of the molecule is broken [conformations characterized by (φ,ψ) and (–φ,–ψ) dihedral angles are equivalent for an achiral amino acid such as Ac₆c but not for the non-symmetrical c₆Phe residues], and therefore each minimum energy conformation characterized for Ac₆c should translate, in principle, into two different c₆Phe minima. Obviously, some of the expected minima may be annihilated, in the same way as new minima without precedent in Ac₆c may appear in c₆Phe induced by the presence of the aromatic substituent. In this context, a comparison with the cyclopentane series is instructive: quantum mechanical calculations provided 5 minimum energy conformations for Ac₅c,⁷ while 8 and 10 minima, respectively, were located for cis-c₅Phe and trans-c₅Phe.^4a

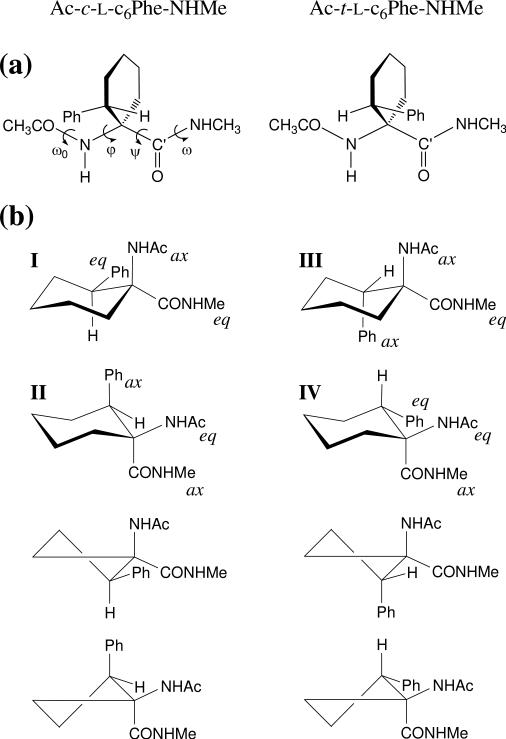
In this work, we present a complete conformational study of the N-acetyl-N’-methylamide derivatives of the cyclohexane analogues of L-phenylalanine exhibiting a cis or a trans relative orientation between the phenyl substituent and the amino function, hereafter denoted as Ac-c-l-c₆Phe-NHMe and Ac-t-l-c₆Phe-NHMe, respectively (Figure 1a). Density functional theory (DFT) calculations at the B3LYP/6-31+G(d,p) level have been used to locate and characterize the minimum energy conformations for these compounds. In order to obtain reliable estimates, the relative energies of all these structures have been re-evaluated using different theoretical levels. Moreover, the influence of the solvent on the conformational preferences of the compounds under study has been analyzed using a self-consistent reaction-field (SCRF) method. The intrinsic conformational preferences calculated in the present work for the c₆Phe derivatives have been compared with those described recently for the unsubstituted Ac₆c residue.⁶

Figure 1.

(a) Structure of the compounds investigated, Ac-c-l-c₆Phe-NHMe and Ac-t-l-c₆Phe-NHMe, that incorporate, respectively, the cis and trans cyclohexane analogues of l-phenylalanine. The backbone dihedral angles are indicated for the cis derivative. (b) Chair and half-chair conformations considered as starting geometries for the cyclohexane ring in the compounds under study. The substituents located in axial (ax) or equatorial (eq) positions are indicated for the chair conformations.

Methods

All the calculations were performed using the Gaussian 03 computer program.⁸ In order to characterize the minimum energy conformations of Ac-c-l-c₆Phe-NHMe and Ac-t-l-c₆Phe-NHMe, a systematic exploration of the conformational space was performed. Given that each flexible backbone dihedral angle (φ,ψ) is expected to exhibit three minima, 9 minima can be anticipated for the potential energy surface E=E(φ,ψ). Regarding the cyclohexane ring, the two possible chair conformations (Figure 1b) were initially considered for each compound. Additionally, two half-chairs (Figure 1b) were included as starting geometries. Although the latter arrangement is very high in energy and is not expected to be found in any energy minima, it is a good starting point to explore cyclohexane conformations different from chair, such as boat or twist. Accordingly, for each c₆Phe derivative under study, 9 (φ,ψ minima) × 4 (2 chair + 2 half-chair cyclohexane conformations) = 36 structures were used as starting points for subsequent full geometry optimizations.

All geometry optimizations were performed using the B3LYP functional^9,10 combined with the 6-31+G(d,p) basis set,¹¹ i.e. B3LYP/6-31+G(d,p). Frequency analyses were carried out to verify the nature of the minimum state of all the stationary points obtained and to calculate the zero-point vibrational energies (ZPVE) and both thermal and entropic corrections. These statistical terms were then used to compute the conformational Gibbs free energies in the gas phase at 298K (ΔG_gp). To analyze the influence of the size of the basis set and the theoretical method used on the conformational energies, single point calculations at the HF/6-31+G(d,p), MP2/6-31+G(d,p),¹² and B3LYP/6-311++G(d,p)¹³ levels were further performed on all the minima.

To obtain an estimation of the solvation effects on the relative stability of the most relevant minima, single-point calculations were conducted on the optimized structures using a SCRF model. Specifically, the Polarizable Continuum Model (PCM) developed by Tomasi and co-workers¹⁴ was used to describe chloroform and water as solvents. The PCM method represents the polarization of the liquid by a charge density appearing on the surface of the cavity created in the solvent. This cavity is built using a molecular shape algorithm. PCM calculations were performed in the framework of the B3LYP/6-31+G(d,p) level using the standard protocol and considering the dielectric constants of chloroform (ε = 4.9) and water (ε = 78.4) to obtain the free energies of solvation (ΔG_solv) of the minimum energy conformations. Within this context, it should be emphasized that previous studies indicated that solute geometry relaxations in solution and single-point calculations on the optimized geometries in the gas phase give almost identical ΔG_solv values.¹⁵ The conformational free energies in solution (ΔG_Chl and ΔG_water) at the B3LYP/6-31+G(d,p) level were then estimated using the classical thermodynamics scheme, i.e. by adding the ΔG_solv and ΔG_gp values.

Results and Discussion

Complete geometry optimizations and frequency calculations led to the characterization of 17 and 21 minimum energy conformations in the gas phase for Ac-c-l-c₆Phe-NHMe and Ac-t-l-c₆Phe-NHMe, respectively. They are listed in Tables 1 and 2, where the conformation adopted by the peptide backbone and the cyclohexane ring, as well as the relative energy (ΔE_gp) and free energy (ΔG_gp) calculated at the B3LYP/6-31+G(d,p) level are indicated for each minimum. Perczel's nomenclature¹⁶ has been used to identify the different peptide backbone conformations.

Table 1.

Backbone dihedral angles,^a,^b relative energy^c in the gas phase (ΔE_gp), and relative free energy^c in the gas phase (ΔG_gp) for the minimum energy conformations of Ac-c-l-c₆Phe-NHMe characterized at the B3LYP/6-31+G(d,p) level. The arrangement adopted by the peptide backbone and the cyclohexane ring^d is indicated.

#	ω0	ϕ	ψ	ω	backbone	cyclohexane	ΔEgp	ΔGgp
1	−175.3	−71.0	35.2	172.9	γL	chair I	0.0e	0.0f
2	−173.6	−73.6	67.4	−176.0	γL	chair II	2.6	2.7
3	−174.6	−73.5	46.7	176.1	γL	twist	3.1	3.4
4	174.5	71.9	−68.5	175.0	γD	chair II	3.7	4.1
5	171.5	46.9	−13.7	177.4	γD	chair I	4.9	4.7
6	161.1	−63.7	162.0	−177.7	εL	chair I	5.1	3.8
7	177.4	−178.2	179.8	−178.3	βL	chair I	5.6	4.9
8	166.2	59.3	40.2	−175.5	αD	chair II	5.7	5.4
9	−168.5	−61.8	−35.9	175.6	αL	chair II	6.1	5.3
10	166.8	167.4	−27.1	−171.9	δD	chair I	7.9	7.7
11	−165.4	32.9	−124.0	175.5	εD	chair I	8.0	7.5
12	−170.9	−166.4	31.5	171.5	δL	twist	8.6	7.5
13	169.9	56.1	42.4	−175.0	αD	twist	9.3	9.0
14	−174.4	−142.7	110.5	−174.1	δL	chair II	9.7	7.7
15	165.3	−61.5	150.8	−177.3	εL	twist	9.8	8.8
16	169.5	−171.3	−46.1	−174.1	δD	twist	10.3	9.7
17	178.6	−146.0	−68.6	178.3	δD	twist	13.9	12.5

^aIn degrees.

^bSee Figure 1a for definition.

^cIn kcal/mol.

^dSee Figure 1b.

^eE=−883.014845 a.u.

^fG=−882.701540 a.u.

Table 2.

Backbone dihedral angles,^a,^b relative energy^c in the gas phase (ΔE_gp) and relative free energy^c in the gas phase (ΔG_gp) for the minimum energy conformations of Ac-t-l-c₆Phe-NHMe characterized at the B3LYP/6-31+G(d,p) level. The arrangement adopted by the peptide backbone and the cyclohexane ring^d is indicated.

#	ω0	ϕ	ψ	ω	backbone	cyclohexane	ΔEgp	ΔGgp
1	−175.2	−73.5	52.2	178.4	γL	chair IV	0.0e	0.0f
2	179.7	−179.2	175.2	−178.6	βL	chair IV	2.7	2.5
3	177.6	71.4	−58.2	−178.7	γD	chair III	3.5	3.1
4	−169.7	−170.6	29.9	171.7	δL	chair IV	4.1	3.7
5	169.5	177.2	−30.9	−173.2	δD	chair IV	4.3	3.8
6	168.1	53.0	−16.9	−177.6	γD	chair IV	5.9	5.5
7	167.1	−59.6	131.7	−177.7	εL	chair III	6.0	5.3
8	164.6	48.1	42.5	−174.4	αD	chair IV	6.2	6.3
9	175.7	−69.2	89.5	−172.5	γL	chair III	6.9	6.1
10	−167.3	58.0	−123.9	175.8	εD	chair III	7.4	6.3
11	−170.0	−61.6	−37.5	176.7	αL	chair III	7.4	6.7
12	−176.2	−54.3	72.4	177.6	γL	twist	9.3	9.4
13	177.3	72.8	−54.2	−176.0	γD	twist	9.3	9.4
14	−176.2	176.2	164.0	175.0	βL	chair III	10.3	10.1
15	179.9	−172.1	159.7	174.3	βL	twist	11.5	11.2
16	176.8	−68.8	85.7	−172.3	γL	twist	13.2	12.5
17	−172.4	179.4	−47.5	−172.8	δD	twist	13.3	12.7
18	−171.0	−168.7	32.4	172.2	δL	twist	13.5	12.4
19	−169.1	−61.7	−38.0	178.3	αL	twist	13.6	12.7
20	164.5	−61.8	149.3	177.8	εL	twist	14.4	13.0
21	−163.0	59.5	−166.7	−177.5	εD	twist	14.6	14.4

^aIn degrees.

^bSee Figure 1a for definition.

^cIn kcal/mol.

^dSee Figure 1b.

^eE=−883.014189 a.u.

^fG=−882.701217 a.u.

Ac-cl-c₆Phe-NHMe

The 17 minimum energy conformations characterized for this compound in the gas phase are distributed within a relative energy interval of 13.9 kcal/mol (Table 1). Eight of them present ΔE_gp values lower than 6 kcal/mol, and are depicted in Figure 2. The contribution of the remaining minima in Table 1 to the conformational equilibrium of Ac-c-l-c₆Phe-NHMe is expected to be negligible not only in the gas phase but also in solution, given that solute-solvent interactions typically mean a stabilization of several kcal/mol.

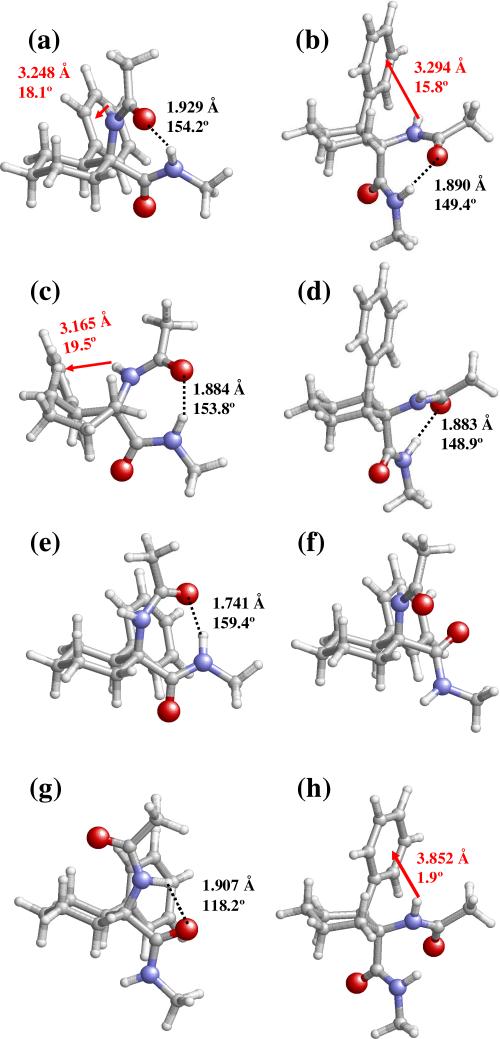
Figure 2.

Selected minimum energy conformations characterized for Ac-c-l-c₆Phe-NHMe at the B3LYP/6-31+G(d,p) level: (a) 1; (b) 2; (c) 3; (d) 4; (e) 5; (f) 6; (g) 7; and (h) 8. Conformational parameters are provided in Table 1. Intramolecular N–H···O hydrogen bonds and N–H···π interactions are indicated by black dashed lines and red arrows, respectively. The geometrical parameters correspond to the d(H···O) and <N–H···O (in Å and degrees, respectively) for hydrogen bonds and to d_H···Ph and θ (in Å and degrees, respectively; see text for definition) for N–H···π interactions.

The lowest energy minimum of Ac-c-l-c₆Phe-NHMe (1) adopts a γ_L backbone arrangement (inverse γ-turn or equatorial C₇ conformation), in which the terminal acetyl CO and methylamide NH sites form an intramolecular hydrogen bond [d(H···O)= 1.929 Å, <N–H···O= 154.2°] defining a seven-membered cycle (Figure 2a). In this conformation, the phenyl substituent and the amino group of cis-c₆Phe lie in close proximity, thus allowing the formation of a weak attractive interaction of the N–H···π type. The geometry of this interaction is defined by the distance between the amide hydrogen and the center of the aromatic system (d_H···Ph= 3.248 Å) and the angle formed by the N–H bond and the phenyl ring plane (θ= 18.1°). The ability of the π electron density of aromatic systems to interact with proton donors has long been recognized,¹⁷ and more recently has been identified as a stabilizing factor of peptide and protein structures.¹⁸ Importantly, interactions of this type have been observed experimentally in small peptides containing c₃Phe^4f and c₆Phe,^4e and characterized theoretically for the former residue.^4c

The same γ_L backbone conformation is found in minima 2 and 3, which are stabilized by similar hydrogen bonding and NH-aromatic interactions (Figures 2b and 2c). Indeed, the three γ_L structures in Table 1 differ mainly in the shape of the cyclohexane ring. The global minimum presents a chair of type I (Figure 1b), which is expected to be that preferred by Ac-c-l-c₆Phe-NHMe according to the axial/equatorial arrangement of the substituents and the tendency of bulky groups to avoid axial positions because they are known to produce a higher steric hindrance with the rest of the cyclohexane system. In chair I, the bulky phenyl ring is equatorially located and only one of the three cyclohexane substituents (–NHCOMe) occupies an axial position. In minimum 2, the six-membered ring assumes the alternate chair arrangement (II, Figure 1b), that bears the phenyl and –CONHMe groups in axial whereas the amino moiety occupies an equatorial position. The less favorable orientation of the cyclohexane substituents in this case is associated to an energy penalty of 2.6 kcal/mol in terms of ΔE_gp. It is highly remarkable that the six-membered ring in minimum 3 adopts a twist conformation, that is, a slightly distorted boat. The high stability of this structure, which is only 0.5 kcal/mol above minimum 2, may be related to the presence of two substituents –among which is the sterically more demanding one (the phenyl group)– in pseudoequatorial positions, and the non-existence of steric conflicts between the peptide backbone and either the cyclohexane moiety or the phenyl substituent.

The next two minima, 4 (Figure 2d) and 5 (Figure 2e), also exhibit a hydrogen bond linking the terminal acetyl CO and methylamide NH groups and closing the seven-membered cycle typical of a γ-turn. However, in this case, the sign of the (φ,ψ) dihedral angles corresponds to a γ_D conformation (axial C₇ or classical γ-turn). Inversion of the γ-turn type results in the disruption of the interaction between the aromatic π orbitals and the cis-c₆Phe NH site. Moreover, only chair arrangements of the cyclohexane ring are found to be compatible with this backbone conformation. Surprisingly enough, the most stable γ_D minimum (4) presents a type II chair, with the bulky phenyl group located axially. The a priori unexpected higher stability observed for this conformer is due to the fact that chair I in 5 brings in close proximity the acetyl oxygen atom of the –NHCOMe peptide fragment and the aromatic ring, thus introducing a very strong steric and electronic repulsion. To minimize this repulsive interaction, the peptide backbone geometry in minimum 5, (φ,ψ) = (47,–14), is highly distorted with respect to that corresponding to a standard γ_D conformation, (φ,ψ) ≈ (70,–60).

The unfavorable interactions between the –NHCOMe oxygen and the phenyl substituent for a chair I-shaped cyclohexane are not present when the peptide backbone assumes semi-extended or fully-extended structures characterized by large ψ values. Thus, minima 6 and 7 combine, respectively, an ε_L (also called polyproline II) or a β_L (C₅) conformation with a chair I disposition for the cyclohexane ring. In contrast, none of these backbone arrangements seem to be compatible with chair II (Table 1). Minimum 6 (Figure 2f) lacks stabilizing interactions either of the hydrogen bond or N–H···π type, whereas a weak intramolecular hydrogen bond [d(H···O)= 1.907 Å, <N–H···O= 118.2°] connecting the amide functions is present in 7 (Figure 2g). It is interesting to note that 6 presents a ΔG_gp value considerably low (3.8 kcal/mol), and is the fourth most stable minima –instead of the sixth– in terms of relative free energy.

The last conformer in Figure 2 (8, Figure 2h) exhibits a ΔE_gp value of 5.7 kcal/mol and falls into the left-handed α-helix region (α_D) of the Ramachandran map. This backbone conformation combined with a cyclohexane chair II arrangement allows the formation of a stabilizing interaction between the π cloud of the axially-oriented phenyl ring and the NH group of cis-c₆Phe. Although not included in Figure 2, a minimum with an α_L backbone geometry and very close in energy (9, Table 1) was also characterized. Notably enough, none of the α-helical minima located present a cyclohexane accommodating the alternate chair conformation.

Ac-t-l-c₆Phe-NHMe

Table 2 describes the most relevant geometrical parameters corresponding to the 21 minimum energy conformations characterized for the trans-c₆Phe derivative in the gas phase, which show ΔE_gp and ΔG_gp values of up to 14.6 and 14.4 kcal/mol, respectively. The 8 most stable minima are displayed in Figure 3.

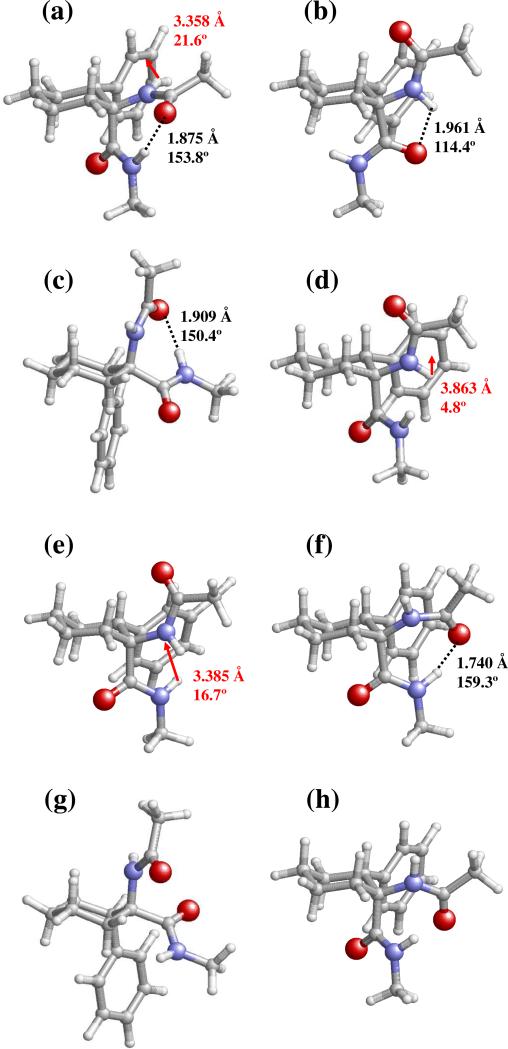
Figure 3.

Selected minimum energy conformations characterized for Ac-t-l-c₆Phe-NHMe at the B3LYP/6-31+G(d,p) level: (a) 1; (b) 2; (c) 3; (d) 4; (e) 5; (f) 6; (g) 7; and (h) 8. Conformational parameters are provided in Table 2. Intramolecular N–H···O hydrogen bonds and N–H···π interactions are indicated by black dashed lines and red arrows, respectively. The geometrical parameters correspond to the d(H···O) and <N–H···O (in Å and degrees, respectively) for hydrogen bonds and to d_H···Ph and θ (in Å and degrees, respectively; see text for definition) for N–H···π interactions.

As observed before for the cis-c₆Phe derivative, the global minimum of Ac-t-l-c₆Phe-NHMe (1, Figure 3a) combines a γ_L backbone conformation and a cyclohexane ring assuming the most favorable chair arrangement, namely that with the bulky aromatic substituent equatorially located (chair IV, Figure 1b). This structure is stabilized by the intramolecular hydrogen bond typical of the γ-turn conformation and by an NH-aromatic interaction, with geometrical parameters similar to those described for the global minimum of cis-c₆Phe.

Other energy minima exhibiting a γ_L backbone and differing from the global minimum in the cyclohexane shape were also located for Ac-t-l-c₆Phe-NHMe (Table 2). However, in this case, reversal of the chair type from IV to III results in a destabilization of 6.9 kcal/mol (minimum 9). Also a six-membered ring with a twist arrangement was found to be compatible with the γ_L structure for this compound, but at a high energy cost (minima 12 and 16). This is in sharp contrast to that described before for Ac-c-l-c₆Phe-NHMe. Thus, although cis- and trans-c₆Phe present global minima with high structural similarity, their response to changes in the cyclohexane conformation for this backbone disposition is notably different. The reason for this distinct behavior lies in the relative orientation of the phenyl ring, which for the trans derivative is next to the carboxyl terminus. Thus, the chair III arrangement combined with a γ_L backbone conformation (minimum 9) results in a high proximity between the carbonyl oxygen of trans-c₆Phe and the aromatic substituent.

A parallel situation, although less marked, is found when comparing the minima exhibiting a γ_D structure for Ac-c-l-c₆Phe-NHMe and Ac-t-l-c₆Phe-NHMe. Thus, for the latter compound, changing the most favorable cyclohexane arrangement for this backbone (chair III, minimum 3) to other shapes results in an energy increase of at least 2.4 kcal/mol. In comparison, for the cis derivative, the two alternate chairs are separated by an energy gap of 1.2 kcal/mol for the same γ_D conformation. Interestingly, for both compounds, this backbone type is more stable when combined with the chair bearing the aromatic substituent in axial (II for cis-c₆Phe and III for trans-c₆Phe).

Another remarkable feature in Table 2 is that three different conformational regions are visited by the minima with ΔE_gp below 5 kcal/mol, namely γ, β and δ. In comparison, only the former appears in Table 1 for the same energy limit. This indicates that the presence of the phenyl substituent produces a less severe restriction of the peptide backbone flexibility for the trans compound, at least, in the gas phase. A similar trend was observed for the c₃Phe^4c and c₅Phe^4a residues investigated before, indicating that the introduction of a phenyl group in Ac_nc to give the corresponding c_nPhe analogue produces more intense conformational constraints when the aromatic substituent is located in the neighborhood of the amino moiety (cis-c_nPhe).

The location of δ minima for the trans-c₆Phe derivative at about 4 kcal/mol (minima 4 and 5) is noteworthy, since this type of peptide backbone geometry was not detected among the energy minima of the c_nPhe residues studied before.^4a,c Although minima with a δ structure are also present in Table 1 for cis-c₆Phe, their relative energy is much higher (7.9 kcal/mol and above). The same holds true for the fully-extended conformation (β). Indeed, minimum 2 in Table 2 exhibits the intramolecularly hydrogen-bonded five-membered ring [d(H···O)= 1.961 Å, <N–H···O= 114.4°] typical of a β backbone conformation, and is destabilized with respect to the global minimum by only 2.7 kcal/mol. In comparison, the most stable structure with a β backbone found for Ac-c-l-c₆Phe-NHMe is 5.6 kcal/mol less stable than the lowest energy minimum. This distinct behavior must be ascribed to the different steric hindrance produced between the cyclohexane ring (the axial hydrogen atoms attached to the γ and γ’ carbons, mainly) and the –NHCOMe or –CONHMe peptide fragments when the latter are axially located (as occurs in the chairs of the most stable β conformers of cis- c₆Phe and trans-c₆Phe, respectively) and adopt a fully-extended conformation, that is, φ and ψ angles close to 180°.

Influence of the thermodynamic corrections, the quantum mechanical method and the basis set on the relative stabilities

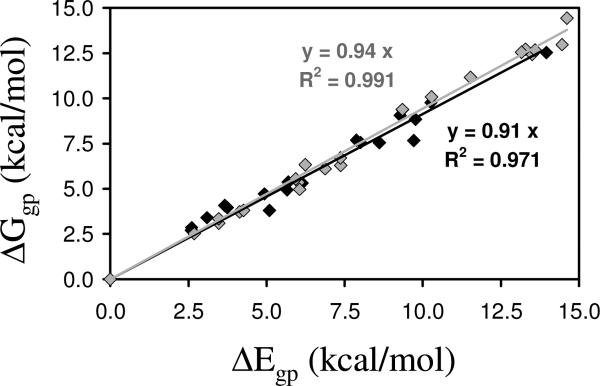
Figure 4 represents ΔE_gp vs. ΔG_gp for the minimum energy conformations of Ac-c-l-c₆Phe-NHMe and Ac-t-l-c₆Phe-NHMe at the B3LYP/6-31+G(d,p) level of theory (Tables 1 and 2). As can be seen, there is a strong correlation between the two parameters, the incorporation of ZPVE, thermal, and entropic corrections leading to a systematic reduction of the ΔE_gp values. Thus, ΔG_gp is on average 7% lower than ΔE_gp, with an average reduction of 9% and 6%, respectively, for the cis and trans derivatives.

Figure 4.

Graphical representation of ΔE_gp vs. ΔG_gp calculated at the B3LYP/6-31+G(d,p) level for Ac-c-l-c₆Phe-NHMe (black diamonds) and Ac-t-l-c₆Phe-NHMe (grey diamonds). The regressions (y= c·x) and correlation coefficients (R²) are displayed for each compound.

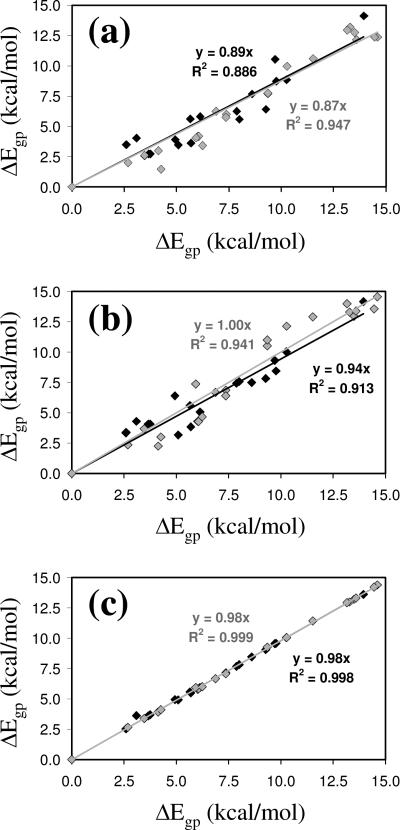
Tables 3 and 4 compare the ΔE_gp values calculated for the compounds under study at different theoretical levels: B3LYP/6-31+G(d,p), MP2/6-31+G(d,p), HF/6-31+G(d,p) and B3LYP/6-311++G(d,p), with molecular geometries optimized at the B3LYP/6-31+G(d,p) level in all cases. Comparison of the results obtained using the B3LYP and MP2 methods combined with the 6-31+G(d,p) basis set (Figure 5a) reveals an excellent agreement. Thus, the ΔE_gp values provided by the former method are overestimated by about 11–13% only. The difference between these two methods should be mainly attributed to the N–H···π interaction, which is better described at the MP2 level, because the strength of interactions involving the π cloud of aromatic systems is typically underestimated by the B3LYP functional.¹⁵ A very significant concordance is also displayed by the ΔE_gp values calculated using the B3LYP and HF methods combined with the 6-31+G(d,p) basis set (Figure 5b). On the other hand, the negligible influence of the size of the basis set is reflected in Figure 5c, which compares the ΔE_gp values obtained using the B3LYP functional combined with the 6-31+G(d,p) and 6-311++G(d,p) basis sets. The overall of these results indicates that the B3LYP/6-31+G(d,p) theoretical level is suitable for the evaluation of energies in the gas phase.

Table 3.

Relative energy in the gas phase^a (ΔE_gp) calculated at different theoretical levels^b for the minimum energy conformations of Ac-c-l-c₆Phe-NHMe.

	6-31+G(d,p)			6-311++G(d,p)
#	B3LYP	MP2	HF	B3LYP
1	0.0c	0.0d	0.0e	0.0f
2	2.6	3.5	3.3	2.5
3	3.1	4.0	4.3	3.6
4	3.7	2.7	4.1	3.6
5	4.9	3.9	6.4	4.9
6	5.1	3.5	3.2	4.9
7	5.6	5.6	5.6	5.6
8	5.7	3.6	3.8	5.5
9	6.1	5.8	5.1	5.9
10	7.9	6.2	7.4	7.7
11	8.0	7.8	5.6	7.6
12	8.6	7.7	7.5	8.5
13	9.3	6.4	7.8	9.1
14	9.7	10.5	9.3	9.6
15	9.8	8.7	8.4	9.6
16	10.3	8.9	10.0	10.0
17	13.9	14.1	14.1	13.6

^aIn kcal/mol.

^bEnergies at the MP2/6-31+G(d,p), HF/6-31+G(d,p) and B3LYP/6-311++G(d,p) levels were derived from single point calculations on B3LYP/6-31+G(d,p) geometries.

^cE=−883.014845 a.u.

^dE=−880.353232 a.u.

^eE=−877.425595 a.u.

^fE=−883.196342 a.u.

Table 4.

Relative energy in the gas phase^a (ΔE_gp) calculated at different theoretical levels^b for the minimum energy conformations of Ac-t-l-c₆Phe-NHMe.

#	6-31+G(d,p)			6-311++G(d,p)
	B3LYP	MP2	HF	B3LYP
1	0.0c	0.0d	0.0e	0.0f
2	2.7	2.0	2.3	2.6
3	3.5	2.6	3.7	3.4
4	4.1	3.0	2.2	3.9
5	4.3	1.5	3.0	4.2
6	5.9	4.1	7.3	5.9
7	6.0	4.2	4.3	5.8
8	6.2	6.0	3.4	4.7
9	6.9	6.7	6.2	6.7
10	7.4	7.1	6.0	6.9
11	7.4	5.7	6.4	7.1
12	9.3	7.7	10.5	9.2
13	9.3	7.7	11.0	9.3
14	10.3	9.9	12.1	10.0
15	11.5	10.6	12.9	11.4
16	13.2	12.9	14.0	12.9
17	13.3	13.2	13.3	13.0
18	13.5	12.7	12.9	13.2
19	13.6	12.1	13.4	13.3
20	14.4	12.4	13.6	14.2
21	14.6	12.3	14.6	14.4

^aIn kcal/mol.

^bEnergies at the MP2/6-31+G(d,p), HF/6-31+G(d,p) and B3LYP/6-311++G(d,p) levels were derived from single point calculations on B3LYP/6-31+G(d,p) geometries.

^cE=−883.014189 a.u.

^dE=−880.351683 a.u.

^eE=−877.424807 a.u.

^fE=−883.195613 a.u.

Figure 5.

Graphical representation of ΔE_gp calculated at the B3LYP/6-31+G(d,p) level vs. ΔE_gp predicted at the (a) MP2/6-31+G(d,p), (b) HF/6-31+G(d,p) and (c) B3LYP/6-311++G(d,p) levels for Ac-c-l-c₆Phe-NHMe (black diamonds) and Ac-t-l-c₆Phe-NHMe (grey diamonds). The regressions (y= c·x) and correlation coefficients (R²) are displayed for each compound.

Influence of the solvent

The influence of chloroform and water on the conformational preferences of the c₆Phe derivatives was evaluated using the PCM method. The conformational free energy in a given solvent was approximated by adding ΔG_solv to the best estimation of ΔG_gp, which is abbreviated as ΔG_gp,* and was determined by combining the ΔE_gp value calculated at the MP2/6-31+G(d,p) level with the thermodynamic corrections obtained at the B3LYP/6-31+G(d,p) level. The values of ΔG_gp,* and the conformational free energies in chloroform and aqueous solutions (ΔG_Chl and ΔG_water, respectively) for all the minimum energy conformations of Ac-c-l-c₆Phe-NHMe and Ac-t-l-c₆Phe-NHMe are given in Tables 5 and 6, respectively. In general, the solvent plays a stabilizing role, which is reflected by a reduction of the relative free energies interval. Specifically, for Ac-c-l-c₆Phe-NHMe, the ΔG_gp,* interval is wider than the ΔG_Chl and ΔG_water ones by 2.5 and 2.1 kcal/mol, respectively. For Ac-t-l-c₆Phe-NHMe, this feature is detected in chloroform solution only (1.6 kcal/mol). It is also interesting to note that the ΔG_gp,* value for some conformers is significantly lower than that of ΔG_gp provided in Tables 1 and 2.

Table 5.

Relative conformational free energies^a at 298 K for the minimum energy conformations of Ac-c-l-c₆Phe-NHMe in the gas phase (ΔG_gp,*),^b chloroform solution (ΔG_Chl) and aqueous solution (ΔG_water). The solvation free energies^a in chloroform and aqueous solutions [ΔG_solv(Chl) and ΔG_solv(water), respectively] are also given.

#	ΔGgp,*	ΔGsolv(Chl)	ΔGChl	ΔGsolv(water)	ΔGwater
1	0.0c	2.8	0.6	4.7	5.5
2	3.6	2.5	3.9	4.5	8.9
3	4.3	3.1	5.2	5.5	10.6
4	3.1	1.0	2.0	1.2	5.2
5	3.7	2.0	3.5	1.5	6.0
6	2.2	0.0	0.0	−2.2	0.8
7	4.9	0.3	3.0	−1.5	4.2
8	3.3	−1.0	0.1	−4.1	0.0
9	5.0	0.9	3.7	−0.5	5.3
10	6.1	1.4	5.3	−0.4	6.5
11	5.1	0.4	3.3	−0.5	5.4
12	6.6	1.3	5.7	0.2	7.6
13	6.2	−1.4	2.6	−5.0	2.0
14	8.5	0.5	6.8	−0.6	8.7
15	7.8	1.0	6.6	−0.4	8.2
16	8.4	−1.4	4.8	1.1	10.3
17	12.7	−0.3	10.2	−4.6	8.9

^aIn kcal/mol.

^bΔG_gp,* corresponds to the best estimation of ΔG_gp, which was obtained by combining the ΔE_gp value calculated at the MP2/6-31+G(d,p) level with the thermodynamic corrections obtained at the B3LYP/6-31+G(d,p) level.

^cG= −880.039927 a.u.

Table 6.

Relative conformational free energies^a at 298 K for the minimum energy conformations of Ac-t-l-c₆Phe-NHMe in the gas phase (ΔG_gp,*),^b chloroform solution (ΔG_Chl) and aqueous solution (ΔG_water). The solvation free energies^a in chloroform and aqueous solutions [ΔG_solv(Chl) and ΔG_solv(water), respectively] are also given.

#	ΔGgp,*	ΔGsolv(Chl)	ΔGChl	ΔGsolv(water)	ΔGwater
1	0.0c	3.3	1.0	5.3	6.2
2	1.8	1.3	0.8	1.7	4.4
3	2.2	1.0	0.9	0.5	3.6
4	2.6	1.7	1.9	−0.7	2.7
5	1.0	1.5	0.2	0.4	2.3
6	3.7	1.4	2.8	0.0	4.6
7	3.5	−0.3	0.9	−2.1	2.3
8	3.5	−1.2	0.0	−4.4	0.0
9	5.5	0.6	3.8	−0.8	5.6
10	4.9	0.9	3.5	0.3	6.1
11	5.1	−1.3	1.5	−5.5	0.5
12	7.7	1.2	6.6	1.1	9.7
13	7.8	0.5	5.9	0.5	9.1
14	9.7	1.3	8.7	2.1	12.7
15	10.2	1.3	9.2	2.5	13.6
16	12.3	0.2	11.5	−0.8	10.2
17	13.1	0.6	11.4	−1.5	12.5
18	11.7	0.2	9.6	−0.9	11.7
19	11.2	−1.8	7.1	−6.7	5.4
20	10.9	−1.1	7.5	−3.4	8.4
21	12.2	−0.5	9.3	0.2	13.2

^aIn kcal/mol.

^bΔG_gp,* corresponds to the best estimation of ΔG_gp, which was obtained by combining the ΔE_gp value calculated at the MP2/6-31+G(d,p) level with the thermodynamic corrections obtained at the B3LYP/6-31+G(d,p) level.

^cG= −880.038710 a.u.

Furthermore, solvation induces important changes in the stability order of the different conformers. Thus, 6 and 8 become the most favored structures for the cis-c₆Phe derivative in chloroform (Table 5). Although the relative stability of 1 decreases significantly in this organic solvent (ΔG_Chl= 0.6 kcal/mol), it is still significantly populated at room temperature. Indeed, the populations of 6, 8 and 1 in chloroform according to a Boltzmann distribution are 44.3%, 37.3% and 15.5%, respectively. The stability of 8 increases with the polarity of the environment, and it becomes the lowest energy minimum in aqueous solution, with an estimated population of 77.3%. Conformer 6 is unfavored by 0.8 kcal/mol in water and accounts for 20.0% of the population, while the 15 remaining minima contribute by 2.7% only. Thus, the conformation preferred by Ac-c-l-c₆Phe-NHMe moves from the γ-turn in the gas phase to structures lacking an intramolecular hydrogen bond, namely polyproline II and α-helix, in condensed phases. It should be noted that conformers with the six-membered ring arranged in twist are destabilized by more than 4.5 kcal/mol in solution, with 13 being the only exception. This conformer exhibits ΔG_Chl= 2.6 kcal/mol and ΔG_water= 2.0 kcal/mol, which correspond to an estimated population of 0.5% and 2.6% in chloroform and water, respectively.

The data in Table 6 reveal that the conformational flexibility of Ac-t-l-c₆Phe-NHMe is greatly increased by the presence of chloroform. Thus, seven structures are predicted to present significant populations in this organic solvent, namely 8 (36.6%), 5 (26.1%), 2 (9.3%), 3 (8.2%), 7 (8.0%), 1 (6.9%), and 11 (3.0%). In comparison, only 8 (66.7%) and 11 (29.7%) are expected to be significantly populated (≥ 3.0%) in aqueous solution. Accordingly, almost all types of peptide backbone arrangements are accessible to Ac-t-l-c₆Phe-NHMe in chloroform, whereas only the α-helical structure (either of the α_L or α_D type) is expected to be present in aqueous solution. Regarding the cyclohexane ring, although the structures exhibiting a twist arrangement are, in general, stabilized by the solvent, they present ΔG_Chl and ΔG_water values above 5.4 kcal/mol, and their populations remain, therefore, negligible at room temperature.

It should be mentioned that the X-ray crystalline structures of small peptides incorporating the c₆Phe residues4b,e actually show conformations corresponding to the α-helical region (occasionally, with some distortion induced by a contiguous proline), which is in agreement with the conformational preferences predicted for the two compounds under study in aqueous solution. In the solid state, the amide moieties of the peptide backbone may interact with the complementary CO and NH sites of neighboring molecules and, as a consequence, intra- and intermolecular hydrogen bonding compete, as happens in the presence of a solvent able to form hydrogen bonds with the peptide.

It is also noteworthy that the great influence exerted by the environment on the conformational preferences of the c₆Phe derivatives under study differs significantly from the behavior observed before for other c_nPhe residues. Thus, solvation was found to alter the conformational profiles of c₃Phe^4c and c₅Phe^4a from a quantitative point of view but not qualitatively and, indeed, the most populated conformations for these residues in the gas-phase were also found to be preferred in aqueous solution.

Comparison with the unsubstituted Ac₆c residue

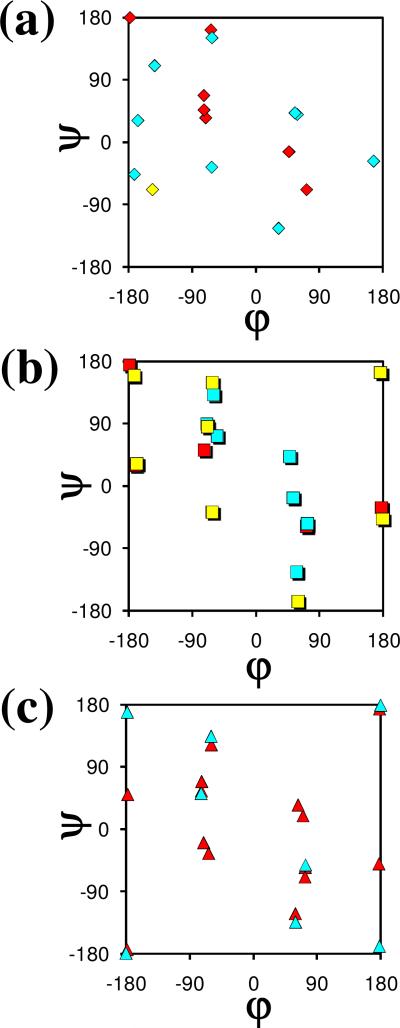
Figure 6 represents a Ramachandran map comparing the distribution of the minimum energy conformations found for Ac-c-l-c₆Phe-NHMe and Ac-t-l-c₆Phe-NHMe in the present work (Tables 1 and 2) and those characterized before for the analogous Ac₆c derivative, Ac-Ac₆c-NHMe, at the same level of theory.⁶ A color code has been used to identify the stability range of the different minima, which have been classified into three categories: ΔG_gp < 5 kcal/mol (red), 5 kcal/mol ≤ ΔG_gp < 10 kcal/mol (blue) and ΔG_gp ≥ 10 kcal/mol (yellow).

Figure 6.

Comparison between the minimum energy conformations predicted for (a) Ac-c-l-c₆Phe-NHMe, (b), Ac-t-l-c₆Phe-NHMe and (c) Ac-Ac₆c-NHMe at the B3LYP/6-31+G(d,p) level. Color code: red, ΔG_gp < 5 kcal/mol; blue, 5 kcal/mol ≤ ΔG_gp < 10 kcal/mol; yellow, ΔG_gp ≥ 10 kcal/mol. For the Ac₆c derivative, both the (φ,ψ) and (–φ,–ψ) positions are indicated for each minimum.

The incorporation of the phenyl side group, either in cis or in trans with respect to the amino terminus, produces a drastic reduction in the conformational diversity accessible to the peptide main chain. Thus, for Ac-Ac₆c-NHMe, four different types of backbone arrangements (namely, γ, α, ε, and β, with the L and D forms being energetically indistinguishable) were found within a ΔG_gp interval of 2.1 kcal/mol above the global minimum.⁶ In contrast, only the γ_L conformation appears below this energy level for the two c₆Phe derivatives (Tables 1 and 2). The effect is particularly pronounced in the case of the cis compound, for which the most stable conformer with a peptide backbone other than γ_L exhibits a ΔG_gp value of 3.8 kcal/mol.

The destabilization induced by the aromatic substituent is clearly seen when comparing the minimum energy structures located in the α-helix region. The most stable minimum of this type found for Ac-Ac₆c-NHMe⁶ presents the cyclohexane ring in a chair conformation with the –NHCOMe substituent axially oriented and shows a ΔG_gp value of 1.6 kcal/mol. In comparison, the most stable α-helical minima characterized for Ac-c-l-c₆Phe-NHMe (Table 1) and Ac-t-l-c₆Phe-NHMe (Table 2) display ΔG_gp values of 5.4 and 6.3 kcal/mol, respectively. Moreover, in the Ac₆c derivative, reversal of the cyclohexane chair leads to another α-helical minimum 1.9 kcal/mol higher in energy. In contrast, only one chair is compatible with each type of α-helical backbone arrangement for the c₆Phe-containing compounds.

Minima exhibiting a twist-shaped cyclohexane ring were characterized for some backbone types in Ac₆c, with the α-helix not among these.⁶ In contrast, such twist conformations are found to be compatible with the α-helix for both cis- and trans-c₆Phe. Moreover, in the case of the cis compound, a twist minimum was characterized at a ΔG_gp value as low as 3.4 kcal/mol (Table 1), whereas the most stable twist arrangement for Ac₆c exhibits a ΔG_gp value close to 6 kcal/mol.⁶

The incorporation of the phenyl substituent produces other effects, such as the modification of the geometry of minima with an ε backbone conformation. Minima of this type were characterized for Ac-Ac₆c-NHMe⁶ with a chair-shaped cyclohexane at (φ,ψ) angles near (–60,120), or the equivalent (60,–120). When a phenyl group is incorporated in cis with the amino moiety, repulsive interactions arise between the aromatic group and the carbonyl oxygen of either the –NHCOMe or the –CONHMe substituent, depending on the ε_D or ε_L backbone type, respectively. To alleviate these, the φ or ψ angle, respectively, deviates by about 30° from the value observed in Ac₆c. Accordingly, the ε_D and ε_L minima in Ac-c-l-c₆Phe-NHMe with a cyclohexane ring arranged as a chair appear at (33,–124) and (–64,162), respectively (Table 1).

Conclusions

Quantum mechanical calculations have been used to characterize the intrinsic conformational preferences of Ac-c-l-c₆Phe-NHMe and Ac-t-l-c₆Phe-NHMe, incorporating the cyclohexane analogues of phenylalanine that bear the aromatic substituent in a cis or a trans orientation, respectively, relative to the amino group. A total of 17 and 21 energy minima have been found and characterized using B3LYP/6-31+G(d,p) calculations for Ac-c-l-c₆Phe-NHMe and Ac-t-l-c₆Phe-NHMe, respectively. Single point calculations at the MP2/6-31+G(d,p), HF/6-31+G(d,p), and B3LYP/6-311++G(d,p) levels were also performed. In the gas phase, the only significantly populated structures at room temperature for both compounds are those exhibiting a γ_L backbone conformation. Comparison with the results previously reported for the unsubstituted cyclohexane residue (Ac₆c) provides evidence for the ability of the aromatic group to interact with the peptide backbone not only sterically but also electronically through the aromatic π orbitals. Moreover, the additional phenyl group exerts a strong influence on the conformational equilibrium of the cyclohexane ring, which, in turn, affects the peptide backbone arrangement. As a consequence, the incorporation of the aromatic group in Ac₆c induces a severe restriction of the peptide backbone flexibility, which, in the gas phase, is less intense for the trans than for the cis c₆Phe analogue.

Solvation effects have been considered through a SCRF method and have been shown to alter significantly the conformational preferences of the c₆Phe derivatives under study. Thus, in aqueous solution, structures lacking any intramolecular hydrogen bond, such as polyproline II and α-helix, are preferred. It should be noted that the conformational preferences predicted in this environment are in agreement with the experimental data available from X-ray diffraction structures of small peptides containing the c₆Phe residues investigated.