MODELING AND BIOLOGICAL CONTROL OF MOSQUITOES

Abstract

Models can be useful at many different levels when considering complex issues such as biological control of mosquitoes. At an early stage, exploratory models are valuable in exploring the characteristics of an ideal biological control agent and for guidance in data collection. When more data are available, models can be used to explore alternative control strategies and the likelihood of success. There are few modeling studies that explicitly consider biological control in mosquitoes; however, there have been many theoretical studies of biological control in other insect systems and of mosquitoes and mosquito-borne diseases in general. Examples are used here to illustrate important aspects of designing, using and interpreting models. The stability properties of a model are valuable in assessing the potential of a biological control agent, but may not be relevant to a mosquito population with frequent environmental perturbations. The time scale and goal of proposed control strategies are important considerations when analyzing a model. The underlying biology of the mosquito host and the biological control agent must be carefully considered when deciding what to include in a model. Factors such as density dependent population growth in the host, the searching efficiency and aggregation of a natural enemy, and the resource base of both have been shown to influence the stability and dynamics of the interaction. Including existing mosquito control practices into a model is useful if biological control is proposed for locations with current insecticidal control. The development of Integrated Pest Management (IPM) strategies can be enhanced using modeling techniques, as a wide variety of options can be simulated and examined. Models can also be valuable in comparing alternate routes of disease transmission and to investigate the level of control needed to reduce transmission.

INTRODUCTION

Modeling could be a valuable tool in developing biological control methods and strategies for mosquitoes, but there has been relatively little work done directly on this subject. However, there are many modeling studies on other organisms relevant to biological control of mosquitoes. Many models of mosquitoes and mosquito-borne disease have been developed which do not directly consider biocontrol strategies but which can be used to identify features that would be important in developing biocontrol agents and strategies. This chapter will illustrate ideas that may be of value in developing biological control theory for mosquitoes, including the general theory of biological control, models of biocontrol in other insects, and models of mosquitoes and vector-borne diseases. Rather than an exhaustive review of all modeling of biocontrol or vectors, this chapter will use selected examples to highlight useful techniques and models applicable to biocontrol of mosquitoes. It will generally restrict attention to process-based models rather than statistical models; the latter are, of course, very valuable but beyond the scope of this review.

An important consideration when identifying features of biocontrol systems is the goal of the control strategy. Although eradication is occasionally the actual goal, in general we are trying to reduce (and maintain) an insect population below a critical threshold: an economic level for pests of crops or livestock, a threshold for disease transmission for vectors, a comfort level for nuisance species. Therefore, it is important to note that long-term coexistence of the host (e.g., a mosquito species) and a biocontrol agent is highly desirable, to extend the time between releases or applications while maintaining the pest population at a low level. This is a different concept from the development of biological pesticides, such as Bacillus thuringiensis israelensis (Bti). For these agents, the mode of action is more like a pesticide and the agent (the bacterium) is not expected to replicate or be maintained in the field; recurrent applications are required. Some issues pertaining to biological pesticides will be discussed here, but the primary focus will be on true biological control agents, with the goal of long-term persistence of the agent in the environment following release.

MODELING BASICS

A brief review of some modeling terms and structures will aid in understanding how models can be used to study biocontrol of mosquitoes. There are several useful texts for those interested in learning more about modeling (e.g., Anderson and May 1991, Scott and Smith 1994, Gurney and Nisbet 1998). Analytical models are relatively simple and can be solved mathematically; more complex models must be solved numerically by computer simulation of one type or another. The state variables are the variables being tracked explicitly in the model; frequently these are counts of individuals in different classes, such as the number of adult female mosquitoes, number of pupae, or number of infected birds. Analytical models are often solved for their equilibrium points; these are solutions to the equations where the state variables are not changing with respect to a dimension of interest; usually this is time (i.e., the number of adult females is constant). A population at equilibrium is not changing in size over time (mathematically, the first derivatives with respect to time are zero). Depending on the goals of the model, the equilibrium properties of population size may be also studied with respect to another population (e.g., are the populations changing in size with respect to each other, such as an increase in the number of mosquitoes per bird?), or, in a model of evolutionary change, the frequency of genes over time may be considered. An equilibrium point is stable if the system returns to this point after a disturbance (Fig. 1); this return can be monotonic or oscillatory (May 1974). Transient behavior is the behavior exhibited before the system comes to an equilibrium; if a system in nature is highly disturbed (due to environmental perturbations, human actions, or other ecological dynamics), the populations may continually exhibit transient behavior and never reach equilibrium. This is of particular interest in a biological control situation, as humans are likely to continue to perturb the system by applying insecticides, changing the environment, etc. Parameters are the rates that govern movement between the classes in the model; for example, the mortality rate of adult female mosquitoes. If a particular rate is not varied during a particular analysis, it may be referred to as a constant; constants can also include universal constants such as π. It is important to identify the parameters, variables and constants in a model to determine if you agree with the values or ranges used, and if the source of the information is reliable. Sensitivity analysis, of which there are many types, considers the effect on the model output of variation in the estimates of the parameters. This uncertainty can come from biological variation (i.e., the mortality rate may vary between species, or by temperature), measurement error (the standard error associated with an empirical study of mortality rates), or gaps in our knowledge (i.e., if there are no estimates available for the species of interest, it may be necessary to consider a wide range of possible values). In an epidemiological model, the basic reproduction number, or R₀, is defined as the number of secondary infections deriving from a single primary infection in a population of susceptible hosts. This number is often used to estimate the control measures necessary to eradicate (or prevent the introduction) of a disease.

Fig. 1.

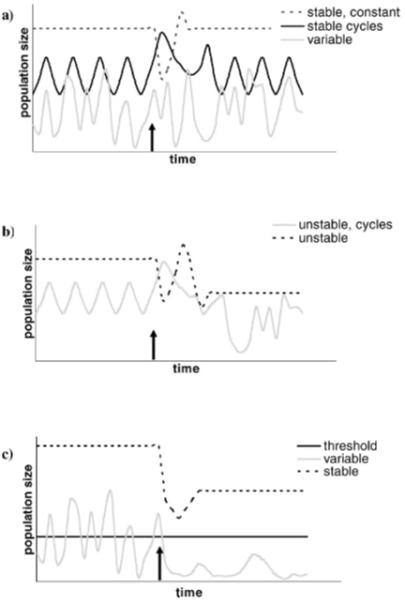
Stability and control in populations. a) Examples of stable equilibria: If an equilibrium point is stable and constant (dashed line), the population size is constant and will return to the same size following a disturbance (imposed at the time marked by the arrow; e.g., control reducing the population). There can also be cyclical equilibria (solid black line), where the population size cycles between different values. Again, the population returns to this same cycle following a disturbance (in this case, an increase in the population; this could be caused by environmental conditions, a supplemental release of a biocontrol agent, etc.). For illustration, an unstable population (grey line) is shown; in this case the population fluctuates with no equilibrium. b) Examples of unstable equilibria: If a population is at an unstable equilibrium, the size of the population will not return to the original value following a disturbance (arrow). It may settle to a new equilibrium point, or become unstable. Two possibilities are illustrated here: an unstable, constant equilibrium settling to a new, constant equilibrium (which may be stable or unstable) following a disturbance, and an equilibrium cycle becoming chaotic following a disturbance. c) Some possible outcomes of control measures: A stable equilibrium is not always the ideal goal for control. Here, a population at equilibrium is disturbed by a control strategy and settles to a new equilibrium; however, the new population size is still above the threshold for concern (set by economics, disease transmission, or nuisance issues). Conversely, an unstable population with unpredictable dynamics could be depressed below the threshold. Other scenarios are possible, including a controlled population that undergoes outbreaks that exceed the threshold.

Figure 1 illustrates some aspects of population stability and variation. It is important to note that a stable population can still be of concern, if the population size is large enough to cause economic, health or nuisance problems (Fig. 1c). Conversely, a biological control agent may be able to suppress a pest below the threshold of concern, but the population may be unstable and the population size variable. Cycles can be stable or unstable (Fig. 1a, b), based on the response to perturbation and whether the cycle size or periodicity changes. Outbreaks, where the target population escapes control and reaches high population sizes, can occur if any of the interacting populations are perturbed (by human or environmental factors). Thus, it is critical to note that stability in the mathematical sense, although important in understanding model behavior and the factors influencing population dynamics, is not always the primary goal for a biological control system.

MODEL VALIDATION

An important aspect of a modeling study is validation. As with the model analysis, this can take many forms and depends on the goals of the model, the type of model, and the data available. If the goal of the study is to make specific predictions, whether of population size, disease transmission, or optimal control strategies, then the model must be validated by comparison to field data before relying on the predictions. This validation must be done with a data set that is independent of all data used in developing the model and parameter estimates. In the initial development of a model, parameter estimates may be “tuned,” i.e., refined by iterative adjustments to the estimates based on comparisons between model output and an appropriate data set. This is appropriate in model development, but the model still must be validated against an independent data set before being used elsewhere. If, however, the goals of the model are more general, such as to explore alternative hypotheses for relationships between elements of the biological system, investigate broad theories of disease transmission or control, or study the stability properties of an analytical model, model validation may not be necessary. Some form of sensitivity analysis is also critical in understanding how a model can be used, because if there is no understanding of how the outcomes of a model (e.g., mosquito populations, disease prevalence, or the success of a proposed control strategy) vary with changes in parameter values, then there can be no valid extrapolation to new situations. It should be noted, however, that it is often difficult to relate the population sizes in a model (generally defined as the absolute total number of individuals in the population) to field collections such as trap catches; the relationship between these values will depend on the efficiency of the trap and other particulars of the system. For model validation, we are usually looking for good correlation between model predictions and field observations (concurrent increases and decreases over time, for example), not absolute agreement.

With any model, the most important aspect of model development is deciding which biological details to include and which to leave out. These decisions must be made based on the goals of the model, available data, and plans for model analysis. Generally, the more that is included in a model, the more data required for parameter estimates and the more difficult it is to understand and analyze the outcome. In assessing a model, the key question to ask is whether the assumptions and structure are suitable for the goals of the model and are reasonable given the biology of the system.

TYPES OF CONTROL AGENTS

Natural Enemies: Predators, Parasitoids and Parasites

The classification of a natural enemy as a predator, parasitoid or parasite depends largely on the number of prey or hosts attacked or consumed, the reproductive strategy of the natural enemy, and other details of the system. While some interactions can be clearly classified, others are not as apparent and the natural enemy has characteristics of more than one type. Here, I will consider the natural enemies together, with the exception of microparasites (bacteria, viruses and fungi), which will be considered later. There are many similarities in the characteristics of these natural enemies and in the properties of the models used to study them.

Some predators, such as copepods and predatory mosquitoes, have been suggested for mosquito control. Mermethid nematodes, macroparasites, have also been explored as mosquito control agents. True parasitoids have not, but will be discussed here since host-parasitoid dynamics are the basis for many biological control models. There have been several books on the subject of host-parasitoid and predatorprey interactions and models (e.g., Hassell 1978, Hochberg and Ives 2000) and numerous reviews (e.g., Hassell and May 1973, Murdoch and Briggs 1996), and interested readers are referred to those sources for further information.

Host-parasitoid models are the backbone of classical biological control theory, and parasitoids have been suggested or used as biological control agents for many pests. Parasitoids are good candidates for biological control, as they frequently have the desired characteristics of specificity for the pest, ability to rear in culture, and a life stage that is relatively easy to distribute. In addition, they have long been used as model systems to study ecological factors. As a result, there is an extensive literature on host-parasitoid dynamics, including theoretical studies on ideal characteristics for biological control, stability analysis, and the effect of stage structure in hosts and parasitoids. Many of the same properties apply to some insect predators. Numerous theoretical studies have considered factors affecting the stability of these systems and the impact on biological control, such as searching efficiency (e.g., Hassell and May 1973), density dependence (e.g., May et al. 1981), age or stage structure (e.g., Murdoch and Briggs 1996 and references therein, Bonsall and Eber 2001) and spatial heterogeneity or structure (e.g., Hassell and May 1988, Hassell et al. 1991). The addition of such complexities to the system is often stabilizing, but their effects can depend on the details of the interaction, such as whether density dependence acts before or after parasitism (May et al. 1981).

An example and review of how models can be used to investigate host-parasitoid systems is provided by Murdoch and Briggs (1996). They identified 4 areas (parasitoid aggregation, population stability, refuges, and density dependence) that affected the stability of host-parasitoid systems, would affect the success of a biological control program, and warranted further research. All of these factors should be investigated for any parasitoid considered for mosquito control. Parasitoid aggregation can be a stabilizing factor, but depends on the specific assumptions of how the aggregation occurs (host or parasitoid movement, responses to density, etc.). Considering biological control situations at the metapopulation level was also an area they addressed; unstable local populations may interact to produce persistence at the metapopulation level. Refuges can also be important in the dynamics of host-parasitoid interactions and can affect the persistence of both species. The refuge is defined based on the host-parasitoid interaction (e.g., only hosts of a certain size are parasitized, or only those in particular environments), and this definition determines the effect of the refuge on the stability properties of the system. Finally, density dependence in the parasitoid attack rate (i.e., density-dependent regulation in the parasitoid population as well as in the host population) can act as a stabilizing factor, but may not be a strong factor at the densities typical in a biological control operation. Murdoch and Briggs (1996) also discuss the importance of stage-structured populations; the stage of host attacked by a parasitoid is important in the stability, persistence, and degree of control provided. This can also have major effects on the outcome of using more than one parasitoid species to control a host species and on the choice of a parasitoid to use; apparently small differences in the life history of a parasitoid can have a strong impact on successful biological control. Many of these factors would also apply to predator-prey systems, and, indeed, aggregation has been shown to stabilize insect predator-prey systems as well (e.g., Hassell and May 1974).

There have been several models investigating the effectiveness of entomopathogenic nematodes for control of crop pests. Fenton et al. (2000) extended a basic nematode-insect model and examined the stability properties of the model with respect to parameter values derived from the literature. This is a nice example of a modeling study, with the assumptions clearly stated and the derivation of the parameter values provided in detail. They showed that, for the range of parameter values derived from a nematodesciarid fly system in mushroom houses, the nematodes cannot regulate the host population. Instead, the system exhibits oscillations that are likely to result in the extinction of the nematode, host population, or both, and long-term control is unlikely. However, this indicates that the nematode may be efficacious for short-term inundative control, essentially as a biological pesticide. With this approach, the long-term stability of the system is of less interest than the short-term dynamics. This is likely to also be the case in many mosquito control situations, where immediate control of the anticipated emergence of a brood is of more concern than long-term reduction of the population. Further studies with the nematode-sciarid fly model and other insectnematode systems (Fenton et al. 2001, 2002) explored the transient dynamics and optimal application strategies, and combined models with empirical research to identify timing and application rates which provide suitable control. A key feature in this analysis was the extension of the model to include the life stages of the insect pests; this can be critical in assessing the timing and efficacy of control when the pest age distribution is not constant (see also Briggs and Godfray 1995, Murdoch and Briggs 1996 for age-structured insect-pathogen models). The optimal timing of nematode applications and the level of control achieved is dependent on the duration of the larval stage; since this is often temperature-dependent, the ideal application schedule may depend on the time of year. It should be noted that there are differences in the life cycle of these nematodes and some of the nematodes suggested for mosquito control; in this case the nematode can achieve multiple generations within one larval fly cadaver (and so thousands of infective juvenile nematodes can ultimately be released from one cadaver), and the insect does not continue to develop after infection. These differences will affect the spread of the nematode through the population in space and time. However, a similar modeling approach could be used to investigate the impact of nematodes or other parasites on mosquito populations, providing information on whether long-term regulation is possible and the level of infection required for short-term inundative control with nematodes.

Insect Pathogens

Insect pathogens have also been considered extensively for biological control. This includes numerous viruses, fungi, and bacteria, and there have been suggestions for all of these as mosquito control agents (Service 1983).

There have been numerous models of insect-pathogen dynamics, from general analytical models to detailed models of specific systems. A key feature in these models is that the outcome of the interaction often depends on the assumptions made about the growth rate of the host in the absence of the pathogen. If the host population is assumed to grow exponentially in the absence of the pathogen, the interaction tends to be unstable and results in the extinction of the pathogen alone or of both species (e.g., Brown 1984, Hochberg 1989, Briggs and Godfray 1995). If there is density-dependent regulation in the host population (a much more likely scenario, particularly for mosquito populations), the interactions are more stable and likely to lead to long-term coexistence of both species (e.g., Begon et al. 1992). As was observed with host-parasitoid models, the stage of the host population attacked can also affect the dynamics of the interaction (e.g., Briggs and Godfray 1995, Moerbeek and Van Den Bosch 1997).

One of the more extensive studies of insect-pathogen dynamics, using both models and empirical studies, has been conducted on nuclear polyhedrosis virus (NPV) and gypsy moths (Lymantria dispar). Dwyer and colleagues began with simple models of natural epizootics (Dwyer and Elkinton 1993). Then, in a series of papers (reviewed in Dwyer et al. 2000), they added complexities to the models to investigate how details of the interaction between NPV and gypsy moth affected insect outbreaks. The models were used in combination with empirical studies to examine the details of the transmission rate, host heterogeneity in susceptibility, and overwinter survival. While these models are most applicable to forest defoliators, this series of papers is a nice illustration of how the combination of empirical and theoretical work strengthens both. Dwyer et al. (1998) also considered a fungal pathogen of gypsy moth, examining how extrapolation to the large spatial scale usually involved in gypsy moth outbreaks affects the dynamics of the system. In another paper (Dwyer et al. 2004), they considered the effects of combining pathogens and predators. The combination of pathogens and predators can lead to complex dynamics, and the system alternates between predator-maintained equilibrium and cycles driven by the pathogen. This is of interest, since rarely do natural populations exist in isolation. Any introduced biological control agent will have to interact not only with the target host population, but with other species as well.

Another aspect to insect-pathogen dynamics is the resource for the pest insect. Xiao and Van Den Bosch (2003) demonstrated that the presence of an alternative, wild host plant for a crop pest affects the stability of the plant-pest-pathogen system. The structure of this model has some similarities to some mosquito systems, where the mosquitoes feed on domestic and wild animals as well as humans. In the crop system, the biological control by a pathogen tends to stabilize the system, allowing coexistence of the wild host plant and the pest, at levels below the threshold for maintenance of the pest on the crop alone.

Interactions and Non-target Effects

Many models, and also many empirical studies, consider one host and one enemy. However, as was illustrated by Dwyer et al. (2004), natural systems are generally much more complex and involve multiple species. Models can be very useful in investigating these complex systems, and can be used to identify areas of potential interaction or non-target effects. Hochberg et al. (1990) considered interactions between a parasitoid and a predator acting on the same host, examining the factors affecting the stability of the system at equilibrium. They demonstrated that each natural enemy can exclude the other, or both can coexist; this is dependent on the degree of competition between them (e.g., who “wins” in a host attacked by both), the growth rate of the host population, and the searching behavior of the parasitoid. Obviously, the outcome of such a system will depend on the details of the biology of the species involved; for a biocontrol system it will also depend on the ability of other interventions to control the pest species. Models can be valuable tools in understanding how multiple populations may interact, and in determining the information most critical to predicting the outcome.

When a parasitoid or predator is introduced to control a particular pest, there is always the concern that it will also attack other non-target species. Just as with the use of pesticides, this must be considered before any release. Lynch et al. (2002) used a host-parasitoid model to consider the effects of an introduced parasitoid on a non-target species. In this model, they focused on transient impacts, since immediately after the release is when the biocontrol agent is likely to have its highest population (in response to the high population size of the pest). They showed that this high density may result in an impact on a non-target species, even if the non-target species is not well accepted by the parasitoid and is not capable of supporting a parasitoid population on its own.

Pearson and Callaway (2003) reviewed the broader indirect effects of biological control, focusing on a natural enemies model for insects used to control invasive plants. This is similar to a host-parasitoid or predator-prey model, although there are obvious differences between an herbivorous insect feeding on a weed and a parasitoid feeding on an insect. They use the example of a system involving an invasive plant, knapweed, and a control agent, gall fly (Urophora spp.). The gall fly can also be a food source for native deer mice (Peromyscus leucopus). Increasing deer mouse populations in turn can increase the prevalence of hantavirus. This is a complex system, and the indirect effects depend on the strength of the biological control (in this case, the gall fly was not successful in controlling knapweed) as well as the interactions between members of the native community. This is used as a cautionary example, and demonstrates an area where modeling could be valuable to assess the potential indirect effects from an introduction to an existing system.

MODELS OF VECTORS AND VECTOR-BORNE DISEASES

There have been numerous models of mosquitoes and mosquito-borne disease, beginning with the classic Ross-Macdonald malaria models (Ross 1911, Macdonald 1952, 1957) and extending to present day models of malaria, (e.g., Roberts et al. 2000, McKenzie and Samba 2004), arboviruses (e.g., Kay et al. 1987, Focks et al. 1995, Wonham 2004, Lord and Day 2001a, 2001b; Strickman and Kittayapong 2003), and other vectors and vector-borne diseases (e.g., Chagas disease, Cohen and Gürtler 2001; onchocerciasis, Habbema et al. 1992; black-legged ticks and Lyme disease, Mount et al. 1997, Schmidt and Ostfeld 2001, Brownstein et al. 2003; tick-borne encephalitis, Randolph et al. 1999, 2002). In addition, there are numerous models of vector populations or aspects of vector biology, not directly considering disease (e.g., Weidhaas 1974, Focks et al. 1988a, 1988b; Focks and McLaughlin 1988, Fry et al. 1989, Eisenberg et al. 1995a, 1995b; Mount et al. 1991, Randolph et al. 1992, Randolph and Rogers 1997, Randolph 1999). Few if any of these models have directly considered biological control, although several include generic “control,” assessing the impacts of increased mortality of the vector, usually assumed to be by pesticide spraying or other treatment. Space precludes an extensive review of these models, and I will simply use a few models to illustrate how biological control could be incorporated into model frameworks and investigated.

POPULATION MODELING

The population size of the vector is often a dominating feature in models of vector-borne disease (e.g., Anderson and May 1991, Lord et al. 1996a, 1996b; Lord and Day 2001a, 2001b). Clearly, reduction in the population size by biocontrol agents will have an impact not only on the nuisance aspects of mosquito populations, but also on the transmission potential for disease. The mortality rate of female vectors also is frequently identified as an important feature in vector-borne disease models (e.g., Kay et al. 1987, Anderson and May 1991, Koella 1991, Lord and Day 2001a) and this would be one target for biological control. The success of a biological control agent in reducing the population size will depend on many aspects of a particular system, and it is often difficult to translate the population sizes used in a model to actual trap catches in field studies (and vice versa).

Several models of mosquito populations have been developed and used to investigate population dynamics and their sensitivity to parameter estimates. A few examples will illustrate this process. Fry et al. (1989) developed a model to examine control options for Culex quinquefasciatus in Orange County, CA. Because the goal of this model was to examine control strategies in a local environment, breeding sites were modeled explicitly along with the probability that the mosquito control operators “knew” about the site. Control is then superimposed as an increased mortality of larval stages, depending on the type of breeding site. Specifics of visits by control personnel are also included. The model was compared to trap collections over 5 years. While no explicit sensitivity analysis or model testing of control strategies was performed, this explicit inclusion of current mosquito control practices is valuable and deserves further investigation in models of biological control of mosquitoes.

Another example of a mosquito population dynamics model is the Culex tarsalis model by Eisenberg et al. (1995a, 1995b). In this model, sensitivity analysis of parameter estimation was conducted using Monte Carlo simulations, where simulations using randomly generated parameter sets (from specified distributions) were compared to a set of criteria based on field data. Simulations that passed (i.e., were sufficiently similar to the field data) were then used for further analysis; this allowed refinement of the parameter estimates for the 2 specific sites considered. It is worth noting that, while not explicitly included in the dynamics of the model, predation was considered as a density-dependent mortality factor acting on larvae. However, the sensitivity analysis indicated a more important role of temperature-dependent (density-independent) larval mortality; over the range studied, predation was not a key factor. Control strategies were not explicitly included, but were implicitly included in mortality rates since the data sets used for comparison were collected in locations with active mosquito control. Further control strategies and biological control agents could be incorporated into the model framework and a systematic sensitivity analysis used to examine their effectiveness.

A model of Psorophora columbiae dynamics by Focks et al. (1988a, 1988b) began with the hydrology of the rice field ecosystem. In a series of papers, Focks and colleagues (Focks et al. 1988a, 1988b; Focks and McLaughlin 1988, Focks 1991) developed the model, studied the dynamics of the population, considered standard control strategies such as larviciding and adulticiding, and finally considered a novel control strategy of treating the dominant blood meal host (cattle) with ivermectin. While not explicitly considering biological control, this series of papers demonstrates how a model can be developed and used for targeted questions. Of particular interest is the analysis of potential ivermectin treatment of hosts; this simulation study indicated that relatively small reductions in survival and fecundity from ivermectin treatment could have significant effects on the need for additional insecticidal control. Models are an ideal way to consider how different methods of control can be combined into an IPM strategy and to identify important informational needs. While the detailed information required for a local model may not be available, the general strategies developed using a more general model can then be fine-tuned based on sensitivity analysis and local information.

A final example of modeling mosquito population dynamics is also by Focks and colleagues (Focks et al. 1993a, 1993b), examining the biology of Aedes aegypti. This is an exceptionally detailed model, with numerous types of containers for larval development. Hydrology (water levels and drying), temperature-dependent larval development, food availability and survival are explicitly tracked in each container type. Detailed weather data are used to drive the hydrological and biological functions. This level of detail has both costs and benefits; it enables consideration of detailed aspects of the mosquito biology, but also makes true sensitivity analysis of the model difficult or impossible. Thus, to develop a model with this level of detail, it is necessary to have extensive data available for parameter estimates and validation. In the case of Ae. aegypti, a well-studied mosquito, such detail was available. Predation is included, as a mortality factor in egg survival, but no other control was included in the initial models (but see the later expansion of the model into dengue transmission, discussed below). However, it would be relatively simple (given the availability of appropriate data) to add various types of biological control to the model. The difficulty would be, as mentioned above, in the analysis; particularly if, with the addition of biological control agents, the model is too complex for many types of sensitivity analysis. If, however, the model were sufficiently validated in the location of interest, many parts of the system could be kept constant and the model analyzed just with respect to the addition of the biocontrol agent. This would allow estimation of the likelihood of successful establishment and mosquito population regulation by the agent, and some analysis of the factors contributing to the success or failure. Careful simulation strategies and analysis would be required to then extrapolate these results to other locations.

In most of these models, control was imposed by reducing survivorship of different life stages, with no direct attention to the method. If appropriate estimates of immediate lethality of a biological control agent can be developed, these models can be used to estimate the short-term effects of the release of such an agent. However, if a biocontrol agent is intended to reproduce in the field and provide long-term control, its population dynamics must also be included in models. This allows the models to be used to understand the factors affecting the likelihood of establishment of the agent and the long-term level of control.

PATHOGEN TRANSMISSION AND CONTROL

Frequently, the goal underlying mosquito or vector control is to reduce the transmission of a disease, and the level of control required depends on the biology of the pathogen as well as the mosquito or vector population. The degree of entomological detail in models of disease transmission varies greatly, from simple models with little entomology (e.g., the Ross-Macdonald malaria models and others; see Anderson and May 1991 for further details) to detailed simulations (e.g., dengue models based on the Ae. aegypti models described above, Focks et al. 1995, 2000; Strickman and Kittayapong 2003). These models are often used to assess criteria for disease invasion or persistence (e.g., each primary case produces at least one secondary case; R₀ >1) either analytically or by simulations. In analytical models, this often takes the form of a threshold population size of vectors, along with other possible criteria on vector mortality rates and vector competence derived from the mathematical expression for R₀ (Anderson and May 1991). In simulation models, a population threshold may be identified (e.g., Lord and Day 2001a), but the level of control required may not be as obvious, depending on the complexity of the model. Explicit control is rarely included in such models, beyond discussion of simple reduction of vector numbers. While this can be directly applied to questions about immediate control (pesticide application or inundative control), understanding the consequences of persistent biological control requires the addition of the control agent to an explicit model of the vector, not simply assuming a reduction in survival or fecundity. This is of particular importance if the long-term impacts of a biological control agent, intended to reproduce in the environment, are of concern.

Models can be used to go beyond simple population dynamics and address how other aspects of mosquito biology affect disease transmission. The long history of malaria models serves to illustrate this point. In the original Ross-Macdonald malaria model, the importance of the biting rate, separate from the total number of mosquitoes, was recognized; it is squared in the expression for R₀ and so has a strong influence on the behavior of the system (Ross 1911, Macdonald 1952, 1957; Anderson and May 1991). This has been used to consider control strategies beyond population reduction, directed at reducing the human biting rate, such as the use of bednets (e.g., Koella 1991 and references therein) and zooprophylaxis (diverting mosquito bites to alternate hosts) (e.g., Killeen et al. 2001; see also Sota and Mogi 1989, Lord et al. 1996a). Vector behavior following DDT spray was modeled by Roberts et al. (2000); this model demonstrated that the repellent aspects of DDT will influence the location of vector biting activity and will affect the apparent efficacy of the spray as measured by indoor host-seeking. Such changes in behavior in response to control efforts can have a major effect on the success of control, and should be considered for any proposed biological control strategies. Other aspects of malaria models are reviewed in Koella (1991), McKenzie and Samba (2004) and McKenzie (2000).

The model by Wonham et al. (2004) is an example of using an analytical model with equilibrium analysis to estimate the threshold mosquito population required for disease invasion. They considered the invasion of West Nile (WN) virus into New York City in 1999, and concluded that reducing the mosquito population to below 4.6 mosquitoes per bird would have limited the WN virus invasion. This estimate, however, is sensitive to the estimates of the parameter values and to whether the mosquito population is assumed to be constant or fluctuating seasonally between a high or low level. While not explicitly considering biological control, this type of model can be used to estimate the level of control required to achieve a specific aim, and thus whether particular biological control agents can achieve the necessary control. However, control in this model can only be considered by increasing the mortality rate of adult mosquitoes; extensions would be required to consider biological control agents acting on other parts of the mosquito life cycle.

Focks et al. (2000) considered the impact of source reduction on dengue transmission using their Ae. aegypti population model. This demonstrates how models can be used to estimate the effort needed to achieve a reduction in disease transmission. Their estimates of the source reduction required to reduce transmission were higher than the effort generally reported during control campaigns, and highlight the difficulty of reducing (and maintaining at these levels) vector populations sufficiently to break transmission cycles.

Many vector-borne diseases have multiple reservoir or amplification hosts, and infection in humans and domestic animals may not directly affect the transmission cycle. In these cases, understanding (and modifying) the risk of disease depends on understanding the natural transmission cycle, and models have been used extensively for this purpose (e.g., Lord and Day 2001a, 2001b; Randolph and Rogers 2000, Schmidt and Ostfeld 2001, Wonham 2004). Ostfeld and colleagues have used models to investigate an interesting concept, the dilution effect, primarily in investigations of Lyme disease and the black-legged tick (Giardina et al. 2000, Schmidt and Ostfeld 2001, Schauber and Ostfeld 2002). These models consider the role of biodiversity in the amplification and transmission of the pathogen in the natural system. The distribution of bites from the vector over the different species in the model system affects the transmission potential, as not all host species for the vector are equally good hosts for the bacteria. In this system, areas with lower diversity (due to environmental fragmentation or other habitat modifications) tend to have fewer host species, but the most competent host (the white-footed mouse) generally remains in the community. Thus, as biodiversity decreases, transmission potential increases as the mice receive more of the vector bites. A similar process may occur with other zoonotic diseases, but the specifics will vary depending on relative host competence and on how changes in biodiversity affect host competence. Similar issues have been studied in models with fewer (but more than one) host species considered (e.g., Rogers 1988, Lord et al. 1996a). These models have shown that the effects of reducing the abundance of a reservoir species depend on the assumptions of the relationship between host and vector abundance. These issues should be considered further, and models can be useful tools if host manipulation is suggested as a control measure.

Integrated pest management is a cornerstone of many control programs, and biological control is likely to be implemented as part of a broader control program, not alone. Models have been used to investigate IPM of tick populations (e.g., Amblyomma americanum, Mount et al. 1999), including pesticide treatment, treatment of hosts with acaricides, vegetation reduction and host population reduction. This model demonstrated that combinations of techniques are often useful, and that cost-benefit analysis can be done in the model framework to assess how to mix methods for an effective IPM. For another tick species Boophilus microplus Beugnet et al. (1998) focused on factors affecting the encounter rate between tick larvae and cattle (B. microplus is a one-host tick, so this encounter rate determines the tick burden) and considered acaricide application strategies and how a vaccine could decrease tick reproduction below the point where the population is sustained. Sterile male releases have also been considered for control of vectors. Weidhaas (1974) demonstrated the use of a simple population model to analyze the level of control needed and the impact of sterile male releases. In a model of Anopheles albimanus, Haile and Weidhaas (1977) examined the efficacy of combining insecticides with sterile male releases. These models illustrate how a quantitative framework can be used to explore combining control options, whether biological or chemical.

Models were used extensively in a large control project for onchocerciasis, the Onchocerciasis Control Programme (OCP) in West Africa (Birley et al. 1983, Birley and Davies 1984, Plaisir et al. 1990, 1991; Habbema et al. 1992). A simulation model was developed (Plaisier et al. 1990) and used to explore the reduction in disease produced for different combinations of larviciding (against the Simulium vectors) and chemotherapy of humans. The models were also used to consider recolonization of areas by flies when control was interrupted (Birley et al. 1983), and the consequences to the human population of changes in control strategies. As more data were made available, the model and parameter estimates were refined and control options re-evaluated (Habbema et al. 1992, Birely and Davies 1984). Although primarily considering larvicidal treatment with pesticides, this project demonstrates how a well-designed model can be used and expanded as part of a larger program to control disease. Other onchocerciasis models have been developed to explore the specifics of the disease in other locations (reviewed by Basáñez and Ricárdez-Esquinca 2001). These models have been used to consider control strategies focused on the human host (ivermectin treatment or removal of nodules), the effect of differing vector competence of Simulium species, and the distribution of worms in flies and humans. Again, these models illustrate how a quantitative framework can be valuable in exploring alternative control strategies and investigating the effects of differences in vectors and environments.

A final example of the use of models to investigate control strategies for vector-borne disease is for Chagas disease, or American trypanosomiasis. The vectors for these parasites are triatomine bugs, which live in the domestic environment and feed on other animals as well as humans. Cohen and Gürtler (2001) developed a model of the transmission season, including humans, dogs, and chickens as hosts, and explicitly tracking the bug population. Human behavior (time spent indoors at different times of year) was also an integral part of the model. They demonstrated that the presence of infected dogs was a major influence on transmission to humans; at low dog numbers dogs provided a source of infection and increased transmission, but when dogs were more common they diverted sufficient bug bites away from humans to reduce transmission. The presence of chickens also influenced transmission, but in complex ways. A more complex model (Castañera et al. 2003) considered detailed interactions between bugs and hosts. These models demonstrated that environmental manipulation (changes in host density, house type), along with insecticide use (reducing the number of bugs present in a house) could affect the intensity of transmission.

OTHER USES OF MODELS

Models are not restricted to investigating population dynamics or transmission cycles, but can be used to investigate many other aspects of vector biology or disease incidence. One example is given by Shaman and colleagues (Shaman et al. 2002a, 2002b, 2003, 2004a, 2004b). In a series of papers, they used a dynamic hydrology model to simulate water table depth and looked for statistical relationships between water table patterns and mosquito abundance (Shaman et al. 2002b) or St. Louis encephalitis (SLE) virus transmission (Shaman et al. 2002a, 2003, 2004a, 2004b). This analysis supports an association between SLE virus transmission and hydrological patterns of a spring drought and later wetting. While not directly considering control issues, this type of model is valuable in developing theories and testing possible patterns of virus transmission. Control strategies could then be superimposed, to determine if they would be sufficient to break the observed associations.

Models can be used to investigate the consequences of new theories, modes of transmission, or hypotheses when they are proposed, even when data are limited. An example is the recent interest in nonsystemic transmission—transmission of a pathogen between two vectors feeding simultaneously on a host without the host becoming viremic. First described in ticks (Jones et al. 1987) and now demonstrated for several tick-borne pathogens (e.g., Gordon et al. 1993, Labuda et al. 1993, Gern and Rais 1996), it was later observed in black flies with vesicular stomatitis virus (Mead et al. 2000). Models have been used to investigate how this may affect transmission cycles (Randolph et al. 1996, 1999; Lord and Tabachnick 2002, Norman et al. 2004), providing a framework for further research and suggestions regarding the most critical information needed. Recently, nonsystemic transmission has been found in mosquitoes with West Nile virus (Higgs et al. 2005). Models are being developed to investigate the relative roles of different transmission routes in the epidemiology of WN and other arbovirus systems (Lord, unpublished data).

There are a number of other areas where models can inform control decisions. Models have been used to investigate resistance management of drugs and insecticides (e.g., Gardner et al. 1998, Lenormand et al. 1999), and could be used more extensively to consider rotational strategies and the spread of resistance alleles. As new biological agents are identified, the release strategies can be modeled and alternatives investigated (e.g., Shea and Possingham 2000), even with relatively little information about the agent. Finally, there is great interest in the development of transgenic mosquitoes and in the use of Wolbachia symbionts to affect populations. There are many models of the spread and maintenance of genes and transformations in populations, and I will simply mention a few to illustrate the utility of models in this area. Cellular automata techniques have been used to model transposon-based genetic drive mechanisms (Kiszewski and Spielman 1998). Models have been used to assess how Wolbachia symbionts could be used to affect populations, through cytoplasmic incompatibility (Dobson et al. 2002a, 2002b), or by engineering to increase mortality (Rasgon et al. 2003), and how ecological factors in the natural population will affect the success of releases of transgenic mosquitoes (Rasgon and Scott 2004). Models will be a critical tool in addressing questions about driving transgenes through populations, the factors that affect the spread of the transgene, and the resulting effect on population size, structure and transmission of pathogens. It must be stressed, however, that models can only assess the factors included in them; actual releases of transgenic insects are likely to produce some unanticipated interactions and results.

FUTURE DIRECTIONS

This chapter has illustrated where models have been and could be used to address biological control of mosquito populations. As new ideas and agents for biological control are found and developed, models will be of increasing value. Models at different scales and incorporating different biological factors can 1) identify areas requiring further research; 2) indicate the strategies most likely to be successful in establishing an agent and achieving control; 3) suggest methods for monitoring releases and effectiveness of control; and 4) highlight potential problems before releases occur, saving time and money. These models may not be easy to develop, as the systems are complex and much of the needed data are not available. We are confident, however, that researchers in the mosquito control community and in modeling can work together to develop the necessary information.