Near-Infrared Microspectroscopic Analysis of Rat Skin Tissue Heterogeneity in Relation to Noninvasive Glucose Sensing

Abstract

Background

Noninvasive glucose measurements are possible by analysis of transmitted near-infrared light over the 4000- to 5000-cm^-1 spectral range. Such measurements are highly sensitive to the exact position of the fiber-optic interface on the surface of the skin sample. A critical question is the degree of heterogeneity of the major chemical components of the skin matrix in relation to the size of the fiber-optic probed used to collect noninvasive spectra. Microscopic spectral mapping is used to map the chemical distribution for a set of excised sections of rat skin.

Method

A Fourier transform near-infrared microspectrometer was used to collect transmission spectra from 16 tissue samples harvested from a set of four healthy Harlan–Sprague male rats. A reference point in the center of the tissue sample was probed regularly to track dehydration, changes in tissue composition, and changes in instrument performance. Amounts of the major skin constituents were determined by fitting microspectra to a set of six pure component absorbance spectra corresponding to water, type I collagen protein, keratin protein, fat, an offset term, and a slope term.

Results

Microspectroscopy provides spectra with root mean square noise levels on 100% lines between 418 and 1475 microabsorbance units, which is sufficient for measuring the main chemical components of skin. The estimated spatial resolution of the microscope is 220 μm. The amounts of each tissue matrix component were determined for each 480 × 360-μm² location of a 4.8 × 3.6-mm² rectangular block of skin tissue. These spectra were used to generate two-dimensional distribution maps for each of the principal skin components.

Conclusions

Distribution of the chemical components of rat skin is significant relative to the dimensions of noninvasive glucose sensing. Chemical distribution maps reveal that variations in the chemical composition of the skin samples are on the same length scale as the fiber-optic probe used to collect noninvasive near-infrared spectra. Analysis of variance between tissue slices collected for one animal and analysis of variations between animals indicate that animal-to-animal variation for all four chemical components is significantly higher than variations between samples for a given animal. These findings justify the collection and interpretation of near-infrared microspectroscopic maps of human skin to establish chemical heterogeneity and its impact on noninvasive glucose sensing for the management of diabetes.

Introduction

Several approaches are being actively pursued to develop technology for measuring glucose noninvasively in human subjects.¹ Spectroscopic approaches involve passing a selected band of optical radiation through a vascular region of the body and then extracting the corresponding glucose concentration from the resulting spectrum. Examples of contemporary spectroscopic approaches include near-infrared absorption spectroscopy,² Raman scattering spectroscopy,³ and photoacoustic infrared spectroscopy.⁴ In all cases, the principal challenge is to extract glucose-specific quantitative information from noninvasive spectra that are dominated by much larger sources of spectral variance.⁵

A major source of spectral variance is the tissue sample itself. The heterogeneity of the chemical composition of the tissue matrix is responsible for the scattering and absorption of propagating photons.⁶ As a result, the chemical composition of the tissue matrix and the physical distribution of the principal chemical constituents have a major impact on the spectrum collected during a noninvasive experiment. The relative amount of each chemical constituent within the path of propagating photons and the heterogeneous distribution of these chemicals heavily impact the absorption and scattering of photons that compose each noninvasive spectrum. Furthermore, the spectroscopic and scattering properties of living tissue are strongly affected by temperature and pressure, thereby producing additional sources of tissue-related spectral variance.⁷

An example is the measurement of glucose by near-infrared absorption spectroscopy where light is transmitted across a fold of rat skin. In this experiment, an optical fiber delivers the incident light to one side of the skin fold and a second optical fiber collects the transmitted light for detection.⁸ As noted previously,⁸ accurate predictions of glucose concentration are possible when noninvasive spectra are collected repeatedly and the fiber-optic interface remains stationary during the collection of noninvasive spectra. When the fiber-optic interface is removed and repositioned before each spectrum, the predicted glucose concentrations are highly scattered.⁸

We are interested in understanding how the heterogeneity of the chemical composition of skin impacts the spectral variance of noninvasive near-infrared transmission spectra. Such a study requires the ability to map the distribution of chemical components within the skin matrix in order to ascertain differences in this distribution and to determine the impact of this distribution on spectral variance. This report describes a mapping procedure used to establish the chemical distribution of the principal chemical components of skin samples. Tissue maps are generated using microspectroscopy to collect near-infrared spectra for 480 × 360-μm² sections of excised skin samples. An analysis of the resulting chemical distribution maps reveals information pertaining to the spectral variance within and between selected measurement sites.

Methods

Instrumentation

Tissue maps were prepared using a Nicolet Magna 560 Fourier transform infrared spectrometer (Nicolet Instrument Corp., Madison, WI) coupled with an IR-Plan^® Advantage microscope (SpectraTech, Inc., Shelton, CT). This microscope was equipped with Cassegrain optics (0.58 numerical aperture, 160/0) and provided a 15-fold magnification of the tissue section. The microscope had been modified by installing a liquid nitrogen-cooled InSb detector equipped with a K-band interference filter. This filter was used to block all light other than the region between 4000 and 5000 cm^-1 (2.0–2.5 μm).

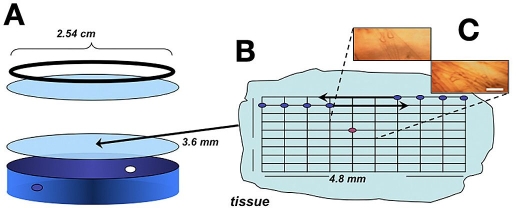
A compression cell was used to hold the tissue samples on the stage of the microscope. A schematic diagram of this compression cell is provided in Figure 1. This custom-made cell consisted of a 1-inch-diameter cylinder that held a sapphire window at one end. The tissue slice was placed on top of this window after which a second sapphire window was placed on top of the tissue slice. A metal ring-screw was used to hold the sandwiched tissue slice in place. The thickness of the sample could be varied by screwing the ring-screw tighter and compressing the tissue between the sapphire windows. Pressure between the windows was relieved by a pair of small holes positioned on the outer circumference of the cylinder, as illustrated in Figure 1. While spectra were collected, these holes were covered with Parafilm to slow the rate of tissue dehydration. After assembly, the compression cell was placed on a motorized XY mapping stage (SpectraTech, Inc.).

Figure 1.

Schematic diagram of the mapping experiment showing (A) the compression cell, (B) tissue slice with measurement array, and (C) charge-coupled device camera images of two measurement locations (bar size: 100 µm). Red dot on the tissue slice array denotes reference location.

Tissue Samples

Experiments were performed on a group of rat skin samples taken from a section of skin on the back of the animal's neck. These skin samples were excised from euthanized retired breeder Harlan–Sprague male rats weighing between 400 and 500 grams. Immediately following euthanasia, skin between the shoulders was shaved with an electric razor and 6 × 6-mm² pieces of skin tissue were excised. Precaution was taken to minimize the amount of blood in these samples. Four skin samples were taken from each animal. Each sample was immediately snap-frozen in liquid nitrogen, submerged in chilled phosphate buffer saline, and stored frozen. This procedure was performed according to a protocol approved by the University of Iowa Animal Care and Use Committee.

Just before each measurement, a tissue sample was thawed at room temperature, patted dry, and positioned inside the compression cell, as described earlier. Sample thickness was adjusted by compressing the tissue between the two sapphire windows until a reasonable infrared signal was obtained from the microscope. Generally, sample thickness ranged from 0.5 to 1 mm by this procedure. Care was taken not to squeeze the sample too hard to avoid displacing the tissue components within the tissue matrix. Each sample was left at room temperature inside the compression cell for at least 15 minutes to stabilize the temperature of the tissue. During the course of these measurements, the room temperature ranged from 21.2 to 23.0°C and more exact temperature control was not attempted.

Absorbance Spectra

Absorbance spectra were calculated as the negative logarithm of the ratio of the tissue single beam spectrum relative to an air reference single beam spectrum. Air reference spectra were obtained by replacing the tissue slice in the compression cell with a 0.95-mm-thick spacer ring composed of Teflon. Air reference spectra were collected at room temperature prior to the mapping of each tissue slice. The same air reference spectrum was used for each absorbance spectrum in the tissue map.

All spectral data were collected in triplicate as 128 co-added, 8k interferograms. Prior to applying Fourier transformation, interferograms were treated with a triangular apodization and Mertz phase correction. After Fourier transformation, the resulting single beam spectra covered the spectral range from 4000 to 5000 cm^-1 with a nominal point spacing of 3.8 cm^-1 and a resolution of 7.6 cm^-1. No external aperture was used to maximize the instrumental signal-to-noise ratio for each spectrum. Spatial resolution of the system was determined experimentally to be about 220 μm.

After collecting reference air spectra, the cell was loaded with the tissue slice and mapping was performed by starting at the northwest corner of the tissue slice. An array of tissue spectra was collected by moving the stage in X and Y directions in fixed increments of 480 and 360 μm, respectively, as indicated schematically in Figure 1. In all, spectra were collected for a 10 × 10 array of locations on the tissue slice. This corresponds to 100 locations across an area of 4.8 × 3.6 mm². Approximately 2 minutes were required to set the stage position and to collect a single spectrum at each map point. After every 30 minutes, the stage was moved to align the center point of the tissue slice at the focal point, and microscopic spectra were recorded for reference purposes.

OMNIC^® Atlμs™ software (Version 1.1, Nicolet Instrument Corp.) was used for data collection. All spectral processing and map construction were accomplished with MATLAB^® (Version 7.0, The MathWorks, Inc., Natick, MA).

Spectral Quality

Spectral quality was assessed as root mean square (RMS) noise on 100% lines between 4400 and 4600 cm^-1. A 100% line was obtained by calculating the negative logarithm of the ratio between two back-to-back single beam spectra collected from an identical location. The resulting 100% line was then fitted to a second-order polynomial, and the RMS error of this fit was obtained using Equation (1):

$$\text{RMS}=\sqrt{\frac{{\displaystyle {\sum }_{i=1}^n{\left(x_i-{\widehat{x}}_i\right)}^2}}{n}}$$ (1)

where n is the number of wavelengths in the fitted region, x_i is the measured absorbance value, and ◯_i is the fitted absorbance value.

The 100% lines and the corresponding RMS noise values were determined for triplicate air single beam spectra and triplicate single beam spectra collected at the center reference point of the tissue slice. For each case, the average value (± standard deviation) is reported for the three possible combinations of these single beam spectra (e.g., ratios of first to second, second to third, and third to first).

Spectral Fitting

Quantitative information can be extracted from each spectrum by fitting it to a set of standard spectra that represent the main chemical components of the skin matrix. In this work, each skin spectrum was fitted to a set of standard spectra representing water, collagen protein, keratin protein, and fat. Additional terms were included in the regression analysis to account for a constant offset and a sloping baseline.

Standard spectra were collected in a conventional transmission geometry at room temperature. The water spectrum (A_water) was obtained from a sealed 1-mm thick transmission cell. Collagen spectrum (A_collagen) was collected from a 1-mm thick pressed pellet composed of type I collagen protein dispersed in a matrix of potassium bromide. Keratin spectrum (A_keratin) was obtained by transmitting near-infrared radiation through a 0.4-mm thick sample of human fingernail. Human fingernail is reported to be composed primarily of keratin protein but may also contain smaller amounts of water and lipids.⁹ Moreover, keratin in nail (known as hard keratin) varies in its cystine content compared to soft keratin in skin.¹⁰ Fat spectrum (A_fat) was collected from a 1-mm thick sample of bovine fat as described elsewhere.¹¹

Spectra corresponding to each of the 100 positions along the tissue slice were fitted by a least-squares regression to the following equation:

$$\begin{array}{l}{\text{A}}_{\text{skin}}=\left({\beta }_{\text{water}}\times {\text{A}}_{\text{water}}\right)+\left({\beta }_{\text{collagen}}\times {\text{A}}_{\text{collagen}}\right)+\hfill \\ \left({\beta }_{\text{fat}}\times {\text{A}}_{\text{fat}}\right)+\left({\beta }_{\text{keratin}}\times {\text{A}}_{\text{keratin}}\right)+\hfill \\ \left({\beta }_{\text{offset}}\times {\text{A}}_{\text{offset}}\right)+\left({\beta }_{\text{slope}}\times {\text{A}}_{\text{slope}}\right)+\epsilon \hfill \end{array}$$ (2)

where A _skin is the measured skin spectrum ,A_slope and A_offset correspond to the slope and offset terms, respectively, β_water, β_collagen, β_keratin, β_fat, β_offset, and β_slope represent regression coefficients from fitting the corresponding standard absorbance spectrum, and ε is the residual spectrum. The resulting six regression coefficients represent the relative amount of each component (water, collagen, keratin, fat, slope, and offset) for each location on the skin slice.

Each spectrum was fitted by least-squares regression over the 4200- to 4900-cm^-1 spectral range.

One-Way Analysis of Variance (ANOVA)

A balanced one-way ANOVA was performed to statistically compare changes in the magnitude of the regression coefficients between locations in one sample and between skin samples obtained from different animals. Maps from each of the four samples from each animal constituted a group that consisted of four sets of 100 spectra per tissue slice. A linear model was used that assumes the means of the different groups are statistically the same. The ANOVA model is described by Equation (3):

$${\mathit{y}}_{ij}={\mathit{\alpha }}_j+{\mathit{\epsilon }}_{ij}$$ (3)

where y_ij is a matrix of coefficients with each column representing data for a different group, α_j is a matrix whose columns are the group means (mean values for a given animal), and ε_ij is the matrix of unmodeled residuals. MATLAB^® software (Version 7.0, The MathWorks, Inc.) was used to calculate probability (p values) for the null hypothesis that the regression coefficients for a particular chemical component obtained from the four animals belong to the same population. In other words, this p value corresponds to the probability of the null hypothesis being true or that the mean values are the same for each group. If the p value is equal to one, this indicates that sample means of all groups come from the same population distribution and that the variance between groups (in this case between animals) is statistically larger than the variance within groups (between map locations for a single tissue slice). A p value near zero indicates that at least one group is significantly different than the others.

Results and Discussion

In all, 1930 single beam spectra were collected for this initial study. These spectra correspond to both air and tissue spectra collected from 16 individual skin slices taken from four separate animals. For each skin slice, spectra were collected at 100 evenly spaced locations over a 4.80 × 3.60-mm² area. Spectra were measured repeatedly from the center position to determine variations in the composition and integrity of the tissue matrix. Data collection for each map required approximately 3 hours, including 30 minutes for the tissue to thaw to room temperature and 2.5 hours to collect spectra from 100 locations for the map.

Single Beam and Absorption Spectra

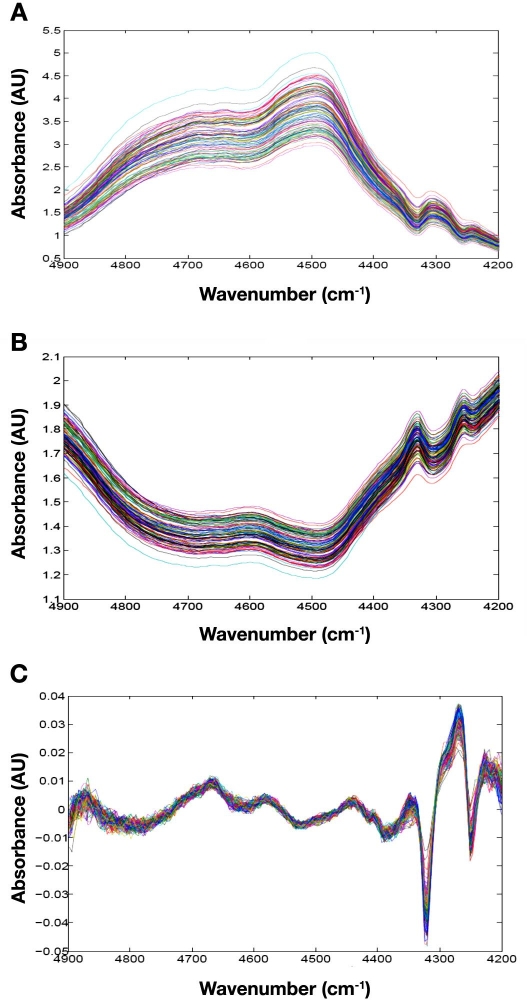
Raw single beam spectra collected from one tissue slice and the corresponding absorption spectra are presented in Figure 2. These spectra are representative of the full data set, as the map for this skin slice is neither more nor less heterogeneous than the others. The basic shape of each spectrum is controlled by the relative amounts of water, protein, and fat at each location. The broad absorption properties of water create the overall curved structure of each spectrum.¹² Absorption bands around 4600 cm^-1 correspond to protein molecules, and those centered at approximately 4350 and 4270 cm^-1 correspond to the long aliphatic chains associated with fat molecules within the tissue matrix.¹¹

Figure 2.

Representative spectral data from Slice 1 for Rat 3 showing (A) raw, single beam spectra, (B) absorbance spectra referenced to air, and (C) residual spectra after regression fitting. AU, absorbance units.

In addition to the chemical features noted earlier, spectral offsets are also evident in both single beam and absorbance spectra presented in Figure 2. These offsets correspond primarily to the scattering of incident radiation as this light propagates through the tissue slice. No significant variations are evident in the slope of the underlying baseline for these spectra.

Spectral quality is of paramount importance for successful noninvasive glucose monitoring.¹³ A key indicator of spectral quality is the RMS noise on 100% lines. RMS noise values are summarized in Table 1 for each of the 16 maps. Values are provided for both air and tissue measurements associated with each map.

Table 1.

Root Mean Square Noise on 100% Lines over the 4600- to 4400-cm^-1 Spectral Range

	Rat 1				Rat 2
Slice	Air		Tissue		Air		Tissue
	Meana	RSDb	Mean	RSD	Mean	RSD	Mean	RSD
1	31 ± 4	14%	922 ± 61	6.6%	30 ± 1	3.3%	830 ± 20	2.4%
2	31 ± 6	20%	640 ± 130	20%	34 ± 1	2.9%	448 ± 32	7.1%
3	33 ± 5	15%	703 ± 37	5.3%	31 ± 1	3.2%	569 ± 28	4.9%
4	30 ± 4	14%	625 ± 8	1.3%	32 ± 4	12%	911 ± 44	4.8%

	Rat 3				Rat 4
Slice	Air		Tissue		Air		Tissue
	Mean	RSD	Mean	RSD	Mean	RSD	Mean	RSD
1	42 ± 8	19%	1040 ± 55	5.3%	52 ± 5	9.6%	1095 ± 65	5.9%
2	41 ± 8	19%	1090 ± 40	3.7%	49 ± 8	16%	1470 ± 49	3.3%
3	32 ± 4	12%	792 ± 23	2.9%	48 ± 5	10%	418 ± 25	6.0%
4	44 ± 6	14%	1130 ± 49	4.0%	47 ± 2	4.2%	1475 ± 76	5.2%

^aMean ± standard deviation (2 degrees of freedom for air, 12 degrees of freedom for tissue).

^bRelative standard deviation.

Root mean square noise values for air give an indication of the basic spectrometer performance. Results in Table 1 indicate that the spectrometer performance was essentially the same for samples associated with the first two animals and then performance degraded slightly for the third and fourth animals. As indicated in Table 1, average values are 31.3, 32.0, 39.7, and 49.3 microabsorbance units (μAU) for each animal. For this particular instrumental configuration, the InSb detector is susceptible to minor shifts in position, which results in slight misalignment over time, which is likely responsible for the degradation in performance indicated in these air 100% lines.

Likewise, values for the RMS noise on 100% lines are significantly higher for the third and fourth animals compared to the first and second animals. Average values across skin slices for each animal are 723, 690, 1037, and 1115 μAU. For these tissue spectra, differences in RMS noise levels are primarily an indication of the thickness of the specific tissue section being analyzed. Scattering by the tissue matrix and absorption by water are related exponentially to the thickness of the skin slice. Both cause a reduction in radiant power reaching the detector, thereby reducing the measured signal, lowering the signal-to-noise ratio, and increasing the RMS noise on 100% lines. Results in Table 1 indicate that, on average, thickness of the skin tissue slices is greatest for the fourth animal and thinnest for the second animal.

In general, values for the RMS noise on 100% lines are 22 to 26 times higher for tissue spectra than for corresponding air spectra. This increase in RMS noise is caused by strong attenuation of the propagating radiation by the tissue matrix, caused primarily by scattering and water absorption. Lower RMS noise levels can be realized using thinner slices of skin. According to the Beer–Lambert law, thinner tissue samples result in smaller absorption signals for protein and fat, thereby degrading sensitivity for analysis of the chemical composition of the tissue slice. In practice, a compromise is needed in regards to the thickness of the tissue slice in order to balance spectral quality (RMS noise on 100% lines) and chemical sensitivity.

It is important to underscore a principal limitation of spectra collected in this experiment. RMS noise levels for these tissue spectra range from 418 to 1475 μAU. Even the lowest level of RMS noise is at least a factor of 10 too high for the measurement of glucose in these slices of skin tissue.¹⁴ RMS noise levels must be on the order of tens of microabsorbance units for successful glucose measurements. Nevertheless, these RMS noise levels are sufficiently low to estimate levels of the major components within the skin matrix, therefore providing a means to map spatial distribution of these components.

Chemical Distribution Maps

Chemical distribution maps are created by analyzing 100 near-infrared spectra collected over an area of 4.8 × 3.6 mm². Each spectrum corresponds to a 480 × 360-μm² rectangular block of tissue within this overall area, as illustrated schematically in Figure 1. The relative amount of each component (water, collagen, keratin, fat, constant offset, and baseline slope) is estimated by fitting each spectrum to a set of standard spectra. The resulting regression coefficients constitute an estimate of the amount of each component in the measured block of tissue.

Quantitative estimates from the regression coefficients are related directly to the amount of the component used to generate the standard spectrum. For example, a 1-mm thick sample of water was used to determine the standard water spectrum that was used in the regression analysis. If the resulting regression coefficient is 0.5, then the estimated thickness of water in that block of the skin slice is 0.5 mm. Similarly, a 1-mm thick layer of bovine fat was used to create the standard fat spectrum, and a 0.4-mm thick section of human fingernail was used for the standard keratin spectrum. Unfortunately, the amount of protein used to generate the standard spectrum for collagen cannot be quantified in the same manner because a mixture of protein and potassium bromide was used to generate this spectrum. Nevertheless, relative changes in the amount of collagen can still be obtained from the corresponding regression coefficients, even though the absolute amount of protein cannot be determined in this case.

For each rectangular block, the incident near-infrared radiation penetrates through the epidermis and dermis layers of the skin slice. Of course, each of these layers, as well as the corresponding sublayers, possesses a different distribution of water, protein, and fat, which is consistent with their different physiological functions.¹⁵ The microspectroscopic measurements used here cannot distinguish between these different layers, so the fitted regression coefficients represent a weighted average through all tissue layers.

Figure 2C shows residual spectra obtained after subtracting fitted spectra from original tissue absorption spectra. The magnitude of these residual spectra is approximately 75-fold lower than the original absorbance values. Such small residuals indicate that the fitting procedure removes a large fraction of the original absorption features and that the principal features in the skin slice spectra are well modeled by the proposed set of six standard spectra. Nevertheless, nonrandom spectral features are evident in the residual spectra, which indicate that more chemical information is embedded within these tissue spectra.

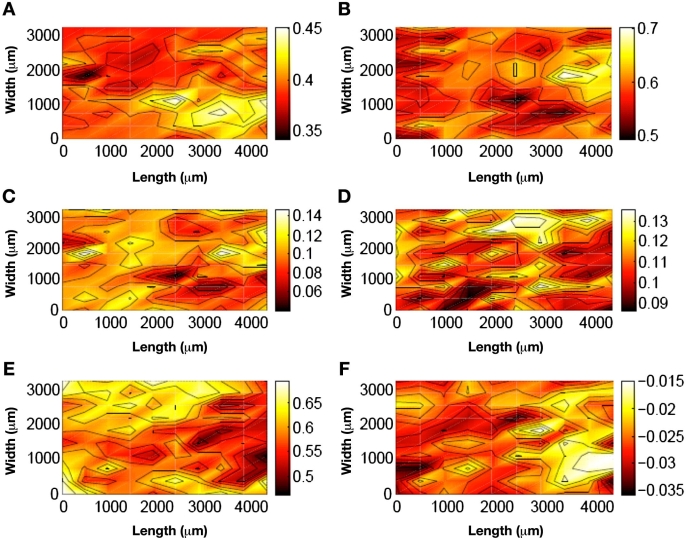
Chemical distribution maps are presented in Figure 3 for a representative tissue slice (Slice 1 for Rat 3 in Table 1). Separate maps illustrate the distribution of water (Figure 3A), collagen protein (Figure 3B), keratin protein (Figure 3C), fat (Figure 3D), spectral offset (Figure 3E), and sloping baseline (Figure 3F) within this slice of skin tissue. These two-tone distribution maps plot a density of color at each pixel to represent the average of the four surrounding tissue locations. Contour lines represent regions where the difference across the line either increases or decreases by one-tenth of the overall change. Finally, a pair of white-dotted circles is included in Figure 3A to indicate the relative size of the optical fibers used to collect noninvasive spectra from living rats in the past.⁸ In this case, the fiber diameter is 1.8 mm.

Figure 3.

False color distribution maps for Slice 1 for Rat 3 for (A) water (dashed circles represent fiber-optic size), (B) collagen type I, (C) keratin, (D) fat, (E) spectral offset, and (F) slope. Solid black contours denote 10% of the overall change in coefficient magnitude.

The maps in Figure 3 clearly illustrate variation in the component distribution across the tissue slice. Larger amounts of each component are indicated by a lighter shade of color. A higher density of contour lines indicates greater variation across the tissue slice. Based on visual inspection, the component demonstrating the largest degree of variation is the spectral offset term, while variations in the baseline slope are the smallest. In terms of the chemical components, the order of variation across the tissue slice is collagen > fat > water > keratin.

For each of the measured components, the degree of heterogeneity is relevant in relation to the diameter of the fiber-optic probe, or the dimension of the incident near-infrared light. These maps illustrate that moving the fiber-optic probe will result in the probing of skin tissue with different chemical compositions. Such variations in the chemical composition of the sample will certainly alter the nature of near-infrared absorption spectra collected noninvasively.

Analysis of Tissue Heterogeneity

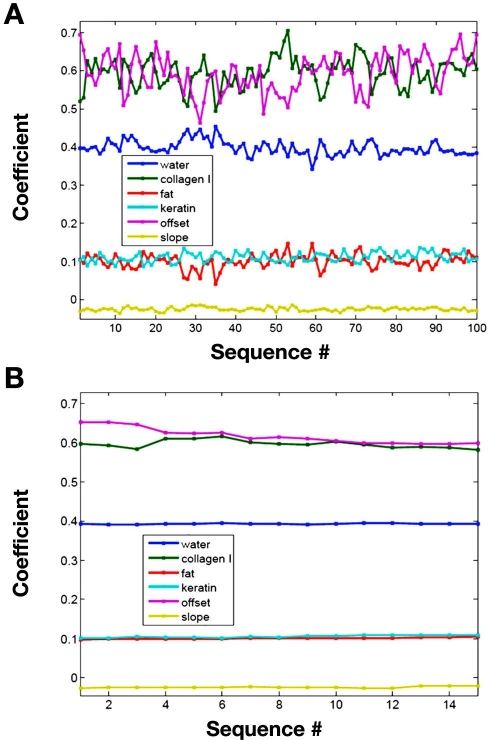
Aside from evaluating chemical distribution maps, the degree of tissue heterogeneity can be assessed by comparing the magnitude of the different regression coefficients at different positions within each tissue slice. The different regression coefficients measured for Slice 1 from Rat 3 are presented graphically in Figure 4. In Figure 4A, the magnitude of each regression coefficient is plotted for the 100 different spatial locations within the tissue slice. Although such a plot provides no spatial information concerning the variation in these coefficients, it clearly displays the degree of variation of each regression coefficient. This plot clearly reveals that the coefficient for the constant term has the highest degree of variation relative to all other coefficients.

Figure 4.

Magnitude of regression coefficients for Slice 1 from Rat 3 for (A) 100 locations of the map and (B) central reference point.

In comparison, Figure 4B plots the magnitude of the regression coefficients obtained from tissue spectra collected repeatedly from the center location of the tissue slice. These reference tissue spectra are collected periodically throughout the course of the data collection session for each map. Over the course of the data collection, little difference is observed for each coefficient. Certainly, the magnitude of variation is significantly less for this reference location compared to the different locations within the tissue matrix. These findings indicate that variations observed in Figure 4A correspond to differences in the tissue composition and not variations caused by degradation of the tissue matrix over time or changes in performance of the instrumentation.

Table 2 summarizes the mean, standard deviation, and relative standard deviation for each coefficient for Slice 1 of Rat 3. Values are provided across the entire tissue matrix as well as for the reference point. Lower relative standard deviations are noted for reference point spectra. Small standard deviations demonstrate the stability of both tissue integrity and instrument performance.

Table 2.

Regression Coefficient Statistics for Slice 1 of Rat 3

Component	Tissue matrix		Reference point
	Mean (±SD)a	RSDb	Mean (±SD)c	RSD
Water	0.40 ± 0.02	5.0%	0.393 ± 0.001	0.3%
Collagen I	0.59 ± 0.04	7.0%	0.6 ± 0.01	2.0%
Fat	0.1 ± 0.02	20%	0.101 ± 0.002	1.9%
Keratin	0.11 ± 0.01	11%	0.105 ± 0.003	3.0%
Offset	0.59 ± 0.05	8%	0.62 ± 0.02	3%
Slope	−0.025 ± 0.005	18.8%	−0.025 ± 0.002	8.1%

^aDegree of freedom = 99.

^bRelative standard deviation.

^cDegree of freedom = 14.

The chemical distribution collected for each tissue slice can be pooled to examine the tissue heterogeneity between animals. The corresponding ANOVA evaluation was performed where the variability of data was analyzed corresponding to the following two groupings: (1) variability between animals and (2) variability between locations for an individual animal. This analysis indicates that animal-to-animal variation for all four chemical components is significantly higher than variations between samples for a given animal or for variations between locations within a single tissue slice, with more than 99% probability (p values < 0.01). On the basis of these results, skin tissue samples from different animals must be treated as different distributions with significantly different values for both mean and standard deviation.

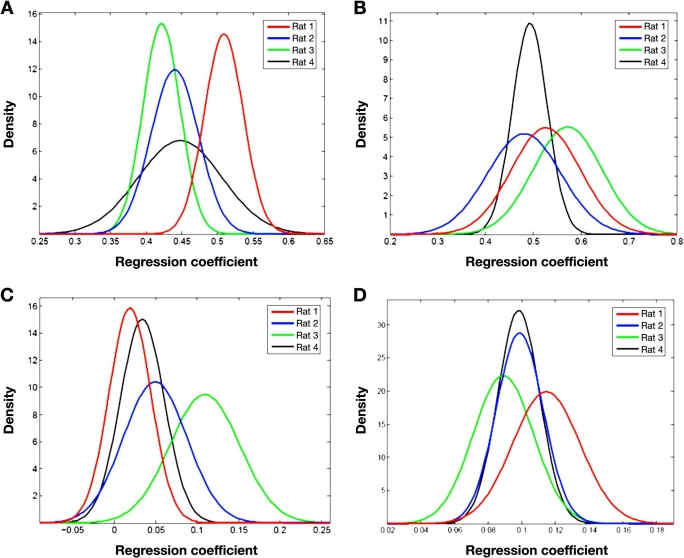
Distributions within and between animals can be visualized in the Gaussian distribution curves presented in Figure 5. Each graph provides a set of Gaussian curves for each animal where each Gaussian curve represents the pooled regression coefficients for each chemical component (water, collagen protein, keratin protein, and fat). This presentation of data clearly illustrates that significant differences exist between animals. Although considerable overlap is observed in some cases, such as in the collagen distribution for Rats 2 and 4 shown in Figure 5D, major differences are observed for each set of distribution curves. These findings are consistent with the ANOVA results presented earlier.

Figure 5.

Gaussian distribution profiles of fitted regression coefficients for (A) water, (B) collagen type I protein, (C) fat, and (D) keratin protein for individual animals: Rat 1 (red), Rat 2 (blue), Rat 3 (green), and Rat 4 (black).

Table 3 summarizes the measured regression coefficients for each component for each animal. As noted earlier, these values can be related quantitatively to the amount of each component within the optical path. Given that the pure component samples used for water and fat were 1 mm thick, the magnitude of the coefficient is equivalent to the estimated thickness of water and fat within the optical path in millimeter units. These values represent the effective optical path length for these components. The thickness of the standard keratin material was 0.4 mm, which corresponds to a range of sample keratin thicknesses of 35–42 μm. This range is a reasonable estimate of the epidermis layer thickness for rat skin.¹⁶

Table 3.

Composite Regression Coefficients for Each Set of Animal Skin Samples^a

Component	Animal
	Rat 1	Rat 2	Rat 3	Rat 4
Water	0.51 ± 0.03	0.44 ± 0.03	0.42 ± 0.03	0.45 ± 0.06
Collagen	0.53 ± 0.07	0.48 ± 0.08	0.57 ± 0.07	0.49 ± 0.04
Fat	0.02 ± 0.03	0.05 ± 0.04	0.10 ± 0.04	0.03 ± 0.03
Keratin	0.12 ± 0.02	0.10 ± 0.01	0.09 ± 0.02	0.10 ± 0.01
Offset	0.53 ± 0.08	0.54 ± 0.08	0.67 ± 0.07	0.6 ± 0.2
Slope	−0.005 ± 0.007	−0.01 ± 0.01	−0.023 ± 0.008	−0.01 ± 0.01

^aMean value (± standard deviation) with 396 degrees of freedom for each value.

Discussion

Magnitude of Tissue Heterogeneity

Fourier transform infrared microspectroscopy is used in this work to measure the distribution of chemical components in rat skin. This method provides micrometer-scale resolution with chemically sensitive detection.¹⁷ Measurement in the near-infrared range requires no special tissue treatment or staining. Thus, the sample is studied in a condition that is close to the actual in vivo environment. Freezing tissue in liquid nitrogen stops biochemical processes and preserves tissue composition for the optical measurement. Two main modes are used to obtain spatial information about tissue: mapping and imaging.¹⁸ Although the imaging approach reduces the collection time dramatically, mapping and imaging supply essentially the same chemical information.¹⁹ In this work, large areas of skin are characterized by limiting each map to 100 locations and spacing them sufficiently apart to provide distribution maps in reasonable time periods.

The distribution maps in Figure 3 illustrate that the measured heterogeneity of the chemical components is certainly significant on the length scale of the optical measurement. With a diameter of 1.8 mm, light exiting the optical fibers will encounter different distributions of water, protein, and fat, depending on the specific location of the fiber-optic probe. The degree to which this magnitude of chemical heterogeneity impacts noninvasive glucose measurements has yet to be determined in a quantitative manner.

The distribution maps in Figures 3E and 3F also reveal significant changes in the offset and slope terms of the regression function. The offset term accounts for differences in optical throughput as light propagates through the tissue. The offset term mainly models scattering processes and is related to the number of interfaces within the tissue matrix with differences in the refractive index. The slope term, however, models changes in the shape of the spectral baseline, which is highly sensitive to changes in the temperature of the sample.²⁰ Again, the distributions of offset and slope terms are significant relative to the diameter of the optical fiber probes.

Component Correlations

Correlations between the different components can be investigated through an analysis of collected data. Inspection of the distribution maps presented in Figures 3B and 3D reveals an inverse correlation between the distributions of water and fat. The darker shaded areas in the water distribution map (higher water content) correspond to the lighter shaded area in the fat map (lower fat content).

A more complicated picture is revealed from a correlation analysis between all measured regression coefficients. In this analysis, coefficients of correlation (R) were calculated for all fitted components for each map on the basis of the regression coefficients measured from the 100 spectra collected across each tissue slice. In some cases, a strong correlation is obtained between two components, while the same components have limited or no correlation in other skin samples. Table 4 provides an indication of the magnitude of each correlation and lists the maximum, minimum, and median correlation coefficients for each component correlation over all 16 tissue samples. Table entries are sorted by the absolute value of the median.

Table 4.

Selected Coefficients of Correlation (R) for Fitted Skin Components^a

Component correlation	Maximum		Minimum		Median
	R	Sample	R	Sample
Fat to slope	−0.1793	Rat 4 Slice 1	−0.7805	Rat 2 Slice 3	−0.5750
Water to fat	−0.1152	Rat 1 Slice 1	−0.8762	Rat 2 Slice 1	−0.5719
Offset to slope	0.0281	Rat 3 Slice 2	−0.7318	Rat 2 Slice 3	−0.5394
Water to collagen	−0.0282	Rat 4 Slice 2	−0.9007	Rat 2 Slice 1	−0.4866
Fat to keratin	−0.1165	Rat 1 Slice 4	−0.6935	Rat 1 Slice 1	−0.4574
Fat to offset	0.7377	Rat 1 Slice 1	−0.3550	Rat 3 Slice 2	0.3911
Keratin to slope	0.7171	Rat 1 Slice 1	−0.1727	Rat 2 Slice 4	0.3866
Water to offset	0.3251	Rat 1 Slice 1	−0.7830	Rat 4 Slice 2	−0.3715
Water to slope	0.6289	Rat 2 Slice 3	−0.0083	Rat 4 Slice 1	0.3327
Collagen to offset	0.3136	Rat 4 Slice 4	−0.5516	Rat 1 Slice 3	−0.2998
Keratin to offset	0.4933	Rat 1 Slice 3	−0.9085	Rat 1 Slice 1	−0.1731
Collagen to slope	0.3320	Rat 4 Slice 3	−0.6939	Rat 4 Slice 4	−0.1114
Collagen to fat	0.8514	Rat 2 Slice 1	−0.3653	Rat 4 Slice 3	0.0830
Water to keratin	0.4328	Rat 3 Slice 2	−0.7100	Rat 1 Slice 3	−0.0712
Collagen to keratin	0.5555	Rat 4 Slice 3	−0.6179	Rat 4 Slice 4	0.0342

^aShaded rows correspond to negative values for the median, indicating a negative correlation.

Although a complete analysis of the values in Table 4 is beyond the scope of this article, a number of interesting features can be pointed out. First, the strongest correlations are negative; in fact, most of the median correlation coefficients are negative. Second, the strongest correlations for 12 of the 15 correlation pairs were observed with samples taken from either Rat 1 or Rat 2. None of the strongest correlations were taken from Rat 3. Seven of the weakest correlations for the 15 correlation pairs were obtained from Rat 4. Third, fat-to-slope, water-to-fat, and offset-to-slope correlation pairs have the most consistent and strongest correlations (median magnitude >0.5) across all samples. Fourth, water, fat, and collagen are strongly correlated for Slice 1 from Rat 2. Fifth, for every correlation pair, at least one maximum or minimum value exists that shows a strong correlation. Finally, a larger sample population is needed to enable a more rigorous analysis and to permit identification of statistical outliers.

Limitations of Microspectroscopic Analysis

Accuracy of fitted data and relevance of distribution maps are related to two important parameters. First, transmission measurements, like those used here, tend to broaden the features seen in microscopic maps.¹⁶ Such a broadening effect will affect spatial resolution adversely, thereby degrading accuracy of the distribution maps. Second, the spectral standards used to fit tissue slice spectra must match the spectral features associated with the main chemical components within the skin tissue matrix accurately. The structure in residual spectra presented in Figure 2C is a clear indication that tissue spectra are not completely modeled by the six component spectra used in this study. This systematic difference between the fitted spectra and skin spectra can correspond to either a mismatch between standard spectra and in situ spectra of the tissue components or an insufficient number of standard spectra.

Despite the aforementioned complications, the tissue matrix is reasonably well characterized by microspectroscopy. Indeed, microspectroscopy provides a spatial resolution of 220 μm, which is sufficient to detect changes in the biochemical makeup within the tissue matrix, as demonstrated in Figure 3. The degree of chemical heterogeneity is on the same length scale as common noninvasive glucose measurements, including near-infrared spectroscopy, Raman spectroscopy, and methods based on changes in the scattering properties of skin. Indeed, as optical throughout is critical for all optical approaches, the distribution presented in Figure 3E clearly illustrates that all optical methods will be sensitive to the exact location of the measurement.

Relevance of the Animal Model

A major research objective of ours is to improve our understanding of this animal model for noninvasive glucose measurements. This model involves the collection of transmission spectra across a thin pinch of skin from the back of the neck of the animal. Near-infrared spectra collected from this region of the rat body match noninvasive transmission spectra collected from a pinch of skin from the back of the hand of human subjects.⁸

The location on the animal is critical because the composition of rat skin varies significantly in thickness from site to site and the biochemical composition of rat skin is location dependent.²¹ Variations in fatty acid and ceramide content of rat epidermal culture and human skin have been reported.²² The selected measurement site is selected to reduce the amount of adipose tissue within the transmission region. Adipose tissue contains molecules with long aliphatic chains that exhibit strong absorption bands in the region of 4200–4400 cm^-1. The absorption of light at these frequencies by the fat molecules adversely affects the signal-to-noise ratio in the spectral region most important for glucose measurements.

Our previously published findings illustrate that transmission spectra collected over the combination spectral region from rat neck skin match those collected from skin on the back of the hand of human subjects.⁸ The most pronounced difference is in scattering offset that is incorporated into the regression model. The six components used in the current study can successfully model near-infrared spectra from the back of the human hand with a spectral residual similar to that of the rat skin residual presented in Figure 2C.

Although this rat skin model adequately matches the principal spectral features of our noninvasive spectra collected across human skin,⁸ there is no indication that the chemical heterogeneity found for rat skin samples is representative of the distribution in human skin. However, a mid-infrared microspectroscopic study of pig skin revealed spatial distributions of lipid and protein similar to those reported here, which suggests that our findings are not unique to rat skin.¹⁵ Clearly, collection and interpretation of near-infrared tissue maps of human skin tissue are warranted to address this critical issue.

Conclusions

Microspectroscopic methods are established to map the distribution of the major chemical components along two dimensions of 16 samples of excised rat skin tissue. The resulting chemical distribution maps clearly reveal chemical heterogeneity on a length scale that is similar to the dimensions used to collect skin spectra for noninvasive glucose measurements. Results show ordered chemical regions on the order of 500–800 μm for water, collagen protein, keratin protein, and fat. A similar structure is observed for terms that characterize changes in the scattering properties of the tissue, as well as changes in the temperature of the sample matrix. An analysis of variance reveals that the animal-to-animal variation is significant and that the chemical variance cannot be treated as coming from a single distribution.

Future noninvasive glucose techniques must recognize the possible existence of this level of tissue heterogeneity. Although the same level of heterogeneity has not been demonstrated with human skin tissue, the implications of such heterogeneity are significant and cannot be ignored. Appropriate corrections are needed to diminish the impact of tissue heterogeneity on the accuracy of future noninvasive glucose measurements. Still, the impact of this degree of tissue heterogeneity on the ability to measure glucose with near-infrared spectroscopy must be quantified, and the magnitude of heterogeneity in human tissue must be determined to establish its significance more fully.

Abbreviations

ANOVA

analysis of variance

µAU

microabsorbance units

RMS

root mean square