Building a dictionary for genomes: Identification of presumptive regulatory sites by statistical analysis

Abstract

The availability of complete genome sequences and mRNA expression data for all genes creates new opportunities and challenges for identifying DNA sequence motifs that control gene expression. An algorithm, “MobyDick,” is presented that decomposes a set of DNA sequences into the most probable dictionary of motifs or words. This method is applicable to any set of DNA sequences: for example, all upstream regions in a genome or all genes expressed under certain conditions. Identification of words is based on a probabilistic segmentation model in which the significance of longer words is deduced from the frequency of shorter ones of various lengths, eliminating the need for a separate set of reference data to define probabilities. We have built a dictionary with 1,200 words for the 6,000 upstream regulatory regions in the yeast genome; the 500 most significant words (some with as few as 10 copies in all of the upstream regions) match 114 of 443 experimentally determined sites (a significance level of 18 standard deviations). When analyzing all of the genes up-regulated during sporulation as a group, we find many motifs in addition to the few previously identified by analyzing the subclusters individually to the expression subclusters. Applying MobyDick to the genes derepressed when the general repressor Tup1 is deleted, we find known as well as putative binding sites for its regulatory partners.

The availability of complete genome sequences has facilitated whole-genome expression analysis and led to rapid accumulation of gene expression data from high-density DNA microarray experiments. Correlating the information coded in the genome sequences to these expression data are crucial to understanding how transcription is regulated on a genomic scale. A great challenge is to decipher the information coded in the regulatory regions of genes that control transcription. So far the development of computational tools for identifying regulatory elements has lagged behind those for sequence comparison and gene discovery. One approach has been to delineate, as sharply as possible, a group of 10–100 coregulated genes (1–3) and then find a pattern common to most of the upstream regions. The analysis tools used range from general multiple-alignment algorithms yielding a weight matrix (4–6) to comparison of the frequency counts of substrings with some reference set (1). These approaches typically reveal a few responsive elements per group of genes in the specific experiment analyzed.

Although multiple copies of a single sequence motif may confer expression of a reporter gene with a minimal core promoter, real genomes are not designed as disjoint groups of genes each controlled by a single factor. Instead, to tailor a gene's expression to many different conditions, multiple control elements are required and signals are integrated (7). It is assumed that genomewide control is achieved by a combinatorial use of multiple sequence elements. For instance, the microarray experiments for yeast have shown quantitatively that most occurrences of proven binding motifs are in nonresponding genes, and many responding genes do not have the motif (8, 9). Thus there are multiple sequence motifs to be found (10). Other variables such as copy number and motif position relative to translation start cannot single out the active genes. Regulation by long-range changes in chromosome structure cannot explain the observations in several experiments (8, 9), where 500–1,000 genes that respond are uniformly distributed over the 16 chromosomes. Chromatin structure within the regulatory region can influence transcription, but for the few cases analyzed in detail, this structure is itself under the control of cis-acting elements and therefore amenable to the type of analysis we propose (compare ref. 10). The multiple sequence motifs can be missed because of insufficient sequence data if genes are divided into small subgroups and analyzed separately (11). To detect multiple regulatory elements with optimal statistics, all of the regulatory regions in the genome need to be analyzed together. Alternatively, to identify regulatory elements responsive to a specific genetic or environmental change, all genes that respond in a DNA microarray experiment should be analyzed as a group.

We present an algorithm, “MobyDick,” suitable for discovering multiple motifs from a large collection of sequences, e.g., all of the upstream regions of the yeast genome or all of the genes up-regulated during sporulation. The approach we took formalizes how one would proceed to decipher a “text” consisting of a long string of letters written in an unknown language in which words are not delineated. The algorithm is based on a statistical mechanics model that segments the string probabilistically into “words” and concurrently builds a “dictionary” of these words. MobyDick can simultaneously find hundreds of different motifs, each of them present in only a small subset of the sequences, e.g., 10–100 copies within the 6,000 upstream regions in the yeast genome. The algorithm does not need external reference data set to calibrate probabilities and finds the optimal lengths of motifs automatically. We illustrate and validate the approach by segmenting a scrambled English novel, by extracting regulatory motifs from the entire yeast genome, and by analyzing data generated from a few DNA microarray experiments.

Theory and Methods

The regulatory sequences in a eukaryotic genome typically have elements or motifs that are shared by sets of functionally related genes. These motifs are separated by random spacers that have diverged sufficiently to be modeled as a random background. The sequence data are modeled as the concatenation of words w drawn at random with frequency p_w from a probabilistic “dictionary” D; there is no syntax. The words can be of different lengths, and typically regulatory elements emerge as longer words whereas shorter words represent background. Intuitively, to build a dictionary from a text, one starts from the frequency of individual letters, finds over-represented pairs, adds them to the dictionary, determines their probabilities, and continues to build larger fragments in this way. The algorithm loops over a fitting step to compute the optimal assignment of p_w given the entries w in the dictionary, followed by a prediction step, which adds new words and terminates when no words are found to be over-represented above a certain prescribed threshold.

Given the entries w of a dictionary (the lexicon), the optimal p_w is found by maximizing Z(S, p_w), the probability of obtaining the sequence S for a given set of normalized dictionary probabilities p_w. For our model,

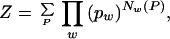1

where the sum is over all possible segmentations P of S, i.e., all possible ways in which the sequence S can be generated by concatenation of words in the dictionary, and N_w(P) denotes the number of times word w is used in a given segmentation. For example, if the dictionary D = {A,T,AT} and the sequence S = TATA, then there are only two possible ways S can be segmented, T.A.T.A and T.AT.A, where “.” denotes a word separator. The corresponding Z(TATA) = (p_A²p_T² + p_Ap_Tp_AT).

For a given set of dictionary words w, we fit the p_w to the sequence S by maximizing the likelihood function in Eq. 1 with the constraint that p_w ≥ 0 and Σ_wp_w = 1. This condition is equivalent to solving for p_w from the equation

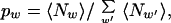2

where 〈N_w〉 = p_w(∂/∂p_w)lnZ is the average number of words w in the ensemble defined by Z. The right hand side of Eq. 2 can, of course, be defined for an arbitrary dictionary, and it is very fruitful to interpret Eq. 2 as a map or discrete dynamical system, i.e., an arbitrary set of p_w is inserted on the right and generates a new set, p′_w, on the left. The fixed point of this map is equivalent to the extremal condition on Eq. 1. Eq. 2 can be solved by simple iteration, and at each step Z increases. This can be quite slow because when the right-hand side of Eq. 2 is linearized around the current value of p_w by taking a derivative, the resulting matrix has eigenvalues close to 1. However, given this matrix we can raise it to the power of 2ⁿ by doing n matrix multiplications. These product matrices can be used to approximate the result of 2ⁿ iterations of Eq. 2, and we take the largest n such that Z increases and all p_w stay positive. When the p_w are close enough to the fixed point so that all of the eigenvalues are less than 1 (the map contracts) we switch to Newton's method to find the fix point to machine accuracy.

A dynamic programming-like technique, similar in spirit to transfer matrix methods in statistical mechanics, permits the computation of Z and its various derivatives (up to the second order) in 𝒪(LDℓ) operations where L is the total sequence length, D the dictionary size, and ℓ the maximum word length. (Further details are available elsewhere§.) Computation of the averages on the right-hand side of Eq. 2 by Monte Carlo methods would be hopelessly inaccurate for our purposes. If the defining words are known, the statistical errors on p_w are set by the Gaussian fluctuations of the background, e.g., if p_A,C,G,T = 1/4 and there is only one other word in the text of length ℓ, its probability is uncertain by (L4^ℓ)^−1/2. Our algorithm handles dictionaries up to 10³ words routinely, and we have verified that the maximum is unique by randomizing the starting p_w and reconverging.

In the prediction step, we do statistical tests on longer words based on their predicted frequencies from the current dictionary. For example, if the current dictionary D is {A,T,AT}, then the expected frequency of the length-3 word TAT (assumed to be embedded in a longer string) can be deduced from the various ways it can be made by concatenations of the words in the dictionary: AT.A.T, AT.AT, T.A.T, and T.AT. Note that the occurrence of a word is contingent on a partition; its frequency is the total probability of all partitions that delimit it, which has no simple relation to the number of times the substring occurs in the data. In practice, to check the completeness of the dictionary, we consider all pairs of dictionary words w,w′ and ask whether the average number of occurrences of the composite word w,w′ created by juxtaposition exceeds by a statistically significant amount the number predicted by the model¶, 〈N_w〉p_w′ (or equivalently 〈N_w'〉p_w). If so, the composite word is added to the dictionary. Here the statistical significance of longer words is based on the probability of shorter words, thus eliminating the need for an external reference data set to define probability. It should be noted that the background model for the statistical test evolves as the dictionary grows. Most other models assume a static background (1, 4–6, 12).

Although the juxtaposition of dictionary words is a very efficient means for narrowing the search for underpredicted strings, it can miss words that are not built from fragments already in the dictionary. Thus we have designed routines to search for over-represented motifs exhaustively within certain classes^¶. In addition to specific strings, we search for clusters of strings defined by including up to two International Union of Pure and Applied Chemistry symbols representing the 12 distinct subsets of two or more bases. Even if the frequency distribution of all strings up to a given length is consistent with Gaussian fluctuations, there can be correlations among the fluctuations and thus meaningful signals in the cluster. Motivated by many biological examples, we also searched for motifs consisting of two short strings separated by a gap, so-called dimers. Once new motifs are added to the dictionary, the new maximization step tests the relevance of all words in parallel and sets to zero the probabilities of less specific words when a more specific one will account for the over-represented string. Once a piece of a motif has been found, it can be grown or contracted (by adding or removing letters) again in parallel for all motifs. In this way words with optimal lengths will emerge.

Having the dictionary still does not permit one to “read” the text in a unique way, because the decomposition into words is probabilistic, and there are many ways to segment the data into words; yet key words do emerge. Let Ξ_w be the number of matches to the word w anywhere in the sequence, and 〈N_w〉 the average number of times the string w is delimited as a word among all segmentations of the data; then the ratio 〈N_w〉/Ξ_w serves as a quality factor. When the ratio is close to one, almost all occurrences of the string w are attributed to the word w itself, instead of being made by concatenations of other words; thus the word w can be clearly delineated from the background. The dictionary does not distinguish between signal and background, although shorter words typically have lower quality. Methods based on frequency counts Ξ will register as significant (i.e., over-represented) any substring overlapping with a dictionary word, whereas our fit will assign p_w > 0 only to the dictionary word itself.

Results

It is instructive to validate the performance of our algorithm with English text. We took a portion of the novel Moby Dick comprising ≈10⁵ characters (the first 10 chapters) and reduced it to a lowercase string containing no spaces or other punctuation characters. The starting dictionary was just the English alphabet; words were added by juxtaposition only and were required to have at least two copies in the data. The original text had 4,214 unique words of which 2,630 were a single copy, which our algorithm was forced to break up. The final dictionary had 3,600 words. Among the most significant 1,800 were 800 English words, 800 were concatenations of English words, and only 200 were fragments. Virtually all of the 1,600 text words with two or more copies occurred somewhere in our dictionary. To mimic the biological situation, we also introduced random letters (whose frequency matched the text) between each word to increase L by a factor of 3. The final dictionary then had 2,450 words. Among the most significant 1,050 were 700 English words and 40 composite words.

In a sense English is too simple: as the probability of obtaining longer words by chance is very small, simply checking for all strings with two or more copies would identify many words. Biological data are different: virtually all 8-mers have two or more copies in the combined upstream regions in yeast, yet less than 1% occur in our dictionary as described below.

A dictionary was prepared for all of the upstream regions in the yeast genome. To maximize the homogeneity of our data, we define control regions to extend upstream from the translation start site to the next coding region on either strand but not more than 600 bp. All exact repeats longer than 16 bases were removed with the program reputer (http://bibiserv.techfak.uni-bielefeld.de/reputer/) and fragments of fewer than 100 bases were ignored. This operation removed 14% of the data.

Starting from a single-base dictionary, words were added via an exhaustive search procedure. We experimented with many ways of adding words to the dictionaries. For the data presented here, we added over-represented n-mers for lengths increasing from n = 1 to n = 8; subsequently, words in the dictionary were allowed to grow one base at a time if the extended word was over-represented. All significant motifs with at most two International Union of Pure and Applied Chemistry symbols, and a total of eight characters then were added. We imposed a minimum of two copies for any dictionary entry.

The final dictionary had 1,200 words, of which 100 were clusters of similar oligonucleotides. On average, two-thirds of the sequence data were segmented into single-letter words and an additional 15% into words of length 4 or less. About 500 dictionary entries fell above a plausible significance level as defined by the quality factor. These included good matches to about half of the motifs found in refs. 1, 8, and 9, including the MCB, SCB, and MCM1 cell-cycle motifs and the URS1 motif for sporulation (Table 1). We also found ≈400 words in the form of two short segments separated by a gap, the most significant of which clustered together to generate the motifs in Table 2.

Table 1.

Known cell cycle sites (lines 1–6; from ref. 8) and some metabolic sites (lines 7–12; from ref. 1) that match words from our genomewide dictionary

Name	Consensus sequence	Dictionary words
MCB	ACGCGT	AAACGCGTACGCGTCGCGT CGCGACGCGT TGACGCGT
SCB	CRCGAAA	ACGCGAAA
SCB′	ACRMSAAA	ACGCGAAAACGCCAAA AACGCCAA
Swi5	RRCCAGCR	GCCAGCG GCAGCCAG
SIC1	GCSCRGC	GCCCAGCC CCGCGCGG
MCM1	TTWCCYAAWNNGGWAA	TTTCCNNNNNNGGAAA
NIT	GATAAT	TGATAATG
MET	TCACGTG	RTCACGTGTCACGTGM CACGTGAC CACGTGCT
PDR	TCCGCGGA	TCCGCGG
HAP	CCAAY	AACCCAAC
MIG1	KANWWWWATSYGGGGW	TATATGTGCATATATGGTGGGGAG
GAL4	CGGN11CCG	CGGN11CCG

The strings in the dictionary words that match the consensus sequence are underlined. 

Table 2.

A sample of the motifs assembled by clustering the most statistically significant word pairs of length 4–5 with a spacing of 3–30 from a genomewide dictionary

Motif	Factor (13)	−log10(P)
KHCGTHTNNNNTGAYW	ABF1	28
ATRTCACTNNNNACGD	RAP1, ABF1	52
TTTCCNNNNNNGGAAA	MCM1	6
ATACANNNNTACAT	?	10
CCGTNNNNNGCGAT	?	9
GGGCNNNNNNACCCG	?	7
CACGTGNNNNNCACGTG	?	7

The clusters were sharp enough that all the word pairs in a cluster aligned. The probability cutoff is log₁₀ of the total number of the pairs sampled, (533)² for the heterodimers and 30 × 533 for the homodimers, where 533 is the total number of words of length 4–5. The probability score for the most significant dimer in the cluster is tabulated. 

Table 3 gives a more comprehensive measure of the extent to which our dictionary is predicting functional biological sites by comparing it with a database of experimentally determined sites (13). This database of experimentally confirmed regulatory sites in yeast has entries covering ≈200 genes and ≈110 factors. Almost all sites occur upstream of the translation start. For comparison with this database, we filtered our dictionaries based on a significance score [N_w/Ξ_w > 0.2 and Ξ_w ≤ 100, to filter out poly(A) and similar strings] and matched (by inclusion) against the 443 nonrepetitive sites of length 5–30. The number of sites hit by chance is calculated by marking the dictionary words on the sequence data (to account for correlations) and then treating the database entries as intervals to be placed at random.

Table 3.

Statistics of matches to the yeast promoter database of ref. 13

Data set	Observed	Expected ± SD
Compact words	94	23  ± 4.8
Dimers	26	2.7  ± 1.8
Scrambled dictionary	33	14  ± 3.3
Ref. 12	30	9  ± 2.9

The first two entries list the matches by the compact words (words with no gap) and dimers (two short segments separated by a variable gap) in our dictionary. The third entry gives the statistics after the words are scrambled by a random permutation of the letters in each word. For the last entry, we cut off the list of motifs from ref. 12 ordered by significance when the total number of Ξ counts in the data equaled that for the dictionary set (approx. 21,000). All other filters were identical. 

Of the 443 nonredundant sites in the database, we hit 114 with a combination of compact words (words with no gaps in the middle) and dimers (two short segments separated by a variable gap), which is 18 standard deviations beyond expectation. As an additional control for the statistical significance of our matches, we scrambled the dictionary words by randomly permuting the letters in each word, and then matched them against the database. In contrast to less systematic assignments of probability, our dictionary correctly predicts the copy number of all strings of length 8 or less, plus certain classes of clusters of which the members are related by a couple of single-base mutations. Thus we can say that for the categories of motifs that we searched for exhaustively, ≈74% of the experimental sites are not statistically over-represented. This statistic, of course, does not exclude the possibility that some of these experimental sites escape our detection because of their great variability or that some of the experimental assignments are incorrect. It is difficult to assess our false-positive rate, because the database covers such a small fraction of the genome.

The above whole-genome analysis uses only information from the genome sequence and is independent of context. For cases in which the responses of all of the genes to a specific genetic or environmental perturbation are measured, a context-dependent dictionary can be constructed by applying MobyDick to a subset of genes that are active under a particular condition, and words in the dictionary can be more readily correlated with the existing knowledge base. We illustrate this approach by analyzing two DNA microarray experiments carried out on yeast: sporulation and TUP1 deletion.

A dictionary was built for the ≈500 genes that are up-regulated during sporulation (9). Using the most stringent criterion for word addition, the sporulation dictionary had only 250 unique words, of which 150 were significant; 66% of the data were segmented into single-letter words and an additional 22% by words of length 4 or less.

The two known principal sporulation elements, URS1 and MSE, have consensus motifs 5′-DSGGCGGC and 5′-CRCAAAW (9). Dictionary words that strongly overlap with these patterns are TCGGCGGC, GGCGGCAAA, TGGGCGGCTA, CTTCGGCGGC, GGCGGCTAAA, and CACAAAA, CGTCACAAA, GTCACAAAA, where the overlap with the consensus sequence is underlined, plus several words that match the reverse complements. We have verified in this instance that the frequency of all 8-mers containing GGCGGC or the MSE consensus are fit by the dictionary to within expected statistical fluctuations. For example, there are 35 copies of CGCAAAW in our data set vs. 28 predicted from the dictionary, although CGCAAAW itself is not a dictionary word.

We have predicted many additional motifs in the sporulation gene data set as well as identified known ones. There are about 20 clusters of dictionary words (with 10 or more copies among the sporulation genes) and 16 specific words whose probability of occurrence in some temporal classes as defined in ref. 9 is less than 10⁻⁴, based on their genomewide frequency. These are likely to be sporulation-specific elements, for example, elements mediating mid-late or late modes of transcription. A subset is shown in Table 4. The TGTG cluster is similar to the one summarized by Mitchell (14). We also matched the significant words in the sporulation dictionary against the yeast promoter database (13) and hit 56 sites; 14 are expected by chance. Thus many words in the sporulation dictionary are biologically meaningful, yet not specific to sporulation. A parallel dictionary fit to the 3′ untranslated region gave much less signal.

Table 4.

Several of the most significant word clusters from our sporulation dictionary that also are over-represented in one or more of the subgroups of the sporulation genes

Motif	Observed	Expected	Classes
TGTCACCT|TGTGTCA|TGTGTCAC|TTGTGTC	35	7	4
GTCAGTAA|TCAGTAAT	14	3	4
GACACA|GCCACA	52	2	4
CGCGACGC|GACGCGA|GACGCGAA|GAGGCGA|GAGGCGAC|GCGACGCG	18	3	1, 2, 5
GCGGCTAA|GGCGGCAAA|GGCGGCTAAA	10	1	1
CGTCACAAA|GTCACAAAA	17	1	4

Seven subgroups (temporal classes) were defined in ref. 9 based on their temporal expression profiles. A motif is defined by a cluster of similar dictionary words; the remaining columns represent the temporal class(es) in which the motif is over-represented (column 4), the number of copies of the motif in the corresponding temporal class(es) (column 2), and number expected based on the total counts in all promoters (column 3). The last two entries are elaborations of the URS1 and MSE motifs that better discriminate responding from nonresponding genes. 

An interesting example of combinatorial control in yeast is the general repression system involving Tup1-Ssn6 repressor (15). This repressor does not bind to DNA itself, but is brought to specific gene sets by a number of sequence-specific DNA-binding proteins. For example, Tup1-Ssn6 binds to the α2-Mcm1 complex, which recognizes specific regulatory elements in a-specific genes and represses these genes in α and a/α cells. Similarly, the combination of Tup1-Ssn6 and the DNA binding protein Mig1 represses glucose-repressible genes when glucose concentration is high. We have built a dictionary for the ≈220 genes that are derepressed by a factor of more than 2-fold when TUP1 is deleted (16). It contains 160 significant motifs, of which 42 occurred in the tup1 deletion data set with high frequency, with chance probability less than 10⁻⁴ based on their genomewide counts. These are potential binding sites for the regulatory partners of Tup1-Ssn6. Among our top five motifs we found the binding sites for Mig1, α2-Mcm1, and a motif that is specific to genes in the seripauperin family. By contrast, the Mig1 binding site was detected in the Tup1 deletion data set in ref. 1 by restricting to a subset of 25 genes that also are up-regulated during diauxic shift.

It is known that Tup1-Ssn6 binds to Rox1 to repress hypoxic genes (17). However, nine of 11 genes listed in ref. 17 exhibit less than a 2-fold change in response to the Tup1 deletion and thus are not included in the data set. As a result, we missed the Rox1 site in the Tup1 dictionary, but we did capture several versions of the Rox1 site in our genomewide dictionary. A similar situation occurred for a1/α2, which represses haploid-specific genes. These results suggest that Tup1 deletion is probably not sufficient to derepress certain classes of genes and that certain activators also are required. We also missed the binding site for another Tup1 partner, Crt1, which represses DNA damage-inducible genes, of which several examples are in the data set. The frequency of the Crt1 site is fit well by our dictionary and thus is not over-represented.

Discussion

We have implemented an algorithm that does a maximum-likelihood fit of data sets as large as several megabases to a probabalistic model: words drawn at random from a dictionary with prescribed frequency. The algorithm loops over a frequency estimation step for a known set of words, followed by the generation of new words by comparing the model predictions with the data. The first step quantifies the probabilities attached to each segmentation of the data, the number of which scales exponentially with the data length. The average base in the sequence typically will be part of several words. Although the probability estimation step converges to a unique global optimum, the word addition step is more heuristic. Namely, we only check that the model fits the data for a limited set of patterns, i.e., n-mers (up to length 8), clusters thereof, dimers, and words formed by juxtaposing dictionary entries.

The dictionary words can be ordered by their quality factor, 〈N_w〉/Ξ_w, which represents the fraction of occurrences of the string w in the data that are delineated as words by our model, not the result of a chance juxtaposition of other words or word fragments. It is natural to use the quality factor to distinguish words of potential biological significance from those that parameterize the “background.” Our fit is very sensitive; p_w will be nonzero if Ξ_w differs by more than 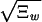from the value expected for when the word w is absent. Words at the limit of detection will have a quality factor that scales as 1/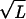. Short words invariably have low quality factors, but certain long words such as poly(A) do also, when there is a large size range of such sites in the data.

Our algorithm has extracted with high statistical significance many known cis-regulatory elements from data sets as large as the entire yeast genome, using no other empirical information. By contrast for the much smaller sporulation data set, MEME (6) only found the URS1 and MSE sequences (and a weak third motif) after the data were further divided into seven clusters (9). We found these, plus ≈20 others, several of which matched experiments (14, 18, 19) plus a statistically significant portion of ref. 13. Algorithms that contrast oligonucleotide frequencies have extracted regulatory elements from small groups of coregulated genes (1), but cannot be applied genomewide and will register many substrings overlapping with the true motif. They also require one to preselect a cluster of genes to examine rather than letting the co-occurrence of high-quality words define the clusters. Our algorithm also provides a model for the data in that it generates the same statistics as the original sequence. We have verified this for the number of occurrences of all n-mers up to length 8, clusters defined by motifs with a couple of International Union of Pure and Applied Chemistry symbols and dimers composed of words of length 4–5 separated by a fixed number of N-symbols.

Searching for regulatory elements by enumerating repeated patterns without reference to an internal or intrinsic probabalistic model can be biased if a random sample of the yeast genome is used to assign significance, because gross differences between coding and noncoding dominate the comparison (12) (Table 3). A code that enumerates regular expressions selects patterns based on absolute counts rather than probability and requires input of several parameters (20). Data compression algorithms, despite a similarity in terminology (e.g., adaptive dictionary for the Ziv-Lempel code family), satisfy very different design criteria (an invertible coding constructed on a single pass; ref. 21) than the data model that we fit to. They would attempt to compress data constructed by randomly drawing single bases (e.g., p_A = p_T = 0.4, p_C = p_G = 0.1), by encoding repeated substrings [e.g., poly(A) and poly(T)], whereas our fit would just return the single base frequencies. Formal models of language as schematized by the Chomsky hierachy have been applied to DNA sequence for some time and have proved useful for discovering sequences with interesting secondary structure at the RNA level, but syntactic rules for regulatory regions have yet to be defined (22). Hidden Markov models (23) are a common way to segment biological data, but they generally are used with relatively few segment types (e.g., promoter, exon, intron) each described by many parameters; we work with many segments, most described by a single parameter.

Our algorithm admits many elaborations such as identifying reverse complements and incorporating an additional degree of freedom into our maximum-likelihood method to segment the data into regions each with a different dictionary. Weight matrices also can be introduced in this way. Even in its present form, our algorithm, if allowed to fit an entire yeast chromosome with all words length 4 or less, will put 99% of the weight into length 3 words (codons) and place almost all of the other length words into noncoding regions.

We cannot yet treat long, fuzzy patterns such as protein motifs over the 20-letter alphabet, for which weight matrix methods were designed (4–6). There are many interesting motifs in yeast, however, which are less than 10 bp long and have only a few variable sites, which we can readily detect.