CURRENT STATUS DATA WITH COMPETING RISKS: LIMITING DISTRIBUTION OF THE MLE

Abstract

We study nonparametric estimation for current status data with competing risks. Our main interest is in the nonparametric maximum likelihood estimator (MLE), and for comparison we also consider a simpler ‘naive estimator’. Groeneboom, Maathuis and Wellner [8] proved that both types of estimators converge globally and locally at rate n^1/3. We use these results to derive the local limiting distributions of the estimators. The limiting distribution of the naive estimator is given by the slopes of the convex minorants of correlated Brownian motion processes with parabolic drifts. The limiting distribution of the MLE involves a new self-induced limiting process. Finally, we present a simulation study showing that the MLE is superior to the naive estimator in terms of mean squared error, both for small sample sizes and asymptotically.

1. Introduction

We study nonparametric estimation for current status data with competing risks. The set-up is as follows. We analyze a system that can fail from K competing risks, where K ∈ ℕ is fixed. The random variables of interest are (X, Y), where X ∈ ℝ is the failure time of the system, and Y ∈ {1,…,K} is the corresponding failure cause. We cannot observe (X,Y) directly. Rather, we observe the ‘current status’ of the system at a single random observation time T ∈ ℝ, where T is independent of (X,Y). This means that at time T, we observe whether or not failure occurred, and if and only if failure occurred, we also observe the failure cause Y. Such data arise naturally in cross-sectional studies with several failure causes, and generalizations arise in HIV vaccine clinical trials [see 10].

We study nonparametric estimation of the sub-distribution functions F₀₁,…,F_0K, where F_0k(s) = P(X ≤ s,Y = k), k = 1,…,K. Various estimators for this purpose were introduced in [10, 12], including the nonparametric maximum likelihood estimator (MLE), which is our primary focus. For comparison we also consider the ‘naive estimator’, an alternative to the MLE discussed in [12]. Characterizations, consistency, and n^1/3 rates of convergence of these estimators were established in Groeneboom, Maathuis and Wellner [8]. In the current paper we use these results to derive the local limiting distributions of the estimators.

1.1. Notation

The following notation is used throughout. The observed data are denoted by (T, Δ), where T is the observation time and Δ = (Δ₁,…,Δ_K+1) is an indicator vector defined by Δ_k = 1{X ≤ T,Y = k} for k = 1,…,K, and Δ_K+1 = 1{X > T}. Let (T_i, Δⁱ), i = 1,…,n, be n i.i.d. observations of (T, Δ), where ${\Delta }^i=({\Delta }_1^i,\dots ,{\Delta }_{K+1}^i).$ Note that we use the superscript i as the index of an observation, and not as a power. The order statistics of T₁,…,T_n are denoted by T₍₁₎,…,T_(n). Furthermore, G is the distribution of T, G_n is the empirical distribution of T_i, i = 1,…,n, and ℙ_n is the empirical distribution (T_i, Δⁱ), i = 1,…,n. For any vector (x₁,…,x_K) ∈ ℝ^K we define $x_{+}={\displaystyle {\sum }_{k=1}^K{x}_k,}$ so that, for example, ${\Delta }_{+}={\displaystyle {\sum }_{k=1}^K{\Delta }_k}$ and $F_{0+}(s)={\displaystyle {\sum }_{k=1}^K{F}_{0k}(s).}$ For any K-tuple F = (F₁,…,F_K) of sub-distribution functions, we define F_K+1(s) = ∫_u>sdF₊(u) = F₊(∞) – F₊(s).

We denote the right-continuous derivative of a function f : ℝ ⟼ ℝ by f′ (if it exists). For any function f : ℝ ⟼ ℝ, we define the convex minorant of f to be the largest convex function that is pointwise bounded by f. For any interval I, D(I) denotes the collection of cadlag functions on I. Finally, we use the following definition for integrals and indicator functions:

Definition 1.1

Let dA be a Lebesgue-Stieltjes measure, and let W be a Brownian motion process. For t < t₀, we define $1_{[t_0,t)}(u)=-1_{[t,t_0)}(u),$ ${\displaystyle {\int }_{[t_0,t)}f(u)dA(u)=-{\displaystyle {\int }_{[t,t_0)}f(u)dA(u),}}$ and ${\displaystyle {\int }_{t_0}^{t}f(u)dW(u)=-{\displaystyle {\int }_t^{t_0}f(u)dW(u).}}$

1.2. Assumptions

We prove the local limiting distributions of the estimators at a fixed point t₀, under the following conditions: (a) The observation time T is independent of the variables of interest (X,Y); (b) For each k = 1,…,K, 0 < F_0k(t₀) < F_0k(∞), and F_0k and G are continuously differentiable at t₀ with positive derivatives f_0k(t₀) and g(t₀); (c) The system cannot fail from two or more causes at the same time. Assumptions (a) and (b) are essential for the development of the theory. Assumption (c) ensures that the failure cause is well-defined. This assumption is always satisfied by defining simultaneous failure from several causes as a new failure cause.

1.3. The estimators

We first consider the MLE. The MLE F̂_n = (F̂_n1,…,F̂_nK) is defined by $l_n({\widehat{F}}_n)={\max }_{F\in {ℱ}_{\kappa }}{l}_n(F),$ where

$$l_n(F)={\displaystyle \int \{{\displaystyle \sum _{k=1}^K{\delta }_k\log F_k(t)+(1-{\delta }_{+})\log (1-F_{+}(t))}\}d{\mathbb{P}}_n(t,\delta ),}$$ (1)

and ℱ_K is the collection of K-tuples F = (F₁,…,F_K) of sub-distribution functions on ℝ with F₊ ≤ 1. The naive estimator F̃_n = (F̃_n1,…,F̃_nK) is defined by $l_{\mathit{\text{nk}}}({\tilde{F}}_{\mathit{\text{nk}}})={\max }_{F_k\in ℱ}{l}_{\mathit{\text{nk}}}(F_k),$ for k = 1,…,K, where ℱ is the collection of distribution functions on ℝ, and

$$l_{nk}(F_k)={\displaystyle \int \{{\delta }_k\log F_k(t)+(1-{\delta }_k)\log (1-F_k(t))\}d{\mathbb{P}}_n(t,\delta ),k=1,\dots ,K.}$$ (2)

Note that F̃_nk only uses the kth entry of the Δ-vector, and is simply the MLE for the reduced current status data (T, Δ_k). Thus, the naive estimator splits the optimization problem into K separate well-known problems. The MLE, on the other hand, estimates F₀₁,…,F_0K simultaneously, accounting for the fact that ${\displaystyle {\sum }_{k=1}^K{F}_{0k}(s)=P(X\le s)}$ is the overall failure time distribution. This relation is incorporated both in the object function l_n(F) (via the term log(1 – F₊)) and in the space ℱ_K over which is maximized (via the constraint F₊ ≤ 1).

1.4. Main results

The main results in this paper are the local limiting distributions of the MLE and the naive estimator. The limiting distribution of F̃_nk corresponds to the limiting distribution of the MLE for the reduced current status data (T, Δ_k). Thus, it is given by the slope of the convex minorant of a two-sided Brownian motion process plus parabolic drift [9, Theorem 5.1, page 89], known as Chernoff's distribution. The joint limiting distribution of (F̃_n1,…,F̃_nK) follows by noting that the K Brownian motion processes have a multinomial covariance structure, since Δ|T ∼ Mult_K+1(1, (F₀₁(T),…,F_0,K+1(T))). The drifted Brownian motion processes and their convex minorants are specified in Definitions 1.2 and 1.5. The limiting distribution of the naive estimator is given in Theorem 1.6, and is simply a K-dimensional version of the limiting distribution for current status data. A formal proof of this result can be found in [14, Section 6.1].

Definition 1.2

Let W = (W₁,…,W_K) be a K-tuple of two-sided Brownian motion processes originating from zero, with mean zero and covariances

$$E\{W_j(t)W_k(s)\}=(\text{|}s\text{|}\wedge \text{|}t\text{|})1\{st>0\}{\Sigma }_{jk},s,t\in ℝ,j,k\in \{1,\dots ,K\},$$ (3)

where Σ_jk = g(t₀)⁻¹ {1{j = k}F_0k(t₀) – F_0j(t₀)F_0k(t₀)}. Moreover, V = (V₁,…,V_K) is a vector of drifted Brownian motions, defined by

$$V_k(t)=W_k(t)+\frac{1}{2}{f}_{0k}(t_0)t^2,k=1,\dots ,K.$$ (4)

Following the convention introduced in Section 1.1, we write $W_{+}={\displaystyle {\sum }_{k=1}^K{W}_k}$ and $V_{+}={\displaystyle {\sum }_{k=1}^K{V}_k.}$ Finally, we use the shorthand notation a_k = (F_0k(t₀))⁻¹, k = 1,…,K + 1.

Remark 1.3

Note that W is the limit of a rescaled version of W_n = (W_n1,…,W_nK), and that V is the limit of a recentered and rescaled version of V_n = (V_n1,…,V_nK), where W_nk and V_nk are defined by (17) and (6) of [8]:

$$\begin{array}{cc}{W}_{nk}(t)={\displaystyle {\int }_{u\le t}\{{\delta }_k-F_{0k}(t_0)\}d{\mathbb{P}}_n(u,\delta ),}& t\in ℝ,k=1,\dots ,K,\\ V_{nk}(t)={\displaystyle {\int }_{u\le t}{\delta }_{k}d{\mathbb{P}}_n(u,\delta ),}& t\in ℝ,k=1,\dots ,K.\end{array}$$ (5)

Remark 1.4

We define the correlation between Brownian motions W_j and W_k by

$$r_{jk}=\frac{{\Sigma }_{jk}}{\sqrt{{\Sigma }_{jj}{\Sigma }_{kk}}}=-\frac{\sqrt{F_{0j}(t_0)F_{0k}(t_0)}}{\sqrt{(1-F_{0j}(t_0))(1-F_{0k}(t_0))}}.$$

Thus, the Brownian motions are negatively correlated, and this negative correlation becomes stronger as t₀ increases. In particular, it follows that r₁₂ → −1 as F₀₊(t₀)→ 1, in the case of K = 2 competing risks.

Definition 1.5

Let H̃ = (H̃₁,…,H̃_K) be the vector of convex minorants of V, i.e., H̃_k is the convex minorant of V_k, for k = 1,…,K. Let F̃ = (F̃₁,…,F̃_K) be the vector of right derivatives of H̃.

Theorem 1.6

Under the assumptions of Section 1.2, n^1/3{F̃_n(t₀ + n^−1/3t) – F₀(t₀)} →_d F̃(t) in the Skorohod topology on (D(ℝ))^K.

The limiting distribution of the MLE is given by the slopes of a new self-induced process Ĥ = (Ĥ₁,…,Ĥ_K), defined in Theorem 1.7. We say that the process Ĥ is ‘self-induced’, since each component Ĥ_k is defined in terms of the other components through ${\widehat{H}}_{+}={\displaystyle {\sum }_{j=1}^K{\widehat{H}}_j.}$ Due to this self-induced nature, existence and uniqueness of Ĥ need to be formally established (Theorem 1.7). The limiting distribution of the MLE is given in Theorem 1.8. These results are proved in the remainder of the paper.

Theorem 1.7

There exists an almost surely unique K-tuple Ĥ = (Ĥ₁,…,Ĥ_K) of convex functions with right-continuous derivatives F̂ = (F̂,…,F̂_K), satisfying the following three conditions:

1. a_kĤ_k(t) + a_K+1Ĥ₊(t) ≤ a_kV_k(t) + a_K+1V₊(t), for k = 1,…,K, t ∈ ℝ,

2. ∫{a_kĤ_k(t) + a_K+1Ĥ₊(t) – a_kV_k(t) – a_K+1V₊(t)}dF̂_k(t) = 0, k = 1,…,K,

3. For all M > 0 and k = 1,…,K, there are points τ_1k < −M and τ_2k > M so that a_kĤ_k(t) + a_K+1Ĥ₊(t) = a_kV_k(t) + a_K+1V₊(t) for t = τ_1kand t = τ_2k.

Theorem 1.8

Under the assumptions of Section 1.2, n^1/3{F̂_n(t₀ + n^−1/3t) – F₀(t₀)} →_d F̂(t) in the Skorohod topology on (D(ℝ))^K. Thus, the limiting distributions of the MLE and the naive estimator are given by the slopes of the limiting processes Ĥ and H̃, respectively. In order to compare Ĥ and H̃ we note that the convex minorant H̃_k of V_k can be defined as the almost surely unique convex function H̃_k with right-continuous derivative F̃_k that satisfies (i) H̃_k(t) ≤ V_k(t) for all t ∈ ℝ, and (ii) ∫{H̃_k(t) – Ṽ_k(t)}dF̃_k(t) = 0. Comparing this to the definition of Ĥ_k in Theorem 1.7, we see that the definition of Ĥ_k contains the extra terms Ĥ₊ and V₊, which come from the term log(1 – F₊(t)) in the log likelihood (1). The presence of Ĥ₊ in Theorem 1.7 causes Ĥ to be self-induced. In contrast, the processes H̃_k for the naive estimator depend only on V_k, so that H̃ is not self-induced. However, note that the processes H̃₁,…,H̃_K are correlated, since the Brownian motions W₁,…,W_K are correlated (see Definition 1.2).

1.5. Outline

This paper is organized as follows. In Section 2 we discuss the new self-induced limiting processes Ĥ and F̂. We give various interpretations of these processes and prove the uniqueness part of Theorem 1.7. Section 3 establishes convergence of the MLE to its limiting distribution (Theorem 1.8). Moreover, in this proof we automatically obtain existence of Ĥ, hence completing the proof of Theorem 1.7. This approach to proving existence of the limiting processes is different from the one followed by [5, 6] for the estimation of convex functions, who establish existence and uniqueness of the limiting process before proving convergence. In Section 4 we compare the estimators in a simulation study, and show that the MLE is superior to the naive estimator in terms of mean squared error, both for small sample sizes and asymptotically. We also discuss computation of the estimators in Section 4. Technical proofs are collected in Section 5.

2. Limiting processes

We now discuss the new self-induced processes Ĥ and F̂ in more detail. In Section 2.1 we give several interpretations of these processes, and illustrate them graphically. In Section 2.2 we prove tightness of {F̂_k – f_0k(t₀)t} and {Ĥ_k(t) – V_k(t)}, for t ∈ ℝ. These results are used in Section 2.3 to prove almost sure uniqueness of Ĥ and F̂.

2.1. Interpretations of Ĥ and F̂

Let k ∈ {1,…,K}. Theorem 1.7 (i) and the convexity of Ĥ_k, imply that a_kĤ_k + a_K+1Ĥ₊ is a convex function that lies below a_kV_k + a_K+1V₊. Hence, a_kĤ_k + a_K+1Ĥ₊ is bounded above by the convex minorant of a_kV_k + a_K+1V₊. This observation leads directly to the following proposition about the points of touch between a_kĤ_k + a_K+1Ĥ₊ and a_kV_k + a_K+1V₊:

Proposition 2.1

For each k = 1,…,K, we define 𝒩_k and 𝒩̂_k by

$${\mathcal{N}}_k=\{pointsoftouchbetween{a}_k{V}_k+a_{K+1}V+anditsconvexminorant\},$$ (6)

$${\widehat{\mathcal{N}}}_k=\{pointsoftouchbetween{a}_k{V}_k+a_{K+1}{V}_{+}and{a}_k{\widehat{H}}_k+a_{K+1}{\widehat{H}}_{+}\}.$$ (7)

Then the following properties hold: (i) 𝒩̂_k ⊂ 𝒩_k, and (ii) At points t ∈ 𝒩̂_k, the right and left derivatives of a_kĤ_k(t) + a_K+1Ĥ₊(t) are bounded above and below by the right and left derivatives of the convex minorant of a_kV_k(t) + a_K+1V₊(t).

Since a_kV_k + a_K+1V₊ is a Brownian motion process plus parabolic drift, the point process 𝒩_k is well-known from [4]. On the other hand, little is known about 𝒩̂_k, due to the self-induced nature of this process. However, Proposition 2.1 (i) relates 𝒩̂_k to 𝒩_k, and this allows us to deduce properties of 𝒩̂_k and the associated processes Ĥ_k and F̂_k. In particular, Proposition 2.1 (i) implies that F̂_k is piecewise constant, and that Ĥ_k is piecewise linear (Corollary 2.2). Moreover, Proposition 2.1 (i) is essential for the proof of Proposition 2.16, where it is used to establish expression (30). Proposition 2.1 (ii) is not used in the sequel.

Corollary 2.2

For each k ∈ {1,…,K}, the following properties hold almost surely: (i) 𝒩̂_k has no condensation points in a finite interval, and (ii) F̂_k is piecewise constant and Ĥ_k is piecewise linear.

Proof. 𝒩_k is a stationary point process which, with probability one, has no condensation points in a finite interval [see 4]. Together with Proposition 2.1 (i), this yields that with probability one, 𝒩̂_k has no condensation points in a finite interval. Conditions (i) and (ii) of Theorem 1.7 imply that F̂_k can only increase at points t ∈ 𝒩_k. Hence, F̂_k is piecewise constant and Ĥ_k is piecewise linear.

Thus, conditions (i) and (ii) of Theorem 1.7 imply that a_kĤ_k + a_K+1H^₊ is a piecewise linear convex function, lying below a_kV_k + a_K+1V₊, and touching a_kV_k + a_K+1V₊ whenever F̂_k jumps. We illustrate these processes using the following example with K = 2 competing risks:

Example 2.3 Let K = 2, and let T be independent of (X,Y). Let T,Y and X|Y be distributed as follows: G(t) = 1 – exp(−t), P(Y = k) = k/3 and P(X ≤ t|Y = k) = 1 – exp(−kt) for k = 1,2. This yields F_0k(t) = (k/3){1 – exp(−kt)} for k = 1,2.

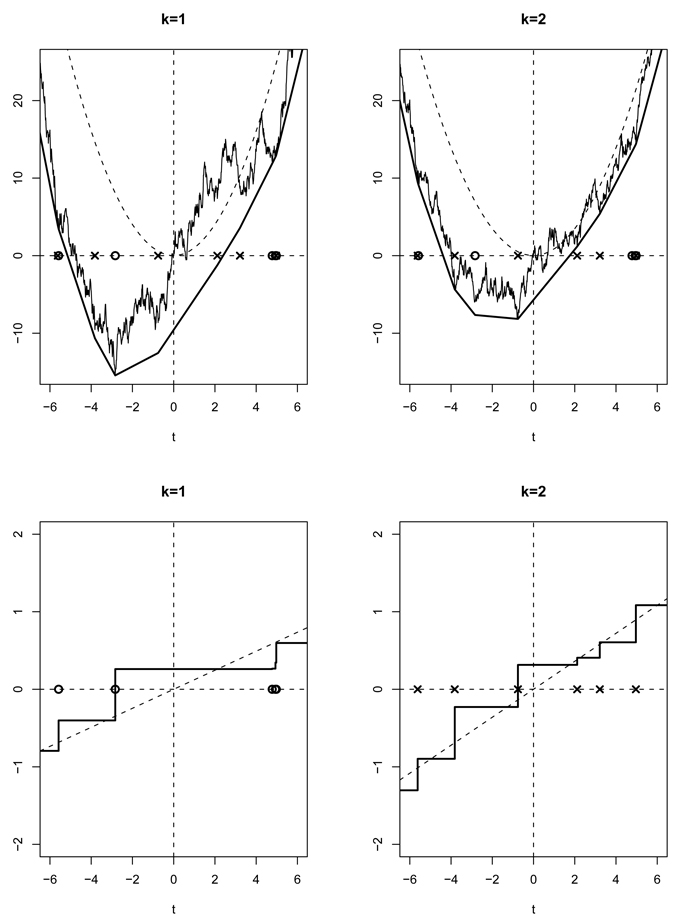
Figure 1 shows the limiting processes a_kV_k + a_K+1V₊, a_kĤ_k + a_K+1Ĥ₊, and F̂_k, for this model with t₀ = 1. The relevant parameters at the point t₀ = 1 are:

$$F_{01}(1)=0.21,F_{02}(1)=0.58,f_{01}(1)=0.12,f_{02}(1)=0.18,g(1)=0.37.$$

F₀₁(1) = 0.21, F₀₂(1) = 0.58, f₀₁(1) = 0.12, f₀₂(1) = 0.18, g(1) = 0.37.

FIG 1.

Limiting processes for the model given in Example 2.3 for t₀ = 1. The top row shows the processes a_kV_k + a_K+1V₊ and a_kĤ_k + a_k+1Ĥ₊, around the dashed parabolic drifts a_kf_0k(t₀)t²/2 + a_K+1f₀₊(t₀)t²/2. The bottom row shows the slope processes F̂_k, around dashed lines with slope f_0k(t₀). The circles and crosses indicate jump points of F̂₁ and F̂₂, respectively. Note that a_kĤ_k + a_k+1Ĥ₊ touches a_kV_k + a_K+1V₊ whenever F̂_k has a jump, for k = 1, 2.

The processes shown in Figure 1 are approximations, obtained by computing the MLE for sample size n = 100,000 (using the algorithm described in Section 4), and then computing the localized processes $V_{nk}^{loc}$ and ${\widehat{H}}_{nk}^{loc}$ (see Definition 3.1 ahead).

Note that F̂₁ has a jump around −3. This jump causes a change of slope in a_kĤ_k + a_K+1Ĥ₊ for both components k ∈ {1,2}, but only for k = 1 is there a touch between a_kĤ_k + a_K+1Ĥ₊ and a_kV_k + a_K+1V₊. Similarly, F̂₂ has a jump around −1. Again, this causes a change of slope in a_kĤ_k + a_K+1Ĥ₊ for both components k ∈ {1,2}, but only for k = 2 is there a touch between a_kĤ_k + a_K+1Ĥ₊ and a_kV_k + a_K+1V₊. The fact that a_kĤ_k + a_K+1Ĥ₊ has changes of slope without touching a_kV_k + a_K+1V₊ implies that a_kĤ_k + a_K+1Ĥ₊ is not the convex minorant of a_kV_k + a_K+1V₊.

It is possible to give convex minorant characterizations of Ĥ, but again these characterizations are self-induced. Proposition 2.4 (a) characterizes Ĥ_k in terms of ${\displaystyle {\sum }_{j=1}^K{\widehat{H}}_j,}$ and Proposition 2.4 (b) characterizes Ĥ_k in terms of ${\displaystyle {\sum }_{j=1,j\ne k}^K{\widehat{H}}_j.}$

Proposition 2.4

Ĥ satisfies the following convex minorant characterizations:

1. For each k = 1,…,K, Ĥ_k(t) is the convex minorant of

   $$V_k(t)+\frac{a_{K+1}}{a_k}\{V_{+}(t)-{\widehat{H}}_{+}(t)\}.$$ (8)
2. For each k = 1,…,K, Ĥ_k(t) is the convex minorant of

   $$V_k(t)+\frac{a_{K+1}}{a_k+a_{K+1}}\{V_{+}^{(-k)}(t)-{\widehat{H}}_{+}^{(-k)}(t)\},$$ (9)

   where $V_{+}^{(-k)}(t)={\displaystyle {\sum }_{j=1,j\ne k}^K{V}_j(t)}$ and ${\widehat{H}}_{+}^{(-k)}(t)={\displaystyle {\sum }_{j=1,j\ne k}^K{\widehat{H}}_j(t).}$

Proof. Conditions (i) and (ii) of Theorem 1.7 are equivalent to:

$$\begin{array}{l}{\widehat{H}}_k(t)\le V_k(t)+\frac{a_{K+1}}{a_k}\{V_{+}(t)-{\widehat{H}}_{+}(t)\},t\in ℝ,\\ {\displaystyle \int \{{\widehat{H}}_k(t)-V_k(t)-\frac{a_{K+1}}{a_k}\{V_{+}(t)-{\widehat{H}}_{+}(t)\}\}d{\widehat{F}}_k(t)=0,}\end{array}$$

for k = 1,…,K. This gives characterization (a). Similarly, characterization (b) holds since conditions (i) and (ii) of Theorem 1.7 are equivalent to:

$$\begin{array}{l}{\widehat{H}}_k(t)\le V_k(t)+\frac{a_{K+1}}{a_k+a_{K+1}}\{V_{+}^{(-k)}(t)-{\widehat{H}}_{+}^{(-k)}(t)\},t\in ℝ,\\ {\displaystyle \int \left\{{\widehat{H}}_k(t)-V_k(t)-\frac{a_{K+1}}{a_k+a_{K+1}}\{V_{+}^{(-k)}(t)-{\widehat{H}}_{+}^{(-k)}(t)\}\right\}d{\widehat{F}}_k(t)=0,}\end{array}$$

for k = 1,…,K.

Comparing the MLE and the naive estimator, we see that H̃_k is the convex minorant of V_k, and Ĥ_k is the convex minorant of V_k + (a_K+1/a_k){V₊ – Ĥ₊}. These processes are illustrated in Figure 2. The difference between the two estimators lies in the extra term (a_K+1/a_k){V₊ – Ĥ₊}, which is shown in the bottom row of Figure 2. Apart from the factor a_K+1/a_k, this term is the same for all k = 1,…,K. Furthermore, a_K+1/a_k = F_0k(t₀)/F_0,K+1(t₀) is an increasing function of t₀, so that the extra term (a_K+1/a_k){V₊ – Ĥ₊} is more important for large values of t₀. This provides an explanation for the simulation results shown in Figure 3 of Section 4, which indicate that MLE is superior to the naive estimator in terms of mean squared error, especially for large values of t. Finally, note that (a_K+1/a_k){V₊ – Ĥ₊} appears to be nonnegative in Figure 2. In Proposition 2.5 we prove that this is indeed the case. In turn, this result implies that H̃_k ≤ Ĥ_k (Corollary 2.6), as shown in the top row of Figure 2.

FIG 2.

Limiting processes for the model given in Example 2.3 for t₀ = 1. The top row shows the processes V_k and their convex minorants H̃_k (grey), together with V_k + (a_k+1/a_k)(V₊–Ĥ₊ and their convex minorants Ĥ_k (black). The dashed lines depict the parabolic drift f_0k(t₀)t²/2. The middle row shows the slope processes F̃_k (grey) and F̂_k (black), which follow the dashed lines with slope f_0k(t₀). The bottom row shows the ‘correction term’ (a_k+1/a_k)(V₊–Ĥ₊) for the MLE.

FIG 3.

Relative MSEs, computed by dividing the MSE of the MLE by the MSE of the other estimators. All MSEs were computed over 1000 simulations for each sample size, on the grid 0, 0.01, 0.02,…, 3.0.

Proposition 2.5

Ĥ₊ (t) ≤ V₊(t) for all t ∈ ℝ.

Proof. Theorem 1.7 (i) can be written as

$${\widehat{H}}_k(t)+\frac{F_{0k}(t_0)}{1-F_{0+}(t_0)}{\widehat{H}}_{+}(t)\le V_k(t)+\frac{F_{0k}(t_0)}{1-F_{0+}(t_0)}{V}_{+}(t),k=1,\dots ,K,t\in ℝ.$$

The statement then follows by summing over k = 1,…,K.

Corollary 2.6

H̃_k(t) ≤ Ĥ_k(t) for all k = 1,…,K and t ∈ ℝ.

Proof. Let k ∈ {1,…,K} and recall that H̃_k is the convex minorant of V_k. Since V₊ – Ĥ₊ ≥ 0 by Proposition 2.5, it follows that H̃_k is a convex function below V_k + (a_K+1/a_k){V₊ – Ĥ₊}. Hence, it is bounded above by the convex minorant Ĥ_k of V_k + (a_K+1/a_k){V₊ – Ĥ₊}.

Finally, we write the characterization of Theorem 1.7 in a way that is analogous to the characterization of the MLE in Proposition 4.8 of [8]. We do this to make a connection between the finite sample situation and the limiting situation. Using this connection, the proofs for the tightness results in Section 2.2 are similar to the proofs for the local rate of convergence in [8, Section 4.3]. We need the following definition:

Definition 2.7

For k = 1,…,K and t ∈ ℝ, we define

$${\overline{F}}_{0k}(t)=f_{0k}(t_0)t\text{ and }{S}_k(t)=a_k{W}_k(t)+a_{K+1}{W}_{+}(t).$$ (10)

Note that S_k is the limit of a rescaled version of the process S_nk = a_kW_nk + a_K+1W_n+, defined in (18) of [8].

Proposition 2.8

For all k = 1,…,K, for each point τ_k ∈ 𝒩̂_k (defined in (7)) and for all s ∈ ℝ we have:

$${\displaystyle {\int }_{{\tau }_k}^s\left\{a_k\{{\widehat{F}}_k(u)-{\overline{F}}_{0k}(u)\}+a_{K+1}\{{\widehat{F}}_{+}(u)-{\overline{F}}_{0+}(u)\}\right\}du\le {\displaystyle {\int }_{{\tau }_k}^{s}d{S}_k(u),}}$$ (11)

and equality must hold if s ∈ 𝒩̂_k.

Proof. Let k ∈ {1,…,K}. By Theorem 1.7 (i), we have

$$a_k{\widehat{H}}_k(t)+a_{K+1}{\widehat{H}}_{+}(t)\le a_k{V}_k(t)+a_{K+1}{V}_{+}(t),t\in ℝ,$$

where equality holds at t = τ_k ∈ 𝒩̂_k. Subtracting this expression for t = τ_k from the expression for t = s, we get:

$${\displaystyle {\int }_{{\tau }_k}^s\{a_k{\widehat{F}}_k(u)+a_{K+1}{\widehat{F}}_{+}(u)\}du\le {\displaystyle {\int }_{{\tau }_k}^s\{a_{k}d{V}_k(u)+a_{K+1}d{V}_{+}(u)\}.}}$$

The result then follows by subtracting ${\displaystyle {\int }_{{\tau }_k}^s\{a_k{\overline{F}}_{0k}(u)+a_{K+1}{\overline{F}}_{0+}(u)\}du}$ from both sides, and using that dV_k(u) = F̄_0k(u)du + dW_k(u) (see (4)).

2.2. Tightness of Ĥ and F̂

The main results of this section are tightness of {F̂_k(t) – F̄_0k(t)} (Proposition 2.9) and {Ĥ_k(t) – V_k(t)} (Corollary 2.15), for t ∈ ℝ. These results are used in Section 2.3 to prove that Ĥ and F̂ are almost surely unique.

Proposition 2.9

For every ϵ > 0 there is an M > 0 such that

$$P(\left|{\widehat{F}}_k(t)-{\overline{F}}_{0k}(t)\right|\ge M)<ϵ,fork=1,\dots ,K,t\in ℝ.$$

Proposition 2.9 is the limit version of Theorem 4.17 of [8], which gave the n^1/3 local rate of convergence of F̂_nk. Hence, analogously to [8, Proof of Theorem 4.17], we first prove a stronger tightness result for the sum process {F̂₊(t) – F̄₀₊(t)}, t ∈ ℝ.

Proposition 2.10

Let β ∈ (0,1) and define

$$v(t)=\{\begin{array}{cc}1,& if\text{|}t\text{|}\le 1,\\ \text{|}t{\text{|}}^{\beta },& if\text{|}t\text{|}>1.\end{array}$$ (12)

Then for every ϵ > 0 there is an M > 0 such that

$$P\left(\underset{t\in ℝ}{\sup }\frac{|{\widehat{F}}_{+}(t)-{\overline{F}}_{0+}(t)}{v(t-s)}\ge M\right)<ϵ,fors\in ℝ.$$

Proof. The organization of this proof is similar to the proof of Theorem 4.10 of [8]. Let ϵ > 0. We only prove the result for s = 0, since the proof for s ≠ 0 is equivalent, due to stationarity of the increments of Brownian motion.

It is sufficient to show that we can choose M > 0 such that

$$\begin{array}{l}P\left(\exists t\in ℝ:{\widehat{F}}_{+}(t)\notin ({\overline{F}}_{0+}(t-Mv(t)),{\overline{F}}_{0+}(t+Mv(t)))\right)\\ =P\left(\exists t\in ℝ:|{\widehat{F}}_{+}(t)-{\overline{F}}_{0+}(t)|\ge f_{0+}(t_0)Mv(t)\right)<ϵ.\end{array}$$

In fact, we only prove that there is an M such that

$$P\left(\exists t\in [0,\infty ):{\widehat{F}}_{+}(t)\ge {\overline{F}}_{0+}(t+Mv(t))\right)<\frac{ϵ}{4},$$

since the proofs for the inequality F̂₊(t) ≤ F̄₀₊(t – Mv(t)) and the interval (−∞,0] are analogous. In turn, it is sufficient to show that there is an m₁ > 0 such that

$$P\left(\exists t\in [j,j+1):{\widehat{F}}_{+}(t)\ge {\overline{F}}_{0+}(t+Mv(t))\right)\le p_{j}M,j\in \mathbb{N},M>m_1,$$ (13)

where p_jM satisfies ${\displaystyle {\sum }_{j=0}^{\infty }{p}_{jM}\to 0}$ as M → ∞. We prove (13) for

$$p_{jM}=d_1\exp \{-d_2{(Mv(j))}^3\},$$ (14)

where d₁ and d₂ are positive constants. Using the monotonicity of F̂₊, we only need to show that P(A_jM) < p_jM for all j ∈ ℕ and M > m₁, where

$$A_{jM}=\{\widehat{F}+(j+1)\ge {\overline{F}}_{0+}(s_{jM})\}\text{ and }{s}_{jM}=j+Mv(j).$$ (15)

We now fix M > 0 and j ∈ ℕ, and define τ_kj = max{𝒩̂k ∩ (−∞,j + 1]}, for k = 1,…,K. These points are well defined by Theorem 1.7 (iii) and Corollary 2.2 (i). Without loss of generality, we assume that the sub-distribution functions are labeled so that τ_1j ≤ ⋯ ≤ τ_Kj. On the event A_jM, there is a k ∈ {1,…,K} such that F̂_k(j + 1) ≥ F̄_0k(s_jM). Hence, we can define ℓ ∈ {1,…,K} such that

$${\widehat{F}}_k(j+1)<{\overline{F}}_{0k}(s_{jM}),k=\ell +1,\dots ,K,$$ (16)

$${\widehat{F}}_{\ell }(j+1)\ge {\overline{F}}_{0\ell }(s_{jM}).$$ (17)

Recall that F̂ must satisfy (11). Hence, P(A_jM) equals

$$\begin{array}{l}P\left({\displaystyle {\int }_{{\tau }_{\ell j}}^{s_{jM}}\{a_{\ell }\{{\widehat{F}}_{\ell }(u)-{\overline{F}}_{0\ell }(u)\}+a_{K+1}\{{\widehat{F}}_{+}(u)-{\overline{F}}_{0+}(u)\}\}du\le {\displaystyle {\int }_{{\tau }_{\ell j}}^{s_{jM}}d{S}_{\ell }(u),A_{jM}}}\right)\\ \le P\left({\displaystyle {\int }_{{\tau }_{\ell j}}^{s_{jM}}{a}_{\ell }\{{\widehat{F}}_{\ell }(u)-{\overline{F}}_{0\ell }(u)\}du\le {\displaystyle {\int }_{{\tau }_{\ell j}}^{s_{jM}}d{S}_{\ell }(u),A_{jM}}}\right)\end{array}$$ (18)

$$+P\left({\displaystyle {\int }_{{\tau }_{\ell j}}^{s_{jM}}\{{\widehat{F}}_{+}(u)-{\overline{F}}_{0+}(u)\}du\le 0,A_{jM}}\right).$$ (19)

Using the definition of τ_ℓj and the fact that F̂_ℓ is monotone nondecreasing and piecewise constant (Corollary 2.2), it follows that on the event A_jM we have, F̂_ℓ(u) ≥ F̂_ℓ(τ_ℓj) = F̂_ℓ(j + 1) ≥ F̄_0ℓ(s_jM), for u ≥ τ_ℓj. Hence, we can bound (18) above by

$$\begin{array}{c}P\left({\displaystyle {\int }_{{\tau }_{\ell j}}^{s_{jM}}{a}_{\ell }\{{\overline{F}}_{0\ell }(s_{jM})-{\overline{F}}_{0\ell }(u)\}du\le {\displaystyle {\int }_{{\tau }_{\ell j}}^{s_{jM}}d{S}_{\ell }(u)}}\right)\\ =P\left(\frac{1}{2}{f}_{0\ell }(t_0){(s_{jM}-{\tau }_{\ell j})}^2\le {\displaystyle {\int }_{{\tau }_{\ell j}}^{s_{jM}}d{S}_{\ell }(u)}\right)\\ \le P\left(\underset{w\le j+1}{\inf }\left\{\frac{1}{2}{f}_{0\ell }(t_0){(s_{jM}-w)}^2-{\displaystyle {\int }_w^{s_{jM}}d{S}_{\ell }(u)}\right\}\le 0\right).\end{array}$$

For m₁ sufficiently large, this probability is bounded above by p_jM/2 for all M > m₁ and j ∈ ℕ, by Lemma 2.11 below. Similarly, (19) is bounded by p_jM/2, using Lemma 2.12 below.

Lemmas 2.11 and 2.12 are the key lemmas in the proof of Proposition 2.10. They are the limit versions of Lemmas 4.13 and 4.14 of [8], and their proofs are given in Section 5. The basic idea of Lemma 2.11 is that the positive quadratic drift b(s_jM – w)² dominates the Brownian motion process S_k and the term C(s_jM – w)^3/2. Note that the lemma also holds when C(s_jM – w)^3/2 is omitted, since this term is positive for M > 1. In fact, in the proof of Proposition 2.10 we only use the lemma without this term, but we need the term C(s_jM – w)^3/2 in the proof of Proposition 2.9 ahead. The proof of Lemma 2.12 relies on the system of component processes. Since it is very similar to the proof of Lemma 4.14, we only point out the differences in Section 5.

Lemma 2.11

Let C > 0 and b > 0. Then there exists an m₁ > 0 such that for all k = 1,…,K, M > m₁and j ∈ ℕ,

$$P\left(\underset{w\le j+1}{\inf }\left\{b{(s_{jM}-w)}^2-{\displaystyle {\int }_w^{s_{jM}}d{S}_k(u)-C{(s_{jM}-w)}^{3/2}}\right\}\le 0\right)\le p_{jM},$$

where s_jM = j + Mv(j), and S_k(·), v(·) and p_jM are defined by (10), (12) and (14), respectively.

Lemma 2.12

Let ℓ be defined by (16) and (17). There is an m₁ > 0 such that

$$P\left({\displaystyle {\int }_{{\tau }_{\ell j}}^{s_{jM}}\{{\widehat{F}}_{+}(u)-{\overline{F}}_{0+}(u)\}du\le 0,A_{jM}}\right)\le p_{jM},forM>m_1,j\in \mathbb{N},$$

where s_jM = j + Mv(j), τ_ℓj = max{𝒩̂_ℓ ∩ (−∞,j + 1]} and v(·), p_jM and A_jM are defined by (12), (14) and (15), respectively.

In order to prove tightness of {F̂_k(t) – F̄_0k(t), t ∈ ℝ, we only need Proposition 2.10 to hold for one value of β ∈ (0,1), analogously to [8, Remark 4.12]. We therefore fix β = 1/2, so that $v(t)=1\vee \sqrt{\text{|}t\text{|}}.$ Then Proposition 2.10 leads to the following corollary, which is a limit version of Corollary 4.16 of [8]:

Corollary 2.13

For every ϵ > 0 there is a C > 0 such that

$$P\left\{\underset{u\in {ℝ}_{+}}{\sup }\frac{{\displaystyle {\int }_{s-u}^s\left|{\widehat{F}}_{+}(t)-{\overline{F}}_{0+}(t)\right|dt}}{u\vee u^{3/2}}\ge C\right\}<ϵ,fors\in ℝ.$$

This corollary allows us to complete the proof of Proposition 2.9.

Proof of Proposition 2.9

Let ϵ > 0 and let k ∈ {1,…,K}. It is sufficient to show that there is an M > 0 such that P(F̂_k(t) ≥ F̄_0k(t + M)) < ϵ and P(F̂_k(t) ≤ F̄_0k(t – M)) < ϵ for all t ∈ ℝ. We only prove the first inequality, since the proof of the second one is analogous. Thus, let t ∈ ℝ and M > 1, and define

$$B_{kM}=\{{\widehat{F}}_k(t)\ge {\overline{F}}_{0k}(t+M)\}\text{ and }{\tau }_k=\max \{{\widehat{\mathcal{N}}}_k\cap (-\infty ,t]\}.$$

Note that τ_k is well-defined because of Theorem 1.7 (iii) and Corollary 2.2 (i). We want to prove that P(B_kM) < ϵ. Recall that F̂ must satisfy (11). Hence,

$$\begin{array}{c}P({{\displaystyle B}}_{kM})=P({\displaystyle {\int }_{\tau k}^{t+M}\left\{{{\displaystyle a}}_k\{{\widehat{F}}_k(u)-{\overline{F}}_{0k}(u)\}+a_{K+1}\{{\widehat{F}}_{+}(u)-{\overline{F}}_{0+}(u)\}\right\}du}\\ \le {\displaystyle {\int }_{\tau k}^{t+M}d{S}_k(u),{{\displaystyle B}}_{kM}).}\end{array}$$ (20)

By Corollary 2.13, we can choose C > 0 such that, with high probability,

$${\displaystyle {\int }_{{\tau }_{\kappa }}^{t+M}\left|{\widehat{F}}_{+}(u)-{\overline{F}}_{0+}(u)\right|du\le C{(t+M-{\tau }_k)}^{3/2},}$$ (21)

uniformly in τ_k ≤ t, using that u^3/2 > u for u > 1. Moreover, on the event B_kM, we have ${\displaystyle {\int }_{{\tau }_{\kappa }}^{t+M}\{{\widehat{F}}_k(u)-{\overline{F}}_{0k}(u)\}du\ge {\displaystyle {\int }_{{\tau }_k}^{t+M}\{{\overline{F}}_{0k}(t+M)-{\overline{F}}_{0k}(u)\}du=f_{0k}(t_0){(t+M-{\tau }_k)}^2/2,}}$ yielding a positive quadratic drift. The statement now follows by combining these facts with (20), and applying Lemma 2.11.

Proposition 2.9 leads to the following corollary about the distance between the jump points of F̂_k. The proof is analogous to the proof of Corollary 4.19 of [8], and is therefore omitted.

Corollary 2.14

For all k = 1,…,K, let${\tau }_{\kappa }^{-}(s)$and${\tau }_k^{+}(s)$be, respectively, the largest jump point ≤ s and the smallest jump point > s of F̂_k. Then for every ϵ > 0 there is a C > 0 such that$P({\tau }_k^{+}(s)-{\tau }_k^{-}(s)>C)<ϵ,$for k = 1,…,K, s ∈ ℝ. Combining Theorem 2.9 and Corollary 2.14 yields tightness of {Ĥ_k(t) – V_k(t)}:

Corollary 2.15

For every ϵ > 0 there is an M > 0 such that

$$P\left(\left|{\widehat{H}}_k(t)-V_k(t)\right|>M\right)<ϵ,fort\in ℝ.$$

2.3. Uniqueness of Ĥ and F̂

We now use the tightness results of Section 2.2 to prove the uniqueness part of Theorem 1.7, as given in Proposition 2.16. The existence part of Theorem 1.7 will follow in Section 3.

Proposition 2.16Let Ĥ and H satisfy the conditions of Theorem 1.7. Then Ĥ ≡ H almost surely.

The proof of Proposition 2.16 relies on the following lemma:

Lemma 2.17

Let Ĥ = (Ĥ₁,…,Ĥ_K) and H = (H₁,…,H_K) satisfy the conditions of Theorem 1.7, and let F̂ = (F̂₁,…,F̂_K) and F = (F₁,…,F_K) be the corresponding derivatives. Then

$$\begin{array}{l}{\displaystyle \sum _{k=1}^K{a}_k{\displaystyle \int {\{F_k(t)-{\widehat{F}}_k(t)\}}^{2}dt+a_{K+1}{\displaystyle \int {\{F_{+}(t)-{\widehat{F}}_{+}(t)\}}^{2}dt}}}\\ \le \underset{m\to \infty }{\lim \inf }{\displaystyle \sum _{k=1}^K\{{\psi }_k(m)-{\psi }_k(-m)\},}\end{array}$$ (22)

where ψ_k : ℝ → ℝ is defined by

$${\psi }_k(t)=\{F_k(t)-{\widehat{F}}_k(t)\}[a_k\{H_k(t)-{\widehat{H}}_k(t)\}+a_{K+1}\{H_{+}(t)-{\widehat{H}}_{+}(t)\}].$$ (23)

Proof. We define the following functional:

$$\begin{array}{c}{{\displaystyle \varphi }}_m(F)={\displaystyle \sum _{k=1}^K{{\displaystyle a}}_k}\left\{\frac{1}{2}{\displaystyle {\int }_{-m}^m{{\displaystyle F}}_k^2(t)dt-{\displaystyle {\int }_{-m}^m{{\displaystyle F}}_k(t)d{{\displaystyle V}}_k(t)}}\right\}\\ +{{\displaystyle a}}_{K+1}\left\{\frac{1}{2}{\displaystyle {\int }_{-m}^m{{\displaystyle F}}_{+}^2(t)dt-{\displaystyle {\int }_{-m}^m{{\displaystyle F}}_{+}(t)dV+(t)}}\right\},m\in \mathbb{N}.\end{array}$$

Then, letting

$$D_k(t)=a_k\{H_k(t)-V_k(t)\}+a_{K+1}\{H_{+}(t)-V_{+}(t)\},$$ (24)

$${\widehat{D}}_k(t)=a_k\{{\widehat{H}}_k(t)-V_k(t)\}+a_{K+1}\{{\widehat{H}}_{+}(t)-V_{+}(t)\},$$ (25)

and using $F_k^2-{\widehat{F}}_k^2={(F_k-{\widehat{F}}_k)}^2+2{\widehat{F}}_k(F_k-{\widehat{F}}_k),$ we have

$$\begin{array}{c}{\varphi }_m(F)-{\varphi }_m(\widehat{F})={\displaystyle \sum _{k=1}^K\frac{a_k}{2}{\displaystyle {\int }_{-m}^m{{\displaystyle \{F_k(t)-{\widehat{F}}_k(t)\}}}^{2}dt+\frac{a_{K+1}}{2}{\displaystyle {\int }_{-m}^m{{\displaystyle \{F_{+}(t)-{\widehat{F}}_{+}(t)\}}}^{2}dt}}}\\ +{\displaystyle \sum _{k=1}^K{\displaystyle {\int }_{-m}^m\{F_k(t)-{\widehat{F}}_k(t)\}d{\widehat{D}}_k(t).}}\end{array}$$ (26)

Using integration by parts, we rewrite the last term of the right side of (26) as:

$$\begin{array}{c}{\displaystyle \sum _{k=1}^k\{F_k(t)-{\widehat{F}}_k(t)\}{\widehat{D}}_k(t){|}_{-m}^m-{\displaystyle \sum _{k=1}^K{\displaystyle {\int }_{-m}^m{\widehat{D}}_k(t)d\{F_k(t)-{\widehat{F}}_k(t)\}}}}\\ \ge {\displaystyle \sum _{k=1}^K\{F_k(t)-{\widehat{F}}_k(t)\}{\widehat{D}}_k(t){|}_{-m}^m.}\end{array}$$ (27)

The inequality on the last line follows from: (a) ${\displaystyle {\int }_{-m}^m{\widehat{D}}_k(t)d{\widehat{F}}_k(t)=0}$ by Theorem 1.7 (ii), and (b) ${\displaystyle {\int }_{-m}^m{\widehat{D}}_k(t)d{F}_k(t)\le 0,}$ since D̂_k(t) ≤ 0 by Theorem 1.7 (i) and F_k is monotone nondecreasing. Combining (26) and (27), and using the same expressions with F and F̂ interchanged, yields

$$\begin{array}{l}0={\phi }_m(\widehat{F})-{\phi }_m(F)+{\phi }_m(F)-{\phi }_m(\widehat{F})\\ \ge {\displaystyle \sum _{k=1}^K{a}_k}{\displaystyle {\int }_{-m}^m{\{F_k(t)-{\widehat{F}}_k(t)\}}^{2}dt+a_{K+1}{\displaystyle {\int }_{-m}^m{\{F_{+}(t)-{\widehat{F}}_{+}(t)\}}^{2}dt}}\\ +{{\displaystyle \sum _{k=1}^K\{{\widehat{F}}_k(t)-F_k(t)\}{D}_k(t)}|}_{-m}^m+{{\displaystyle \sum _{k=1}^K\{F_k(t)-{\widehat{F}}_k(t)\}{\widehat{D}}_k(t)}|}_{-m}^m.\end{array}$$

By writing out the right side of this expression, we find that it is equivalent to

$$\begin{array}{c}{\displaystyle \sum _{k=1}^K{a}_k{\displaystyle {\int }_{-m}^m{{\displaystyle \{F_k(t)-{\widehat{F}}_k(t)\}}}^{2}dt+a_{K+1}{\displaystyle {\int }_{-m}^m{{\displaystyle \{F_{+}(t)-{\widehat{F}}_{+}(t)\}}}^{2}dt}}}\\ \le {\displaystyle \sum _{k=1}^K[\{F_k(m)-{\widehat{F}}_k(m)\}\{D_k(m)-{\widehat{D}}_k(m)\}}\\ -\{F_k(-m)-{\widehat{F}}_k(-m)\}\{D_k(-m)-{\widehat{D}}_k(-m)\}].\end{array}$$ (28)

This inequality holds for all m ∈ ℕ, and hence we can take lim inf_m→∞. The left side of (28) is a monotone sequence in m, so that we can replace lim inf_m→∞. by lim_m→∞. The result then follows from the definitions of ψ_k, D_k, and D̂_k in (23) – (25).

We are now ready to prove Proposition 2.16. The idea of the proof is to show that the right side of (22) is almost surely equal to zero. We prove this in two steps. First, we show that it is of order O_p(1), using the tightness results of Proposition 2.9 and Corollary 2.15. Next, we show that the right side is almost surely equal to zero.

Proof of Proposition 2.16

We first show that the right side of (22) is of order O_p(1). Let k ∈ {1,…,K}, and note that Proposition 2.9 yields that {F_k(m) – F̄_0k(m)} and {F̂_k(m) – F̄_0k(m)} are of order O_p(1), so that also {F_k(m) – F̂_k(m)} = O_p(1). Similarly, Corollary 2.15 implies that {H_k(m) – Ĥ_k(m)} = O_p(1). Using the same argument for −m, this proves that the right side of (22) is of order O_p(1).

We now show that the right side of (22) is almost surely equal to zero. Let k ∈ {1,…,K}. We only consider |F_k(m) – F̂_k(m)‖H_k(m) – Ĥ_k(m)|, since the term |F_k(m) – F̂_k(m)‖H₊(m) – Ĥ₊(m)| and the point –m can be treated analogously. It is sufficient to show that

$$\underset{m\to \infty }{\text{lim inf}}P\left(\left|F_k(m)-{\widehat{F}}_k(m)\right|\left|H_k(m)-{\widehat{H}}_k(m)\right|>\eta \right)=0,\text{ for all }\eta >0.$$ (29)

Let τ_mk be the last jump point of F_k before m, and let τ̂_mk be the last jump point of F̂_k before m. We define the following events

$$\begin{array}{c}{E}_m=E_m(ϵ,\delta ,C)=E_{1m}(ϵ)\cap E_{2m}(\delta )\cap E_{3m}(C),\text{ where}\\ E_{1m}=E_{1m}(ϵ)=\left\{{\displaystyle {\int }_{{\tau }_{mk}\vee {\widehat{\tau }}_{mk}}^{\infty }{\{F_k(t)-{\widehat{F}}_k(t)\}}^{2}dt<ϵ}\right\},\\ E_{2m}=E_{2m}(\delta )=\{m-({\tau }_{mk}\vee {\widehat{\tau }}_{mk})>\delta \},\\ E_{3m}=E_{3m}(C)=\left\{\left|H_k(m)-{\widehat{H}}_k(m)\right|<C\right\}.\end{array}$$

Let ϵ₁ > 0 and ϵ₂ > 0. Since the right side of (22) is of order O_p(1), it follows that ∫{F_k(t) – F̂_k(t)}²dt = O_p(1) for every k ∈ {1,…,K}. This implies that ${\displaystyle {\int }_m^{\infty }{\{F_k(t)-{\widehat{F}}_k(t)\}}^{2}dt{\to }_{p}0}$ as m → ∞ . Together with the fact that m – {τ_mk ∨ τ̂_mk} = O_p(1) (Corollary 2.14), this implies that there is an m₁ > 0 such that P(E_1m(ϵ₁)^c) < ϵ₁ for all m > m₁. Next, recall that the points of jump of F_k and F̂_k are contained in the set 𝒩_k, defined in Proposition 2.1. Letting τ′_mk = max{𝒩_k ∩ (–∞, m]}, we have

$$P(E_{2m}^c(\delta ))\le P(m-{{\tau }^{\prime }}_{mk}<\delta ).$$ (30)

The distribution of m – τ′_mk is independent of m, non-degenerate and continuous [see 4]. Hence, we can choose δ > 0 such that the probabilities in (30) are bounded by ϵ₂/2 for all m. Furthermore, by tightness of {H_k(m) – Ĥ_k(m)}, there is a C > 0 such that P(E_3m(C)^c) < ϵ₂/2 for all m. This implies that P(E_m(ϵ₁,δ,C)^c) < ϵ₁ + ϵ₂ for m > m₁.

Returning to (29), we now have for η > 0:

$$\begin{array}{c}\underset{m\to \infty }{\text{lim inf}}P\left(\left|F_k(m)-{\widehat{F}}_k(m)\right|\left|H_k(m)-{\widehat{H}}_k(m)\right|>\eta \right)\\ \le {ϵ}_1+{ϵ}_2+\underset{m\to \infty }{\lim \inf }P\left(\left|F_k(m)-{\widehat{F}}_k(m)\right|\left|H_k(m)-{\widehat{H}}_k(m)\right|>\eta ,E_m({ϵ}_1,\delta ,C)\right)\\ \le {ϵ}_1+{ϵ}_2+\underset{m\to \infty }{\lim \inf }P\left(\left|F_k(m)-{\widehat{F}}_k(m)\right|>\frac{\eta }{C},E_m({ϵ}_1,\delta ,C)\right),\end{array}$$

using the definition of E_3m(C) in the last line. The probability in the last line equals zero for ϵ₁ small. To see this, note that F_k(m) – F̂_k(m) > η/C, m – {τ_mk ∨ τ̂_mk} > δ, and the fact that F_k and F̂_k are piecewise constant on m – {τ_km ∨ τ̂_mk} imply that

$${\displaystyle {\int }_{{\tau }_{mk}\vee {\widehat{\tau }}_{mk}}^{\infty }{\{F_k(u)-{\widehat{F}}_k(u)\}}^{2}du\ge }{\displaystyle {\int }_{{\tau }_{mk}\vee {\widehat{\tau }}_{mk}}^m{\{F_k(u)-{\widehat{F}}_k(u)\}}^{2}du>\frac{{\eta }^2\delta }{C^2},}$$

so that E_1m(ϵ₁) cannot hold for ϵ₁ < η²δ/C².

This proves that the right side of (22) equals zero, almost surely. Together with the right-continuity of F_k and F̂_k, this implies that F_k ≡ F̂_k almost surely, for k = 1,…,K. Since F_k and F̂_k are the right derivatives of H_k and Ĥ_k, this yields that H_k = Ĥ_k + c_k almost surely. Finally, both H_k and Ĥ_k satisfy conditions (i) and (ii) of Theorem 1.7 for k = 1,…,K, so that c₁ = ⋯ = c_K = 0 and H ≡ H^ almost surely.

3. Proof of the limiting distribution of the MLE

In this section we prove that the MLE converges to the limiting distribution given in Theorem 1.8. In the process, we also prove the existence part of Theorem 1.7.

First, we recall from [8, Section 2.2] that the naive estimators F˜_nk, k = 1,…,K, are unique at t ∈ {T₁,…,T_n}, and that the MLEs F̂_nk, k = 1,…,K, are unique at t ∈ 𝒯_K, where ${\mathcal{T}}_k=\{T_i,i=1,\dots ,n:{\Delta }_k^i+{\Delta }_{K+1}^i>0\}\cup \{T_{(n)}\}$ for k = 1,…,K [see 8, Proposition 2.3]. To avoid issues with non-uniqueness, we adopt the convention that F̃_nk and F̂_nk, k = 1,…,K, are piecewise constant and right-continuous, with jumps only at the points at which they are uniquely defined. This convention does not affect the asymptotic properties of the estimators under the assumptions of Section 1.2. Recalling the definitions of G and G_n given in Section 1.1, we now define the following localized processes:

Definition 3.1

For each k = 1,…,K, we define:

$${\widehat{F}}_{nk}^{loc}(t)=n^{1/3}\{{\widehat{F}}_{nk}(t_0+n^{-1/3}t)-F_{0k}(t_0)\},$$ (31)

$$V_{nk}^{loc}(t)=\frac{n^{2/3}}{g(t_0)}{\displaystyle {\int }_{u\in (t_0,t_0+n^{-1/3}t)}\{{\delta }_k-F_{0k}(t_0)\}d{\mathbb{P}}_n(u,\delta ),,}$$ (32)

$${\overline{H}}_{nk}^{loc}(t)=\frac{n^{2/3}}{g(t_0)}{\displaystyle {\int }_{t_0}^{t_0+n^{-1/3}t}\{{\widehat{F}}_{nk}(u)-F_{0k}(t_0)\}dG(u),}$$ (33)

$${\widehat{H}}_{nk}^{loc}(t)={\overline{H}}_{nk}^{loc}(t)+\frac{c_{nk}}{a_k}-F_{0k}(t_0){\displaystyle \sum _{k=1}^K\frac{c_{nk}}{a_k},}$$ (34)

where c_nk is the difference between $a_k{V}_{nk}^{loc}+a_{K+1}{V}_{n+}^{loc}$ and $a_k{H}_{nk}^{loc}+a_{K+1}{H}_{n+}^{loc}$ at the last jump point τ_nk of ${\widehat{F}}_{nk}^{loc}$ before zero, i.e.,

$$c_{nk}=a_k{V}_{nk}^{loc}({\tau }_{nk}-)+a_{K+1}{V}_{n+}^{loc}({\tau }_{nk}-)-a_k{\overline{H}}_{nk}^{loc}({\tau }_{nk})-a_{K+1}{\overline{H}}_{n+}^{loc}({\tau }_{nk}).$$ (35)

Moreover, we define the vectors ${\widehat{F}}_n^{loc}=({\widehat{F}}_{n1}^{loc},\dots ,{\widehat{F}}_{nK}^{loc}),V_n^{loc}=(V_{n1}^{loc},\dots ,V_{nK}^{loc}),$ and ${\widehat{H}}_n^{loc}=({\widehat{H}}_{n1}^{loc},\dots ,{\widehat{H}}_{nK}^{loc}).$

Note that ${\widehat{H}}_{nk}^{loc}$ differs from ${\overline{H}}_{nk}^{loc}$ by a vertical shift, and that $({\widehat{H}}_{nk}^{loc}{)}^{\prime }(t)=({\overline{H}}_{nk}^{loc}{)}^{\prime }(t)={\widehat{F}}_{nk}^{loc}(t)+o(1).$ We now show that the MLE satisfies the characterization given in Proposition 3.2, which can be viewed as a recentered and rescaled version of the characterization in Proposition 4.8 of [8]. In the proof of Theorem 1.8 we will see that, as n → ∞, this characterization converges to the characterization of the limiting process given in Theorem 1.7.

Proposition 3.2

Let the assumptions of Section 1.2 hold, and let m > 0. then

$$\begin{array}{l}{a}_k{\widehat{H}}_{nk}^{loc}(t)+a_{K+1}{\widehat{H}}_{n+}^{loc}(t)\le a_k{V}_{nk}^{loc}(t-)+a_{K+1}{V}_{n+}^{loc}(t-)+R_{nk}^{loc}(t),fort\in [-m,m],\\ {\displaystyle {\int }_{-m}^m\{a_k{V}_{nk}^{loc}(t-)+a_{K+1}d{V}_{n+}^{loc}(t-)+R_{nk}^{loc}(t)-a_k{\widehat{H}}_{nk}^{loc}(t)-a_{K+1}{\widehat{H}}_{n+}^{loc}(t)\}d{\widehat{F}}_{nk}^{loc}(t)=0,}\end{array}$$

where $R_{nk}^{loc}(t)=o_p(1),$uniformly in t ∈ [–m, m].

Proof. Let m > 0 and let τ_nk be the last jump point of F̂_nk before t₀. It follows from the characterization of the MLE in Proposition 4.8 of [8] that

$$\begin{array}{l}{\displaystyle {\int }_{{\tau }_{nk}}^s\left\{a_k\{{\widehat{F}}_{nk}(u)-F_{0k}(u)\}+a_{K+1}\{{\widehat{F}}_{n+}(u)-F_{0+}(u)\}\right\}dG(u)}\\ \le {\displaystyle {\int }_{[{\tau }_{nk},s)}\left\{a_k\{{\delta }_k-F_{0k}(u)\}+a_{K+1}\{{\delta }_{+}-F_{0+}(u)\}\right\}d{\mathbb{P}}_n(u,\delta )+R_{nk}({\tau }_{nk},s),}\end{array}$$ (36)

where equality holds if s is a jump point of F̂_nk. Using that t₀ – τ_nk = O_p(n^−1/3) by [8, Corollary 4.19], it follows from [8, Corollary 4.20] that R_nk(τ_nk, s) = O_p(n^−2/3), uniformly in s ∈ [t₀ – m₁n^1/3,t₀ + m₁n^−1/3]. We now add

$${\displaystyle {\int }_{{\tau }_{nk}}^s\{a_k\{F_{0k}(u)-F_{0k}(t_0)\}+a_{K+1}\{F_{0+}(u)-F_{0+}(t_0)\}\}dG(u)}$$

to both sides of (36). This gives

$$\begin{array}{c}{\displaystyle {\int }_{{\tau }_{nk}}^s\left\{a_k\{{\widehat{F}}_{nk}(u)-F_{0k}(t_0)\}+a_{K+1}\{{\widehat{F}}_{n+}(u)-F_{0+}(t_0)\}\right\}dG(u)}\\ \le {\displaystyle {\int }_{[{\tau }_{nk},s)}\left\{a_k\{{\delta }_k-F_{0k}(t_0)\}+a_{K+1}\{{\delta }_{+}-F_{0+}(t_0)\}\right\}d{\mathbb{P}}_n(u,\delta )+R_{nk}^{\text{'}}({\tau }_{nk},s),}\end{array}$$ (37)

where equality holds if s is a jump point of F^_nk, and where

$$\begin{array}{l}{R^{\prime }}_{nk}(s,t)=R_{nk}(s,t)+{\rho }_{nk}(s,t),\text{ with}\\ {\rho }_{nk}(s,t)={\displaystyle {\int }_{[s,t)}\left\{a_k\{F_{0k}(t_0)-F_{0k}(u)\}+a_{K+1}\{F_{0+}(t_0)-F_{0+}(u)\}\right\}d(G_n-G)(u).}\end{array}$$

Note that ρ_nk(τ_nk, s) = o_p(n^−2/3), uniformly in s ∈ [t₀ – m₁n^−1/3,t₀ + m₁n^−1/3], using (29) in [8, Lemma 4.9] and t₀ – τ_nk = O_p(n^−1/3) by [8, Corollary 4.19]. Hence, the remainder term R′_nk in (37) is of the same order as R_nk. Next, consider (37), and write ${\int }_{[{\tau }_{nk},s)}={\int }_{[{\tau }_{nk},t_0)}+{\int }_{[t_0,s),}$ let s = t₀ + n^−1/3t, and multiply by n^2/3/g(t₀). This yields

$$c_{nk}+a_k{\overline{H}}_{nk}(t)+a_{K+1}{\overline{H}}_{n+}(t)\le R_{nk}^{loc}(t)+a_k{V}_{nk}^{loc}(t-)+a_{K+1}{V}_{n+}^{loc}(t-),$$ (38)

where equality holds if t is a jump point of ${\widehat{F}}_{nk}^{loc}$ and where

$$R_{nk}^{loc}(t)=\{n^{2/3}/g(t_0)\}{R^{\prime }}_{nk}({\tau }_{nk},t_0+n^{-1/3}t),k=1,\dots ,K.$$ (39)

Note that $R_{nk}^{loc}(t)=o_p(1)$ uniformly in t ∈ [−m₁, m₁], using again that t₀ – τ_nk = O_p(n^−1/3). Moreover, note that $R_{nk}^{loc}$ is left-continuous. We now remove the random variables c_nk by solving the following system of equations for H₁,…,H_K:

$$c_{nk}+a_k{\overline{H}}_{nk}(t)+a_{K+1}{\overline{H}}_{n+}(t)=a_k{H}_{nk}(t)+a_{K+1}{H}_{n+}(t),k=1,\dots ,K.$$

The unique solution is $H_{nk}(t)={\overline{H}}_{nk}(t)+(c_{nk}/a_k)+{\displaystyle {\sum }_{k=1}^K(c_{nk}\text{/}{a}_k)\equiv {\widehat{H}}_{nk}^{loc}(t).}$

Definition 3.3

We define ${\widehat{U}}_n=(R_n^{loc},V_n^{loc},{\widehat{H}}_n^{loc},{\widehat{F}}_n^{loc}),$ where $R_n^{loc}=(R_{n1}^{loc},\dots ,R_{nK}^{loc})$ with $R_{nk}^{loc}$ defined by (39), and where $V_n^{loc},{\widehat{H}}_n^{loc}$ and ${\widehat{F}}_n^{loc}$ are given in Definition 34. We use the notation ·|[−m,m] to denote that processes are restricted to [−m,m]. We now define a space for Û_n|[−m,m]:

Definition 3.4

For any interval I, let D⁻(I) be the collection of ‘caglad’ functions on I (left-continuous with right limits), and let C(I) denote the collection of continuous functions on I. For m ∈ ℕ, we define the space

$$\begin{array}{c}E[-m,m]={(D^{-}[-m,m])}^K\times {(D[-m,m])}^K\times {(C[-m,m])}^K\times {(D[-m,m])}^K\\ \equiv I\times II\times III\times IV,\end{array}$$

endowed with the product topology induced by the uniform topology on I × II × III, and the Skorohod topology on IV.

Proof of Theorem 1.8

Analogously to the work of [6, Proof of Theorem 6.2] on the estimation of convex densities, we first show that Û_n|[−m,m] is tight in E[−m,m] for each m ∈ ℕ. Since $R_{nk}^{loc}\text{|}[-m,m]=o_p(1)$ by Proposition 3.2, it follows that $R_n^{loc}$ is tight in (D⁻[−m,m])^K endowed with the uniform topology. Next, note that the subset of D[−m,m] consisting of absolutely bounded nondecreasing functions is compact in the Skorohod topology. Hence, the local rate of convergence of the MLE [see 8, Theorem 4.17] and the monotonicity of ${\widehat{F}}_{nk}^{loc},$k = 1,…,K, yield tightness of ${\widehat{F}}_n^{loc}\text{|}[-m,m]$ in the space (D[−m,m])^K endowed with the Skorohod topology. Moreover, since the set of absolutely bounded continuous functions with absolutely bounded derivatives is compact in C[−m,m] endowed with the uniform topology, it follows that ${\overline{H}}_n^{loc}\text{|}[-m,m]$ is tight in (C[−m,m])^K endowed with the uniform topology. Furthermore, $V_n^{loc}\text{|}[-m,m]$ is tight in (D[−m,m])^K endowed with the uniform topology, since $V_n^{loc}(t){\to }_{d}V(t)$ uniformly on compacta. Finally, c_n1,…,c_nK are tight since each c_nk is the difference of quantities that are tight, using that t₀ – τ_nk = O_p(n^−1/3) by [8, Corollary 4.19]. Hence, also ${\widehat{H}}_n^{loc}\text{|}[-m,m]$ is tight in (C[−m,m])^K endowed with the uniform topology. Combining everything, it follows that Û_n[−m,m] is tight in E[−m,m] for each m ∈ ℕ.

It now follows by a diagonal argument that any subsequence Û_n′ of Û_n has a further subsequence Û_n″ that converges in distribution to a limit

$$U=(0,V,H,F)\in {(C(ℝ))}^K\times {(C(ℝ))}^K\times {(C(ℝ))}^K\times {(D(ℝ))}^K.$$

Using a representation theorem (see, e.g., [2], [15, Representation Theorem 13, page 71], or [17, Theorem 1.10.4, page 59]), we can assume that Û_n″ →_a.s U. Hence, F = H′ at continuity points of F, since the derivatives of a sequence of convex functions converge together with the convex functions at points where the limit has a continuous derivative. Proposition 3.2 and the continuous mapping theorem imply that the vector (V,H,F) must satisfy

$$\begin{array}{l}\underset{[-m,m]}{\text{inf}}\{a_k{V}_k(t)+a_{K+1}{V}_{+}(t)-a_k{H}_k(t)-a_{K+1}{H}_{+}(t)\}\ge 0,\\ {\displaystyle {\int }_{-m}^m\{a_k{V}_k(t)+a_{K+1}{V}_{+}(t)-a_k{H}_k(t)-a_{K+1}{H}_{+}(t)\}d{F}_k(t)=0,}\end{array}$$

for all m ∈ ℕ, where we replaced V_k(t–) by V_k(t), since V₁,…,V_K are continuous.

Letting m → ∞ it follows that H₁,…,H_K satisfy conditions (i) and (ii) of Theorem 1.7. Furthermore, Theorem 1.7 (iii) is satisfied since t₀ – τ_nk = O_p(n^−1/3) by [8, Corollary 4.19]. Hence, there exists a K-tuple of processes (H₁,…,H_K) that satisfies the conditions of Theorem 1.7. This proves the existence part of Theorem 1.7. Moreover, Proposition 2.16 implies that there is only one such K-tuple. Thus, each subsequence converges to the same limit H = (H₁,…,H_K) = (Ĥ₁,…,Ĥ_K) defined in Theorem 1.8. In particular, this implies that ${\widehat{F}}_n^{loc}(t)=n^{1/3}({\widehat{F}}_n(t_0+n^{-1/3}t)-F_0(t_0)){\to }_d\widehat{F}(t)$ in the Skorohod topology on (D(ℝ))^K.

4. Simulations

We simulated 1000 data sets of sizes n = 250, 2500 and 25000, from the model given in Example 2.3. For each data set, we computed the MLE and the naive estimator. For computation of the naive estimator, see [1, pages 13–15] and [9, pages 40–41]. Various algorithms for the computation of the MLE are proposed by [10, 11, 12]. However, in order to handle large data sets, we use a different approach. We view the problem as a bivariate censored data problem, and use a method based on sequential quadratic programming and the support reduction algorithm of [7]. Details are discussed in [13, Chapter 5]. As convergence criterion we used satisfaction of the characterization in [8, Corollary 2.8] within a tolerance of 10⁻¹⁰. Both estimators were assumed to be piecewise constant, as discussed in the beginning of Section 3.

It was suggested by [12] that the naive estimator can be improved by suitably modifying it when the sum of its components exceeds one. In order to investigate this idea, we define a ‘scaled naive estimator’ ${\tilde{F}}_{nk}^s$ by

$${\tilde{F}}_{nk}^s(t)=\{\begin{array}{cc}{\tilde{F}}_{nk}(t)& \text{if }{\tilde{F}}_{n+}(s_0)\le 1,\\ {\tilde{F}}_{nk}(t)/{\tilde{F}}_{n+}(s_0)& \text{if }{\tilde{F}}_{n+}(s_0)>1,\end{array}$$

for k = 1,…,K, where we take s₀ = 3. Note that ${\tilde{F}}_{n+}^s(t)\le 1$ for t ≤ 3. We also defined a ‘truncated naive estimator’ ${\tilde{F}}_{nk}^t.$ If F̃_n+(T_(n)) ≤ 1, then ${\tilde{F}}_{nk}^t\equiv {\tilde{F}}_{nk}$ for all k = 1,…,K. Otherwise, we let s_n = min{t : F̃_n+(t) > 1} and define

$$\begin{array}{c}{\tilde{F}}_{nk}^t(t)=\{\begin{array}{cc}{\tilde{F}}_{nk}(t)& \text{for }t<s_n,\\ {\tilde{F}}_{nk}(t)+{\alpha }_{nk}& \text{for }t\ge s_n,\end{array}\\ \text{where }{\alpha }_{\kappa }=\frac{{\tilde{F}}_{nk}(s_n)-{\tilde{F}}_{nk}(s_n-)}{{\tilde{F}}_{n+}(s_n)-{\tilde{F}}_{n+}(s_n-)}\{1-{\tilde{F}}_{n+}(s_n-)\},\end{array}$$

for k = 1,…,K. Note that ${\tilde{F}}_{n+}^t(t)\le 1$ for all t ∈ ℝ.

We computed the mean squared error (MSE) of all estimators on a grid with points 0, 0.01, 0.02,…,3.0. Subsequently, we computed relative MSEs by dividing the MSE of the MLE by the MSE of each estimator. The results are shown in Figure 3. Note that the MLE tends to have the best MSE, for all sample sizes and for all values of t. Only for sample size 250 and small values of t, the scaled naive estimator outperforms the other estimators; this anomaly is caused by the fact that this estimator is scaled down so much that it has a very small variance. The difference between the MLE and the naive estimators is most pronounced for large values of t. This was also observed by [12], and they explained this by noting that only the MLE is guaranteed to satisfy the constraint F₊(t) ≤ 1 at large values of t. We believe that this constraint is indeed important for small sample sizes, but the theory developed in this paper indicates that it does not play any role asymptotically. Asymptotically, the difference can be explained by the extra term (a_K+1/a_k){V₊ – Ĥ₊} in the limiting process of the MLE (see Proposition 2.4), since the factor a_K+1/a_k = F_0k(t)/F_0,K+1(t) is increasing in t.

Among the naive estimators, the truncated naive estimator behaves better than the naive estimator for sample sizes 250 and 2500, especially for large values of t. However, for sample size 25000 we can barely distinguish the three naive estimators. The latter can be explained by the fact that all versions of the naive estimator are asymptotically equivalent for t ∈ [0, 3], since consistency of the naive estimator ensures that lim_n→∞ F̃_n+(3) ≤ 1 almost surely. On the other hand, the three naive estimators are clearly less efficient than the MLE for sample size 25000. These results support our theoretical finding that the form of the likelihood (and not the constrained F₊ ≤ 1) causes the different asymptotic behavior of the MLE and the naive estimator.

Finally, we note that our simulations consider estimation of F_0k(t), for t on a grid. Alternatively, one can consider estimation of certain smooth functional of F_0k. The naive estimator was suggested to be asymptotically efficient for this purpose [12], and [14, Chapter 7] proved that the same is true for the MLE. A simulation study that compares the estimators in this setting is presented in [14, Chapter 8.2].

5. Technical proofs

Proof of Lemma 2.11

Let k ∈ {1,…,K} and j ∈ ℕ = {0,1,…}. Note that for M large, we have for all w ≤ j + 1:

$$C(s_{jM}-w\vee {(s_{jM}-w)}^{3/2}\le \frac{1}{2}b{(s_{jM}-w)}^2.$$

Hence, the probability in the statement of Lemma 2.11 is bounded above by

$$P\left\{\underset{w\le j+1}{\sup }\left\{{\displaystyle {\int }_w^{s_{jM}}d{S}_k(u)-\frac{1}{2}b{(s_{jM}-w)}^2}\right\}\ge 0\right\}.$$

In turn, this probability is bounded above by

$${\displaystyle \sum _{q=0}^{\infty }P\left\{\underset{w\in (j-q,j-q+1]}{\sup }{\displaystyle {\int }_w^{s_{jM}}d{S}_k(u)\ge {\lambda }_{kjq}}\right\},}$$ (40)

where λ_kjq = b(s_jM – (j – q + 1))²/2 = b(Mu(j) + q – 1)²/2.

We write the qth term in (40) as

$$\begin{array}{l}P\left(\underset{w\in [j-q,j-q+1)}{\sup }{S}_k(s_{jM}-w)\ge {\lambda }_{kjq}\right)\le P\left(\underset{w\in [0,Mv(j)+q)}{\sup }{S}_k(w)\ge {\lambda }_{kjq}\right)\\ =P\left(\underset{w\in [0,1)}{\sup }{S}_k(w)\ge \frac{{\lambda }_{kjq}}{\sqrt{Mv(j)+q}}\right)\le P\left(\underset{w\in [0,1]}{\sup }{B}_k(w)\ge \frac{{\lambda }_{kjq}}{b_k\sqrt{Mv(j)+q}}\right)\\ \le 2P\left(N(0,1)\ge \frac{{\lambda }_{kjq}}{b_k\sqrt{Mv(j)+q}}\right)\le 2b_{kjq}\exp \left(-\frac{1}{2}{\left(\frac{{\lambda }_{kjq}}{b_k\sqrt{Mv(j)+q}}\right)}^2\right),\end{array}$$

where b_k is the standard deviation of S_k(1) and $b_{jkq}=b_k\sqrt{Mv(j)+q}/({\lambda }_{kjq}\sqrt{2\pi }),$ and B_k(·) is standard Brownian motion. Here we used standard properties of Brownian motion. The second to last inequality is given in for example [16, equation 6, page 33], and the last inequality follows from Mills’ ratio [see 3, Equation (10)]. Note that b_kjq ≤ d all j ∈ ℕ, for some d > 0 and all M > 3. It follows that (40) is bounded above by

$${\displaystyle \sum _{q=0}^{\infty }d\exp \left(-\frac{1}{2}{\left(\frac{{\lambda }_{kjq}}{b_k\sqrt{Mv(j)+q}}\right)}^2\right)\approx {\displaystyle \sum _{q=0}^{\infty }d\exp \left(-\frac{1}{2}\frac{{(Mv(j)+q)}^3}{b_k^2}\right),}}$$

which in turn is bounded above by d₁ exp(−d₂(Mu(j))³), for some constants d₁ and d₂, using (a + b)³ ≥ a³ + b³ for a, b ≥ 0.

Proof of Lemma 2.12

This proof is completely analogous to the proof of Lemma 4.14 of [8], upon replacing F̂_nk(u) by F^_k(u), F_0k(u) by F̄_0k(u), dG(u) by du, S_nk(·) by S_k(·), τ_nkj by τ_kj, s_njM by s_jM, and A_njM by A_jM. The only difference is that the second term on the right side of [8, equation (69)] vanishes, since this term comes from the remainder term R_nk(s,t), and we do not have such a remainder term in the limiting characterization given in Proposition 3.2.