Experimental Validation of a Theoretical Model of Cytokine Capture Using a Hemoadsorption Device

Abstract

Sepsis, a systemic inflammatory response in the presence of an infection, is characterized by overproduction of inflammatory mediators called cytokines. Removal of these cytokines using an extracorporeal hemoadsorption device is a potential therapy for sepsis. We are developing a cytokine adsorption device (CAD) filled with microporous polymer beads and have previously published a mathematical model which predicts the time course of cytokine removal by the device. The goal of this study was to show that the model can experimentally predict the rate of cytokine capture associated with key design and operational parameters of the CAD. We spiked IL-6, IL-10, and TNF into horse serum and perfused it through an appropriately scaled-down CAD and measured the change in concentration of the cytokines over time. These data were fit to the mathematical model to determine a single model parameter, Γ_i, which is only a function of the cytokine-polymer interaction and the cytokine effective diffusion coefficient in the porous matrix. We compared Γ_i values, which by definition should not change between experiments. Our results indicate that the Γ_i value for a specific cytokine was statistically independent of all other parameters in the model, including initial cytokine concentration, flow rate, serum reservoir volume, CAD size, and bead size. Our results also indicate that competitive adsorption of cytokines and other middle-molecular weight proteins, which is neglected in the model, does not affect the rate of removal of a given cytokine. The model of cytokine capture in the CAD developed in this study will be integrated with a systems model of sepsis to simulate the progression of sepsis in humans and to develop a therapeutic CAD design and intervention protocol that improves patient outcomes in sepsis.

INTRODUCTION

Severe sepsis is an acute inflammatory reaction which arises due to the host response to infection¹, resulting in systemic inflammation and organ failure. Up to 750,000 patients are affected annually in the US alone, and over one-third die as a result². Sepsis is characterized by the redundant release of multiple inflammatory mediators including cytokines into the bloodstream^{3, 4}. Increased expression of pro-inflammatory cytokines such as tumor necrosis factor (TNF) and interleukin-6 (IL-6) and anti-inflammatory cytokines such as interleukin-10 (IL-10) in the circulation is strongly associated with death⁵.

Although several drug therapies have been developed for the treatment of sepsis via blockage of one or more mediators, they have been ineffective because they cannot attenuate the entire response^6-8. One possible solution that would non-selectively lower the concentration of circulating cytokines is hemofiltration. Hemofiltration, the removal of plasma solutes after convective filtration from whole blood in hollow fibers, has been shown to lower cytokine concentrations in septic patients^{9, 10}. Much of the success of using hemofiltration, however, can be attributed to solute adsorption on to the hollow fiber membranes¹¹, and therefore new techniques focus on hemoadsorption in addition to filtration.

We are developing a hemoadsorption device consisting of polymer beads packed in a column through which whole blood is directly perfused. This device has been effective in removing TNF, IL-6, and IL-10, and other middle-molecular weight proteins in both in vitro and ex vivo studies^{12, 13}. We have also developed a mathematical model¹⁴ which uses a simple analytic expression to predict the removal rate of cytokines by the hemoadsorption device. The rate of removal depends on one unknown parameter, ${\Gamma }_i\equiv K_i{q}_i^{\max }{D}_i$, where K and $q_i^{max}$ are the affinity and capacity of the polymer surface for the cytokine in question, respectively, and D_i is the effective diffusion coefficient of the cytokine in the pore structure.

The model we have developed, once validated, will enable us to perform simulations of various experimental scenarios. Eventually this model will be combined with a systems model of sepsis in human patients to evaluate the efficacy of the CAD for various cytokine expression profiles. This method of device design will enable us to develop the most efficient device both quickly and without using costly resources such as cytokines and assay kits. In this paper, we experimentally test the validity of our theoretical model of cytokine capture. As part of our validation, we also justify two key assumptions of the model: 1) that the single parameter gamma is independent of the concentration of the cytokine being captured, and 2) that other adsorbing species do not affect capture of a given cytokine. Our results indicate that the theoretical model predicts cytokine removal well in our hemoadsorption device.

THEORETICAL MODEL

We have previously developed a simple mathematical model¹⁴ which uses the following analytic expression to predict the concentration C_i of an individual cytokine i over time, t:

$$-\frac{d{C}_i}{dt}=\frac{Q}{V_r}\left[1-\exp \frac{-3}{\sqrt{\pi }}\frac{m_b}{Q}\frac{1}{R}\sqrt{\frac{{\Gamma }_i}{\rho t}}\right]C_i\left(t\right)$$ (1)

where Q is the volumetric flow rate, V_r is the blood or serum reservoir volume, m_b is the mass of beads in the column, R is the radius of beads in the column, and ρ is the density of the polymer. The only unknown parameter in the model is Γ_i which is specific to cytokine i and its interaction with the bead pore and outer surfaces. By definition,

$${\Gamma }_i\equiv D_i{q}_i^{\max }{K}_i$$ (2)

where D_i represents the diffusion coefficient of cytokine i within the beads, $q_i^{max}$ is the maximum capacity of cytokine i per unit mass of each bead, and K_i is the affinity constant from the Langmuir equilibrium adsorption isotherm. In the experiments described below, we measure Γ_i for IL-6, IL-10, and TNF and test that its value is independent of all other experimental parameters.

MATERIALS AND METHODS

The cytokine adsorption device (CAD) consists of a cartridge filled with porous polymer beads. The beads are made up of a polystyrene divinylbenzene (PSDVB) copolymer and covered in a biocompatible polyvinylpyrrolidone (PVP) coating.

General in vitro recirculation experiments

For each recirculation experiment, an unused CAD was packed with fresh polymer and connected in line with a peristaltic pump (Figure 1). The inlet and outlet tubing ports were connected to a reservoir containing 8ml of horse serum or phosphate buffered saline (PBS) spiked with one or more adsorbable proteins. The reservoir fluid was pumped through the CAD at a set flow rate and samples were taken from the reservoir at times t=0, 15, 30, 60, 90, 120, 180, and 240min. Samples were stored at −70°C for subsequent assay using enzyme-linked immunosorbent assay (ELISA). Concentrations of IL-6, IL-10, and TNF were determined using BioSource ELISA kits (Invitrogen, USA) according to the instructions of the manufacturer. The concentration of β₂-microglobulin was measured using a Quantikine IVD ELISA kit (R&D Systems, USA), also according to the instructions of the manufacturer.

Figure 1.

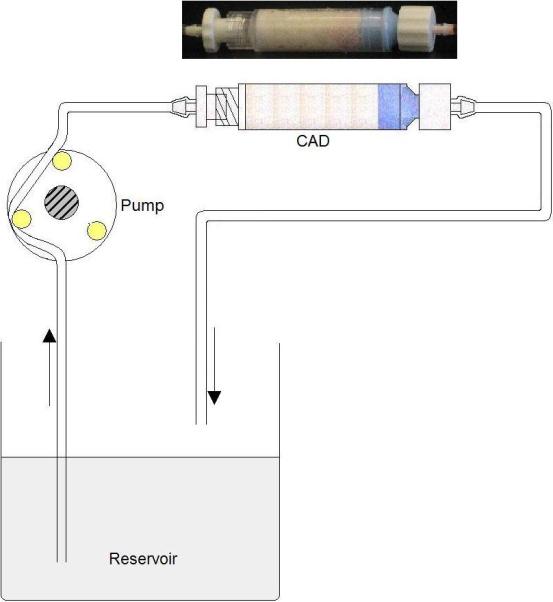
Recirculation loop used to test cytokine removal from cytokine-spiked serum flowing through the CAD.

Experimental validation of theoretical model

Three trials of each model validation experiment described below were performed, and all experimental parameters were set at the baseline values shown in Table 1 unless otherwise specified.

Table 1.

Description of baseline parameters and their values.

Parameter name	Description	Baseline value
C0	Initial concentration of cytokine, pg/ml	1000
Q	Volumetric flow rate, ml/min	0.8
R	Average bead radius, μm	289.1
mb	Mass of beads in cartridge, g	1.5
Vr	Reservoir volume, ml	8.0

In the first set of experiments, we wanted to test whether the model was able to predict changes in cytokine capture rate associated with changes in the model parameters (Eq. 1), including the initial cytokine concentration in the reservoir, perfusion rate through the cartridge, bead mass in the cartridge, and bead size. To test the effect of initial cytokine concentration, we performed experiments of IL-6 removal using a serum reservoir spiked with either 1000pg/ml or 5000pg/ml, with all other parameters at their baseline values as indicated by Table 1. Typically, cytokine concentrations in septic patients do not exceed 5000 pg/ml. We tested the effect of changes in flow rate by perfusing serum spiked with IL-6 at a flow rate of 0.8ml/min or 0.08ml/min while keeping all other parameters at their baseline values. We chose to validate the model for a flow rate below the baseline value as opposed to above it because capture of IL-6 falls into an intermediate regime between perfusion and diffusion-limited capture. Capture is more dependent on flow rate at lower perfusion rates whereas at high flow rates, capture becomes entirely diffusion limited and independent of flow rate.

To test the effect of increasing bead mass in the CAD, we measured capture of IL-6 from serum using devices containing either 1.5g or 10g of beads. In the case of the 10g device, a reservoir volume of 80ml and a flow rate of 8.0ml/min were used in order to accommodate the larger device. Smaller beads were tested because of the advantage they offer due to their greatly increased surface area and the likelihood that such beads would be included in the final device design. We tested the effect of changes to bead size by performing capture of IL-6 using 289.1μm radius beads and 58.4μm radius beads in the CADs. All other parameters remained at their baseline values.

In the second series of experiments, we tested whether competitive binding effects arise due to the presence of multiple adsorbing species, including other cytokines and middle-molecular weight molecules that can diffuse into the porous beads. β2-microglobulin (β2-m) was chosen as the additional adsorbing species because it is the most abundant middle-molecular weight protein in blood that adsorbs onto the CytoSorb beads. We examined whether the presence of β2-m affected the capture rate of IL-6. We performed recirculation experiments using IL-6 alone or with an additional 1.5μg/ml β2-m spiked into a solution of PBS and 50mg/ml bovine serum albumin (BSA) with all other parameters at baseline. To directly examine interaction effects between key cytokines of interest, we performed simultaneous IL-6, IL-10, and TNF capture from serum with all parameters at their baseline values.

Model fitting and statistical analysis

The concentrations of TNF, IL-6, and IL-10 over time were normalized to the initial concentration of each cytokine. This data was fit to the model by integrating Eq. 1 using Matlab so that the change in the reservoir volume due to sampling could be incorporated. The integration was subject to the constraint that at t=0 normalized concentration is 1. The integrated value of C_i(t) was then fit to the experimental data. The value of Γ_i found to most closely model cytokine removal for each set of data was obtained via nonlinear regression using Matlab. 95% confidence intervals for both Γ_i and initial concentration were determined along with the R² value for each fit. The average Γ_i value was calculated for each set (n=3) of experiments and compared using a student's t-test.

RESULTS

Varying model parameters

Figure 2 compares IL-6 capture experiments using a serum reservoir spiked with either 1000 or 5000 pg/ml. The average Γ_IL–6 values obtained over three trials were 1.05e-4±2.34e-5 and 1.17e-4±3.58e-5 cm²·ml·min⁻¹·g⁻¹ for the low and high concentrations, respectively. There was no significant difference between the average Γ_IL–6 values (p=0.63).

Figure 2.

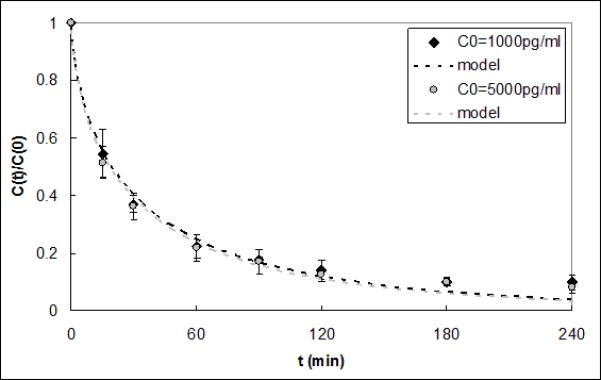
IL-6 capture data and respective model fits for initial concentrations of 1000pg/ml and 5000pg/ml. The model Γ_IL-6 fits were 1.05e-4 and 1.17e-4 cm²·ml·min⁻¹·g⁻¹ and were not statistically different (p=0.63).

Figure 3 shows the results of IL-6 capture from serum perfused through the CAD at 0.8ml/min or 0.08ml/min. Γ_IL–6 for the lower flow rate was 1.77e-4±1.62e-4 cm²·ml·min⁻¹·g⁻¹ and was not significantly different from that for the baseline flow rate (1.05e-4±2.34e-5 cm²·ml·min⁻¹·g⁻¹, p=0.49).

Figure 3.

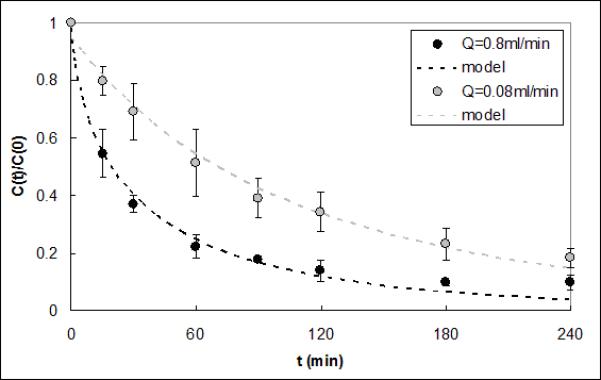
IL-6 capture data and respective model fits for serum flow rates of 0.8ml/min and 0.08ml/min. The model Γ_IL-6 fits were 1.05e-4 and 1.77e-4 cm²·ml·min⁻¹·g⁻¹ and were not statistically different (p=0.49).

Figure 4 shows IL-6 capture data from serum obtained using a CAD containing either 1.5g or 10g of beads. Reservoir volume and flow rate were increased proportionally to the increase in bead mass, just as they would be for a full scale-up of the device for use in a clinical setting. The average Γ_IL–6 for the larger device was 7.14e-5±4.28e-5 cm²·ml·min⁻¹·g⁻¹, which is not statistically different compared to the value for the smaller device (1.05e-4±2.34e-5 cm²·ml·min⁻¹·g⁻¹, p=0.39). Capture of IL-6 from serum in CADs packed with either 289.1μm or 58.4μm radius CytoSorb beads is shown in Figure 5. The average Γ_IL–6 value was 8.14e-5±5.78e-5 cm²·ml·min⁻¹·g⁻¹ for the devices packed with the smaller beads; this value was not significantly different from that obtained with the larger beads (1.05e-4±2.34e-5 cm²·ml·min⁻¹·g⁻¹, p=0.56).

Figure 4.

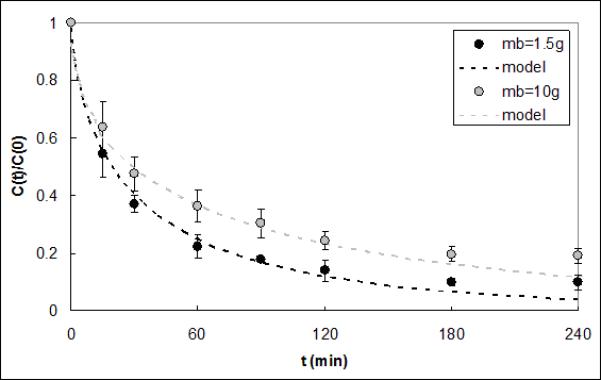
IL-6 capture data and respective model fits for CADs containing 1.5g and 10g of polymer beads. The model Γ_IL-6 fits were 1.05e-4 and 7.15e-5 cm²·ml·min⁻¹·g⁻¹ and were not statistically different (p=0.39).

Figure 5.

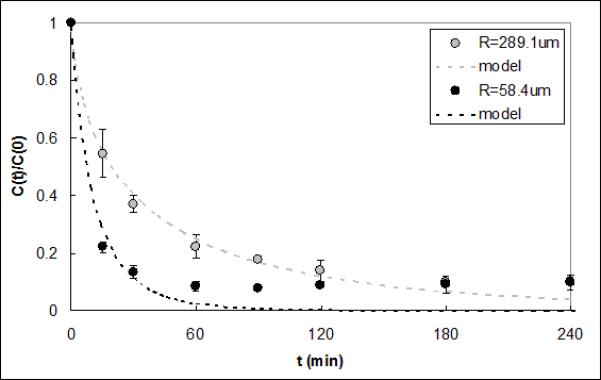
IL-6 capture data and respective model fits for CADs containing 289.1μm and 58.4μm radius polymer beads. The model Γ_IL-6 fits were 1.05e-4 and 8.14e-5 cm²·ml·min⁻¹·g⁻¹ and were not statistically different (p=0.56).

Competitive adsorption effects

In Figure 6 capture results are shown for IL-6 in a solution of PBS (pH 7.4) and BSA alone or with 1.5μg/ml β2-m. No statistical difference was found between the average Γ_IL–6 values of 9.59e-5±2.11e-5 and 8.75e-5±5.84e-6 cm²·ml·min⁻¹·g⁻¹ for the experiments with and without β2-m, respectively (p=0.29). Figure 6 also shows that despite its relative abundance in the reservoir, β2-m was rapidly removed by the CAD. Cytokine capture experiments were done using serum spiked with TNF, IL-10, and IL-6 alone or in combination (Figure 7). The average Γ_i values for each cytokine in the multicomponent solution were statistically the same as those of the corresponding cytokine alone in solution. These Γ_i values are shown in Table 2, along with the Γ_i values calculated from all of the model validation experiments in this study. P values for the comparison of Γ_i in single-cytokine and three-cytokine solution for IL-6, IL-10, and TNF were 0.99, 0.15, and 0.99, respectively.

Figure 6.

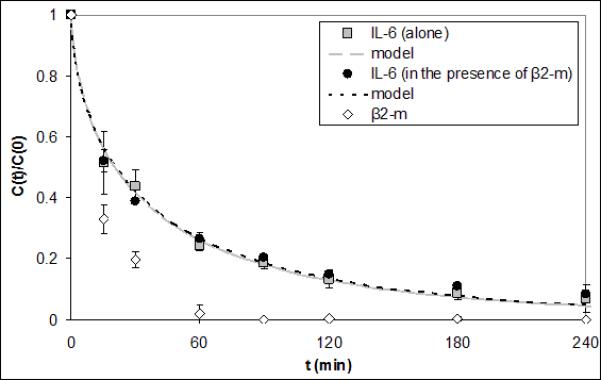
IL-6 capture data and respective model fits for PBS/BSA reservoirs with or without an additional spike of 1.5μg/ml β2-m. The model Γ_IL-6 fits were 9.59e-5 and 8.75e-5 cm²·ml·min⁻¹·g⁻¹ and were not statistically different (p=0.29). β2-m capture data is also shown.

Figure 7.

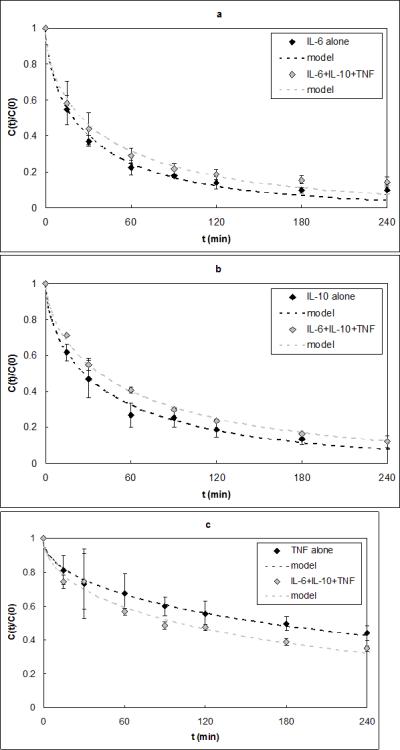
a) IL-6 capture data alone and in a three-cytokine solution. The model Γ_IL-6 fits were 1.05e-4 and 6.22e-5 cm²·ml·min⁻¹·g⁻¹ and were not statistically different (p=0.99). b) IL-10 capture data alone and in a three-cytokine solution. The model Γ_IL-10 fits were 6.66e-5 and 3.69e-5 cm²·ml·min⁻¹·g⁻¹ and were not statistically different (p=0.15). c) TNF capture data alone and in a three-cytokine solution. The model Γ_TNF fits were 5.85e-6 and 9.05e-6 cm²·ml·min⁻¹·g⁻¹ and were not statistically different (p=0.99).

Table 2.

Γ_i values for baseline and validation experiments.

	Baseline, 1 cytokine	Baseline, 3 cytokines	C0=5000 pg/ml	Q=0.08 ml/min	mb=10g	R=58.4 μm	IL-6 in PBS/BSA	IL-6+β2-m in PBS/BSA
ΓIL-6	1.05E-4±2.34E-5	6.22E-5±1.92E-5	1.17E-4±3.58E-5	1.77E-4±1.62E-4	7.14E-5±4.28E-5	8.14E-5±5.78E-5	9.59E-5±2.11E-5	8.75E-5±5.84E-6
ΓIL-10	6.66E-5±2.27E-5	3.69E-5±2.04E-6	----	----	----	----	----	----
ΓTNF	5.85E-6±1.22E-6	9.05E-6±4.71E-7	----	----	----	----	----	----

DISCUSSION

Sepsis is a complex disease characterized by overproduction of cytokines. Cytokine removal using hemoadsorption has demonstrated in animal models some potential as a treatment for sepsis^{13, 15}. We are developing a cytokine adsorption device (CAD) based on direct blood perfusion through a cartridge containing novel biocompatible, highly adsorbent polymer beads. We previously developed a theoretical model that can be used to predict the time course of removal of cytokines from extracorporeal circulation through the CAD. The primary goal of this study was to demonstrate experimentally that the model can predict the rate of cytokine capture associated with key design variables of the CAD. These include initial cytokine concentration, perfusion rate through the CAD, and the size of the CAD and of its adsorbing beads. Our experiments indicate that over a clinically relevant range of these parameters the single unknown model parameter (Γ_i), which accounts for the specific interaction of a particular cytokine i with the adsorbent beads, is statistically unaffected by changes in these parameters. The second goal of this study was to demonstrate experimentally that competitive adsorption of solutes, which is neglected in the model, does not affect the rate of removal of a given cytokine. The results indeed indicate that the presence of either multiple cytokines or relatively high concentrations of β2-m had no effect on the capture rate of cytokines.

The development of our simple model of cytokine capture in the CAD was based on a perturbation analysis in which the effects of competitive adsorption of other solutes on cytokine adsorption were predicted to be secondary. We addressed this experimentally in several different ways. First, we compared the removal rates of IL-6, IL-10, and TNF spiked individually into serum to their respective removal rates when spiked collectively into serum. Γ_i values for each of the three cytokines alone in solution were determined to be statistically the same as Γ_i values for each cytokine in the multiple cytokine solution. Cytokine levels, however, are relatively small (~1000pg/ml) compared to other middle-molecular weight proteins that can be adsorbed within the beads of the CAD. Accordingly, we also investigated whether the removal rate of cytokines could be affected by the presence of β2-microglobulin (β2-m), which is among the most abundant middle-molecular weight proteins (~1.5μg/ml)¹⁶. We compared removal rate of IL-6 spiked individually into a solution of PBS and BSA to its removal rate spiked together with 1.5μg/ml β2-m into the same solution. The Γ_IL-6 values in the two solutions were statistically the same. Finally, we can also compare the Γ_IL-6 value for IL-6 spiked in PBS/BSA solution with that for IL-6 spiked in serum, which would specifically account for possible effects of all other serum proteins. Γ_IL-6 for capture of IL-6 from PBS and BSA was, which was not significantly different from that in serum (9.59e-5 cm²·ml·min⁻¹·g⁻¹ vs. 1.05e-4 cm²·ml·min⁻¹·g⁻¹, respectively, see Table 1).

We chose to validate our mathematical model by fitting values of the cytokine-specific parameter Γ_i to removal rate data and comparing those fit values for changes to other parameters in the model, as discussed above. A more fundamental way to validate the model would be to measure independently the parameters comprising Γ_i, which include D_i, the effective cytokine diffusion coefficient within the beads, and K_i and $q_i^{\max }$, the Langmuir adsorption isotherm parameters. Measurement of these parameters, however, is neither feasible nor practical. Effective diffusion coefficients in polymer matrices are typically measured in a diffusion chamber apparatus in which a cast polymer film separates a solute-containing chamber from an initially solute-free chamber. Our hemoadsorption polymer cannot be cast into films while maintaining the same pore morphology as in bead form. Advanced microscopy techniques based on visualizing diffusion of labeled proteins directly within individual beads^{17, 18} do not provide D_i independent of the Langmuir adsorption parameters. Obtaining the Langmuir adsorption isotherm in order to determine K_i and $q_i^{\max }$ is not feasible because the amount of cytokine required to reach equilibrium within a measurable amount of bead material is prohibitive.

The model and the experiments did deviate at later time points for the 58.4μm radius beads but not for the 289.1μm radius beads. The deviation occurred only after 90% of IL-6 was removed, and the Γ_IL-6 values were statistically the same for both the large and small beads. This discrepancy may be due to diffusion hindrance caused by partial blocking of the bead pores by cytokines which have already adsorbed. If so, the model could use a variable diffusion coefficient that decreases in proportion to the mass of adsorbed cytokine. Several models for a diffusion coefficient decreasing as a function of adsorbed species already exist^{19, 20}. While unlikely to be critical for future applications of the model, studies could be done to incorporate and validate a variable diffusivity.

Our cytokine adsorption device contains a biocompatible polymer and is designed for direct whole blood perfusion. We validated our model using human cytokines spiked into horse serum instead of blood. Our model was developed only to predict the removal rate of cytokines from the plasma phase of blood. Other complexities associated with cytokine release and other interactions with cellular components of blood are incorporated in a systems model of cytokine dynamics in sepsis being developed by our colleagues²¹. Once validated, our model does apply to blood flow through the CAD provided the flow rate and volume parameters in the model (Eq. 1) are those associated with plasma flow and plasma volume. We are currently evaluating this by performing cytokine capture experiments using red blood cells suspended in a PBS/BSA solution spiked with cytokines. Horse serum was used rather than human serum to avoid the interactions between cytokines and their soluble receptors, which are also accounted for in the systems model of sepsis. The model of cytokine capture in the CAD developed here will be integrated with the systems model of sepsis to simulate the progression of sepsis in humans and to develop a therapeutic CAD intervention protocol that improves patient outcomes in sepsis.