Buffer Standards for the Biochemical pH of 3-(N-morpholino)-2-hydroxypropanesulfonic Acid from (278.15 to 328.15) K

Abstract

The values of the second dissociation constant pK₂ and related thermodynamic quantities of the ampholyte 3-(N-morpholino)-2-hydroxypropanesulfonic acid (MOPSO) have been previously determined at temperatures from (278.15 to 328.15) K. In this study, the pH values of two buffer solutions without NaCl and three buffer solutions with NaCl having ionic strengths (I = 0.16 mol·kg⁻¹) similar to those in blood plasma, have been evaluated at 12 temperatures from (278.15 to 328.15) K using an extended form of the Debye-Hückel equation, since the Bates-Guggenheim convention is valid up to I = 0.1 mol·kg⁻¹. The liquid junction potentials (E_j) between the buffer solutions of MOPSO and saturated KCl solution of the calomel electrode at (298.15 and 310.15) K have been estimated by measurement with a flowing junction cell. These values of E_j have been used to ascertain the operational pH values at (298.15 and 310.15) K. Three buffer solutions of MOPSO are recommended as useful reference solutions for pH measurements in saline media of ionic strength I = 0.16 mol·kg⁻¹.

Introduction

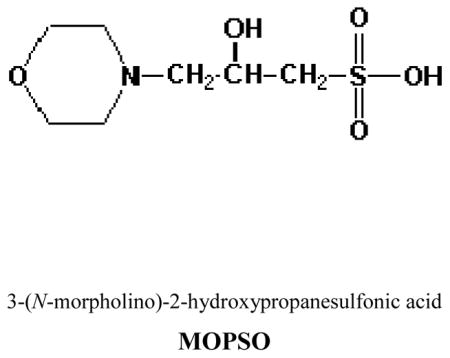
The buffer substances recommended by Good et al.^1,2 have proven very useful for the measurement of the pH of blood and the control of pH in the region close to that of physiological solutions. Very recently, we have reported the pH values of 3-[(1, 1-dimethyl-2-hydroxymethyl)amino]-2-hydroxypropanesulfonic acid (AMPSO)³ at temperatures from (278.15 to 328.15) K including 310.15 K. The zwitterionic buffer N-[tris(hydroxymethyl)methyl-3-amino]propanesulfonic acid (TAPS)⁴ has also been recommended for use as a physiological buffer at (298.15 and 310.15) K. In the present investigation, we are interested in providing reliable pH values for the ampholyte 3-(N-morpholino)-2-hydroxypropanesulfonic acid, (MOPSO), which has the structure as follows:

Bates and his associates⁵ reported pH values of N-tris(hydroxymethyl)methyl-2-aminoethanesulfonic acid (TES) at (298.15 and 310.15) K. These buffer solutions are recommended as standard buffers for pH measurements.

For the highest reproducibility and accuracy, the glass electrode pH meter assembly at a point close to the pH of blood (7.407) can be obtained within the framework of the National Institute of Standards and Technology (NIST/NBS) by using physiological phosphate pH buffer as a primary standard.⁶ The pH of this physiological phosphate buffer standard is 7.415 at 298.15 K and 7.395 at 310.15 K, and has been internationally used for standardization at or close to the pH of the clinical sample.

Various attempts to establish a suitable primary reference standard at an isotonic saline solution, I = 0.16 mol·kg⁻¹ and near the pH of blood plasma have been met with difficulty. The commonly accepted physiological phosphate standard solutions are mixtures of KH₂PO₄ (0.008695 mol·kg⁻¹) and Na₂HPO4 (0.03043 mol·kg-1). The problems associated with the use of the physiological phosphate solutions are: (i) phosphates interact unfavorably with biological media, (ii) phosphate precipitates with blood ingredients (Mg²⁺ and Ca²⁺), and (iii) the temperature coefficient of blood is (−0.015 pH unit/K) as compared to 1:3.5 phosphate standard (−0.0028 pH unit/K).⁷ The compound MOPSO is not expected to have any undesirable side effects (no precipitation with Ca²⁺ and Mg²⁺), but the possibility of complex formation with cations such as Ca²⁺ and Mg²⁺ exists. We have attempted to minimize it with high concentration of sodium chloride-buffer ratio for an isotonic saline solution of I = 0.16 mol·kg⁻¹.

Good and his associates^1,2 introduced a series of new hydrogen ion buffers for use in the physiological pH range. The authors took the liberty of citing some published works by various investigators for structurally related zwitterionic buffer compounds with a view to comparing the effects of substituents on pK₂ and pH values. Wu and coworkers⁸ have published the values of pK₂ and pH of the zwitterionic buffer N-(2-hydroxyethyl)piperazine-N-2-ethanesulfonic acid (HEPES), and a second zwitterionic buffer, 3-(N-morpholino)-2-hydroxypropanesulfonic acid (MOPSO).⁹ Roy et al.¹⁰ reported results for pK₂ and pH for 3-(N-morpholino)propanesulfonic acid (MOPS) and 4-N-(morpholino)butanesulfonic acid (MOBS).¹¹ The pH of these solutions closely match that of the common biological media. In 1973, Bates et al.¹² suggested the use of tris(hydroxymethyl)methylglycine (TRICINE) as a secondary buffer standard for the physiological range of pH 7.2 to 8.5. The pH of 0.06 m TRICINE + 0.02 m sodium TRICINEate buffer solution at 310.15 K is 7.407, matching exactly the pH of blood. Goldberg et al.,¹³ in their excellent review article of the thermodynamic quantities of the biological buffers, indicated that the results for pK₂ are available in the literature for MOPSO. To the authors’ knowledge, no reliable pH values of MOPSO for the buffer compositions under study have been reported.

In order to provide accurate and reproducible pH values for physiological pH standards, we have studied the buffer compound, MOPSO, with the following compositions on the scale of molality (m), where m = mol·kg⁻¹, and I is the ionic strength in the unit of mol·kg⁻¹:

1. MOPSO (0.02 mol·kg⁻¹) + NaMOPSO (0.06 mol·kg⁻¹), I = 0.06 mol·kg⁻¹

2. MOPSO (0.02 mol·kg⁻¹) + NaMOPSO (0.04 mol·kg⁻¹), I = 0.04 mol·kg⁻¹

3. MOPSO (0.01 mol·kg⁻¹) + NaMOPSO (0.03 mol·kg⁻¹) + NaCl (0.13 mol·kg⁻¹), I = 0.16 mol·kg⁻¹

4. MOPSO (0.02 mol·kg⁻¹) + NaMOPSO (0.06 mol·kg⁻¹) + NaCl (0.10 mol·kg⁻¹), I = 0.16 mol·kg⁻¹

5. MOPSO (0.04 mol·kg⁻¹) + NaMOPSO (0.04 mol·kg⁻¹) + NaCl (0.12 mol·kg⁻¹), I = 0.16 mol·kg⁻¹

The detailed procedure for the preparation of these buffer solutions for MOPSO is described in the following section.

Experimental

MOPSO was purchased from the Sigma Chemical Co. (St. Louis, Missouri). The purification procedure (using further crystallization) and the assay have been reported in a previous paper.⁵ The assay showed that the MOPSO buffer used was (99.91 to 99.97) % pure. All buffer solutions were prepared by massing the MOPSO, NaCl (ACS reagent grade), a standard solution of NaOH for the preparation of NaMOPSO, and calculated amounts of CO₂- free doubly distilled water. Buoyancy corrections were made for all masses used to prepare solutions.

The cell design, the preparation procedure of the hydrogen electrodes using chloroplatinic acid, the silver-silver chloride thermal, electrolytic electrodes,¹⁴ hydrogen gas purification, and preparation of the solutions have been described previously.^3,10 Details about the control of temperature (within ± 0.005 K)³ using a digital platinum resistance thermometer (Guildline Model 9540), a digital voltmeter (Hewlett-Packard 2000 multimeter), and other experimental procedures, will also be found elsewhere.³

Methods and Results

The values of cell potential for the calculations of pH are given in Tables 1 and 2 for cell (A) containing 2 buffer solutions lacking NaCl, and 3 buffer solutions in which NaCl had been added to make I = 0.16 mol·kg⁻¹, respectively. These values have been corrected to a hydrogen pressure of 101.325 kPa. At 298.15 K, cell potential values are the average of at least 2 readings at the beginning, the middle, and sometimes at the end of the temperature sequence. Duplicate cells usually gave readings on the average within 0.04 mV in the temperature range (278.15 to 328.15) K.

Table 1.

Cell Potential of Cell A (in Volts): Pt(s); H₂ (g), 101.325 kPa | MOPSO (m₁), NaMOPSO (m₂), NaCl (m₃) | AgCl(s), Ag(s)

mol·kg−1			T/K
m1	m2	m3	278.15	283.15	288.15	293.15	298.15	303.15	308.15	310.15	313.15	318.15	323.15	328.15
0.02	0.06	0.005	0.78522	0.78765	0.79014	0.79235	0.79454	0.79663	0.79830	0.79933	0.80035	0.80232	0.80380	0.80535
0.02	0.06	0.010	0.76992	0.77207	0.77410	0.77617	0.77823	0.78003	0.78121	0.78229	0.78327	0.78461	0.78576	0.78689
0.02	0.06	0.015	0.76144	0.76351	0.76535	0.76706	0.76951	0.77114	0.77179	0.77318	0.77395	0.77514	0.77614	0.77704
0.02	0.06	0.020	0.75575	0.75787	0.75966	0.76130	0.76347	0.76500	0.76522	0.76684	0.76750	0.76854	0.76941	0.77017
0.02	0.04	0.005	0.77350	0.77583	0.77798	0.78017	0.78180	0.78395	0.78552	0.78626	0.78709	0.78859	0.78954	0.79070
0.02	0.04	0.010	0.75766	0.75980	0.76168	0.76337	0.76456	0.76681	0.76821	0.76883	0.76953	0.77118	0.77149	0.77203
0.02	0.04	0.015	0.74873	0.75053	0.75232	0.75389	0.75495	0.75704	0.75830	0.75885	0.75946	0.76139	0.76116	0.76182
0.02	0.04	0.020	0.74283	0.74447	0.74609	0.74752	0.74821	0.75063	0.75175	0.75220	0.75274	0.75489	0.75422	0.75478

Table 2.

Cell Voltage of Cell A (in Volts): Pt(s); H₂ (g), 101.325 kPa | MOPSO (m₁), NaMOPSO (m₂), NaCl (m₃) | AgCl(s), Ag(s)

mol·kg−1			T/K
m1	m2	m3	278.15	283.15	288.15	293.15	298.15	303.15	308.15	310.15	313.15	318.15	323.15	328.15
0.01	0.03	0.13	0.71369	0.71524	0.71636	0.71726	0.71798	0.71858	0.71905	0.71918	0.71932	0.71944	0.71945	0.71934
0.02	0.06	0.10	0.71951	0.72100	0.72226	0.72333	0.72429	0.72504	0.72568	0.72592	0.72616	0.72651	0.72666	0.72680
0.04	0.04	0.12	0.74072	0.74249	0.74407	0.74558	0.74704	0.74812	0.74920	0.74955	0.75007	0.75078	0.75132	0.75171

The pH of MOPSO Buffer

The conventional standard pH values have been evaluated by the method of Bates et al. ^{3, 9–10, 15–17} for 5 standard buffer solutions, stated in the introduction section, (a to e). For accurate calculations of the second dissociation constants, pK₂; and pH values of the 5 buffer solutions, the following cell (A) is used for the collection of cell potential data

$$\text{Pt}(\text{s}),{\text{H}}_2(\text{g}),101.325\text{kPa})\mid \text{MOPSO}(m_1)+\text{NaMOPSO}(m_2)+\text{NaCl}(m_3)\mid \text{AgCl}(\text{s}),\text{Ag}(\text{s})$$ (A)

where m₁, m₂, and m₃ indicate molalities of the respective species, and 1 atm = 101.325 kPa in SI units. The cell (A) is known as the Harned-type cell.

The flowing junction cell (B), was used for the evaluation of the liquid junction potential at the contact between the buffer solution and the heavier saturated KCl solution shown with a double vertical line.

$$\begin{array}{l}\text{Pt}(\text{s}),{\text{H}}_2(\text{g}),101.325\text{kPa}\mid \text{MOPSO}(m_1)+\text{NaMOPSO}(m_2),\text{NaCl}(m_3)\mid \mid \text{KCl}(\text{satd}),\\ \mid {\text{Hg}}_2{\text{Cl}}_{\text{2}}\text{(s)},\text{Hg}(\text{l})\end{array}$$ (B)

where the abbreviations (s), (l), and (g) denote solid, liquid, and gaseous state, respectively. In routine laboratory measurements, the hydrogen electrode is commonly replaced by a glass electrode. For the cell (B), the values of the standard electrode potential, $E_{\mathit{SCE}}^{\circ }$, of the saturated calomel electrode were taken as: −0.2415 V, and −0.2335 V at (298.15 and 310.15) K, respectively. These values are periodically rechecked with experiments.

For cell (C), the phosphate salts were NIST standard reference materials with the composition [KH₂PO₄ (0.008695 mol·kg⁻¹) + Na₂HPO₄ (0.03043 mol·kg⁻¹)] and its solutions are recommended for pH measurements in physiological solutions.

$$\text{Pt}(\text{s});{\text{H}}_2(\text{g}),101.325\text{kPa}\mid \text{phosphate}\text{buffer}\mid \mid \text{KCl}(\text{satd})\mid {\text{Hg}}_2{\text{Cl}}_2(\text{s}),\text{Hg}(\text{l})$$ (C)

It should be emphasized that the difference in values between the liquid junction potential when one solution (the pH standard) is replaced by another (the unknown) is important. The values of the liquid junction potential, E_j, for the physiological phosphate solutions and other buffer solutions of MOPSO from cell (B) were obtained^8,10 using the flowing junction cell. The equation for the calculation of E_j¹⁰ is

$$E_{\text{j}}=E+E_{\mathit{SCE}}^{\circ }-k\text{pH}$$ (1)

where $E_{\mathit{SCE}}^{\circ }=-0.2415\text{V}$, k = 0.059156, and pH = 7.415 (physiological phosphate buffer solution) at 298.15 K; $E_{\mathit{SCE}}^{\circ }=-0.2335$, k = 0.061538, and pH = 7.395 at 310.15 K. The operational definition of pH, designated as pH(x), is

$$\text{pH}(\text{x})=\text{pH}(\text{s})+\frac{E_x-E_s-\delta E_j}{k}$$ (2)

where “x” refers to the unknown buffer MOPSO + NaMOPSO; “s” is the reference solution (NBS/NIST physiological phosphate buffer) of known pH, and δE_j = E_j(s) − E_j(x). If δE_j = 0, then eq 3 takes the form

$$\text{pH}(\text{x})=\text{pH}(\text{s})+\frac{E_x-E_s}{k}$$ (3)

It is important to mention that eq 3 is more common, as δE_j (the difference) is all that is needed, not E_j in mV.

In order to calculate pH(s) values for all 5 buffer solutions, calculations for the acidity function p(a_Hγ_Cl) values were made in the temperature range (278.15 to 328.15) K, from the cell potential (E) listed in Tables 1 and 2, the molality of the chloride ion, and E°, the standard potential of the silver-silver chloride electrode.³ The Nernst equation^12,14,17 for cell (A) is given by:

$$p(a_H{\gamma }_{Cl})=\frac{E-E^{\circ }}{k}+{log}_{10}{m}_{Cl}$$ (4)

where k is the Nernst slope.

From the plot of the acidity function, p(a_Hγ_Cl), for each buffer solution against the molality of the chloride ion employing linear regression analysis, the intercept, p(a_Hγ_Cl)°, at m_Cl = 0 was obtained. These values of p(a_Hγ_Cl)° for 2 chloride-free buffer solutions listed above are given in Table 3. The uncertainty (mean deviation) introduced in this type of graphical extrapolation appeared to be slightly greater than 0.001 from the lines drawn. For 3 buffer solutions in the presence of NaCl (c to e), the values of p(a_Hγ_Cl) are entered in Table 4 from (278.15 to 328.15) K.

Table 3.

p(a_Hγ_Cl)^o of (MOPSO + NaMOPSO) Buffer Solutions from (278.15 to 328.15) K Obtained by Extrapolation for Chloride-Free Solutions ^a

T(K)	0.02 m MOPSO + 0.04 m NaMOPSO	0.02 m MOPSO + 0.06 m NaMOPSO
	I = 0.04 m	I = 0.06 m
278.15	7.455	7.662
283.15	7.374	7.575
288.15	7.293	7.496
293.15	7.219	7.420
298.15	7.142	7.344
303.15	7.073	7.275
308.15	7.002	7.208
310.15	6.978	7.181
313.15	6.937	7.142
318.15	6.868	7.084
323.15	6.807	7.022
328.15	6.743	6.964

^am = 1 mol·kg⁻¹

Table 4.

p(a_Hγ_Cl) of (MOPSO + NaMOPSO) Buffer Solutions from (278.15 to 328.15) K Computed Using Eqs 4–7

T(K)	0.01 m MOPSO + 0.03 m NaMOPSO + 0.13 m NaCl	0.02 m MOPSO + 0.06 m NaMOPSO + 0.10 m NaCl	0.04 m MOPSO + 0.12 m NaMOPSO + 0.04 m NaCl
	I = 0.16 ma	I = 0.16 ma	I = 0.16 ma
278.15	7.803	7.794	7.781
283.15	7.725	7.713	7.698
288.15	7.645	7.634	7.617
293.15	7.566	7.557	7.541
298.15	7.491	7.483	7.470
303.15	7.417	7.411	7.397
308.15	7.346	7.341	7.327
310.15	7.318	7.314	7.300
313.15	7.277	7.273	7.260
318.15	7.210	7.208	7.194
323.15	7.144	7.143	7.130
328.15	7.080	7.081	7.066

^am = 1 mol·kg⁻¹

Conventional pH(s) values determined from the cell potential of cells without liquid junction for the solution without the presence of the chloride ion were determined by the equation

$$\text{pH}(\text{s})=p{(a_{\text{H}}{\gamma }_{\text{Cl}})}^{\circ }+{log}_{10}{\gamma }_{Cl}^{\circ }$$ (5)

where the single-ion activity coefficient, ${\gamma }_{Cl}^{\circ }$, cannot be measured experimentally. The estimation of ${\gamma }_{Cl}^{\circ }$ for the calculation of pH(s) by eq 6 has been outlined before.¹⁰ The pH values obtained from the liquid junction cell are indicated by pH, whereas the “conventional” pH calculated from eq 6 is designated as pH(s). The “pH convention,” commonly known as Bates-Guggenheim convention,¹⁸ is expressed by the following equation

$$-{log}_{10}{\gamma }_{Cl}^{\circ }=\frac{A\sqrt{I}}{1+1.5\sqrt{I}}$$ (6)

The International Union of Pure and Applied Chemistry¹⁹ has recommended this convention. It has been assumed that eq 6 is valid up to I = 0.1 mol·kg⁻¹. For I > 0.1 mol·kg⁻¹, there is no widely accepted (agreed-upon) convention. Perhaps a linear dependent CI term from eq 7 along with a variation of the ion-size parameter as a function of temperature would provide a more logical choice when I > 0.1 mol·kg⁻¹.

Thus a “pH convention”^8,10 based on an extended Debye-Hückel equation⁸ has been assumed to be more logical when I > 0.1 mol·kg⁻¹ up to I = 1.0 mol·kg⁻¹ in the calculation of ${log}_{10}{\gamma }_{Cl}^{\circ }$ for all of the buffer-chloride solutions. The following equation is preferred:

$${log}_{10}{\gamma }_{Cl}^{\circ }=-\frac{A\sqrt{I}}{1+B{a}^{\circ }\sqrt{I}}+CI$$ (7)

where I is the ionic strength of the buffer solution, A and B are the Debye-Hückel constants, C is an adjustable parameter, Ba° was assumed to be 1.38 kg^½·mol^−½ for all the experimental temperatures, corresponding to an (ion-size parameter) a° of 4.2 Å.^{8, 10} The empirical equation given below for the calculation of the parameter C^8,10 was obtained from a curve-fitting method:

$$C=C_{298.15}+6.2\times {10}^{-4}(T-298.15)-8.7\times {10}^{-6}{(T-298.15)}^2$$ (8)

where C_298.15 = 0.032⁸ kg·mol⁻¹ at 298.15 K and T is the absolute temperature.

The values of pH(s), listed in Table 5 for two buffer solutions of MOPSO without NaCl were computed from eqs 4 – 8 and are represented by the following equations:

$$\begin{array}{l}\text{For}\text{MOPSO}(0.02\text{mol}·{\text{kg}}^{-1})+\text{NaMOPSO}(0.06\text{mol}·{\text{kg}}^{-1}):\\ \text{pH}(\text{s})=7.254-1.4578\times {10}^{-2}(T-298.15)+5.98\times {10}^{-5}{(T-298.15)}^2\end{array}$$ (9)

$$\begin{array}{l}\text{For}\text{MOPSO}(0.02\text{mol}·{\text{kg}}^{-1})+\text{NaMOPSO}(0.04\text{mol}·{\text{kg}}^{-1}):\\ \text{pH}(\text{s})=7.066-1.4714\times {10}^{-2}(T-298.15)+4.12\times {10}^{-5}{(T-298.15)}^2\end{array}$$ (10)

where (278.15 ≤ T ≤ 328.15) K. The standard deviations of regression for the pH(s) of the chloride-free buffer solutions, obtained from the fits with eqs 12 – 13, are 0.0019, and 0.0015, respectively.

Table 5.

pH(s) of (MOPSO + NaMOPSO) Buffer Solutions from (278.15 to 328.15) K Computed Using Eqs 4–7

T(K)	0.02 m MOPSO + 0.06 m NaMOPSO	0.02 m MOPSO + 0.04 m NaMOPSO
	I = 0.06 ma	I = 0.04 ma
278.15	7.572	7.378
283.15	7.484	7.297
288.15	7.405	7.215
293.15	7.329	7.141
298.15	7.252	7.065
303.15	7.182	7.994
308.15	7.115	7.922
310.15	7.088	7.898
313.15	7.049	7.857
318.15	6.990	6.787
323.15	6.927	6.725
328.15	6.869	6.661

^am = 1 mol·kg⁻¹

For 3 buffer solutions containing NaCl at an isotonic saline media total ionic strength of I = 0.16 mol·kg⁻¹, the values of pH(s) calculated using eq 4 – 8 and from the acidity function data listed in Table 4 are entered in Table 6. These values of pH(s) are expressed by the following equations:

$$\begin{array}{l}\text{For}\text{MOPSO}(0.01\text{mol}·{\text{kg}}^{-1})+\text{NaMOPSO}(0.03\text{mol}·{\text{kg}}^{-1})+\text{NaCl}(0.13\text{mol}·{\text{kg}}^{-1}):\\ \text{pH}(\text{s})=7.365-1.4968\times {10}^{-2}(T-298.15)+3.7\times {10}^{-5}{(T-298.15)}^2\end{array}$$ (11)

$$\begin{array}{l}\text{For}\text{MOPSO}(0.02\text{mol}·{\text{kg}}^{-1})+\text{NaMOPSO}(0.06\text{mol}·{\text{kg}}^{-1})+\text{NaCl}(0.10\text{mol}·{\text{kg}}^{-1}):\\ \text{pH}(\text{s})=7.357-1.4773\times {10}^{-2}(T-298.15)+4.04\times {10}^{-5}{(T-298.15)}^2\end{array}$$ (12)

$$\begin{array}{l}\text{For}\text{MOPSO}(0.04\text{mol}·{\text{kg}}^{-1})+\text{NaMOPSO}(0.04\text{mol}·{\text{kg}}^{-1})+\text{NaCl}(0.12\text{mol}·{\text{kg}}^{-1}):\\ \text{pH}(\text{s})=7.343-1.4739\times {10}^{-2}(T-298.15)+3.93\times {10}^{-5}{(T-298.15)}^2\end{array}$$ (13)

where T is the temperature in K. The standard deviations for regression of the “observed” results from eqs 11 – 13 are 0.0009, 0.0004, and 0.0014, respectively.

Table 6.

pH(s) of (MOPSO + NaMOPSO) Buffer Solutions from 278.15 to 328.15 K Computed Using Eqs 4–7

T(K)	0.01 m MOPSO + 0.03 m NaMOPSO + 0.13 m NaCl	0.02 m MOPSO + 0.06 m NaMOPSO + 0.10 m NaCl	0.04 m MOPSO + 0.12 m NaMOPSO + 0.04 m NaCl
	I = 0.16 ma	I = 0.16 ma	I = 0.16 ma
278.15	7.677	7.669	7.655
283.15	7.599	7.588	7.572
288.15	7.519	7.508	7.492
293.15	7.441	7.432	7.416
298.15	7.364	7.357	7.343
303.15	7.290	7.284	7.270
308.15	7.219	7.213	7.200
310.15	7.190	7.186	7.172
313.15	7.148	7.144	7.131
318.15	7.080	7.078	7.065
323.15	7.014	7.013	7.999
328.15	7.949	6.950	7.934

^am = 1 mol·kg⁻¹

The operational pH values at (298.15 and 310.15) K were evaluated from cells with liquid junctions cells (B and C) by means of the flowing junction cell.^8,10 The cell potential values of the cells (B and C) at (298.15 and 310.15) K are given in Table 7. The values of E_j listed in Table 8 were obtained by using eq 1. The widely used equation for the calculation of ${log}_{10}{\gamma }_{Cl}^{\circ }$ is based on the Bates - Guggenheim convention,^{3, 5, 7–8} and is valid up to I = 0.1 mol·kg⁻¹.^6,17–19 The combined standard uncertainty for the pH(s) values was accounted for by combining the various known sources of error: (i) assumption for the calculation of the ${log}_{10}{\gamma }_{Cl}^{\circ }$ using eq 7 (± 0.004 pH unit), (ii) extrapolation of the p(a_Hγ_Cl)° plot for chloride-free solutions (less than ± 0.002 pH unit), and (iii) error in the experimental measurement from the multimeter (± 0.02 mV). Thus the overall estimated uncertainty is ± 0.006 and ± 0.012 pH unit for buffers without the presence of NaCl and with the ionic strength I = 0.16 mol·kg⁻¹, respectively. Errors in the values of E_j are irrelevant to the values of pH(s) determined from cell (A) without liquid junction; however, the δE_j of eq 2 does affect the operational pH values listed in Table 9 at (298.15 and 310.15) K. These are recommended as useful secondary pH standards for calibrating electrodes for pH measuring assembly in the range of physiological interest. The consistency of the three sets of experiments listed in Table 9 leads credence in the pH values of MOPSO buffer solutions.

Table 7.

Cell Voltage of Cell B for MOPSO buffer

mol·kg−1			E/V
m1	m2	m3	298.15 K	310.15 K
0.02	0.06	0.10	0.67722	0.69514
0.04	0.04	0.12	0.67633	0.67556
0.01	0.03	0.13	0.67745	0.67672

Cell Voltage of Cell Ca
Cell C	E, V
0.008695 m KH2PO4	298.15 K	310.15 K
+ 0.03043 m Na2HPO4	0.68275	0.69147

^aCorrected to a hydrogen pressure of 101.325 kPa, for physiological phosphate buffer solutions (primary reference standard buffer) at (298.15 and 310.15) K.

Table 8.

Values of the liquid junction potentials for MOPSO at (298.15 and 310.15) K

	Eja/mV
System	298.15 K	310.15 K
Physiological phosphate (0.008695 m KH2PO4 + 0.03043 m NaCl)	2.6	2.9
0.02 m MOPSO + 0.06 m NaMOPSO + 0.10 m NaCl	0.5	0.7
0.04 m MOPSO + 0.04 m NaMOPSO + 0.12 m NaCl	0.5	0.8
0.01 m MOPSO + 0.03 m NaMOPSO + 0.13 m NaCl	0.4	0.8

^a $E_j=E+E_{\mathit{SCE}}^{\circ }$ - k pH from eq 1, E is the cell voltage from Table 5, k = Nernst slope with values 0.059156 at 298.15 K, and 0.061538 at 310.15 K; the pH of the primary reference standard phosphate buffer is 7.415 and 7.395 at (298.15 and 310.15) K; $E_{\mathit{SCE}}^{\circ }$ = electrode potential of the saturated calomel electrode = −0.2415 V and −0.2335 V at (298.15 and 310.15) K, respectively.

Table 9.

Values of pH at (298.15 to 310.15) K for MOPSO Buffer Solutions

Cell B				T = 298.15 K			T = 310.15 K
mol·kg−1				pH
m1	m2	m3	I	WithoutaEj corr	WithbEj corr	Calcc	WithoutaEj corr	WithbEj corr	Calcc
0.02	0.06	0.10	0.16	7.322	7.357	7.357	7.149	7.185	7.186
0.04	0.04	0.12	0.16	7.307	7.342	7.343	7.137	7.171	7.172
0.01	0.03	0.13	0.16	7.326	7.363	7.364	7.156	7.190	7.190

^apH = 7.415 + [(E − 0.68275)/0.059156] at 298.15 K, and pH = 7.395 + [(E − 0.69144)/0.061538] at 310.15 K; the cell potential values (Table 7) are 0.68275 V and 0.69144 V at (298.15 to 310.15) K for the physiological phosphate buffer standard solution.

^bValues obtained from eq 2 and E_j data of Table 8.

^cObtained from Tables 5 and 6.