Motion Planning Under Uncertainty for Image-guided Medical Needle Steering

Abstract

We develop a new motion planning algorithm for a variant of a Dubins car with binary left/right steering and apply it to steerable needles, a new class of flexible bevel-tip medical needles that physicians can steer through soft tissue to reach clinical targets inaccessible to traditional stiff needles. Our method explicitly considers uncertainty in needle motion due to patient differences and the difficulty in predicting needle/tissue interaction. The planner computes optimal steering actions to maximize the probability that the needle will reach the desired target. Given a medical image with segmented obstacles and target, our method formulates the planning problem as a Markov Decision Process based on an efficient discretization of the state space, models motion uncertainty using probability distributions, and computes optimal steering actions using Dynamic Programming. This approach only requires parameters that can be directly extracted from images, allows fast computation of the optimal needle entry point, and enables intra-operative optimal steering of the needle using the pre-computed dynamic programming look-up table. We apply the method to generate motion plans for steerable needles to reach targets inaccessible to stiff needles, and we illustrate the importance of considering uncertainty during motion plan optimization.

1 Introduction

Advances in medical imaging modalities such as MRI, ultrasound, and X-ray fluoroscopy are now providing physicians with real-time, patient-specific information as they perform medical procedures such as extracting tissue samples for biopsies, injecting drugs for anesthesia, or implanting radioactive seeds for brachytherapy cancer treatment. These diagnostic and therapeutic medical procedures require insertion of a needle to a specific location in soft tissue. We are developing motion planning algorithms for medical needle insertion procedures that can utilize the information obtained by real-time imaging to accurately reach desired locations.

We consider a new class of medical needles, composed of a flexible material and with a bevel-tip, that can be steered to targets in soft tissue that are inaccessible to traditional stiff needles (Webster III et al., 2006a, 2005a; Alterovitz et al., 2005a,b). Steerable needles are controlled by 2 degrees of freedom actuated at the needle base: insertion distance and bevel direction. Webster III et al. (2006a) experimentally demonstrated that, under ideal conditions, a flexible bevel-tip needle cuts a path of constant curvature in the direction of the bevel, and the needle shaft bends to follow the path cut by the bevel tip. In a plane, a needle subject to this nonholonomic constraint based on bevel direction is equivalent to a Dubins car that can only steer its wheels far left or far right but cannot go straight.

The steerable needle motion planning problem is to determine a sequence of actions (insertions and direction changes) so the needle tip reaches the specified target while avoiding obstacles and staying inside the workspace. Given a segmented medical image of the target, obstacles, and starting location, the feasible workspace for motion planning is defined by the soft tissues through which the needle can be steered. Obstacles represent tissues that cannot be cut by the needle, such as bone, or sensitive tissues that should not be damaged, such as nerves or arteries.

We consider motion planning for steerable needles in the context of an image-guided procedure: real-time imaging and computer vision algorithms are used to track the position and orientation of the needle tip in the tissue. Recently developed methods can provide this information for a variety of imaging modalities (Cleary et al., 2003; DiMaio et al., 2006a). In this paper, we consider motion plans in an imaging plane since the speed/resolution trade-off of 3-D imaging modalities is generally poor for 3-D real-time interventional applications. With imaging modalities continuing to improve, we will explore the natural extension of our planning approach to 3-D in future work.

Whereas many traditional motion planners assume a robot’s motions are perfectly deterministic and predictable, a needle’s motion through soft tissue cannot be predicted with certainty due to patient differences and the difficulty in predicting needle/tissue interaction. These sources of uncertainty may result in deflections of the needle’s orientation, which is a type of slip in the motion of a Dubins car. Real-time imaging in the operating room can measure the needle’s current position and orientation, but this measurement by itself provides no information about the effect of future deflections during insertion. Since the motion response of the needle is not deterministic, success of the procedure can rarely be guaranteed.

We develop a new motion planning approach for steering flexible needles through soft tissue that explicitly considers uncertainty in needle motion. To define optimality for a needle steering plan, we introduce a new objective for image-guided motion planning: maximizing the probability of success. In the case of needle steering, the needle insertion procedure continues until the needle reaches the target (success) or until failure occurs, where failure is defined as hitting an obstacle, exiting the feasible workspace, or reaching a state in which it is impossible to prevent the former two outcomes. Our method formulates the planning problem as a Markov Decision Process (MDP) based on an efficient discretization of the state space, models motion uncertainty using probability distributions, and computes optimal actions (within error due to discretization) for a set of feasible states using infinite horizon Dynamic Programming (DP).

Our motion planner is designed to run inside a feedback loop. After the feasible workspace, start region, and target are defined from a pre-procedure image, the motion planner is executed to compute the optimal action for each state. After the image-guided procedure begins, an image is acquired, the needle’s current state (tip position and orientation) is extracted from the image, the motion planner (quickly) returns the optimal action to perform for that state, the action is executed and the needle may deflect due to motion uncertainty, and the cycle repeats.

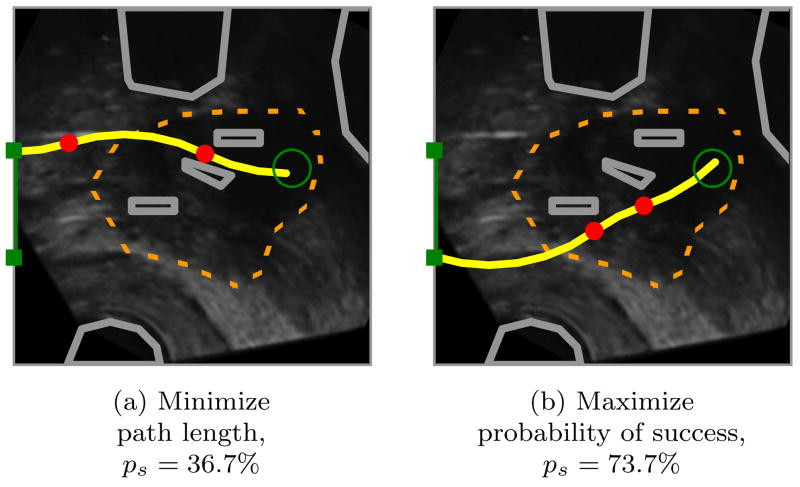
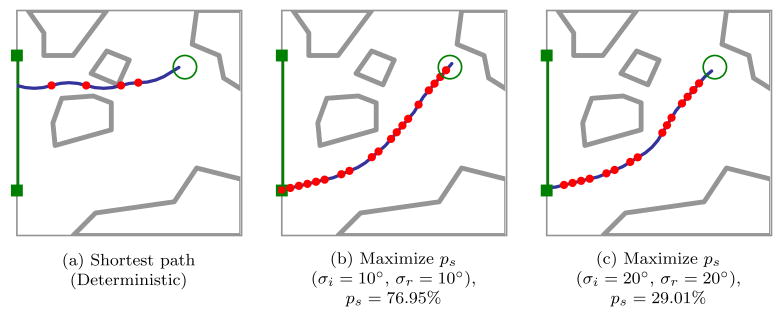
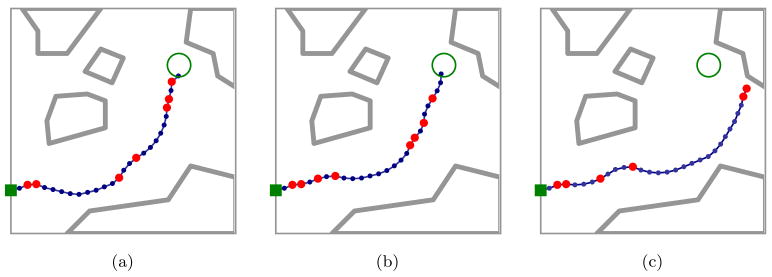
In Fig. 1, we apply our motion planner in simulation to prostate brachytherapy, a medical procedure to treat prostate cancer in which physicians implant radioactive seeds at precise locations inside the prostate under ultrasound image guidance. In this ultrasound image of the prostate (segmented by a dotted line), obstacles correspond to bones, the rectum, the bladder, the urethra, and previously implanted seeds. Brachytherapy is currently performed in medical practice using rigid needles; here we consider steerable needles capable of obstacle avoidance. We compare the output of our new method, which explicitly considers motion uncertainty, to the output of a shortest-path planner that assumes the needles follow ideal deterministic motion. Our new method improves the expected probability of success by over 30% compared to shortest path planning, illustrating the importance of explicitly considering uncertainty in needle motion.

Figure 1.

Our motion planner computes actions (insertions and direction changes, indicated by dots) to steer the needle from an insertion entry region (vertical line on left between the solid squares) to the target (open circle) inside soft tissue, without touching critical areas indicated by polygonal obstacles in the imaging plane. The motion of the needle is not known with certainty; the needle tip may be deflected during insertion due to tissue inhomogeneities or other unpredictable soft tissue interactions. We explicitly consider this uncertainty to generate motion plans to maximize the probability of success, p_s, the probability that the needle will reach the target without colliding with an obstacle or exiting the workspace boundary. Relative to a planner that minimizes path length, our planner considering uncertainty may generate longer paths with greater clearance from obstacles to maximize p_s.

1.1 Related Work

Nonholonomic motion planning has a long history in robotics and related fields (Latombe, 1991, 1999; Choset et al., 2005; LaValle, 2006). Past work has addressed deterministic curvature-constrained path planning where a mobile robot’s path is, like a car, constrained by a minimum turning radius. Dubins showed that the optimal curvature-constrained trajectory in open space from a start pose to a target pose can be described using a discrete set of canonical trajectories composed of straight line segments and arcs of the minimum radius of curvature (Dubins, 1957). Jacobs and Canny (1989) considered polygonal obstacles and constructed a configuration space for a set of canonical trajectories, and Agarwal et al. (2002) developed a fast algorithm to compute a shortest path inside a convex polygon. For Reeds-Shepp cars with reverse, Laumond et al. (1994) developed a nonholonomic planner using recursive subdivision of collision-free paths generated by a lower-level geometric planner, and Bicchi et al. (1996) proposed a technique that provides the shortest path for circular unicycles. Sellen (1998) developed a discrete state-space approach; his discrete representation of orientation using a unit circle inspired our discretization approach.

Our planning problem considers steerable needles, a new type of needle currently being developed jointly by researchers at The Johns Hopkins University and The University of California, Berkeley (Webster III et al., 2005b). Unlike traditional Dubins cars that are subject to a minimum turning radius, steerable needles are subject to a constant turning radius. Webster et al. showed experimentally that, under ideal conditions, steerable bevel-tip needles follow paths of constant curvature in the direction of the bevel tip (Webster III et al., 2006a), and that the radius of curvature of the needle path is not significantly affected by insertion velocity (Webster III et al., 2005a).

Park et al. (2005) formulated the planning problem for steerable bevel-tip needles in stiff tissue as a nonholonomic kinematics problem based on a 3-D extension of a unicycle model and used a diffusion-based motion planning algorithm to numerically compute a path. The approach is based on recent advances by Zhou and Chirikjian in nonholonomic motion planning including stochastic model-based motion planning to compensate for noise bias (Zhou and Chirikjian, 2004) and probabilistic models of dead-reckoning error in nonholonomic robots (Zhou and Chirikjian, 2003). Park’s method searches for a feasible path in full 3-D space using continuous control, but it does not consider obstacle avoidance or the uncertainty of the response of the needle to insertion or direction changes, both of which are emphasized in our method.

In preliminary work on motion planning for bevel-tip steerable needles, we proposed an MDP formulation for 2-D needle steering (Alterovitz et al., 2005b) to find a stochastic shortest path from a start position to a target, subject to user-specified “cost” parameters for direction changes, insertion distance, and obstacle collisions. However, the formulation was not targeted at image-guided procedures, did not include insertion point optimization, and optimized an objective function that has no physical meaning. In this paper, we develop a 2-D motion planning approach for image-guided needle steering that explicitly considers motion uncertainty to maximize the probability of success based on parameters that can be extracted from medical imaging without requiring user-specified “cost” parameters that may be difficult to determine.

MDP’s and dynamic programming are ideally suited for medical planning problems because of the variance in characteristics between patients and the necessity for clinicians to make decisions at discrete time intervals based on limited known information. In the context of medical procedure planning, MDP’s have been developed to assist in decisions such as timing for liver transplants (Alagoz et al., 2005), discharge times for severe sepsis cases (Kreke et al., 2005), and start dates for HIV drug cocktail treatment (Shechter et al., 2005). MDP’s and dynamic programming have also been used in a variety of robotics applications, including planning paths for mobile robots (Dean et al., 1995; LaValle and Hutchinson, 1998; Ferguson and Stentz, 2004; LaValle, 2006).

Past work has investigated needle insertion planning in situations where soft tissue deformations are significant and can be modeled. Several groups have estimated tissue material properties and needle/tissue interaction parameters using tissue phantoms (DiMaio and Salcudean, 2003a; Crouch et al., 2005) and animal experiments (Kataoka et al., 2002; Simone and Okamura, 2002; Okamura et al., 2004; Kobayashi et al., 2005; Heverly et al., 2005; Hing et al., 2007). Our past work addressed planning optimal insertion location and insertion distance for rigid symmetric-tip needles to compensate for 2-D tissue deformations predicted using a finite element model (Alterovitz et al., 2003a,b,c). We previously also developed a different 2-D planner for bevel-tip steerable needles to explicitly compensate for the effects of tissue deformation by combining finite element simulation with numeric optimization (Alterovitz et al., 2005a). This previous approach assumed that bevel direction can only be set once prior to insertion and employed local optimization that can fail to find a globally optimal solution in the presence of obstacles.

Past work has also considered insertion planning for needles and related devices capable of following curved paths through tissues using different mechanisms. One such approach uses slightly flexible symmetric-tip needles that are guided by translating and orienting the needle base to explicitly deform surrounding tissue, causing the needle to follow a curved path (DiMaio and Salcudean, 2003b; Glozman and Shoham, 2007). DiMaio and Salcudean (2003b) developed a planning approach that guides this type of needle around point obstacles with oval-shaped potential fields. Glozman and Shoham (2007) also addressed symmetric-tip needles and approximated the tissue using springs. Another steering approach utilizes a standard biopsy cannula (hollow tube needle) and adds steering capability with an embedded pre-bent stylet that is controlled by a hand-held, motorized device (Okazawa et al., 2005). A recently developed “active cannula” device is composed of concentric, pre-curved tubes and is capable of following curved paths in a “snake-like” manner in soft tissue or open space (Webster III et al., 2006b).

Integrating motion planning for needle insertion with intra-operative medical imaging requires real-time localization of the needle in the images. Methods are available for this purpose for a variety of imaging modalities (Cleary et al., 2003; DiMaio et al., 2006a). X-ray fluoroscopy, a relatively low-cost imaging modality capable of obtaining images at regular discrete time intervals, is ideally suited for our application because it generates 2-D projection images from which the needle can be cleanly segmented (Cleary et al., 2003).

Medical needle insertion procedures may also benefit from the more precise control of needle position and velocity made possible through robotic surgical assistants (Howe and Matsuoka, 1999; Taylor and Stoianovici, 2003). Dedicated robotic hardware for needle insertion is being developed for a variety of medical applications, including stereotactic neurosurgery (Masamune et al., 1998), CT-guided procedures (Maurin et al., 2005), MR compatible surgical assistance (Chinzei et al., 2000; DiMaio et al., 2006b), thermotherapy cancer treatment (Hata et al., 2005), and prostate biopsy and therapeutic interventions (Fichtinger et al., 2002; Schneider et al., 2004).

1.2 Our Contributions

In Sec. 3, we first introduce a motion planner for Dubins cars with binary left/right steering subject to a constant turning radius rather than the typical minimum turning radius. This model applies to an idealized steerable needle whose motion is deterministic: the needle exactly follows arcs of constant curvature in response to insertion actions. Our planning method utilizes an efficient discretization of the state space for which error due to discretization can be tightly bounded. Since any feasible plan will succeed with 100% probability under the deterministic motion assumption, we apply the traditional motion planning objective of computing a shortest path plan from the current state to the target.

In Sec. 4, we extend the deterministic motion planner to consider uncertainty in motion and introduce a new planning objective: maximize the probability of success. Unlike the objective function value of previous methods that consider motion uncertainty, the value of this new objective function has physical meaning: it is the probability that the needle tip will successfully reach the target during the insertion procedure. In addition to this intuitive meaning of the objective, our problem formulation has a secondary benefit: all data required for planning can be measured directly from imaging data without requiring tweaking of user-specified parameters. Rather than assigning costs to insertion distance, needle rotation, etc., which are difficult to estimate or quantify, our method only requires the probability distributions of the needle response to each feasible action, which can be estimated from previously obtained images.

Our method formulates the planning problem as a Markov Decision Process (MDP) and computes actions to maximize the probability of success using infinite horizon Dynamic Programming (DP). Solving the MDP using DP has key benefits particularly relevant for medical planning problems where feedback is provided at regular time intervals using medical imaging or other sensor modalities. Like a well-constructed navigation field, the DP solver provides an optimal action for any state in the workspace. We use the DP look-up table to automatically optimize the needle insertion point. Integrated with intra-operative medical imaging, this DP look-up table can also be used to optimally steer the needle in the operating room without requiring costly intra-operative re-planning. Hence, the planning solution can serve as a means of control when integrated with real-time medical imaging.

Throughout the description of the motion planning method, we focus on the needle steering application. However, the method is generally applicable to any car-like robot with binary left/right steering that follows paths composed of arcs of constant curvature, whose position can be estimated by sensors at regular intervals, and whose path may deflect due to motion uncertainty.

2 Problem Definition

Steerable bevel-tip needles are controlled by 2 degrees of freedom: insertion distance and rotation angle about the needle axis. The actuation is performed at the needle base outside the patient (Webster III et al., 2006a). Insertion pushes the needle deeper into the tissue, while rotation turns the needle about its shaft, re-orienting the bevel at the needle tip. For a sufficiently flexible needle, Webster III et al. (2006a) experimentally demonstrated that rotating the needle base will change the bevel direction without changing the needle shaft’s position in the tissue. In the plane, the needle shaft can be rotated 180° about the insertion axis at the base so the bevel points in either the bevel-left or bevel-right direction. When inserted, the asymmetric force applied by the bevel causes the needle to bend and follow a curved path through the tissue (Webster III et al., 2006a). Under ideal conditions, the curve will have a constant radius of curvature r, which is a property of the needle and tissue. We assume the needle moves only in the imaging plane; a recently developed low-level controller using image feedback can effectively maintain this constraint (Kallem and Cowan, 2007). We also assume the tissue is stiff relative to the needle and that the needle is thin, sharp, and low-friction so the tissue does not significantly deform. While the needle can be partially retracted and re-inserted, the needle’s motion would be biased to follow the path in the tissue cut by the needle prior to retraction. Hence, in this paper we only consider needle insertion, not retraction.

We define the workspace as a 2-D rectangle of depth z_max and height y_max. Obstacles in the workspace are defined by (possibly nonconvex) polygons. The obstacles can be expanded using a Minkowski sum with a circle to specify a minimum clearance (LaValle, 2006). The target region is defined by a circle with center point t and radius r_t.

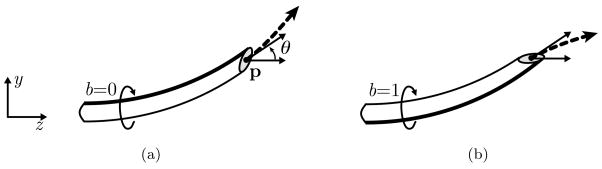
As shown in Fig. 2, the state w of the needle during insertion is fully characterized by the needle tip’s position p = (p_y, p_z), orientation angle θ, and bevel direction b, where b is either bevel-left (b=0) or bevel-right (b=1).

Figure 2.

The state of a steerable needle during insertion is characterized by tip position p, tip orientation angle θ, and bevel direction b (a). Rotating the needle about its base changes the bevel direction but does not affect needle position (b). The needle will cut soft tissue along an arc (dashed vector) based on bevel direction.

We assume the needle steering procedure is performed with image guidance; a medical image is acquired at regular time intervals and the state of the needle (tip position and orientation) is extracted from the images. Between image acquisitions, we assume the needle moves at constant velocity and is inserted a distance δ. In our model, direction changes can only occur at discrete decision points separated by the insertion distance δ. One of two actions u can be selected at any decision point: insert the needle a distance δ (u = 0), or change direction and insert a distance δ (u = 1).

During insertion, the needle tip orientation may be deflected by inhomogeneous tissue, small anatomical structures not visible in medical images, or local tissue displacements. Additional deflection may occur during direction changes due to stiffness along the needle shaft. Such deflections are due to an unknown aspect of the tissue structure or needle/tissue interaction, not errors in measurement of the needle’s orientation, and can be considered a type of noise parameter in the plane. We model uncertainty in needle motion due to such deflections using probability distributions. The orientation angle θ may be deflected by some angle β, which we model as normally distributed with mean 0 and standard deviations σ_i; for insertion (u = 0) and σ_r for direction changes followed by insertion (u = 1). Since σ_i and σ_r are properties of the needle and tissue, we plan in future work to automatically estimate these parameters by retrospectively analyzing images of needle insertion.

The goal of our motion planner is to compute an optimal action u for every feasible state w in the workspace to maximize the probability p_s that the needle will successfully reach the target.

3 Motion Planning for Deterministic Needle Steering

We first introduce a motion planner for an idealized steerable needle whose motion is deterministic: the needle perfectly follows arcs of constant curvature in response to insertion actions.

To computationally solve the motion planning problem, we transform the problem from a continuous state space to a discrete state space by approximating needle state w = {p, θ, b} using a discrete representation. To make this approach tractable, we must round p and θ without generating an unwieldy number of states while simultaneously bounding error due to discretization.

3.1 State Space Discretization

Our discretization of the planar workspace is based on a grid of points with a spacing Δ horizontally and vertically. We approximate a point p = (p_y, p_z) by rounding to the nearest point q = (q_y, q_z) on the grid. For a rectangular workspace bounded by depth z_max and height y_max, this results in

$$N_s=\lfloor \frac{z_{\mathit{max}}+\mathrm{\Delta }}{\mathrm{\Delta }}\rfloor \lfloor \frac{y_{\mathit{max}}+\mathrm{\Delta }}{\mathrm{\Delta }}\rfloor$$

position states aligned at the origin.

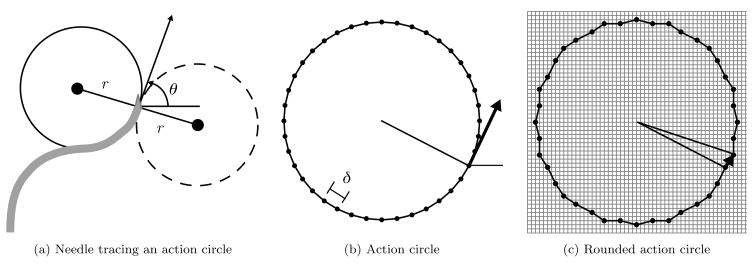
Rather than directly approximating θ by rounding, which would incur a cumulative error with every transition, we take advantage of the discrete insertion distances δ. We define an action circle of radius r, the radius of curvature of the needle. Each point c on the action circle represents an orientation θ of the needle, where θ is the angle of the tangent of the circle at c with respect to the z-axis. The needle will trace an arc of length δ along the action circle in a counter-clockwise direction for b = 0 and in the clockwise direction for b = 1. Direction changes correspond to rotating the point c by 180° about the action circle origin and tracing subsequent insertions in the opposite direction, as shown in Fig. 3(a). Since the needle traces arcs of length δ, we divide the action circle into N_c arcs of length δ = 2πr/N_c. The endpoints of the arcs generate a set of N_c action circle points, each representing a discrete orientation state, as shown in Fig. 3(b). We require that N_c be a multiple of 4 to facilitate the orientation state change after a direction change.

Figure 3.

A needle in the bevel-left direction with orientation θ is tracing the solid action circle with radius r (a). A direction change would result in tracing the dotted circle. The action circle is divided into N_c = 40 discrete arcs of length δ (b). The action circle points are rounded to the nearest point on the Δ-density grid, and transitions for insertion of distance δ are defined by the vectors between rounded action circle points (c).

At each of the N_s discrete position states on the Δ grid, the needle may be in any of the N_c orientation states and the bevel direction can be either b = 0 or b = 1. Hence, the total number of discrete states is N = 2N_sN_c.

Using this discretization, a needle state w = {p, θ, b} can be approximated as a discrete state s = {q, Θ, b}, where q = (q_y, q_z) is the discrete point closest to p on the Δ-density grid and Θ is the integer index of the discrete action circle point with tangent angle closest to θ.

3.2 Deterministic State Transitions

For each state and action, we create a state transition that defines the motion of the needle when it is inserted a distance δ. We first consider the motion of the needle from a particular spatial state q. To define transitions for each orientation state at q, we overlay the action circle on a regular grid of spacing Δ and round the positions of the action circle points to the nearest grid point, as shown in Fig. 3(c). The displacement vectors between rounded action circle points encode the transitions of the needle tip. Given a particular orientation state Θ and bevel direction b = 0, we define the state transition using a translation component (the displacement vector between the positions of Θ and Θ − 1 on the rounded action circle, which will point exactly to a new spatial state) and a new orientation state (Θ − 1). If b = 1, we increment rather than decrement Θ. We create these state transitions for each orientation state and bevel direction for each position state q in the workspace. This discretization of states and state transitions results in 0 discretization error in orientation when new actions are selected at δ intervals.

Certain states and transitions must be handled as special cases. States inside the target region and states inside obstacles are absorbing states, meaning they have a single self-transit ion edge of zero length. If the transition arc from a feasible state exits the workspace or intersects an edge of a polygonal obstacle, a transition to an obstacle state is used.

3.3 Discretization Error

Deterministic paths designated using this discrete representation of state will incur error due to discretization, but the error is bounded. At any decision point, the position error due to rounding to the Δ workspace grid is $E_0=\mathrm{\Delta }\sqrt{2}/2$. When the bevel direction is changed, a position error is also incurred because the distance between the center of the original action circle and the center of the action circle after the direction change will be in the range $2r\pm \mathrm{\Delta }\sqrt{2}$. Hence, for a needle path with h direction changes, the final orientation is precise but the error in position is bounded above by $E_h=h\mathrm{\Delta }\sqrt{2}+\mathrm{\Delta }\sqrt{2}/2$.

3.4 Computing Deterministic Shortest Paths

For the planner that considers deterministic motion, we compute an action for each state such that the path length to the target is minimized. As in standard motion planning approaches (Latombe, 1991; Choset et al., 2005; LaValle, 2006), we formulate the motion planning problem as a graph problem. We represent each state as a node in a graph and state transitions as directed edges between the corresponding nodes. We merge all states in the target into a single “source” state. We then apply Dijkstra’s shortest path algorithm (Bertsekas, 2000) to compute the shortest path from each state to the target. The action u to perform at a state is implicitly computed based on the directed edge from that state that was selected for the shortest path.

4 Motion Planning for Needle Steering Under Uncertainty

We extend the deterministic motion planner from Sec. 3 to consider uncertainty in motion and to compute actions to explicitly maximize the probability of success p_s for each state. The planner retains the discrete approximation of the state space introduced in Sec. 3.1, but replaces the single deterministic state transition per action defined in Sec. 3.2 with a set of state transitions, each weighted by its probability of occurrence. We then generalize the shortest path algorithm defined in Sec. 3.4 with a dynamic programming approach that enables the planner to utilize the probability-weighted state transitions to explicitly maximize the probability of success.

4.1 Modeling Motion Uncertainty

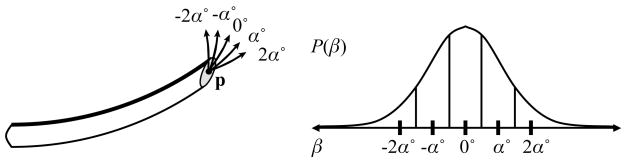
Due to motion uncertainty, actual needle paths will not always exactly trace the action circle introduced in Sec. 3.1. The deflection angle β defined in Sec. 2 must be approximated using discrete values. We define discrete transitions from a state x_i, each separated by an angle of deflection of α = 360°/N_c. In this paper, we model β using a normal distribution with mean 0 and standard deviation σ_i or σ_r, and compute the probability for each discrete transition by integrating the corresponding area under the normal curve, as shown in Fig. 4. We set the number of discrete transitions N_pi such that the areas on the left and right tails of the normal distribution sum to less than 1%. The left and right tail probabilities are added to the left-most and right-most transitions, respectively. Using this discretization, we define a transition probability matrix P(u), where P_ij(u) defines the probability of transitioning from state x_i to state x_j given that action u is performed.

Figure 4.

When the needle is inserted, the insertion angle θ may be deflected by some angle β. We model the probability distribution of β using a normal distribution with mean 0 and standard deviation σ_i; for insertion or σ_r for direction change. For a discrete sample of deflections (β = {−2α, −α, 0, α, 2α}), we obtain the probability of each deflection by integrating the corresponding area under the normal curve.

4.2 Maximizing the Probability of Success using Dynamic Programming

The goal of our motion planning approach is to compute an optimal action u for every state w (in continuous space) such that the probability of reaching the target is maximized. We define p_s(w) to be the probability of success given that the needle is currently in state w. If the position of state w is inside the target, p_s(w) = 1. If the position of state w is inside an obstacle, p_s(w) = 0. Given an action u for some other state w, the probability of success will depend on the response of the needle to the action (the next state) and the probability of success at that next state. The expected probability of success is

$$p_s(w)=E[p_s(v)\mid w,u],$$ (1)

where the expectation is over v, a random variable for the next state. The goal of motion planning is to compute an optimal action u for every state w:

$$p_s(w)=\underset{u}{max}\{E[p_s(v)\mid w,u]\}.$$ (2)

For N discrete states, the motion planning problem is to determine the optimal action u_i for each state x_i, i = 1, …, N. We re-write Eq. 2 using the discrete approximation and expand the expected value to a summation:

$$p_s(x_i)=\underset{u_i}{max}\left\{\sum _{j=1}^N{P}_{ij}(u_i)p_s(x_j)\right\},$$ (3)

where P_ij (u_i) is the probability of entering state x_j after executing action u_i at current state x_i.

We observe that the needle steering motion planning problem is a type of MDP. In particular, Eq. 3 has the form of the Bellman equation for a stochastic maximum-reward problem (Bertsekas, 2000):

$$J^{\ast }(x_i)=\underset{u_i}{max}\sum _{j=1}^N{P}_{ij}(u_i)(g(x_i,u_i,x_j)+J^{\ast }(x_j)).$$ (4)

where g(x_i, u_i, x_j) is a “reward” for transitioning from state x_i to x_i after performing action u_i. In our case, we set J* (x_i) = p_s(x_i), and we set g(x_i, u_i, x_j) = 0 for all x_i, u_i, and x_j. Stochastic maximum-reward problems of this form can be optimally solved using infinite horizon Dynamic Programming (DP).

Infinite horizon DP is a type of dynamic programming in which there is no finite time horizon (Bertsekas, 2000). For stationary problems, this implies that the optimal action at each state is purely a function of the state without explicit dependence on time. In the case of needle steering, once a state transition is made, the next action is computed based on the current position, orientation, and bevel direction without explicit dependence on past actions.

To solve the infinite horizon DP problem defined by the Bellman Eq. 4, we use the value iteration algorithm (Bertsekas, 2000), which iteratively updates p_s(x_i) for each state i by evaluating Eq. 3. This generates a DP look-up table containing the optimal action u_i and the probability of success p_s(x_i) for i = 1, …, N.

Termination of the algorithm is guaranteed in N iterations if the transition probability graph corresponding to some optimal stationary policy is acyclic (Bertsekas, 2000). Violation of this requirement will be rare in motion planning since a violation implies that an optimal action sequence results in a path that, with probability greater than 0, loops and passes through the same point at the same orientation more than once. As in the deterministic shortest path planner case, the planner does not explicitly detect self-intersections of the needle path in the plane.

To improve performance, we take advantage of the sparsity of the matrices P_ij(u) for u = 0 and u = 1. Each iteration of the value iteration algorithm requires matrixvector multiplication using the transition probability matrix. Although P_ij (u) has N² entries, each row of P_ij (u) has only k nonzero entries, where k ≪ N since the needle will only transition to a state j in the spatial vicinity of state i. Hence, P_ij(u) has at most kN nonzero entries. By only accessing nonzero entries of P_ij(u) during computation, each iteration of the value iteration algorithm requires only O(kN) rather than O(N²) time and memory. Thus, the total algorithm’s complexity is O(kN²). To further improve performance, we terminate value iteration when the maximum change ε over all states is less than 10⁻³, which in our test cases occurred in far fewer than N iterations, as described in Sec. 5.

5 Computational Results

We implemented the motion planner in C++ and tested it on a 2.21GHz Athlon 64 PC. In Fig. 1, we set the needle radius of curvature r = 5.0, defined the workspace by z_max = y_max = 10, and used discretization parameters N_c = 40, Δ = 0.101, and δ = 0.785. The resulting DP problem contained N = 800,000 states. In all further examples, we set r = 2.5, z_max = y_max = 10, N_c = 40, Δ = 0.101, and δ = 0.393, resulting in N = 800,000 states.

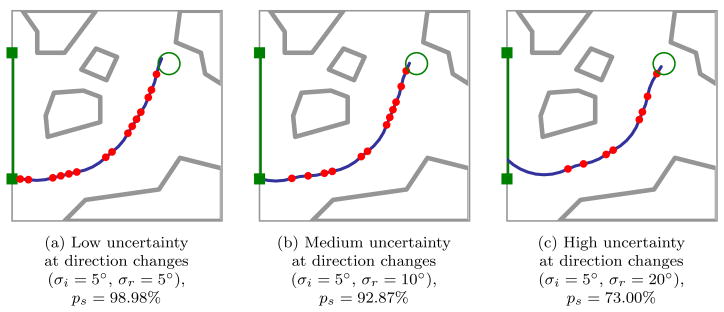
Optimal plans and probability of success p_s depend on the level of uncertainty in needle motion. As shown in Figs. 1 and 5, explicitly considering the variance of needle motion significantly affects the optimal plan relative to the shortest path plan generated under the assumption of deterministic motion. We also vary the variance during direction changes independently from the variance during insertions without direction changes. Optimal plans and probability of success p_s are highly sensitive to the level of uncertainty in needle motion due to direction changes. As shown in Fig. 6, the number of direction changes decreases as the variance during direction changes increases.

Figure 5.

As in Fig. 1, optimal plans maximizing the probability of success p_s illustrate the importance of considering uncertainty in needle motion. The shortest path plan passes through a narrow gap between obstacles (a). Since maximizing p_s explicitly considers uncertainty, the optimal expected path has greater clearance from obstacles, decreasing the probability that large deflections will cause failure to reach the target. Here we consider medium (b) and large (c) variance in tip deflections for a needle with smaller radius of curvature than in Fig. 1.

Figure 6.

Optimal plans demonstrate the importance of considering uncertainty in needle motion, where σ_i; and σ_r are the standard deviations of needle tip deflections that can occur during insertion and direction changes, respectively. For higher σ_r relative to σ_i, the optimal plan includes fewer direction changes. Needle motion uncertainty at locations of direction changes may be substantially higher than uncertainty during insertion due to transverse stiffness of the needle.

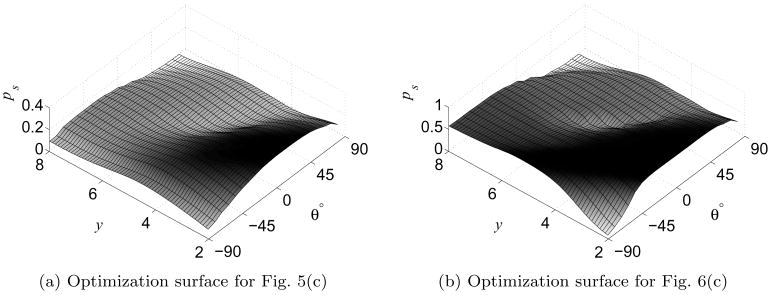
By examining the DP look-up table, we can optimize the initial insertion location, orientation, and bevel direction, as shown in Figs. 1, 5, and 6. In these examples, the set of feasible start states was defined as a subset of all states on the left edge of the workspace. By linearly scanning the computed probability of success for the start states in the DP look-up table, the method identifies the bevel direction b, insertion point (height y on the left edge of the workspace), and starting orientation angle θ (which varies from −90° to 90°) that maximizes probability of success, as shown in Fig. 7.

Figure 7.

The optimal needle insertion location y, angle θ, and bevel direction b are found by scanning the DP look-up table for the feasible start state with maximal p_s. Here we plot optimization surfaces for b = 0. The low regions correspond to states from which the needle has high probability of colliding with an obstacle or exiting the workspace, and the high regions correspond to better start states.

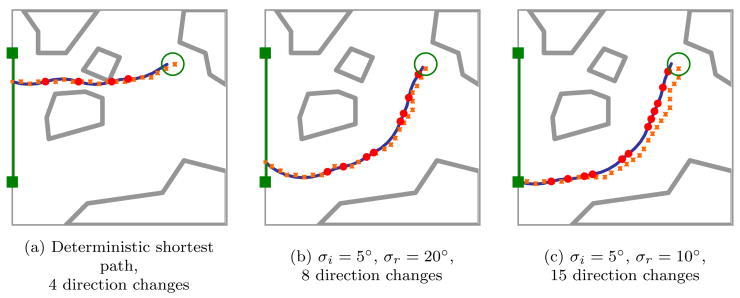
Since the planner approximates the state of the needle with a discrete state, the planner is subject to discretization errors as discussed in Sec. 3.3. After each action, the state of the needle is obtained from medical imaging, reducing the discretization error in position of the current state to $\mathrm{\Delta }\sqrt{2}/2$. However, when the planner considers future actions, discretization error for future bevel direction changes is cumulative. We illustrate the effect of cumulative discretization error during planning in Fig. 8, where the planner internally assumes the expected needle path will follow the dotted line rather than the actual expected path indicated by the solid line. The effect of cumulative errors due to discretization, which is bounded as described in Sec. 3.3, is generally smaller when fewer direction changes are planned.

Figure 8.

The small squares depict the discrete states used internally by the motion planning algorithm when predicting the expected path from the start state, while the solid line shows the actual expected needle path based on constant-curvature motion. The cumulative error due to discretization, which is bounded as described in Sec. 3.3, is generally smaller when fewer direction changes (indicated by solid circles) are performed.

As defined in Sec. 4.2, the computational complexity of the motion planner is O(kN²). Fewer than 300 iterations were required for each example, with fewer iterations required for smaller σ_i; and σ_r. In all examples, k, the number of transitions per state, is bounded such that k ≤ 25. Computation time to construct the MDP depends on the collision detector used, as collision detection must be performed for all N states and up to kN state transitions. Computation time to solve the MDP for the examples ranged from 67 sec to 110 sec on a 2.21GHz AMD Athlon 64 PC, with higher computation times required for problems with greater variance, due to the increased number of transitions from each state. As computation only needs to be performed at the pre-procedure stage, we believe minutes of computation time is reasonable for the intended applications. Intra-operative computation time is effectively instantaneous since only a memory access to the DP look-up table is required to retrieve the optimal action after the needle has been localized in imaging.

Integrating intra-operative medical imaging with the pre-computed DP look-up table could permit optimal steering of the needle in the operating room without requiring costly intra-operative re-planning. We demonstrate the potential of this approach using simulation of needle deflections based on normal distributions with mean 0 and standard deviations σ_i; = 5° and σ_r = 20° in Fig. 9. After each insertion distance δ, we assume the needle tip is localized in the image. Based on the DP look-up table, the needle is either inserted or the bevel direction is changed. The effect of uncertainty can be seen as deflections in the path, i.e., locations where the tangent of the path abruptly changes. Since σ_r > σ_i, deflections are more likely to occur at points of direction change. In practice, clinicians could monitor p_s, insertion length, and self-intersection while performing needle insertion.

Figure 9.

Three simulated image-guided needle insertion procedures from a fixed starting point with needle motion uncertainty standard deviations of σ_i = 5° during insertion and σ_r = 20° during direction changes. After each insertion distance δ we assume the needle tip is localized in the image and identified using a dot. Based on the DP look-up table, the needle is either inserted (small dots) or a direction change is made (larger dots). The effect of uncertainty can be seen as deflections in the path, i.e., locations where the tangent of the path abruptly changes. Since σ_r > σ_i, deflections are more likely to occur at points of direction change. In all cases, p_s = 72.35% at the initial state. In (c), multiple deflections and the nonholonomic constraint on needle motion prevent the needle from reaching the target.

6 Conclusion and Future Work

We developed a new motion planning approach for steering flexible needles through soft tissue that explicitly considers uncertainty: the planner computes optimal actions to maximize the probability that the needle will reach the desired target. Motion planning for steerable needles, which can be controlled by 2 degrees of freedom at the needle base (bevel direction and insertion distance), is a variant of nonholonomic planning for a Dubins car with no reversals, binary left/right steering, and uncertainty in motion direction.

Given a medical image with segmented obstacles, target, and start region, our method formulates the planning problem as a Markov Decision Process (MDP) based on an efficient discretization of the state space, models motion uncertainty using probability distributions, and computes actions to maximize the probability of success using infinite horizon DP. Using our implementation of the method, we generated motion plans for steerable needles to reach targets inaccessible to stiff needles and illustrated the importance of considering uncertainty in needle motion, as shown in Figs. 1, 5, and 6.

Our approach has key features particularly beneficial for medical planning problems. First, the planning formulation only requires parameters that can be directly extracted from images (the variance of needle orientation after insertion with or without direction change). Second, we can determine the optimal needle insertion start pose by examining the pre-computed DP look-up table containing the optimal probability of success for each needle state, as demonstrated in Fig. 7. Third, intra-operative medical imaging can be combined with the pre-computed DP look-up table to permit optimal steering of the needle in the operating room without requiring time-consuming intra-operative re-planning, as shown in Fig. 9.

Extending the motion planner to 3-D would expand the applicability of the method. Although the mathematical formulation can be naturally extended, substantial effort will be required to geometrically specify 3-D state transitions and to efficiently handle the larger state space when solving the MDP. We plan to consider faster alternatives to the general value iteration algorithm, including hierarchical and adaptive resolution methods (Chow and Tsitsiklis, 1991; Bakker et al., 2005; Moore and Atkeson, 1995), methods that prioritize states (Barto et al., 1995; Dean et al., 1995; Hansen and Zilberstein, 2001; Moore and Atkeson, 1993; Ferguson and Stentz, 2004), and other approaches that take advantage of the structure of our problem formulation (Bemporad and Morari, 1999; Branicky et al., 1998, 1999).

In future work, we also plan to consider new objective functions, including a weighted combination of path length and probability of success that would enable the computation of higher risk but possibly shorter paths. We also plan to develop automated methods to estimate needle curvature and variance properties from medical images and to explore the inclusion of multiple tissue types in the workspace with different needle/tissue interaction properties.

Our motion planner has implications beyond the needle steering application. We can directly extend the method to motion planning problems with a bounded number of discrete turning radii where current position and orientation can be measured but future motion response to actions is uncertain. For example, mobile robots subject to motion uncertainty with similar properties can receive periodic “imaging” updates from GPS or satellite images. Optimization of “insertion location” could apply to automated guided vehicles in a factory setting, where one machine is fixed but a second machine can be placed to maximize the probability that the vehicle will not collide with other objects on the factory floor. By identifying a relationship between needle steering and infinite horizon DP, we developed a motion planner capable of rigorously computing plans that are optimal in the presence of uncertainty.