External compression-induced fracture patterning on the surface of poly(dimethylsiloxane) cubes and microspheres

Abstract

This paper describes a method for creating sub-micron surface patterns on cubes and microspheres. In this method, PDMS cubes and microspheres are exposed to oxygen plasma, which creates a very thin, hard, surface-modified layer on a compliant substrate. These are then compressed, causing the layer to crack in patterns dictated by the distribution of tensile stresses in the surface layer. Cracks with sub-micron widths were generated on 1 cm³ cubes and 800 µm-diameter microspheres, and the resulting crack patterns were observed. Finite-element simulations of the tensile stress distributions reveal that the fracture patterns arise from different mechanisms in the cubes and spheres. In particular, pattern formation is associated with frictional contact in the cubes; but not in the microspheres where geometrical effects associated with changes in the cross-sectional area along the axis lead to generation of tensile stress. These observations and analyses provide a foundation on which to predict and guide crack pattern formation on a wide variety of small 3D objects. In anticipation of future applications in materials science and biology, we demonstrate selective deposition of compounds into the cracks to make them functionally differentiable from the rest of the surface.

Introduction

The controlled fabrication of two- and three-dimensionally (2D and 3D) ordered structures is important for the micro/nano-engineering of materials and devices.^1–6 One of the most accessible and useful technologies for laboratory micro/nanofabrication is the set of methods commonly referred to as soft lithography, where patterning is performed using structures constructed on an elastomeric polymer, typically polydimethylsiloxane (PDMS). Microcontact printing (µCP), for example, is a versatile soft lithographic technique in which molecular patterns are transferred to flat,⁷ smoothly curved,⁸ or spherical⁹ surfaces using PDMS stamps. Akin to µCP, a transfer printing method has been developed to deposit single-walled carbon nanotubes onto a variety of surface configurations.¹⁰ Other surface patterning methods include those of a class intended for the subsequent flexibility of the patterned substrates where a tensile pre-strain in the substrate is used to create buckled surface layers of silicon¹¹ or gold¹² for application in flexible electronics. Surface patterning methods have also been devised for curved and colloidal surfaces. The deposition and subsequent cross-linking of self-assembled monolayers onto flat, spherical, or cylindrical surfaces has been performed such that the layer can be removed from the template on which it was formed retaining its original configuration.¹³ Micropatterned polygons have also been created where 2D patterned sheets has been folded up to create 3D structures.^2,3 Finally, a combination of chemical vapor deposition (CVD) and projection lithography can be used to produce colloids (100 µm< diameter < 400 µm) with high-precision surface structures.¹⁴

Recently, we developed a fabrication method where external stretching-induced fracture of PDMS-supported brittle thin films generates parallel nano-scale cracks over large (1 cm² or larger) flat substrates.^15,16 The distinguishing feature of this approach is that differences in surface chemistry between the brittle thin film and the newly exposed crack surfaces enable the selective deposition of nanoparticles, organic molecules or proteins for applications that require metallic microfeatures, functionally active molecules or extra-cellular matrices for the reconfigurable patterning of living cells.¹⁵ Although experimentally straightforward and able to provide interesting features, the technology was limited for patterning on small objects due to the requirement for clamping parts of the substrate to be patterned and then stretching it. Here, we describe a variation of this method that overcomes this limitation where crack patterns are formed by external compression rather than by stretching. We anticipate that the functionalized patterns on these small objects will be beneficial for applications such as formation of microparticles with metallic features and electrical circuitry,^1,3 patterning small 3D objects with cell adhesion ligands and cells,¹⁷ and the self-assembly of 3-D structures, for example, of patchy adhering microspheres.⁴ Before developing these applications, however, it is critical to develop the patterning technology and understand the underlying principles that guide formation of various fracture patterns on different types of small objects. Thus, in this paper, we characterize this method using two representative objects: cubes with sides with lengths of about 10 mm, and microspheres with diameters of about 800 µm. Importantly, and non-intuitively, we find that there are different mechanisms by which compression-induced tensile strains, and thus crack patterns, are generated on the two different shapes of objects.

Materials and methods

Compression of oxidized PDMS cubes and microspheres

Polydimethylsiloxane prepolymer (Sylgard 184, Dow Corning) was prepared by mixing the curing agent and polymer base in weight ratios of 1:30 for the cubes and 1:10 for the microspheres. The pre-polymer for the cubes was poured into Petri dishes to a thickness of 1 cm and cured in an oven at 60°C for 24 hours. After curing, the 1 cm-thick sheet was manually cut into cubes. The pre-polymer for the microspheres was placed in a glass bottle in a weight ratio of 1:10 with DI water containing 0.1 wt% Pluronic F108 (an ethylene oxide/propylene oxide block copolymer surfactant). The container was vibrated for approximately 5 to 10 seconds with a vortex mixer (Fisher Vortex Genie 2, Fisher Scientific) to produce a suspension of PDMS prepolymer microspheres by emulsification.¹⁸ The emulsion was cured for 24 hours in an oven at 60°C.

In preparation for surface modification and subsequent patterning, the cured cubes and microspheres were washed with de-ionized (DI) water and dried. Surface modification was performed with radio frequency oxygen plasma (3 minutes, 0.5 Torr, maximum power, Plasma Prep II, SPI supplies) to generate a thin, silica-like film on the surface. Individual oxidized PDMS cubes were compressed using a manual micrometer-screw-driven compression apparatus (Micro Vice Holder; S. T. Japan USA, LLC. FL, USA). Compression of the microspheres was performed using a homemade system described in the main text. This compression induced periodic cracks in the surface layer, exposing the hydrophobic substrate in both the cubes and spheres.

Observation of the crack-patterns

An optical microscope (Nikon, TE 300) with a 2x objective lens was used to observe a cracked cube (Fig. 1). A typical pattern immediately after it had been released from approximately 35–40% compression, can be seen in Fig. 1C. Imaging of the microspheres after patterning (Fig. 2) was performed using the scanning-electron microscope (Philips/FEI XL30FEG). Prior to imaging, the relaxed PDMS microspheres were carbon coated (SPI Supplies, Module Carbon Coater; carbon density 2.2 g/cc) for 2 minutes.

Figure 1.

A) An oxidized cube of PDMS (each edge: 10 mm, 1:30 curing agent-to-base ratio in weight). B) Compression of the cube. C) An optical micrograph of crack patterns on the oxidized cube. Compression with significant friction at the contacts (top and bottom) yields a non-uniform tensile stress oriented perpendicular to the direction of compression; consequently, cracks were produced in the brittle oxidized layer. D) Relationship between the average crack spacing in the middle of the cubes (averaged from five cubes at each compression ratio) and the applied compressive strain.

Figure 2.

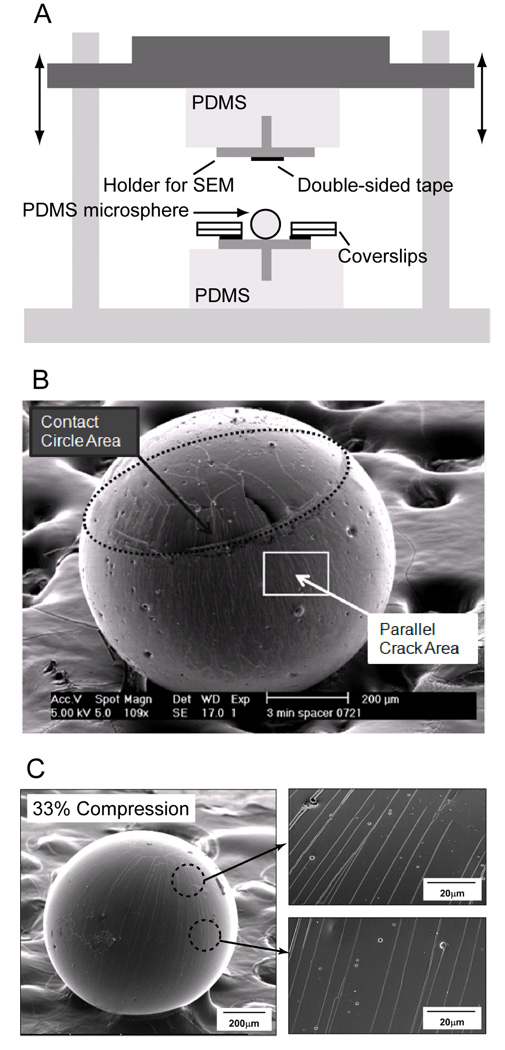
A) The device for controlled compression of the microspheres. A microsphere is compressed between a movable mount and a static stage. Double-sided tape is attached only on the upper mount. Compression between adhesive (upper) and nonadhesive (lower) surfaces enables selective adhesion of the microsphere to the upper mount after relaxation. Coverslips were used as spacers to determine the amount of compression. B) SEM image of a microsphere that has been compressed by 79%. The contact circle area (2D random orientation of cracks) and the area between the two contact circles (parallel cracks running from pole to pole) are marked with arrows on the image. C) Additional SEM images showing the cracks generated at a compression ratio of 33%, showing that the crack spacing is essentially constant throughout the region between the contact and equator.

Results and discussion

Experimental results

Oxidized PDMS cubes were uniaxially compressed to between 10 and 50% of their original side length (Figs. 1A & 1B). This generated an ordered series of parallel cracks aligned with the direction of compression. An optical image of a representative crack pattern is shown in Fig. 1C. The relationship between the nominal compressive strain (compression ratio) and the crack spacing was investigated by measuring the average crack spacing in the middle of a face of the compressed cubes. The average crack spacing at each strain was determined from measurements taken from five different cubes. Figure 1D shows the relationship between the amount of compression and the average crack spacing. Consistent with prior analyses and observations of thin-film cracking,^19–22 the average spacing systematically decreased with increasing amount of compression. As shown in Fig. 1D, the average crack spacing systematically decreased as the applied compressive strain increased. For compressive strains of 30% and greater, the standard deviation in the measured crack spacing was less than 15% of the average value. The variability was more significant at lower values of applied strain, with the standard deviation increasing to as much as 40% of the average value at a compressive strain of 10%. This decrease in uniformity of the spacing under reduced loading is an expected feature of thin-film cracking phenomena, owing to the influence of the initial defect density.

Microspheres have many uses as building blocks for assembled structures,^4,23–27 carrier beads for culture of adherent cells,^{17, 28, 29} and encoded beads for multiplexed assays.^10,30 Crack patterns were induced manually on microspheres by the following procedure. An adhesive-covered specimen mount used for the scanning-electron microscope (SEM), was fixed into a PDMS slab on a movable upper stage of a custom-built jig (Fig. 2A). A microsphere was placed on a bare specimen mount before it was oxidized. Following oxidation of the microsphere, the mount was fixed beneath the upper stage. The microsphere was then compressed between the two specimen mounts by lowering the upper stage. The amount of compression of the microsphere was controlled by using different numbers of glass cover slips (each 170 µm thick) as spacers between the specimen mounts (Fig. 2A). The nominal compressive strain (or compression ratio) was calculated as

$$\mathit{\text{Compression}}(\%)=\frac{d-t}{d}\times 100$$ (1)

where d and t are the diameter of microsphere and the thickness of spacers, respectively. During the compression test, the microsphere was transferred to the upper mount due to the adhesive coating, facilitating its subsequent transportation and handling. In addition, it ensured that the orientation of the microsphere relative to the compression direction was known when obtaining images.

Oxidized PDMS microspheres were compressed to 33 ± 1%, 58 ± 1%, and 79 ± 1%, and the resulting crack patterns were studied in the SEM (Fig. 2). Several features are of note. (i) The contact circle formed during compression is visible at the top pole of the microsphere (Fig. 2B & Fig 3B). The extent of this contact circle provided confirmation of the degree of compression imposed. (ii) The cracks inside and along this contact circle are randomly oriented, most likely due to contact stresses. (iii) Outside this contact circle, a pattern of relatively uniform and parallel cracks aligned with the compression direction (i.e., longitudinal cracks) was formed. Figure 2C shows SEM images of a whole sphere, compressed to 33%, and close-up images of the crack patterns near the equator and closer to the region of contact. One point that should be made in conjunction with this figure is that the average crack spacing on an individual microsphere is independent of distance from the equator, when measured anywhere outside of the contact circles. Based on thin-film fracture mechanics, this indicates that the tensile strain in the surface layer must be approximately constant in this region.^19–22

Figure 3.

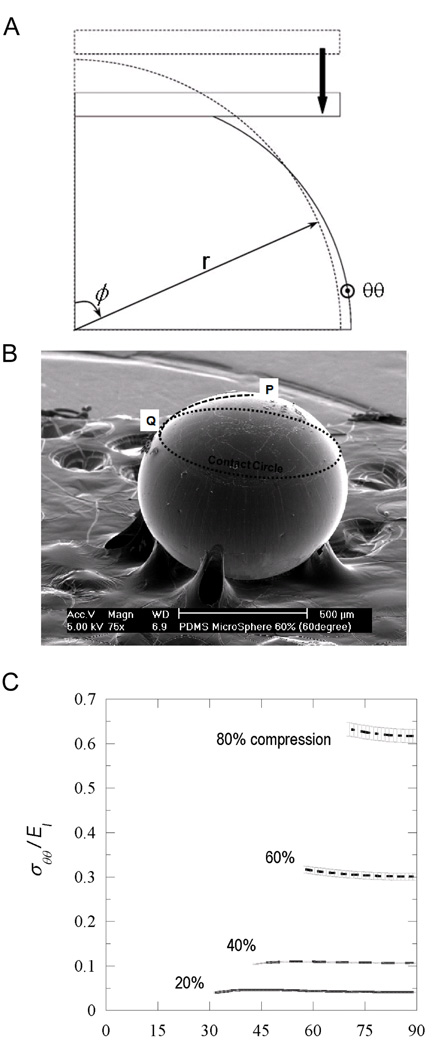
A) A quarter axisymmetric model of the sphere and the upper compressing plate in the relaxed and compressed states. The direction θθ is oriented pointing out of the page at the edge of the 2D representation of the microsphere. B) The experimentally observed contact circle whose radius was measured as the distance between P and Q, after relaxation, as noted schematically on the SEM image of a sphere patterned with 58% compression. C) The circumferential stress (normalized by PDMS modulus, E) as a function of meridional position, ϕ, at 20, 40, 60, and 80% compression (ϕ = 90° is coincident with the equator of the sphere). The plots are terminated at the boundary of the contact circle.

Finite-element calculations

Finite-element calculations were performed (using the commercial package ABAQUS) to understand the origin of the tensile stress that produced crack patterns in the oxidized layers. These calculations also allowed the magnitude of the induced tension to be related to the level of applied compression, so that comparisons could be made to experiments in which the tension was applied directly. The bulk PDMS was modeled using 3-D hybrid brick elements for the cubes and axisymmetric hybrid elements for the spheres. The oxidized layer was modeled using 3-D linear-elastic shell elements for the cubes and axisymmetric shell elements for the sphere. The properties of the bulk PDMS and the surface layer were taken to be those obtained in earlier studies, with the thickness of the oxidized layer being assumed to be 200 nm.¹⁶ When the surface layer is thin compared to the dimensions of the substrates, crack formation doesn't affect the overall deformation of the object. It is this overall deformation that controls the average local tension that leads to crack patterns. Therefore, the effects of crack formation were not included in the finite-element analyses.

Compression was applied to the cubes in the numerical model by imposing nodal displacements in the direction of compression on the top surface of the cube and constraining the nodes on the bottom surface from moving in this direction. Two extreme cases were modeled: one in which the nodes on the top and bottom surface were free to translate perpendicular to the direction of compression (the frictionless case) and one in which the nodes were constrained perpendicular to the direction of compression (the no-slip case).

Compression was applied to the spheres through a 2-D model of the aluminum compressing plates, assuming an elastic modulus of 70 GPa. The contact between the plate and the sphere was modeled as frictionless. Displacement control was used to model compression of the sphere to compression ratios of 20, 40, 60, and 80%. After compression, the sphere was allowed to relax elastically in the numerical model, since the constitutive properties of the PDMS have been shown to be elastic.¹⁶ The radius of the contact circle was equated to the length of the arc along the surface of the relaxed sphere that had been in contact with the compressing plates at the maximum extent of compression. This corresponds to the arc between the points P and Q shown in Fig. 3. A comparison between this distance obtained from the numerical calculations and the equivalent distance obtained from SEM images was used as confirmation that the extent of compression deduced from Eqn. 1 was correct. For example, as shown in Table 1, the radius of contact was numerically determined to be equal to 460 µm for a sphere that had been compressed by 80%, which agreed with the experimentally measured contact radius of 435 ± 15 µm.

Table 1.

Relationship between the extent of applied compression, contact circle radius, crack spacing, and induced circumferential normalized tensile stress in the equatorial plane. In addition, the crack spacing obtained in earlier work by directly applying tensile strains are compared to the spacing obtained in the present work. Microspheres were chosen to have a radius equal to approximately 400 µm.

Compression	79%	58%	33%
Microsphere radius, µm ± 2 µm	400	412	395
Contact circle radius, µm ± 15 µm	435	330	140
Crack spacing, µm	1.9 ± 0.3	3.8 ± 0.7	7.3 ± 0.6
Approximate equatorial circumferential normalized tensile stress (σθθ/E)	60%	25%	7%
Crack spacing of Zhu, et al. 2005, µm	2.7 ± 0.6	6.4 ± 0.8	12.3 ± 5
Crack spacing of Mills, et al. 2007, µm	--	1.9 ± 0.6	7.5 ± 3

The finite-element calculations showed that the origin of the tensile stress responsible for the cracking is different in the cubes and spheres. In the case of frictionless contact, tensile stresses can be induced in the surface layer of the cube only if Poisson's ratio for bulk PDMS is greater than that of the oxidized layer. In this case, the tensile stresses are uniform over all portions of the surface and depend on the elastic properties of the surface layer and the bulk PDMS. Conversely, if there is significant friction at the contact, the resultant constraint keeps the ends of the specimen from expanding in a lateral direction, while the middle section is free to bulge out. This induces a lateral tensile stress in the middle section that can cause cracking. The magnitude of the tensile stress depends on the level of friction at the contacts, and it varies over the free surface of the cube—higher stresses are induced in the center of the cube face than near the constrained ends (See supporting information). (It should be noted that if a long rectangular prism were compressed, then the tensile stress would only be induced near the constrained regions; the tensile stress in the middle would be reduced as the aspect ratio of the prism increased.)

Oxygen plasma treatment of PDMS creates compositional changes in the oxidized layer consistent with a silica-like structure^31–32 which may also produce a decrease in the Poisson’s ratio at the surface layer. However, experimental observations of the free surfaces of the cube bowing out under the applied compression indicate that friction at the contacts plays a significant role in inducing the tensile stress. Additionally, the crack patterns on the surface of a cube (Fig. 1C) confirm the predicted non-uniform distribution of tensile stresses on the cube face, as the cracks were concentrated in the center 2/3 to 1/2 of the free cube face. Furthermore, when the relationship between the tensile strains induced in the mid-sections of the cubes and the applied compression ratio was computed (See supporting information), it was found that these induced tensile strains were consistent with the tensile strains that were directly applied in the earlier work of Zhu et al.¹⁵ and Mills et al.¹⁶ to obtain similar crack spacings to those shown in Fig. 1D.

The results of the finite-element calculations for the spheres demonstrated that a circumferential tensile stress was generated in the absence of any friction. The circumferential stress normalized by the modulus of the surface layer, σ_θθ/E_l, is plotted as a function of the meridional coordinate ϕ in Fig. 3C. It was noted that the circumferential stress is tensile in the absence of friction, even if there is no mismatch in the Poisson's ratio between the surface layer and the bulk PDMS. In this regard, the generation of tensile stresses is much more robust in the spheres than in the cubes since, unlike long rectangular prisms that when compressed would generate tensile stress only near the constrained regions, a large sphere develops tensile stress uniformly across the surface outside the contact region. Furthermore, it is noted from Fig. 3C that the magnitude of the circumferential stress outside the contact region is constant (to within 10%) and independent of the distance from the equator of the sphere (ϕ) for all compression ratios. This is consistent with the experimental observation that the crack spacing was independent of ϕ.

Discussion

Table 1 summarizes some values for the radii of the microspheres, the radius of the contact circle, and the average crack spacing at the equator for three different percentages of compression, as defined by Eqn. (1). The measured values of the contact radius agreed with the calculated values from the finite-element calculations—indicating that the compression ratios deduced from the dimensions of the glass spacers were correct. Added to this table are calculations of the tensile strain computed from the finite-element calculations. Also added to this table are the measured crack spacing at the corresponding levels of tensile strain obtained in the previous work^15,16 in which the tensile strains were directly imposed by applied tension—an approach that can not be used with the three-dimensional objects examined in this work. While the same trends in crack spacing as a function of tensile strain are seen between the two approaches, it should be noted that there are several possible reasons why some discrepancies exist in the measurements between the different experiments: (i) the oxidation conditions between runs could not be controlled reliably; (ii) the curvature of the spheres may have some influence on the crack pattern; and (iii) the technique for fabricating the PDMS microspheres had to be different from the technique for created 2-D plates, resulting in different properties—the properties of the bulk material are known to control the crack spacing.²²

The mechanics responsible for inducing tensile stresses within the oxidized layer differs between the spherical and cubic geometries. In the course of this study, we recognized three mechanisms by which a tensile stress may be induced in the surface layer of a 3-D shape subjected to an applied compression: (i) the constraint induced by a Poisson's ratio mismatch between the surface layer and the bulk material; (ii) the constraint induced by frictional effects at the contacts; and (iii) the constraint induced by geometrical effects associated with a change in the cross-sectional area along the axis of compression. It is this final mechanism that is primarily responsible for generating the tensile stresses necessary to induce cracks on the sphere. To summarize, in right prismatic shapes, such as the cube, uniform axial compression alone does not induce a tensile stress perpendicular to the axis of compression. For this class of shapes, tensile stresses can be induced by compression only if there is a Poisson's ratio mismatch between the surface layer and the bulk material, or if there is friction at the contact. Alternatively, in non-prismatic shapes, such as the sphere, when the cross-sectional area changes along the axis of compression, tensile stresses can be generated in the surface layer solely from the constraint induced by geometry. Although the details of the stress distributions depend on the shape, this provides a general guideline for predicting which shapes will produce crack patterns using compression techniques similar to those described here.

Finally, we demonstrated two simple applications of how the crack patterns might be used. (See supporting information). First, we preferentially adsorbed a fluorescent synthetic organic molecule in the parallel cracks. Successful patterning was achieved by hydrophobic interactions between the molecule and the exposed crack surface which is hydrophobic^{33, 34} . Micropatterning of synthetic organic molecules onto three-dimensional substrates enhances or enables many applications in biosensing, cell patterning, and nanotechnology.^35,36 This simple cracking based method of patterning custom-synthesized organic molecules thus has future potential in bioscience for patterning cell-adhesion ligands and other bioactive molecules. The crack-patterned surfaces can also serve as a template for the assembly of metallic nanoparticles.¹⁵ Second, we decorated the cracks using template-assisted self-assembly (TASA)^{37, 38} of aqueous gold nanoparticle (GNP) suspensions. These results are interesting given recent advances in the use of ordered arrays of micro- or nano-sized metallic particles^39–44 for photonic-crystals, miniaturized sensors, and cell patterning.⁴⁵

Conclusions

In summary, we have presented the development of ordered crack patterns on the surface of PDMS cubes and microspheres by compression of the elastomeric polymer with a brittle oxidized surface layer. The conditions required to induce suitable tensile stresses orthogonal to the applied compression have been elucidated by means of finite-element calculations. In particular, it was observed that compression cracking of prismatic shapes is generally only possible in a limited region that is affected by the presence of frictional constraints. Conversely, geometrical constraints in geometries such as spheres can lead to compression cracking even in the absence of friction. The fabrication technique that we propose has three features that make it attractive: (i) it is easy and fast to implement and does not require expensive equipment; (ii) it can create ordered patterns on small objects where lithography, µCP, or stretch-induced patterning are difficult; and (iii) the patterning method is scalable and increasing the number of microspheres or other objects that can be patterned simultaneously should be straightforward. Such capabilities may be particularly beneficial for applications such as self-assembly of patchy microspheres, where many patterned objects are needed.⁴⁶ Although it is difficult to generate uniform patterns over the entire object, this technique is unique in its capabilities and has potential to be used to engineer functional small objects for materials science and biological applications.^47,48

Supplementary Material

1_si_001. Supporting Information.

We additionally present the chemical structure and synthesis information for the fluorescent compound used to selectively absorb onto the crack faces, procedures for gold nanoparticle patterning, as well as selected results from finite-element calculations performed on the cube geometry. This information is available free of charge via the Internet at http://pubs.acs.org.