Bayesian variable selection using an adaptive powered correlation prior

Abstract

The problem of selecting the correct subset of predictors within a linear model has received much attention in recent literature. Within the Bayesian framework, a popular choice of prior has been Zellner's g-prior which is based on the inverse of empirical covariance matrix of the predictors. An extension of the Zellner's prior is proposed in this article which allow for a power parameter on the empirical covariance of the predictors. The power parameter helps control the degree to which correlated predictors are smoothed towards or away from one another. In addition, the empirical covariance of the predictors is used to obtain suitable priors over model space. In this manner, the power parameter also helps to determine whether models containing highly collinear predictors are preferred or avoided. The proposed power parameter can be chosen via an empirical Bayes method which leads to a data adaptive choice of prior. Simulation studies and a real data example are presented to show how the power parameter is well determined from the degree of cross-correlation within predictors. The proposed modification compares favorably to the standard use of Zellner's prior and an intrinsic prior in these examples.

1. Introduction

Consider the linear regression model with n independent observations and let y = (y₁,…,y_n)′ be the vector of response variables. The canonical linear model can be written as

$$\mathit{y}=\mathit{X}\mathit{\beta }+\mathbf{ϵ},$$ (1.1)

where X = (x₁,…,x_p) is an n × p matrix of explanatory variables with x_j = (x_1j,…,x_nj)′ for j = 1,…, p. Let β = (β₁,…, β_p)′ be the corresponding vector of unknown regression parameters, and ϵ ~ N(0, σ²I). Throughout the paper, we assume y to be empirically centered to have mean zero, while the columns of X have been standardized to have mean zero and norm one, so X′X will be the empirical correlation matrix.

Under the above regression model, it is assumed that only an unknown subset of the coefficients are non-zero, so that the variable selection problem is to identify this unknown subset. Bayesian approaches to the problem of selecting variables/predictors within a linear regression framework has received considerable attention over the years, for example see, Mitchell and Beauchamp (1988), Geweke (1996), George and McCulloch (1993, 1997), Brown et al. (1998), George (2000), Chipman et al. (2001) and Casella and Moreno (2006).

For the linear model, Zellner (1986) suggested a particular form of a conjugate normal-Gamma family called the g-prior which can be expressed as

$$\begin{array}{c}\mathit{\beta }|{\sigma }^2,\mathit{X}~\mathrm{N}\left(0,\frac{{\sigma }^2}{g}{(\mathit{X}\prime \mathit{X})}^{-1}\right),\hfill \\ {\sigma }^2~\mathit{\text{IG}}(a_0,b_0),\hfill \end{array}$$ (1.2)

where g > 0 is a known scaling factor and a₀ > 0, b₀ > 0 are known parameters of the inverse Gamma distribution with mean a₀/(b₀−1). The prior covariance matrix of β is the scalar multiple σ²/g of the inverse Fisher information matrix, which concurrently depends on the observed data through the design matrix X.

This particular prior has been widely adopted in the context of Bayesian variable selection due to its closed form calculations of all marginal likelihoods which is suitable for rapid computations over a large number of submodels, and its simple interpretation that it can be derived from the idea of a likelihood for a pseudo-dataset with the same design matrix X as the observed sample (see, Zellner, 1986; George and Foster, 2000; Smith and Kohn, 1996; Fernandez et al., 2001).

In this paper, we point out a drawback of using Zellner's prior on β particularly when the predictors (x_j) are highly correlated. The conditional variance of β given σ² and X is based on the inverse of the empirical correlation of predictors and puts most of its prior mass in the direction that causes the regression coefficients of correlated predictors to be smoothed away from each other. So when coupled with model selection, Zellner's prior discourages highly collinear predictors to enter the models simultaneously by inducing a negative correlation between the coefficients.

We propose a modification of Zellner's g-prior by replacing (X′X)⁻¹ by (X′X)^λ where the power λ ∈ ℝ, controls the amount of smoothing of collinear predictors towards or away from each other accordingly as λ > 0 or λ < 0, respectively. For λ > 0, the new conditional prior variance of β puts more prior mass in the direction that corresponds to a strong prior smoothing of regression coefficients of highly collinear predictors towards each other. Therefore, by choosing λ > 0 our proposed modification in contrast, forces highly collinear predictors entering or exiting the model simultaneously (see Section 2). Hence, the use of the power hyperparameter λ to the empirical correlation matrix helps us to determine whether models with high collinear predictors are preferred or not.

The hyperparameter λ is further incorporated into the prior probabilities over model space with the same intentions of encouraging or discouraging the inclusion of groups of correlated predictors. The choice of hyperparameter is obtained via an empirical Bayes approach and the inference regarding model selection is then made based on the posterior probabilities. By allowing the power parameter λ to be chosen by the data, we let the data decide whether to include collinear predictors or not.

The remainder of the paper is structured as follows. In Section 2, we describe in detail the powered correlation prior and provide a simple motivating example, when p = 2. Section 3, describes the choice of new prior specifications for model selection. The Bayesian hierarchical model and the calculation of posterior probabilities are presented in Section 4. The superior performance of using the powered correlation prior over Zellner's g-priors is illustrated with the help of simulation studies and real data examples in Section 5. Finally, in Section 6 we conclude with a discussion.

2. The adaptive powered correlated prior

Consider again a normal regression model as in (1.1), where X′X represents the correlation matrix. Let X′X = ΓDΓ′ be the spectral decomposition, where the columns of Γ are the p orthonormal eigenvectors and D is the diagonal matrix with eigenvalues d₁ ≥ … ≥ d_p ≥ 0 as the diagonal entries. The powered correlation prior for β conditioned on σ² and X is defined as

$$\mathit{\beta }|{\sigma }^2,\mathit{X}~\mathrm{N}\left(0,\frac{{\sigma }^2}{g}{(\mathit{X}\prime \mathit{X})}^{\lambda }\right),$$ (2.1)

where (X′X)^λ = ΓD^λΓ′, with g > 0 and λ ∈ ℝ controlling the strength and the shape, respectively, of the prior covariance matrix, for a given σ² > 0.

There are several priors which are special cases of the powered correlation prior. For instance, λ = −1 produces the Zellner's g-prior (1.2). By setting λ =0 we have (X′X)⁰ = I which gives us the ridge regression model of Hoerl and Kennard (1970), under this model β_j are given independent N(0, σ²/g) priors. Next we illustrate how λ controls the model's response to collinearity which is the main motivation for using the powered correlation prior.

Let T = XΓ and θ = Γ′β. The linear model can be written in terms of the principal components as

$$\mathit{y}~\mathrm{N}(\mathit{T}\mathit{\theta },{\sigma }^2)\text{\hspace{1em}with}\mathit{\theta }~\mathrm{N}\left(0,\frac{{\sigma }^2}{g}{\mathit{D}}^{\lambda }\right).$$ (2.2)

The columns of the new design matrix T are the principal components, and so the original prior on β can be viewed as independent mean zero normal priors on the principal component regression coefficients, with prior variance proportional to the power of the corresponding eigenvalues, $d_1^{\lambda },\dots ,d_p^{\lambda }$. Principal components with d_i near zero indicate a presence of a near-linear relationship between the predictors, and the direction determined by the corresponding eigenvectors are those which are uninformative from the data. A classical frequentist approach to handle collinearity is to use principal component regression, and eliminate those dimensions with very small eigenvalues. Then transform back to the original scale, so that no predictors are actually removed. Along the same lines, we shall illustrate on how changing the value of λ would affect the prior correlation and demonstrate the intuition behind our proposed modification. For a simple illustration consider the case with p = 2 with a positive correlation ρ between them so that

$${(\mathit{X}\prime \mathit{X})}^{\lambda }={\left[\begin{array}{cc}1\hfill & \rho \hfill \\ \rho \hfill & 1\hfill \end{array}\right]}^{\lambda }.$$ (2.3)

It easily follows that in this case,

$$\mathbf{\Gamma }=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1\hfill & 1\hfill \\ 1\hfill & -1\hfill \end{array}\right]\text{ and }{\mathit{D}}^{\lambda }=\left[\begin{array}{cc}{(1+\rho )}^{\lambda }\hfill & \hfill 0\hfill \\ \hfill 0\hfill & {(1-\rho )}^{\lambda }\hfill \end{array}\right].$$ (2.4)

The first principal component of our new design matrix T can be written as the sum of the predictors and the second as the difference

$$\mathit{T}=\frac{1}{\sqrt{2}}{\left[\begin{array}{c}{\mathit{x}}_1+{\mathit{x}}_2\hfill \\ {\mathit{x}}_1-{\mathit{x}}_2\hfill \end{array}\right]}^{\prime }\text{\hspace{1em}with}\mathit{\theta }~\mathrm{N}\left(\left[\begin{array}{c}0\hfill \\ 0\hfill \end{array}\right],\frac{{\sigma }^2}{g}\left[\begin{array}{cc}{(1+\rho )}^{\lambda }\hfill & \hfill 0\hfill \\ \hfill 0\hfill & {(1-\rho )}^{\lambda }\end{array}\right]\right),$$ (2.5)

for λ > 0 the prior on the coefficient for the sum has mean zero and variance (1 + ρ)^λ, while the prior on the coefficient for the difference has mean zero and variance (1 − ρ)^λ.

As ρ in (2.5) increases, a smaller prior variance is given to the coefficient for the difference of the two predictors, and hence introduces more shrinkage to the principal component directions that are associated with small eigenvalues. So that larger λ forces the difference to be more likely closer to the prior mean (zero). On the original β scale this corresponds to strong prior smoothing of regression parameters corresponding to highly collinear predictors.

On the other hand λ < 0 places a large prior variance on the coefficient for the difference, and a smaller variance on the coefficient of the sum, thereby shrinking those directions which correspond to large eigenvalues. This has an effect of smoothing the regression parameters corresponding to highly collinear predictors away from each other, forcing the two predictors to be negatively correlated.

Hence in dimensions greater than two, in the presence of collinear predictors, λ has the flexibility to introduce more shrinkage in the directions that correspond to the small eigenvalues. This behavior motivates us to allow for the possibility of choosing alternative values for λ. In particular, we allow the data to determine the choice of λ using an empirical Bayes approach. We note that in the context of principal components regression, West (2003) allows for different prior variances on the principal component coefficients. However, our interest lies in the collinearity on the original scale.

3. Model specification

The main focus of this paper is to use this powered correlation prior in a model selection problem. For the linear regression model in (1.1), it is typically the case that only an unknown subset of the coefficients β_j are non-zero, so in the context of variable selection we begin by indexing each candidate model with one binary vector δ = (δ₁,…,δ_p)′ where each element δ_j takes the value 1 or 0 depending on whether it is included or excluded from the model. More specifically, let

$${\delta }_j=\{\begin{array}{cc}1\hfill & \text{if}{\mathit{x}}_j\text{is included in the model},\hfill \\ 0\hfill & \text{if}{\mathit{x}}_j\text{is excluded from the model}.\hfill \end{array}$$ (3.1)

We now rewrite the linear regression model, given δ as

$$\mathit{y}={\mathit{X}}_{\mathit{\delta }}{\mathit{\beta }}_{\mathit{\delta }}+\mathbf{ϵ},$$ (3.2)

where ϵ ~ N(0, σ²I), and X_δ and β_δ are the design matrix and the regression parameters of the model only including the predictors with δ_j = 1. In the context of variable selection we can write the powered correlation prior as

$${\mathit{\beta }}_{\mathit{\delta }}|\mathit{\delta },{\sigma }^2,\mathit{X}~\mathrm{N}\left(0,\frac{{\sigma }^2}{g}{({\mathit{X}\prime }_{\mathit{\delta }}{\mathit{X}}_{\mathit{\delta }})}^{\lambda }\right)\text{\hspace{1em}with}{({\mathit{X}\prime }_{\mathit{\delta }}{\mathit{X}}_{\mathit{\delta }})}^{\lambda }={\mathbf{\Gamma }}_{\mathit{\delta }}{\mathit{D}}_{\mathit{\delta }}^{\lambda }{\mathbf{\Gamma }\prime }_{\mathit{\delta }},$$ (3.3)

where Γ_δ is the matrix of eigenvectors and ${\mathit{D}}_{\mathit{\delta }}^{\lambda }$ is a diagonal matrix with diagonal entries as the eigenvalues of ${({\mathit{X}\prime }_{\mathit{\delta }}{\mathit{X}}_{\mathit{\delta }})}^{\lambda }$ .

Now that we have defined the prior for the coefficients given the model we now incorporate the same idea into the choice of prior for the inclusion indicators. With respect to Bayesian variable selection, a common prior for the inclusion indicators is p(δ) ∝ π^p_δ (1 − π)^p−p_δ (George and McCulloch, 1993, 1997; George and Foster, 2000) where $p_{\delta }={\displaystyle {\sum }_{j=1}^p{\delta }_j}$ is the number of predictors in the model defined by δ, and π is the prior inclusion probability for each covariate. We can see this being equivalent to placing Bernoulli (π) priors on δ_j and thereby giving equal weight to any pair of equally sized models. Setting $\pi =\frac{1}{2}$ yields the popular uniform prior over model space formed by considering all subsets of predictors and under this prior the posterior model probability is proportional to the marginal likelihood. A drawback of using this prior is that it puts most of its mass on models of size ≃ p/2 and it does not take into account the correlation between the predictors. Yuan and Lin (2005) proposed an alternative prior over model space:

$$P(\mathit{\delta }|\pi )\mathrm{\propto }{\pi }^{p_{\delta }}{(1-\pi )}^{p-p_{\delta }}{|{\mathit{X}\prime }_{\mathit{\delta }}{\mathit{X}}_{\mathit{\delta }}|}^{1/2},$$ (3.4)

where | · | denotes the determinant, and $|{\mathit{X}\prime }_{\mathit{\delta }}{\mathit{X}}_{\mathit{\delta }}|=1$ if p_δ = 0. Since $|{\mathit{X}\prime }_{\mathit{\delta }}{\mathit{X}}_{\mathit{\delta }}|$ is small for models with highly collinear predictors, this prior discourages these models. We follow Yuan and Lin in that we use the information from the design matrix to build a prior for the model space. However, we do not necessarily want to penalize models with collinear predictors. We propose to incorporate the power parameter λ into a prior for δ that could encourage or discourage inclusion of groups of correlated predictors. So we propose the following prior on model space:

$$P(\mathit{\delta }|\lambda ,\pi )\mathrm{\propto }{\pi }^{p_{\delta }}{(1-\pi )}^{p-p_{\delta }}{|{\mathit{X}\prime }_{\mathit{\delta }}{\mathit{X}}_{\mathit{\delta }}|}^{-\lambda /2}.$$ (3.5)

So for large values of λ, the prior puts more of its mass on models with highly collinear predictors; while for λ < 0, penalizing models with collinear predictors. Hence coupled with the powered correlation prior, positive (negative) λ encourages (discourages) highly collinear predictors to enter the model simultaneously. Note that λ = −1 gives us Zellner's prior on the coefficients coupled with the prior of Yuan and Lin on the models.

3.1. Choice of g

The parameter g defines the strength of the powered correlation prior. The choice of g is complicated in that large values of g will result in the prior dominating the likelihood, and small values of g would favor the null model (George and Foster, 2000). Various choices of g have been proposed over the years. For example, Smith and Kohn (1996) performed variable selection involving splines with a fixed value of g = 0.01. However, the choice of g may also depend on the sample size n, or the number of predictors p. George and Foster (2000) propose an empirical Bayes method for estimating g from its marginal likelihood. Foster and George (1994) recommended using g = 1/p² based on a risk inflation criterion (RIC). Kass and Wasserman (1995) suggests the unit information prior, where the amount of information in the prior corresponds to the amount of information in one observation, leading to g = 1/n. This leads to the Bayes factor as an approximation of the BIC. Fernandez et al. (2001) suggest g = 1/max(n, p²) called the benchmark prior (BRIC), which is a combination of RIC and BIC. More recently Liang et al. (2008) suggest a mixture of g-priors as an alternative to the default g-priors.

Since the scale of ${({\mathit{X}\prime }_{\mathit{\delta }}{\mathit{X}}_{\mathit{\delta }})}^{\lambda }$ will depend on λ, we first standardize so that we may separate out the scale of g from that of ${({\mathit{X}\prime }_{\mathit{\delta }}{\mathit{X}}_{\mathit{\delta }})}^{\lambda }$ . To do so we modify (3.3) as

$${\mathit{\beta }}_{\mathit{\delta }}|\mathit{\delta },{\sigma }^2,\mathit{X}~\mathrm{N}\left(0,\frac{{\sigma }^2}{g}k{({\mathit{X}\prime }_{\mathit{\delta }}{\mathit{X}}_{\mathit{\delta }})}^{\lambda }\right)\text{\hspace{1em}with}k\equiv k(\lambda ,\mathit{\delta },\mathit{X})=\frac{\text{Tr}[{({\mathit{X}\prime }_{\mathit{\delta }}{\mathit{X}}_{\mathit{\delta }})}^{-1}]}{\text{Tr}[{({\mathit{X}\prime }_{\mathit{\delta }}{\mathit{X}}_{\mathit{\delta }})}^{\lambda }]}.$$ (3.6)

This has an effect of setting the trace of ${({\mathit{X}\prime }_{\mathit{\delta }}{\mathit{X}}_{\mathit{\delta }})}^{\lambda }$ to be equal to that of using λ = −1 regardless of the choice of λ. We then choose g = 1/n, as in the unit information prior (Kass and Wasserman, 1995).

For ${({\mathit{X}\prime }_{\delta }{\mathit{X}}_{\delta })}^{\lambda }={\mathbf{\Gamma }}_{\delta }{\mathit{D}}_{\delta }^{\lambda }{\mathbf{\Gamma }}_{\delta }$ , k can be considered as the ratio of the average eigenvalues with those of $\lambda =-1,({\sum }_j{\mathit{D}}_{{\delta }_j}^{-1}/n)/{\sum }_j{\mathit{D}}_{{\delta }_j}^{\lambda }/n$. Instead of the trace one could have opted to choose the determinant, i.e. the ratio of the product of the eigenvalues. An advantage of using the average of the eigenvalues is that it provides more stability and in turn helps prevent the prior from dominating the likelihood. We note that other choices of standardization and choice of g are possible and are left for future investigations.

4. Model selection using posterior probabilities

In the Bayesian framework, a set of prior distributions is specified on the parameters θ_δ = (β_δ, σ²) for each model, along with a meaningful set of prior model probabilities P(δ|λ, π) over the class of all models. Model selection is then done based on the posterior probabilities. Using the set of priors defined in the previous section, we can now construct a hierarchical Bayesian model to perform variable selection

$$\begin{array}{c}\mathit{y}|\mathit{\beta },\mathit{\delta },{\sigma }^2,\mathit{X}\mathit{~}\mathrm{N}({\mathit{X}}_{\mathit{\delta }}{\mathit{\beta }}_{\mathit{\delta }},{\sigma }^{2}I),\hfill \\ {\mathit{\beta }}_{\mathit{\delta }}|\mathit{\delta },{\sigma }^2,\mathit{X}~\mathrm{N}\left(0,\frac{{\sigma }^2}{g}k{({\mathit{X}\prime }_{\mathit{\delta }}{\mathit{X}}_{\mathit{\delta }})}^{\lambda }\right),\hfill \\ {\sigma }^2~\mathit{\text{IG}}\left(\frac{{\gamma }_0}{2},\frac{{\gamma }_0}{2}\right),\hfill \\ P(\mathit{\delta }|\lambda ,\pi )\mathrm{\propto }{\pi }^{p_{\delta }}{(1-\pi )}^{p-p_{\delta }}{|{\mathit{X}\prime }_{\mathit{\delta }}{\mathit{X}}_{\mathit{\delta }}|}^{-\lambda /2},\hfill \end{array}$$ (4.1)

where k is as defined in (3.6) The key idea in computing the posterior model probabilities is to obtain the marginal likelihood of the data under model δ by integrating out the model parameters

$$P(\mathit{y}|\mathit{\delta },\mathit{X})={\displaystyle \int P(\mathit{y}|{\mathit{\theta }}_{\mathit{\delta }},\mathit{\delta },\mathit{X})}P({\mathit{\theta }}_{\delta }|\mathit{\delta },\mathit{X})\mathrm{d}{\mathit{\theta }}_{\mathit{\delta }}.$$ (4.2)

The choice of conjugate priors allows us to analytically compute the above integral. Using the hierarchical model and integrating out θ_δ we obtain the conditional distribution of y given δ and X,

$$\mathit{y}|\mathit{\delta },\mathit{X}~{\mathit{t}}_{({\gamma }_0+n)}\left\{0,\left({\mathit{I}}_n+\frac{k}{g}{\mathit{X}}_{\mathit{\delta }}{({\mathit{X}\prime }_{\mathit{\delta }}{\mathit{X}}_{\mathit{\delta }})}^{\lambda }{\mathit{X}\prime }_{\mathit{\delta }}\right)\right\}.$$ (4.3)

Then model comparison is done via the posterior probabilities,

$$P(\mathit{\delta }|\mathit{y},\mathit{X})\mathrm{\propto }P(\mathit{y}|\mathit{\delta },\mathit{X})P(\mathit{\delta }|\lambda ,\pi ).$$ (4.4)

In order to fully specify our prior distribution we need to specify g, γ₀, π and λ.We choose g = 1/n the unit information prior proposed by Kass and Wasserman (1995). For γ₀, after trying various choices, we saw that the model selected was not sensitive to the value of γ₀ chosen, and since there is little or no information about this hyperparameter we decided to set γ₀ to a constant, which has led to reasonable results as pointed out by George and McCulloch (1997). Following these lines, we set γ₀ = 0.01 for the rest of the article, which corresponds to placing a non-informative prior on σ².

The parameters (λ, π) are very influential and informative with respect to the model selected and it is of utmost importance that we choose them carefully. Thus, we propose an empirical Bayes approach to select π ∈ (0, 1) and λ ∈ ℝ by marginalizing over δ and maximizing the marginal likelihood function given by

$$m(\mathit{y}|\mathit{X},\pi ,\lambda )={\displaystyle \sum _{\mathit{\delta }}P(\mathit{y}|\mathit{\delta },\mathit{X})P(\mathit{\delta }|\lambda ,\pi ).}$$ (4.5)

When the number of predictors, p is of moderate size (e.g., p≤20) the above sum can be computed by evaluating (4.2) for each model via complete enumeration for a given (π, λ). Numerical optimization is then used to maximize m(y|X, π, λ) defined in (4.5) to obtain the pair (π̂, λ̂). Specifically, we fix λ on a fine grid and for each λ, we maximize over π ∈ (0, 1), and obtain π̂ (λ) and obtain λ̂ = argmax m(y|X, π̂ (λ), λ).

5. Simulations and real data

We shall now compare our proposed method to the standard use of Zellner's prior with a uniform prior over model space, i.e. the common approach

$$\begin{array}{l}{\mathit{\beta }}_{\mathit{\delta }}|{\mathit{\sigma }}^2,\mathit{\delta },\mathit{X}~\mathrm{N}\left(0,{\sigma }^2{({\mathit{X}\prime }_{\mathit{\delta }}{\mathit{X}}_{\mathit{\delta }})}^{-1}/g\right)\text{\hspace{1em}where}g=1/n,\\ {\sigma }^2~\mathit{\text{IG}}\left(\frac{{\gamma }_0}{2},\frac{{\gamma }_0}{2}\right), {\gamma }_0=0.01,\\ P(\mathit{\delta })={(1/2)}^p.\end{array}$$ (5.1)

We also compared our method to the fully automatic Bayesian variable selection procedure proposed by Casella and Moreno (2006) where posterior probabilities are computed using intrinsic priors (Berger and Pericchi, 1996) which eliminates the need for tuning parameters. However, we note that this procedure was not specifically designed to handle correlated predictors.

In this section we evaluate the performance of using our proposed method in selecting the correct subset of predictors as compared to the two abovementioned methods, based on a simulated data involving highly collinear predictors. Comparisons are also presented for one real dataset.

5.1. Simulation study

For the simulated example, we consider the true model

$$y=x_1+x_2+\epsilon \text{\hspace{1em}where}\epsilon ~\mathrm{N}(0,1).$$ (5.2)

We generate p predictors from a multivariate normal with Cov(x_j, x_k) = ρ^|j−k|, for ρ = 0.9. For Case 1, we fixed p = 4, while for Case 2 we used p = 12, so that in the first case there were two unimportant predictors, while in Case 2, there were 10. For both cases, we generated 1000 datasets each with n = 30 observations.

5.1.1. Case 1: p = 4

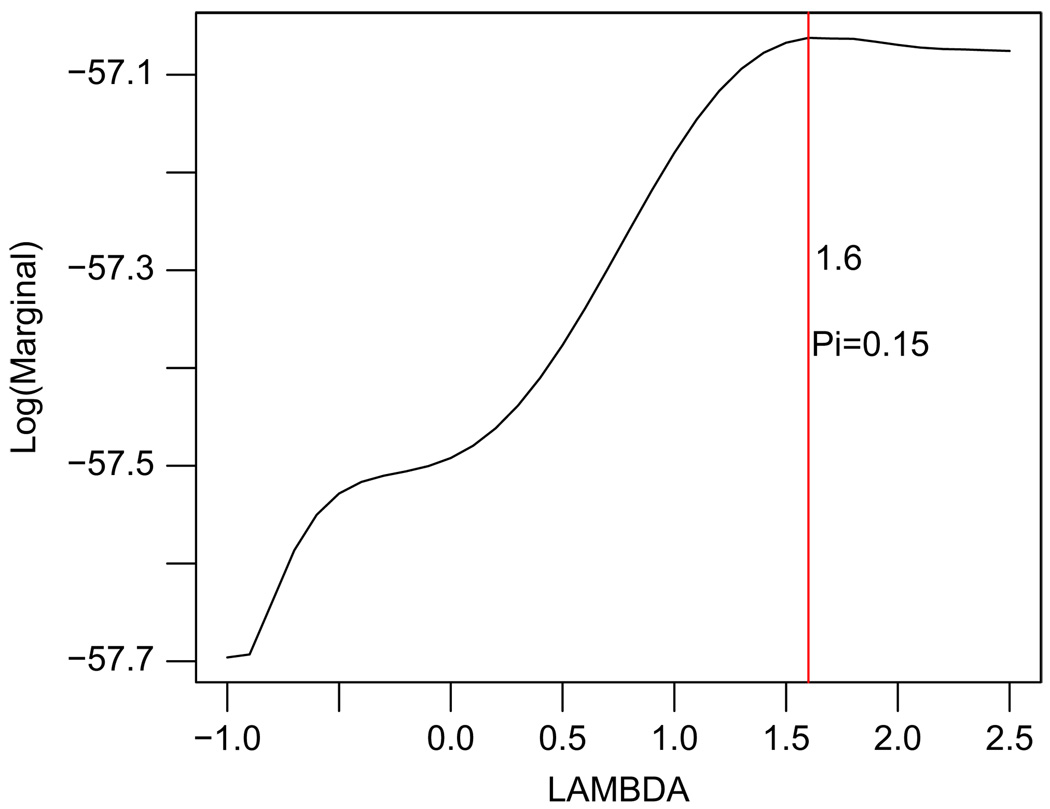
Using the empirical Bayes approach mentioned earlier we compute the optimal pair λ̂ = 1.6 and π̂ = 0.15 which maximizes the marginal likelihood obtained under complete enumeration of all possible 2⁴ − 1 models. The estimates (λ̂, π̂) are the values obtained after averaging over the 1000 replications (Fig. 1).

Fig. 1.

Plot of λ vs. Log[m(y|X, π, λ)], maximized over π ∈ (0, 1), corresponding to case 1: p = 4. Averaged over 1000 simulations. The vertical line represents the location of the global maximum.

From Table 1, the performance of our proposed method appears quite good compared to the other two methods. We see that Zellner's as well as the intrinsic prior's chooses single variable models with over half of its posterior probability. In contrast, using the powered correlation prior smoothes the regression parameters of the correlated variables towards each other, by giving more prior information in the direction that are less determined by the data, and selects the correct model, (x₁, x₂) with an overwhelming 0.622 posterior probability.

Table 1.

For Case 1, comparing average posterior probabilities, corresponding to the case 1: p = 4, averaged across 1000 simulations.

Zellner's			PoCor			Intrinsic Prior
Subset	Avg Post Prob	% Selected	Subset	Avg Post Prob	% Selected	Subset	Avg Post Prob	% Selected
x2	0.321	37.6	x1, x2	0.622	68.7	x1	0.468	51.9
x1	0.221	20.4	x2	0.116	10.4	x2	0.410	44.2
x1, x2	0.105	11.2	x1, x2, x3	0.089	3.4	x1, x2	0.039	0.62
x1, x2, x4	0.074	5.9	x1, x2, x4	0.040	3.1	x1, x3	0.020	0.36
x1, x2, x3	0.055	4.4	x1, x2, x3, x4	0.039	2.5	x3	0.020	0.24
x2, x4	0.052	2.8	x1	0.030	2.3	x1, x4	0.017	1.07
x2, x3	0.045	2.6	x1, x3	0.009	1.4	x2, x3	0.010	0.26
x1, x3	0.035	2.1	x2, x3	0.003	1.0	x2, x4	0.008	0.20
x1, x3, x4	0.024	1.4	x2, x3, x4	0.002	0.9	x4	0.002	0.12
x1, x2, x3, x4	0.019	1.1	x1, x3, x4	0.002	0.6	x1, x2, x4	0.003	0.08

% Selected is the number of times (in %) each model was selected as the highest posterior model out of 1000 replications. Zellner's represents use of Zellner's prior as in (5.1). PoCor represents our proposed modification as in (4.1). Intrinsic Prior represents the fully automatic procedure proposed by Casella and Moreno (2006).

Table 1 also lists the number of times (in %) each model was selected as the model with highest posterior probability out of 1000 replications by the three methods. We see that the powered correlation prior based method picks the correct model, (x₁, x₂), 68.7% of the time.

5.1.2. Case 2: p = 12

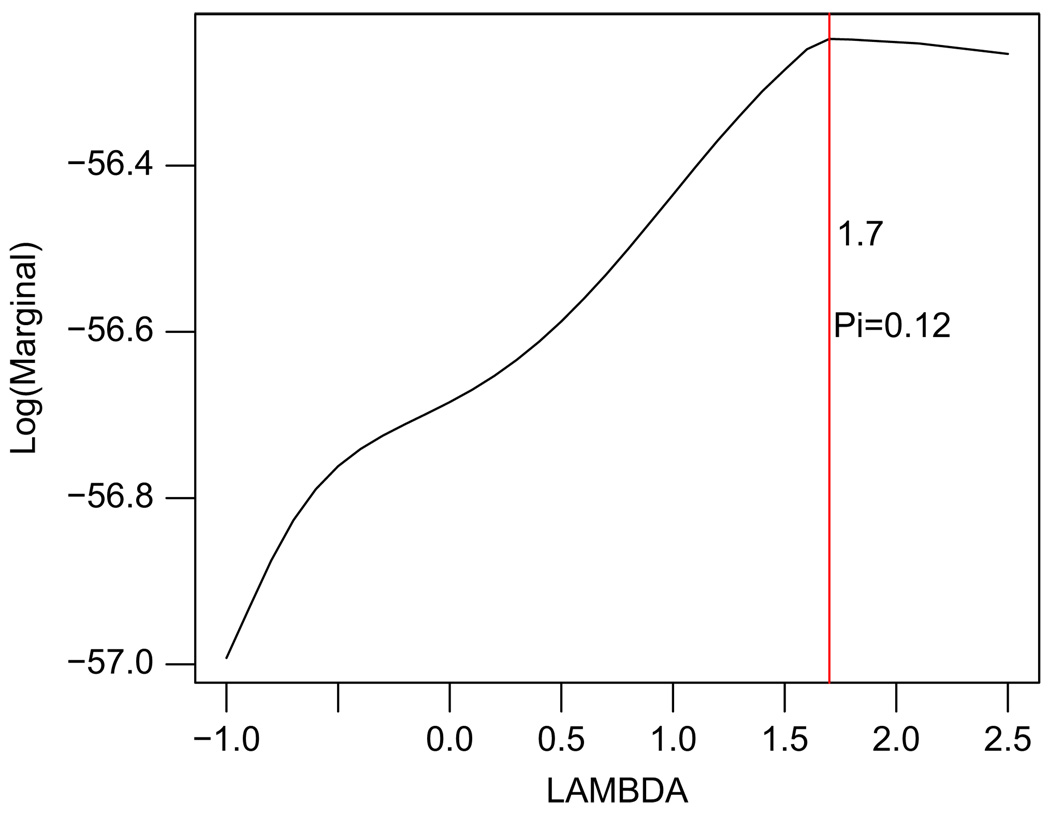
Similar to the previous case, the optimal values (λ̂ = 1.7, π̂ = 0.12) were obtained by averaging over 1000 replications (Fig. 2) which maximizes the marginal likelihood function. The performance of the powered correlation priors in terms of selecting correlated predictors is also similar to the previous case.

Fig. 2.

Plot of λ vs. Log[m(y|X, π, λ)], maximized over π ∈ (0, 1), corresponding to case 2: p = 12, averaged over 1000 simulations. The vertical line represents the location of the global maximum.

From Table 2 it is clear that Zellner's prior penalizes models with high collinearity, thereby putting more posterior mass on single variable models. In contrast, the powered correlation prior method favors the true model (x₁, x₂) with maximum average posterior probability of 0.145 and the correct model was selected 46.1% of the time. For the intrinsic prior, the maximum posterior model is the model including only x₁ and the correct model is selected only 9.8% of the time.

Table 2.

Case 2, comparing average posterior probabilities, corresponding to the case 2: p = 12, averaged over 1000 simulations.

Zellner's			PoCor			Intrinsic Prior
Subset	Avg Post Prob	% Selected	Subset	Avg Post Prob	% Selected	Subset	Avg Post Prob	% Selected
x1	0.068	28.9	x1, x2	0.145	46.1	x1	0.039	33.2
x1, x2	0.051	10.6	x1, x2, x3	0.109	12.4	x2	0.016	14.5
x1, x3	0.025	10	x1, x3	0.090	7.8	x1, x2	0.013	9.8
x1, x4	0.016	5.9	x2, x3	0.078	5.5	x1, x2, x3	0.011	5.4
x1, x5	0.0133	5.4	x1	0.056	5.1	x1, x3	0.009	2.3
x1, x2, x5	0.013	4.4	x1, x2,x4	0.020	4.7	x1, x2, x4	0.008	0.89
x1, x2, x6	0.012	3.5	x1, x2, x3, x4	0.016	3.6	x1, x3, x4	0.008	0.76
x2, x2, x8	0.011	3.5	x1, x2, x5	0.010	3.4	x1, x2, x5	0.007	0.54

% Selected is the number of times (in %) each model was selected as the highest posterior model out of 1000 replications. Zellner's represents use of Zellner's prior as in (5.1). PoCor represents our proposed modification as in (4.1). Intrinsic Prior represents the fully automatic procedure proposed by Casella and Moreno (2006).

In this simulation study the true model contains two highly correlated predictors x₁ and x₂. Given that we know the true data-generating mechanism, an objective comparison criterion is the ability of the methods to correctly identify the underlying true model. We see from Table 1 and Table 2 that the posterior probability for the true model using our proposed method is much larger than for any other model. Hence our method is able to correctly identify the true set of predictors even when they are highly correlated. Alternatively, the two other approaches choose a single predictor model and give very little posterior probability to the true model. Model performance could be further evaluated based on prediction accuracy, but we have not explored that aspect in this simulation study, as the main goal was to examine whether the methods identify the entire correct set of variables that contribute to the explanation of the response y.

5.2. Real data example

We consider a real dataset to demonstrate the performance of our method. For our real data example we use the data on NCAA graduation rates (Mangold et al., 2003) where there are 97 observations and 19 predictors. The response variable is the average graduation rates for each of the 97 colleges (see Appendix for a description of the dataset). Mangold, Bean and Adams used this dataset with the goal of showing that successful sports programs raise graduation rates. This dataset is of specific interest to us, due to the presence of high correlation among the variables. We fit a main effects only model with the 19 possible predictors.

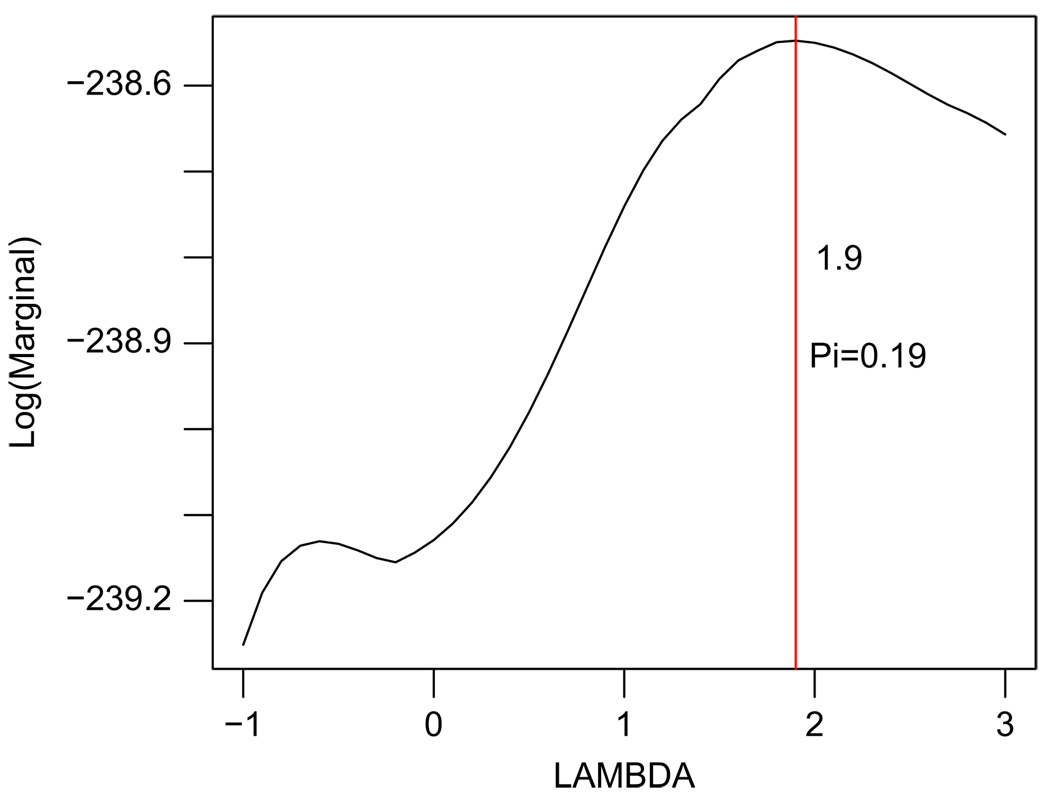
For this dataset we obtain the optimal values of λ̂ = 1.9 and π̂ = 0.19 (Fig. 3). Posterior probabilities are computed using these optimal values by complete enumeration of all 2¹⁹ − 1 possible models.

Fig. 3.

Plot of λ vs. Log[m(y|X, π, λ)], maximized over π ∈ (0, 1), corresponding to the NCAA Dataset. The vertical line represents the location of the global maximum.

In Table 3 we compare the posterior model probabilities by using our proposed method to those obtained using the standard Zellner's g-prior and the fully automatic intrinsic priors. The highest posterior model selected using the powered correlation prior to predict the average graduation rates is a 6 variable model, as compared to Zellner's which selects a 5 variable model by dropping x₁₇ (acceptance rate) from the model chosen by our approach. This could be attributed to the high correlation between x₂ and x₁₇ (ρ = 0.81). The intrinsic prior approach picks out a simpler (fewer predictors) model as its highest posterior probability model.

Table 3.

Comparing posterior probabilities and average prediction errors for the models of the NCAA data.

Zellner's			PoCor			Intrinsic Prior
Subset	Post Prob	C.V. Pred Err	Subset	Post Prob	C.V. Pred Err	Subset	Post Prob	C.V. Pred Err
x2, x3, x4, x5, x7	0.042	54.38 (0.615)	x2, x3, x4, x5, x7, x17	0.036	51.53 (0.561)	x2, x4, x7	0.066	53.97 (0.530)
x2, x3, x4, x7	0.041	55.57 (0.646)	x2, x3, x4, x5, x7, x17, x18	0.030	52.38 (0.619)	x2, x3, x4, x5, x7	0.040	52.94 (0.541)
x2, x3, x4, x5	0.028	56.74 (0.599)	x1,x2, x3, x4, x5, x7	0.028	53.46 (0.608)	x2, x3, x4, x5	0.028	54.09 (0.602)
x2, x3, x4, x5, x7, x18	0.017	55.17 (0.609)	x2, x3,x4, x5, x7, x18	0.021	54.08 (0.572)	x2, x4, x5, x7	0.022	54.82 (0.576)
x2, x3, x4, x5, x7, x17	0.015	54.89 (0.623)	x2, x3, x4, x5, x7	0.018	54.51 (0.568)	x2, x3, x4	0.016	58.71 (0.617)
x1, x2, x3, x4, x5, x7	0.013	55.64 (0.611)	x1, x2, x3, x4, x5	0.015	56.13 (0.601)	x2, x4, x7, x11	0.011	58.67 (0.594)
x2, x3,x4, x7, x8, x9	0.011	56.54 (0.628)	x2, x3,x4, x5, x7, x10	0.009	54.75 (0.554)	x2, x4, x11	0.010	60.08 (0.581)

The entries in parenthesis are the standard errors obtained by 1000 replications.

Model comparison and validation are now made based on the average predicted error, where the parameter estimates are obtained by computing the posterior mean of β_δ for each given configuration of δ and y for each of the three methods. Table 3 reports the average mean square predictive error along with their standard errors obtained using 5-fold cross-validation (CV), whose estimates are first averaged across 10 CV splits to reduce variability, and then replicated 1000 times. We see that the top two models picked out by the powered correlation prior's posterior probabilities has a significantly lower prediction error than that of the models selected using the two other methods. Hence, both the simulation and the real data example show strong support for the use of our proposed powered correlation prior.

6. Discussion

In this paper we have demonstrated that within a linear model framework the powered correlation prior helps to resolve the problem of selecting subsets using a suitable modification of Zellner's g-prior when the predictors are highly correlated. By using simulated and the real data examples we have illustrated that the powered correlation prior tends to perform better in terms of choosing the correct model than the standard Zellner's prior and the intrinsic prior for correlated predictors. The choice of hyperparameter λ obtained using a empirical Bayes method controls the degree of smoothing of correlated predictors towards or away from each other.

For a large number of predictors (e.g. p > 30), a attractive feature of this prior is that all the parameters can be integrated out analytically to obtain a closed form for the unnormalized posterior model probabilities. Hence a simple Gibbs sampler over model space (George and McCulloch, 1997) can be implemented to approximate the marginal for each pair (λ, π). This can be implemented on a two-dimensional grid, and although it may take significant computation time, it remains feasible.

Model averaging for linear regression models has received considerable attention (Raftery et al., 1997). This method accounts for model uncertainty by averaging over all possible models. It is possible to extend the use of our proposed prior to perform model averaging via the use of posterior probabilities.

There has also been considerable interest in Bayesian variable selection for generalized linear models. The selection criteria are based on extensions of Bayesian methods used in linear regression framework. While beyond the scope of this paper, one can extend the powered correlation prior used here to generalized linear models.

Appendix A. Brief description of NCAA data

Data from Mangold et al. (2003), Journal Of Higher Education, pp. 540–562, “The Impact of Intercollegiate Athletics on Graduation Rates Among Major NCAA Division I Universities.” The data were taken from the 1996–1999 editions of the US News “Best Colleges in America” and from the US Department of Education data and includes 97 NCAA Division 1A schools. The authors hoped to show that successful sports programs raise graduation rates. Here is a list describing briefly the response variable and 19 predictors.

Y	average 6 yr graduation rate for 1996, 1997, 1998
x1	% students in top 10 Percent HS
x2	ACT COMPOSITE 25TH
x3	% on living campus
x4	% first-time undergraduates
x5	total enrollment/1000
x6	% courses taught by TAs
x7	composite of basketball ranking
x8	in-state tuition/1000
x9	room and board/1000
x10	avg. BB home attendance
x11	full professor salary
x12	student to faculty ratio
x13	% white
x14	assistant professor salary
x15	population of city where located
x16	% faculty with PHD
x17	acceptance rate
x18	% receiving loans
x19	% out of state