An Adaptive Design for Identifying the Dose with the Best Efficacy/Tolerability Profile with Application to a Crossover Dose-Finding Study

SUMMARY

Proof-of-concept in clinical trials has traditionally focused on identification of a maximum tolerated dose with the assumption that the higher doses provide better efficacy. However adverse events associated with a maximum tolerated dose may have a negative effect on efficacy. We present an efficient adaptive dose-finding strategy which concentrates patient assignments at and around the dose which has the best efficacy/tolerability profile based on a utility function. The strategy is applied within the setting of a crossover design. While the strategy may also be applied to parallel studies, a crossover design provides more power for a given sample size for comparisons between the optimal dose versus placebo and/or active control when it is reasonable to assume no carryover effects.

1. Introduction

The goal of a phase II dose-finding study is to find the best dose to investigate in subsequent trials. Such a dose should have good efficacy, which is established by comparing response to treatment with drug versus placebo and/or active control. Doses with superior efficacy might also have higher rates of adverse events, hence both outcomes should be taken into consideration for dose selection. A utility function which incorporates both positive benefit for efficacy and negative benefit for intolerability may be constructed. If both outcomes are binary, a natural way of combining these is to consider an outcome of success defined as the therapeutic response without toxicity. Such strategy was considered by many in the context of oncology trials [1-4]. The value of the utility function at each dose is then equal to a success rate at that dose. Other ways of defining the utility function for binary outcomes have been suggested [5, 6]. When one or both outcomes are non-binary, there are various ways of defining utility. Fedorov and Wu [7] for example, suggest defining utility using the conditional mean of efficacy (conditional on no toxicity), or dichotomizing the efficacy variable if binary outcomes are of primary interest to a regulatory agency. Utilities may also be inferred from discussions with physicians. Thall and Cook [5] give an excellent description of such a process in the context of two different clinical trial settings. Usually the utility function is specified in such a way that the doses with the most favorable response and lowest rates of adverse events have higher values of the utility function. The goal of the trial is then to identify the dose for which the maximum of the utility function is achieved. We will refer to this dose as the optimal dose. An additional goal is to compare the mean efficacy and tolerability at this optimal dose to active control and/or placebo.

This work was motivated by a proof-of-concept trial conducted by Merck Research Laboratories. The goal of the trial is to identify an effective, tolerable dose of an investigational drug in patients with the indication of interest and also to provide evidence of non-inferiority to an active control. Because of confidentiality issues and for ease of presentation some non-essential features of the trial description have been modified. The efficacy of the new drug in the trial is measured by a continuous variable at the end of a two-week treatment period, while the occurrence of selected adverse events is measured as a binary variable over this same period.

This Merck trial used a 3-period, 6-sequence crossover Williams Latin square design to enable evaluation of the key objectives related to efficacy and tolerability of the experimental treatment compared to placebo and active control. Each patient was randomized to one of the following 6 treatment sequences, which specifies the order of treatments received by the patient: ABC, BCA, CAB, ACB, BAC, CBA, where A=Experimental Treatment, B=Placebo and C=Active Control. For example, a patient randomized to sequence BCA receives placebo in Period 1, active control in Period 2 and one of five doses of experimental treatment in Period 3. The specific dose of the experimental treatment received by the patient is determined by the adaptive procedure. The design is balanced for first order carryover effect [8] at the treatment level (but not for dose). Given the therapeutic area and pharmacokinetic properties of the experimental treatment, it was reasonable to conduct this crossover study (with appropriate washout between periods) and assume no carryover effect. Crossover designs are often used in first in man studies [9] and in proof of concept or dose finding studies for a variety of therapeutic areas [10]. When used appropriately, crossover designs have some advantages over parallel designs including: higher power and independence to variability between investigative sites. In a crossover study, patients act as their own control which allows the use of within-subject comparisons and results in more power than a parallel study. Variability between investigative sites also becomes irrelevant, which is important since this Merck study included about 20 sites. Lastly, the dose associated with the experimental treatment period can be changed in real time for subsequent allocation to new patients entering the trial; therefore, the crossover design is also compatible with dose adaptation which is important since the best dose for testing proof of concept was not known.

Disadvantages of a crossover design include longer trial duration and potential carryover effects. A three-period crossover study is more than three times longer than a parallel study because it includes two sufficiently long washout periods between the three treatment periods. Therefore, crossover studies are advantageous in therapeutic areas where enrollment rates are slow (a requirement for an adaptive design) and patient retention is high.

Adaptive designs require adequate time to “search” for the best dose. In a parallel design setting, this means being able to observe the response relatively quickly with respect to enrollment rate. In a crossover setting, one can exploit the long trial duration to benefit the adaptive design by determining the dose of the experimental treatment “just-in-time” or immediately prior to the appropriate treatment periods. Adaptive dose-finding designs are widely used in oncology. In non-oncology setting, adaptive designs have been shown to be beneficial in various dose-finding problems [6,11]. We developed an adaptive design to use in dose-finding trials with the goal of maximizing the utility function. The new adaptive design improves the quality of estimation of the optimal dose and increases the power of its comparison with placebo and/or active control as compared to equal allocation. Though adaptive designs create logistical challenges in the execution of a trial, especially for multi-center trials like the one in the motivating example, improved precision and efficiency brought by adaptive designs may outweigh the logistical challenges.

2. Model for the data and specification of the utility function

Denote a fixed ordered set of dose levels chosen for the trial by {d₁, …, d_K}, with d₁ denoting placebo. For ease of notation we will refer to active control as treatment K+1. In this three-period, six sequence crossover design each subject receives placebo, control and one of five doses of the drug according to the order prescribed by the sequence to which the subject was randomized. Let Y_ijk be the efficacy outcome of subject i in period j, j = 1,2,3, receiving treatment k, k = 1,…, K+1. Then

$$E\left(Y_{ijk}\right)={\mu }_k+{\pi }_j,$$ (2.1)

where μ_k is a treatment effect, k = 1,…, K+1, and π_j is a period effect, j = 1,2,3. The outcomes Y_ijk are assumed to be normally distributed with Var (Y_ijk) = σ² and corr(Y_ijk, Y_ij’k’) = ρ, for j ≠ j’. That is, efficacy outcomes are correlated within each subject and observations from different subjects are independent.

Tolerability outcome V_ijk of subject i in period j, j = 1,2,3, receiving treatment k, k = 1,…, K+1, is binary indicating the occurrence of an adverse event. Tolerability outcomes were correlated within each patient corr(V_ijk, V_ij’k') = τ. No period effect is assumed for tolerability outcome with E (V_ijk) = p_i.

Efficacy and tolerability were modeled separately but considered jointly through the utility function. To determine the utility function, we received extensive input from physicians over a plausible efficacy and tolerability region. We also studied utility functions appearing in the literature on dose-finding [1-5]. A “base case” was identified that provided an acceptable balance of efficacy and tolerability; this was defined as the experimental treatment with adverse event rate 0.1 and efficacy of 20. To consider tolerability from the “base case” physicians decided that a dose with efficacy of 21 and adverse event rate of 0.2 is as good as the “base case”. That is, 1 unit increase in efficacy is balanced by 0.1 increase in adverse event rate. Similarly, it was decided that 1 unit decrease in efficacy is balanced by 0.1 decrease in adverse event rate, that is, a dose with efficacy of 19 and adverse event rate of 0 is as good as the “base case” Therefore, the utility function can be written as

$$U\left(d_k\right)={\mu }_k-10p_k.$$ (2.2)

Based upon previous studies conducted with the experimental treatment it was assumed that the mean efficacy response was increasing with dose with the possibly of a downturn at higher doses. Therefore, it was assumed that the mean response followed the model

$${\mu }_1\le \dots \le {\mu }_{h-1}\le {\mu }_h\ge {\mu }_{h+1}\ge \dots \ge {\mu }_K,$$ (2.3)

where the response at dose h is called the peak of the dose-response function. If the peak is at the highest dose, d_K, the function is non-decreasing, if the peak is at the lowest dose, the function is non-increasing. Mild to moderate severity adverse events were expected. The adverse event rate of interest was assumed to be non-decreasing with dose

$$p_1\le \dots \le p_K$$ (2.4)

Unlike the natural utility for binary outcomes (e.g., success), which is unimodal under broad conditions [12], the utility defined in (2.2) is not necessarily unimodal. We investigated plausible scenarios for mean efficacy and adverse events rates in the planned trial and concluded that the assumption of a unimodal utility (2.2) was viable.

3. Allocation procedure

3.1. Allocation design

The goals of the trial were 1) to identify the optimal dose and 2) to compare this dose with active control and placebo. To improve the power of comparisons with active control and placebo one needs as many patients as possible on the optimal dose. Therefore the goal of our adaptive strategy is to assign as many subjects as possible in the neighborhood of the optimal dose. The proposed allocation procedure is not specific to a crossover study and may be used in other types of designs.

Kpamegan and Flournoy [13] suggested an up-and-down design for maximizing a function over a fixed set of doses with binary outcomes. Their sequential procedure estimates the difference between the two most recent observations and then determines the direction in which to locate the next pair of observations. Our sequential procedure, though similar in spirit, utilizes all outcome data available so far and can be used with any type of outcome. We refer to our procedure as the maximizing procedure and describe it below.

Maximizing procedure

A new subject is randomized to one of two designated adjacent doses with equal probabilities, with an exception listed below in (iv). Suppose the most recent designated pair of doses was (d_j, d_j+1), j∈{2,…,K−1}. Let ${\widehat{S}}_j$ be the estimated difference in the utility function between d_j and d_j+1. Then

1. if ${\widehat{S}}_j<0$, the next designated pair of designated doses is (d_j−1, d_j);

2. if ${\widehat{S}}_j>0$, the next designated pair of doses is (d_j+1, d_j+2);

3. if ${\widehat{S}}_j=0$, the next designated pair of doses is (d_j+1, d_j+2) with probability φ = (K − 1 − j)/(K − 3) and doses (d_j−1, d_j) with probability 1 − φ.

4. The following adjustments are implemented at the highest and lowest doses. If the current pair is (d₁,d₂) and ${\widehat{S}}_1<0$, the randomization to (d₁,d₂) is with the randomization ratio of 2:1. If the current pair is (d_K−1,d_K) and ${\widehat{S}}_{K-1}>0$, the randomization is to (d_K−1,d_K) the randomization ratio of 1:2.

If the optimal dose is dose d_h, 2 < h < K, as the design zooms-in onto the maximum, the allocation starts oscillating between (d_h−1,d_h) and (d_h,d_h+1), yielding the allocation to (d_h−1,d_h,d_h+1) in proportions 1:2:1. Provision (iii) allows the design to move from the spot where the utility function is flat to explore other areas. Provision (iv) facilitates the assignment of 2:1 to the maximum, if the maximum is at d₂ or d_K.

The difference S_j was estimated by modeling utility as a quadratic function of dose. The goal was to fit a local quadratic model around the current dose that uses some information from the doses that are further away. It is noted that a recursive search of the mode of a function based on quadratic approximation might be more efficient, especially in a non-adaptive setting. Another possibility is to estimate the utility function (2.2) by computing maximum likelihood estimates (MLEs) of mean efficacy under restriction (2.3) and of tolerability means under restriction (2.4) (see Section 3.2 for more details). The observations at doses (d_h−1,d_h,d_h+1) where given weight 1, while the observations at the remaining doses were assigned weight 0.5 and placebo was given a weight of 0.2. When the designated current pair of doses was (d₂,d₃), placebo was given weight 1. The model included a period effect and was fitted using generalized estimating equations [14].

3.2. Estimating the optimal dose at the end of the trial

In this section we describe how to identify the optimal dose at the end of the adaptive trial and also for a non-adaptive trial with equal allocation to the same doses for comparison. Let (n₁, …, n_K+1) be the vector of sample sizes at {d₁, …, d_K+1} after the adaptive crossover trial. For a non-adaptive crossover trial with equal allocation each subject receives placebo, active control and one of the {d₂, …, d_K} with equal number of subjects allocated to each of these doses, n₂ = … = n_K.

We will describe two approaches for estimating the optimal dose. The first approach can be used with any design and is based on computing MLEs of efficacy means under restriction (2.3) and MLEs for tolerability proportions under restriction (2.4) and plugging them into the utility function. Such an approach is a middle ground between using a parsimonious model in estimation and not using any assumptions, and generally yields better estimates. The second estimation procedure is used with the data obtained in an adaptive fashion and is based on selecting the dose with the highest utility from the two adjacent doses with the highest numbers of patients allocated. This approach is preferred for the adaptive design since it insures that the optimal dose will be selected from doses with an adequate sample size.

In the first estimation approach we computed MLEs of efficacy means under restriction (2.3) and of tolerability means under restriction (2.4). The quadratic model we used in Section 3.1 works well to estimate the difference in utility function between doses locally, but such a parsimonious model is not flexible enough to summarize all available data after the trial. This is in agreement with the previous finding that, in the case of a simple order, isotonic methods were shown to be superior to fitting parsimonious models such as a two-parameter logistic regression [15, 16]. For a given vector X = (x₁, …, x_K and positive weights W = (w₁,…, w_K), an isotonic function Z is said to be an isotonic regression of X under restriction (2.3) with weights w and peak h if it minimizes ${\sum }_{j=1}^K{w}_j{(x_j-z_j)}^2$ for Z satisfying the ordering (2.3). Since the location of the peak h is unknown, isotonic estimates under restriction (2.3) are computed for every h = 1, …, K. The estimated location of the peak is the one that maximizes the likelihood.

The mean efficacy at each dose in {d₁,…, d_K+1} was estimated by fitting a linear model to all available efficacy data as a function of treatment (2.1). The model was fitted using generalized estimating equations (GEE) to take into account the exchangeable correlation structure of the outcome and a period effect for the crossover design. To compute estimates of the efficacy outcome under restriction (2.3) the algorithm described in Shi [17] and Geng and Shi [18] was applied to the fitted means of the efficacy outcome from the GEE model for {d₁,…, d_K} with weights (n₁, …, n_K). Such computation does not necessarily yield the estimates that maximize the likelihood under restriction, but each does provide a good approximation. Restricted MLEs of the tolerability outcome on {d₁,…, d_K} were computed using a pooled adjacent violator algorithm [19]. Then the estimates of the utility function were computed using formula (2.2). The estimated optimal dose was the dose with the highest value of the estimated utility.

This adaptive design increases the allocation around the optimal dose, hence sample size itself is very informative for determining the location of the optimal dose. To estimate the optimal dose after the adaptive trial (second estimation approach), a best set of two doses was determined and then the estimated optimal dose was chosen from that set. To determine the best set of two, first, the smallest dose among those with the most assignments was chosen: d_τ = min{arg max_{i=2, …K} n_i}. If d_τ was d₂ or d_K, then the best set was defined as {d₂,d₃} and {d_K−1,d_K}, respectively. If 2 < τ < K, the second dose in the best set was the dose d_τ’ = max{arg max (n_τ−1,n_τ+1)}. Of the two doses in the best set of two, the one with the larger estimated utility was selected as the estimated optimal dose. To avoid ties, we used fitted means of the efficacy outcome to estimate the utility.

3.3. Comparison with placebo and active control

An important goal of the trial was to compare the mean response with active control and placebo. When the optimal dose is selected based on the value of response, the estimated mean response at that dose is most likely biased upward [20] and therefore type one error rate might be inflated. Each of the two tests was performed at 0.05 level. The critical values were adjusted by setting the critical values equal to the 95th percentile of the distribution of the test statistic under the null hypothesis.

4. Simulation study

A simulation study was conducted to compare the adaptive crossover design with a non-adaptive crossover trial with equal allocation to the doses under study. In collaboration with physicians, several plausible scenarios for the true underlying response means were designed (Figure 1). Scenarios included both monotonic and unimodal shapes of dose-response curve and various resulting locations of the optimal dose. The utility functions for six scenarios are shown in Figure 1. Scaled doses levels were {0, 0.25, 0.42, 0.67, 0.83, 1}. In all scenarios the efficacy at the optimal dose was equal to 20 and the intolerability rate at the optimal dose was 0.1. At the end of the trial the efficacy at the estimated optimal dose, d_h, was compared to active control efficacy that was set to equal to 20 (non-inferiority) as well as compared to placebo (superiority). Alternatively, one can combine the data from the best set of two and compare mean response of the combined sample with placebo and active control. The primary efficacy null hypothesis compared to placebo, μ_k = μ₁, was tested against a one-sided alternative, μ_k > μ₁, at the 0.025 significance level. The secondary efficacy hypothesis compared the active control with placebo. The null hypothesis, μ_h = μ_K+1 + Δ_μ, was tested against a one-sided alternative, μ_h > μ_K+1 − Δ_μ, at the 0.025 significance level with Δ_μ = 3. Another secondary hypothesis was tolerability comparison with placebo. The null hypothesis, p_h = p₁ + Δ_p, was tested against a one-sided alternative, p_h < p₁ + Δ_p, at the 0.025 significance level with Δ_p = 0.2. The joint hypothesis involved the combination of the latter two secondary hypotheses.

Figure 1.

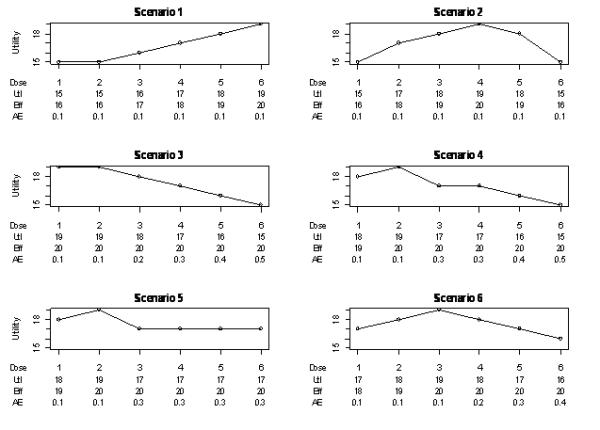
Six efficacy-tolerability scenarios showing the values for utility (Utl), efficacy (Eff) and tolerability (AE). Utility is computed as Efficacy − 10×Tolerability.

Table I displays simulation results for σ = 7, ρ = 0.5, period effect π₃ = 2π₂ = 1, and the total sample size of 200. Table I displays results where tolerability outcomes are independent within a patient. In the actual trial the potential for carryover effects was deemed low, therefore we present simulations assuming no carryover effect. The length of each treatment was two weeks with results on both efficacy and tolerability being available on day 14 after the start of the treatment. The accrual rate was 3 patients per week for the first four weeks and 5 patients per week after that. The adaptation was performed once every two weeks. Based on results of prior studies, all doses were expected to be generally well tolerated, and d₄ and d₅ were considered to be the most promising; therefore, the starting pair of doses was {d₄,d₅}. Simulations were repeated for other pairs of starting doses and the results were very similar (simulation results are available from the authors). The first adaptation was performed when at least two observations were available on each of placebo, d₄ and d₅. The period effect was fitted as linear. Simulation results are based on 3000 runs.

Table I.

Proportion of runs when the correct optimal dose was selected (CS); proportion of runs when the estimated optimal dose was shown to have efficacy no worse than active control and tolerability no worse than placebo (JOINT POWER); power to compare efficacy at the estimated optimal dose with active control (POWER RESPONSE CONTROL); power to compare adverse event rate at the estimated optimal dose with placebo (POWER AE PLACEBO); power to compare efficacy at the estimated optimal dose with placebo (POWER RESPONSE PLACEBO); and 25%, median, and 75% of the number of trials at the estimated optimal dose (SAMPLE SIZE QUANTILES). The two estimators of the optimal dose are presented: isotonic estimator (Adaptive 1) and best set of 2 doses estimator (Adaptive 2).

	CS	Joint Power	Power Response Control	Power AE Placebo	Power Response Placebo	Sample Size Quantiles (25%, median, 75%)
Scenario 1
Adaptive 1	0.74	0.86	0.90	0.95	0.97	68	81	89
Adaptive 2	0.72	0.86	0.89	0.97	0.96	70	81	89
Equal	0.70	0.70	0.82	0.86	0.99	40	40	40
Scenario 2
Adaptive 1	0.69	0.87	0.93	0.93	0.99	53	63	72
Adaptive 2	0.75	0.90	0.94	0.96	0.99	58	65	84
Equal	0.63	0.73	0.87	0.85	0.99	40	40	40
Scenario 3
Adaptive 1	0.77	0.80	0.96	0.82	0.025	69	84	94
Adaptive 2	0.78	0.87	0.99	0.88	0.025	77	85	95
Equal	0.80	0.58	0.81	0.74	0.025	40	40	40
Scenario 4
Adaptive 1	0.83	0.78	0.94	0.81	0.24	62	82	93
Adaptive 2	0.89	0.85	0.97	0.88	0.25	73	84	95
Equal	0.82	0.56	0.82	0.72	0.18	40	40	40
Scenario 5
Adaptive 1	0.73	0.65	0.92	0.71	0.24	44	76	92
Adaptive 2	0.72	0.68	0.97	0.70	0.26	65	81	93
Equal	0.72	0.53	0.87	0.65	0.24	40	40	40
Scenario 6
Adaptive 1	0.59	0.72	0.94	0.75	0.74	48	69	82
Adaptive 2	0.69	0.80	0.97	0.82	0.76	60	74	83
Equal	0.52	0.62	0.91	0.69	0.61	40	40	40

The primary goal was to estimate the optimal dose well. Column 1 of Table I displays the proportion of runs where the optimal dose was identified correctly. We illustrate the performance of the adaptive design based upon the two estimators: isotonic (Adaptive 1) and using the best set of two doses (Adaptive 2). In the set-up and scenarios considered, the ‘best set of two doses’ yields slightly better estimates than does isotonic. When equal allocation is used isotonic estimation is considerably better than using just the fitted means in estimation of the utility function (results are available from the authors). Identification of the optimal dose is generally better for the adaptive design as compared to the equal allocation crossover design.

The second goal of the trial was hypothesis testing regarding efficacy and tolerability at the optimal dose. Column 3 of Table I displays the power to compare efficacy at the estimated optimal dose with active control, while Columns 4 and 5 display the power to compare adverse event rates and the power for efficacy comparison at the estimated optimal dose with placebo. The adaptive design has higher power than equal allocation for nearly every scenario evaluated (columns 3, 4 and 5) primarily due to increased allocation at the optimal dose compared to equal allocation. Since an increase in power for efficacy (columns 3 and 5) can be achieved by selecting a dose with a very high mean response, and an increase in power for tolerability (column 4) can be achieved by selecting a dose with a low adverse event rate, we computed the power for the joint hypothesis of both efficacy and tolerability to illustrate the performance of the new design. The power of the joint hypothesis is displayed in column 2 and is the proportion of trials where both tolerability (compared to placebo) and efficacy (compared to active control) null hypotheses were rejected. Doses other than optimal have either worse tolerability or lower efficacy, therefore column 2 reflects not only the sample size at the estimated optimal dose but also the precision of estimation. The larger the number of subjects at the estimated optimal dose and the better the precision, the higher is the value in column 2. The adaptive design substantially increases the joint power compared to the equal allocation design with absolute increase in power varying from 15% to 29%. The joint power for the adaptive design is higher than the equal allocation design for all scenarios considered.

Column 6 of Table I displays quantiles of the number of subjects at the estimated optimal dose. On average, the adaptive design assigns substantially more subjects to the estimated optimal dose. This translates into the increase in power of rejecting the hypotheses regarding the efficacy and tolerability parameters. The minimum number of subjects at the optimal dose for the best set of two estimation procedure varied from 32 to 42. At the same time, the minimum number of subjects at the optimal dose using the isotonic estimation procedure can be as low as 1 or 2. This happens very rarely and does not affect the performance of the procedure on average (Table I), however it is a concern if this procedure is used in the trial. We recommend using the ‘best set of two’ estimation procedure.

The average allocation of patients to doses is displayed in Table II. The adaptive design assigns more subjects on average to and around the optimal dose as compared to equal allocation. By assigning more patients to the doses with more favorable efficacy/tolerability profiles the adaptive design assigns fewer patients to doses with higher rates of adverse events compared to allocating equally to all doses (Table II, scenarios 3-6).

Table II.

Average number of subjects assigned to each dose in adaptive allocation. The allocation at the optimal dose is in bold.

	d1	d2	d3	d4	d5	d6
Scenario 1	200	7	16	26	78	73
Scenario 2	200	26	61	64	34	14
Scenario 3	200	85	76	16	13	9
Scenario 4	200	80	74	19	15	11
Scenario 5	200	65	63	21	28	23
Scenario 6	200	50	73	43	21	13

In crossover studies missing data are likely. We performed simulations with missing data assuming that the data were missing at random. Trials with missing data were simulated to ensure that the upcoming trial would have an adequate precision and power. As far as comparison with the equal allocation crossover design the results were very similar to the case of no missing data. In simulations with various values of σ and ρ adaptive design was always superior to the equal allocation. All results are available from the authors.

If more rapid accrual is expected in the beginning of the trial, a lead-in phase before reverting to the adaptive design may be employed. Subjects are assigned equally to doses {d₂,…, d_K} in the lead-in phase. The starting dose for an adaptive design is then estimated from the lead-in phase data using the isotonic method. Our investigation shows that the lead-in phase with up to 25% of the total sample size improves the likelihood of selecting the correct optimal dose at the end of the trial.

5. Discussion

There has been a recent increase in interest in adaptive designs in hope of improving the efficiency of drug development [21]. One promising area of application is in dose-finding studies. One of the reasons is because the focus of dose-finding designs is estimation where adaptive designs can be quite helpful. Adaptive trials are logistically feasible [6, 22] and can be quite beneficial in phase I studies in healthy volunteers [22] and dose ranging studies [11]. In this paper we described an adaptive design for maximizing the allocation of patients to an optimal dose on the basis of a utility function which incorporates information on efficacy and safety. This approach provides increased power for assessing superiority of the optimal dose to placebo or non-inferiority of the optimal dose to an active control. We demonstrated the advantages of using this adaptive design in such trials compared to equal allocation. Simulations suggest that correct identification of the optimal dose is generally better than an equal allocation design and that this adaptive design provides considerably higher power for the treatment comparisons of interest. Applied to the Merck study in conjunction with crossover allocation, this adaptive design used approximately 1/5 the sample size of a traditional design and maintained similar power for the primary comparison to placebo. The savings were due to both adaptive and crossover design components. While the maximizing procedure provides information for evaluating dose-response, it may be more limited than that provided by equal allocation to all doses because the adaptive design zooms-in on the ‘best’ dose.

A key decision in preparing for the trial was to define the utility function. If both outcomes are binary, a natural way to define utility is the success rate where success is an event of observing therapeutic response without toxicity. If the efficacy variable is independent of the tolerability variable, such utility can be written as U₁(d_k) = μ_k(1−p_k) = μ_k − μ_kp_k, where μ_k and p_k are mean efficacy and tolerability correspondingly. Utility U₁ resembles the one we used in the trial, U(d_k) = μ_k − 10 p_k ; in fact, in all 6 scenarios we considered, U₁ and U have the same maximum. We also considered various forms of utility functions, and the investigational team felt that the utility U, where tolerability is equally weighted rather than weighing it by the value of mean response μ_k, reflected the objectives of the trial in the best way. The utility U is similar to the one in reference [5]. The utility function should be carefully considered and constructed for each new study; U and U₁ are only provided as examples. The adaptive crossover trial was conducted at Merck Research Laboratories in 2008-2009.