The reduced [2Fe-2S] clusters in adrenodoxin and Arthrospira platensis ferredoxin share spin density with protein nitrogens, probed using 2D ESEEM

Summary

We have used X-band ESEEM to study the reduced [2Fe-2S] cluster in adrenodoxin and Arthrospira platensis ferredoxin. By use of a 2D approach (HYSCORE), we have shown that the cluster is involved in weak magnetic interactions with several nitrogens in each protein. Despite substantial difference in the shape and orientational dependence of individual crosspeaks, the major spectral features in both proteins are attributable to two peptide nitrogens (N1 and N2) with similar hyperfine couplings ∼1.1 and ∼0.70 MHz. The couplings determined represent to a small fraction (0.0003–0.0005) of the unpaired spin density of the reduced cluster transferred to these nitrogens over H-bond bridges or the covalent bonds of cysteine ligands. Simulation of the HYSCORE spectra has allowed us to estimate the orientation of the nuclear quadrupole tensors of N1 and N2 in the g-tensor coordinate system. The most likely candidates for the role of N1 and N2 have been identified in the protein environment by comparing magnetic-resonance data with crystallographic structures of the oxidized proteins. A possible influence of redox-linked structural changes on ESEEM data is analyzed using available structures for related proteins in two redox states.

Introduction

Iron-sulfur proteins occur widely in nature, and most are involved in electron transfer reactions with various partners. Several cluster classes have been identified, including proteins with [2Fe-2S], [3Fe-4S], and [4Fe-4S], where the iron ions are tetrahedrally coordinated with bridging sulfide ions and generally with cysteinyl residues as ligands, or histidines in Rieske-type [2Fe-2S] proteins.^1–5 Most proteins exhibit reversible oxidation-reduction between different oxidation states of their iron-sulfur cluster. Because of their role in electron transport, the redox potentials of the clusters of Fe-S protein are among the characteristics most pertinent to their biological function. Redox potentials of Fe-S clusters in proteins, even those with essentially the same liganding pattern, vary over a wide range between +400 mV and −600 mV.⁵ This implies that the redox potential of each particular cluster is determined by other factors in the protein environment. Those factors that influence redox potential should therefore be considered individually for each protein at the atomic level. A variety of factors have been proposed to contribute to variations in the redox potentials of Fe-S clusters including hydrogen bonding, solvent accessibility, and the folding of the polypeptide around the cluster, which may affect the orientation of cysteine ligands and main chain peptide groups.^6,7

Correlation of redox properties with structural features is often limited by the availability of detailed structural information. Even when X-ray structures exist, the detailed structure is arrived at by refinement from the raw electron density data, and this can give rise to substantial changes in the positions and conformations of light atoms. In many cases, the X-ray structure is determined with the protein in a specific oxidation state, and contains no information on the geometric and electronic changes accompanying reduction/oxidation processes. In addition, crystallography provides no information about the electronic structure of the redox center itself or about the distribution of the unpaired spin density over the cluster in paramagnetic states, and over atoms in the protein environment. Since these are major determinants of reactivity, the absence of this structural information translates to uncertainties in theoretical analysis.

Although the two approaches are complementary, high-resolution EPR techniques probing interaction between the electron spin of a paramagnetic cluster and magnetic nuclei of the protein can provide structural information about local spatial and electronic structure relevant to function, independent of a complete crystallographic structure. Thus, the ESEEM spectra of [2Fe-2S], [3Fe-4S] and [4Fe-4S] clusters with cysteine ligands in paramagnetic states show protein nitrogens involved in weak interactions with the electron spin of the cluster, with hyperfine couplings of ∼1 MHz or less, which result from the transfer of unpaired spin density onto the nitrogen nuclei.^8–14 Usually, these nitrogens have been identified as peptide nitogens, but without any confirmed assignment to a particular residue in the protein structure. This has also precluded the detail analysis of the path involved in transfer of the spin density creating the observed coupling. So far, only one study¹² has attempted to identify the nitrogens interacting with reduced [2Fe-2S] cluster in Porphira umbilicalis ferredoxin. In this study, the intensity of the lines in 1D orientation-selected C-band ESEEM spectra provided the spectroscopic data, and this was compared to the X-ray structure of the closely related ferredoxin from Arthrospira (Spirulina) platensis. However, the structural model was significantly revised when a later refinement appeared.^15,16

Difficulties in analysis and interpretation of the ¹⁴N ESEEM of the iron-sulfur clusters often result from the complexity of the multicomponent spectra, and the congestion and overlap of the lines, probably produced by more than one interacting nucleus. New opportunities for characterization of such systems have appeared with the application of 2D ESEEM, which makes it possible to resolve the spectra produced by several nitrogens.¹⁷

In the present work we have applied X-band ESEEM spectroscopy, taking advantage of the 2D approach, in a comparative study of the interaction of the reduced [2Fe-2S] cluster with protein nitrogens in adrenodoxin (adx) and Arthrospira platensis ferredoxin (fdx). Adrenodoxin was the first vertebrate ferredoxin for which a high-resolution X-ray structure became available.¹⁸ It is synthesized in the cytoplasm of the adrenal cortex and is subsequently imported into mitochondria where it is used in electron transfer to various cytochromes of the P450 family. The A. platensis plant type ferredoxin is representative of a wide range of electron-transfer proteins and enzymes. Within the class, the electronic structures of the plant- and vertebrate [2Fe-2S] ferredoxins in the reduced state are highly conserved, but between classes they show dramatic differences. The 1D and 2D ESEEM spectra of these proteins also show differences in the interactions between the unpaired spin and the protein nitrogens. Analysis of spectroscopic data using the available X-ray structures of these proteins has allowed us to determine which protein nitrogens are likely to carry most of the transferred spin density.

Experimental procedures

Sample preparation

Adx proteins were produced in the host E. coli BL21 using the plasmid pKKHC.¹⁹ Overnight cultures of the cells were used to inoculate 4 liters of culture and heterologous protein production was induced by addition of IPTG (final concentration of 1 mM) after the cells had reached an optical density (at 600 nm) between 0.7 – 1. The cultures were grown at 30°C for at least 12 h and cells were harvested by centrifugation at 4000 g (4°C) for 15 min and then stored at −20°C. E. coli pellets were resuspended in 100 ml lysis-buffer (20 mM Tris/HCl, pH 8, 10 mM EDTA, 20 mM NaCl, 100 (µg/ml PMSF) and the cell lysis was performed by a sonication step. In order to precipitate cell debris, the suspension was then centrifugated for 45 min at 20000 g and the subsequent purification of adx from the supernatant was conducted by using a combination of hydrophobic-interaction, ion-exchange and size-exclusion chromatographic methods.

Samples of A. platensis ferredoxin were isolated and purified by a modification of the method of Lojero and Krogmann.²⁰

Both proteins were reduced with sodium dithionite solution under an argon atmosphere.

EPR experiments

Pulsed EPR measurements were carried out using an X-band Bruker ELEXSYS E580 spectrometer with an Oxford CF 935 cryostat at 10–11 K. Several types of ESEEM experiments with different pulse sequences were employed, with appropriate phase cycling schemes to eliminate unwanted features from experimental echo envelopes. Among the pulse sequences used were two pulse and 1D and 2D three- and four-pulse sequences. In the two pulse electron spin echo (ESE) experiment (π/2-τ-π-τ-echo), the intensity of the echo signal at a fixed interval, τ, between two microwave pulses with spin vector rotation angles π/2 and π was measured as a function of magnetic field. In the 1D three-pulse experiment (π/2-τ-π/2- T-π/2-τ-echo), the intensity of the stimulated echo signal after the third pulse is recorded as a function of time, T, at constant time, τ. The set of three-pulse envelopes recorded at different τ values forms a 2D three-pulse data set. In the 2D four-pulse experiment (π/2-τ-π/2-t₁-π-t₂-π/2-τ-echo, also called HYSCORE), the intensity of the stimulated echo after the fourth pulse was measured with variation of t₂ and t₁ whilst τ remained constant. The length of a π/2 pulse was nominally 16 ns and that of a π pulse was 32 ns. The repetition rate of pulse sequences was 1000 Hz. HYSCORE data were collected in the form of 2D time-domain patterns containing 256×256 points with a step16 ns. Spectral processing of three- and four-pulse ESEEM patterns, including subtraction of relaxation decay (fitting by polynoms of 3–4 degree), apodization (Hamming window), zero filling, and fast Fourier transformation (FT), was performed using Bruker WIN-EPR software.

Spectral simulations

HYSCORE simulations were performed using home-written software based on the density matrix formalism in the approximation of ideal strong pulses and taking into account the phase interference effects in powder HYSCORE spectra. The software uses numerical diagonalization of the full spin-Hamiltonian involving an electron spin S=1/2 interacting with one nuclear spin up to I=9/2 and taking into account their hyperfine and nuclear quadrupole interactions with arbitrary orientations of the tensors in the electron gtensor frame. Orientation averaging for powder spectra is done taking into account orientation selectivity in HYSCORE experiment, e.g. using the excitation bandwidth of microwave pulses and the g-factor anisotropy. This software was developed by Dr. Alexei Tyryshkin (currently Princeton University) and can be used on a PC without any additional commercial software.

Nitrogen ESEEM and HYSCORE

The three-pulse ESEEM experiment detects nuclear frequencies of the magnetic nuclei interacting with the unpaired electron of the reduced cluster. For samples of native protein, the interaction of each ¹⁴N atom (with nuclear spin I=1) is characterized by six nuclear frequencies corresponding to two single-quantum (sq) and one double-quantum (dq) transitions from two electron spin manifolds m_S = ±1/2 (Fig. S1, ESI). However, under certain conditions of orientation, some of these transitions can be formally forbidden and have a negligible intensity in the spectra. This phenomenon depends upon the strength of nuclear Zeeman, hyperfine and quadrupole interactions, and their relative orientation in the g-tensor coordinate system. In an orientation-disordered system, an additional factor influencing the intensity of the different transitions is their orientation dependence. Strong orientation dependence of some transitions often prevents the appearance of observable lines with well-pronounced maxima. As a consequence, the ¹⁴N nucleus interacting with an unpaired electron spin S=1/2 can produce up to six lines in an ESEEM spectrum. These lines are from transitions between three nuclear energy sublevels in each of the two electron spin manifolds, which have m_S =+½ or −½. Because of their different orientational dependence, in ESEEM measurements of amorphous samples (as in the case of the frozen solutions of the proteins used in these experiments), not all transitions contribute equally to the spectra.

The powder ESEEM spectrum expected from ¹⁴N with predominantly isotropic hyperfine coupling A is governed by the ratio between the effective nuclear frequency in each manifold, ν_ef±, given by ν_ef± = ∣ν_I ± A/2∣, and the quadrupole coupling constant, K, (given by K=e² qQ/4h).^21–23 If ν_ef±/K∼0, i.e. ν_ef± ≅ 0 (the situation called a cancellation condition, because ν_I≅A/2) then the three nuclear frequencies from a corresponding manifold will be close to three pure nuclear quadrupole resonance (NQR) frequencies

$${\mathrm{\nu }}_{+}=K(3+\eta ),{\mathrm{\nu }}_{-}=K(3-\eta ),{\mathrm{\nu }}_{\mathrm{o}}=2K\eta$$ (1)

of ¹⁴N transitions between the energy levels defined by the principal values of the nqi tensor (above). In this case, three narrow peaks at the frequencies shown in eq. (1) will be present in the powder ESEEM spectra. These frequencies possess the property ν₊ = ν₋ + ν_o, and can appear in spectra up to a ratio of ν_ef±/K ∼ 0.75 – 1.

If ν_ef±/K>1, only a single line without pronounced orientation dependence from each corresponding manifold is expected. This line is produced by a transition at the maximum frequency, which is actually a double-quantum transition between the two nuclear outer states with m_I = −1 and 1. The frequency of this transition is well described by the following equation²¹:

$${\mathrm{\nu }}_{\text{dq}\pm }=2{[{\mathrm{\nu }}_{\text{ef}\pm }^2+\mathrm{\kappa }]}^{1/2}$$ (2)

where κ= K²(3+η²), η- asymmetry parameter. Two other single-quantum transitions, involving the central level with m_I=0, usually do not show any resolved peaks due to significant orientation dependence from quadrupole interaction.

The general advantage of the two-dimensional HYSCORE technique lies in the creation of non-diagonal cross-peaks whose coordinates are nuclear frequencies from opposite electron spin manifolds. HYSCORE spectra are sensitive to the relative signs of the correlated frequencies and are usually presented as two quadrants (+,+) and (+,−). ¹⁴N nucleus can produce up to 18 cross-peaks in each of two quadrants, (+−) and (++), of the HYSCORE spectra including two [dq_±,dq_−/+], eight [dq_±,sq^(1,2)_−/+], and eight [sq^(1,2)_±,sq^(1,2)_−/+] correlations.²⁴ However, as in the case above, only some of the possible cross-features will have observable intensity. Those cross-peaks are distributed in two quadrants, (++) and (+−), depending on the relative values of nuclear magnetic interactions and orientation dependence of nuclear frequencies. In addition, the intensity of cross-peaks is significantly influenced by the time τ between the first and second pulses, which is kept constant in each HYSCORE experiment. Due to this property, several measurements at different times τ are usually required for the detection of all cross-peaks contributing to the spectra. In the present work the cross-peaks from nitrogens were located in (+,+) quadrant only.

Moreover, the ESEEM intensity of the nuclear transition and the intensity of cross-peaks involving this transition are described by different coefficients. As a result, the absence of a line from some transitions in three-pulse ESEEM spectra does not rule out the existence of HYSCORE cross-peaks. HYSCORE also has an enhanced ability to detect peaks of low intensity relative to the three-pulse spectra. The experiment separates overlapping peaks along a second dimension and enhances the signal-to-noise ratio by the second FT. Observation of a few cross-features from ¹⁴N is often enough for the construction of nuclear frequencies in both manifolds. These frequencies can then be used for calculating the nitrogen hyperfine and quadrupole couplings as shown below.

Results

EPR spectra of the reduced clusters. Orientation selection

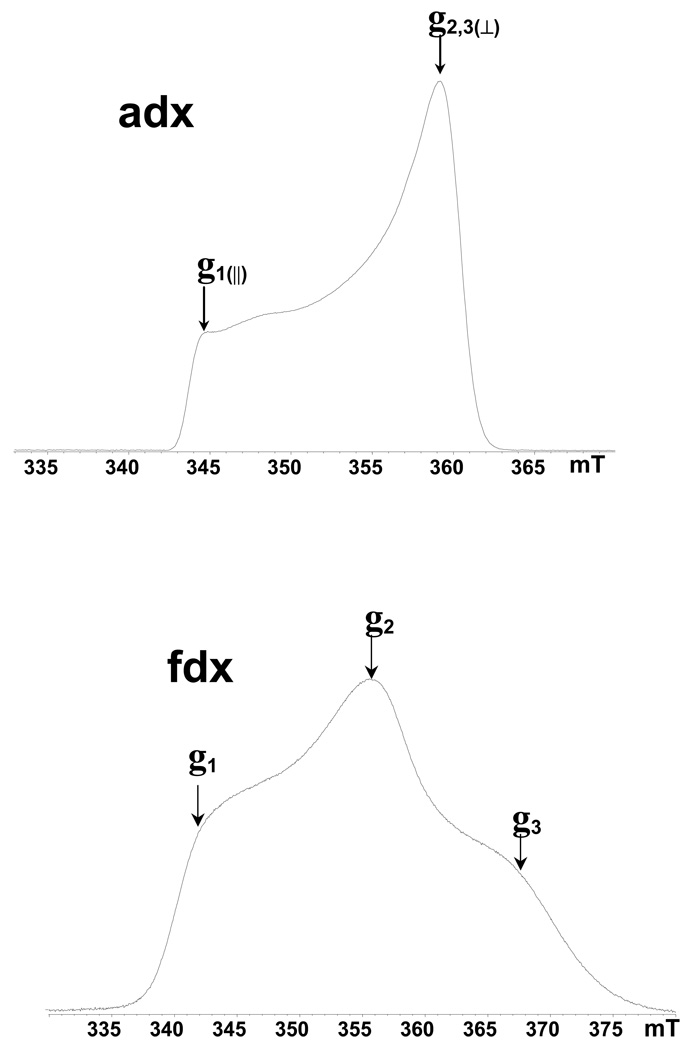
Strong antiferromagnetic coupling between the electron spins of two irons in [2Fe-2S] cluster via bridging sulfide atoms produces an EPR silent ground state in the oxidized Fe³⁺(S=5/2)-Fe³⁺(S=5/2) form of the cluster, and a paramagnetic S=1/2 ground state of the reduced form Fe³⁺(S=5/2)-Fe²⁺(S=2).²⁵ The field-sweep X-band two-pulse ESE spectra of dithionite-reduced [2Fe-2S] cluster in adx and fdx are shown in Fig. 1. The field-sweep spectrum of adx corresponds to the absorption mode of CW EPR with a lineshape typical for axial symmetry of the g-tensor with principal values g_‖(1)=2.024, g_⊥(2,3)=1.934.²⁶ The spectrum of fdx has a rhombic lineshape with principal values g₁=2.052, g₂=1.957, g₃=1.887.²⁷ The total widths of the spectrum are ∼20 and 35 mT, respectively, both of which are much greater than the spectral interval excited by the microwave pulses (∼0.5–1 mT). The ESEEM and HYSCORE measurements under such conditions are therefore orientation-selective experiments, because the magnetic field fixed at any point within the EPR line selects clusters with particular orientations of the g-tensor relative to the magnetic field direction. Thus, the spectra taken at the high and low extreme edges near the maximal (for adx and fdx) and minimal (for fdx only) g values (Fig. 1) give “single-crystal-like” patterns from the reduced clusters, whose g₁ and g₃ axes are directed along the magnetic field. In contrast, the resonance condition at the point corresponding to g_⊥(2,3) and g₂ value is fulfilled by many different, yet well-defined, orientations.

Figure 1.

Two-pulse field-sweep ESE spectra of the reduced Rieske-type cluster in adx and fdx recorded with τ = 200 ns. Arrows show the positions where orientation-selected ESEEM and HYSCORE spectra were measured. The microwave frequency of the pulsed EPR spectrometer was ∼9.7 GHz. Slight variation of the ESE amplitude is seen in the weak slope of the adx spectrum in the low-field region. Similar changes in regions of the spectrum with steeper slopes would not be so visible. It is likely to be produced by the dependence of the ESEEM depth on the field and/or orientation.

¹⁴N ESEEM and HYSCORE

The two-pulse echo envelopes of adx and fdx exhibit periodical variations of high−frequency, which originate from protons in the local environment of the [2Fe–2S] cluster (Fig. S2, ESI). In addition, the echo envelopes show some low-frequency features produced by nitrogen nuclei because ¹⁴N are the only nuclei in the protein environment of the cluster at natural abundance (∼100%), which could produce observable deep ESEEM. In order to obtain quantitative information about interacting nuclei, we applied more sophisticated 1D and 2D ESEEM techniques, because a simple two-pulse experiment does not provide sufficient resolution of all contributions to spectra due to the relatively short relaxation time of the echo decay.

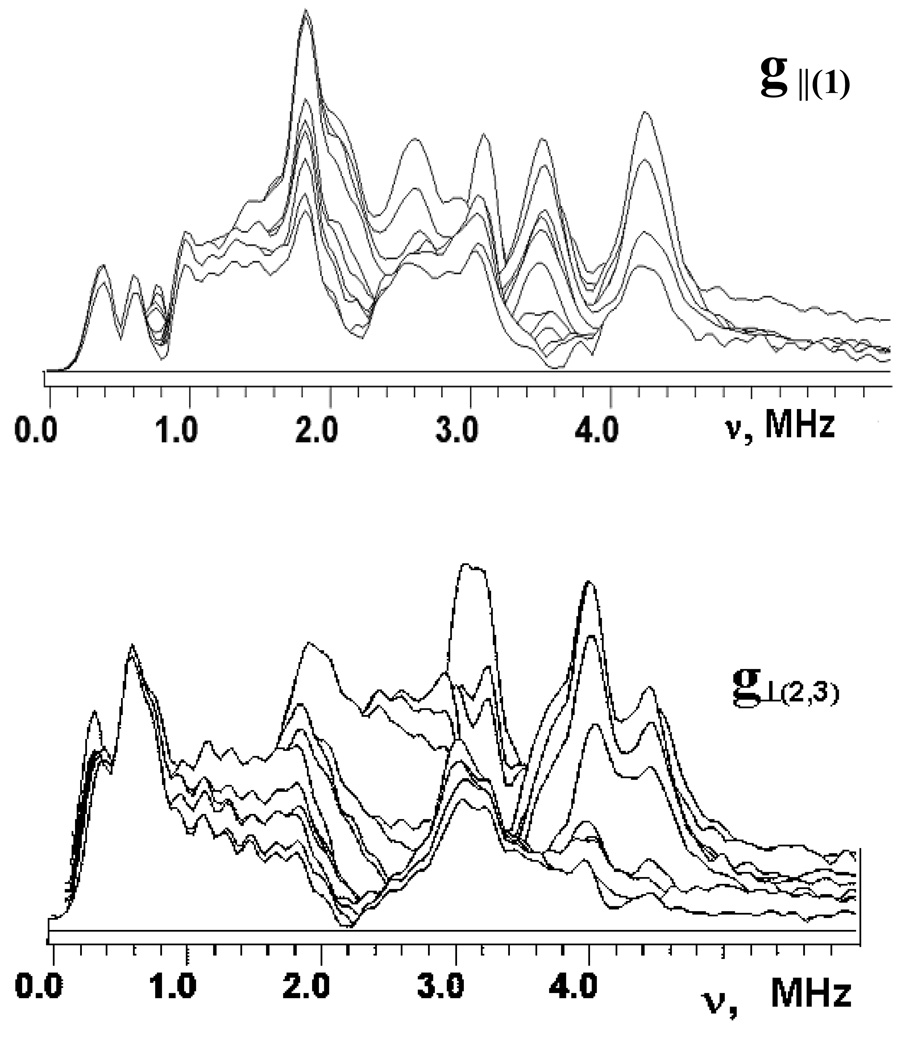
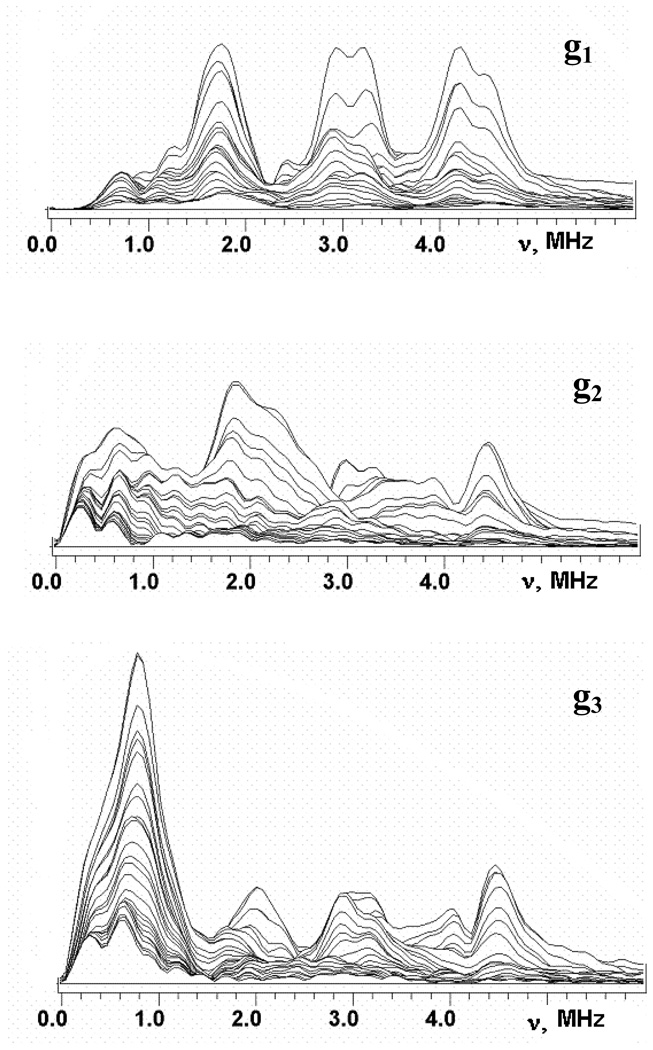
Fig. 2 and Fig. 3 show the stacked plots of the three-pulse ESEEM spectra of reduced adx and fdx at frequencies <6 MHz, appropriate for ¹⁴N nuclei, recorded as a function of time, τ, between the first and second pulses at the points of EPR spectra shown in Fig. 1. The spectra have a complex shape with multiple peaks. They do not conform to those cases of cancellation condition, or hyperfine couplings that significantly exceed the ¹⁴N Zeeman frequencies from a single nucleus^21–23, that are well-understood, and this prevents a straightforward interpretation. The frequencies of the major peaks observed in three-pulse spectra of adx and fdx are collected in Table 1. One can note that the maximum intensities of the ESEEM frequencies are comparable in all three-pulse spectra except the fdx spectrum recoded at g₃. In this spectrum the peak at 0.7–0.8 MHz significantly exceeds all other lines. In particular, peaks at this frequency are practically absent in the “single-crystal like” spectra of adx and fdx recorded in the g₁ region.

Figure 2.

Stacked plots of 3-pulse ESEEM spectra after modulus FT along time T between the second and third microwave pulses for adx. (Fig. 1). Spectra measured near g_1(∥)=2.024 and g_2,3(⊥)=1.934 at the fields 343.8 and 359.0 mT, respectively. The last spectrum corresponds to initial time τ=100 ns and successive spectra are obtained with increasing steps of 16 ns.

Figure 3.

Stacked plots of 3-pulse ESEEM spectra after modulus FT along time T between the second and third microwave pulses for fdx. Spectra measured near g₁=2.052, g₂= 1.957, g₃=1.887 at the fields 341.8, 356.2 and 370.0 mT, respectively (Fig. 1). The last spectrum corresponds to initial time τ=100 ns and successive spectra are obtained with increasing steps of 16 ns.

Table 1.

Nitrogen Frequencies (MHz) in three-pulse ESEEM and HYSCORE spectra of adx and fdx

Protein	EPR position	Three-pulse ESEEM	Major cross-peaks in HYSCORE
adx	g∥(1)	4.23, 3.55, 3.01, 2.56, 1.83	(4.23, 3.17) (1); (3.50, 2.44) (2)
	g⊥(2,3)	4.48, 4.03, 3.2, 3.1, 1.8–2.0	(4.4, 3.17) (1); (4.03, 3.24) (2)
fdx	g1	4.48, 4.19, 3.26, 2.93, 1.5–2.0	(4.52, 3.22) (1), (4.32, 3.01) (2)
	g2	4.52, 3.2–3.85, 1.8–2.4	(4.35, 2.97) (1), (3.99, 3.09) (2)
	g3	4.46, 4.03, 3.3, 2.93, 2.0–2.26, 0.8	(4.44, 3.01) (1), (4.15, 3.05) (2)

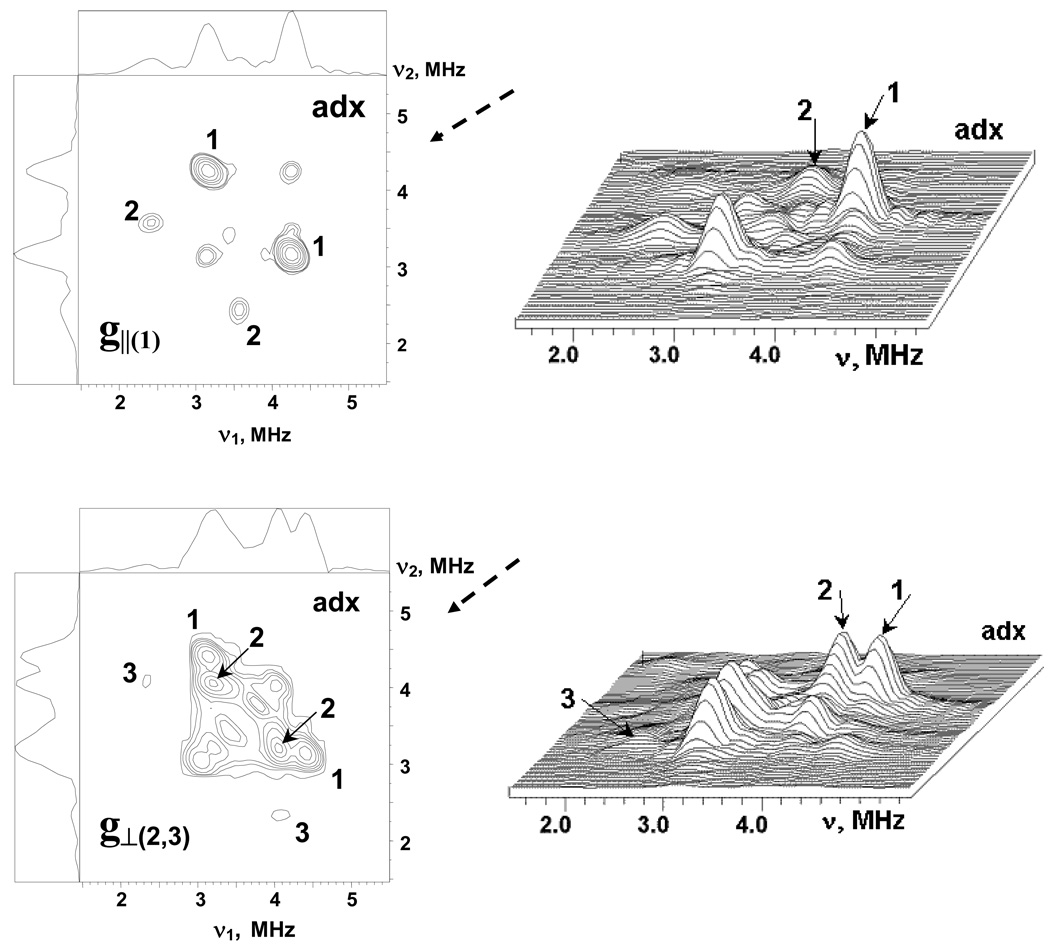
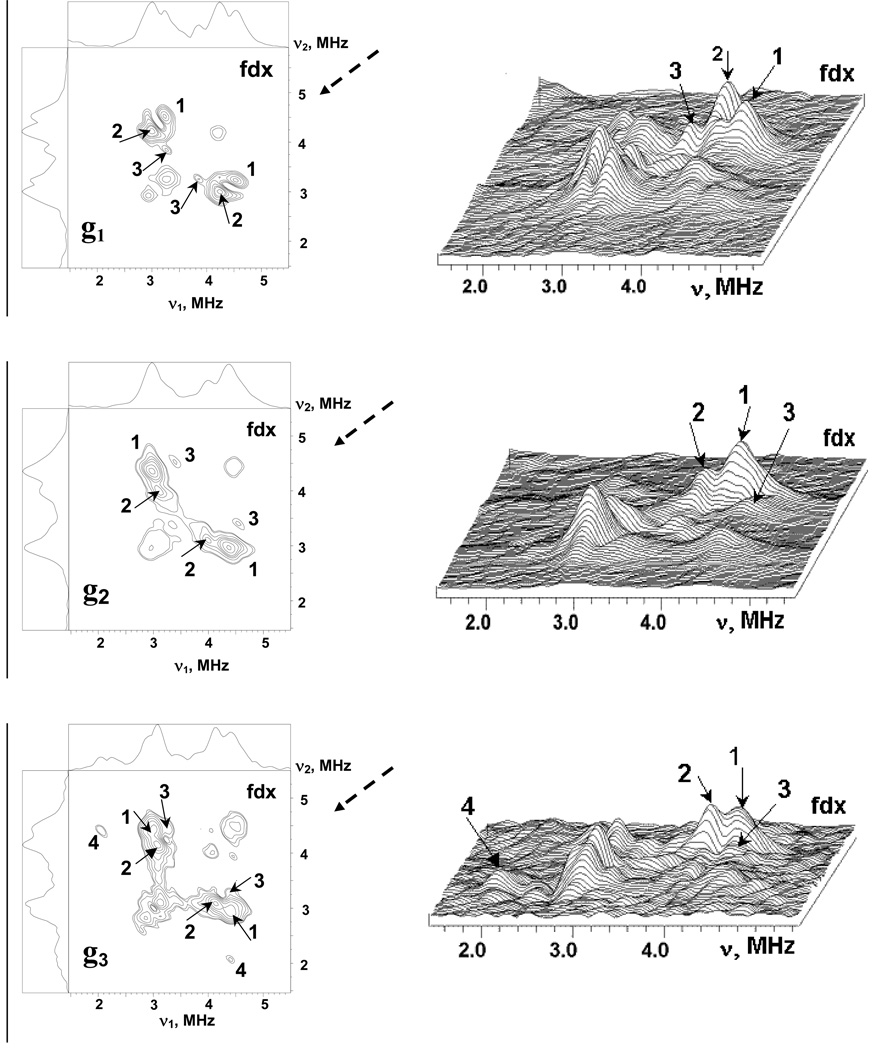
Additional information about relations between nitrogen frequencies was obtained from the 2D ESEEM (HYSCORE) spectra recorded at similar points of EPR line. Fig. 4 shows HYSCORE spectra in contour and stacked presentation for adx. The nondiagonal cross-peaks in these spectra correlate nuclear frequencies from opposite electron spin manifolds belonging to the same nucleus. In the HYSCORE spectra of adx and fdx all ¹⁴N cross-peaks are located in the (++) quadrant only. The spectrum of adx recorded near g_‖(1) contains two pairs of cross-peaks at (4.23, 3.17) MHz (1) and (3.50, 2.44) MHz (2) (top panels). The cross-peaks 1 and 2 are well separated due to difference in the frequencies of both coordinates of the order ∼0.7 MHz.

Figure 4.

The contour (left) and stacked (right) presentations of ¹⁴N HYSCORE spectra of the reduced [2Fe-2S] cluster in the adx. Spectra measured near g_1(∥)=2.024 and g_2,3(⊥)=1.934 at the fields 343.8 and 359.0 mT, respectively. The time τ between first and second microwave pulses is equal to 136 ns for both spectra. Arrows indicate the direction from which the 3D stacked perspective is viewed.

The HYSCORE spectrum of adx measured in the g_⊥(2,3) region (bottom panels) exhibits two closely located pairs of cross-peaks of high intensity at (4.4, 3.17) MHz (1), and (4.03, 3.24) MHz (2), as well as a pair of weak cross-peaks (3) at (4.03, 2.32) MHz. One can note that the difference between the frequencies of cross-peaks 1 and 2 observed in the g_⊥(2,3) is much smaller than that in the g_‖(1) region. The cross-peaks 3 seen in the g_⊥(2,3) region probably belong to the same nitrogen as cross-peaks 2 because they have a common coordinate. These peaks define all three nuclear frequencies, at 3.24, 2.32, 0.92 MHz, in one manifold of this nitrogen, although the cross-peaks involving lowest frequency are not seen in the three-pulse and HYSCORE spectra. Observation of the peaks 3 allows us also to conclude that cross-peaks 1 and 2 are produced by two different nitrogens. The fact that the similarly marked cross-peaks 1 and 2 in both spectra belong to the same nucleus (N1 or N2) does not follow from the spectra; the conclusion is based on the results from spectral simulations described below. The cross-peaks 1 and 2 in both spectra correlate two transitions of maximum frequency, i.e. nominally double-quantum transitions, from opposite manifolds for two different nuclei (see Fig. S1, ESI).

The cross-peaks in HYSCORE spectra of the fdx recorded at the points of the EPR spectrum corresponding to the principal directions of the rhombic g-tensor (Fig. 5) contain a group of closely located and partly overlapping cross-peaks with complex lineshapes. However, two major peaks 1 and 2 are present in all three spectrum, surrounded by features of lower intensity (marked for instance as 3, which we cannot assign currently, and 4 which could belong to the same nucleus as 1 or 3). In contrast to the adx, the frequencies of peaks 1 and 2 show small variations not exceeding ∼0.2–0.3 MHz in the spectra recorded at different fields (Table 1). As in the case of the adx spectra, we suggest that peaks 1 and 2 in the different spectra are produced by two different nitrogens.

Figure 5.

The contour (left) and stacked (right) presentations of ¹⁴N HYSCORE spectra of the reduced [2Fe-2S] cluster in the fdx. Spectra measured near g₁=2.052, g₂= 1.957, g₃=1.887 at the fields 341.8, 356.2 and 370.0 mT, respectively. The time τ between first and second microwave pulses is equal to 136 ns for all spectra. Arrows indicate the direction from which the 3D stacked perspective is viewed.

The HYSCORE spectra at each field were measured at several τ values between 100 and 400 ns. However, they did not resolve any other features other than the ones seen in Figure 4 and Figure 5 recorded with τ =136 ns. The frequencies of the cross-peaks 1 and 2 in HYSCORE spectra of both proteins are consistent with higher frequencies seen in the interval ∼2.5–4.5 MHz in three-pulse spectra. There are also other peaks in three-pulse spectra around 1.8–2.0 MHz and less, which were not involved in cross-correlations. They may belong to single-quantum transitions of the nitrogens producing cross-peaks 1 and 2 but cross-peaks from these transitions will have low intensity in HYSCORE. A second possibility is that these lines are produced by some other nitrogens with smaller hyperfine couplings.

To summarize the experimental data provided here, we conclude that the ¹⁴N ESEEM spectra of both adx and fdx arise from the interaction, predominantly isotropic, of the reduced cluster’s spin with at least two nitrogens possessing close nuclear frequencies. The spectral patterns are more complex for fdx suggesting additional contributions from other nitrogens. Below we will analyze the spectra described with the aim of characterizing the magnetic interactions with nitrogens, and we will use this information for identification of particular N-atoms by correlating the magnetic resonance data with available X-ray structures of adx and fdx.

Discussion

Estimate of hyperfine couplings

The ¹⁴N HYSCORE spectra obtained at g_⊥(2,3) or g₂ region for the two proteins provide a convenient start of the discussion. Because a broad set of orientations contributes to these spectra, it seems appropriate to analyze them and to estimate the nitrogen couplings using approaches developed for the orientation disordered systems. We suggest that the cross-peaks (1) and (2) closely located in the spectra of adx and fdx correlate two transitions of maximum frequency ν_dq+ and ν_dq− (Fig. S1, ESI) from opposite manifolds of two different nuclei N1 and N2. In this case, the formal expressions for the frequency of double-quantum transitions (eq.2) would provide an estimate of the hyperfine coupling with the nitrogen:

$$A=({\mathrm{\nu }}_{\text{dq}+}^2-{\mathrm{\nu }}_{\text{dq}-}^2)/8{\mathrm{\nu }}_{\mathrm{I}}$$ (3)

This gives hyperfine couplings A ∼ 1.1 and 0.7 MHz for N1 and N2, respectively, in adx and fdx (Table 2). Using these couplings the parameter κ=K²(3+η²) from (eq.2) is also calculated. It varies between 1.8–2.16 MHz for different nitrogens (Table 2). Those correspond to quadrupole coupling constant K∼0.68–0.83 MHz, for the asymmetry parameter between 0≤η≤1. This interval of K is consistent with peptide nitrogens, which demonstrate stable, high values for quadrupole coupling constant, with K∼0.75–0.85 MHz and κ=1.82–2.37 MHz² in free peptides, metal complexes of diglycine, and in protein H-bonds with sulfur and oxygen atoms.^28–35 The results provided in the Table 2 show that value of κ is consistently smaller for nitrogens with smaller hyperfine coupling. It might be because equation (2) for the frequency of the dq-transition is less accurate for the smaller couplings than for the larger ones. On the other hand, this result might reflect the difference in the H-bond structure leading to correlated hyperfine and quadrupole characteristics of the donor nitrogen.

Table 2.

Estimated hyperfine and nuclear quadrupole couplings of the nitrogens contributing to HYSCORE spectra of adx and fdx

Protein	Field,mT/ νI, MHz	Cross-peak, MHz	A (+/−0.03), MHz	κ, MHz2	K (+/−0.05), MHz
adx	359.0/1.105	(4.40, 3.17) (1)	1.05	2.11	0.78
		(4.03, 3.24) (2)	0.65	1.83	0.73
fdx	356.2/1.096	(4.35, 2.97) (1)	1.16	2.13 6	0.78
		(3.99, 3.09) (2)	0.72	1.8	0.73

One can also note that, for the estimated values of hyperfine couplings and quadrupole coupling constant, the ratio ν_ef-/K varies within 0.7–1.0 MHz, indicating significant deviation from the cancellation condition, which occurs when ν_ef- /K ∼0. Such a deviation would prevent the appearance of intensive narrow lines at exact nqi frequencies of peptide nitrogen(s) from this manifold in “powder-like” spectra. For the other manifold, the ratio ν_ef+/K has a value ∼2, which might lead to expectation of dq-transitions in the spectra, together with sq-transitions in the “single-crystal like spectra”.

Model calculations

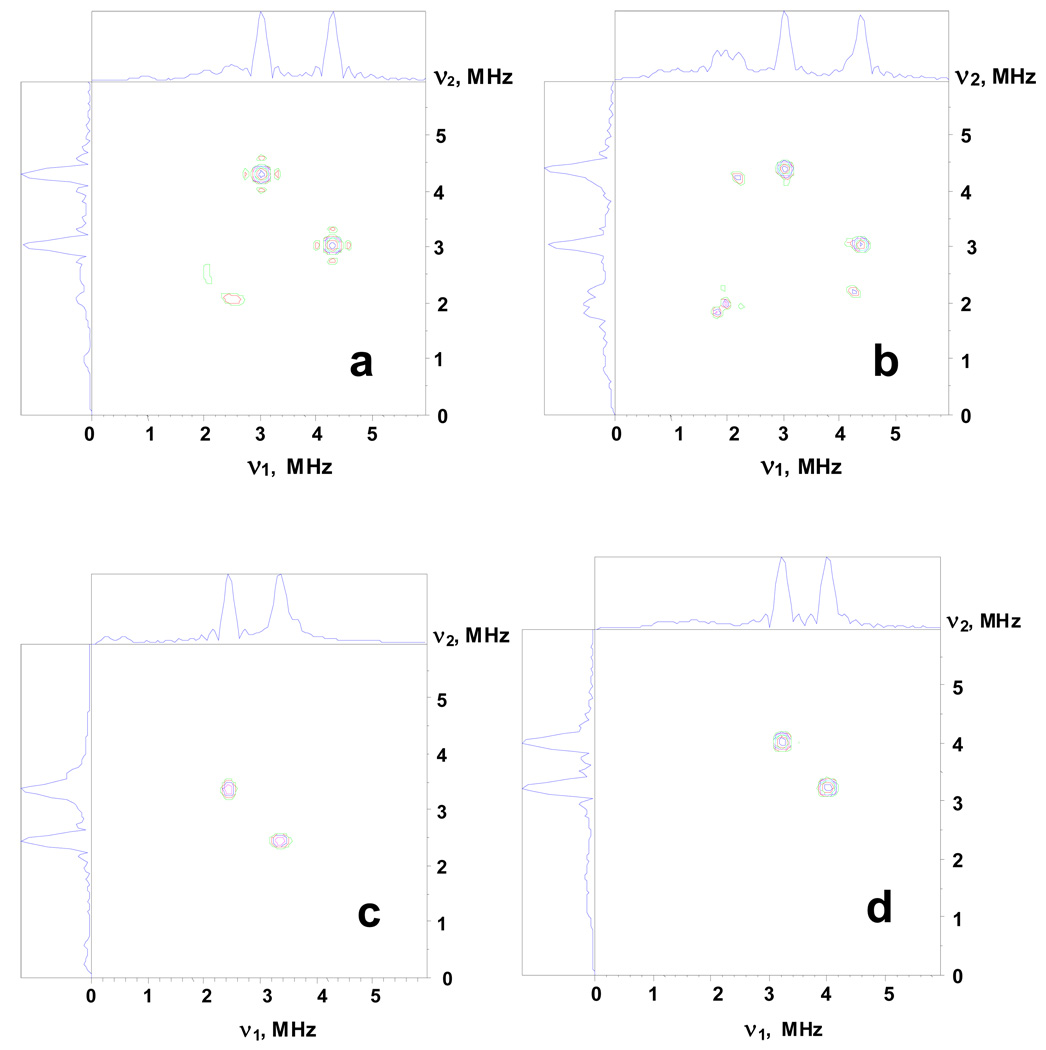
¹⁴N HYSCORE spectra of adx consistently show the presence of two nitrogens near the reduced [2Fe-2S] cluster possessing largest hyperfine couplings ∼1.05 MHz (N1) and 0.65 MHz (N2). For more specific characterization of these nitrogens we have performed model calculations of the orientation-selected HYSCORE spectra at g_║(1) and g_⊥(2,3) positions using hyperfine couplings given in Table 2 and typical average quadrupole characteristics of the peptide nuclei K=0.8 MHz, and η=0.5 MHz. The nitrogen peaks 1 and 2 in both HYSCORE spectra of adx possess almost symmetrical line shape, with approximately rounded contours indicating that the anisotropic hyperfine coupling for N1 and N2 is significantly smaller than the isotropic constants. Therefore, in the model calculations, we initially consider only isotropic hyperfine coupling. In this situation the intensity of different transitions and their appearance in spectra depend on the relative orientation of the g-tensor, and the principal directions of the ¹⁴N nqi tensor. The choice of a particular value for the external magnetic field within the EPR lineshape selects a particular orientation(s) of the g-tensor (i.e. cluster), relative to the magnetic field direction. The aim of simulations was to find orientations of the ¹⁴N nqi tensor relative to the g-tensor at which each of two particular nitrogens would produce spectra dominated by the single pair of cross-peaks seen experimentally (among nine possible cross-combinations). These peaks are from dq-dq correlations involving the maximal frequency from each manifold (Fig. S1, ESI). An additional feature that had to be accounted for in the simulations was the significant difference up to ∼0.8–0.9 MHz between the frequencies of cross-peaks 2 in the spectrum recorded at g_║(1) and the cross-peaks 1 and 2 in the spectrum recorded at g_⊥(2,3). There is no such large difference between the frequencies of cross-peaks 1 in the spectrum recorded at g_║(1) and the cross-peaks 1 and 2 in the spectrum recorded at g_⊥(2,3). Our model simulations for the HYSCORE spectra from the nitrogens with the hyperfine coupling ∼1.1 MHz (N1) and 0.65 MHz (N2) with the parameters of nuclear quadrupole tensor indicated above have shown that the cross-features at the low frequencies (3.5, 2.4) MHz could not be obtained for the nitrogen N1 at any relative orientation of the g- and nqi-tensors. This result has allows us to conclude that the cross peaks 1 in the HYSCORE spectra recorded at g_║(1) and g_⊥(2,3) belong to N1, while cross-peaks 2 in these spectra belong to N2.

The relative orientation of the g (principal values g₁ ≥ g₂ ≥ g₃) and nqi (principal values Q_max ≥ Q_int ≥ Q_min) tensors was defined by Euler angles (α,β,γ), where the angle α corresponds to the rotation around the g₁ axis, the angle β defines the rotation about g₃ axis, and the angle γ describes the rotation about g₁ axis again. It is important to note that in this definition, β specifies an angle between the maximal axes of g and nqi tensors. We were able to reproduce reasonably the intensity and location of the different spectral lines seen in the three-pulse spectra, and as cross-peaks (1) in HYSCORE spectra, within a narrow interval of angles β = ±(55º–65º) or ±(115º–125º) and α = ± (60º–70º) or ±(110º–120º) for the nitrogen (N1) with the larger coupling ∼1.1 MHz. The angle γ could have arbitrary value. On the other hand, the location of the cross-peaks 2 from nitrogen N2 with a coupling ∼0.65 MHz in the spectra at g_‖(1) and g_⊥(2,3), and in particular the decrease of the frequencies at the g_║(1), was reproduced with a value for angle β (between the maximal principal axes of the g and nqi tensors) close to ∼± (90º±5º), and angle α ∼(0–10)°. Examples of the simulated spectra are shown in Fig. 6.

Figure 6.

¹⁴N HYSCORE spectra calculated with the following parameters: (a,b) Magnetic field B_o=343.5 mT, B_o∥g_1(||) (a) and B_o=359.0 mT, B_o⊥ g_1(∥) (right); relative orientation of the g-tensor and nqi tensor is described by the Euler angles (60º, 60º,0º), isotropic hyperfine constant a=1.1 MHz, quadrupole coupling constant K=0.8 MHz, asymmetry parameter η=0.5, cross-peak frequencies (4.20, 3.03) MHz (a), and (4.4, 3.03), (4.2, 2.25) MHz (b). These spectra reproduce the location of cross-peaks 1 in the spectra in Figure 4.

(c,d) Magnetic field B_o=343.5 mT, B_o∥g_1(∥) (c) and B_o=359.0 mT, B_o⊥ g_1(∥) (d); relative orientation of the g-tensor and nqi tensor is described by the Euler angles (0º, 90º,0º), isotropic hyperfine constant a=0.65 MHz, quadrupole coupling constant K=0.8 MHz, asymmetry parameter η=0.5, cross-peak frequencies (3.37, 2.44) MHz (c), and (4.0, 3.23) MHz (d). These spectra reproduce the location of cross-peaks 2 in the spectra inFigure 4. The time τ between first and second microwave pulses is equal to 136 ns for all spectra. The weak anisotropic hyperfine interaction up to T∼0.15 MHz does not affect the spectra calculated in the approximation of the isotropic coupling only.

We have also tested that the structural parameters found from the simulations in the isotropic approximation would not be affected by small anisotropic hyperfine couplings (of the order 10–15% of the isotropic constant), with different and arbitrary orientations of the hyperfine tensor principal axes. Our calculations of the anisotropic hyperfine tensors based on a point dipole model of the interaction of each nitrogen with Fe(III) and Fe(II) spins (using X-ray coordinates, see below) have shown that the average perpendicular component of the anisotropic hyperfine tensor would not exceed 0.16 MHz for any nitrogen in adx and 0.13 MHz in fdx (Table S4 and Table S5, ESI).

The frequencies of the cross-peaks 1 and 2 in the orientation-selected HYSCORE spectra of the fdx do not show significant variations, and have values similar to those for cross-peaks 1 in adx. Therefore, the maximal quadrupole principal axis of these nitrogens forms angle β of the same order, with the g₁ axis as for the N1 in adx, i.e. β=±(50º–70º) or ±(110º–130º). An additional spectral feature, which can be used for the identification of the interacting nitrogens in fdx, is the dominating intensity of the peak at low frequency ∼0.7 MHz in the three-pulse ESEEM spectra recorded near the g₃ principal value (Fig. 3). The value of this frequency is consistent with the lowest frequency, ν_2sq-, in the ν_ef- manifold.^12,32 Theoretical considerations^22,23 supported by the simulations indicate that the increase of ν_2sq- intensity occurs when both vectors B_o and g₃ closely coincide with the axis of the maximal principal value of the nqi tensor. This coincidence of tensor axes is characteristic of nitrogen(s) producing such a line (at ∼0.7 MHz) in the spectrum. However, despite the high intensity of this line in the three-pulse spectrum, the experimental HYSCORE spectra do not show any intensive cross-peaks involving this frequency, so that it can not be accounted for in terms of nitrogens N1 and N2, suggesting that more detailed examination of other nitrogens based on other experimental approaches might be called for.

Information about the principal directions of the g-tensor of the [2Fe-2S] cluster, and of the nuclear quadrupole tensor of the peptide nitrogen, can be correlated with the available crystallographic structural models of the cluster environment in adx and fdx. However, we should note that the crystallographic structures determined for adx and fdx are those of the oxidized state of the protein. The influence of redox state on the structure, and conclusions obtained from comparison of the magnetic resonance data and X-ray structural models, will be discussed more extensively below.

Identification of the interacting nitrogens

The angles characterizing the relative orientation of g and nqi tensors, determined from the simulation of the ESEEM spectra, make it possible to identify possible candidates among the peptide nitrogens around the [2Fe-2S] cluster that have the largest hyperfine couplings, and hence carry the maximal unpaired spin density.

As stated above, peptide nitrogens in different compounds possess a narrow range of quadrupole coupling constants, K=0.75–0.85 MHz, determined by the electronic structure and the geometry of the planar peptide group.^28–35 This coupling constant is only slightly perturbed by hydrogen bonding, as confirmed by calculations of the quadrupole coupling tensor.^36–38 Calculations based on molecules in vacuo yield quadrupole coupling tensors for peptide nitrogen very close to experimental values, confirming the negligible influence of hydrogen bonding. From these calculations, the maximum principal value is normal to the local peptide plane; the intermediate element almost coincides with the C(O)-N(H) bond, and the minimal element points about 30º from the N-H bond.

In order to interpret the magnetic resonance data in conjunction with crystal structures, one needs to know the orientation of the g-tensor principal axes. Orientation of the g-tensor principal directions for the reduced [2Fe-2S] cluster in adx and fdx was previously determined from the simulation of the orientation selected proton ENDOR spectra.^26,27 According to these studies, the g-tensor principal axes are displaced from those theoretically predicted^39,40 as exactly along the S-S, Fe-Fe, and nearly normal to the cluster plane directions. For instance, the g₁ direction in adx is about 24º, with the normal of the averaged plane spanned by the FeSSFe core. The plane spanned by two other principal directions is tilted by about 21º with respect to the FeSSFe plane, so that g₂ forms an angle of 28º with the Fe-Fe direction.²⁶ In fdx the corresponding angles were 25º and 16º, respectively.²⁷ These results are supported by g-tensor skewing of a similar order reported in a single-crystal EPR study of the reduced [2Fe-2S] Rieske cluster in cytochrome bc₁ complex with stigmatellin.⁴¹ The direction cosines defining the orientation of the g-tensor principal axes in the coordinate system of the X-ray structure of adx (1ayf.pdb¹⁸) and fdx (4fxc.pdb¹⁶), respectively, are shown in Table S1, ESI. We have used these orientations of the g-tensor axes in the analysis of ESEEM data.

Available crystallographic structures for adrenodoxin and A. platensis ferredoxin open the way for some tentative conclusions about the nitrogens in the environment nearest the [2Fe-2S] that is responsible for the observed ESEEM/HYSCORE features. These nitrogens possess predominantly isotropic hyperfine couplings and thus carry the unpaired spin density transferred onto their nuclei from the reduced cluster. The preferred mechanism for transfer of unpaired spin density from the cluster onto the protein nitrogens is the formation of the hydrogen bond between N-H groups and bridging sulfurs or sulfurs of cysteine ligands. The second mechanism is the transfer of the spin density over the covalent bonds of cysteine ligands to the peptide nitrogen of cysteine residues.

Using the X-ray structures for adx and fdx, we have calculated the distances between the bridging sulfurs, or the sulfurs of cysteine ligands of the [2Fe-2S] cluster, and the nitrogens of the residues located in the nearest cluster environment (Table S2 and Table S3, ESI). The peptide nitrogens of residues 46, 48–56, and 92 as well as two nitrogens from Gln93 (including the side-chain N_ε2) located at <3.9–4.0 Å from at least one of the sulfurs of the cluster are possible candidates for H-bond formation in adx (as follow from NMR results discussed below), thirteen nitrogens in all. For some of them, the distances are within <4.0 Å from two sulfurs simultaneously (Table 1). The peptide nitrogens of the ligands Cys46, Cys52, Cys55 and Cys92 are located 3.19–3.49 Å from the coordinating sulfurs and are separated from them by three bonds.

Using the properties of peptide planes and the atomic coordinates of adx (1ayf), an angle, β, between the maximal principal direction of the nqi tensor and g₁ principal axis of the cluster’s g-tensor was calculated for different nitrogens (β in Table 3). Comparison of these angles with the angle β∼±(55º–65º) or ±(115º–125º) defined for N1 from numerical simulations indicates that the nitrogens of Gly48, Thr49, Leu50, Thr54, Cys55, Cys92 and Gln93 are appropriate for nitrogen N1. Additional characteristics that can be considered in selection of suitable candidates are the direction cosines between the g₁ axis and other principal axes of the nqi tensor, and the geometry of the potential hydrogen bond defined by the relative location of N-H and S atoms (Table 3). Strong hydrogen bonds show a linear geometry, with the proton located in the plane of the C-N-C (or O-C-N for the glutamine amide) structure.⁴² Thus, we characterize the relative location of N-H and S atoms by two angles: θ = θ’-90º, where θ is the deviation from the plane (given in terms of θ’, the angle between the N-S vector, and a vector normal to the plane above for the particular residue), and ϕ, which is the angle between N-S and N-H vectors, - effectively the deviation from linearity. One can note that deviations from linearity, with values for θ and ϕ up to 40–50º, were reported for H-bonds in proteins where the location of the H-bonded protons was precisely determined from magnetic resonance experiments.⁴³

Table 3.

Characteristics of the nitrogens with shortest N…S distances in adx.

Nitrogen Residue	N-S, Å	S atom	β, deg	cint	cmin	θ, deg	ϕ, deg
Cys46	3.47	Cys52	97	−0.57	0.81	−17	13
	3.49	Cys46	97	−0.57	0.81
Gly48	3.25	S2	66	0.36	0.84	7	26
	3.79	Cys46	66	0.36	0.84	−58	58
Thr49	3.13	Cys46	64	−0.11	0.89	15	13
Leu50	3.55	S1	117	0.86	0.22	−17	47
	3.48	Cys46	117	0.86	0.22	64	61
Ala51	3.26	Cys46	29	0.47	0.09	−2	10
Cys52	3.78	Cys46	84	0.65	−0.76	−66	66
	3.49	Cys52	84	0.65	−0.76
Ser53	3.52	Cys52	80	0.98	−0.06	48	87
Thr54	3.65	Cys52	125	−0.06	−0.81	25	20
Cys55	3.19	Cys55	63	−0.77	−0.45
His56	3.80	Cys55	28	0.44	−0.19	−42	92
Cys92	3.62	Cys55	127	−0.52	0.61	−11	7
	3.25	Cys92	127	−0.52	0.61
Gln93	3.65	Cys92	60	0.11	0.86	−47	80
Gln93*	3.40	Cys92	101	0.03	0.98	−3	17

^*N_ε2

β is an angle between the g₁ axis of the g-tensor and maximum principal value axis of the nitrogen nqi tensor. C_int and C_min are direction cosines defining angles between the g₁ axis and intermediate and mimimum principal value axes of the nitrogen nqi tensor.

θ=θ’-90º, θ’ is the angle between the N-S vector and the normal vector to the peptide plane of the particular residue, ϕ is the angle between N-S and N-H vectors.

The absolute values of the direction cosines, between the g₁ axis, and the principal axes of the intermediate and the minimal principal values of the nqi tensor, calculated from Euler angles found in model simulations, vary within 0.28–0.58 and 0.64–0.85, respectively. The direction cosines determined from atomic coordinates are close to these intervals for nitrogens of Gly48 and Cys92 only. The nitrogen of Gly48 is located at a distance suitable for H-bond formation with the bridging S2 and the sulfur of Cys46. However, the H-bond to S2 has a significantly shorter S… N distance (3.25 Å vs. 3.79 Å), and satisfies the requirement for H-bond linearity better than the H-bond to Cys46. On the other hand, the H-bond model between the nitrogen of Cys92 and the sulfur of Cys55 has the characteristics of a strong H-bond, with θ and ϕ ∼10º. An additional possibility for this nitrogen, which belongs to the coordinating cysteine, is that spin density might be transferred over molecular bonds without participation in H-bond formation (Fig. 7).

Figure 7.

Amino acid sequences of adx (top) and fdx (bottom) showing residues located around the [2Fe-2S] cluster. Cysteine ligand residues are marked in Bold. The nitrogens of the underlined residues indicate candidates for the N1 and N2 carrying largest unpaired spin density (see text). The structures of adx and fdx are shown in Fig. S4, ESI.

Simulations that reproduce the frequency variations between the spectra at g_1(‖) and g_2,3(⊥) of cross-peaks 2 reasonably well, give β ∼90º and α ∼0º, with possible deviations up to 10º for N2 that allow one to select the nitrogens of Cys46, Cys52, Ser53, and Gln93 (N_ε2) as candidates for this role (Table 3). Analysis of other structural characteristics shown in Table 3 for these nitrogens indicates that only the nitrogen of Ser53 has direction cosines between the g_1(‖) and the principal axes of the intermediate and minimum principal values of the nqi tensor close to the estimated |c_int|∼1 and |c_min|∼0. On the other hand, the location of the N-H group of Ser53 relative to the sulfur of Cys52 is far from ideal in geometry for a strong H-bond. In contrast, the location of the N-H group of Cys46 is more appropriate for the formation of a strong H-bond with the sulfur of Cys52 (Table 3), but the direction cosines significantly deviate from those determined from the simulations. The difference in direction cosines excludes also the second option for this nitrogen, i.e. spin density transfer from ligating sulfur. Some additional comments on the Gln93 (N_ε2) are provided in the next section.

Unfortunately, the g-tensor axiality in adx means that we cannot perform orientation selection experiments along the g₃ axis and, this therefore precludes discussion in relation to the orientation of g₂ and g₃ axes relative to the principal axes of the nuclear quadrupole tensor of different nitrogens.

In contrast to adx, the HYSCORE spectra of fdx are more complex, with significant overlap of the individual cross-peaks from different nitrogens. In this situation, it is hard even to assign cross-peaks produced by the same nucleus in the spectra recorded at field positions corresponding to the different principal directions of the g-tensor. However, some conclusions can be reached about possible participants in the H-bonding associated with the largest spin density transfer. There are 12 peptide nitrogens with N…S distances between 2.79 and 3.67 Å, suitable for the formation of the H-bonds in this protein (Table S3). The frequencies of the cross-peaks in the spectra do not change significantly when recorded at different fields; the changes are in the range of the variations of the Zeeman frequency, and proportional to the changes of the external magnetic field. Together with the simulations performed for adx, this result allows us to conclude that the nitrogens producing the observed peaks are characterized by an angle β ∼±(50º–70º) or ±(110º–130º) between the directions of the maximal principal values of the g- and nqi tensors. Five of the 12 peptide nitrogens (Ser40, Cys41, Ala43, Cys49, Cys79, and Val80) possess angles, β (see above), close to this range (Table 4). However, among them the location of nitrogens from Ser40, Ala43, and Cys79 are suitable for formation of H-bonds only if these are close to linear. The nitrogen from Cys49 would be unlikely to participate in H-bond formation, but unpaired spin density could be transferred to this nitrogen through cysteine bonds (Fig. 7).

Table 4.

Characteristics of the nitrogens with shortest N…S distances in fdx.

Nitrogen Residue	N–S, Å	S atom	β, deg	ξ, deg	θ, deg	ϕ, deg
Ser40	3.11	S1	135	123	0	2
Cys41	3.35	S1	79	95	52	41
	3.13	Cys41	79	95
Arg42	3.33	S1	85	168	−16	13
	2.82	Cys41	85	168	−68	72
Ala43	3.02	Cys41	55	65	−10	17
Gly44	3.30	S2	93	81	−14	36
	3.78	Cys41	93	81	−49	45
Ala45	3.87	Cys41	11	100	31	36
Cys46	3.64	S2	83	14	−36	37
	3.53	Cys46	83	14
Ser47	2.79	Cys46	100	141	51	61
Thr48	3.67	Cys46	132	112	40	43
Cys49	3.37	Cys49	72	19
Cys79	3.65	Cys49	118	37	21	19
	3.47	Cys79	118	37
Val80	3.38	Cys79	59	83	−50	73

β is an angle between the g₁ axis of the g-tensor and maximum principal value axes of the nitrogen nqi tensor. ξ is an angle between the g₃ axis of the g-tensor and maximum principal value axes of the nitrogen nqi tensor. θ=θ’-90º, θ’ is the angle between the N-S vector and the normal vector to the peptide plane of the particular residue, ϕ is the angle between N–S and N–H vectors.

Several nitrogens in this protein have β-angles close to 90º, but the spectra do not show the strong variation of nuclear frequencies as a function of field position seen in adx. Among them is the peptide nitrogen of Arg42, which is characterized by the smallest deviation from a co-linearity for the g₃ direction and the axis of maximal principal value of the nqi tensor (168º, Table 4). Thus, this nitrogen could be responsible for the intensive line at low frequency (0.7 MHz) in three-pulse spectra at g₃. In addition it is located at 3.32 Å from the bridging S1 and 2.81 Å from the sulfur of Cys41. However, the H-bond geometry with S1 is preferable. This nitrogen could also produce some additional features in HYSCORE spectra which have not yet been interpreted.

Redox-linked structural changes in [2Fe-2S] ferredoxins

For the analysis of the magnetic resonance data obtained for the reduced adx and fdx we have used crystallographic structures obtained for oxidized proteins. Since the oxidized structures leave some ambiguity in assignment, it might be useful to consider another possibility, - that the reduced protein might have structural differences that would allow a resolution of these ambiguities. Crystallographic structures reported during the last few years for oxidized and reduced forms of other [2Fe-2S] ferredoxins provide a database for analysis of possible contributions of redox-linked conformational changes that might provide clues.

So far, high-resolution crystal structures in oxidized and reduced states were reported for a plant-type ferredoxin, Anabaena PCC7119 Fd (AnFd)⁴⁴, and two bacterial [2Fe–2S] ferredoxins that are vertebrate-like, i.e. Putidaredoxin (Pdx) from Pseudomonas putida⁴⁵ and FdVI from the photosynthetic bacterium Rhodobacter capsulatus.⁴⁶. Despite diverse functions of vertebrate-type ferredoxins, sequence alignment highlighted the conserved cluster-binding sequence, Cys-X₅-Cys-X-Thr-Cys-X_36–38-Cys.⁴⁷ However, in fdx, the first loop is of 4 residues (X₄), and the second 30 (X₃₀), while in adx, the longer loop is X₃₇ compared to X₃₈ in Pdx and FdVI.

In AnFd, reduction gave rise to relatively limited conformational changes around residues Cys46, Ser47 and Phe65.⁴⁴ The major difference between the redox forms of AnFd lies in the orientation of the carbonyl group of Cys46, which points toward (“CO in”) and away (“CO out”) from the [2Fe-2S] cluster in the oxidized and reduced protein, respectively. The flip of the Cys46-Ser47 peptide bond in the crystal structure of reduced AnFd was proposed to be a signature of the reduction of the Fe1 iron atom in the [2Fe-2S] iron-sulfur proteins. Moreover, the flip leads to the formation of a new (additional) hydrogen bond between the nitrogen of Ser47 and S2 with N…S distance 3.7 Å. Mechanistically, the flip in the Cys46–Ser47 link influences the Phe65, which plays a crucial role in electron transfer.

The difference between AnFd and other vertebrate and vertebrate-type ferredoxins is that structural rearrangement in the vertebrate-type proteins is more obvious and involves peptides and residues distant from the active site.^45,46 However, again the flip of the carbonyl is the most visible change in the environment close to the cluster. In oxidized Pdx, the Cys45 carbonyl points towards the cluster (CO in). In reduced Pdx, the conformational shift of the Cys45 carbonyl (CO out) is accompanied by a new hydrogen bond (in the oxidized form) between the peptide nitrogen of Ala46 and the bridging S1 atom of the cluster, which leads to readjustment of bonding interactions between the reduced metal center, electron-enriched S_γ of the cysteinyl ligands, and the backbone amide nitrogen atoms. Because of the orientation of the new H-bond in the reduced form, this conformational reorganization narrows the binding “box” in the dimension normal to the cluster plane by changing the distances between nitrogens and sulfur atoms, and the angles between different atoms (particularly N…H…S), though these changes do not exceed 0.15 Å and ∼5º, respectively, compared to the oxidized protein.⁴⁵ Particularly, positions of the residues of the more C-terminal metal binding loop, Cys85-Gln87, and that of Cys48 are little changed during redox transition in Pdx. Also these differences do not significantly modify the relative orientation of the peptide planes and FeSSFe plane of the cluster (or the g-tensor principal axes).

In the oxidized FdVI, in contrast to Pdx, the CO of Ala44 (next to cysteinyl ligand Cys45) pointed away from the cluster (CO out), whereas in the reduced protein, Ala44 showed two conformations, in one of which the carbonyl came closer to the cluster S1 atom, at a distance of 3.9 Å (CO in). In this conformation, the Ala44 carbonyl turned towards Met70, thus reducing the distance from Ala44 O to Met70 S from 4.7 to 3.0 Å. Interestingly, Met70 occupies a position similar to Phe65 in AnFd, and it is inferred that the CO switch of Ala44 might be involved in the interaction of FdVI with its natural partner.⁴⁶ The conformational change on redox transition modified the configuration of the cluster domain substantially, with changes in H-bond distances from all the backbone N-atoms within 3.5 Å of the cluster, and introduction of an additional bond to Met24 with a distance of 2.73 Å.

NMR structures are available for the oxidized and reduced forms of adx (1L6U, 1L6V).⁴⁸ However, we note that the ‘best representative conformers’ in the NMR structures differ substantially in the liganding of the cluster, and deviate substantially from the crystallographic structures both in cysteine-S to cluster-Fe distances, and in the H-bonding patterns for the groups discussed here. The authors note that these regions are ill-defined due to paramagnetic interactions.

In considering the conformational changes above, it is clear that we must take into account the possibility of differences between the oxidized, and reduced structures of adx, the latter being the protein observed by EPR. Residues could undergo substantial relocation associated with a carbonyl flip (observed so far in all ferredoxins for which a structure of the reduced state is available), leading to formation of a new H-bond with a bridging sulfur, which could not otherwise be inferred from the structure of the oxidized protein. If this flip occurred, it would be at the residue immediately after the second cysteine ligand of the cluster. On the basis of homology, it seems likely that on reduction of adx, in association with a flip of Cys52 carbonyl, the nitrogen of Ser53 would move closer to the cluster, breaking the H-bond with Cys52 -SH, and forming a new H-bond between N-H and the bridging sulfur S1. If such a conformational change occurred, it would require reconsideration of the H-bonding possibilities for the peptide nitrogen of Ser 53.

A special caveat is also needed for the N_ε of Glutamine-93 of adx. The H-bond between this nitrogen and the sulfur of the nearest cysteine ligand (Cys92) is a conserved motif for vertebrate-type ferredoxins, which is absent in the plant-type ferredoxins. This H-bond exists in oxidized and reduced forms, although the data for Pdx allow one to suggest that it is weaker in the reduced form. The N… S distance and N… H… S angle are 3.39 Å and 174º, respectively, in oxidized protein in comparison with 3.44 Å and 170º, for reduced form.⁴⁵ It is tempting to assign N_ε to N2 because no nitrogen with similar characteristics is present in fdx spectra. The only argument against this assignment is that the values of direction cosines are interchanged, i.e. the values calculated were |c_int |∼0 and |c_min |∼1, instead of the values |c_int |∼1 and |c_min |∼0 expected if intermediate principal value of the nuclear quadrupole tensor is coincident with C-N direction. One can note, however, that some NMR data for the H-bonded C-NH₂ group have allowed an interpretation in which the orientation of intermediate and minimal principal directions could be interchanged.⁴⁹ This uncertainty still allows us to keep N_ε of Gln among the possible candidates for the role of the N2. One can suggest that the hyperfine coupling with this nitrogen could be measured directly using selective ¹⁵N labeling.

Transferred spin density

Detailed NMR studies of the hydrogen bonds between ligating cysteine sulfurs and peptide nitrogens in Clostridium pasteurianum rubredoxin (CpRd) have found important relations between unpaired spin density, the strength of hydrogen bonds and redox potential.^50–52 The ¹⁵N NMR spectra from wild-type CpRd and nine mutants of rubredoxin showed multiple hyperfine-shifted resonances from four ligating cysteines, and from amides forming H-bonds with cysteine sulfurs that ligate the iron in the oxidized (Fe(III)) and reduced (Fe(II)) forms. The Fermi contact chemical shifts were linearly proportional to the calculated unpaired spin density at the peptide (amide) nitrogens. The unpaired spin density at any particular nitrogen does not exceed 0.0022 in the oxidized state and 0.0018 in the reduced state at room temperature. Furthermore, calculations showed that the shorter the H…S distance (which varied within 2.5–3.0 Å for different H-bonds), the greater the unpaired spin density on N. In addition it was found, that the aggregate lengths of these hydrogen bonds were shorter in both oxidation states in variants with higher reduction potential than in those with lower reduction potential, and that differences in aggregate hydrogen bonding upon reduction correlated linearly with the published reduction potentials for the 10 CpRd variants, which span 126 mV. Interestingly, the peptide nitrogens of cysteine ligands showed more complex behavior, due to transfer of spin density via two pathways. These results show the importance of the distribution of unpaired electron spin density via hydrogen bonds on the peptide nitrogens around the iron-sulfur cluster in determination of redox properties. The structural difference between rubredoxin and ferredoxins is that all sulfurs belong to cysteine ligands in first structure, but there are two additional bridging sulfurs in [2Fe-2S] clusters, which could form H-bonds with the peptide nitrogens of non-liganding residues.

The results obtained in the present work allow some preliminary conclusions about the H-bonding of peptide nitrogens with the [2Fe-2S] cluster. We have suggested two possible candidates for the role of the N1 (with the largest coupling ∼1.1 MHz) in adx. These are peptide nitrogen of Gly48, H-bonded to S2, and that of Cys92, H-bonded to Cys52. The latter could also carrying spin density transferred via molecular bonds from Fe(III). We favor the first of these possibilities, i.e. Gly48 nitrogen H-bonded with S2. The HYSCORE spectra of the [2Fe-2S] cluster in ¹⁵N labeled Rieske fragment isolated from the bc₁ complex of Rhodobacter sphaeroides showed the presence of a weakly coupled nitrogen with a coupling ∼1 MHz (recalculated for ¹⁴N). The ¹⁴N S-band ESEEM study of this protein has identified this nitrogen as the peptide N of Leu132, which structures show to be involved in an H-bond with one of the bridging sulfurs. A similar coupling observed in the spectra of other Rieske proteins^32,53 and in classical ferredoxins, including adx and fdx in this work, may indicate the presence of a similar hydrogen bond with a bridging sulfur, transferring an excess of unpaired spin density onto the peptide nitrogen. If so, this configuration might be a common structural motif of all [2Fe-2S] clusters, not linked specifically to the differences in cluster potential. In agreement with this hypothesis, nitrogens with structural characteristics suitable for the H-bonding with a bridging sulfur, i.e. Ser40 and Arg42, were among the candidates for H-bonding in fdx, selected on the basis of the ESEEM parameters.

Estimated values of the hyperfine couplings with predominantly isotropic character for the two nitrogens discussed above are ∼0.6–0.7 and 1.0–1.1 MHz. The experimentally determined hyperfine couplings reflect multiplication by a coefficient of order ∼((-1) – (+1.5)) to take account of the interaction with individual magnetic moments of Fe(III) or Fe(II) (see ESI, rescaling of hyperfine couplings). The nonzero isotropic constant, a, for the interacting peptide nitrogen indicates that unpaired electron spin density is transferred from the reduced cluster onto this atom. The isotropic constant is determined mainly by the unpaired spin density in the 2s orbital of N. It is proportional to the value of 1811 MHz for ¹⁴N, which is computed for unit spin density in this orbital.⁵⁴ Thus, the isotropic hyperfine couplings 0.7 and 1.0 MHz determined from HYSCORE spectra correspond to the transfer of only a very small fraction of this computed spin density, with ρ_s ∼ 0.33.10⁻³ and 0.55.10⁻³ , respectively, on the 2s orbital of nitrogen. The fraction of spin density on the two nitrogens near the reduced [2Fe-2S] cluster in adx and fdx is ∼4–6 times smaller than the spin densities found in CpRd. This difference might reflect the electron spin S=1/2 of the cluster in its ground state compared to S=5/2 and S=2 of oxidized and reduced rubredoxin respectively. In addition, the NMR data were obtained at room temperature when excited states could have contributed to the electronic structure.

In analogy with the NMR spectra, one can suggest that other nitrogens involved in the H-bond formation around the clusters in adx and fdx carry even smaller unpaired spin density. Partial support for this comes from spectra of fdx, which show additional features near cross-peaks 1 and 2. More adequate information about all interacting nitrogens and their hyperfine couplings can be directly obtained from experiments with ¹⁵N uniformly labeled proteins. This approach has been recently applied to the Rieske clusters in two different proteins, where the ¹⁵N HYSCORE spectra clearly show the presence of nitrogens with couplings ∼1.0 MHz, but also nitrogens showing 5–10 times weaker coupling.^32,53 However, this approach still leaves the assignment of the observed couplings questionable, and needs to be combined with other methodological or spectroscopic approaches (particularly experiments at lower S-band microwave frequencies). Of particular interest would be selective labeling of the different residues, which could help in direct measurement of hyperfine couplings, and in construction of a density map of transferred spin on different peptide nitrogens for the [2Fe-2S] cluster in its ground electronic state. This would certainly be of interest in addressing the participation of new H-bonds formed on reduction, as discussed above. The information obtained from spectroscopy of the local N atoms, combined with data about hyperfine couplings of protons involved in H-bonds, would help in a general understanding of the nature of hydrogen bonds and their role in stabilization of the cluster in its reduced state.

Conclusion

The X-band 1D and 2D ¹⁴N ESEEM study of the reduced [2Fe-2S] cluster in two ferredoxins has shown that it is involved in weak interactions with protein nitrogens carrying unpaired spin density transferred presumably via H-bond bridges or covalent bonds of cysteine ligands. The hyperfine couplings ∼0.65–0.70 and ∼1.05–1.1 MHz were attributed to two nitrogens in each of the two proteins, but these similar couplings revealed different spatial locations relative to the cluster, as follows from the different behavior of their cross-peaks in orientation-selected spectra. These couplings are comparable with or less than the ¹⁴N Zeeman frequency (∼1.05–1.1 MHz in X-band) in both proteins. As a result, the X-band spectra observed are dominated by double-quantum peaks from two nitrogens, and their cross-correlations in 2D spectra. Observation of only these peaks prevents the exact determination of the hyperfine and nuclear quadrupole tensors. The 1D and 2D ESEEM spectra show obvious differences between the two proteins, although the maximal couplings with two nitrogens are similar. The patterns are more complex in fdx, prompting the suggestion that additional nitrogens with smaller hyperfine couplings must interact with the cluster.

Comparing the results of ESEEM analysis with the X-ray structure of the oxidized proteins, we have selected nitrogens suitable for the properties of N1 and N2 detected by spectroscopy. Those are peptide nitrogen of Gly48 and Cys92 as N1 and peptide nitrogen of Ser53 and Cys46 as N2 in adx. The peptide nitrogens of Ser40, Cys41, Ala43, Cys49, and Cys79 are selected for the role N1 or N2 in fdx.

We were not able to identify these nitrogens unambiguously. This is because of the complex character of the orientation-selected spectra, which have a limited number of resolved cross-peaks produced by several peptide nitrogens, with an unfavorable relation between the effective nuclear hyperfine frequencies and quadrupole coupling constant.

In order to resolve additional spectral features in 1D and 2D spectra, and to obtain more precise information about the interacting nitrogens, one can propose the use of ESEEM and HYSCORE at lower microwave frequencies (C- and S-band experiments were previously performed^12,32), and uniformly and selectively ¹⁵N labeled proteins. These approaches would help to reveal the difference in the electronic structure of plant and vertebrate ferredoxins, and lead to a deeper understanding of the role of hydrogen bonds with peptide nitrogens.

Other factors influencing the results of the spectroscopic study are related to the methodology of the data analysis. The analysis is based on comparison between the X-ray structure and the magnetic-resonance parameters, referred to the coordinate system of the g-tensor. The accuracy of the analysis depends on two basic methodological limitations: accuracy in determination of the g-tensor principal axes, and of the atomic coordinates, which depend on the resolution of X-ray structure. An additional problem arises from ambiguity in the reduction state of the protein. Most available X-ray structures are obtained for the oxidized proteins. Particularly, we have used the X-ray structures of the oxidized proteins for the data analysis obtained for reduced protein. However, the experimental data discussed above indicate that some changes of the structure, specifically in the cluster environment, might accompany the reduction. Thus, the most favorable situation for correlation of the structural and magnetic-resonance characteristics would be the availability of a high-resolution X-ray structure for the reduced protein together with the g-tensor determined from EPR measurements with a similar single-crystal.