De novo computational prediction of non-coding RNA genes in prokaryotic genomes

Abstract

Motivation: The computational identification of non-coding RNA (ncRNA) genes represents one of the most important and challenging problems in computational biology. Existing methods for ncRNA gene prediction rely mostly on homology information, thus limiting their applications to ncRNA genes with known homologues.

Results: We present a novel de novo prediction algorithm for ncRNA genes using features derived from the sequences and structures of known ncRNA genes in comparison to decoys. Using these features, we have trained a neural network-based classifier and have applied it to Escherichia coli and Sulfolobus solfataricus for genome-wide prediction of ncRNAs. Our method has an average prediction sensitivity and specificity of 68% and 70%, respectively, for identifying windows with potential for ncRNA genes in E.coli. By combining windows of different sizes and using positional filtering strategies, we predicted 601 candidate ncRNAs and recovered 41% of known ncRNAs in E.coli. We experimentally investigated six novel candidates using Northern blot analysis and found expression of three candidates: one represents a potential new ncRNA, one is associated with stable mRNA decay intermediates and one is a case of either a potential riboswitch or transcription attenuator involved in the regulation of cell division. In general, our approach enables the identification of both cis- and trans-acting ncRNAs in partially or completely sequenced microbial genomes without requiring homology or structural conservation.

Availability: The source code and results are available at http://csbl.bmb.uga.edu/publications/materials/tran/.

Contact: xyn@bmb.uga.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Non-coding RNA (ncRNA) or small RNA (sRNA) genes, which encode functional RNA molecules that are not translated into proteins, are involved in a variety of cellular processes ranging from regulation of gene expression to RNA modification and editing (Gottesman, 2005; Huttenhofer et al., 2002). In humans, it is estimated that ∼98% of the genome can be transcribed, of which only ∼2% encodes protein genes (Szymanski et al., 2003), suggesting the possibility that a large percentage of the genome may encode ncRNA genes. Although the vital importance of ncRNA genes in cellular activities is well recognized, our current knowledge about the collection of all ncRNA genes encoded in a particular genome is very limited because of the lack of effective capabilities, either computational or experimental, for elucidating them.

It is generally believed that the identification of ncRNA genes, particularly in bacterial genomes, is more challenging than protein-coding genes. Unlike protein-coding genes, ncRNA genes do not contain easily detectable signals such as open reading frames (i.e. a sequence between an in-frame start codon and the first in-frame stop codon going from the 5′ to the 3′ end of the sequence), codon biases, or ribosome binding sites. Although some ncRNA genes have recognizable promoters and terminators (Argaman et al., 2001; Chen et al., 2002), the identification of such regulatory signals is quite challenging. This identification problem is further complicated by the fact that most ncRNA genes are much shorter than protein-coding genes.

A number of computational methods for identifying ncRNA genes have been developed and reported (Argaman et al., 2001; Chen et al., 2002; Klein et al., 2002; Livny et al., 2005; Pichon and Felden, 2003; Schattner, 2002; Washietl et al., 2005; Wassarman et al., 2001; Yachie et al., 2006; Zhang et al., 2004). These methods generally fall into two classes: (i) methods that identify members of an ncRNA family based on homology information (Argaman et al., 2001; Wassarman et al., 2001); and (ii) methods that find novel ncRNAs based on general features common to ncRNA genes. We focus on the latter class of methods since it relates to our approach.

Two classes of methods have been developed to predict novel ncRNAs. The first one identifies conserved and relatively long sequences in the intergenic regions across closely related genomes. This type of method is based on the assumption, which is generally true for prokaryotic genomes, that such conserved regions encode functional RNAs and not cis-regulatory DNA motifs. Such a strategy has been used to mine Escherichia coli (Zhang et al., 2004) and other bacterial genomes (Pichon and Felden, 2003) for novel ncRNAs. By limiting the search to intergenic regions, one could realistically search for ncRNA genes on a genome-wide scale. However, this approach will miss ncRNAs that overlap protein-coding genes, either sense or antisense, and ncRNA genes that are unique to a genome. For example, it is known that ∼25% of the C/D snoRNA genes overlap protein-coding genes in the Pyrococcus abyssi genome (Gaspin et al., 2000). A generalization of this type of method is to predict novel ncRNA genes through the identification of conserved RNA secondary structures across related genomes and further analyze their mutational patterns (Rivas and Eddy, 2001; Rivas et al., 2001) or evaluate the folding energy of their predicted structures (Coventry et al., 2004; di Bernardo et al., 2003; Pedersen et al., 2006; Washietl et al., 2005). These structure-based methods rely on the need for homology as well as having high quality alignments.

The second class of approach predicts novel ncRNA genes based on identifying both common and distinguishing features of known ncRNA genes in target genomic regions. The features used have included predicted promoters and terminators, as well as the base compositions of target sequences. Typical requirements mandate that such a region be short and flanked by promoter and terminator signals (Argaman et al., 2001; Chen et al., 2002). Clearly, such methods are limited in their effectiveness in reliable prediction of novel ncRNA genes for two main reasons: (i) accurate prediction of such signals is very challenging and unreliable; and (ii) only a fraction of terminators, namely, rho-independent terminators in prokaryotes, can be computationally predicted (Kingsford et al., 2007).

Although nucleotide composition-based methods have had some success in ncRNA gene prediction, these methods are limited to organisms with compositional bias in their ncRNA genes in relation to their underlying genome. For example, in A/T-rich hyperthermophilic genomes, the ncRNA genes are relatively more GC-rich (Klein et al., 2002; Larsson et al., 2008; Schattner, 2002). In addition to base composition (or mono-nucleotide composition), some programs have employed di- and tri-nucleotide frequencies to distinguish ncRNA genes from the genomic background (Wang et al., 2006). Such information has also been further enhanced through the use of folding energy and known RNA motifs (Carter et al., 2001) for the prediction of ncRNA genes in E.coli.

In this article, we present a de novo method for predicting ncRNAs in bacterial genomes that employs a number of novel structural features associated with known ncRNA genes. Our method does not require prior homology, multiple sequence alignments, or structural conservation but uses only sequence and structure-based features easily derivable from the genome itself, which is a major advantage since the method can be directly applied to any organism that may be newly sequenced or partially sequenced. A neural network (NN)-based classifier was trained to predict the ncRNA genes on a genome-wide scale. We have applied this classifier to RNA gene prediction in E.coli and have compared our predictions to other existing programs. Furthermore, we also experimentally investigated six of the novel candidate ncRNAs predicted by the algorithm using Northern blot analysis, and identified a potential new ncRNA located downstream of the ydgA gene as well as a cis-acting regulatory element that helps control the expression of the essential mreB operon.

2 METHODS

To train a classifier for the de novo prediction of ncRNAs genes, we first generated a positive data set containing known ncRNA genes and identified a set of sequence and structural-based features that could distinguish the positive data set from non-ncRNA genes. We assumed that ncRNA genes are no longer than 1000 nucleotides (nt), which covers the vast majority of the known ncRNAs in prokaryotes. We refer the reader to the Supplementary Material for additional details presented in each of the following subsections.

2.1 Data set generation

Our positive ncRNA data set was derived from three existing sources: (i) the NONCODE database (Liu et al., 2005); (ii) published literature; and (iii) GenBank. These searches yielded 427, 426 and 1105 ncRNAs from NONCODE, published literature, and NCBI, respectively, for a total of 1540 non-overlapping ncRNAs, which we refer to as ‘Positive1540’ for future reference.

To remove redundant sequences from within this data set, we applied the Markov cluster (MCL) algorithm to group together similar sequences using the default inflation parameter and a BLAST bit-score cutoff of 5 (Enright et al., 2002). Our application of this algorithm resulted in 936 clusters from which we randomly selected one ncRNA from each cluster to use in our final training data set. We refer to this data set as ‘Positive936’ to represent our positive controls.

The generation of the negative control represented a challenge in our work since there are no known negative sets, i.e. regions of the genome known not to contain ncRNA genes. Approaches using segments of the genomic background (Carter et al., 2001; Saetrom et al., 2005; Schattner, 2002) as the control inherently assume that ncRNA genes make up only a small portion of the entire genome, which may not be correct. Other methods use randomly shuffled permutations of known ncRNA genes to build a negative training data set (Clote et al., 2005; Klein et al., 2002; Rivas and Eddy, 2000; Workman and Krogh, 1999). We constructed our negative set by shuffling sequences of known ncRNA genes, while preserving both the mono- and di-nucleotide frequencies. This approach prevented the negative set from being biased to certain regions of the genome. The rationale for preserving the compositional frequencies was that it enabled the calculation of the minimum folding energy (MFE) without biasing the stabilizing and destabilizing energy from stacked base pairs or loops, respectively (Clote et al., 2005; Freyhult et al., 2005; Workman and Krogh, 1999). We used the shuffling strategy implemented in (Clote et al., 2005), based on the Altschul and Erickson algorithm (Altschul and Erickson, 1985). We use the term ‘di-shuffle’ to represent the shuffling procedure that preserves the mono- and di-nucleotide frequencies of the input sequence. For each known ncRNA sequence in ‘Positive936’, we generated 1000 di-shuffled sequences, to which we refer as ‘Dishuffle936’.

2.2 Features used

Secondary structures play a key role in the functions of ncRNAs and are more highly conserved than the primary sequences. Accordingly, we investigated a number of secondary structure-based features in terms of their power to differentiate between ncRNAs and their di-shuffled sequences, including novel features such as structural and ensemble statistics, plus a few previously used features such as folding statistics.

2.2.1 Folding statistics

We examined the MFE (Carter et al., 2001; Wang et al., 2006; Washietl et al., 2005) distributions for real ncRNAs and their di-shuffled sequences. Although useful, the current thermodynamic model used in RNA secondary structure prediction is accurate to only within 5–10% of the actual MFE, making the accuracy of the current MFE-based structure predictions ∼50–70% (Eddy, 2004). Therefore we used other features in conjunction with MFE to assess the reliability of the secondary structure prediction. One of these features was the Shannon base-pairing entropy measure (Freyhult et al., 2005; Huynen et al., 1997). Given an RNA sequence, the Shannon entropy can be computed from the ensemble of predicted secondary structures, as shown in Equations (1) and (2), where P_i,j is the probability of base-pairing between nucleotides at sequence positions i and j, and n is the length of the RNA sequence. Note that the higher the entropy, the lower the structural prediction reliability.

(1)

(2)

Supplementary Figure S1 shows the folding statistics (MFE and Shannon entropy) for each ncRNA in Positive936 compared to Dishuffle936. In agreement with (Clote et al., 2005; Freyhult et al., 2005), the ncRNAs in our data set were observed to have lower MFE and Shannon entropy than their di-shuffled sequences.

2.2.2 Ensemble statistics

Besides the Shannon base-pairing entropy, we investigated three other ensemble-based features to assess the global folding reliability among all structures in the Boltzmann ensemble. These features included (i) the free energy of the thermodynamic ensemble; (ii) the ensemble diversity statistic computed by RNAfold; and (iii) the frequency of the MFE structure. These features measured the average free energy, base-pair distance and uniqueness of the MFE structure (Gruber et al., 2008). The free energy of the ensemble for ncRNAs tends to be lower and hence more stable, while the ensemble of ncRNA structures tends to be less diverse, indicating that the ncRNA structures were more unique compared to their di-shuffled decoys, as shown in Supplementary Figure S2.

Since the prediction accuracy of secondary structures can improve substantially with the inclusion of suboptimal structures near the MFE (Jaeger et al., 1989), we applied an RNA secondary structure clustering algorithm, RNACluster (Liu et al., 2008), to cluster 1000 predicted structures sampled from all possible secondary structures according to the Boltzmann equilibrium probability distribution (Ding and Lawrence, 2003). Using the base-pairing distance between predicted secondary structures (Liu et al., 2008), we calculated various statistics to assess the cluster quality of the sampled structures. One statistic measured the compactness of each cluster (or cluster density) as defined in (Liu et al., 2008) and shown in Equation (3),

(3)

where d_ij is the base-pair distance and m is the number of structures within a cluster.

Unlike the clustering analysis of the predicted secondary structures done by the authors of Sfold (Chan and Ding, 2008; Ding et al., 2005, 2006), our approach used a rigorous and unique clustering method employed in RNACluster (Liu et al., 2008). RNACluster identifies dense clusters in the space of all predicted structures by representing the structures as a minimum spanning tree (MST) and by identifying subtrees of the MST that form statistically significant clusters. We calculated five statistics, based on (Chan and Ding, 2008), for discriminating structural RNAs from their decoys using RNACluster: (i) the number of high-frequency base-pairs in the ensemble; (ii) the average number of high-frequency base-pairs per cluster; (iii) the average base-pair distance between the MFE structure and the ensemble, (iv) the between-cluster sum of squares (BSS); and (v) the within-cluster sum of squares (WSS). The BSS statistic measures the base-pair distance between the cluster centroid and the ensemble centroid, while the WSS statistic measures the base-pair distance between the cluster centroid with all structures within that cluster (Chan and Ding, 2008). The centroid definitions may be found in the Supplementary Material.

We also calculated the BSS and WSS statistics based on a non-optimal ‘centroid’ structure, which we denoted as BSS_point and WSS_point, respectively. The BSS_point measures the between-cluster sum of squares distance between a cluster centroid and the ensemble centroid where the centroid is an existing structure unlike the optimal centroid used in (Chan and Ding, 2008). The WSS_point measures the within-cluster sum of squares distance between the cluster centroid (an actual structure) to all structures within that cluster. In addition, we incorporated the following novel statistics related to the compactness of a cluster: (i) the average compactness; (ii) the maximum compactness; (iii) the minimum compactness; (iv) the compactness of the largest cluster; and (v) the overall compactness to assess the cluster quality generated by RNACluster. Note that the average compactness is the mean of the compactness statistics over all the clusters, while the overall compactness is taken over the entire collection of structures, i.e. the sum of all the distances normalized by the number of structures in the entire collection of structures. The average compactness gives a more localized view of the density of the clusters while the overall compactness gives a more global view of the density of all the structures. Finally, we examined the number of clusters as found by RNACluster.

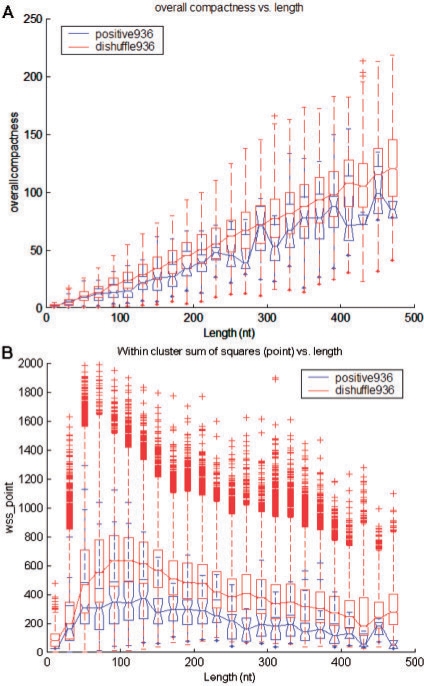
The statistics calculated by RNACluster were found to be highly discriminatory for separating ncRNAs from their di-shuffled versions, as shown by the P-values in Supplementary Table S1. Using the RNACluster method, the structures of known ncRNAs tend to form fewer clusters and be more densely clustered than their di-shuffled versions, as shown in Figure 1A. Additional compactness-related boxplots are shown in Supplementary Figure S3. The statistics from the largest cluster, as shown in Supplementary Figure S4, also reflect the same trend for lower compactness statistics in the positive set compared to the di-shuffled set. Our calculation of the relevant statistics from (Chan and Ding, 2008), utilizing RNACluster, agrees with the authors' results, as shown in Supplementary Figures S5–S7. We showed that our calculation of the WSS_point statistic using RNACluster was more discriminative than the WSS statistic from Sfold in Figure 1B and Supplementary Figure S6B, respectively. These results are also reflected in the P-value in Supplementary Table S1.

Fig. 1.

Ensemble statistics. Boxplots for the (A) overall compactness and (B) within cluster sum of squares versus sequence lengths for ncRNAs (Positive936) and their decoys (Dishuffle936). The outliers indicated by the tick marks are values more than two times the inter-quartile range. In general, ncRNAs tended to have fewer clusters that were denser (lower compactness measure) than their decoys, and their within-cluster sum of squares were generally smaller than that of their decoys.

2.2.3 Structural statistics

We also considered another set of novel structural features derived from the predicted RNA secondary structures that are useful for the identification of ncRNAs. We examined various properties of known RNA secondary structural elements, i.e. stems and loops for their possible discerning power between actual ncRNAs and their di-shuffled sequences. For each stem, loop, internal-loop and bulge structural element, as shown in Supplementary Figure S8, we computed the 18 statistics defined in Supplementary Table S2. To the best of our knowledge, these features have not been applied in the de novo identification of ncRNAs.

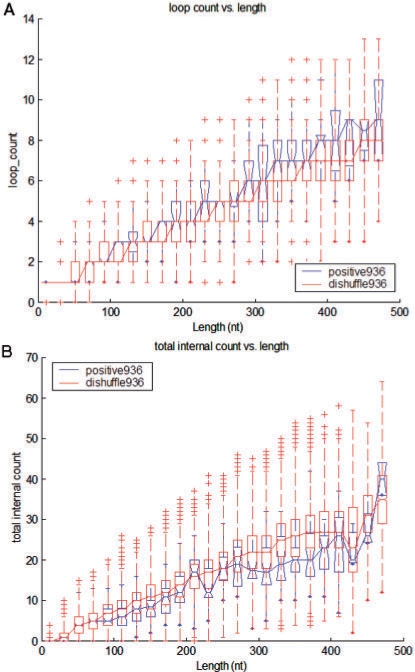
From the structural statistics shown in Supplementary Figure S9, real ncRNAs tend to have fewer stem branches, but the stems tend to be longer on average. This longer stem preference contributes to more stability in the RNA secondary structure. Real ncRNAs in our dataset also tend to have more loops, as shown in Figure 2A. The presence of more loops may also be related to the functional role of the ncRNAs. When multiloops are present, there tend to be more loops in real ncRNAs than in their di-shuffled version, as shown in Supplementary Figure S10. Not all single-stranded regions were more dominant in real ncRNAs. As seen in Figure 2B, the total internal-loops consisting of internal loops and bulge regions were actually less in ncRNAs than in their di-shuffled sequences. This tendency for ncRNAs to have fewer of such structural elements may have some functional interpretation that can be applied to ncRNA gene finding. Additional boxplots for loop-related structures are shown in Supplementary Figures S11–S12.

Fig. 2.

Structural statistics. Boxplots for the (A) hairpin-loop count and (B) total internal-structure count (internal-loop and bulges) versus lengths for ncRNAs (Positive936) and their decoys (Dishuffle936). The outliers indicated by the tick marks are values more than two times the inter-quartile range. In general, ncRNAs tended to have more loop regions and fewer internal-loops on average than their decoys.

2.2.4 Significant features

For all the features examined above, we used hypothesis testing to identify those features that can potentially distinguish known ncRNAs from their di-shuffled sequences. We performed a paired t-test, comparing the mean of the features from the Positive936 data set with the mean from the Dishuffle936 data set, and computed the P-value estimating the probability that these samples have the same means, as summarized in Supplementary Table S1. Since the t-test assumes distributions of equal variances, we also computed the significance according to the Wilcoxon signed rank because the rank sum test is not based on this assumption; the rank sum test gave similar results. We manually selected a set of 25 features with significant P-values below 0.05, which we refer as the f25 feature set. This set included two-folding statistics, two ensemble statistics, 14 RNACluster statistics and seven structural statistics, as shown in Supplementary Table S1. All features were length normalized (when applicable) before using them for genome-wide prediction. We have also calculated the mean and the variance area under the receiver operating curve (AUROC) for each of the f25 features in Table 1. The AUROC is a qualitative measure of the performance not dependent on a specific threshold. Generally, the underlying predictor has higher AUROC for higher sensitivity and specificity. Over 10 of our features have consistent AUROC values above 0.6. Of additional interest is that some ensemble statistics-based features are found to have higher AUROC values than the commonly used single structure-based MFE measures.

Table 1.

The mean and variance for each feature's AUROC value

Features	Mean (AUROC)	Var (AUROC)
rnacluster_wss_point	0.7316	5.09E-05
rnacluster_maxcompactness	0.6437	7.14E-05
entropy_entropy	0.6329	5.54E-05
structuralstatistics_stem_ave	0.6325	4.51E-05
diversity_ensemble_diversity	0.6263	8.10E-05
rnacluster_overallcompactness	0.6249	8.07E-05
rnacluster_avecompactness	0.6059	3.18E-05
rnacluster_num_hifreq_bp_ensemble	0.6041	6.27E-05
rnacluster_bss_point	0.6039	7.73E-05
rnacluster_ave_bpdist_mfe_ensemble	0.6011	7.29E-05
rnacluster_compactnesslargest	0.5988	8.54E-05
structuralstatistics_stem_count	0.5960	6.55E-05
rnacluster_ave_num_hifreq_bp_percluster	0.5901	2.00E-05
structuralstatistics_mfe	0.5900	7.04E-06
diversity_free_energy_thermo_ensemble	0.5856	5.94E-06
structuralstatistics_total_internal_count	0.5848	7.69E-05
rnacluster_bss	0.5747	7.59E-05
rnacluster_nclusters	0.5630	3.99E-05
rnacluster_wss	0.5601	6.19E-05
structuralstatistics_total_internal_nt	0.5551	7.77E-05
structuralstatistics_loop_ave	0.5402	8.60E-05
rnacluster_nlargest	0.5292	7.93E-05
rnacluster_mincompactness	0.5237	7.99E-06
structuralstatistics_multiloop_ave	0.5169	5.11E-05
structuralstatistics_loop_count	0.5133	5.96E-05

The normalized feature values from ‘Positive936’ were compared to 1000 runs of its ‘Dishuffle936’ to assess each feature's ability to discriminate between ncRNAs and the corresponding di-shuffled set. The performance shown is organism-independent to allow for an unbiased comparison among the features. Over 10 features have an average AUROC value above 0.6 that is highly stable across 1000 runs, each of which uses a different negative set.

2.3 Application to genome-wide prediction

In order to construct an unbiased positive set for genome-wide prediction, we included in it all 93 known ncRNAs in E.coli from the Positive1540 data set. Using these ncRNAs as queries, we ran an all-versus-all BLASTN search against the Positive936 data set and removed all the Positive936 hits with E-values below 10⁻⁵. We reduced the original Positive936 data set to 800 unique ncRNAs after removing sequences homologous to the 93 known ncRNAs. We then used this data set without known ncRNAs in E.coli for training and refer to it as Positive800_ecoli.

For the negative set, we di-shuffled 800 randomly selected sequence segments in E.coli with the same length distribution as Positive800_ecoli to ensure no ncRNA-related secondary structures were present. Other negative training sets were examined but the results were not as significant as the final negative set used. Details of the other negative sets tested can be found in the Supplementary Materials. We computed all the f25 significant features and an additional 20 sequence-based statistics, namely, four mono- and 16 di-mer frequencies because they were useful in distinguishing between real ncRNAs and decoys by previous algorithms (Carter et al., 2001; Klein et al., 2002; Liu et al., 2006; Schattner, 2002; Wang et al., 2006).

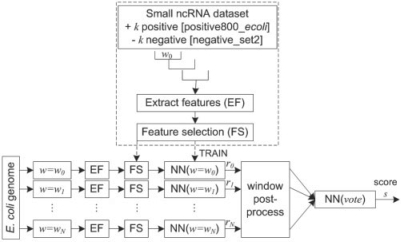
2.3.1 Meta-learner classifier to combine information from different window sizes

We applied the genome-wide prediction classifier approach shown in Figure 3 as follows. For each sample in the training data set, we calculate all 45 features (f25 significant features +20 sequence-based features) within a sliding window of length w which slides from left to the right with step size = w/2. The features can undergo a feature ranking selection method before being used to train a window length-specific NN classifier. The AUROC values of our method using different feature sizes are compared in Supplementary Table S6.

Fig. 3.

A schematic of the classifier architecture used for genome-wide prediction. The results of each NN-based classifier were then post-processed and combined into a final NN-based classifier to make the final prediction. The output of the length-specific NN-based classifiers and voting classifier were labeled by score r_i for 0 ≤ i ≤ N and score s, respectively.

NNs are a class of machine learning algorithms, widely used for solving classification problems based on multiple sources of information without assuming the underlying relationships among the individual information sources. This technique is robust for noisy data and has been widely used for many biological data analysis problems (Carter et al., 2001; Tran et al., 2007). We have trained an NN-based classifier using MATLAB®'s NN toolbox using 45 features derived from our data set. The network parameters were optimized using the Levenberg–Marquardt algorithm to obtain the desired binary (1/0) classification label depending on whether each sample contains an ncRNA or not. Our classifier has a single layer, one-neuron architecture using a logsig activation function. Other NN architectures with more neurons in the current one-layer and two- and three-layer networks were also examined, but the performance improvements were negligible (data not shown). Our NN classifier is able to account for the discerning power of each feature and its redundancy in the context of the other features during its training to select an optimal combination of features. We found that using a smaller subset of features (∼10–15), we can train a classifier with only slightly lower prediction accuracy (details omitted). We have also used support vector machines to train our classifier but found that the results were not as good (data not shown).

The results from different window length-specific classifiers are combined through a meta-learner NN classifier to predict the final score. We omit further details about dealing with overlapping windows of different sizes. For testing, we repeated the same procedure using overlapping sliding windows on the entire genome of E.coli. By training multiple window length-specific classifiers, each classifier was tuned to distinguish the positive (ncRNAs) from the negative training data for genes of different lengths.

The main computational cost of our approach is in computing the feature set. It takes less than one minute per window to calculate all the features used in the classifier on a 2.2 GHz, 2 GB RAM AMD Opteron dual-processor single-core computer. In order to scan the whole E.coli genome using window size w = 120 requires ∼54 days on a single processor. Distributed computing is required to make the computation practically feasible.

2.3.2 Filter with positional information to compare with other prediction programs

To reduce the false positive rate in our prediction, we have analyzed the position of known ncRNAs in E.coli by classifying all ncRNAs into four classes based on their locations: (i) intergenic; (ii) cds_samestrand; (iii) antisense; and (iv) other cases. The cases of antisense and cds_samestrand were further subcategorized into those ncRNAs that fully or partially overlapped a protein-coding region. We focused on the partially overlapping subcategory because (i) in both Positive800_ecoli; and our E.coli data set, the partially overlapping case was approximately twice as common as the fully overlapping case; and (ii) experimental validation of fully overlapping cases is difficult (Huttenhofer and Vogel, 2006). For the partially overlapping cases, we computed the log likelihood score using Equation (4), where nt_overlap is the number of overlapped nucleotides between the ncRNA and the protein-coding region. The log likelihood for the antisense and cds_samestrand cases with partial overlap is shown for the Positive800_ecoli dataset in Supplementary Figure S13. We noted that for the vast majority cases, ncRNA genes partially overlapped protein-coding regions by no more than ∼50-nt, which is good for discriminating between the positive and negative sets.

(4)

2.4 Experimental validation

To identify a manageable list of candidates for experimental validation, we employed data from positional, conservation, promoter, terminator and a high-density tiling array (Argaman et al., 2001; Chen et al., 2002). Conservation denotes candidates with BLASTN hit sequences with E-value <10⁻⁵. Promoter and transcription factor binding site information from RegulonDB was used to compile promoter regions within 300 nt upstream of the predicted ncRNA. TransTermHP (Kingsford et al., 2007) was used to predict rho-independent transcription terminators downstream of our predicted ncRNAs. A tiling array permits an unbiased analysis of complete genomic transcription, including ncRNAs. The whole genome-tiling array data set was derived by comparing an RNase E deletion strain of E.coli with a wild-type control (Stead et al., manuscript in preparation). This strain was chosen because RNase E has been shown to play an important role in general RNA metabolism in E.coli (Bernstein et al., 2004; Ow and Kushner, 2002). The authors identified 402 possible ncRNA candidates based on increased steady-state RNA levels in the RNase E deletion strain compared to a wild-type control (Stead et al., manuscript in preparation). Overall, we filtered our program's predictions based on the following conditions: (i) the potential ncRNA was conserved; (ii) it contained either a predicted promoter or terminator; (iii) its overlap with a protein-coding region (if applicable) was <50 nt; and (iv) it overlapped candidates derived from the tiling array.

2.4.1 Bacterial strains, isolation of total RNA and Northern analysis

The E.coli strains used in this study were MG1693 (thyA715 rph-1), which was provided by the E.coli Genetic Stock Center (Yale University) and an isogenic derivative, SK3564 (rneΔ1018::bla thyA715 rph-1 recA56 srlD::Tn10/pDHK30(rng-219 Sm^r/Sp^r)/pWSK129 (Km^r) which has been described previously (Mohanty and Kushner, 2008). Both strains were grown in Luria broth supplemented with thymine (50 μg/ml) at 37°C. For MG1693, cells were harvested at 3.5, 6, 8 and 10 h post-inoculation, corresponding to mid-log, early stationary, mid stationary and late stationary phase growth. For SK3564 the cells were grown in the same manner, but in order to account for its slower growth rate, were harvested at 11.5, 17.5, 20 and 23 h post-inoculation. Harvested cells were mixed with an equal volume of crushed frozen TM buffer [10 mM Tris (pH 7.2)/5 mM MgCl₂] containing 20 mM NaN₃ and 0.4 mg/ml chloramphenicol (O'Hara et al., 1995). The cells were then centrifuged at 5000 rpm for 10 min at 4°C. The cell pellets were subsequently resuspended in Trizol® (Invitrogen) and total RNA was extracted according to the manufacturer's instructions.

The RNA samples were treated with DNase I using a DNA-free kit™ (Ambion), ethanol precipitated, quantitated with a Nanodrop apparatus (NanoDrop Technologies) and visualized on 1.0% agarose gels. For Northern analysis, 30 μg of total RNA were loaded in each lane and separated on either 6 or 8% polyacrylamide/8.3 M urea gels and subsequently transferred onto Magnacharge nylon membranes (GE Water & Processing technologies) by electroblotting (1 h, 80 V, 4°C). Membranes were prehybridized in ULTRAhyb® Ultrasensitive Hybridization Buffer (Ambion) at 68°C and probed with internally labeled, in vitro transcribed RNA oligomers (oligonucleotide sequences used to generate the probes are available on request). Hybridization was visualized on a Storm 840 PhosphorImager (GE Healthcare).

3 RESULTS

By utilizing folding, ensemble and structure-based features, we developed an NN-based meta-learner for the de novo prediction of ncRNAs on a genome-wide scale. We compared our prediction results in E.coli to existing programs relying on homology and other information. We found that our results are as good or in some cases better than these methods.

3.1 ncRNA prediction in prokaryotes

Table 2 summarizes the detailed prediction performance of the meta-learner. Our trained meta-learner achieved an average prediction sensitivity of 68%, specificity of 70%, and an overall accuracy of 70% for predicting windows containing ncRNAs in E.coli. By combining prediction results from individual window-specific NN-based classifiers, our meta-learner improved the prediction performance of the best individual window-specific classifier. The optimal AUROC performance was achieved using three window sizes, w = 100, 120 and 160 nt, corresponding to the three peaks of the ncRNA-length distribution in E.coli, as shown in Supplementary Figure S14. The AUROC curve for E.coli is given in Supplementary Figure S15. For other organisms, users can select a threshold necessary to obtain a desired sensitivity and specificity trade-off for their application.

Table 2.

AUROC values of our predictions for E.coli and S.solfataricus using its optimal three window sizes for both the direct and reverse complement strands

Organism	Strand	Sn	Sp	AUROC
E.coli	+	0.7182	0.6638	0.7557
E.coli	−	0.6457	0.7275	0.7628
S.solfataricus	+	0.6235	0.7614	0.7502
S.solfataricus	−	0.5149	0.8224	0.7214

We then obtained a unique list of candidates for the genome by labeling continuous regions with NN scores above the user-chosen threshold. The cutoff for the NN threshold will vary depending on the application and the user's preference in trading off the prediction sensitivity and specificity. For our study, we bias in favor of sensitivity rather than missing potential candidates by selecting a low threshold resulting in 16 571 positive candidates. After filtering with positional information by requiring the prediction to (i) fall into an antisense case; and (ii) have nucleotide overlap <50 nt with a protein-coding region, we obtained 601 candidates and recovered 41% of known ncRNAs in E.coli with a PPV of 6%. Twenty-three of our 601 predicted candidates overlap known strand-specific ncRNAs, four candidates overlapped annotated tRNAs, and 574 novel predictions. A summary of the prediction sensitivity (S_n) and positive prediction values (PPV) for the different programs is summarized in Table 3.

Table 3.

Comparison of prediction accuracies by different programs for E.coli

Program	No. of predictions	Sn	PPV
Carter	563	0.3441	0.0568
Chen	227	0.2903	0.1189
Rivas	275	0.4086	0.1382
Saestrom	306	0.1183	0.0359
Wang	420	0.0753	0.0167
Tran	601	0.4086	0.0632

The number of predictions, sensitivity [S_n = TP/(TP + FN)] and positive prediction value [PPV = TP/(TP + FP)] is given for each program (Carter et al., 2001; Chen et al., 2002; Rivas et al., 2001; Saetrom et al., 2005; Wang et al., 2006).

Rivas et al. (2001) had an overall better sensitivity and PPV than ours. However, their program relied on prior knowledge of multiple alignments for identification of conserved regions, which may not be generally available for all genomes. Chen et al. (2002) had better PPV but lower sensitivity than our program. Compared to Carter et al. (2001), we had over 6% improvement in sensitivity with approximately the same PPV. Our predictions were also significantly better in S_n and PPV compared to (Saetrom et al., 2005) and (Wang et al., 2006). The results of our de novo prediction using structure and sequence-based features is highly promising given the fact that we do not rely on additional promoter/terminator or sequence alignment information as required by other programs. We also illustrated the robustness of our ncRNA predictor by searching for ncRNAs in the thermophilic archaeon, S.solfataricus (NC_002754). Our application to S.solfataricus yielded an average prediction sensitivity of 57%, specificity of 79% and an overall accuracy of 71% for predicting windows containing ncRNAs, as shown in Table 2. Additional discussion can be found in the Supplementary Material.

3.2 Experimental verification of selected ncRNA candidates in E.coli

As an application of our de novo prediction for use in wet lab studies, we incorporated additional information available to an experimentalist and filtered by conservation, promoter/terminator, positional and tiling array data to further narrow down our predicted candidates in E.coli. Using this filtering approach, we identified 31 candidates as summarized in the Supplementary Figure S16 for further validation. Out of the 31 candidates, 17 overlapped with known ncRNA genes or annotated tRNA/rRNA genes in E.coli. From the 14 remaining novel predictions, eight were excluded because they overlapped with predicted ncRNA genes derived from other programs (Carter et al., 2001; Chen et al., 2002; Rivas et al., 2001; Saetrom et al., 2005; Tjaden et al., 2006; Wang et al., 2006). The remaining six candidates (5, 6, 8, 9, 11 and 12), as shown in Supplementary Table S7, did not overlap with predictions by the other prediction programs, and had higher steady-state levels in the RNase E mutant. Based on our Northern analysis, three of the candidates (5, 6 and 8) were not observed in either the RNase E mutant or the wild-type control (data not shown). Since the tiling array has a higher sensitivity than the Northern analysis, we suspect that these potential ncRNAs are transcribed at such low levels that they could not be detected even in the RNase E deletion mutant.

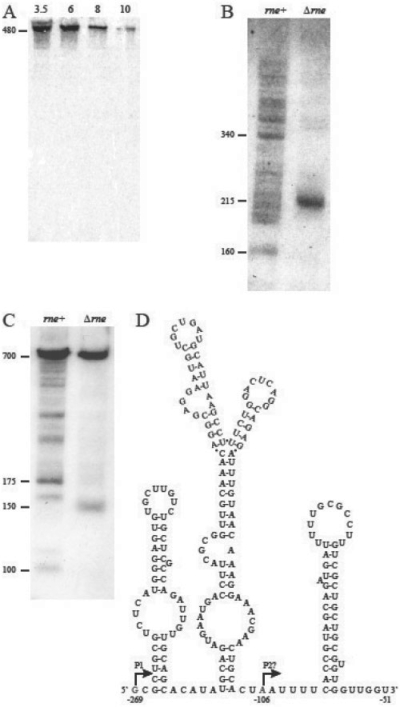
Candidate 9 maps to a region downstream of a predicted strong rho-independent transcription terminator associated with the ydgA gene. It also overlaps a repetitive extragenic palindrome called RIP126 (Rudd, 1999). Using an RNA probe of 130 nt, a large species of 480 nt was observed in mid-log phase cells in a wild-type strain (data not shown). In addition, significant amounts of smaller species of 140, 170 and 215 nt appeared as the cells entered stationary phase (data not shown). However, because there is considerable nucleotide sequence conservation among the various RIP elements, we designed a second RNA probe (a 30-mer) that was specific for RIP126. With this probe, we observed only the 480 nt species, which was most abundant in both mid-log and early stationary phase cells (Fig. 4A). While we cannot rule out at this time that this species is a stable decay intermediate of the upstream ydgA mRNA, based on the predicted strength of the ydgA rho-independent transcription terminator, we hypothesize that candidate 9 is indeed a ncRNA that contains a significant region of antisense sequence to the 3′ terminus of the adjacent uidC mRNA, which is transcribed in the opposite direction.

Fig. 4.

Analysis of predicted ncRNA candidates 9, 11 and 12. For the Northern analysis, 30 μg of total RNA was loaded in each lane and transcript sizes were estimated using a New England Biolabs low range ssRNA ladder. (A) Analysis of candidate 9. RNA isolated from a culture of MG1693 (rne⁺) at various times throughout exponential and stationary phase and separated on a 6% PAGE as described in ‘Methods’ section. (B) Analysis of candidate 11. Total RNA from exponentially growing MG1693 (rne⁺) and SK3564 (Δrne) was separated on an 8% PAGE. (C) Analysis of candidate 12. Total RNA from exponentially growing MG1693 (rne⁺) and SK3564 (Δrne) were separated on a 6% PAGE. (D) Candidate 11 falls within the 5′ UTR of the mreB gene. RNAstar secondary structure prediction of a portion of the mreB leader (nucleotides from −269 to −51). Nucleotides shown in red at positions −269 and −106 correspond to the primer extension products detected by Wachi et al. (2006). Position −106 was originally identified as a potential transcription start site but may in fact represent an RNase E cleavage site since it occurs in a single-stranded A/U rich region and there is no apparent σ⁷⁰ upstream of this site. Furthermore, we hypothesize that the distal stem-loop that ends of −51 represents a rho-independent transcription terminator that is functional in the Δrne strain.

Candidate 12 is located in the 5′ untranslated region (UTR) of the crp gene, encoding the catabolite repressor protein. Previous experiments have shown the existence of three potential promoters (P1, P2 and P3) for this gene (Ishizuka et al., 1994). Transcription initiation from P3 would generate a 5′ UTR of 167 nt. The RNA probe used was 89 nt in length and would detect RNA species arising from all three promoters. As shown in Figure 4C, in exponentially growing wild-type cells a large number of discrete species were detected, but most of them rapidly disappeared as the cells entered stationary phase (data not shown). Strikingly, in the RNase E deletion mutant the ∼700 nt transcript was the predominant species, demonstrating that almost all of the smaller products observed in the wild-type control probably arose from RNase E cleavages. An ∼150 nt species was still detected in the RNase E mutant and could have arisen from inefficient cleavages by another endoribonuclease such as RNase G. Since the large species detected in both the RNase E mutant and the wild-type control was the approximate size of the full-length crp mRNA, we speculate that all of the species observed in wild-type cells (Fig. 4C) are probably stable mRNA decay products that retain some or all of the 5′ UTR.

Candidate 11 falls within the 5′ UTR of the mreB gene, an essential locus that is involved in establishment of cell shape and cell division (Shih et al., 2005). Transcriptional analysis of this gene has identified three potential promoters based on primer extension analysis (Wachi et al., 2006). Transcription from the most distal promoter would generate a 5′ UTR of 267 nt. Using an RNA probe of 145 nt specific for the 5′ UTR, we detected numerous species in exponentially growing wild-type cells (Fig. 4B). However, in the RNase E deletion mutant, only a single 215 nt species was detected (Fig. 4B). When this 5′ UTR fragment was folded using the RNAstar program, a highly structured molecule was predicted (Fig. 4D). We hypothesize that the 215 nt species observed in the RNase E mutant represents a premature termination of transcription of the mreBCD operon that arises because of a defect in cell division that is an indirect effect of the reduction in RNase E activity. In wild-type cells, where the mreB protein is required for normal cell division, transcription proceeds beyond the putative terminator shown in Figure 4D. Thus our algorithm described here has identified either a riboswitch or a transcription attenuator that is important in the process of bacterial cell division.

4 DISCUSSION

In this study, we identified a number of sequence and structure-based features that can distinguish known ncRNAs from their di-shuffled versions, which do not rely on a priori knowledge of sequence alignments, conservation with closely related organisms, or structural conservation. By utilizing these novel features, we developed a classifier for ncRNA gene prediction. The use of training samples from a large class of ncRNAs from diverse organisms enabled us to find different categories of ncRNAs from various organisms. We have successfully applied our de novo predictor to E.coli and S.solfataricus.

Application of our program has led to a number of novel ncRNA gene predictions. Using Northern blot analysis for E.coli, we were able to find expression in three out of six target candidates under our tested conditions. We believe the expressed candidates are stable decay products and one has the potential to be a riboswitch. Further functional experimental studies will be needed in order to fully verify these as real ncRNAs since transcription does not imply function.

The results of our ncRNA prediction in E.coli are shown to be highly competitive with or better than the existing prediction programs as we have well demonstrated in this study. Overall our genome-scale prediction results indicate that there may be many more ncRNAs in E.coli, particularly in non-intergenic regions, which have been missed by previous studies. Further functional studies on these predicted ncRNA genes are needed to better understand its role and mechanism in regulation.

The promising set of features identified in this study could possibly aid in predicting ncRNAs in eukaryotic genomes. Additional changes to the training set and methodology of the current windowing approach must be made to account for more complex genomic organization in higher-order genomes. Future studies may involve the comparison of other machine learning algorithms and meta-learning approaches.

The de novo aspect of our approach makes it easily applicable to newly or partially sequenced genomes since it is not homology-based nor it requires the computation of multiple sequence alignments among related organisms. The ensemble-based features identified in our study perform significantly better than established MFE-based methods. All these capabilities led to the identification of two new regulatory RNAs among other possibly new ncRNA genes.