Experimental validation of Monte Carlo (MANTIS) simulated x-ray response of columnar CsI scintillator screens

Abstract

Purpose:MANTIS is a Monte Carlo code developed for the detailed simulation of columnar CsI scintillator screens in x-ray imaging systems. Validation of this code is needed to provide a reliable and valuable tool for system optimization and accurate reconstructions for a variety of x-ray applications. Whereas previous validation efforts have focused on matching of summary statistics, in this work the authors examine the complete point response function (PRF) of the detector system in addition to relative light output values.

Methods: Relative light output values and high-resolution PRFs have been experimentally measured with a custom setup. A corresponding set of simulated light output values and PRFs have also been produced, where detailed knowledge of the experimental setup and CsI:Tl screen structures are accounted for in the simulations. Four different screens were investigated with different thicknesses, column tilt angles, and substrate types. A quantitative comparison between the experimental and simulated PRFs was performed for four different incidence angles (0°, 15°, 30°, and 45°) and two different x-ray spectra (40 and 70 kVp). The figure of merit (FOM) used measures the normalized differences between the simulated and experimental data averaged over a region of interest.

Results: Experimental relative light output values ranged from 1.456 to 1.650 and were in approximate agreement for aluminum substrates, but poor agreement for graphite substrates. The FOMs for all screen types, incidence angles, and energies ranged from 0.1929 to 0.4775. To put these FOMs in context, the same FOM was computed for 2D symmetric Gaussians fit to the same experimental data. These FOMs ranged from 0.2068 to 0.8029. Our analysis demonstrates that MANTIS reproduces experimental PRFs with higher accuracy than a symmetric 2D Gaussian fit to the experimental data in the majority of cases. Examination of the spatial distribution of differences between the PRFs shows that the main reason for errors between MANTIS and the experimental data is that MANTIS-generated PRFs are sharper than the experimental PRFs.

Conclusions: The experimental validation of MANTIS performed in this study demonstrates that MANTIS is able to reliably predict experimental PRFs, especially for thinner screens, and can reproduce the highly asymmetric shape seen in the experimental data. As a result, optimizations and reconstructions carried out using MANTIS should yield results indicative of actual detector performance. Better characterization of screen properties is necessary to reconcile the simulated light output values with experimental data.

INTRODUCTION

Thallium-activated cesium iodide (CsI:Tl) scintillator screens coupled with optical readout arrays are currently the most commonly implemented detection method for digital x-ray imaging.¹ X rays are absorbed by the CsI:Tl crystal, which then produces a shower of optical photons that are detected with a flat panel array of amorphous silicon photodiodes. The crystal itself has a complex columnar structure that directs the optical photons down the thickness of the crystal and improves the detector resolution as compared with unstructured crystals.^{1, 2, 3} This columnar structure also affects the point response function (PRF) of the detector in a complex manner that is difficult to model. The PRF fully describes the blurring behavior of the scintillator and is simply the image that results from x rays that are incident on the detector at a single, infinitesimally small point. This definition of the PRF is ambiguous since x rays with different incidence angles will result in dissimilar responses. This fact has lead investigators to provide a more formal analysis of the response function of x-ray detectors that include directionality of the primary beam (see, for instance, Ref. 4). Therefore, for the purpose of the analysis included in this paper, our definition of PRF includes the direction of the incoming x rays. Proper modeling of the PRF and its dependence on scintillator properties is critical to performing rigorous system optimizations that correctly predict image quality and forward-problem image reconstructions that accurately reproduce the imaged object.

To the authors’ knowledge, the only computational model that provides a detailed treatment of the internal structure of CsI:Tl columnar scintillators and is capable of predicting the full two-dimensional (2D) PRF as a function of the scintillator properties is a package called MANTIS (Monte Carlo x-ray electron optical imaging simulation).⁵ Several studies have investigated models of detector performance for megavoltage photons for radiotherapy applications.^{6, 7, 8, 9, 10} These studies focus on single- or segmented-crystal scintillators and have been used to simulate light output as well as symmetric detector spread via the modulation transfer function (MTF). Experimental validation of both light output and symmetric detector response has been reported in the cited works. A recently developed Monte Carlo code, PHOTON, for simulating optical photon transport in scintillation detectors was used to model the light output of a single-crystal plastic scintillator for 662 keV gamma rays and was validated with experimental data.¹¹ The main difference between the code MANTIS and the work cited above is the fact that MANTIS uses a list-mode approach for accounting of energy depositions and optical photon generation in the scintillator and can accommodate a structure with a large number of columns in the scintillator device. A recent study by Blakesley and Speller¹² implemented a Monte Carlo-based model of the full x-ray detection process in flat panel arrays (both indirect and direct detection types) from generation of the x-ray photons to charge readout and electronic noise in the photodiode layer. However, their model was meant to provide broad comparisons between theoretical detectors and not to give detailed descriptions of detector image quality. For this reason, while their model does provide a simplified treatment of the scintillator internal columnar structure, their model does not produce two-dimensional PRFs capable of fully capturing the blurring behavior of the detector.

MANTIS is a publicly available Monte Carlo simulation code capable of tackling the problem of detailed simulation of the imaging properties of these columnar CsI:Tl scintillator screens.⁵ It provides a complete Monte Carlo simulation of the entire experimental setup including sources and objects in their respective geometries and is the only tool that can accurately predict the anisotropic nature of the columnar scintillator response. Comprehensive validation of the code is necessary to have confidence in the derived results. Once validated, MANTIS can be used to perform system optimizations and accurate reconstructions of data for a variety of applications. It has already been applied to characterize breast tomosynthesis¹³ and breast computed tomography (CT) systems.¹⁴ Incorporation of the complete, anisotropic scintillator response has the potential to substantially improve system design and reconstruction techniques.

Previous validation work on this and other detector models has focused on reproducing summary measures of the scintillator performance (i.e., MTF, Swank factor).^{7, 8, 10, 13, 15} In this paper, we approach the validation of the MANTIS package from the perspective of comparing the complete PRFs of the system, while maintaining the information (Swank) factor I and the light output consistent with previously published data. Typically, experimental measures of detector PRFs are performed using edge or slit devices, which cannot completely reproduce angular variations in the true PRFs.⁴ Here, we use a pinhole-based experimental setup to perform a complete measurement of the PRFs of four different CsI:Tl screens at four incidence angles (0°, 15°, 30°, and 45°) and two x-ray spectra (40 and 70 kVp). In addition, simulated PRFs, that incorporate the detailed experimental setup parameters and CsI:Tl structural information, are produced by MANTIS for each of these screens. A quantitative comparison of the experimental and analogous simulation results is then performed. Note that while the pinhole-based measurements (using a 30 μm diameter pinhole) provide an approximation to the true PRF, since the true PRF requires an infinitesimal incidence point, the simulated data use the same system setup and therefore also produce an analogous response.

Section 2 provides a description of the experimental setup and MANTIS code. The results are presented in Sec. 3 and a discussion is given in Sec. 4. Finally, conclusions are given in Sec. 5.

MATERIALS AND METHODS

Validation of columnar CsI detector response as simulated by MANTIS was performed by experimentally measuring both relative light output and PRF shape using two different experimental setups. Simulations mimicking those experimental setups as closely as possible were then performed with MANTIS, and the results were compared. In the following subsections we first describe the experimental setups then the corresponding MANTIS simulations and the FOM used for evaluating the data.

Experiments

We have designed a custom imaging system that allows us to capture high-resolution images of screen output with the additional benefit of having an open faceplate where different screens can easily be mounted. The optical detector setup consists of a high-resolution CCD camera with a one-to-one fiber optic faceplate (FOP) that allows measurements on different screens by providing an interface between the detector inside of the thermoelectrically cooled vacuum Dewar and the outside environment. The CCD is a Quantix 6303 Photometrics 3072 × 2048 imaging array with 9 × 9 μm pixels. A standard Quantix 6303 camera was modified with a 4.5 cm length one-to-one fiber optic faceplate, with 4.5 μm fibers, bonded to the CCD chip on one side, and leaving the other side accessible (outside the vacuum) so that scintillator screens can be positioned and measured (see Fig. 1).

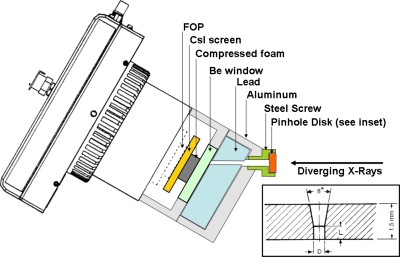
Figure 1.

Schematic of CCD setup with a 30° pinhole holder (not to scale). Diverging x rays enter from the right. The pinhole is mounted in a caphead screw and positioned in an aluminum holder at the desired angular orientation. Lead lining within the aluminum holder provides shielding from background signal and has a hole oriented to allow the primary signal through. The signal then passes through a Be window and compressed foam before impacting the screen and producing the optical signal that travels down the FOP to the optical detector. A cross-sectional view (not to scale) of the pinhole disk is shown in the inset (Ref. ¹⁶). The manufacturer specifies L=75±10 μm and D=30±5 μm for the 30 μm pinhole. Note that, when drawn to scale, the size of the straight edged portion of the pinhole is much smaller than the angled opening.

Individual scintillator screens are held in pressure contact with the FOP by a piece of dense foam inserted between the 0.025 in. thick beryllium window cap and the screen. The use of optical index-matching fluid was investigated to improve contact between the screen and FOP (data not shown), but did not improve the image quality. The indices of refraction were 1.48 for the FOP (Incom, Inc., Charlton, MA) and 1.55 for the optical index-matching fluid (NYE optical fluid OCF-455, NYE Lubricants, Inc., Fairhaven, MA).

Relative light output

For the light output experiments, four different screens (screens 1–4) were investigated (see Sec. 2A3 for more detail on the screens). Two screens were placed directly against the FOP of the CCD camera, side by side, at the same time and a set of 11 exposures was taken with the x-ray tube at 70 kVp (see Section2A4 for more details about the x-ray source) and an exposure of 50 mA and 100 ms. One of the screens was always screen 1, so that the light output relative to screen 1 could be measured. The light output was then calculated, on the median of the 11 exposures, as the ratio of the average of values within a circular region of interest (ROI) on the screen area.

Point response function

For the PRF experiments, an additional aluminum cap with lead shielding was bolted onto the beryllium window cap to hold a pinhole (see Sec. 2A5 for details about the pinhole) as close to the screen as possible. A total of four aluminum caps were manufactured, each holding the pinhole at a different fixed angles (0°, 15°, 30°, and 45°) with respect to the screen. Figure 1 shows a schematic of the 30° pinhole holder in place. These four angles were chosen to cover the range of typical incidence angles seen in mammography, tomosynthesis, and breast CT systems (see Ref. 13). Additional shielding is provided by a lead sleeve that fits around the outside of the camera and a lead window near the end of the CCD assembly.

This entire camera∕screen∕pinhole assembly is bolted to a motorized rotation stage controlled via a LABVIEW (National Instruments, Austin, TX) program to allow accurate angular alignment with the x-ray source. Alignment at zero degrees is achieved with a laser assembly between the beryllium window cap and the x-ray tube window. A small laser is mounted in a circular cap that bolts onto the window cap and a circular mirror is secured in front of the x-ray tube window with two plastic pressure tabs. Positions of the x-ray tube and detector are adjusted until the reflected laser beam coincides with the original laser beam location. Once this condition is achieved all stages controlling the x-ray tube and detection position are locked in place except for the rotational stage that controls the angle of the CCD camera. For all measurements, the distance from the source to the pinhole was 130.0 cm. The distance from the screen to the pinhole varied in the range 0.7–1.0 in., depending on what angle was being measured and the thickness of the measured screen.

PRFs were measured on all four screens with 40 and 70 kVp spectra for each of the four incidence angles (0°, 15°, 30°, and 45°). Eleven images were acquired for each of the experimental conditions so that error bars could be estimated from the sample variance. Pixels in the individual experimental images that were more than five standard deviations from the median over all 11 images were replaced with the median value for that spatial pixel location before further analysis.

Screens

A total of four different columnar CsI scintillator screens (provided by Radiation Monitoring Devices, Inc., Watertown, MA) were measured. Their manufacturer’s specifications are given in Table 1. In order to characterize screen morphology, cross-sectional views were imaged with a scanning electron microscope (SEM) (model ISI SS40, now Topcon, Tokyo). This allowed measurements of not only the thickness of the CsI layer but also of the approximate diameter and angle of the columns relative to the substrate. Note that, while SEM measurements provide a means of probing the internal structure of the screens, they do have several important shortcomings. First, a SEM can never be acquired of exactly the same position that is used to acquire an image. Second, only a very small number of SEM measurements can be performed on a single screen, resulting in a poor sampling of the crystal structure. Finally, the act of acquiring the SEM image for a cross-sectional view can modify the structure of the crystal itself. All of these shortcoming arise from the fact that acquisition of a SEM image for a cross-sectional view requires the screen to be physically broken, and is, therefore, inherently destructive. Figure 2 shows the SEM measurements of each of the screens. From this figure we can see how the tilt angles and layer thicknesses vary between the different screens. In addition, we can see the transition from columnar to amorphous CsI close to the substrate. This figure demonstrates the variety of structures seen in the different screens as well as allows the reader to evaluate the ability of the simulation code to reproduce these complicated structures.

Table 1.

Manufacturer specifications and model parameters of the four measured CsI scintillator screens.

Screen	Manufacturer	Part No.a	CsI thickness (μm)b	Screen dims (mm)	Substrate	Estimated column tilt (deg)c	Simulated layers
1	RMD Inc.d	B31-3	208	50 × 50 × 1	Graphite	6.0	4 μm organic polymer 166.4 μm columnar CsI 41.6 μm homogeneous CsI
2	RMD Inc.	B39-2	170	50 × 50 × 1	Graphite + Al	2.6–4e	4 μm organic polymer 136.0 μm columnar CsI 34.0 μm homogeneous CsI
3	RMD Inc.	B40-3	450	50 × 50 × 1	Graphite + Al	6.5	4 μm organic polymer 360.0 μm columnar CsI 90.0 μm homogeneous CsI
4	RMD Inc.	B40-7	380	50 × 50 × 1	Graphite	2.0	4 μm organic polymer 304.0 μm columnar CsI 76.0 μm homogeneous CsI

^aManufacturer’s part number.

^bDetermined from SEM measurements for screen 1 and by optical microscopy for screens 2–4.

^cEstimated from SEM measurements.

^dRadiation Monitoring Devices, Inc., Watertown, MA, http://www.rmdinc.com/products/p005.html.

^eA constant value of 3.3° was used in the simulations.

Figure 2.

SEM measurements of all screens. The physical size of the white scale bar at the bottom of each SEM as well as the magnification are given following the screen number. (a) Screen 1 (77.4 μm, 200×), (b) screen 2 (56.44 μm, 300×), (c) screen 3 (151.36 μm, 100×), and (d) screen 4 (151.36 μm, 100×)

The measured screens cover a range of different properties including reflective and absorptive substrates, thin and thick columnar scintillator layers, a variety of different layer structures, and varying columnar tilt angles. An estimate of the columnar tilt angle of each of the screens was performed by using a graphics program to measure the angle of a line drawn over the SEM following a column judged to be representative of the area imaged by the SEM. The error in estimation of this tilt angle was approximately ±0.5°. In Sec. 4E we discuss the importance of accurately determining this parameter and find that an error of as large as ±6° does not significantly affect the results.

For one of the screens (screen 3), a second SEM measurement was taken at a different orientation (data not shown), approximately perpendicular to the first orientation, to provide a more accurate characterization of the CsI structure. For the two corners of screen 3, the measured columnar tilt angles were 2.5° and 6.0°. The combination of these two tilt angles gave the final tilt angle of 6.5° as indicated in Table 1. For screen 2, the range in columnar tilt angle is due to the fact that the tilt angle varied over the area imaged in the SEM. Overall, the measured tilt angles of the screens varied from between approximately 2.0° and 6.5°. In all but one of the screens (screen 3) the magnitude of the tilt angle was only measured in one direction and is therefore a lower limit to the true tilt angle at that location. Additional uncertainty arises from the fact that the columnar tilt angle may vary over the screen surface. See Sec. 4A for further discussion of errors associated with quantification of the SEM structure.

X-ray source

The x-ray source is a Varian B180 (Varian Corp., Salt Lake City, UT) x-ray tube with a tungsten anode, a 0.3 mm focal spot, 1.0 mm Al internal filtration, and no additional filtration. For the current measurements, data were taken with peak energies of 40 and 70 kVp.

Pinhole

The pinhole assembly consists of a small, 90:10 gold-platinum alloy disk with a pinhole aperture machined through the center of the disk face and mounted in the head of a cap screw (Fluke Biomedical X-Ray Pinhole Assembly #07-613, Everett, WA). The manufacturer’s specifications are shown in the inset of Fig. 1 (L=75±10 μm, D=30±5 μm).¹⁶

Simulations

The simulations were performed using MANTIS, a tool for modeling x-ray imaging systems with CsI:Tl columnar scintillator screens. MANTIS simulates the transport of x-ray photons, electrons, and optical photons within the same geometric model.^{17, 18} The code MANTIS, which is publicly available online (a current version of the code, tutorials, and examples are available from ftp://150.148.3.14/mantis) incorporates the PENELOPE (Ref. ¹⁹) physics for x ray and electron interaction physics models, along with the optical transport models and geometry descriptors. For validation of previous versions of the code, we have focused on the statistics of the screen optical signal using Swank factor measurements.¹⁵ Results of that validation show that the predictions of MANTIS are well within the uncertainties of experimental measurements.

In this paper, we have incorporated the detailed geometrical structure of each specific scintillator screen (see Table 1). Additional parameters, such as material and surface optical properties and columnar packing density, remain unchanged from previous simulations and are listed in Table 2. Details we can model include scintillator thickness, additional top and bottom layers that are present in the overall detector such as the substrate and protective layers, and uniform tilt angle and direction of the CsI:Tl columns. For this study, each individual PRF was produced with 5×10⁵ histories and required approximately 14 min of CPU time on a 768-core Linux cluster with MANTIS version 2.0. This number of histories produced PRFs with low enough uncertainties to allow for precise comparisons of the figures of merit (FOMs) for the different cases compared in this study.

Table 2.

Simulation parameters of the MANTIS model.

Column diameter	10.2 μm
Packing density	85% (approx)
Photodiode thickness	10 μm
FOP	Slab of glass (material #171 in PENELOPE)
Column surface roughness parameter a	0.2
Optical properties	n	μabsorption (cm−1)	μscatter (cm−1)
Scintillator	1.8	1.0	1.0
Nitrogen gas between columns	1.0	0.0	0.0
Photodiode	1.7	0.1	10.0

Relative light output

Relative light output values were calculated by counting the number of detected optical photons from PRF simulations for 0° and 70 kVp and dividing by the value for screen 1 with a substrate reflectivity of 10%. Reflectivities of 10%, 17%, and 40% were investigated for the graphite substrates and 35%, 80%, and 90% for the aluminum-coated substrates. A range of reflectivities was investigated in simulation since it was not possible to directly measure the substrate reflectivities of the actual screens.

Point response function

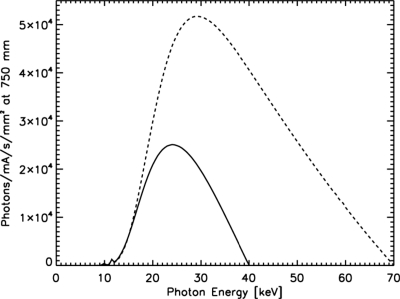
Here, the incoming beam was modeled as a parallel beam from a circular source of 100 μm diameter. The x-ray spectra used in the simulations were calculated using IPEM Report 78 (Ref. ²⁰) for 40 and 70 kVp spectra with 1.0 mm Al filtration. The spectra are shown in Fig. 3. The mean photon energy (MPE) and half-value layer (HVL) for the 40 kVp spectrum are 25.6 keV and 0.8926 mm Al, respectively. For the 70 kVp spectrum, the MPE and HVL are 36.5 keV and 1.593 mm Al. The pinhole disk and Be window were both simulated using the exact material composition and geometrical measurements as provided by the manufacturers.

Figure 3.

Spectra used in MANTIS simulations of the experimental PRFs: 40 kVp (solid line) and 70 kVp (dashed line). Both spectra include 1.0 mm Al filtration.

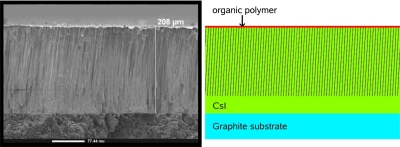
Measurements of the columnar tilt angle and layer thicknesses for each individual screen, as described in Sec. 2A3, were incorporated in the geometric model implemented in MANTIS. In the current version of the code (version 2), the columnar shape and tilt angle are required to be constant for the entire array of columns across the screen. From inspection of Figs. 24 we can see that this is an oversimplification since both the columnar shape and tilt angle can change in a complicated manner over the screen surface. We are currently working on more sophisticated geometrical models for future versions of the code. Figure 4 shows a side-by-side comparison of the SEM measurement of screen 1 and the corresponding model structure used in MANTIS. All of the measured screens were modeled with four different layers; a 4 μm planar protective layer of organic polymer, a variable thickness layer (depending on the SEM-derived thickness of the individual screens) of columnar CsI, a layer of homogeneous CsI crystal with 20% the thickness of the total CsI layer, and a 1-mm-thick substrate of either graphite or aluminum-coated graphite depending on the individual screen. The CsI columns in the columnar layer had a uniform diameter and tilt angle over the entire screen. The tilt angle of the columns was along the same direction as the oblique angle of x-ray incidence. The reflectivities of the graphite and aluminum-coated graphite substrates were assumed to be 10% and 90%, respectively, in MANTIS.

Figure 4.

(left) SEM of screen 1 (white scale bar = 77.4 μm, magnification =200×) (right) Schematic of MANTIS model of the same screen (to scale). The thin layer at the top of the image represents the organic polymer. The organic polymer layer is followed by the columnar zone, where light gray indicates CsI and dark gray is the intercolumnar space. The next layer is the homogeneous CsI and, finally, the bottom layer is the substrate.

The photodiode layer was placed immediately following the screens. This was then followed by as a solid glass slab (PENELOPE material 171) to model the FOP. We chose to model the FOP and photodiode layer in this manner to capture the scatter associated with the FOP. We are currently unable to simulate the transmission properties of the FOP itself. Although in reality, the photodiode layer is after the FOP, we do not expect this inconsistency to significantly affect the results, as discussed later in Sec. 4D.

Using the above-mentioned parameters, PRFs were simulated on all four screens with 40 and 70 kVp spectra for each of the four incidence angles (0°, 15°, 30°, and 45°). Eleven images were simulated for each of the cases to allow for estimation of error bars.

Figure of merit

A quantitative comparison of the experimental and simulated PRFs was performed by computing a FOM for each of the 11 pairs of experimental and simulated images for each different screen∕spectrum∕incidence angle combination. The mean and standard deviation of the eleven independent FOMs were taken as estimates of the FOM and its error. The FOM was calculated as

$$\mathrm{FOM}=\sqrt{\frac{1}{N_{\mathrm{ROI}}}\sum _{i=1}^{N_{\mathrm{ROI}}}{\Delta }_i^2},$$ (1)

where N_ROI is the number of pixels in the ROI and Δ is the normalized difference. The normalized difference is defined as

$${\Delta }_i=1-\frac{\raisebox{1ex}{$s_i$}\!\left/ \!\raisebox{-1ex}{$\sum _i{s}_i$}\right.}{\raisebox{1ex}{$(e_i-b)$}\!\left/ \!\raisebox{-1ex}{$\sum _i(e_i-b)$}\right.},$$ (2)

where b is a background value calculated by summing the values in a corner of the image where there is no signal and s_i and e_i are elements of the vectors s and e that contain all the simulated and experimental PRF values, respectively, within the selected ROI. The vectors s and e are defined by

$$\mathbf{s}=\{\mathbf{P}\mathbf{R}{\mathbf{F}}^{\mathrm{sim}};{\mathrm{PRF}}_j^{\exp }⩾50\sigma \text{and}{\mathrm{PRF}}_j^{\mathrm{sim}}>0,j∊[1,N_{\mathrm{PRF}}]\}$$ (3)

and

$$\mathbf{e}=\{\mathbf{P}\mathbf{R}{\mathbf{F}}^{\exp };{\mathrm{PRF}}_j^{\exp }⩾50\sigma \text{and}{\mathrm{PRF}}_j^{\mathrm{sim}}>0,j∊[1,N_{\mathrm{PRF}}]\},$$ (4)

respectively, where PRF^sim is the simulated PRF, PRF^exp is the experimental PRF, ${\mathrm{PRF}}_j^{\exp }$ is an element of the experimental PRF image, ${\mathrm{PRF}}_j^{\mathrm{sim}}$ is an element of the simulated PRF image, N_PRF is the number of pixels in the PRFs (the simulated and experimental PRFs have the same number of pixels), and σ is the noise in the experimental image calculated as the standard deviation of the lower left corner of the image. Therefore, the ROI is identical for both the simulated and experimental images and consists of those pixels with a signal-to-noise ratio (SNR), ${\mathrm{PRF}}_j^{\exp }∕\sigma$, of greater than or equal to 50 in the experimental data and a nonzero value in the simulated data. Note that the ROI is not square or circular, rather it only includes pixels that satisfy the SNR condition. Figure 9 in Section 3B gives an indication of the ROI size since all pixels outside of the ROI are set to zero in these images. The number of pixels in the ROI ranged from 206 to 736 pixels (equivalent to 16 686–59 616 μm²) over all PRFs investigated.

To ensure that the two PRFs were correctly aligned before calculation of the FOM, the maximum of the two-dimensional (2D) cross-correlation function was used to determine the optimal relative shifts and rotations of the two images prior to calculation of the FOM. The resolution of the cross-correlation algorithm was one pixel (9 μm) for x and y shifts and 1° for rotations.

Finally, to provide a benchmark to put the FOM values in context, the same FOM was also calculated using a symmetric 2D Gaussian, fit to the zero-angle experimental data, as the simulated data. The Gaussian fit was performed using a modified version of the program gauss2dfit in the software package IDL (ITT Visual Information Solutions, Boulder, CO) that forced the widths of the 2D Gaussian in the x and y directions to be equal.

RESULTS

Relative light output

The experimental light output values were compared with light output values derived from MANTIS simulations with a variety of substrate reflectivities. The substrate reflectivities used in MANTIS for the PRF comparisons were 10% for the graphite substrates and 90% for the aluminum-coated substrates. We have investigated additional reflectivities (17% and 40% for graphite and 35% and 80% for aluminum) to observe their effect on the light output values. The measured and simulated relative light output values for graphite and aluminum-coated substrates are shown in Table 3. For the graphite substrates, we only have a single independent measurement of light output (for screen 4). The results seem to indicate that a very large reflectivity (much greater than 40%) is necessary to match the experimental results. For the aluminum-coated substrates, we have two independent measurements of light output (screens 2 and 3), and we see that no single reflectivity value can reproduce the experimental results of both of the screens. Results from screen 2 seem to indicate an aluminum reflectivity of between 80% and 90%, while screen 3 implies a reflectivity of much greater than 90%, however, these results are less discordant since the simulated light output values at 80% and 90% are the same to within two error bars. This inconsistency is probably a result of one of two or both effects; the fact that reflectivity is only one of numerous parameters in MANTIS that affects the light output of a screen and the fact that different screens from different manufacturing batches can have highly variable light outputs depending on slight differences in the manufacturing process that are not easily controlled or quantified. See Sec. 4B for a discussion of variability of screen performance with manufacturing process. In future studies it will be important to provide independent measurements of substrate reflectivity to reduce the number of variables needed to validate light output. However, these measurements must be carefully controlled since substrate reflectivity can vary depending on handling conditions and substrate production methods. For all other MANTIS-generated PRFs presented in this paper, we have used substrate reflectivities of 10% for graphite and 90% for aluminum-coated graphite because those values were used in previous validation efforts and have been crucial in matching Swank factors (see Ref. 13). In the future, we plan to perform reflectivity measurements on the individual substrates themselves during the screen production process, so that these values can be included in MANTIS and the number of unknown parameters in the simulations can be reduced.

Table 3.

Measured and simulated relative screen output for screens with graphite and aluminum coated substrates. All values are normalized to screen 1 at 10% reflectivity.

Graphite substrates
Screen No.	Measured light output	Simulated light output
		Refl: 10	Refl: 17	Refl: 40
1	1.000 ± 0.000	1.000 ± 0.021	1.011 ± 0.054	1.149 ± 0.051
4	1.469 ± 0.042	1.148 ± 0.020	1.183 ± 0.049	1.300 ± 0.055
Aluminum-coated substrates
Screen No.	Measured light output	Simulated light output
		Refl: 35	Refl: 80	Refl: 90
2	1.456 ± 0.043	1.046 ± 0.060	1.393 ± 0.068	1.504 ± 0.031
3	1.650 ± 0.050	1.214 ± 0.050	1.465 ± 0.047	1.522 ± 0.027

Point response functions

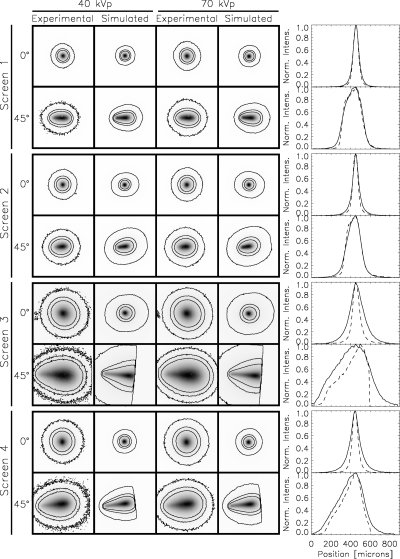
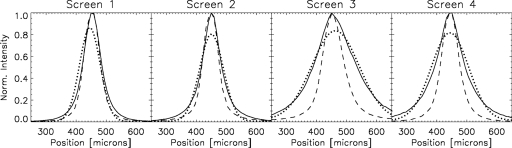
Figure 5 shows the experimental and simulated PRFs for the screens in Table 1 at 40 and 70 kVp x-ray source energies and 0° and 45° incidence angles. Here, the 11 individual experimental and simulated results have been combined to produce a single PRF for each spectrum∕incidence angle combination. The PRFs have all been normalized by their maximum value and contours at 0.01, 0.05, and 0.1 times the maximum value are shown. Also shown are plots of horizontal cuts through the experimental and simulated PRFs for 40 kVp. The experimental data are shown with a solid line and the simulated data are shown with a dashed line. The sharp cutoffs seen in the simulated data of screens 3 and 4 are because the simulations were not run past this spatial location. The most noticeable quality of the PRFs is their highly non-Gaussian shape at large incidence angles. This tear-drop shape, seen especially well in the thick screens, is due to the increasing spread of the secondary photons produced by x rays deposited at shallow depths in the CsI crystal. There is also a large variation evident between the individual screens. These large differences make it clear that one PRF model does not fit all CsI scintillator screens and that each screen must be individually modeled according to its specific structure. In particular, we can see that MANTIS clearly does a better job of reproducing experimental data for the thinner screens (screens 1 and 2).

Figure 5.

Experimental and simulated PRFs for screens 1–4. (first column) 40 kVp, experimental (second column) 40 kVp, simulations from MANTIS (third column) 70 kVp, experimental (fourth column) 70 kVp, simulations from MANTIS (fifth column) 40 kVp, horizontal cuts through the center of the PRFs, experimental data are shown with a solid line and MANTIS results are shown as a dashed line. The different screens are labeled as well as the incidence angles. Only incidence angles of 0° and 45° are shown. Contour lines shown on the plots are for levels of 0.01, 0.05, and 0.1 (the maximum is always 1). All PRFs are 101 × 101 pixels with 9 μm∕pixel.

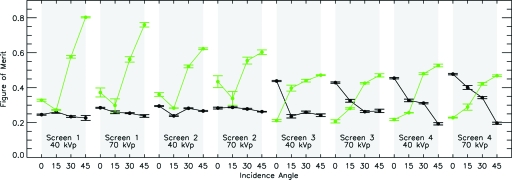
Figures 6789 show the results of quantitative comparisons between experimental and simulated data. Figure 6 shows a plot of all the FOMs for all the screens, energies, and angles investigated. We see that the FOMs comparing experimental data with MANTIS simulations are between about 0.1929 and 0.4775 for all cases. There does not seem to be a significant difference in the FOM values with energy. For the thicker screens (screens 3 and 4), MANTIS tends to reproduce PRFs with larger incidence angles better than those with smaller incidence angles. In this case, the cause may be due to the principal determinant of the PRF shape. At large incidence angles, the PRF shape is largely determined by the geometry of the system (the angle of the x ray entering the crystal), whereas at small incidence angles the principal determinant of the PRF shape is the optical transport. Since geometry is much easier to model than optical transport, PRFs at large angles may be easier to predict. For the same substrate type and energy, MANTIS tends to perform better for thin screens than for thick screens at small incidence angles.

Figure 6.

FOMs for all screens, energies, and incidence angles. Black indicates the results from the comparison of experimental data with MANTIS-generated PRFs and green indicates the results from the comparison with a 2D symmetric Gaussian fit to the zero-angle experimental data. The values displayed are means of FOMs calculated from 11 independent experimental and simulated images, while the error bars represent the standard deviation of those 11 different FOMs.

Figure 7.

Comparison of experimental, MANTIS, and Gaussian fit PRFs at zero degrees for 40 kVp. One-dimensional, horizontal cuts through the center of the PRFs are shown for each screen. The experimental data are shown as a solid line, MANTIS as a dashed line, and the Gaussian fits as a dotted line. We can see in all cases that the Gaussian fit underestimates the peak of the PRF. For the thicker screens (screens 3 and 4), MANTIS provides a much sharper PRF than the experimental data and, as a result, the FOM calculation indicates a better match to the experimental data for the Gaussian fit than MANTIS.

Figure 8.

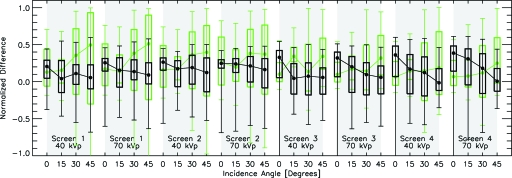
The normalized difference of the PRFs is plotted as a function of incidence angle for all screens, energies, and incidence angles. Normalized differences from the comparison with MANTIS are plotted in black, while normalized differences from the 2D Gaussian fit are plotted in green. The box plots show the median normalized difference (in the ROI) as the filled circle, the bottom and top of the box are the first and third quartiles, and the bottom and top error bars show the minimum and maximum normalized differences.

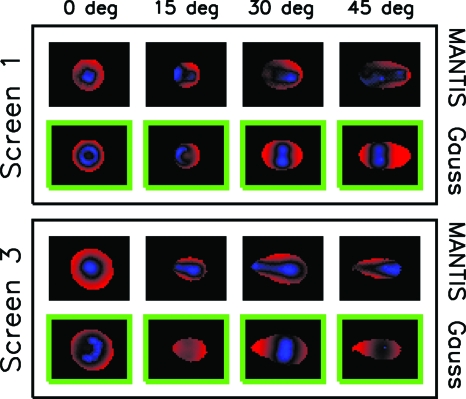
Figure 9.

Images showing the spatial distribution of the normalized differences for all incidence angles of screens 1 and 3 with the 40 kVp spectrum. Images from the comparison of experimental data with MANTIS are outlined in black and labeled “MANTIS,” while images from the comparison with the 2D Gaussian fit are outlined in a green box and labeled “Gauss.” Negative normalized differences are mapped to shades of blue, positive to shades of red, and zero to black. The images are all scaled to have red, blue, and black as corresponding to the most positive, most negative, and zero data values, respectively. As a result, these images simply indicate the spatial location and relative magnitude of differences and not the absolute magnitude of the difference which is indicated in Fig. 8.

For the comparison with Gaussian fits, we find that the FOM ranges between about 0.2068 and 0.8029. It is notable that the FOM for the Gaussian fits to the experimental data are, in general, worse than the MANTIS simulated PRFs. The exception is that the symmetric Gaussian fit tends to match the experimental data better for the thicker screens than for the thinner screens at small incidence angles, which suggests that as the screens get thicker their response becomes more Gaussian. Note that, for the thicker screens, MANTIS still outperforms the Gaussian fit for larger incidence angles. It is interesting to note that, for the thinner screens, even at an incidence angle of zero degrees, MANTIS outperforms the Gaussian fit. Figure 7 shows a closer examination of the experimental data, MANTIS simulation results, and Gaussian fits at zero degrees for 40 kVp. Horizontal, one-dimensional cuts through the centers of the PRFs are shown for each of the four screens. We can see in all cases that the Gaussian fit underestimates the peak of the experimental data and MANTIS provides a better estimate of the PRF shape. Therefore, the better performance of the Gaussian fit for small incidence angles for the thicker screens seems to be due to the fact that MANTIS is underestimating the width of the PRF.

Figures 89 show a more detailed breakdown of the normalized differences [Δ_i as given in Eq. 2]. In Fig. 8 the normalized difference is plotted on the y axis and the angle of incidence on the x axis for every screen and energy investigated. The objective of this plot is to show the distribution of normalized difference values that make up the single FOM values. The FOM is calculated by taking the rms of the normalized difference values. The box plots show the median normalized difference (in the ROI) as the filled circle, the bottom and top of the box are the first and third quartiles, and the bottom and top error bars show the minimum and maximum normalized difference. Results for the MANTIS comparison are shown in black and for the Gaussian fit are shown in green. A selected set of the corresponding images are displayed in Fig. 9 that show the spatial distribution and relative magnitude of the normalized differences for each incidence angle investigated. In these plots the normalized difference is shown in the ROI where a normalized difference of zero is mapped to black, negative differences are shown as shades of blue, and positive differences are shown as shades of red. The images are all scaled to the minimum and maximum of the normalized differences for each particular PRF. Therefore, Fig. 9 shows the spatial distribution of the normalized differences over the ROI, while Fig. 8 shows the distribution of the actual numerical normalized difference values. These figures allow a more detailed analysis of the differences between the experimental and MANTIS model data.

As an example of the type of information conveyed in Fig. 8, we can compare screen 1 at 70 kVp and 0° with screen 3 at 40 kVp and 45°. From Fig. 6 we can see that the FOMs of the comparison with the Gaussian are larger than the FOMs from the comparison with MANTIS results in both cases. Now, if we examine Fig. 8 we can see that the reason for the disparity in FOMs of the two cases (screen 1∕70 kVp∕0° versus screen 3∕40 kVp∕45°) is very different. In the case of screen 1 (70 kVp∕0°), the average normalized differences are very similar and the difference in FOM arises from the fact that the range of normalized difference values is much larger for the Gaussian comparison than for the MANTIS comparison. Conversely, for screen 3 (40 kVp∕45°) the range of the normalized difference values are very similar for the Gaussian and MANTIS comparisons, but the difference in FOMs arises from the fact that the mean normalized difference values are very different. The data in Figures 89 also demonstrate that the main reason for the differences between the experimental and MANTIS PRFs is that MANTIS tends to produce PRFs that are too sharp compared to the experimental data. This can be seen particularly well in Fig. 9 in the images with the black outline (labeled “MANTIS”) since the central portion of the difference image tends to be blue (or negative) and the outer region tends to be red (or positive). In fact, this effect is also easily visualized in the individual PRF images in Fig. 5. This trend is evident for all screens, energies, and incidence angles.

DISCUSSION

Examination of the experimental and MANTIS-generated PRFs shows that MANTIS provides a good fit to the experimental data for all energies, incidence angles, and screens measured. The match between experimental and MANTIS PRFs is especially good for the thinner screens. However, we do see that a 2D Gaussian fit to the zero incidence angle data outperforms MANTIS for small incidence angles for the thicker screens. In addition, MANTIS consistently predicts sharper PRFs than those measured experimentally.

Another point that should be made is that, for this study, the parameters used in MANTIS were taken from previous studies where pulse-height spectra had been validated. The only parameters that were modified were related to geometry of the system components. In effect, this approach answers the question of how well MANTIS can predict detector performance with only basic geometrical information about the screen and no additional modification of the other model parameters. We anticipate that MANTIS can match experimental data more closely by optimizing various parameters of the code (e.g., reflectivities, bulk absorption, amorphous layer fraction), however, unless these parameters are obtained through physical measurements, this would not indicate the ability of the code to predict performance. Therefore, the results presented in this study represent a conservative estimate of accuracy for the estimation of the PRF of CsI screens.

To our knowledge, only two other models have been validated against experimental data from columnar CsI scintillators.^{12, 21} In the model produced by Blakesley and Speller,¹² zero incidence angle simulation results were compared against experimental data from two systems with different columnar CsI screens. The validation was performed by overplotting the experimental MTF with simulated results, no quantitative FOM was used. For one of these systems, the screen had an unspecified thickness, so the model was adjusted to provide the best fit to the experimental data. For the other system, simulations were compared with two CsI screens that had the same thickness, but were deposited on different substrates. Their model predicted a MTF that was in between the experimental measurements of the two screens. The authors emphasize the inability of the model to include all the details of the screen properties and the fact that properties of screens with the same thickness and scintillator material can vary widely due to a variety of factors. In the first system they discuss the experimental data itself were used to determine the model parameters and are, therefore, not a representation of the predictive abilities of the model. In the second case, the model parameters were determined independent of the experimental data, but the model was not detailed enough to distinguish between the two types of screens investigated. The authors acknowledge that there are many different parameters not included in the model that can affect screen performance. In our validation efforts, we have avoided using the experimental data to determine any model parameters so that the validation addresses the predictive abilities of the model. In addition, we have attempted to include more parameters that may affect screen performance, such as the detailed structure of the CsI crystal. However, our validation efforts are still subject to a number of uncertainties as will be discussed in the following subsections.

Mainprize et al.²¹ developed an analytical model for the one-dimensional MTF of a scintillator as a function of angle of incidence of an incoming x-ray beam. This was compared with experimental MTFs measured on a structured CsI flat panel detector at four different incidence angles and two different x-ray spectra after dividing by the zero-angle MTF. In this case, since the thickness of the CsI was not known, it was determined by a fit with the experimental data itself. Again, the model was validated by qualitatively comparing the MTFs of the simulated and experimental data. In this study, the experimental data were also used to determine model parameters since the thickness of the CsI was not known. Therefore, as in the Blakesley and Speller¹² study, the validation is not of the predictive ability of the model. In addition, the model was only meant to simulate the effects of incidence angle and did not include optical transfer properties of the crystal.

Our study is a validation of the predictive abilities of the MANTIS software since the experimental results were not used to determine model parameters. In addition, MANTIS includes effects of both optical transfer as well as incidence angle and details of the columnar structure of the CsI crystal. In order to fully characterize the asymmetric detector blur that can be generated with MANTIS, we have chosen to validate the model against 2D experimental PRFs, which are not subject to the limitations of MTF analysis. In addition, we have developed a quantitative FOM to facilitate comparison of different screens and imaging systems. Examination of this FOM across the four investigated screens has shown that although MANTIS provides a good fit to the experimental data, there still exist some uncertainties that cause MANTIS to predict sharper PRFs than those seen experimentally. In the following sections we discuss possible sources of error that may contribute to the differences seen in Sec. 3 between the experimental data and MANTIS model results. Details of the scintillator screen layers and their geometry, variation in screen properties due to the manufacturing process, geometry of the x-ray source and pinhole, blur due to the FOP, and orientation between the columnar tilt angle and the incoming x-ray beam are all considered.

Accurate knowledge of screen details

The ability of MANTIS to incorporate detailed structure of the CsI scintillator screens requires that the true structure be accurately quantified. For this purpose, SEM measurements were taken and analyzed. However, there are limitations in both the ability of MANTIS to incorporate high levels of detail and for the SEMs to accurately quantify the CsI structure. In the case of MANTIS, the CsI crystal must be cleanly divided into two regions, a homogeneous region (in contact with the substrate) and a columnar region that extends beyond that. In reality there is a smooth transition between the solid and columnar structures in the CsI crystal. MANTIS also requires that the columns all have the same circular diameter and tilt angle and that all layers have a uniform planar thickness. However, inspection of the SEM images clearly shows that all of these characteristics are, at some level, inaccurate. In reality, the CsI columns have irregular, noncircular cross sections that vary along the depth of the CsI layer, the thicknesses of layers can vary over the crystal width, some deposited layers form a nonplanar surface that dips down into the layers below, and tilt angles of the columns are nonuniform even over the small field of view of the SEM images. While these inaccuracies do exist, the reasonable approximation employed by MANTIS should allow for representative results.

With respect to the size and shape of the columnar bases, our previous work has shown that column base shape does not affect medium or long range blur (> 10 μm) (Ref. ²²) for a model that does not include columnar tilt. However, the effect of intracolumnar spacing, presence of cracks and dislocations in the columns, and presence of contact between the columns remains to be investigated.

We are currently working to improve the ability of MANTIS to simulate random columnar tilt and shape by developing a geometry definition that generates the columnar structure on the fly as it follows the interaction sites of x rays and electrons. It is possible that the artificial regularity of the Monte Carlo geometry used in this work is contributing to a bias in the resulting PRF images. One way that we have approached this limitation is by introducing variations in the columnar walls to represent the variability in the columnar shape seen in the SEMs. This is implemented with a roughness algorithm that was described in our previous papers.^{5, 14} However, the introduction of this variation in the geometry is not based at the moment on any physical characterization performed on actual screens. To be consistent with results presented in previous papers, we have used the same amount of variability (a=0.2, where a is a user-adjustable parameter that defines the amount of mixing of the surface normal with an isotropic vector) as defined in Ref. 5.

The SEM measurements themselves have some additional sources of error that affect the thickness calculations of different layers. The approximate error in thickness estimation from the SEM measurements is ±10%. For most screens (screens 2–4), optical microscopy images were also taken (on a Leitz Laborlux 12 HL microscope) to provide more accurate thickness measurements (errors of approximately ±3%). Calculation of tilt angles should be unaffected by these thickness inaccuracies since there is no measurable distortion in the images. Quantification of the tilt angles was, however, affected by the limited sampling of the CsI scintillator screens. For all screens, one or two corners were imaged in a single field to determine tilt angles and thicknesses. A limited number of samples were used to produce measurements from the same screens used to collect PRF data. Since the tilt angles are not necessarily aligned with the imaged plane, the tilt angles calculated from a single corner represent a minimum tilt angle. Tilt angles calculated from a second corner (approximately perpendicular to the first imaging plane) provided a more accurate quantification of the true tilt angle. Of course, these calculations assume that the tilt angle is uniform over the screen face, which is probably not true in reality.

The reflectivity of the screen substrate is also a potential source of error. In this paper, we chose reflectivities of 10% for graphite substrates and 90% for aluminum-coated substrates. However, experimental measurements of substrate reflectivity should provide more accurate estimates of this parameter and, in the future, we hope to arrange such measurements for incorporation into the simulations.

While these uncertainties mean that MANTIS cannot exactly reproduce all of the complex details of the SEM structure, the level of complexity modeled in MANTIS represents the most complete modeling of CsI scintillator screens to date and should provide representative results that properly simulate trends in the PRF structure.

Variation in screen properties

Variation in screen properties due to the manufacturing process may be a significant source of error when comparing experimental data with simulations. To quantify this variation, the MTF was measured for a total of 11 screens produced during four different deposition runs (two to three screens per deposition run) with an average CsI thickness of 240 μm. All screens were deposited on a graphite substrate. The range of MTF values at 5.0 lp∕mm for each of the four deposition runs were 0.130–0.134, 0.273–0.327, 0.228–0.321, and 0.316–0.337. Similarly, at 8.1 lp∕mm the MTF values were 0.035–0.038, 0.109–0.148, 0.083–0.156, and 0.146–0.164. There are large variations both within a single deposition as well as between the different deposition runs. The factors responsible for these types of differences may not be included in the MANTIS models and, as a result, may be responsible for some of the discrepancies seen.

Accurate x-ray source and pinhole geometry

Accurately modeling the x-ray source and pinhole geometry is a critical step in the modeling process. Our previous validation work has shown that simplifying the x-ray source and pinhole structure combination to a perpendicular incoming beam produces results that are much sharper than those produced with the correct x-ray source and pinhole geometries.²³

For these simulations, the x-ray focal spot was modeled as a circle with 100 μm diameter and a parallel beam. The true focal spot has a similar shape, but with two bright lobes and does not emit parallel rays. Images of the experimentally measured focal spot of the x-ray tube used in this paper can be found in Fig. 6(a) of Ref. 24.

In order to verify the pinhole structure, digital optical microscopy images (High-Magnification Digital Microscope System VHX-100, Keyence Corporation of America, Woodcliff Lake, NJ) were taken of the front and back surfaces of the pinhole disk. Measurements from the digital images give a diameter of 35.5 μm for the small end of the 30 μm pinhole and a diameter of 215 μm for the large end. These diameters are within approximately two times the pinhole manufacturer’s errors.

Although the actual pinhole diameters were measured before the simulations were performed, the pinhole diameters used in the simulations were taken directly from the manufacturer’s specifications. This decision was made because the optical microscopy measurements did not allow for measurement of the internal structure of the pinhole. However, the measured pinhole outer diameters did deviate slightly from the manufacturer’s specifications (35.5 versus 30 ± 5 μm for the smaller diameter and 215 versus 229 ± 5 μm for the larger diameter).

In order to determine the error incurred by an incorrectly modeled pinhole diameter, we reran simulations similar to those described in Sec. 3B with a pinhole diameter of 36 μm for screen 1 at 0° and 70 kVp. The resultant FOM was 0.3528 ± 0.0089 as compared to 0.3552 ± 0.0133 for the original diameter (30 μm). The difference between these two values is 0.0024 ± 0.0160, so the change in the FOM calculation is negligible. The small change in the FOM with pinhole diameter is due to the fact that the diameter of the pinhole is only determined by a very thin layer at the end of the pinhole, and the majority of the pinhole structure is a larger cone that is unaffected by the specified diameter.

Another potential source of error is the positional error incurred by the manner in which the pinhole is mounted in the cap screw head. This is done by applying superglue between the pinhole disk and the hole machined in the screw head and positioning them by hand. Although the machined hole in the screw head guides the pinhole, it is not an exact fit because the machined hole is somewhat oversized. We anticipate the error in the pinhole disk position to be less than ±0.5 mm horizontally and less than ±1° in angle.

Blur due to FOP

The FOP is a potential source of image degradation, although its effect should be small given that the fibers are 4.5 μm in diameter. To quantify the image degradation imposed by the FOP, a resolution phantom (Edmund Optics 1951 USAF Resolution Target 2^″ Square Negative #NT38-256, Barrington, NJ) was placed in pressure contact with the FOP and a polychromatic, diffuse light source was placed in front of the resolution phantom. The light source was constructed by placing a set of light emitting diodes inside of a white Styrofoam box with a diffuser placed at the output. Note that the resolution phantom was made of glass and of a similar size to the CsI scintillator screens, making the contact of the resolution phantom similar to that of the CsI scintillator screens. In this phantom, the pattern representing 45.3 line pairs per mm (lp∕mm) (group 5, element 4) is resolvable in both axes of the detector. A resolution of 45.3 lp∕mm corresponds to a resolution of 11.0 μm, only slightly greater than the pixel size of the detector (9.0 μm). Therefore, while the FOP may induce a slight blur on the image, its effect should be on the order of the size of a single CCD pixel.

Columnar tilt angle and incident x-ray beam

For the simulations presented in this paper, the tilt angle of the columns was always along the same direction as the oblique angle of x-ray incidence. Experimentally, however, the true orientation of the columns with respect to the incoming x-ray beam is unknown. This leads to a possible inconsistency between the experimental and simulated data that may affect the comparison between the two. To investigate the magnitude of this effect, we also simulated PRFs with a columnar tilt angle directly opposite the oblique angle of the incident x-ray beam (180° rotated from the original data) to explore a range of possible orientations. This was done for screen 2 with a 40 kVp spectrum and all of the incidence angles. For the original PRFs the FOMs were 0.3901 ± 0.0209, 0.4124 ± 0.0310, 0.3932 ± 0.0086, and 0.3685 ± 0.0208 for 0°, 15°, 30°, and 45°, respectively. For the new PRFs, with the modified tilt angle, the FOMs were 0.4015 ± 0.0091, 0.3830 ± 0.0038, 0.3997 ± 0.0079, and 0.4583 ± 0.0400 for 0°, 15°, 30°, and 45°. If we take the difference of each of these values divided by the error in the difference, we get 0.5001, 0.9413, 0.5566, and 1.9918 for 0°, 15°, 30°, and 45°, respectively. This means that changing the orientation of the columnar tilt angle will change the FOM by about the same order as the error in the measurements. Therefore, we do not expect this effect to significantly affect the results.

CONCLUSION

The results presented in this paper provide experimental validation of the MANTIS package for a variety of experimental conditions. Investigators applying MANTIS to various imaging systems now have a better understanding of both its strengths and limitations. Such detailed models of scintillator screen response have important implications in the optimization of x-ray imaging systems and reconstruction of three-dimensional images from planar data. Optimization that does not take into account accurate detector properties may produce misleading results and the inclusion of models like MANTIS can result in more accurate reconstructions since the forward problem is better characterized. Improvements in optimization and reconstructions of x-ray data have the potential to improve image quality and, as a result, detection of abnormalities and disease in these types of images. While the long timescales of MANTIS simulations make rigorous optimizations difficult at present, we are currently developing a fast, analytical model to approximate PRFs produced by MANTIS.²⁵ Such a model will allow for rapid generation of detector PRFs and make inclusion of these detailed detector simulations in complex optimization or forward-problem models of 3D x-ray imaging systems possible and even straightforward.