Kilovoltage beam Monte Carlo dose calculations in submillimeter voxels for small animal radiotherapy

Magdalena Bazalova; Hu Zhou; Paul J Keall; Edward E Graves

doi:10.1118/1.3238465

. 2009 Oct 2;36(11):4991–4999. doi: 10.1118/1.3238465

Kilovoltage beam Monte Carlo dose calculations in submillimeter voxels for small animal radiotherapy

Magdalena Bazalova ^1,^a), Hu Zhou ¹, Paul J Keall ¹, Edward E Graves ¹

PMCID: PMC2773455 PMID: 19994508

Abstract

Purpose: Small animal conformal radiotherapy (RT) is essential for preclinical cancer research studies and therefore various microRT systems have been recently designed. The aim of this paper is to efficiently calculate the dose delivered using our microRT system based on a microCT scanner with the Monte Carlo (MC) method and to compare the MC calculations to film measurements.

Methods: Doses from 2–30 mm diameter 120 kVp photon beams deposited in a solid water phantom with 0.2×0.2×0.2 mm³ voxels are calculated using the latest versions of the EGSnrc codes BEAMNRC and DOSXYZNRC. Two dose calculation approaches are studied: a two-step approach using phase-space files and direct dose calculation with BEAMNRC simulation sources. Due to the small beam size and submillimeter voxel size resulting in long calculation times, variance reduction techniques are studied. The optimum bremsstrahlung splitting number (NBRSPL in BEAMNRC) and the optimum DOSXYZNRC photon splitting (N_split) number are examined for both calculation approaches and various beam sizes. The dose calculation efficiencies and the required number of histories to achieve 1% statistical uncertainty—with no particle recycling—are evaluated for 2–30 mm beams. As a final step, film dose measurements are compared to MC calculated dose distributions.

Results: The optimum NBRSPL is approximately 1×10⁶ for both dose calculation approaches. For the dose calculations with phase-space files, N_split varies only slightly for 2–30 mm beams and is established to be 300. N_split for the DOSXYZNRC calculation with the BEAMNRC source ranges from 300 for the 30 mm beam to 4000 for the 2 mm beam. The calculation time significantly increases for small beam sizes when the BEAMNRC simulation source is used compared to the simulations with phase-space files. For the 2 and 30 mm beams, the dose calculations with phase-space files are more efficient than the dose calculations with BEAMNRC sources by factors of 54 and 1.6, respectively. The dose calculation efficiencies converge for beams with diameters larger than 30 mm.

Conclusions: A very good agreement of MC calculated dose distributions to film measurements is found. The mean difference of percentage depth dose curves between calculated and measured data for 2, 5, 10, and 20 mm beams is 1.8%.

Keywords: small animal radiotherapy, Monte Carlo, bremsstrahlung splitting, microCT

INTRODUCTION

Research in small animal radiation therapy (RT) has been gaining attention in recent years. It is foreseen that small animal radiotherapy will allow for more complex and efficient studies of the biological effects of radiation on tumors and normal tissues following clinically relevant radiation treatments. A number of groups have recently developed systems to treat small animals with image-guided conformal radiotherapy,¹^,²^,³^,⁴^,⁵^,⁶^,⁷^,⁸^,⁹^,¹⁰ rectifying a long-standing deficit of preclinical radiotherapy technology. However, treatment planning and dose calculation methods for small animals have also lagged behind those used in the clinic.

Traditionally, animal models of disease have been treated with radiation using a single beam shaped by lead blocks.¹^,² The dose to normal tissue was relatively high and therefore more effort has been invested to develop new techniques to achieve conformal dose distributions in these subjects. Stojandovic et al.³^,⁴ built a conformal microRT system based on a small high-activity ¹⁹²Ir source, capable of animal irradiation from four angles (0°, 90°, 180°, and 270°) using five different circular collimators (5–15 mm). A decommissioned radiation therapy simulator was modified for small animal radiotherapy in Princess Margaret Hospital in Toronto⁵ and dose to a mouse was delivered with a 225 kVp beam using arc therapy. A small animal radiation research platform was developed at John Hopkins University.⁶^,⁷ An x-ray tube and an amorphous silicon detector are mounted on a gantry that rotates around a translation and rotation stage allowing for cone beam CT imaging and noncoplanar radiotherapy. 80–100 kVp beams are used for imaging and a 225 kVp beam is used for radiotherapy, delivering dose rates between 22–375 cGy∕min depending on the beam size.

We have built a small animal radiotherapy system⁸^,⁹^,¹⁰ based on a GE eXplore Locus microCT scanner (GE Healthcare, London, Ontario, Canada). For conformal radiation therapy, the imaging device has been modified in two ways. First, a two-stage collimator was added in front of the x-ray tube ensuring selective irradiation of the target. Two coaxial hexagonal apertures are rotated by 30° with respect to each other forming an approximately circular beam. The collimator can produce beams of 1–100 mm in diameter, defined at the microCT scanner isocenter. Secondly, a two-dimensional translation stage was mounted on the microCT scanner bed, which enables positioning of any target at the isocenter of the x-ray beam for treatment.

Kilovoltage (kV) photon beams are practical for small animal radiotherapy and have been used in all radiotherapy systems discussed above. Treatment planning for kV beams, however, is not a straightforward task, and because of the low photon beam energy resulting in a significant number of photoelectric interactions, tissue heterogeneities have to be taken into account.¹¹ Dose calculations with kV beams can therefore be accurately performed with the Monte Carlo (MC) method. The aim of this paper is to present a study on efficient MC dose calculations for accurate assessment of the dose delivered with our microRT system and to compare the calculated dose to experimental Gafchromic film measurements.

The latest versions of the EGSnrc (Refs. ¹²^,¹³) MC codes BEAMNRC (Ref. ¹⁴) and DOSXYZNRC (Ref. ¹⁵) are used in this study. Whereas MC simulations of kV beams with the BEAMNRC code have been studied extensively,¹⁶^,¹⁷^,¹⁸ little attention has been given to MC dose calculations in submillimeter voxels.⁵ In this study, two dose calculation approaches, one using phase-space files and one using the full BEAMNRC simulation source, are compared. Transport parameters and variance reduction techniques are studied and recommendations for efficient dose calculations in submillimeter voxels using kV beams are made.

MATERIALS AND METHODS

The x-ray tube of the microCT scanner operates with a maximum tube voltage of 120 kV and a maximum tube current of 50 mA. The tungsten anode, angled at 10°, has a 0.3 mm diameter circular focal spot. According to the manufacturer’s specifications, the x-ray beam is filtered by inherent filtration corresponding to 1.5 mm of aluminum. The distance of the x-ray tube to the isocenter is 35.4 cm and the source-to-detector distance is 41.6 cm.

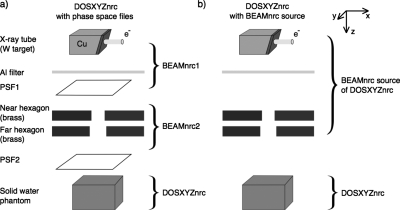
The EGSnrc (Refs. ¹²^,¹³) MC codes BEAMNRC (Ref. ¹⁴) and DOSXYZNRC (Ref. ¹⁵) are used for beam simulations and dose calculations in this paper. Two approaches for calculation of dose delivered by the microCT scanner modified for small animal radiotherapy are taken. In the first approach, in which two phase-space files (PSFs) are used, the microCT scanner geometry is split into three parts: x-ray beam production by the x-ray tube, collimation of this beam by the variable aperture collimator, and the dose calculation itself [Fig. 1a]. In the second approach, a treatment head simulation is used as a source in the DOSXYZNRC calculation [Fig. 1b]. The x-ray beam creation and collimation is simulated in the BEAMNRC part of the simulation which runs simultaneously with the DOSXYZNRC simulation.¹⁹ The main advantage of the latter approach is the elimination of stored phase-space files.

Two approaches for DOSXYZNRC dose calculation for small animal radiotherapy based on a microCT scanner: using two phase-space files (a) and using the BEAMNRC simulation source (b).

The efficiency of dose calculations is calculated in a 4×4×3.5 cm³ solid water phantom with 0.2×0.2×0.2 mm³ voxels throughout this study. More specifically, the optimum bremsstrahlung splitting numbers in the BEAMNRC simulations and photon splitting number in the DOSXYZNRC simulations are studied in greater detail. Beam simulations for the two dose calculation approaches are described in the following sections.

BEAMNRC simulations

Phase-space file simulations

Since the upper part of the x-ray tube geometry [Fig. 1a] is unchanged for all beam sizes, the beam simulation is split into two steps. The BEAMNRC code is used for x-ray beam production and filtration in the first step and for beam collimation in the second step. Finally, the absorbed dose in a solid water phantom is calculated using the DOSXYZNRC code. In this dose calculation approach, the x-ray beam production is simulated only once for a set of beam sizes. The beam collimation is also simulated only once for each beam size, which significantly reduces the calculation time compared to the dose calculation approach with the BEAMNRC simulation source, described in the next section.

Interactions of 120 keV electrons with the tungsten anode and the particle transport through the 1.5 mm aluminum inherent filtration are simulated in the first BEAMNRC simulation. Directional bremsstrahlung splitting²⁰ (DBS) with a 0.7 cm splitting field radius defined at 15 cm from the source is used to increase the beam simulation efficiency. The DBS parameters are set to produce a 30 mm diameter field at the isocenter of the microCT scanner. It is assumed that 1–30 mm field sizes will cover the majority of small animal radiotherapy targets. High-weight bremsstrahlung photons compromising the statistics that fall outside of the defined splitting field are ignored.

Kawrakow²¹ presented a theoretical model for the efficiency of x-ray tube simulations using DBS. From his study and the paper by Mainegra-Hing and Kawrakow,¹⁶ DBS simulation efficiency $ε_{N}^{DBS}$ using N splitting photons can be expressed as

\frac{N}{ε_{N}^{DBS}} = A_{0} + A_{1} (N - 1) + A_{2} {(N - 1)}^{2} .

(1)

The parameters A_i, i=1,2,3, have physical meanings, however, it is impossible to determine them directly. They can be determined by fitting simulated curves, and the optimum N maximizing $ε_{N}^{DBS}$ can be calculated using

N_{\max}^{DBS} = \sqrt{\frac{A_{0}}{A_{2}}} .

(2)

The bremsstrahlung cross-section enhancement (BCSE) variance reduction technique was recently introduced in the BEAMNRC code.²²^,²³ In general, BCSE generates bremsstrahlung photons that are less statistically correlated than split photons generated by DBS. In order to achieve the most efficient simulations, BCSE should be used in combination with DBS. Ali and Rogers²³ showed that for diagnostic x-ray tubes BCSE in combination with DBS can increase the efficiency of bremsstrahlung production by a factor of 2 compared to simulations with DBS alone. However, including BCSE in our simulations does not result in any improvement in simulation efficiency compared to simulations with DBS alone. This is likely due to the fact that few DBS-correlated photons will fall into the same submillimeter voxel.

The electron impact ionization, atomic relaxations, and low energy photon interactions, such as Rayleigh scattering and bound Compton scattering, are included in the simulations. The electron energy cutoff ECUT and the photon energy cutoff PCUT are set to 0.516 and 0.005 MeV, respectively. This BEAMNRC simulation results in a distribution of particles below the aluminum filter stored in the phase-space file PSF1 [Fig. 1a].

PSF1 is set as the particle source for the second step of the beam simulation, the BEAMNRC calculation where particle transport through the collimators is simulated. Two 0.95 cm thick brass hexagonal openings are simulated using the BLOCK component modules.²⁴ Due to the collimator geometry and a low probability of interaction in the air of the collimator opening, recycling of particles results in identical recycled particles in the phase-space files PSF2. Particle recycling is therefore avoided. The outcome of this BEAMNRC simulation is a set of phase-space files for each beam size (PSF2) that are used as the particle source for the final DOSXYZNRC dose calculation. PSF2 is collected as closely to the collimator as possible to allow for MC dose calculations for irradiation of larger animals from an arbitrary x-ray tube angle.

BEAMNRC source simulation

The BEAM treatment head source is used in the second approach to MC dose calculations [Fig. 1b]. A new accelerator is built that encompasses x-ray beam creation, filtration, and collimation. The accelerator is compiled as a shared library. DBS geometrical parameters are adjusted according to the simulated beam size. For each beam size, the DBS splitting radius is set 10% larger than the beam radius defined at SSD below the far hexagon of the collimation system. Such a DBS splitting radius accounts for collimator scatter. The transport parameters are the same as those in the BEAMNRC simulations used to generate phase-space files, with the exception that electron impact ionization is simulated throughout the entire geometry.

The source plane of the DOSXYZNRC simulations is placed as close to the collimator plane as possible. In addition, including the air between the x-ray source and the voxelized phantom∕animal geometry in the DOSXYZNRC portion of the simulation slightly increases the efficiency of the simulation compared to including the air in the BEAMNRC simulation, as shown by Kawrakow and Walters.¹⁹

In this approach, no phase-space files are stored which, especially for large beam sizes requiring extensive disk space, is the main advantage of the BEAMNRC simulation sources compared to the dose calculation approach with phase-space files. On the other hand, each history is simulated starting with an electron striking the x-ray tube target which correspondingly increases the calculation time compared to using phase-space files.

In all MC simulations presented in the paper, the material cross section data are created with the PEGS4 (Ref. ¹⁴) program of the EGSNRC code. The low energy thresholds for electrons and photons AE and AP are set to 0.516 and 0.005, consistent with the ECUT and PCUT parameters, respectively. In order to calculate the cross section data in the kilovoltage range accurately, the upper energy thresholds for electrons and photons UE and UP are set to 300 keV. Simulations for the 2 mm beam with the more accurate XCOM cross sections show negligible differences in dose distributions from simulations with the default Storm-Israel PEGS4 cross sections. The x-ray beam produced with the XCOM cross sections is slightly harder than the beam simulated with the default PEGS4 data. The slightly higher solid water XCOM linear attenuation and mass energy absorption coefficients cause the attenuation of the beam to be the same for both cross-section data. In future studies, however, the XCOM cross sections will be used.

DOSXYZNRC simulations

The dose deposited in a 4×4×3.5 cm³ solid water phantom with 0.2×0.2×0.2 mm³ voxels throughout is calculated for 2, 5, 7, 10, 15, 17, 20, and 30 mm beams using the optimum simulation parameters. The HOWFARLESS (Ref. ²⁵) option for homogeneous phantoms is used in all simulations, which increases the calculation efficiency by approximately 8% for dose calculations with phase-space files. The beams are incident on the top of the phantom, with the source plane perpendicular to the z axis. The simulations are used to evaluate the efficiencies as well as the CPU time and the number of histories with no particle recycling needed to achieve a 1% statistical uncertainty for dose calculations in 0.2×0.2×0.2 mm³ voxels. This voxel size is the resolution of microCT images produced by the hybrid imaging and radiotherapy system that will be used for MC dose calculations for small animal radiotherapy.

The number of electrons in the beam field is very low, less than 0.1% of the total number of particles, and therefore only phase-space file photons are used in all dose calculations. Omitting phase-space file electrons has a negligible effect on the simulated dose distributions.

The continuous slowing down approximation (CSDA) range of 120 keV electrons in solid water is 0.2 mm which is the simulation voxel size. Lower energy electrons with shorter CSDA ranges are more likely to be produced by 120 kVp photons and, therefore, variance reduction techniques using electron energy cutoffs are studied. Electron energy cutoffs ECUT of 0.516 and 0.816 MeV are found to affect the dose in the very first layer of surface voxels, causing less than 5% difference in dose and differences within the statistical uncertainties of 1% at 1σ at larger depths. The DOSXYZNRC calculation time with ECUT of 0.816 MeV decreases by up to a factor of 1.5 compared to 0.516 MeV ECUT. As a result, electrons are not transported in the DOSXYZNRC simulations in this study.

Interactions important for low energy photons, such as Rayleigh scattering and bound Compton scattering, are included in all DOSXYZNRC simulations. Unlike in the x-ray beam calculation, electron impact ionization and relaxation cascades are not simulated. Dose distributions with and without electron impact ionization and relaxation cascades were simulated and found to agree within statistical uncertainties of 1% at 1σ. All MC calculations are submitted to a 2×3 GHz Quad-Core Intel Xeon machine with 4 GB memory.

Simulation efficiency

The optimum simulation parameters are determined using the following definition of simulation efficiency ε:

ε = \frac{1}{σ^{2} T},

(3)

where σ² is the average of squared percentage statistical uncertainties in voxels with dose D>D₅₀ achieved in CPU time T. D₅₀ corresponds to 50% of the maximum dose D_max of the simulation.

BEAMNRC bremsstrahlung photon splitting

The optimum number of bremsstrahlung photons (NBRSPL in BEAMNRC) is investigated using the DOSXYZNRC code for both dose calculation approaches. NBRSPL is varied from 1000 to 1.5×10⁶, the maximum achievable on our machine, and the efficiency ε of the simulation is evaluated using the statistical uncertainties of the dose deposited by a single beam parallel to the z axis in the solid water phantom. The beam is defined by PSF1 for phase-space file simulations and by 2, 5, 10, and 20 mm beam geometries for simulations with the BEAMNRC source. High-weight (fat, unsplit) photons that fall outside of the defined DBS splitting radius are discarded.

Photon splitting

Due to the finite number of phase-space particles, two options for increasing the efficiency of dose calculations can be used: photon recycling and∕or photon splitting. It has been shown that photon splitting is a more efficient technique and that dose calculation results with and without photon splitting agree within statistical uncertainties.¹⁹ More importantly, efficiency achieved by recycling is limited by the latent variance of the phase-space data.²⁶ In order to avoid this limitation, particles are not recycled in this study, and only photon splitting is investigated.

Photon splitting is well documented for MV photons with 2–5 mm voxels. In small animal radiotherapy, where the dose from kV beams in submillimeter voxels is calculated, the optimum photon splitting numbers N_split may differ from those reported for MV beams. In this study, N_split is varied from 0, corresponding to no photon splitting, to 3000, depending on the beam size, and the N_split producing the maximum simulation efficiencies ε [Eq. 3] for the 2, 5, 10, and 20 mm beams are determined.

Film measurements

In the final step of this study, MC dose calculations in a 6×6×3.5 cm³ solid water phantom with 0.2×0.2×1 mm³ voxels are compared to experimental measurements. Depth dose curves and beam profiles calculated with MC are compared to measurements with Gafchromic EBT films.⁸ Films are placed in a 6×6×3.5 cm³ phantom consisting of 3 mm thick 6×6 cm² solid water slabs and irradiated for 1 min with a 120 kVp, 50 mA x-ray beam. The top surface of the phantom is positioned 2.5 cm above the isocenter with the x-ray tube pointing down. Eleven 6×6 cm² EBT films are sandwiched in the slabs of solid water and the central axis depth dose curve is measured. In addition, beam profiles along the heel effect and perpendicular to the heel effect are measured at different depths. The resolution of the film readout is 508 dpi. A factor for conversion of the Monte Carlo dose expressed in Gy∕(incident particle) to the actual dose rate in Gy∕min is determined by a least squares fit using MATLAB (The Mathworks, Natick, MA). More details on the film measurements are given in the paper by Rodriguezet al.⁸

RESULTS AND DISCUSSION

Variance reduction techniques

Directional bremsstrahlung splitting

The efficiency calculated with the 0.2×0.2×0.2 mm³ resolution solid water phantom as a function of the bremsstrahlung splitting number (NBRSPL) is studied for the generation of PSF1. A splitting number of 1×10⁶ resulted in a large phase-space file PSF1 with 8.9×10⁸ particles simulated in 51.1 h of CPU time. Since the CPU time to generate PSF1 is not included in the efficiency calculation, the efficiencies for all studied values of NBRSPL are within 6%.

PSF1 is used as the source for the second BEAMNRC calculation simulating the beam collimation. As a result, a library of phase-space files for beams with 1–30 mm diameters is created. The collimated phase-space files (PSF2) contains from 3.0×10⁶ particles for the 2 mm beam up to 6.9×10⁸ particles for the 30 mm beam calculated in 11.0–5.7 h, respectively.

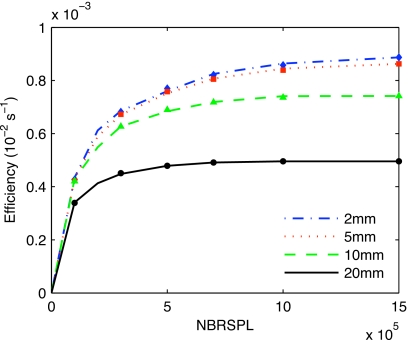
The bremsstrahlung splitting experiment for the BEAMNRC source results in the efficiency curves for the 2, 5, 10, and 20 mm beams presented in Fig. 2. The dose calculation efficiency decreases with increasing beam size, and the optimum splitting number slightly increases with decreasing the beam size.

The efficiency of dose calculations as a function of bremsstrahlung splitting number NBRSPL using DBS for different beam sizes in theBEAMNRC simulation source dose calculation. The symbols represent values calculated using Eq. 1.

According to Eq. 2, the maximum efficiency splitting numbers for the 2, 5, 10, and 20 mm beams are found to be 3.2×10⁶, 2.4×10⁶, 1.4×10⁶, and 1.2×10⁶. The efficiency curve falloff behind the maximum is slow and, therefore, a constant bremsstrahlung splitting number of 1×10⁶ is used for all beam sizes. This caused less than 5% decrease in efficiency.

The optimum splitting number is much higher than what is found for MV beams where optimum values of NBRSPL of ∼1500 are reported.²⁰ This is mainly due to the small beam size and the consequent small solid angle of interest. The conclusions are in agreement with conclusions drawn in the paper by Mainegra-Hing and Kawrakow.¹⁶

Photon splitting

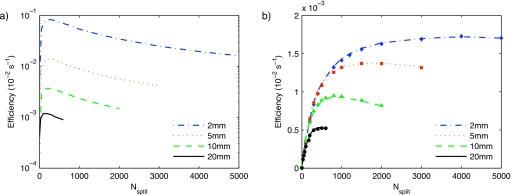
The results for the dose calculation with phase-space files presented in Fig. 3a show that the simulation efficiency significantly increases with decreasing field size. Figure 3a also demonstrates that the optimum N_split slightly increases with decreasing field size, being 300 for the 2 and 5 mm beams and 200 for the 10 and 20 mm beams. Since there is only a less than 1% efficiency drop between N_split values of 200 and 300 for the 10 and 20 mm beams, the splitting number for all dose calculations using phase-space files is set to 300.

The efficiency curves for the BEAMNRC source simulation dose calculations are shown in Fig. 3b. Similar to the simulations with phase-space files, the efficiency increases with decreasing the field size. However, the CPU time for the BEAMNRC source simulation is not negligible and therefore the efficiency difference between various field sizes is not as large as for the simulations with phase-space files. The optimum splitting number strongly depends on the field size for the BEAMNRC simulation sources. It is found to be 4000, 1500, 1000, and 400 for the 2, 5, 10, and 20 mm beams, respectively. These N_split values are at least a factor of 10 larger than for MV beams with larger voxels. Due to the smaller voxel size, the energy from split photons is more likely to be deposited in different voxels. The larger N_split values of kV beams are in agreement with the MV beam study by Kawrakow and Walters.¹⁹

Figure 3 also demonstrates that the efficiency curves for the two dose calculation approaches converge for larger beam sizes, which is due to the large portion of the CPU time spent in phantom particle transport, instead of x-ray beam creation. The optimum splitting number for other field sizes presented in this report is calculated using a linear interpolation and assuming an optimum splitting number of 300 for the 30 mm beam.

OptimumN_splitusingBEAMNRCsource. The total dose calculation time for the BEAMNRC source is T_Bs=T_B+T_D, where T_B is the BEAMNRC source simulation time and T_D is the time for the DOSXYZNRC part of the simulation. Assuming that the CPU time T_D to transport N particles from the phase-space files (or what would be the phase-space file in the BEAMNRC simulation source) through the phantom is the same for both the phase-space file and the BEAMNRC source simulation and that it results in the same statistical uncertainty σ, the efficiency for the BEAMNRC source dose calculation ε_Bs can be expressed using T_D, and σ of the phase-space file simulations using the following:

ε_{B s} = \frac{1}{σ^{2} (T_{B} + T_{D})} .

(4)

The previous equation also assumes that the time required to read phase-space file particles from a hard disk is negligible. If the CPU time T_B to simulate N phase-space particles using the BEAMNRC simulation is known, ε_Bs can be calculated from the efficiency curve of the dose calculations with phase-space files. T_B is found by running the accelerator compiled as a shared library [Fig. 1b] as a stand-alone accelerator.

The symbols in Fig. 3b represent the calculated points and they are in a very good agreement with the simulated data. The mean difference between simulated and calculated points for all beam sizes is 2.8%. Equation 4 can be conveniently used to characterize the optimum N_split forBEAMNRC simulation sources using efficiency curves of phase-space file simulations.

Simulation times

MC dose calculations for small animal radiotherapy are intended to be used for treatment plan optimization, and therefore the calculation times are a valid concern and should be as short as possible. The two MC dose calculation approaches presented in this paper are compared by means of CPU times and number of histories needed to achieve a 1% statistical uncertainty in voxels with doses larger than 50% of the maximum calculated dose. The phase-space and simulation source results agree to within 1%.

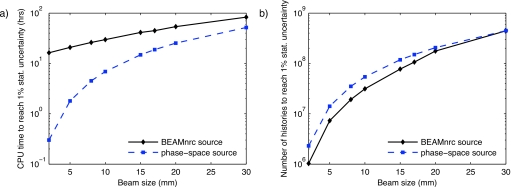
Figure 4 summarizes the results of the simulation efficiency study, showing the CPU time (a) and the number of histories (b) required to achieve a 1% statistical uncertainty. Note that the number of histories is not the number of primary histories but the number of particles incident on the phantom and that the simulation statistics are computed per incident particle.

Efficiency of MC dose calculation with BEAMNRC source and with phase-space files: the CPU time for a 3 GHz machine (a) and the number of histories (b) to achieve 1% statistical uncertainty. The ordinates are logarithmic.

For small beam sizes, the CPU time for dose calculations with the BEAMNRC simulation source is significantly longer than for dose calculations using phase-space files. For example, the 2 mm beam can be simulated in 20 min with the phase-space file. The same simulation with the BEAMNRC source resulting in identical dose distribution takes 16.3 h. This is due to the fact that the DOSXYZNRC part of the simulation is very fast and the simulation time is dominated by the creation of the x-ray beam for small beams. The ratio of the BEAMNRC source model CPU time to the total calculation time decreases with increasing beam size as the DOSXYZNRC simulation uses a larger fraction of the total CPU time. This is due to both an increase in the DOSXYZNRC simulation time and a decrease in the BEAMNRC simulation time. Therefore, the two curves in Fig. 5a approach convergence for large beam sizes.

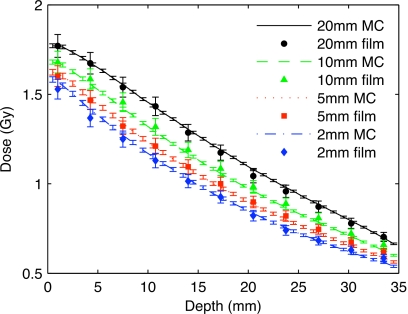
Depth dose curves for a 1 min treatment simulated with phase-space files (lines) and measured with EBT Gafchromic films (markers). The scanner isocenter is at 0 mm depth.

The results of the CPU time study are summarized in Table 1 where, for the phase-space source, the CPU times of the second BEAMNRC calculation simulating the beam collimation are also listed. Including the beam collimation in the calculation of the simulation efficiency would significantly decrease the efficiency, especially for small beams. For the 2 mm beam, the efficiency would decrease by a factor of 28. The simulation parameters for the phase-space file calculation are optimized for the 30 mm beam and all the parameters including the bremsstrahlung splitting number, splitting radius, and photon splitting number are almost identical to the 30 mm beam simulation with the BEAMNRC source. Assuming that a 35 h simulation is needed to create just enough particles in PSF1 to reach 1% statistical uncertainty, the total simulation time for the 30 mm beam using phase-space files is approximately 90 h. Comparison with the 83 hour long 30 mm beam simulation with the BEAMNRC source indicates that I∕O operations take approximately 8% of the total CPU time.

Table 1.

CPU time (h) to achieve 1% statistical uncertainty on a 3 GHz machine.


Beam diameter (mm)		2	5	8	10	15	17	20	30
Phase-space source	Collimation	8.6	8.3	7.9	7.7	6.9	6.6	6.2	3.7
Phase-space source	DOSXYZNRC	0.3	1.8	4.5	6.9	14.8	18.8	25.3	51.7
BEAMNRC source	Total	16.3	20.9	26.1	29.8	41.2	44.8	53.8	83.0

Open in a new tab

The number of phase-space histories needed to achieve a 1% statistical uncertainty for various beam sizes is plotted in Fig. 4b. Due to the lower photon splitting number for the phase-space file dose calculations, the number of histories for 1% statistical uncertainty is larger for small beam sizes than for simulations with BEAMNRC simulation sources.

Since the bremsstrahlung splitting and the photon splitting numbers for the 30 mm beam are identical for both dose calculation approaches, the numbers of histories to reach 1% statistical uncertainty for the 30 mm beam should be equal. Table II demonstrates that the numbers of histories for the two dose calculation approaches differ by only 0.8%. The number of particles available in the phase-space files is at least 30% higher than the minimum required for the 1% dose calculation statistical uncertainty.

Comparison of Monte Carlo dose calculations with film measurements

The comparison of depth dose curves calculated by MC and measured with EBT Gafchromic films is presented in Fig. 5. During the process of matching the MC dose distribution to experimental measurements, it was found that the 1.5 mm aluminum inherent filtration specified by the manufacturer produced a softer beam with a faster attenuation than what is measured by films. This might be caused by the fact that inherent filtration increases with time due to deposition of tungsten on the tube window.²⁷ As a result, the inherent filtration of the microCT tube is modified to 2.5 mm of aluminum which yields a better agreement with film measurements.

The dose rate conversion factor is found to be 7.55×10¹⁸ particles∕min. The mean difference between measured and simulated data points using this conversion factor is 1.8%.

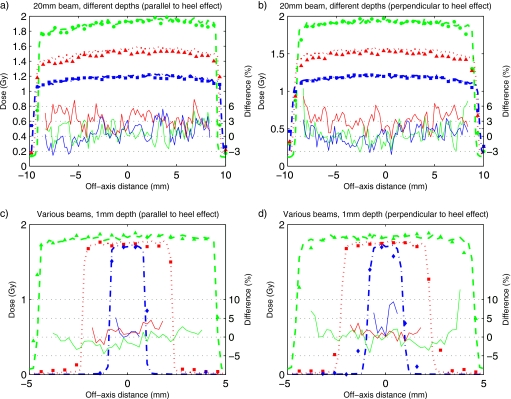
Dose profiles for the 20 mm beam at 0.1, 1.0, and 2.0 cm depths parallel and perpendicular to the heel effect are presented in Figs. 6a, 6b, respectively. The difference curves indicate that, with the exception of the 1.0 cm depth profile that is systematically higher for the MC simulation, the difference between MC and film data is within 3%. Both the film measurements and the MC simulations show that the heel effect flattens out at larger depths.

MC simulated profiles (lines) and measured profiles with films (symbols) for the 20 mm beam at 0.1 (◆), 1.0 (▲), and 2.0 (◼) cm depths parallel (a) and perpendicular to the heel effect (b), and for 10 (▲), 5 (◼), and 2 (◆) mm beams at 1 mm depth parallel (c) and perpendicular to the heel effect (d) in solid water phantom positioned 2.5 cm above the isocenter. Solid lines show the percentage difference between MC and film data. The treatment time is 1 min.

Dose profiles for the 10, 5, and 2 mm beams at 1 mm depth parallel and perpendicular to the heel effect are shown in Figs. 6c, 6d, respectively. The heel effect is only noticeable in the 10 mm beam. Similar to the 20 mm beams, all beam profiles simulated by MC match the measurements within the uncertainties of the film measurements⁸ and the statistical uncertainties (of 1% at 1σ) of the MC simulations. Larger than 10% dose differences in the penumbra region can be explained by small shifts in the positioning of the film and by inaccuracies in the alignment of the collimation system.

All MC simulations of this paper are performed in homogeneous solid water phantoms. It is expected that calculation times of dose deposited in small animals will be longer; however, due to the voxelized geometry used by the DOSXYZNRC code, the calculation times should not be increased significantly. Material∕tissue segmentation for MC dose calculations with kV beams is essential²⁸^,²⁹ and it is currently under investigation.

CONCLUSIONS

In this paper, the efficiency of Monte Carlo dose calculations using the EGSNRC codes for small animal radiotherapy based on a microCT scanner is studied. Dose is calculated in submillimeter resolution geometries, primarily using the practically relevant 0.2×0.2×0.2 mm³ voxels using phase-space files and BEAMNRC sources. To our knowledge, this paper presents the first extensive study on efficient MC dose calculations for kilovoltage beams in submillimeter voxels.

For very small beams, MC dose calculations with phase-space files are significantly more efficient than simulations with BEAMNRC sources. The simulation time to reach 1% statistical uncertainty is faster by a factor of 54 for a 2 mm beam and by a factor of 1.6 for a 30 mm beam (Table 1). This study indicates that the simulation times for the two simulation approaches converge for larger beam sizes.

Simulations for beams with diameters less than or equal to 30 mm can be conveniently performed with a library of precalculated phase-space files. This recommendation will depend on the voxel size used in the simulation. Note that as shown in this study, recycling of phase-space particles can be avoided with sufficiently large phase-space files.

A comparison of MC simulated central axis percentage depth dose curves and profiles to the measured ones using Gafchromic films show that our microCT∕RT beam is modeled with a reasonable accuracy. In this study, phase-space files for beams with diameters of 1–30 mm were calculated and serve as a library for future MC dose calculations

ACKNOWLEDGMENTS

The authors would like to thank to B. Walters for his comments on efficiency curves and to I. Kawrakow for his help with the installation of the new version of the BEAMNRC code. They would also like to thank to E. Ali for his comments on the BCSE variance reduction technique.

References

Khan M., Hill R., and Vandyk J., “Partial volume rat lung irradiation: An evaluation of early DNA damage,” Int. J. Radiat. Oncol., Biol., Phys. 40, 467–476 (1998). [DOI] [PubMed] [Google Scholar]
Hillman G. G., Maughan R. L., Grignon D. J., Yudelev M., Rubio J., Tekyi-Mensah S., Layer A., Che M., and Forman J. D., “Neutron or photon irradiation for prostate tumors: enhancement of cytokine therapy in a metastatic tumor model,” Clin. Cancer Res. 7, 136–144 (2001). [PubMed] [Google Scholar]
Stojadinovic S., Low D. A., Hope A. J., Vicic M., Deasy J. O., Cui J., Khullar D., Parikh P. J., Malinowski K. T., Izaguirre E. W., Mutic S., and Grigsby P. W., “MicroRT—Small animal conformal irradiator,” Med. Phys. 34, 4706–4716 (2007). 10.1118/1.2799887 [DOI] [PubMed] [Google Scholar]
Stojadinovic S., Low D. A., Vicic M., Mutic S., Deasy J. O., Hope A. J., Parikh P. J., and Grigsby P. W., “Progress toward a microradiation therapy small animal conformal irradiator,” Med. Phys. 33, 3834–3845 (2006). 10.1118/1.2349693 [DOI] [PubMed] [Google Scholar]
Chow J. C. L. and Leung M. K. K., “Treatment planning for a small animal using Monte Carlo simulation,” Med. Phys. 34, 4810–4817 (2007). 10.1118/1.2805254 [DOI] [PubMed] [Google Scholar]
Matinfar M., Ford E., Iordachita I., Wong J., and Kazanzides P., “Image-guided small animal radiation research platform: calibration of treatment beam alignment,” Phys. Med. Biol. 54, 891–905 (2009). 10.1088/0031-9155/54/4/005 [DOI] [PMC free article] [PubMed] [Google Scholar]
Wong J., Armour E., Kazanzides P., Iordachita I., Tryggestad E., Deng H., Matinfar M., Kennedy C., Liu Z., Chan T., Gray O., Verhaegen F., McNutt T., Ford E., and DeWeese T. L., “High-resolution, small animal radiation research platform with x-ray tomographic guidance capabilities,” Int. J. Radiat. Oncol., Biol., Phys. 71, 1591–1599 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
Rodriguez M., Zhou H., Keall P. J., and Graves E. E., “Commissioning of a novel microCT∕RT system for small animal conformal radiotherapy,” Phys. Med. Biol. 54, 3727–3740 (2009). 10.1088/0031-9155/54/12/008 [DOI] [PMC free article] [PubMed] [Google Scholar]
Graves E. E., Zhou H., Chatterjee R., Keall P. J., Gambhir S. S., Contag C. H., and Boyer A. L., “Design and evaluation of a variable aperture collimator for conformal radiotherapy of small animals using a microCT scanner,” Med. Phys. 34, 4359–4367 (2007). 10.1118/1.2789498 [DOI] [PubMed] [Google Scholar]
Zhou H., Xu J., Rodriguez M., van den Haak F., Zhu X., Xian Y., Nelson G., Jogani R., Tran P. T., Keall P. J., and Graves E. E., “Development of a microCT-based image-guided conformal radiotherapy system for small animals,” Int. J. Radiat. Oncol., Biol., Phys. (submitted). [DOI] [PMC free article] [PubMed]
Gao W. and Raeside D. E., “Orthovoltage radiation therapy treatment planning using Monte Carlo simulation: Treatment of neuroendocrine carcinoma of the maxillary sinus,” Phys. Med. Biol. 42, 2421–2434 (1997). 10.1088/0031-9155/42/12/009 [DOI] [PubMed] [Google Scholar]
Kawrakow I. and Rogers D. W. O., “The EGSnrc code system: Monte Carlo simulation of electron and photon transport,” NRCC Report No. PIRS-701, 2006.
Kawrakow I., “Accurate condensed history Monte Carlo simulation of electron transport. I. EGSnrc, the new EGS4 version,” Med. Phys. 27, 485–498 (2000). 10.1118/1.598917 [DOI] [PubMed] [Google Scholar]
Rogers D. W. O., Faddegon B. A., Ding G. X., Ma C.-M., We J., and Mackie T. R., “BEAM: A Monte Carlo code to simulate radiotherapy treatment units,” Med. Phys. 22, 503–524 (1995). 10.1118/1.597552 [DOI] [PubMed] [Google Scholar]
Walters B. R. B., Kawrakow I., and Rogers D. W. O., “DOSXYZnrc users manual,” NRCC Report No. PIRS-794 rev B, 2007.
Mainegra-Hing E. and Kawrakow I., “Efficient x-ray tube simulations,” Med. Phys. 33, 2683–2690 (2006). 10.1118/1.2219331 [DOI] [PubMed] [Google Scholar]
Ali E. S. M. and Rogers D. W. O., “Benchmarking EGSnrc in the kilovoltage energy range against experimental measurements of charged particle backscatter coefficients,” Phys. Med. Biol. 53, 1527–2544 (2008). 10.1088/0031-9155/53/6/002 [DOI] [PubMed] [Google Scholar]
Bazalova M. and Verhaegen F., “Monte Carlo simulation of a computed tomography x-ray tube,” Phys. Med. Biol. 52, 5945–5955 (2007). 10.1088/0031-9155/52/19/015 [DOI] [PubMed] [Google Scholar]
Kawrakow I. and Walters B., “Efficient photon beam dose calculations using DOSXYZnrc with BEAMnrc,” Med. Phys. 33, 3046–3056 (2006). 10.1118/1.2219778 [DOI] [PubMed] [Google Scholar]
Kawrakow I., Rogers D. W. O., and Walters B. R. B., “Large efficiency improvements in BEAMnrc using directional bremsstrahlung splitting,” Med. Phys. 31, 2883–2898 (2004). 10.1118/1.1788912 [DOI] [PubMed] [Google Scholar]
Kawrakow I., “On the efficiency of photon beam treatment head simulations,” Med. Phys. 32, 2320–2326 (2005). 10.1118/1.1943808 [DOI] [PubMed] [Google Scholar]
Hasenblag F., Fix M. K., Born E. J., Mini R., and Kawrakow I., “VMC++ versus BEAMnrc: A comparison of simulated linear accelerator heads for photon beams,” Med. Phys. 35, 1521–1531 (2008). 10.1118/1.2885372 [DOI] [PubMed] [Google Scholar]
Ali E. S. M. and Rogers D. W. O., “Efficiency improvements of x-ray simulations in EGSnrc user-codes using bremsstrahlung cross section enhancement (BCSE),” Med. Phys. 34, 2143–2154 (2007). 10.1118/1.2736778 [DOI] [PubMed] [Google Scholar]
Rogers D. W. O., Walters B., and Kawrakow I., “BEAMnrc users manual,” NRCC Report No. PIRS-0509(A) rev K, 2006.
Walters B. R. B. and Kawrakow I., “A “HOWFARLESS” option to increase efficiency of homogeneous phantom calculations with DOSXYZnrc,” Med. Phys. 34, 3794–3807 (2007). 10.1118/1.2776258 [DOI] [PubMed] [Google Scholar]
Sempau J., Sánchez-Reyes A., Salvat F., Oulad ben Tahar H., Jiang S. B., and Fernández-Varea J. M., “Monte Carlo simulation of electron beams from an accelerator head using PENELOPE,” Phys. Med. Biol. 46, 1163–1186 (2001). 10.1088/0031-9155/46/4/318 [DOI] [PubMed] [Google Scholar]
Nagel H. D., “Limitations in the determination of total filtration of x-ray tube assemblies,” Phys. Med. Biol. 33, 271–89 (1988). 10.1088/0031-9155/33/2/006 [DOI] [PubMed] [Google Scholar]
Zhou H., Keall P. J., and Graves E. E., “A bone composition model for Monte Carlo x-ray transport simulations,” Med. Phys. 36, 1008–1018 (2009). 10.1118/1.3077129 [DOI] [PubMed] [Google Scholar]
Bazalova M., Carrier J.-F., Beaulieu L., and Verhaegen F., “Dual-energy CT-based material extraction for tissue segmentation in Monte Carlo dose calculations,” Phys. Med. Biol. 53, 2439–2456 (2008). 10.1088/0031-9155/53/9/015 [DOI] [PubMed] [Google Scholar]

[c1] Khan M., Hill R., and Vandyk J., “Partial volume rat lung irradiation: An evaluation of early DNA damage,” Int. J. Radiat. Oncol., Biol., Phys. 40, 467–476 (1998). [DOI] [PubMed] [Google Scholar]

[c2] Hillman G. G., Maughan R. L., Grignon D. J., Yudelev M., Rubio J., Tekyi-Mensah S., Layer A., Che M., and Forman J. D., “Neutron or photon irradiation for prostate tumors: enhancement of cytokine therapy in a metastatic tumor model,” Clin. Cancer Res. 7, 136–144 (2001). [PubMed] [Google Scholar]

[c3] Stojadinovic S., Low D. A., Hope A. J., Vicic M., Deasy J. O., Cui J., Khullar D., Parikh P. J., Malinowski K. T., Izaguirre E. W., Mutic S., and Grigsby P. W., “MicroRT—Small animal conformal irradiator,” Med. Phys. 34, 4706–4716 (2007). 10.1118/1.2799887 [DOI] [PubMed] [Google Scholar]

[c4] Stojadinovic S., Low D. A., Vicic M., Mutic S., Deasy J. O., Hope A. J., Parikh P. J., and Grigsby P. W., “Progress toward a microradiation therapy small animal conformal irradiator,” Med. Phys. 33, 3834–3845 (2006). 10.1118/1.2349693 [DOI] [PubMed] [Google Scholar]

[c5] Chow J. C. L. and Leung M. K. K., “Treatment planning for a small animal using Monte Carlo simulation,” Med. Phys. 34, 4810–4817 (2007). 10.1118/1.2805254 [DOI] [PubMed] [Google Scholar]

[c6] Matinfar M., Ford E., Iordachita I., Wong J., and Kazanzides P., “Image-guided small animal radiation research platform: calibration of treatment beam alignment,” Phys. Med. Biol. 54, 891–905 (2009). 10.1088/0031-9155/54/4/005 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c7] Wong J., Armour E., Kazanzides P., Iordachita I., Tryggestad E., Deng H., Matinfar M., Kennedy C., Liu Z., Chan T., Gray O., Verhaegen F., McNutt T., Ford E., and DeWeese T. L., “High-resolution, small animal radiation research platform with x-ray tomographic guidance capabilities,” Int. J. Radiat. Oncol., Biol., Phys. 71, 1591–1599 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]

[c8] Rodriguez M., Zhou H., Keall P. J., and Graves E. E., “Commissioning of a novel microCT∕RT system for small animal conformal radiotherapy,” Phys. Med. Biol. 54, 3727–3740 (2009). 10.1088/0031-9155/54/12/008 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c9] Graves E. E., Zhou H., Chatterjee R., Keall P. J., Gambhir S. S., Contag C. H., and Boyer A. L., “Design and evaluation of a variable aperture collimator for conformal radiotherapy of small animals using a microCT scanner,” Med. Phys. 34, 4359–4367 (2007). 10.1118/1.2789498 [DOI] [PubMed] [Google Scholar]

[c10] Zhou H., Xu J., Rodriguez M., van den Haak F., Zhu X., Xian Y., Nelson G., Jogani R., Tran P. T., Keall P. J., and Graves E. E., “Development of a microCT-based image-guided conformal radiotherapy system for small animals,” Int. J. Radiat. Oncol., Biol., Phys. (submitted). [DOI] [PMC free article] [PubMed]

[c11] Gao W. and Raeside D. E., “Orthovoltage radiation therapy treatment planning using Monte Carlo simulation: Treatment of neuroendocrine carcinoma of the maxillary sinus,” Phys. Med. Biol. 42, 2421–2434 (1997). 10.1088/0031-9155/42/12/009 [DOI] [PubMed] [Google Scholar]

[c12] Kawrakow I. and Rogers D. W. O., “The EGSnrc code system: Monte Carlo simulation of electron and photon transport,” NRCC Report No. PIRS-701, 2006.

[c13] Kawrakow I., “Accurate condensed history Monte Carlo simulation of electron transport. I. EGSnrc, the new EGS4 version,” Med. Phys. 27, 485–498 (2000). 10.1118/1.598917 [DOI] [PubMed] [Google Scholar]

[c14] Rogers D. W. O., Faddegon B. A., Ding G. X., Ma C.-M., We J., and Mackie T. R., “BEAM: A Monte Carlo code to simulate radiotherapy treatment units,” Med. Phys. 22, 503–524 (1995). 10.1118/1.597552 [DOI] [PubMed] [Google Scholar]

[c15] Walters B. R. B., Kawrakow I., and Rogers D. W. O., “DOSXYZnrc users manual,” NRCC Report No. PIRS-794 rev B, 2007.

[c16] Mainegra-Hing E. and Kawrakow I., “Efficient x-ray tube simulations,” Med. Phys. 33, 2683–2690 (2006). 10.1118/1.2219331 [DOI] [PubMed] [Google Scholar]

[c17] Ali E. S. M. and Rogers D. W. O., “Benchmarking EGSnrc in the kilovoltage energy range against experimental measurements of charged particle backscatter coefficients,” Phys. Med. Biol. 53, 1527–2544 (2008). 10.1088/0031-9155/53/6/002 [DOI] [PubMed] [Google Scholar]

[c18] Bazalova M. and Verhaegen F., “Monte Carlo simulation of a computed tomography x-ray tube,” Phys. Med. Biol. 52, 5945–5955 (2007). 10.1088/0031-9155/52/19/015 [DOI] [PubMed] [Google Scholar]

[c19] Kawrakow I. and Walters B., “Efficient photon beam dose calculations using DOSXYZnrc with BEAMnrc,” Med. Phys. 33, 3046–3056 (2006). 10.1118/1.2219778 [DOI] [PubMed] [Google Scholar]

[c20] Kawrakow I., Rogers D. W. O., and Walters B. R. B., “Large efficiency improvements in BEAMnrc using directional bremsstrahlung splitting,” Med. Phys. 31, 2883–2898 (2004). 10.1118/1.1788912 [DOI] [PubMed] [Google Scholar]

[c21] Kawrakow I., “On the efficiency of photon beam treatment head simulations,” Med. Phys. 32, 2320–2326 (2005). 10.1118/1.1943808 [DOI] [PubMed] [Google Scholar]

[c22] Hasenblag F., Fix M. K., Born E. J., Mini R., and Kawrakow I., “VMC++ versus BEAMnrc: A comparison of simulated linear accelerator heads for photon beams,” Med. Phys. 35, 1521–1531 (2008). 10.1118/1.2885372 [DOI] [PubMed] [Google Scholar]

[c23] Ali E. S. M. and Rogers D. W. O., “Efficiency improvements of x-ray simulations in EGSnrc user-codes using bremsstrahlung cross section enhancement (BCSE),” Med. Phys. 34, 2143–2154 (2007). 10.1118/1.2736778 [DOI] [PubMed] [Google Scholar]

[c24] Rogers D. W. O., Walters B., and Kawrakow I., “BEAMnrc users manual,” NRCC Report No. PIRS-0509(A) rev K, 2006.

[c25] Walters B. R. B. and Kawrakow I., “A “HOWFARLESS” option to increase efficiency of homogeneous phantom calculations with DOSXYZnrc,” Med. Phys. 34, 3794–3807 (2007). 10.1118/1.2776258 [DOI] [PubMed] [Google Scholar]

[c26] Sempau J., Sánchez-Reyes A., Salvat F., Oulad ben Tahar H., Jiang S. B., and Fernández-Varea J. M., “Monte Carlo simulation of electron beams from an accelerator head using PENELOPE,” Phys. Med. Biol. 46, 1163–1186 (2001). 10.1088/0031-9155/46/4/318 [DOI] [PubMed] [Google Scholar]

[c27] Nagel H. D., “Limitations in the determination of total filtration of x-ray tube assemblies,” Phys. Med. Biol. 33, 271–89 (1988). 10.1088/0031-9155/33/2/006 [DOI] [PubMed] [Google Scholar]

[c28] Zhou H., Keall P. J., and Graves E. E., “A bone composition model for Monte Carlo x-ray transport simulations,” Med. Phys. 36, 1008–1018 (2009). 10.1118/1.3077129 [DOI] [PubMed] [Google Scholar]

[c29] Bazalova M., Carrier J.-F., Beaulieu L., and Verhaegen F., “Dual-energy CT-based material extraction for tissue segmentation in Monte Carlo dose calculations,” Phys. Med. Biol. 53, 2439–2456 (2008). 10.1088/0031-9155/53/9/015 [DOI] [PubMed] [Google Scholar]

PERMALINK

Kilovoltage beam Monte Carlo dose calculations in submillimeter voxels for small animal radiotherapy

Magdalena Bazalova

Hu Zhou

Paul J Keall

Edward E Graves

Abstract

INTRODUCTION

MATERIALS AND METHODS