The effects of longitudinal chromatic aberration and a shift in the peak of the middle-wavelength sensitive cone fundamental on cone contrast

Abstract

Longitudinal chromatic aberration is a well-known imperfection of visual optics, but the consequences in natural conditions, and for the evolution of receptor spectral sensitivities are less well understood. This paper examines how chromatic aberration affects image quality in the middle-wavelength sensitive (M-) cones, viewing broad-band spectra, over a range of spatial frequencies and focal planes. We also model the effects on M-cone contrast of moving the M-cone fundamental relative to the long- and middle-wavelength (L- and M-cone) fundamentals, while the eye is accommodated at different focal planes or at a focal plane that maximizes luminance contrast.

When the focal plane shifts towards longer (650 nm) or shorter wavelengths (420 nm) the effects on M-cone contrast are large: longitudinal chromatic aberration causes total loss of M-cone contrast above 10 to 20 c/d. In comparison, the shift of the M-cone fundamental causes smaller effects on M-cone contrast. At 10 c/d a shift in the peak of the M-cone spectrum from 560 nm to 460 nm decreases M-cone contrast by 30%, while a 10 nm blue-shift causes only a minor loss of contrast. However, a noticeable loss of contrast may be seen if the eye is focused at focal planes other than that which maximizes luminance contrast.

The presence of separate long- and middle-wavelength sensitive cones therefore has a small, but not insignificant cost to the retinal image via longitudinal chromatic aberration. This aberration may therefore be a factor limiting evolution of visual pigments and trichromatic color vision.

Introduction

Longitudinal chromatic aberration (LCA) is a significant feature in physiological optics (Bedford & Wyszecki, 1957). LCA produces large amounts of chromatic defocus, and some species have adapted to counteract the blur: some fish have multifocal lenses (Kröger, Campbell, Fernald & Wagner, 1999), and the jumping spider Plexippus (Salticidae) places different spectral types of receptor at different depths (Blest, Hardie, McIntyre & Williams, 1981) as do firefly squids (Kröger & Gislen, 2004).

Potential advantages of LCA are the increased depth of focus of the visual system and the provision of chromatic defocus cues for accommodation (Kruger, Mathews, Aggarwala, Yager & Kruger, 1995; Rucker & Kruger, 2004). With respect to the first of these, with different wavelengths focusing at different planes within the eye, the eye can focus over a wide range of distances potentially without the need for adjusting focus (accommodation). With respect to the second, it has been shown that LCA provides cues on the sign of defocus for the accommodation mechanism (Kruger et al., 1995); the accommodation mechanism responds to the difference in cone contrast between L- and M-cones when a retinal image is focused in-front or behind the retina (Rucker & Kruger, 2004).

Potential disadvantages of LCA are related to the induced spatial blur. In humans there is around 2.00 D in aberration between 400 and 700 nm (Bedford & Wyszecki, 1957; Wald & Griffin, 1947), which under full spectrum illumination should impair retinal image quality, and hence spatial vision (Boynton, 1979; Mollon, 1982). This effect may be somewhat limited by macular pigment (Reading & Weale, 1974), which absorbs short-wavelength light, and by the scarcity of S-cones (Curcio, Allen, Sloan, Lerea, Hurley, Klock & Milam, 1991; Mollon & Bowmaker, 1992; Roorda & Williams, 1999). Additionally, monochromatic aberrations can compensate to some degree for the effects of LCA (McLellan, Marcos, Prieto & Burns, 2002). As a result of these adaptations the retinal image quality for S-cones may not be as blurred as originally thought.

With respect to L- and M-cones, four main types of explanation have been proposed to account for the relatively small spectral separation of primate L- and M-cones: i) that the small separation is not adaptive, but reflects the recent evolutionary divergence of the two pigments (Goldsmith, 1991); ii) that the small spectral separation is limited by the depth of focus of the eye (Kröger, 2000); iii) that the spectral tuning optimizes color vision in a particular task, such as detecting fruit amongst leaves (Osorio & Vorobyev, 2005; Sumner & Mollon, 2000); and iv) that having widely separated L-cone and M-cone receptors is deleterious for spatial vision, for example because luminance signals are corrupted by chromatic noise (Osorio, Ruderman & Cronin, 1998; Williams, Sekiguchi & Brainard, 1993). Given that chromatic aberration must to some extent degrade spatial information this may also be a significant factor in the evolution of the L- and M-cone spectral sensitivities.

Here we ask whether chromatic aberration has limited the separation of L- and M-cones. We examine the cost, in terms of cone contrast, of having separate L- and M-cones as in normal trichromats (DeMarco, Pokorny & Smith, 1992), or for greater or lesser spectral separations of the cones. We assume that the L-cone and S-cone spectral sensitivity is fixed, and then ask how contrast of the retinal image is affected by varying the peak sensitivity of the M-cone fundamental in the presence of LCA, and how this effect compares to the defocusing effects of LCA.

Methods

This analysis consists of two parts: calculation of the modulation transfer function for the eye to determine the contrast of the retinal image with defocus from LCA, and calculation of M-cone contrast of the defocused retinal image when the peak sensitivity of the M-cone fundamental is varied. Because M-cone contrast varies with the plane of focus we calculated M-cone contrast when the eye is focused to maximize luminance contrast for the different M-cone spectra and for when the eye is focused at 555 nm, the peak of the V(λ) function for the normal M-cone pigment.

Calculation of the modulation transfer function

The modulation transfer function for the diffraction limited eye was calculated (Equation 1 in Appendix) using a model originally described by Hopkins (1955) and Smith (1982) (the program was written by L.R. Stark). This model describes the ability of an optical system to transfer object contrast to the image, and has been previously applied to the human eye by Flitcroft (1989; 1990; 1999). Calculations are based on Emsley's reduced eye (Emsley, 1939) with a radius of curvature of 5.55 mm and a focal length of the eye of 22.4967 mm. Using a square pupil approximation this model provides a theoretical modulation transfer function that can be used to predict the modulation of the retinal image when the image is blurred by the effects of longitudinal chromatic aberration or with lenses. For all calculations a 3 mm pupil was selected because at 3 mm monochromatic aberrations are minimal (Liang & Williams, 1997; Walsh & Charman, 1985) and the deleterious effects of diffraction are minimized relative to the deleterious effects of aberrations (Campbell & Green, 1965; Campbell & Gubisch, 1966; Donnelly & Roorda, 2003). In this analysis the defocus caused by longitudinal chromatic aberration (from the wavelength specified as the focal plane) was calculated using Thibos’ chromatic eye model (Thibos, Ye, Zhang & Bradley, 1992).

The modulation transfer function was calculated as a function of wavelength over the visible spectrum (20 nm intervals from 400 nm to 700 nm) as shown in Figure 1. This calculation was repeated for a range of spatial frequencies (60, 30, 15, 10, 3 and 1 c/d), and with different focal planes (650, 600, 580, 560, 555, 550, 545, 540, 535, 530, 525, 420 nm). Regression curves were fitted to the data for each spatial frequency at each focal plane. Up to 10 c/d the calculated values were fitted with a third-order polynomial regression curve, and the modulation transfer function, at 2 nm intervals, was predicted from these curves. Beyond 10 c/d the values were fitted with higher order polynomials (Matlab). Values for long- and short-wavelength extremes were removed to maintain an r value > 0.95.

Figure 1.

The modulation transfer function (MTF) was calculated as a function of defocus for a range of wavelengths (20 nm intervals from 400 nm to 700 nm) by taking into account the defocusing effects of longitudinal chromatic aberration for a 3 mm pupil. This calculation was repeated for a range of spatial frequencies (60 , 30 , 15, 10, 3 and 1 c/d) and with different focal planes (650, 600, 580, 560, 555, 550, 545, 540, 535, 530, 525, 420 nm). MTF functions are shown for focal planes at 420, 525, 530, 545, 560, 600 nm. Negative values of M-cone modulation indicate spurious resolution.

Calculation of retinal image contrast

We calculated the maximum and minimum radiance (2 nm intervals) of an imaginary stimulus of 100% contrast illuminated with the radiance spectrum of the sun. Other natural radiance spectra could have been used, but Lewis and Zhaoping, (2006) have shown that for color vision there is little variation in the optimal values of the peak of the spectral function with different natural illuminants. In addition, we could have used other data to estimate reflectances in natural scenes, but again, Lewis and Zhaoping, (2006) find that using different reflectance spectra has only a very small affect on the amount of color information available to the visual system when the M-cone fundamental is moved to shorter wavelengths. Of course different spectra would provide different amounts of light to the respective cone types and as such may affect image quality and spatial resolution.

After calculating the maximum and minimum radiance of the imaginary stimulus, we then calculated the contrast of the retinal image b(λ) over the visible spectrum after the effects of LCA. To do this the contrast c(λ) of the imaginary stimulus (100%) was multiplied by the modulation transfer function over the visible spectrum MTF(λ).

Calculation of retinal radiance

Then, to calculate the amplitude of the radiance modulation on the retina ΔB(λ), retinal contrast b(λ) was multiplied by the mean radiance B₀(λ) of the stimulus (assuming 100% reflectance) as shown in Equation 2 (Appendix). This calculation was repeated for each spatial frequency (60, 30, 15, 10, 3 and 1 c/d), at each focal plane (650, 600, 580, 560, 555, 550, 545, 540, 535, 530, 525, 420 nm).

Next we calculated the maximum and minimum radiance of the retinal image as a function of wavelength (λ). To do this the amplitude of the modulation at each wavelength, ΔB, was added or subtracted from the mean radiance values B₀(λ) (Equation 3 in Appendix). This calculation produces two intensity spectrums that include the effects of blur from LCA, one that corresponds to the maximum radiance (B_max) of the retinal image and one that corresponds to the minimum radiance (B_min).

Calculation of M-cone fundamentals

We then created M-cone extinction spectrums with peaks at 560, 550, 540, 530, 520, 500, 490, 480, 470, and 460 nm using Lamb Functions (Lamb, 1995) for calculating abscissa transformations from the average spectrum. The extinction spectrum is the pigment absorption spectrum without the effects of the ocular media and density of the cone pigments. Equal energy extinction spectrums were then converted to log quantal energy spectrums by first dividing by λ/700. The effects of the lens and macular pigments are incorporated into a spectrum that is given more weight at the short end of the spectrum where the pigments have the most effect. This allows for the higher energy of short-wavelength light.

Next we needed to estimate the fraction of the incident light available to the cone photopigments at the retinal level. To do this the log absorption of the ocular media was added to the log quantal extinction spectrum. We used lens absorption data (Pokorny, Smith & Lutze, 1987) for a 32 year-old with a small entrance pupil, and macular pigment absorption data from Wyszecki & Stiles, (1982). Values for macular pigment density and lens density were fixed for all transformations. To recreate M-cone fundamentals, antilog values were calculated, the function was then converted back into an equal energy spectrum (by multiplying the modified quantal energy spectrum by λ/700), and normalized to its peak. Figure 2 shows some of the shifted M-cone fundamentals in relation to the fixed L- and S-cone fundamentals.

Figure 2.

L- and S-cone fundamentals were fixed while the M-cone extinction function was shifted over a range of values (460 to 560 nm). The absorption of short-wavelength light by macular and lens pigments was incorporated to produce M-cone fundamentals with different peak sensitivities.

Calculation of cone excitation and cone contrast

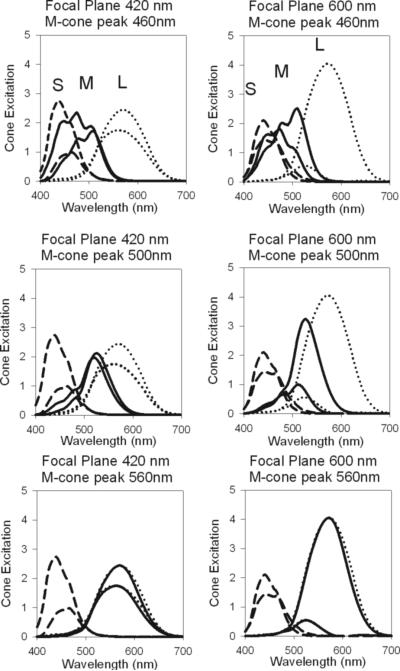
To calculate the cone excitation, produced by the radiance spectrum mentioned above, we used the formula described by Equation 4 (in Appendix). Cone excitation levels for both the maximum and minimum radiance spectra were calculated from the derived M-cone fundamental and the L- and S-cone fundamentals (Smith & Pokorny, 1975) (Equation 5 in Appendix). Cone excitation values were integrated over the 2 nm intervals between radiance spectrum data points. Figure 3 shows the maximum and minimum cone excitation levels as a function of wavelength for when the focal plane is at either 420 nm or 600 nm, when the peak of the extinction function was at 460, 500, or 560 nm.

Figure 3.

The maximum and minimum cone excitation for L- (dotted line), M- (solid line), and S-cones (dashed line), for an imaginary 10 c/d sine wave stimulus with 100% contrast when the focal plane is either at 420 nm (left) or 600 nm (right), and the peak of the M-cone extinction spectrum is at 460 nm (top), 500 nm (middle) or 560 nm (bottom), and the effects of LCA have been taken into consideration. L- and M-cone contrast increases when the focal plane is at 600 nm and decreases at 420 nm. S-cone contrast increases when the focal plane is at 420 nm. As the M-cone peak is shifted towards longer wavelengths (top to bottom) until it is aligned with the L-cone, the cone excitation spectrum follows.

Finally, L-, M-, and S-cone contrast was calculated (Equation 6 in Appendix) using the formula for Michelson contrast for each of the spatial frequencies (1, 3, 6, 10, 15, 30, and 60 c/d) at each focal plane (420, 525, 530, 535, 545, 550, 555, and 620 nm). This procedure was repeated for each of the fundamentals derived from the shifted M-cone extinction functions (460−560 nm).

Calculation of the focal plane of maximal luminance contrast

Next we calculated which focal plane would give maximal luminance contrast when the peak of the M-cone fundamental was shifted. To achieve this, the peak of the combined L- and M-cone fundamentals was calculated for each of the shifted M-cone fundamentals, for a range of different L:M-cone ratios (8, 2, 1.62, 1.23, 0.94). The peak of the combined function was assumed to be the point of maximal luminance contrast. There is a wide variation among subjects in the ratio of L:M cones in the retina (Carroll, McMahon, Neitz & Neitz, 2000; Hagstrom, Neitz & Neitz, 1998; Kremers, Scholl, Knau, Berendschot, Usui & Sharpe, 2000; Roorda & Williams, 1999; Wesner, Pokorny, Shevell & Smith, 1991) and the peak of the V(λ) function changes over a wide range of wavelengths as the ratio changes. A ratio of 1.62:1 is the value used by Smith & Pokorny (1975) in fitting the cone primaries to the V(λ) function and this value of ratio was used to compare the effect on cone contrast of shifting the peak of the M-cone fundamental. The ratio of 1.62:1 is typically considered an average value. As the ratio gets larger, the weighting of the L-cone increases, and the peak of the combined function will be biased towards 560 nm, towards the peak of the L-cone spectrum. An increase in the L:M-cone ratio shifts the focal plane that maximizes luminance contrast towards longer wavelengths; over a range of 15 nm when the cone weighting is changed from 0.94:1 to 8:1 for the normal M-cone pigment (peak of the extinction spectrum at 530 nm).

Calculation of chromatic contrast

To quantify chromatic noise, red/green and blue/yellow chromatic contrast was calculated across the black/white edge of the retinal image. The red/green chromatic signal was calculated as the difference in L- and M-cone excitation (with an L:M-cone ratio of 1:1) in the peak and in the trough of the grating. The blue/yellow chromatic signal was calculated as the difference in S- and L-+M-cone excitation (with an L:M-cone ratio of 1:1). Chromatic contrast across the black/white edge was then calculated using the formula for Michelson contrast. Since a region with higher L-cone excitation will be positive and a region with higher M-cone excitation will be negative, values of Michelson contrast will be greater than one for chromatic contrast if there is more L-cone excitation than M-cone excitation in the peak and more M-cone excitation than L-cone excitation in the trough of the grating or vice versa. A value less than one implies that the L- or M-cone excitation was greater in both the peak and the trough of the grating.

Assumptions

In this analysis it is assumed that there is foveal viewing of an object on the optical axis of the system. As such there will be no transverse chromatic aberration arising from the stimulus, but transverse chromatic aberration can arise from the optics of the eye since the optical axis is about 5 deg from the visual axis; this can be even greater if the pupil is decentered. Nevertheless, transverse chromatic aberration at the fovea is typically less than 1 min arc (Kruger, Mathews, Aggarwala & Sanchez, 1993; Ogboso & Bedell, 1987; Simonet & Campbell, 1990). These small values of transverse chromatic aberration are unlikely to cause deterioration of the retinal image.

The effects of the retinal cone mosaic are not taken into account in this study. The cone aperture size and density will affect the efficiency with which the observer detects the stimulus, and the arrangement of the cones will affect the ability to resolve higher spatial frequencies. S-cones have a much lower density than L- and M-cones and no allowance is made for this factor as only the effect of moving the M-cone fundamental is considered in this manuscript.

It is assumed that all visual stimuli can be broken down into a series of sine-wave gratings (Fourier transformation) with different spatial frequencies, phase, and orientation. It is assumed that if the effect of the visual system on each component is known, then the effect of the visual system on the complete image can be found by reconstructing the retinal image, by summing the effects on the individual components (inverse Fourier transform).

Results and Discussion

The effect on M-cone excitation of changing the focal plane

Cone excitation is maximal when the focal plane corresponds to the peak of the cone sensitivity spectrum. Figure 3 shows the maximum and minimum cone excitation for a 10 c/d sine-wave grating for L-, M-, and S-cones when the eye is focused at 420 or 600 nm and the peak of the M-cone extinction spectrum is at 420, 555, or 650 nm. It is clear that when the focal plane changes from 420 nm to 600 nm there is a corresponding increase in maximum cone excitation for L-cones and M-cones and a decrease in cone excitation for S-cones.

The effect on M-cone contrast of changing the focal plane

When the focal plane is at long-wavelengths contrast is maximal for L-cones, and when the focal plane is at short-wavelengths contrast is maximal for S-cones. Table 1 shows the cone contrast for L-, M- and S-cones when the eye is focused at 460, 500, or 560 nm (for the normal M-cone pigment). As would be expected, cone contrast is higher for S-cones when the plane of focus is at 420 nm (3 c/d: S-cones: 0.93; L-cones: 0.67 modulation) and higher for L-cones when the plane of focus is at 650 nm (3 c/d: S-cones: 0.63; L-cones: 0.97 modulation). The relative change in cone contrast between cone types with focus is the basis of the signal that underlies the chromatic cue for reflex accommodation (Rucker & Kruger, 2004).

Table 1.

Cone contrast for L-,M-, and S-cones when the eye is focused at 420 nm, 555 nm, and 650 nm. These cone contrasts are for the normal M-cone function with a peak of the extinction function at 530 nm.

Focus at 420 nm		1c/d	3c/d	6c/d	10c/d	15c/d	30c/d	60c/d
	L	0.96	0.67	0.11	−0.11	0.06	0.00	0.00
	M	0.96	0.72	0.20	−0.09	0.03	0.01	0.00
	S	0.99	0.93	0.76	0.45	0.38	0.19	0.17
Focus at 555 nm		1c/d	3c/d	6c/d	10c/d	15c/d	30c/d	60c/d
	L	1.00	0.99	0.94	0.86	0.75	0.44	0.21
	M	1.00	0.99	0.94	0.88	0.78	0.50	0.27
	S	0.98	0.82	0.48	0.08	−0.03	−0.01	0.02
Focus at 650 nm		1c/d	3c/d	6c/d	10c/d	15c/d	30c/d	60c/d
	L	1.00	0.97	0.82	0.61	0.40	0.18	0.06
	M	0.99	0.94	0.76	0.47	0.21	0.05	0.02
	S	0.95	0.63	0.15	−0.06	0.01	0.00	0.00

Figure 4A shows the effect of LCA on M-cone contrast for the M-cone fundamental at different focal planes. In this case, M-cone contrast in the retinal image is greatest when the focal plane lies between 555 nm and 535 nm. Accommodating to longer or shorter wavelengths decreases M-cone contrast, which for spatial frequencies of 10 c/d and above ultimately results in spurious resolution (negative modulation values) when the focal plane is at 460 nm. When the focal plane is at 650 nm there is a complete loss of M-cone contrast for spatial frequencies higher than 20 c/d.

Figure 4.

A) The effect on M-cone modulation of changing the focal plane, as a function of spatial frequency, when the eye is affected by LCA. M-cone contrast is only shown for the normal M-cone pigment (M-cone extinction spectrum with a peak at 530 nm). M-cone contrast depends critically on the plane of focus, being maximal at focal planes that lie close to the peak of the M-cone extinction spectrum. B) The effect on M-cone contrast of shifting the peak of the M-cone extinction spectrum, as a function of spatial frequency, when the eye is affected by LCA, and focused to maximize luminance contrast. M-cone modulation is maximal for the normal M-cone pigment (peak at 530 nm).

The effect on M-cone contrast of changing the peak of the M-cone extinction function

If we now vary the M-cone peak and adjust the focal plane to maximize luminance contrast (as described in the Methods) then we can see (Figure 4B) that the effect of a shift in the peak of the M-cone extinction spectrum is smaller than that caused by accommodation to long or short wavelengths. If the eye is focused to maximize luminance contrast (using the focal plane that corresponds to an L:M cone ratio of 1.62) there is a decrease in M-cone contrast when the peak of the M-cone extinction spectrum is shifted towards shorter wavelengths or longer wavelengths. As shown in Figure 4B there is a 28% decrease in M-cone contrast when the peak is shifted from 540 nm to 460 nm at 10 c/d. However, at 10 c/d for peak locations between 520 nm and 560 nm the change in M-cone contrast was only 3-4%. The decrease in M-cone contrast with a shift in the fundamental towards shorter wavelengths is mainly due to the blur induced by LCA.

It might be anticipated that the optimal peak location for maximum cone contrast would be for a single pigment as would be the case when the peak of the extinction function is at 560 nm, but it appears that there is an advantage to having a small separation, despite the blur from LCA that this will incur. For the highest spatial frequencies maximum M-cone contrast is found when the peak of the extinction function is located at 530 nm, as found in the normal M-cone pigment (DeMarco et al., 1992). The decrease in the M-cone contrast when the peak of the extinction spectrum is shifted towards longer or shorter wavelengths suggests that the normal spectral separation of L- and M-cones may optimize image quality for the highest spatial frequencies, though this prediction is limited by the accuracy of the fit.

Comparison of how the defocusing effects of LCA compare to the change in M-cone contrast caused by varying the M-cone peak sensitivity

Although the spectral separation of the L- and M-cones is potentially a factor limiting image quality, the decrease in M-cone contrast due to the shift in the peak of the M-cone spectrum is much smaller than the decrease in M-cone contrast with a change in the focal plane. When the eye is focused optimally for a particular spectrum moving the peak of the spectrum over 80 nm reduces contrast by a maximum of 50%, while the effects of focusing at different planes can reduce M-cone contrast by 100%.

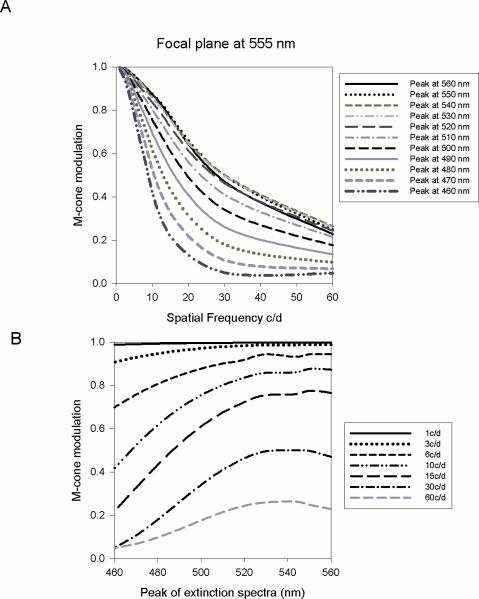
If the focal plane is at 555 nm, at the peak of the average V(λ) function, then the effects of a shift in the peak of the M-cone extinction spectrum are much more pronounced (Figure 5). At 10 c/d there is a drop in M-cone modulation from 0.87 to 0.41 as the peak of the M-cone extinction spectrum is shifted from 560 nm to 460 nm. At 30 c/d the effect on cone contrast is even more pronounced with a drop in M-cone modulation from 0.47 to 0.05 over the same range of M-cone spectrum. The maximum M-cone contrast is found close to 555 nm (Figure 5B) close to the focal plane.

Figure 5.

A) Change in M-cone contrast as a function of spatial frequency with the focal plane at 555 nm. A shift in the peak of the extinction spectrum has a marked effect on M-cone contrast at spatial frequencies above 10 c/d when the focal plane is fixed at 555 nm. B) Change in M-cone contrast as a function of the peak of the extinction spectrum. Maximum contrast is found close to the focal plane at 555 nm.

The relationship between M-cone contrast, the focal plane, and the peak of the M-cone extinction function

Although this may seem obvious it should be noted that the M-cone spectrum that corresponds to maximal M-cone contrast corresponds closely to the focal plane (Figure 6). When the focal plane is at 555 nm maximum contrast is found when the peak of the M-cone extinction spectrum is around 550 to 560 nm, but when the focal plane is at 525 nm or 535 nm, maximum M-cone contrast is found close to M-cone extinction spectrums with peaks around 530 nm and 510 nm. Thus, there may be some visual benefit in the peak of the cone spectrum corresponding to the plane of habitual focus.

Figure 6.

Change in M-cone contrast as a function of the shift in the peak of the M-cone extinction spectrum for focal planes 555 nm, 535 nm, and 525 nm. These graphs emphasize the point that M-cone contrast is maximal when the focal plane corresponds to the peak of the extinction spectrum.

The relationship between M-cone contrast and spatial frequency

It can be seen that M-cone contrast varies with spatial frequency as would be predicted (Figure 6). With low spatial frequencies (3 c/d) there is only a small (1%) change in M-cone contrast, per 10 nm shift in the peak of the M-cone extinction spectrum, when the peak of the M-cone extinction spectrum is shifted below 520 nm (with a focal plane of 555 nm). Not surprisingly, the effect is greater for higher spatial frequencies. For a 15 c/d or 30 c/d grating there is a 7% change in M-cone contrast, per 10 nm shift in the peak of the M-cone extinction spectrum, when the peak of the M-cone extinction spectrum is shifted below 530 nm.

Chromatic noise as a limiter of spectral separation

In the Introduction one of the explanations proposed to account for the relatively small separation of primate L- and M-cones was that having widely separated L-cone and M-cone receptors is deleterious for spatial vision, because luminance signals are corrupted by chromatic noise (Osorio et al., 1998; Williams et al., 1993). The effect of shifting the peak of the M-cone extinction spectrum on red/green chromatic contrast can be seen in Figure 7.

Figure 7.

Luminance and chromatic contrast for a 3 c/d sine wave grating change with the focal plane and with the peak of the M-cone extinction spectrum. When the focal plane is at 555 nm there is a small decrease in luminance contrast with increased separation of the cones (M-cone peak shifted to 460 nm), but little change in red/green chromatic contrast. When the focal plane is at 650 nm there is a greater decrease in luminance contrast with separation of the M-cone and L-cones, while chromatic contrast increases. When the focal plane is at 420 nm, luminance contrast increases with M- and L-cone separation, while red/green chromatic contrast decreases. Blue/yellow chromatic contrast changes in much the same way as the change in luminance contrast.

Luminance contrast, calculated from the weighted sum of L- and M-cone excitation, depends on the spectral separation of the cones and on the focal plane. As might be expected, when the focal plane is at 555 nm luminance contrast is close to 100% for all cone separations, neither the L- nor M-cone peak is far from the plane of focus. When the focal plane is at 650 nm, luminance contrast decreases with increased cone separation as the M-cone peak moves towards 460 nm, in line with the decrease in M-cone contrast arising from LCA. For example, luminance contrast of a 3 c/d grating is reduced to 0.89 for an M-cone peak at 460 nm, compared to 0.97 for an M-cone peak at 560 nm. However, when the plane of focus is at 420 nm, luminance contrast increases slightly for greater spectral separation. Modulation increases from 0.68 when the M-cone peak is at 560 nm to 0.74 when the M-cone peak is at 460 nm. This increase in luminance contrast can be explained by the improvement in focus for the M-cone at short-wavelengths.

Red/green chromatic contrast also depends on the spectral separation of the cones and on the focal plane, while blue/yellow chromatic contrast changes in much the same way as luminance contrast. When the focal plane is at 555 nm red/green modulation is around 1.00 for all separations; since both cone types are focused equally well there is very little color contrast in the retinal image of the grating. When the focal plane is at 650 nm, red/green chromatic contrast ( L-M) of a 3 c/d grating increases with increased separation of the L- and M-cones, as the peak of the M-cone extinction function is moved towards 460 nm. For example, modulation increases from 0.95 for a peak at 560 nm to 1.6 for an M-cone peak at 460 nm. This is easily explained since the retinal image will be more blurred for M-cones at shorter wavelengths, increasing the difference in cone excitation between M-cones and L-cones. When the focal plane is at 420 nm, chromatic contrast decreases with an increase in spectral separation as the retinal image for M-cones becomes more in focus. Chromatic contrast decreases from 0.64 when the M-cone peak is at 560 nm to 0.04 when the M-cone peak is at 460 nm.

This analysis demonstrates that while there are only very small changes in luminance and chromatic contrast with increased cone separation when the focal plane is at 555 nm, focus at other focal planes causes larger antagonistic changes in both components. While luminance contrast decreases with increased separation at a focal plane of 600 nm, chromatic contrast increases. While luminance contrast increases slightly with increased cone separation at a focal plane of 420 nm, chromatic contrast decreases. Chromatic noise would therefore only limit cone separation when the eye is focused away from the plane that maximizes luminance contrast.

Depth of focus as a limiter of spectral separation

Another explanation that was proposed to account for the relatively small separation of the L- and M-cones was the hypothesis described by Kröger (2000). Kröger (2000) suggested that LCA may have limited visual pigment evolution, and that the separation between the wavelengths of maximal absorbance of the average L- (558 nm) and M-cone (530 nm) pigments was limited by the 0.3 D depth of focus of the human eye. This analysis agrees with the hypothesis that the effects of LCA reduce the cone contrast of the retinal image, and as such may limit the separation of the L- and M-cones. However, chromatic blur from LCA, between the two cone types specified above, is equivalent to only 0.19 D when calculated with the chromatic eye (Thibos et al., 1992), and verified with recent measurements of LCA (Marcos, Burns, Moreno-Barriusop & Navarro, 1999). In fact the separation of the L- and M-cones could be increased beyond 520 nm before the chromatic defocus from LCA is greater than the depth of focus of the eye of 0.3 D with a 4 mm pupil (Marcos, Moreno & Navarro, 1999).

Deterioration in spatial contrast as a limiter of spectral separation

Another question we can ask with regard to the question of whether LCA may have affected visual pigment evolution, is whether spatial vision with a 520 nm M-cone pigment would be detectably inferior to that with a 530 nm pigment if the focal plane is at 555 nm. This 10 nm shift would cause a more rapid decline in contrast (Figure 6) equal to an 8% reduction in modulation (from 0.50 to 0.46) for a 30 c/d grating (6/6 Snellen acuity), which is equivalent to the grating being blurred by 0.16 D. In other words the effect of shifting the peak of the M-cone spectrum towards shorter wavelengths is small, but is within detectable limits; the smallest lens power in an optometrist's lens trial case is a 0.12 D lens. However, the reduction of contrast will be smaller (from 0.52 to 0.50) if the eye strives to maximize luminance contrast for the specific cone sensitivity functions (Figure 2). Hence, the limiting effect of LCA on spectral separation depends on accuracy of the accommodation response.

The effect of a shift in the peak of the M-cone extinction function on reflex accommodation

Since the focal plane depends on accurate accommodation, the focal plane will depend on relative cone contrasts between L- and M-cones (Rucker & Kruger, 2004) as well as on luminance contrast. If M-cone contrast is reduced relative to L-cone contrast, the accommodation signal that is derived from the comparison between L- and M-cones will also be affected. It is therefore possible that the spectral location of the peak of the pigment absorption function, which ultimately affects cone contrast, could be a factor limiting not only image quality, but also the reflex accommodation response as proposed by Rucker & Kruger (2006).

Conclusion

When the focal plane maximizes luminance contrast M-cone contrast is maximized and a shift in the M-cone fundamental towards shorter or longer wavelengths causes a small but noticeable reduction in contrast. This effect is, of course, most pronounced at high spatial frequencies. Therefore, relative to other sources of noise the presence of separate M- and L-cones incurs a small, but not insignificant cost via chromatic aberration. As this penalty increases with spectral separation, and different focusing demands, chromatic aberration may be a factor limiting the evolution of visual pigments and color vision that is roughly comparable to other effects on the luminance signal caused by having separate M- and L-cones (Osorio et al., 1998; Williams et al., 1993).

Appendix

$$M(v,D)=\frac{\sin \left[kD\left(1-\frac{s}{2}\right)\right]}{kD}k=\frac{fp}{b}.\frac{360v}{2n}s=\frac{\lambda vf}{2np}.\frac{360}{2\pi b}$$ (1)

Equation (1) calculates the modulation transfer function M(v,D) for a grating of spatial frequency (v) in cycles/degree with defocus (D) measured in diopters. The focal length of the eye (f), the distance from the second nodal point to the image plane (b) and the pupil diameter (p) are measured in meters. The refractive index of the ocular media is (n).

$$\begin{array}{ccc}\text{Michelson contrast (b) equals:}\hfill & \frac{B\max -B\min }{B\max +B\min }=b\hfill & \text{Where Bmax and}\hfill \\ \hfill & \hfill & \text{Bmin are the}\hfill \\ \hfill & \hfill & \text{maximum and}\hfill \\ \hfill & \hfill & \text{minimum}\hfill \\ \hfill & \hfill & \text{reflectances}\hfill \\ \text{While the mean reflectance of the stimulus equals:}\hfill & \frac{B\max +B\min }{2}=Bo\hfill & \text{where Bo is the mean}\hfill \\ \hfill & \hfill & \text{reflectance}\hfill \\ \text{By rearranging:}\hfill & (B\max +B\min )=2^{\ast }Bo\hfill & \hfill \\ \text{And by replacement Michelson contrast equals:}\hfill & \frac{B\max -B\min }{2^{\ast }Bo}=b\hfill & \hfill \\ \text{Rearrangement gives:}\hfill & \frac{(B\max -B\min )}{2}=b^{\ast }Bo\hfill & \hfill \\ \text{And the amplitude of the modulation is:}\hfill & \Delta B=b^{\ast }Bo\hfill & \hfill \end{array}$$ (2)

$$\begin{array}{cc}\hfill \text{B}\max \left(\lambda \right)& ={\text{B}}_0\left(\lambda \right)+\Delta \text{B}\lambda \hfill \\ \hfill \text{B}\min \left(\lambda \right)& ={\text{B}}_0\left(\lambda \right)-\Delta \text{B}\left(\lambda \right)\hfill \end{array}$$ (3)

B_max(λ) and B_min(λ) are the maximum and minimum reflectances of the stimulus for a particular wavelength. To calculate the maximum and minimum reflectance of the stimulus (after the effects of LCA have been taken into account) as a function of wavelength (λ) the amplitude of the modulation at each wavelength, ΔB, was added or subtracted from the mean reflectance values B₀(λ).

The quantum catch (Q) of a receptor (r) for a given stimulus is described by:

$$Qr={\int }_{400}^{700}Sr\left(\lambda \right)R\left(\lambda \right)d\lambda$$ (4)

where S(λ) denotes the spectral sensitivity of the receptor (r) as described by the cone fundamental, at wavelength (λ) from 400 to 700 nm, and R(λ) denotes the reflectance spectrum as described by the maximum (B_max) and minimum (B_min) radiance spectra of the imaginary stimulus.

$$\begin{array}{cc}{\text{L}}_{\text{excit}}\left(\max \right)=\sum \left({\text{B}}_{\max }{\left(\lambda \right)}^{\ast }{\text{L}}_{\text{fund}}\left(\lambda \right)\right)\hfill & {\text{L}}_{\text{excit}}\left(\min \right)=\sum \left({\text{B}}_{\min }{\left(\lambda \right)}^{\ast }{\text{L}}_{\text{fund}}\left(\lambda \right)\right)\hfill \\ {\text{M}}_{\text{excit}}\left(\max \right)=\sum \left({\text{B}}_{\max }{\left(\lambda \right)}^{\ast }{\text{M}}_{\text{fund}}\left(\lambda \right)\right)\hfill & {\text{M}}_{\text{excit}}\left(\min \right)=\sum \left({\text{B}}_{\min }{\left(\lambda \right)}^{\ast }{\text{M}}_{\text{fund}}\left(\lambda \right)\right)\hfill \\ {\text{S}}_{\text{excit}}\left(\max \right)=\sum \left({\text{B}}_{\max }{\left(\lambda \right)}^{\ast }{\text{S}}_{\text{fund}}\left(\lambda \right)\right)\hfill & {\text{S}}_{\text{excit}}\left(\min \right)=\sum \left({\text{B}}_{\min }{\left(\lambda \right)}^{\ast }{\text{S}}_{\text{fund}}\left(\lambda \right)\right)\hfill \end{array}$$ (5)

Cone excitation levels (L_excit, M_excit, S_excit) for both the maximum (B_max) and minimum (B_min) radiance spectra were calculated from the derived M-cone fundamental and the L- and S-cone fundamentals (L_fund, M_fund, S_fund)

$$\begin{array}{cc}\hfill {\text{L}}_{\mathrm{mod}}& =({\text{L}}_{\text{excit}}\left(\max \right)-{\text{L}}_{\text{excit}}\left(\min \right))∕({\text{L}}_{\text{excit}}\left(\max \right)+{\text{L}}_{\text{excit}}\left(\min \right))\hfill \\ \hfill {\text{M}}_{\mathrm{mod}}& =({\text{M}}_{\text{excit}}\left(\max \right)-{\text{M}}_{\text{excit}}\left(\min \right))∕({\text{M}}_{\text{excit}}\left(\max \right)+{\text{M}}_{\text{excit}}\left(\min \right))\hfill \\ \hfill {\text{S}}_{\mathrm{mod}}& =({\text{S}}_{\text{excit}}\left(\max \right)-{\text{S}}_{\text{excit}}\left(\min \right))∕({\text{S}}_{\text{excit}}\left(\max \right)+{\text{S}}_{\text{excit}}\left(\min \right))\hfill \end{array}$$ (6)

L-, M-, and S-cone contrast was calculated (L_mod, M_mod, S_mod) using the formula for Michelson Contrast for each of the spatial frequencies.