Design and Control of a Powered Transfemoral Prosthesis

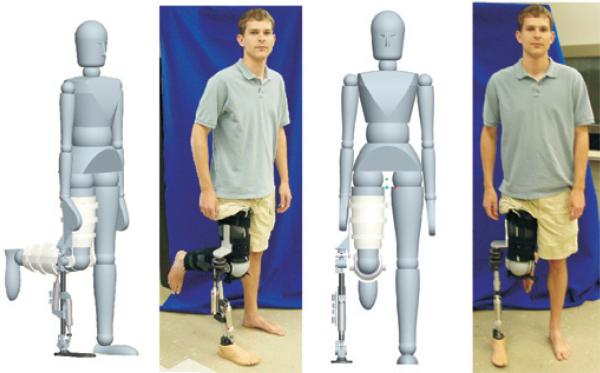
Abstract

The paper describes the design and control of a transfemoral prosthesis with powered knee and ankle joints. The initial prototype is a pneumatically actuated powered-tethered device, which is intended to serve as a laboratory test bed for a subsequent self-powered version. The prosthesis design is described, including its kinematic optimization and the design of a three-axis socket load cell that measures the forces and moments of interaction between the socket and prosthesis. A gait controller is proposed based on the use of passive impedance functions that coordinates the motion of the prosthesis with the user during level walking. The control approach is implemented on the prosthesis prototype and experimental results are shown that demonstrate the promise of the active prosthesis and control approach in restoring fully powered level walking to the user.

1. Introduction

1.1. Motivation

Despite significant technological advances over the past decade, such as the introduction of microcomputer-modulated damping during swing, commercial transfemoral prostheses remain limited to energetically passive devices. That is, the joints of the prostheses can either store or dissipate energy, but cannot provide net power over a gait cycle. The inability to deliver joint power significantly impairs the ability of these prostheses to restore many locomotive functions, including walking up stairs and up slopes, running, and jumping, all of which require significant net positive power at the knee joint, ankle joint or both (Winter and Sienko 1988; DeVita et al. 1996; Jacobs et al. 1996; Prilutsky et al. 1996; Nagano et al. 1998; Riener et al. 1999; Nadeau et al. 2003). Furthermore, although less obvious, even biomechanically normal walking requires positive power output at the knee joint and significant net positive power output at the ankle joint (Winter 1991). Transfemoral amputees walking with passive prostheses have been shown to expend up to 60% more metabolic energy relative to healthy subjects during level walking (Waters et al. 1976) and exert as much as three times the affected-side hip power and torque (Winter 1991), presumably due to the absence of powered joints. A prosthesis with the capacity to deliver power at the knee and ankle joints would presumably address these deficiencies, and would additionally enable the restoration of biomechanically normal locomotion. Such a prosthesis, however, would require: (i) power generation capabilities comparable to an actual limb; and (ii) a control framework for generating required joint torques for locomotion while ensuring stable and coordinated interaction with the user and the environment. This paper describes the authors’ progress to date in pursuing both of these goals. Specifically: Section 2 presents the current prosthesis prototype design and discusses the means by which the authors intend to convert this to a self-powered version Section 3 describes the control approach; and Section 4 presents experimental results that demonstrate the hardware and control approach.

1.2. Background

Though the authors are not aware of any prior work on the development of a powered knee and ankle prosthesis, prior work does exist on the development of powered knee transfemoral prostheses and powered ankle transtibial prostheses. Regarding the former, Flowers (1973), Donath (1974), Flowers and Mann (1977), Grimes et al. (1977), Grimes (1979), Stein (1983) and Stein and Flowers (1988) developed a tethered electrohydraulic transfemoral prosthesis that consisted of a hydraulically actuated knee joint tethered to a hydraulic power source and off-board electronics and computation. They subsequently developed an “echo control” scheme for gait control, as described by Grimes et al. (1977), in which a modified knee trajectory from the sound leg is played back on the contralateral side. Popovic and Schwirtlich (1988) reported on the development of a battery-powered active knee joint actuated by DC motors, together with a finite-state knee controller that utilizes a robust position tracking control algorithm for gait control (Popovic et. al. 1995). With regard to powered ankle joints, Klute et al. (1998, 2000) describe the design of an active ankle joint using pneumatic McKibben actuators, although gait control algorithms were not described. Au et al. (2005) assessed the feasibility of an electromyography (EMG)-based position control approach for a transtibial prosthesis. Finally, although no published literature exists, Ossur, a major prosthetics company based in Iceland, has announced the development of both a powered knee and a self-adjusting ankle. The ankle prosthesis, called the “Proprio Foot”, is not a true powered ankle, because it does not contribute power to gait, but rather is used to quasistatically adjust the angle of the ankle to better accommodate sitting and slopes. The powered knee, called the “Power Knee”, utilizes an echo-type control approach that utilizes sensors on the sound-side leg.

Unlike any prior work, this paper describes a prosthesis design that consists of both a powered knee and ankle, and describes a method of control that enables natural, stable interaction between the user and the powered prosthesis. The control approach is implemented on the prosthesis prototype fit to a user, and experimentally shown to provide powered level walking representative of normal gait.

2. Prosthesis Design

One of the most significant challenges in the development of a powered lower-limb prosthesis is providing self-powered actuation capabilities comparable to biological systems. State-of-the-art power supply and actuation technology such as battery/DC motor combinations suffer from low-energy density of the power source (i.e. heavy batteries for a given amount of energy), low actuator force/torque density and low actuator power density (i.e. heavy motor/gearhead packages for a given amount of force or torque and power output), all relative to the human musculoskeletal system. Recent advances in power supply and actuation for self-powered robots, such as the liquid-fueled approaches described by Goldfarb et al. (2003), Shields et al. (2006), Fite and Goldfarb (2006) and Fite et al. (2006) offer the potential for improved energetic characteristics relative to battery/DC motor combinations, and thus bring the potential of a powered lower limb prosthesis to the near horizon. Specifically, the aforementioned publications describe pneumatic-type actuators, which are powered by the reaction products of a catalytically decomposed liquid monopropellant. The proposed approach has been experimentally shown to provide an order of magnitude greater actuation potential, an energetic figure of merit, than state-of-the-art batteries and motors (Fite and Goldfarb 2006; Shields et al. 2006). Rather than construct a self-powered version directly, the authors have developed a power-tethered version of the prosthesis, which enables laboratory-based controller development and prosthesis testing. The self-powered version should be nearly identical to the power-tethered version, but will include an on-board propellant cartridge and catalyst pack in place of the pneumatic tether. This section describes the design of the power-tethered pneumatically actuated prosthesis prototype.

2.1. Design Specifications

The active joint torque specifications for the prosthesis were based on the torque/angle phase space required for a 75 kg user for fast walking and stair climbing, as derived from body-mass-normalized data from Winter (1991) and Riener et al. (2002), respectively. Minimum range of motion was determined to be 110° of flexion for the knee, and 45° of planterflexion and 20° of dorsiflexion for the ankle. Based on these desired specifications, the joint actuators and their respective kinematic configurations were selected via a design optimization to minimize the actuator volume that would achieve the desired torque/angle phase space. Specifically, each joint was configured as a slider-crank, as shown in Figure 1. The geometric relationship between the actuator (linear) displacement and crank angle is given by the law of cosines:

$$x^2=L_1^2+L_2^2-2L_1{L}_2\cos \theta ,$$ (1)

where L₁ and L₂ are the two fixed-length segments of the slider-crank, θ is the angle between those segments and x is the actuator length. The actuator length in turn can vary between a fully contracted state, x_min = L₀, and a fully extended state, x_max = L + L₀, where L₀ is the cylinder length and L is the stroke length. The relationship between slider force and crank torque is obtained by the method of virtual work as

$$\tau =F\frac{dx}{d\theta }=\frac{F{L}_1{L}_2\sin \theta }{\sqrt{L_1^2+L_2^2-2L_1{L}_2\cos \theta }},$$ (2)

where τ is the joint torque (corresponding to the joint angle θ) and F is the force output from the pneumatic actuator, which is given by the product of the actuator diameter, D, and operating pressure, which in this case is 2 MPa (300 psig). The kinematic configuration of each joint is thus primarily a function of the variables L₁, L₂, L and D, which are obtained based on a multi-tiered design optimization, the primary objective of which was to minimize the actuator volume (note that L₀ is a function of L and D, as given by the manufacturer of the cylinder). Specifically, for a given actuator diameter and stroke length (which determine x_min and x_max), combinations of L₁ and L₂ were determined, based on (1), that provide the requisite range of motion. For each viable combination, the maximum torque envelope was computed. Solutions that could not provide a sufficient torque envelope were eliminated. The optimal solution was determined first as that with the minimum actuator volume second as that which minimized the angle between the peak actuator torque and the angle at which the peak biomechanical torque occurs during gait; and third as that which minimized the length L₁. Note that all three criteria were required, because multiple solutions existed for any subset of the criteria.

Fig. 1.

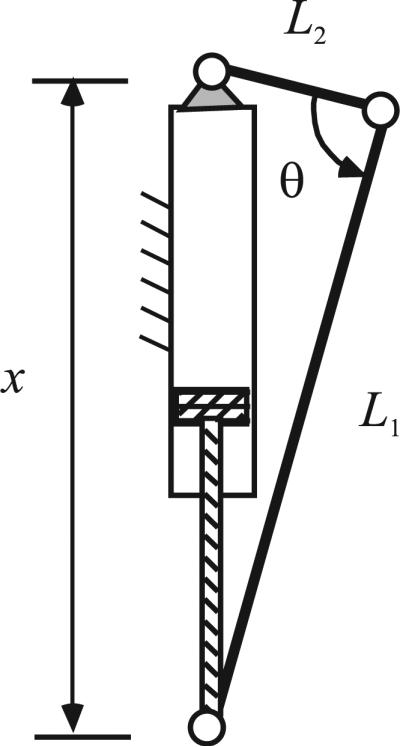
Slider-crank configuration with parameters L₁, L₂, x and θ. From Sup and Goldfarb (2006).

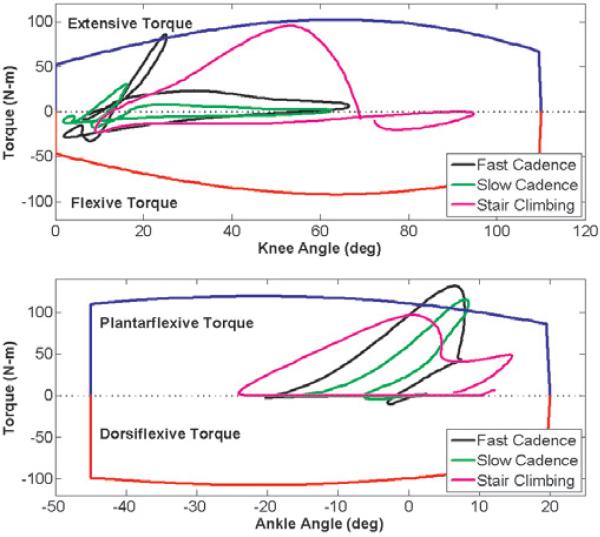
The joint specifications and ranges considered for L₁ and L₂ are given in Table 1, the actuator sizes considered are given in Table 2 and, finally, the optimized solution for each joint is given in Table 3. Note that the ankle actuator can supply only 76% of the torque required for fast walking by a 75 kg user. Although solutions did exist for the full ankle torque, these solutions placed the geometry envelope of the prototype outside of the typical human volumetric envelope. As such, it was decided to trade the peak torque capability of the ankle in order to limit the size of the ankle actuator and the L₁ dimension in order to stay within the volumetric envelope of the anthropomorphic norm and reduce overall weight of the device. Experimental trials with the device will determine whether or not this was a worthwhile design trade-off. The maximum torque envelope of the resulting knee and ankle actuator configurations are shown graphically in Figure 2, along with the data for a 75 kg normal human for slow and fast cadence and stair climbing (Winter 1991; Riener et al. 2002).

Table 1.

Parameters Used for the Optimization of the Actuator Size and Configuration

Parameter	Knee actuator	Ankle actuator
Peak kinematic torque required	86 Nm	130 Nm
Angle at peak kinematic torque	25°	10°
Minimum range of motion	110°	65°
Range of L1	0.001–3.16 cm	0.001–3.16 cm
Range of L2	0.001–30 cm	0.001–30 cm

Table 2.

Actuator Parameters Considered in the Optimization

Actuator diameters	7/8", 17/16", 1.25", 1.5", 1.75", 2"
Actuator stroke length	0.25"–6"
Maximum operating pressure	2 MPa (300 psig)

Table 3.

Results of the Parameter Optimization of Actuator Size and Configuration

Parameter	Knee actuator	Ankle actuator
L1	4.3 cm	5.1 cm
L2	28.8 cm	26.3 cm
Range of actuator motion	125°	87°
Actuator diameter	1.5”	1.5”
Actuator stroke	3”	2.75”
Peak actuator torque	102 Nm	119 Nm
Supplied actuator torque at angle of peak kinematic torque	86 Nm	100 Nm

Fig. 2.

Comparison of maximum torque capability of active joints to the torque requirement during various gaits for a 75 kg normal user, based on an operating pressure of 2 MPa (300 psig). Note that the envelope around the torque trajectories represents the maximum torque capability of the prosthesis.

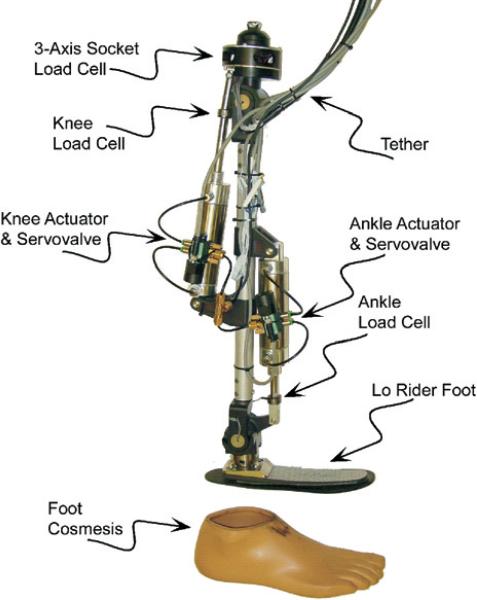
Figure 3 shows the resulting prosthesis prototype in a labeled photograph. Based on the previously mentioned design optimization, the prosthesis incorporates a 7.6 cm (3 in) stroke, 3.8 cm (1.5 in) bore double-acting pneumatic cylinder (Bimba model 17-3-DP), while the ankle joint incorporates a 7 cm (2.75 in) stroke, 3.8 cm (1.5 in) bore double-acting cylinder (Bimba model 17-2.75-DP). Operating at 2 MPa (300 psig), the actuators are capable of producing 2,270 N (510 lbf) of outward axial force and 2,070 N (465 lbf) on the return. Each actuator is controlled by means of a four-way servovalve (Enfield Technologies LS-V05). Sensors on the prosthesis include cylinder force sensors (which indirectly provide joint torque measurement), joint angle sensors and a custom three-axis socket load cell that measures the axial force, sagittal plane moment and frontal plane moment at the interface between the prosthesis and socket. The cylinder force sensors are uniaxial load cells (Honeywell Sensotec model 11) located in line with the actuator piston rods. The ankle and knee joint angles are measured with integrated joint motion sensors (ETI Systems model SP12S precision potentiometer), which are located inside the hollow axle and composite plain bearings (Garlock model DU) in each joint. The custom three-axis socket load cell, used for the measurement of the interaction forces and moments between the user and prosthesis, is described in the following.

Fig. 3.

The power-tethered prototype.

The structural components of the prosthesis were designed to withstand a 2,224 N (500 lbf) load and maximum actuator joint torques. Safe stress conditions were verified using ProE Mechanica finite-element analysis (FEA) software. The results of these analyses indicate that 7075-T6 aluminum, which has a minimum yield strength in excess of 500 MPa, provides a factor of safety between 1.7 and 3.7 for the various parts under the aforementioned design conditions.

The powered prosthesis was designed to fit a broad range of different sized persons, ranging from two standard deviations below the female norm in length, up to two standard deviations above the male norm in length based on data from Gordon et al. (1989). The tibial length is varied by changing the single structural (tibia) tube and the clamping supports for the actuators allow for adjustment to achieve the recommended spacing as dictated by the kinematic configuration optimization. The foot is a low-profile prosthetic foot (Otto Bock Lo Rider), with typical sizes available. In addition, the ankle joint and the three-axis socket load cell incorporate standard pyramid connectors for coupling the prosthesis to the feet and socket, thus enabling a high degree of adjustment in the knee and ankle alignment, as is standard in transfemoral prostheses. Combined with the Otto Bock Lo Rider foot, which weighs 0.37 kg (0.8 lbf), the total weight of the tethered transfemoral prosthesis with pyramid connectors is 2.65 kg (5.8 lbf), which is within the normal and acceptable range for transfemoral prostheses and less than a comparable normal limb segment (Clauser et al. 1969). An untethered version is expected to add an additional 0.9 kg (2 lbf) of weight, which maintains the prosthesis within an acceptable weight range.

2.2. Three-axis Socket Load Cell Design

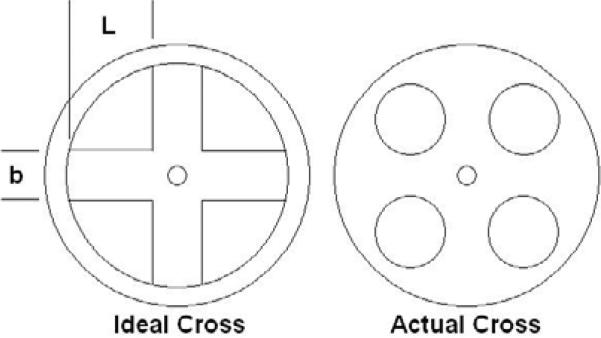
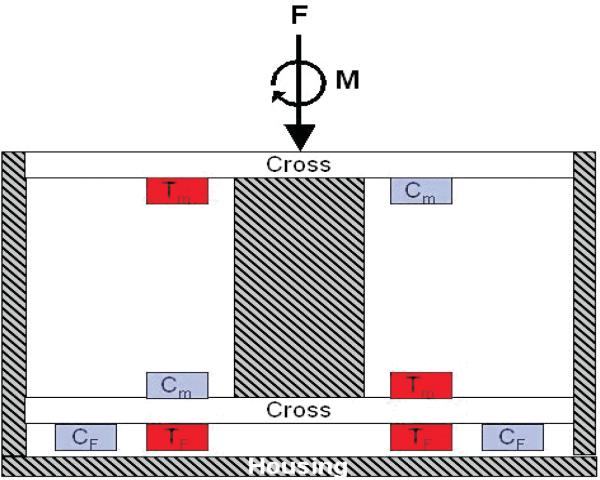
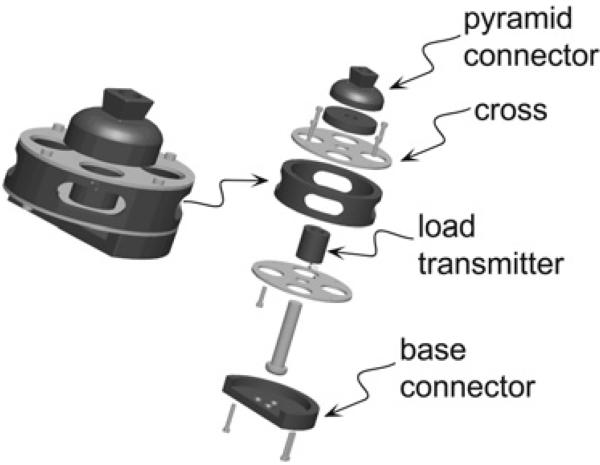
For purposes of prosthesis control and user intent recognition, the prosthesis incorporates a load cell between the prosthesis and user, which measures the interaction forces and moments. Based on the data presented in Winter (1991) and Riener et al. (2002), the required range of measurement for the load cell was determined to be 1000 N of axial force (i.e. along the socket) and 100 Nm of sagittal and frontal plane moments. Relative to commercially available multi-axis load cells (e.g. ATI and JR3), this combination of force and moment is disproportionately weighted toward the moment measurement, and thus would require load cells that are much larger than could be realistically implemented in a prosthetic leg. As such, a custom load cell was designed and fabricated. The basis of the load cell design is a crossed beam spring element, as shown in Figure 4. The design objective was thus to provide similar strain sensitivities for the axial load and moments (e.g. approximately 1,000 microstrain for metal foil gages) for the desired applied force and moment ranges. In order to achieve similar magnitudes, a double cross configuration was developed (as shown in Figure 5) in order to effectively separate, by means of a pair of connected crosses, the fundamental mechanisms by which the moment and axial forces are measured. The moment is counteracted by a force couple transmitted by a connecting rod, which loads the beams in tension and compression, while the force is counteracted by loading the beams in bending. The different mechanisms of loading allow the relative geometry of the pair to be manipulated to generate similar strain sensitivity to the desired force and moments. Based on appropriate analytical descriptions of strain, the double load cell was optimized for the smallest overall device size. The resulting strains were then verified with a ProE Mechanica FEA. The resulting design, which is shown in Figure 6, consists of two single crosses separated by a distance and rigidly held together by a housing on the outside and load transmitter in the center. The device was fabricated from a combination of stainless steel and aluminum using the actual cross design as depicted in Figure 4 and has a total mass of 360 g. The load cell was calibrated utilizing a least-squares method to obtain the transformation matrix between the vector of applied forces and moments and the vector of strain gage outputs, based on a fifth-order polynomial. Coupling between load cell axes produces a maximum error of 2.2% of full scale output (FSO) in the axial force measurement, a maximum error of 6.7% FSO in the sagittal moment measurement and a maximum error of 5.5% FSO in the frontal moment measurement.

Fig. 4.

Ideal versus actual beam patterns of the three-axis socket load cell. From Sup and Goldfarb (2006).

Fig. 5.

Regions of compression (C) and tension (T) in a sectional view of the double cross for an applied force, F, and moment, M, for the three-axis socket load cell. Subscripts denote loading responsible for the compression and tension. From Sup and Goldfarb (2006).

Fig. 6.

Assembled and exploded views of the three-axis socket load cell. From Sup and Goldfarb (2006).

3. Gait Control Strategy

The previously described prosthesis is a fully powered two degree-of-freedom robot, capable of significant joint torque and power, which is rigidly attached to a user. As such, the prosthesis requires a reliable control framework to generate the required joint torques while ensuring stable and coordinated interaction with the user and the environment.

The overarching approach in all prior work has been to generate a desired joint position trajectory, which, by its nature, utilizes the prosthesis as a position source. Such an approach poses several problems for the control of a powered transfemoral prosthesis. First, the desired position trajectories are typically computed based on a measurement of the sound-side leg trajectory, which (i) restricts the approach to unilateral amputees, (ii) requires instrumentation of the sound-side leg, and (iii) generally produces an even number of steps, which can present a problem when the user desires an odd number of steps. A subtler yet significant issue with position-based control is that suitable motion tracking requires a high-output impedance, which forces the amputee to react to the limb rather than interact with it. Specifically, in order for the prosthesis to dictate the joint trajectory, it must assume a high-output impedance (i.e. must be stiff), thus precluding any dynamic interaction with the user and the environment.

Unlike prior works, the approach proposed herein utilizes an impedance-based approach to generate joint torques. Such an approach enables the user to interact with the prosthesis by leveraging its dynamics in a manner similar to normal gait (Mochon and McMahon 1980) and also generates stable and predictable behavior. The essence of the approach is to characterize the knee and ankle behavior with a series of finite states consisting of passive spring and damper behaviors, wherein energy is delivered to the user by switching between appropriate equilibrium positions (of the virtual springs) in each finite state. In this manner, the prosthesis is guaranteed to be passive within each gait mode, and thus generates power simply by switching between modes. As the user initiates mode switching, the result is a predictable controller that, barring input from the user, will always default to passive behavior.

3.1. Impedance Characterization of Gait

Based loosely on the notion of impedance control proposed by Hogan (1985), the torque required at each joint during a single stride (i.e. a single period of gait) can be piecewise represented by a series of passive impedance functions. A regression analysis of gait data from Winter (1991) indicates that joint torques can be sufficiently characterized by functions of joint angle and velocity by the simple impedance model

$$\tau =k_1(\theta -{\theta }_{\mathrm{e}})+k_2{(\theta -{\theta }_{\mathrm{e}})}^3+b\stackrel{.}{\theta }.$$ (3)

Specifically, the joint torques within each gait mode can be described by the combination of linear and cubic stiffness terms, together with a linear damping term, where k₁ and k₂ characterize the linear and cubic stiffness, θ_e is the equilibrium angle, b is the linear damping coefficient, θ is the joint angle and τ is the joint torque, where the positive directions of the angle and torque are defined as in Figure 7. If the coefficients b, k₁ and k₂ are constrained to be positive, then the joint will exponentially converge to a stable equilibrium at θ = θ_e and θ = 0 within each gait mode. That is, within any given mode, the actuators are energetically passive (i.e. the joint will come to rest at a local equilibrium). As the unactuated prosthesis is energetically passive, the combined behavior is likewise passive, and thus will respond in a predictable manner. Note that power is delivered from the prosthesis to the user by switching between modes. As the switching is triggered by direct input from the user, the user maintains direct influence over the power generated by the prosthesis. If the user does not trigger the next mode, the prosthesis will cease to deliver power, and will instead come to rest at the local equilibrium identified with the present mode.

Fig. 7.

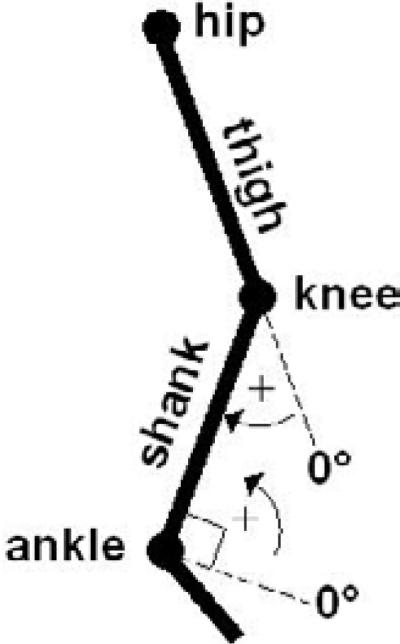
Joint angle and torque convention used. Positive torque is defined in the direction of increasing angle.

3.2. Gait Modes

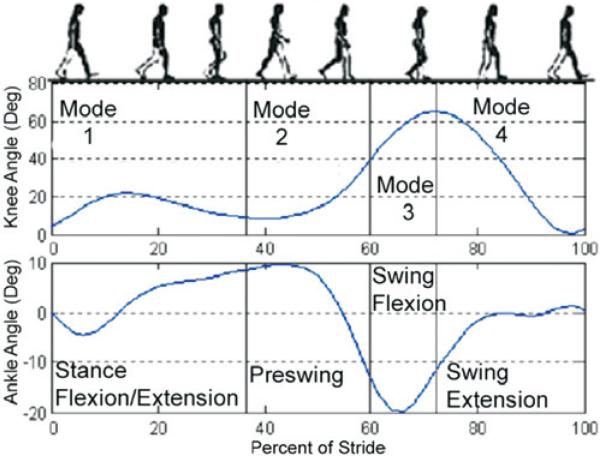
As previously discussed, the decomposition of joint behavior into passive segments requires the division of the gait cycle into modes or “finite states”, as dictated by their functions and the character of the piecewise segments of the impedance functions described previously. Although the number of modes required is not unique, the switching rules between modes must be well defined and measurable, and the number of modes should be sufficient to provide an accurate representation of normal joint function. One can reasonably assert that the swing and stance phase of gait constitute a minimal set of modes for the proposed approach. Based on least-squares regression fitting of (3) to gait data (i.e. from Winter (1991)), we determined that such fits were improved significantly by further dividing swing and stance into two sub-modes, as shown in Figure 8, with switching rules as shown in Figure 9.

Fig. 8.

Subdivision of normal gait into four functional modes. From Sup et al. (2007).

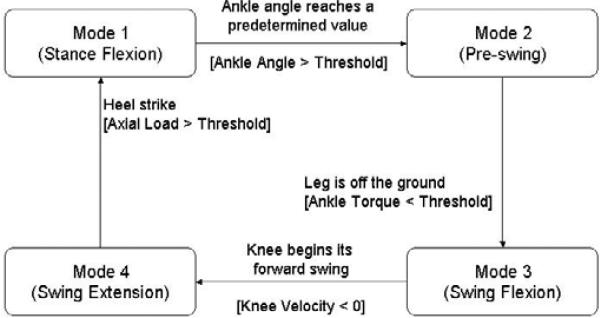
Fig. 9.

A finite-state model of normal gait. Each box represents a state and the transition conditions between states are specified.

Mode 1 begins with a heel strike, upon which the knee immediately begins to flex so as to provide impact absorption and begin loading, while the ankle simultaneously plantarflexes to reach a flat foot state. Both knee and ankle joints have relatively high stiffness during this mode to prevent buckling and allow for appropriate stance knee flexion, because Mode 1 comprises most of the weight bearing functionality. Mode 2 is the push-off phase and begins as the ankle dorsiflexes beyond a given angle (i.e. user's center of mass lies forward of stance foot). The knee stiffness decreases in this mode to allow knee flexion while the ankle provides a plantarflexive torque for push-off. Mode 3 begins as the foot leaves the ground as indicated by the ankle torque load cell and lasts until the knee reaches maximum flexion. Mode 4 is active during the extension of the knee joint (i.e. as the lower leg swings forward), which begins as the knee velocity becomes negative and ends at heel strike (as determined by the three-axis socket load cell). In both of the swing modes, the ankle torque is small and is represented in the controller as a (relatively) weak spring regulated to a neutral position. The knee is primarily treated as a damper in both swing modes (Modes 3 and 4).

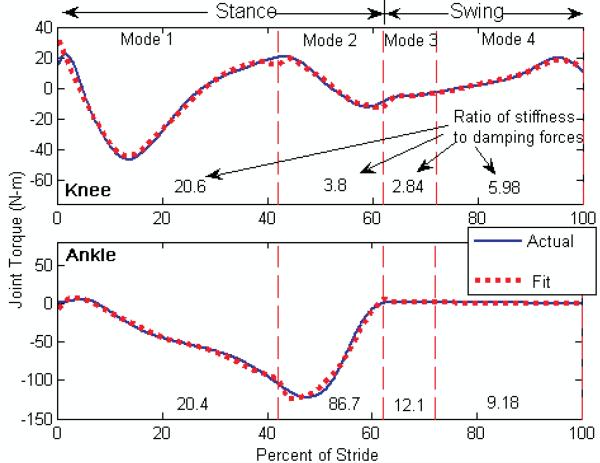
The proposed approach to “impedance modeling” of joint torques was preliminarily validated by utilizing the gait data of a healthy 75 kg subject, as derived from body-mass-normalized data from Winter (1991). Incorporating the four gait modes described previously, along with the motion and torque data for each joint provided by Winter (1991), a constrained least-squares optimization was conducted to generate a set of parameters for (3) in each mode. The resulting parameter set is listed for each mode in Table 4 and the resulting fit to joint torques is shown graphically in Figure 10. The fit shown in Figure 10 clearly indicates that normal joint function can be represented by the use of piecewise passive functions as proposed.

Table 4.

Impedance Parameters for Prototypical Gait (Gait Data from Winter (1991)).

	Knee impedance				Ankle impedance
Mode	k1 (Nm/deg)	k2 (Nm/deg3)	b (N s m–1)	θe (deg)	k1 (Nm/deg)	k2 (Nm/deg3)	b (Nms/deg)	θe (deg)
1	3.78	73 × 10–3	25 × 10–3	12	1.35	25 × 10–3	0.118	–5
2	0	9 × 10–6	30 × 10–3	37	4.50	0	5 × 10–3	–18
3	0	9 × 10–3	16 × 10–3	52	0.04	0	3 × 10–3	23
4	0.093	2 × 10–6	13 × 10–3	44	0.134	0	2 × 10–3	2

Fig. 10.

Piecewise fitting of knee and ankle torques during normal speed level walk (averaged population data from Winter (1991) scaled for a 75 kg adult) to a non-linear spring-damper impedance model. The numbers shown in each mode represent the mean ratio of the stiffness forces to damping forces predicted by the fit. The vertical lines represent the segmentation of a gait stride into four distinct modes.

4. Experimental Results

The impedance based gait control strategy was implemented on the tethered prosthesis prototype on a healthy subject using an able-bodied testing adaptor as shown in Figure 11. The adaptor consists of a commercial adjustable locking knee immobilizer (KneeRANGER-Universal Hinged Knee Brace) with an adaptor bracket that transfers load from the subject to the prosthesis. As the prosthesis remains lateral to the immobilized leg of the healthy subject, the adaptor simulates transfemoral amputee gait without kinematic interference from the immobilized leg. While the adapter allows for preliminary testing of the gait control algorithm, the setup does involve certain drawbacks in simulating prosthetic gait, some of which include: (i) compliance of the soft-tissue interface between the device and user (more so than exhibited by a limb–socket interface); (ii) “parasitic” inertia of the intact lower limb (i.e. in addition to the inertia of the prosthesis); and (iii) asymmetry in the frontal plane (as seen in Figure 11) which results in a larger than normal frontal plane moment. Despite these drawbacks, the adaptor provides a reasonable facsimile of amputee gait and enables the device and proposed impedance-based control approach to be tested.

Fig. 11.

Able-bodied testing adaptor used in development, testing and evaluation of the prosthesis and controllers prior to transfemoral amputee participation. From Sup and Goldfarb (2006).

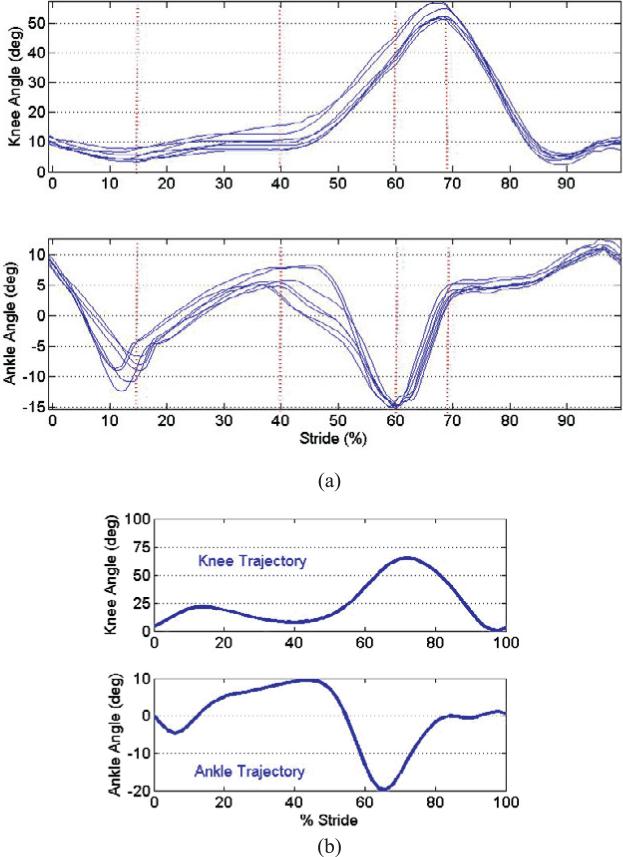
The prosthesis was tethered to a 2 MPa (300 psig) pressure source (i.e. compressed nitrogen) and to a controller implemented on a desktop PC with the real-time interface provided by MATLAB Real Time Workshop. Gait trials were performed on a treadmill, which provided a controlled walking speed and enabled enhanced safety monitoring, including a safety suspension harness and the use of handrails. Unlike the parameter tuning shown in Table 4 and Figure 10, the gait data for the prosthesis and user did not exist apriori. As such, the parameters shown in Table 4 were used as a rough guide and were tuned to the user by means of a combination of joint sensor data, video recordings and user feedback. For example, if the user felt that a joint was not generating necessary torques during support or push-off, the stiffness would be increased or the stiffness set point altered. With this iterative process, the impedance functions were tuned, finally resulting in the set indicated in Table 5. Note that the parameters are notably different from Table 4, owing most likely to the fact that (i) they were obtained primarily by user and sensor feedback (as opposed to a least-squares optimization), (ii) the tuning process was not able to sufficiently differentiate between the linear and cubic stiffness coefficients, (iii) the joints had some (unactuated) damping, which required considerably less feedback damping, (iv) the mass properties of the prosthetic leg are quite different from the native limb and (v) the data in Table 4 represents an averaged set of users, while the data in Table 5 represents the single subject in this trial. Based on this parameter set, the (measured) prosthesis joint angles during level treadmill walking at 0.675 m s^–1 (1.5 mph) are shown in Figure 12(a). An experimental trial can be viewed in the video provided in Extension 1.

Table 5.

Impedance Parameters Derived by Experimental Tuning

	Knee Impedance				Ankle Impedance
Mode	k1 (Nm/deg)	k2 (Nm/deg3)	b (N s m–1)	θe (deg)	k1 (Nm/deg))	k2 (Nm/deg3)	b (Nms/deg)	θe (deg)
1	7.5	0	0	14	4.5	0	0	–8
2	1.0	0.006	0	16	4.5	0	0	–25
3	0	0	0.005	0	0.5	0	0	0
4	0.08	0	0.08	30	0.75	0	0	–3

Fig. 12.

Measured joint angles (in degrees) for (a) six consecutive gait cycles for a treadmill walk at 0.675 m s^–1 (1.5 mph) for powered prosthesis and (b) average trajectory for normal gait.

When comparing the knee and ankle angles of Figure 12(a) with the prototypical data from Winter (1991), shown in Figure 12(b), one can observe that the powered prosthesis and controller provide behavior that is quite similar to normal gait, except in the knee behavior during the first 20% of the stride (i.e. just after heel strike). The difference in behavior during this period is most likely a result of the significant compliance between the adaptor and user. Specifically, the role of the knee during this period is to flex slightly upon impact, which absorbs energy and cushions the impact of heel strike. As such, the knee acts effectively as a stiff spring, first absorbing the energy of impact and shortly after returning this energy to the user. When used with the adaptor, this knee stiffness acts in series with the (much lower) stiffness of the user–adaptor interface, and thus the cushioning role of knee flexion during heel strike is dominated by the compliance in the user–adaptor interface. This behavior is evident in the video of Extension 1 by watching the relative motion between the top of the brace and the subject's hip during heel strike. The authors assume that once the axial compliance between the user and prosthesis is reduced significantly (as would be the case with an amputee subject), the knee joint will exhibit the flexion and subsequent extension evidenced in the prototypical gait kinematics of Figure 12(b).

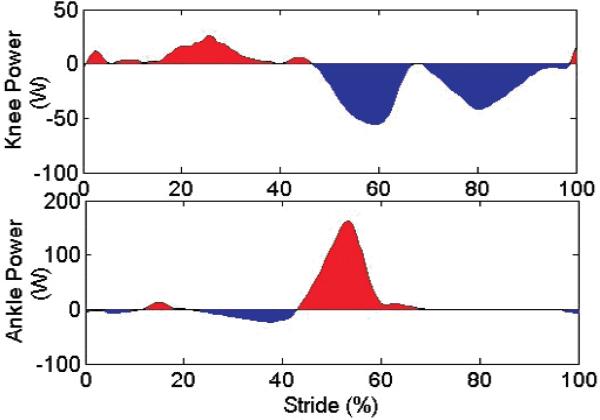
The knee and ankle joint powers, which were computed directly from the torque and differentiated angle data, are shown in Figure 13 and indicate that the prosthesis is supplying a significant amount of power to the user. Note that the measured power compares favorably with that measured in healthy subjects (see Winter (1991)) and thus indicates an enhanced level of functionality relative to existing passive prostheses.

Fig 13.

Averaged measured joint powers (W) for six consecutive gait cycles for a treadmill walk.

5. Conclusion

In this paper we have described the design and control of a tethered pneumatically actuated transfemoral prosthesis. The prosthesis design has been optimized to provide the requisite joint torque/angle requirements with a minimum volume actuator configuration. The control approach segments the gait cycle into four detectable modes and utilizes a passive impedance characterization of each mode to generate the required torques for the knee and ankle joints during walking. The approach was validated against normal gait data and through experimental testing with an able-bodied adaptor. Test results showed the prosthesis was able to produce a near-normal gait pattern, deliver required joint torques and supply a significant amount of power to the user.

Appendix: Index to Multimedia Extensions

The multimedia extension page is found at http://www.ijrr.org

Table of Multimedia Extensions

Extension	Type	Description
1	Video	Level treadmill walking using an able-bodied adaptor at 0.675 m s–1 (1.5 mph).