Robust Generation and Decoding of Morphogen Gradients

Abstract

Morphogen gradients play a key role in multiple differentiation processes. Both the formation of the gradient and its interpretation by the receiving cells need to occur at high precision to ensure reproducible patterning. This need for quantitative precision is challenged by fluctuations in the environmental conditions and by variations in the genetic makeup of the developing embryos. We discuss mechanisms that buffer morphogen profiles against variations in gene dosage. Self-enhanced morphogen degradation and pre-steady-state decoding provide general means for buffering the morphogen profile against fluctuations in morphogen production rate. A more specific “shuttling” mechanism, which establishes a sharp and robust activation profile of a widely expressed morphogen, and enables the adjustment of morphogen profile with embryo size, is also described. Finally, we consider the transformation of the smooth gradient profile into sharp borders of gene expression in the signal-receiving cells. The integration theory and experiments are increasingly used, providing key insights into the system-level functioning of the developmental system.

Modeling of buffering mechanisms and morphogen shuttling can explain how gradients of morphogens are robustly generated and decoded during development.

In order for a uniform field of cells to differentiate into a reproducible pattern of organs and tissues, cells need to receive information about their position within the field. During development, positional information is often conveyed by spatial gradients of morphogens (Wolpert 1989). In the presence of such gradients, cells are subject to different levels of morphogen, depending on their positions within the field, and activate, accordingly, one of several gene expression cassettes. The quantitative shape of the morphogen gradient is critical for patterning, with cell-fate boundaries established at specific concentration thresholds. Although these general features of morphogen-based patterning are universal, the range and form of the morphogen profile, and the pattern of induced target genes, vary significantly depending on the tissue setting and the signaling pathways used.

The formation of a morphogen gradient is a dynamic process, influenced by the kinetics of morphogen production, diffusion, and degradation. These processes are tightly controlled through intricate networks of positive and negative feedback loops, which shape the gradient and enhance its reproducibility between individual embryos and developmental contexts. In the past three decades, many of the components comprising the morphogen signaling cascades have been identified and sorted into pathways, enabling one to start addressing seminal questions regarding their functionality: How is it that morphogen signaling is reproducible from one embryo to the next, despite fluctuations in the levels of signaling components, temperature differences, variations in size, or unequal distribution of components between daughter cells? Are there underlying mechanisms that assure a reproducible response? Are these mechanisms conserved across species, similar to the signaling pathways they control?

In this review, we outline insights we gained by quantitatively analyzing the process of morphogen gradient formation. We focus on mechanisms that buffer morphogen profiles against fluctuations in gene dosage, and describe general means by which such buffering is enhanced. These mechanisms include self-enhanced morphogen degradation and pre-steady-state decoding. In addition, we describe a more specific “shuttling” mechanism that is used to generate a sharp and robust profile of a morphogen activity from a source that is broadly produced. We discuss the implication of the shuttling mechanism for the ability of embryos to adjust their pattern with size. Finally, we consider the transformation of the smooth gradient profile into sharp borders of gene expression in the signal-receiving cells.

CANONICAL PARADIGM OF MORPHOGEN GRADIENT FORMATION: INTERPLAY BETWEEN DYNAMIC RANGE AND ROBUSTNESS

The canonical model of morphogen gradient formation assumes that morphogen is secreted from a localized source, and spreads across the tissue while being degraded. The resulting concentration gradient peaks at the source and decays gradually away from it. This general paradigm applies to a number of well-studied systems, including the Bicoid gradient in the early Drosophila embryo (Driever and Nüsslein-Volhard 1988b) and the Dpp, Hedgehog, and Wingless gradients in the Drosophila wing imaginal disc (Teleman et al. 2001). Quantitative properties of such morphogen profiles are relatively well understood. In the absence of feedbacks, the steady-state gradient is exponential, M ∼ e^−x/λ. The decay length (scale) of the profile is defined by the morphogen diffusion coefficient (D) and its typical degradation time (α) such that $\lambda =\sqrt{D\alpha }$, and its overall level is proportional to the morphogen production rate.

Within this canonical paradigm, the sensitivity to changes in morphogen production rate is easily derived (Eldar et al. 2003). The shift in cell-fate boundaries, δx, upon modulating the morphogen production rate by some factor η, is proportional to the morphogen decay length λ:

$$\delta x=\lambda \text{ ln}\left(\eta \right).$$ (1)

This means that all thresholds are shifted by the precise same amount, independently of their position in the unperturbed system. Thus, a single length scale, λ, controls both the spread of the morphogen (its decay across the field) and the sensitivity of patterning to perturbations in morphogen production rate. Robustness and dynamic range are thus inherently linked: The system can be readily made less sensitive by reducing the decay length λ; but this will inevitably limit the spread of the gradient. A gradient that spreads over most of the field requires λ to be of the order of field size, and consequently will be highly sensitive to fluctuations in morphogen production rate.

UNCOUPLING THE INTERPLAY: “SELF-ENHANCED DEGRADATION” ENHANCES ROBUSTNESS WITHOUT LIMITING THE DYNAMIC RANGE OF THE MORPHOGEN GRADIENT

The distribution of morphogens is typically shaped by feedback loops. Morphogen signaling regulates the abundance or activity of genes coding for receptors, heparan sulfate proteoglycans (HSPGs) or other regulatory proteins, and a feedback loop is established when these molecules regulate the diffusion, degradation, or production of the morphogen (Akiyama et al. 2008; Chen and Struhl 1996; Tsuda et al. 1999). In principle, such feedbacks could buffer the morphogen gradient against genetic and environmental perturbations.

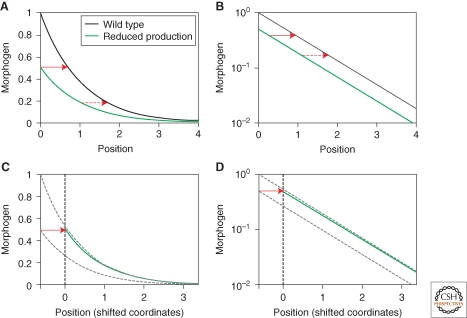
To explore the types of feedback that will uncouple the interplay between robustness and dynamic range, it is instructive to examine more closely the factors that control these two properties in a general morphogen system (Eldar et al. 2003). Consider first the sensitivity of the steady-state profile to changes in morphogen production rate (Fig. 1). Morphogen production is localized to the origin (x = 0), and as such defines the boundary conditions for morphogen dynamics. Importantly, the dynamics (diffusion and degradation) in all other positions is independent of the rate by which morphogen is produced. Consequently, if we shift the perturbed profile (corresponding to the system with modified production rate) by just a bit along the position-axis, such that it will coincide with the nonperturbed profile at just one point (e.g., the origin of the original system), the two profiles must coincide also at all other points. This is because the two profiles (unperturbed and perturbed profiles in shifted x-coordinate) are now defined by precisely the same dynamic equations and the same boundary conditions. A consequence of this simple analysis is that all threshold positions are shifted by the same amount, independent of their absolute position along the position-axis. We have noted this property when discussing the properties of the exponential profile (Equation 1, previously). The present discussion concludes that this property holds more generally for steady-state morphogen profiles, even in the presence of feedbacks (provided that the profile decays sufficiently and rapidly across the field [Eldar et al. 2003]).

Figure 1.

Shift morphogen in profile following perturbation in morphogen production rate. (A–B) Steady-state morphogen profiles. Shown is the steady-state profile of two models, differing only in the rate by which the morphogen is produced. In both models, the morphogen degrades linearly, with the same degradation rate, and diffuses with the same diffusion coefficient. The perturbed profile (green line) corresponds to morphogen that is produced at half the rate by which wild-type morphogen is produced (black line). The profiles are shown in linear scale (A) and log scale (B). The red arrow denotes the shift in profile. (C–D) The two steady-state morphogen profiles are related through a shift in the position coordinates. The perturbed profile is plotted in a new coordinate frame, obtained by shifting the original coordinates along the x-axis (defining new_x = old_x + Δ, with Δ as some fixed value). In these coordinates, the perturbed profile coincides with the wild-type profile (dashed gray line, plotted in the original coordinate system). The profiles are shown in linear scale (C) and log scale (D).

Moreover, it is clear from the above analysis that the shift in the morphogen profile depends only on the rate by which morphogen profile decays close to the source (boundary). Robustness thus depends only on the dynamics properties close to the source. In contrast, the spread of the gradient is a function of the average decay of the profile throughout the field. The case of no-feedback (exponential profile) is unique in the sense that the gradient is defined by a single decay length (λ). Hence, the decay length in the vicinity of the source (which controls robustness) is the same as the decay length everywhere, coupling robustness and dynamic range.

Feedback regulation can result in a morphogen profile that decays at multiple length scales, and can thus break the interplay between robustness and dynamic range (Eldar et al. 2003). A multitude of length scales is achieved, for example, when morphogen signaling enhances morphogen degradation. In such a case, morphogen decays rapidly close to the source (where morphogen levels are highest) but decays at a slower rate further away from the source (where morphogen levels are lower). Robustness is thus improved without comprising the dynamic range. The resulting gradient is not exponential. Rather, it is better approximated by a power-law S(x) ∼ 1/x^m. The same uncoupling can be obtained also if morphogen signaling alters the (local) diffusion coefficient (e.g., by modulating the level of HSPG), such that diffusion becomes smaller in regions of high morphogen signaling (Bollenbach et al. 2005).

The robustness mechanism described above is general, and does not depend on the precise means by which morphogen signaling impacts on morphogen degradation or diffusion. Self-enhanced degradation was described in several developmental contexts. The induction of patched transcription by Hh signaling, for example, enhances the uptake and degradation of Hh (Incardona et al. 2000), leading to enhanced Hh degradation in the vicinity of its source. Specifically in the Drosophila wing imaginal disc, Hh is produced in the posterior compartment and signals to the adjacent cells in the anterior compartment, which, in response, induce Ptc expression (Chen and Struhl 1996). This induction of Ptc results in increased sequestering and degradation of Hh by the receiving cells (Tabata and Kornberg 1994), thus likely increasing the robustness to fluctuations in the level of Hh. Similarly, in the zebrafish embryo, retinoic acid (RA) is produced posterior to the hindbrain, and generates a posterior-to-anterior gradient that specifies rhombomere location. RA signaling leads to induction of cyp26a, a cytochrome p450 enzyme that oxidizes RA to promote its removal from the tissue, thus generating an RA gradient that is robust to fluctuations in RA synthesis (White et al. 2007).

PRE-STEADY-STATE DECODING

Most analyses of morphogen patterning assume that the fate of the responding cells is determined by the morphogen gradient after the gradient had reached its steady state. However, developmental processes often occur rapidly, and it is not clear whether the profile can converge to its steady state within the restricted time frame available. Moreover, temporal averaging throughout the kinetics is also possible and was shown to apply, e.g., in the readout of the sonic hedgehog morphogen gradient in the vertebrate central nervous system (Dessaud et al. 2007). We also realized that feedbacks, which shape morphogen gradients through regulation of transcription or translation, are lengthy, and might not be possible to use during rapid early development. Several theoretical studies suggested that the morphogen signal might be read (decoded) before the profile had reached its steady state (Gursky et al. 2004; Mizutani et al. 2005; Saha and Schaffer 2006). This motivated us to examine whether the time at which the gradient is being decoded affects the sensitivity of the profile-to-morphogen production rate (Bergmann et al. 2007).

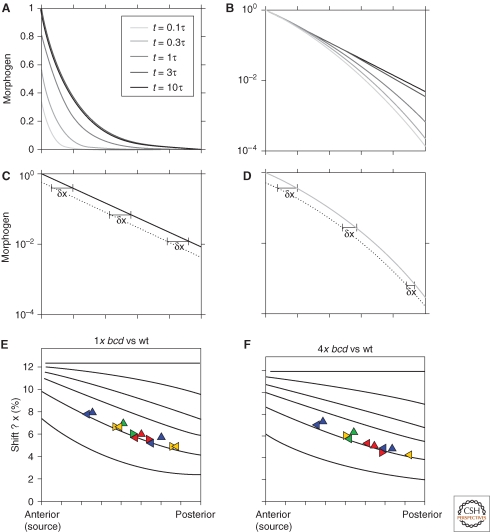
The mathematical formula describing the pre-steady-state morphogen profile is somewhat more complex than that describing the steady-state distribution, precluding meaningful analytical manipulation. Still, the sensitivity of the pre-steady-state profile to changes in morphogen production rate can be predicted using straightforward numerical integration (Bergmann et al. 2007). Two features that distinguish the pre-steady-state profile were described. First, the shift in profile following a change in morphogen production rate is not uniform. Rather, thresholds positioned differently across the field shift to different extents (Fig. 2). This is in contrast to the uniform shift expected of the steady-state profile, as discussed previously. The reason for this difference is that the morphogen profile does not converge to its steady state at a uniform rate everywhere. Rather, positions that are close to the source converge rapidly, whereas positions that are further away take a longer time to converge. Consequently, at any point in time, different positions will be at different stages of their dynamics, and this will affect the shift in their position when morphogen production rate is perturbed.

Figure 2.

Pre-steady-state decoding. (A, B) Temporal evolution of morphogen profile: The morphogen profiles at different time points, as indicated, are shown using either absolute levels (A) or normalized by their maximum at x = 0 (B). The morphogen degrades linearly at a rate f = τ⁻¹. Morphogen production began at time t = 0. Time is in units of morphogen degradation time τ. (C, D) Change in morphogen profile following reduction in production rate: The wild-type morphogen profile is compared with a perturbed profile, corresponding to morphogen that is produced twofold slower. δx denotes the shift between the wild-type and the perturbed profiles. Note the uniform shift for the steady-state profile (C), compared with the position-dependent shift for the pre-steady-state profile (D), where the shift decreases further away from the morphogen source. (E, F) Shifts in morphogen profile following reduction in production rate: Shown are the shifts in threshold positions following twofold reduction (E) or enhancement (F) in morphogen-production rate. The shifts are shown as a function of the position of the threshold in the unperturbed system, with the different lines corresponding to different pre-steady-state profiles, obtained following the initiation of morphogen production, at the indicated times. Symbols correspond to simulation of the full gap-gene system, as described in Bergmann et al. 2007.

A second interesting aspect is that, for most threshold positions, the sensitivity to morphogen production rate is in fact lower when decoding is performed before steady state has been reached (Bergmann et al. 2007). The reason for this smaller shift in the pre-steady-state gradient has to do with differences in the decay profile. Thus, although the steady-state profile decays exponentially, the rate by which the pre-steady-state profile converges to this limiting exponential pattern increases with the distance from the source. Consequently, before the steady state, the local steepness of the gradient increases with the distance from the source. This increased steepness decreases the shift in threshold position upon a change in morphogen production rate. It should be noted, however, that although this increased steepness enhances robustness, it also compromises the dynamic range of the profile because of its more rapid decay away from the source.

PRE-STEADY-STATE DECODING OF THE BICOID MORPHOGEN PROVIDES QUANTITATIVE EXPLANATIONS TO A NUMBER OF UNRESOLVED PROPERTIES OF THIS PATTERNING SYSTEM

One of the best-studied examples of molecular gradients is that of Bicoid (Bcd), a maternally encoded transcription factor that plays a pivotal role in patterning the early Drosophila embryo (reviewed in Ephrussi and Johnston 2004). Visualization of the graded Bcd distribution along the anterior–posterior axis of the embryo provided the first experimental demonstration that molecular gradients exist (Driever and Nüsslein-Volhard 1988a,b). Bcd induces the expression of different target genes (termed “gap genes”) in a concentration-dependent manner, leading to their expression in distinct spatial domains along the anterior–posterior axis (Driever et al. 1989a; Driever and Nüsslein-Volhard 1989; Driever et al. 1989b; Johnston and Nüsslein-Volhard 1992; Struhl et al. 1989). The pattern of gap gene expression is subsequently refined through the cross-regulatory interactions between the gap genes themselves, which, similar to Bcd, function as transcription factors (Rivera-Pomar and Jäckle 1996).

Consistent with Bcd functioning as a morphogen, changes in the dosage of maternal Bcd cause a shift in the expression domains of Bcd-target genes such as hunchback (hb). Reducing Bcd dosage leads to an anterior shift, whereas increasing its dosage shifts the expression domains posteriorly. Surprisingly, however, several studies noted that the observed shifts are significantly smaller than expected by the simple morphogen model (Driever and Nüsslein-Volhard 1988a; Houchmandzadeh et al. 2002). For example, in embryos derived from mothers bearing only one functional allele of bcd, the Hb expression domain shifts by only ∼7% embryo length (EL), about half of what is expected theoretically. These anomalous shifts in cell fates were recognized over two decades ago, in the early analysis of the Bcd gradient (Driever and Nüsslein-Volhard 1988a), and were further emphasized by recent quantitative measurements (Houchmandzadeh et al. 2002).

The simple morphogen model was further challenged by several observations that seemed to decouple the hb-expression domain from the Bcd gradient. First, it was shown that changes in temperature alter the Bcd gradient but do not influence the hb-expression domain (Houchmandzadeh et al. 2002; Lucchetta et al. 2005). An additional difficulty was raised when the stochastic fluctuations in the binding of Bcd to gene promoters were considered (Gregor et al. 2007a; Gregor et al. 2007b). It was argued, based on physical considerations, that this noise is too high to allow distinction between the Bcd levels at two neighboring nuclei at the border of the hb-expression domain. Again, it was proposed that a novel, yet to be determined mechanism is used for ensuring the high precision by which the hb-expression domain is defined, as seen experimentally.

We revisited these issues, and in particular the anomalous shift in gap-gene expression domains, by examining the basic assumptions leading to the apparent inconsistencies between the measured and the predicted shifts (Bergmann et al. 2007). In previous studies, the expected shifts in Hb expression domains following a change in Bcd dosage were calculated using Equation 1. This equation requires two parameters: λ, the decay length of the morphogen, and η, the relative change in Bcd dosage. Both parameters can be readily estimated: λ is deduced from the measured Bcd profile, whereas η is well approximated by the change in the number of maternal copies of bcd. We noted, however, that the use of Equation 1 is justified only if the profile had reached its steady state. As we discussed previously, the expected shifts are different if the Bcd profile is decoded early, before reaching its steady state. A first indication that the steady-state assumption might not hold here was provided by the shifts in gap-gene expression domains upon change in Bcd dosage, which were shown to be strongly position-dependent (Bergmann et al. 2007): Anterior gap genes display a relatively high sensitivity to changes in Bcd dosage, whereas those that are expressed more posteriorly display a lower sensitivity. As discussed above, this position-dependent shift is a signature of a pre-steady-state decoding.

Pre-steady-state decoding provides a parsimonious explanation to other apparent mysteries characterizing the relationship between Hb and Bcd (Bergmann et al. 2007; Bergmann et al. 2008). First and foremost, the measured shifts in Hb expression domain are fully explained by the corresponding changes in Bcd dosage. Second, at early times, greater distances separate the nuclei, increasing the difference in Bcd dosage between neighboring nuclei, and limiting the impact of stochastic fluctuations. Finally, it was shown that Hb profile scales with the natural variations in embryo size whereas the Bcd profile does not (Driever and Nüsslein-Volhard 1988a; Houchmandzadeh et al. 2002). This, again, can be explained by the pre-steady-state theory, under the additional assumption that Bcd transmits rapidly between nucleus and cytoplasm (Gregor et al. 2007b). In such a case, the pre-steady-state profile (defining Hb expression domain) scales with embryo size, whereas the late, steady-state profile of Bcd does not (Bergmann et al. 2007).

Experiments analyzing the Bcd gradient were reported recently (Gregor et al. 2007b), but their interpretation is under debate (Bergmann et al. 2008). Three different approaches for measuring the Bcd diffusion coefficient gave a consistently low value of D ∼0.3 µm²/s (Gregor et al. 2007b). Considering the relevant time scale in which patterning takes place (∼90 min following egg lay), and the scale of the Bcd gradient (∼100 microns), this diffusion coefficient is clearly inconsistent with the steady-state assumption. In fact, even for pre-steady-state decoding, this low diffusion entails a high production of the Bcd protein in order to allow for sufficient accumulation of Bcd at mid-embryo, which enables the determination of Hb transcription at early times. Interestingly, direct measurements of nuclear Bcd-GFP distribution in early embryos did reveal a stable pattern as early as stage 10–11. This apparent contradiction might be reconciled by further analysis, which showed that the total level of Bcd does in fact continue to accumulate in embryos (Bergmann et al. 2008). This analysis suggested that the overall profile has not yet reached its steady state, in accordance with the pre-steady-state hypothesis. Further clarification of these issues will require measuring the Bicoid degradation time, and the time of gap genes determination by the Bcd gradient, which are not yet available.

NONCANONICAL GRADIENT FORMATION: ESTABLISHING A SHARP DISTRIBUTION FROM A SHALLOW SOURCE

Our discussion so far has focused on the canonical model of morphogen gradient formation, which assumes that morphogen is secreted by a localized source, and diffuses to create a gradient that peaks at the source (Fig. 3A). Although this model is applicable to many systems, other cases exist where morphogen is in fact produced in a broad domain but its activity is subsequently restricted to a narrow area that is well within its domain of expression (Fig. 3B). Properties of gradients created by this paradigm are significantly less understood.

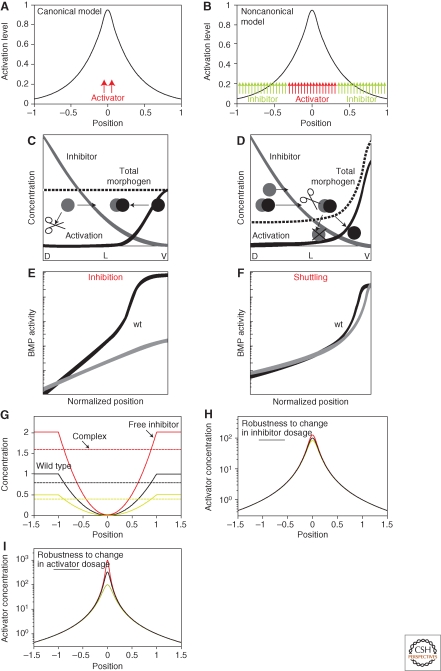
Figure 3.

Shuttling versus inhibition-based mechanism for gradient formation. (A) Canonical model for morphogen gradient formation: Morphogen is produced from a local source. Diffusion and degradation of the morphogen across the field leads to a concentration gradient that picks at the source and decays away from it. (B) Noncanonical model for morphogen gradient formation: Morphogen is produced in a broad domain but its activity is subsequently restricted to a narrow area that is well within its domain of expression. Restricted activity could be because of, e.g., an inhibitor secreted from the adjacent domains. (C) Inhibition-based patterning mechanism: A schematic representation of the inhibition-based mechanism. An inhibition gradient is generated through the localized secretion of an inhibitor and its degradation by a uniform protease. This inhibition gradient is established over a field of an activator. The activator may be uniformly distributed. Note that positive feedback of BMP expression may eventually result in graded BMP expression as well, but this is not required for the generation of the gradient itself, and does not constitute a main aspect of the patterning mechanism. The figure is based on the paradigm of early Xenopus patterning, with D, L, and V standing for dorsal, lateral, and ventral regions of the embryo, respectively. Inhibitor is shown in gray, activator in black, and the total activator (free and in complex with the inhibitor) in dashed black. (D) Shuttling-based patterning mechanism: A schematic representation of the shuttling-based mechanism. Patterning here relies mostly on the physical translocation of the BMP ligands to the ventral region. The activation gradient thus arises primarily from the graded distribution of the BMP ligands themselves. Effective shuttling requires that the binding of ligand to the inhibitor greatly facilitates its diffusion, and that the free ligand is released by cleavage of the complex. Notations are the same as those in A. (E) Inhibition-based profile does not scale: Shown is a typical profile of BMP activation within the inhibition-based model. The profile was solved twice: first for parameters simulating wild-type embryos and second for dorsal-half embryos (same parameters, but embryo’s size halved). The profiles are shown in scaled coordinates. Note the different profiles corresponding to the wild-type versus half embryo. (F) Scaling of shuttling-based profile: A typical profile of BMP activation within the shuttling-based model. The profile was solved twice: First for parameters simulating wild-type embryos and second for dorsal-half embryos (same parameters, but embryo’s size halved). The profiles are shown in scaled coordinates. Note the accurate scaling of the profiles corresponding to the wild-type versus half embryo. (G–I) Robustness of shuttling-based mechanism. (G) Inhibitor profile is not robust: The profile of the inhibitor is not robust to dosage of the inhibitor or the protease. In fact, changing the inhibitor dosage causes a proportional change in its spatial profile, as is shown in the figure. (H) Robustness of the activation profile to the levels of inhibitor: The activation profile is robust to changes in inhibitor or protease because of the fact that the level of inhibitor-activator complex, which is uniform throughout the field and functions as a global integrator, is also altered in proportion to the change in the inhibitor dosage. Because the free activator does not diffuse, its level at any point in space is given by the ratio between the complex and free inhibitor, which is independent of the inhibitor or protease dosages. (I) Robustness of the activation profile to the levels of activator: The activation profile is also robust to the total level of activator. This, again, is because of the fact that the free activator does not diffuse. Lack of diffusion allows the storage of any excess activator in the dorsal-most region, where no inhibitor is present.

The dorsoventral (DV) axis of the early Drosophila embryo is patterned by a graded activity of the bone-morphogenetic protein (BMP) (Ferguson and Anderson 1992). This system provides a well-studied example for the noncanonical strategy for morphogen gradient formation. Two BMP ligands (Screw and Dpp) participate in this patterning, and both are broadly expressed: Dpp is produced in the dorsal domain whereas Screw is produced throughout the embryo (reviewed by Raftery and Sutherland 1999). The key asymmetry leading to the formation of a BMP-activation gradient is the secretion of the BMP inhibitor, Short gastrulation (Sog), from the neuroectoderm regions flanking the dorsal domain (Srinivasan et al. 2002). The resulting activation gradient is sharp enough to subdivide the dorsal domain into several distinct regions of gene expression.

The protein components involved in this patterning system, as well as the interaction between them, are well described. Still, the function of this patterning network depends on the quantitative values of the kinetic parameters. In fact, changing the parameter values might not only alter the quantitative dynamics, but also lead to a qualitatively different mechanism for gradient formation. For example, if only some of the proteins or complexes are allowed to diffuse, a gradient will be established by a mechanism that is distinct from the case where all protein species are allowed to diffuse. The values of these kinetic parameters are largely unknown. How then can modeling assist in our understanding of the patterning mechanism?

Our working hypothesis is that evolution favors a robust network design. Specifically, we assumed that the networks that function in nature display minimal sensitivity to fluctuations in gene dosage or kinetic parameters. Because the subspace of robust networks is typically small, identifying a robust topology can predict the patterning mechanism, which can then be verified experimentally.

The best way to describe the function of a patterning network for an arbitrary set of parameters is to formulate a general enough model, and derive an analytical solution for the concentrations of the different molecular species. Such an analytical solution, however, is typically difficult to obtain, in particular for the noncanonical paradigm for morphogen gradient formation, where several diffusing and interacting species cooperate in establishing the gradient. A numerical screen provides an alternative approach. The idea here is to start from a general (“liberal”) model that is restricted only by the known network topology, and to solve this model systematically over a wide range of parameters. Each parameter choice consists of a particular “network.” The consistency of each network with experimental evidence or some other requirement (e.g., robustness) is then evaluated, and the properties of the “consistent” networks are characterized.

SHUTTLING MECHANISM: GENERATING A SHARP AND ROBUST GRADIENT

We analyzed the BMP patterning network in Drosophila using the numerical screen approach (Eldar et al. 2002). The results of this screen revealed two distinct mechanisms that can be used for establishing an activation gradient. The first class of networks achieved patterning by relying strictly on the inhibition of BMP by its inhibitor Sog. Within this inhibition-based mechanism (Fig. 3C), the inhibitor Sog diffuses into a region of uniform BMP, where it is also cleaved by a protease (Tolloid). A gradient of inhibition is generated, leading to an inverse activation gradient. This mechanism does not require the redistribution of BMP molecules themselves. Rather, BMP may still be uniformly distributed, but its activity is now graded because of the graded distribution of its inhibitor.

An alternative, shuttling-based mechanism was also proposed (Holley et al. 1996), and was found to be implemented by the second class of networks (Fig. 3D). Here, the inhibitor Sog functions to physically translocate the BMP molecules to the dorsal region. The activation gradient now reflects mostly the graded redistribution of the BMP molecules themselves, and not the inhibition of their activity by graded Sog. Shuttling is obtained when BMP diffuses primarily when bound by Sog. This binding is also assumed to facilitate the degradation of Sog by its protease, Tolloid. Conversely, free BMP does not readily diffuse, thus accumulating in the dorsal-most region where the levels of free Sog are low. This lack of diffusion of Dpp could result, for example, from its rapid binding to receptors or to components of the extracellular environment.

As expected, both mechanisms can establish a graded BMP activation profile. The mechanisms differ substantially, however, in the sharpness of the resulting profile and also in its robustness. Gradients established by the inhibition-based mechanism are relatively shallow, and are highly sensitive to the dosages of the inhibitor, activator, or protease. In contrast, the shuttling-based mechanism defines a much sharper profile, and this profile is robust to changes in gene dosage (Eldar et al. 2002; Meinhardt and Roth 2002). The mechanisms ensuring the robustness of the activation profile to the dosage of the inhibitor or the protease, and to the dosage of the activator itself, are explained in Figure 3G,H, respectively. The finding that the shuttling-based mechanism confers a significantly higher robustness led us to propose that this mechanism operates in Drosophila. This prediction was confirmed experimentally in the Drosophila embryo (Eldar et al. 2002; Mizutani et al. 2005; Shimmi et al. 2005; Wang and Ferguson 2005) (review by O’Connor et al. 2006) and was subsequently also shown to be used for patterning the embryonic DV axis in short-germ insects (van der Zee et al. 2006).

Notably, this strategy for creating a pattern is particularly useful for early embryos, where distinct yet broad zygotic gene expression domains are defined, but a highly restricted source for morphogen production has not been generated yet. The physical concentration of ligand by shuttling molecules provided by adjacent tissues can thus generate a sharp and robust morphogen profile, even in the absence of a restricted morphogen expression source.

SHUTTLING OF BMP LIGANDS IN XENOPUS: IMPLICATION FOR THE SCALING OF PATTERN WITH SIZE

So far, we focused on the property of robustness, defined as the quantitative ability to buffer fluctuations in gene dosage or kinetic rate constants. The embryo, however, faces additional sources of variability, most notably fluctuations in size. Embryo size can differ greatly, depending on environmental factors (e.g., nutrition and temperature) or specific genetic polymorphisms. The body plan must be adjusted to these size fluctuations to maintain proper proportions between the different tissues or organs. How this scaling of pattern with size is achieved mechanistically is largely unknown.

The ability of embryos to scale pattern with size was emphasized most dramatically in two classical experiments performed by Hans Spemmann at the beginning of the century (reviewed in De Robertis 2006). The first experiment showed that dorsal-half embryos grow to generate a complete and well-proportioned embryo, albeit smaller in size. The second experiment shows that transplanting a dorsal group of cells from one embryo to the ventral side of a second embryo generates a twinned tadpole. Here also, both axes are well-proportioned and include dorsal, lateral, and ventral tissues. The precision of scaling, and the lack of compensatory growth, was further illustrated in subsequent quantitative experiments (Cooke 1981).

What is the mechanistic basis for scaling? One of our motivations in addressing this question was the fact that the patterning network involved is largely homologous to the network that patterns the dorsal region of the early Drosophila embryo, discussed above (De Robertis and Kuroda 2004; Holley and Ferguson 1997). In fact, in all bilatera, DV patterning of the early embryo involves a graded BMP activation profile, although in vertebrates the positions are inverted with respect to Drosophila, i.e., maximal activation by BMP takes place at the ventral side. Other components of the patterning network are also conserved. For example, the key asymmetry in generating the BMP activation gradient in amphibians relies on the localized secretion of a BMP inhibitor (including Chordin, homologous to Sog), which is produced at the dorsal region by cells of the “Spemman organizer” (De Robertis and Kuroda 2004). An important difference between the Drosophila and vertebrate systems, however, is the use of a unique BMP ligand in vertebrates, Admp (Reversade and De Robertis 2005), which is repressed by BMP signaling and accordingly is expressed together with the BMP inhibitor Chordin in the dorsal region, where pathway activation is lowest.

Using a numeric screen for networks that support scaling, we identified again the shutting mechanism. This mechanism provided a simple, quantitative explanation for the capacity of the Xenopus embryo to scale pattern with size (Ben-Zvi et al. 2008). The key for scaling was the shuttling of two types of BMP ligands, a canonical one (BMP) and noncanonical one (Admp), both of which compete for binding to the inhibitor Chordin. This competition allows for a range of possible activation profiles, depending on the relative amount of the two ligands in the system. The precise activation profile can thus be controlled by modulating the levels of the two BMP ligands. Importantly, these levels are in fact controlled through feedback loops. In particular, Admp expression is repressed by the BMP pathway. This repression provides an effective means for measuring the size of the embryo and adjusting the morphogen profile accordingly.

More precisely, note that the repression of Admp by BMP signaling functions to “pin” the magnitude of BMP activation at the dorsal-most side to a precise value, defined by the threshold at which Admp expression is repressed. Once this boundary level of the activation gradient had been determined, the rest of the gradient will follow, resulting in a robust scaling of the morphogen profile (both length scale and amplitude) with embryo size. Intriguingly, we find that this scaling mechanism functions through an effective implementation of an integral-feedback controller, a key concept in engineering (Barkai and Ben-Zvi 2009).

GRADIENT INTERPRETATION: USING SHALLOW GRADIENTS TO DEFINE SHARP ACTIVATION BORDERS

Because the distribution of a morphogen is governed by diffusion processes, its profile is smooth, decaying gradually between adjacent cells. This continuous distribution is converted to well-defined domains of gene expression, demarcated by sharp borders. This poses a challenge for the responding cells: how to sense small differences in morphogen activation profile, and execute one of several alternative gene expression programs, accordingly. Cooperative binding to the regulatory region of the responding target gene provides one solution, and is used, for example, in the responses to the early Bicoid or Dorsal gradients in Drosophila embryos (Jiang and Levine 1993; Struhl et al. 1989). The degree of cooperativity determines the sharpness of the response, and the binding affinity dictates the position of the borders of expression with respect to the source of the gradient.

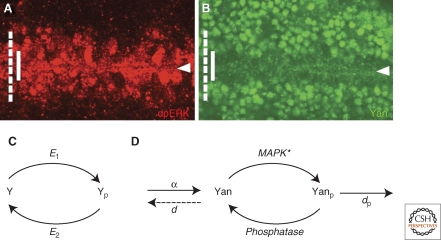
We sought alternative mechanisms for generating threshold responses. The ETS-transcription factor Pointed executes most of the transcriptional responses following EGF receptor activation in Drosophila (Gabay et al. 1996). Different Pointed isoforms are activated at the transcriptional or posttranscriptional level, by MAP kinase phosphorylation. In parallel, the repressor ETS-domain protein Yan is phophorylated by MAP kinase, leading to its nuclear export and degradation. The sharp border of Yan degradation, which is well within the domain of graded activation of the EGF receptor (Fig. 4), prompted us to examine the mechanism in detail.

Figure 4.

Generating threshold responses by zero-order ultrasensitivity. (A) In a wild-type embryo (stage 10), the activating ligand Spi emanates from the ventral midline (arrowhead), triggering EGF receptor in the adjacent cells, and leading to graded activation of MAP kinase that is detected with dpERK antibodies (red). (B) Within the domain of MAP kinase activation (dashed white line), the degradation pattern of Yan (green, full line) at the same stage shows a much more restricted and sharp response. (C) A classical zero-order hypersensitivity model, showing the reversible conversion of a substrate between two states, and the dependence of the final product only on the difference between the rate of opposing enzymatic reactions. (D) In the case of the Yan degradation network, in addition to phosphorylation by MAP kinase (MAPK) and dephosphorylation by unknown proteases, aspects such as synthesis and degradation have to be considered. Similar to the classical model, a switchlike behavior is generated when the substrate is in excess with respect to the dissociation constants for the two opposing enzymes.

Goldbeter and Koshland have suggested that sharp borders can be defined by a mechanism they coined “zero order ultrasensitivity” (Goldbeter and Koshland 1981; Goldbeter and Wolpert 1990). This mechanism considers a reversible reaction in which substrate is, for example, phosphorylated and dephosphorylated, and assumes that the substrate is in excess, allowing both reactions to occur at zero order (saturation). Under these conditions, the rate of reactions is practically independent of the concentration of the substrate. All substrate will thus accumulate as one of the forms, depending simply on the difference in the rates of the forward and backward reactions. Because the rates of the reactions depend on the concentration of the modifying and de-modifying enzymes, this system is ultra-sensitive to small changes in the concentrations of these enzymes, being able to respond to small changes in these concentrations in a switchlike manner (Fig. 4).

In accordance with this model, we were able to show that the degradation of Yan follows zero-order kinetics (Melen et al. 2005). An elevation in the level of Yan did not alter the position of the threshold, but led to an increase in the time to reach steady state, which was directly proportional to the excess level of Yan that was produced. This mechanism provides several advantages. First, it generates a sharp threshold. Second, the same kinase-activity gradient could generate distinct thresholds for different transcription factors, depending on the affinity. Finally, in a noisy and fluctuating environment, having a large substrate pool, which is completely phosphorylated or non-phosphorylated, may buffer against temporal fluctuations in activity, as well as against noise. It will be interesting to determine if sharp thresholds of activated (phosphorylated) transcription factors can be achieved by this mechanism.

CONCLUDING REMARKS

The studies described in this review represent our initial foray to address patterning by morphogens in a quantitative and computational manner. This analysis is enlightening, as the cells sense not only the presence or absence of the morphogen, but elicit a variety of responses that are highly dependent on the level of activation by the morphogen. Most importantly, beyond the quantitative analysis of the response, our approach examines the mechanisms that buffer fluctuations to allow a reproducible output. The feature of robustness imposes constraints on the emerging solutions, and guides us toward the biologically relevant mechanisms.

From what we have learned so far, are there any generalities we can draw on regarding the mechanisms that provide robustness? First, these mechanisms are not absolute, but only minimize the effects of fluctuations. Second, diverse strategies seem to be used, and are adapted to each of the systems. In the case of ligand-induced degradation, the morphogen distribution close to the source is uncoupled from its distribution away from the source. For the Bicoid gradient, early decoding before steady state may minimize fluctuations. Finally, for the early BMP gradients, the physical concentration of the ligand generates not only a graded activation profile, but may also translocate excess ligand to a narrower region, thus minimizing the effects of fluctuations in ligand levels. The striking conservation of robustness mechanisms, e.g., in the case of BMP ligand shuttling, indicates that they are an integral part of the patterning pathways that they regulate.