Abstract
The peak decay method is an affinity chromatographic technique that has been used to examine the dissociation of solutes from immobilized ligands in the presence of excess displacing agent. However, it can be difficult to find a displacing agent that does not interfere with detection of the eluting analyte. In this study, a non-competitive peak decay method was developed in which no displacing agent was required for analyte elution. This method was evaluated for the study of drug-protein interactions by using it along with high-performance affinity chromatography to measure the dissociation rate constants for R- and S-warfarin from columns containing immobilized human serum albumin (HSA). Several factors were considered in the optimization of this method, including the amount of applied analyte, the column size, and the flow rate. The dissociation rate constants for R- and S-warfarin from HSA were measured at several temperatures by this approach, giving values of 0.56 (± 0.01) and 0.66 (± 0.01) s−1 at pH 7.4 and 37°C. These results were in good agreement with previous values obtained by other methods. This approach is not limited to warfarin and HSA but could be employed in studying additional drug-protein interactions or other systems with weak-to-moderate binding.
Keywords: Drug-protein interactions, peak decay analysis, human serum albumin, warfarin, high-performance affinity chromatography, dissociation rate, kinetics
1 Introduction
Information on the kinetics of a biomolecular interaction is useful in the design of many methods that employ biological ligands for chemical separations or analysis. Surface plasmon resonance and other biosensor systems can be utilized to obtain such information [1–3], but affinity chromatography can also be employed for this purpose. Kinetic methods based on affinity chromatography include band-broadening measurements, peak profiling, and split-peak analysis [4–6]. However, each of these techniques has limitations. Band-broadening measurements work well for systems with relatively fast association and dissociation kinetics; however, this technique requires careful control of the system and precise measurement of peak variances at many flow rates [7–11]. Peak profiling is a closely-related method that also requires careful peak variance measurements, but this approach instead uses high flow rates to determine rate constants for an analyte on an affinity column [6]. The split-peak method makes use of area measurements for non-bound analyte fractions and is usually performed at high flow rates; this approach tends to give best results for systems with strong binding and slow dissociation kinetics [12,13].
The peak decay method is an attractive alternative to these other techniques when working with biomolecular systems that have intermediate rates of dissociation [4,5,14]. In past work with this approach, the release of an analyte from an immobilized ligand has been measured under conditions in which analyte reassociation is made negligible by the presence of a high concentration of a competing agent [4]. This analysis has been performed by first saturating the immobilized ligand with the analyte and then quickly changing to a mobile phase that has a high concentration of a competing agent, thus promoting release of the analyte through mass action. For instance, the dissociation rate of fluorescent sugar analogs from immobilized concanavalin A has been examined by this method when using a non-fluorescent sugar as a competing agent [14]. If this method is conducted under appropriate flow rate and competing agent conditions, elution of the displaced analyte can be treated as a first-order process that provides the dissociation rate constant for the release of analyte from the immobilized ligand in the column [4,14].
This report will examine the development of a non-competitive peak decay method that can be performed with weak-to-moderate affinity systems and without the use of a displacing agent. This approach will be tested by using it in high-performance affinity chromatography (HPAC) to examine dissociation of the drug warfarin from columns that contain human serum albumin (HSA). HSA is a 66.5 kDa plasma protein that binds to many drugs and small organic compounds in blood. Warfarin is a chiral anticoagulant drug that is known to bind to HSA at the warfarin-azapropazone site, or Sudlow site I [15,16]. The association equilibrium constants for HSA with the R- and S-enantiomers of warfarin have been determined to be in the range of 2.4–4.1 × 105 M−1 at pH 7.4 and 37°C [17–19]. Information is also available on the rate constants for these interactions [9,20–25]. All of these properties make this system a useful model for developing and evaluating a non-competitive peak decay method for the study of drug-protein interactions. Several theoretical and practical factors will be considered in the optimization of this method, including the effects of varying the amount of applied analyte, the column size, and the flow rate of the mobile phase. The results should provide useful guidelines in the extension of this approach to the study of other drug-protein interactions or additional systems with weak-to-moderate binding.
2 Theory
The reactions shown in Eqs. (1)–(2) have been used previously to describe analyte interactions in an affinity column [4,14]. This model is based on a two-step process involving (1) diffusion of the analyte into and out of the pores of the support and (2) analyte adsorption-desorption with an immobilized ligand that is located on the surface of the support.
| (1) |
| (2) |
In these reactions, Ae and Ap represent the analyte in the flowing mobile phase (or excluded volume) and stagnant mobile phase (or pore volume) of the support, respectively. Mass transport of the analyte between the flowing mobile phase and stagnant mobile phase is described in Eq. (1) by the forward and reverse rate constants k1 and k−1. In Eq. (2), L refers to the immobilized ligand and A−L represents the analyte-ligand complex, while ka and kd are the association and dissociation rate constants for interactions of the analyte with the ligand.
The peak decay method originally reported in Refs. [4] and [14] made use of an affinity column that was first saturated with the analyte. This analyte was then dissociated in the presence of an excess of competing agent. At a sufficiently high flow rate, it was proposed that this dissociation could be described by the two-step process shown in Eqs. (3)–(4), in which reassociation of the analyte with the ligand and mass transfer of analyte from the flowing mobile phase to the stagnant mobile phase are considered to be negligible on the time scale of the experiment [4,14].
| (3) |
| (4) |
In this situation, the elution profile for the analyte is represented by Eq. (5),
| (5) |
where t is the time allowed for elution, mAe is the moles of analyte eluting at time t, and mA0 is the initial moles of bound analyte in the column. If kd is much smaller than k−1 (i.e., the elution of analyte is limited by its rate of dissociation from the ligand), Eq. (5) reduces to Eq. (6).
| (6) |
Eq. (6) makes it possible to obtain the dissociation rate constant for this system by preparing a plot of the natural logarithm of the elution profile versus time, or ln(dmAe/dt) vs. t, which should have a slope equal to −kd [14]. This particular expression is written for a system in which only one type of interaction and a single dissociation rate constant can be used to describe the release of A from the immobilized ligand. If several types of interactions are present (e.g., specific binding plus non-specific binding or multi-site interactions of A with L), Eq. (6) can still be used but would now give a weighted kd value that depends on the relative amount of analyte that is undergoing each type of dissociation process.
One problem with using a competing agent in the peak decay method is this agent may create a significant change in background signal when it is applied, making it difficult to measure the rate of analyte dissociation from the column. This problem was avoided in this current study for weak-to-moderate affinity systems by using a non-competitive peak decay method. This was accomplished by working under column size and flow rate conditions that maximized the chance of washing a retained analyte from the column after the analyte had dissociated from the ligand and exited the stagnant mobile phase. If this process occurs quickly, only a negligible amount of analyte should be able to reenter the stagnant mobile phase. When both the rates of analyte dissociation and reassociation are much slower than this rate of mass transfer (i.e., ka[L]≪ k−1 and kd≪k−1), Eq. (6) can again be used to describe the rate of analyte release from the column. This makes it possible to use a plot of the natural logarithm of the peak decay response to give the dissociation rate constant for the release of the analyte from the ligand (kd). If the association equilibrium constant (Ka) for the binding of the analyte to the ligand is also known, the association rate constant for the analyte with the ligand can also be determined by using the relationship Ka = ka/kd.
As indicated earlier, one assumption made in Eq. (6) is that ka[L] ≪ k−1. This means that the rate of reassociation of the analyte with the ligand is assumed to be negligible compared to the rate of mass transfer of the analyte from the stagnant mobile phase to the flowing mobile phase. The size of the pseudo-first order rate constant for reassociation (ka [L]) can be adjusted by passing through the affinity column a solution with a known, moderate or high concentration of analyte [A]. This concept can be illustrated by using the ideal case in which a local equilibrium is reached between the analyte and ligand for a system with single-site binding. Under these conditions, the amount of analyte that is bound to the ligand (mL,app) can be related to the true binding capacity of the column (mL) through the following relationship [4,26].
| (7) |
In this system, the moles of free ligand sites that remain in the column can be calculated by finding the difference between mL and mL,app. Using the fact that [L] =(mL− mL,app)/VM gives Eq. (8), where VM is the column void volume.
| (8) |
Eq. (8) indicates that a small value for ka [L] (i.e., as needed for slow reassociation) can be obtained if there is a reasonably high concentration of analyte that can bind to the column and produce a low concentration of free ligand. Although Eqs. (7) and (8) were derived for a system at local equilibrium, the same general factor(s) that lead to a small value for ka [L] and slow reassociation will also pertain to a peak decay analysis in which analyte-ligand binding has not yet achieved a local equilibrium.
Caution also must be taken to avoid using too large of a concentration for the applied analyte because the excess analyte in solution can make it difficult to later observe the decay profile for retained analyte as it dissociates from the column. This concept can be represented by the following relationship, as is again derived for a simple system in which a local equilibrium is present between the analyte and ligand for a system with single site binding.
| (9) |
This equation shows that an increase in analyte concentration will eventually cause the ratio of the free analyte to bound analyte in the mobile phase ([A]/[A−L]) to increase. This will make it difficult under such conditions to observe a decay curve due to the excess of free analyte that is washing from the column. The same issue will be present in a system in which the analyte and ligand have not yet reached a local equilibrium. Such a problem can be reduced by decreasing [A], but too large of a decrease in [A] will create a situation in which reassociation is likely to occur, as indicated by Eq. (8). Thus, both the rate of reassociation and the amount of excess analyte in solution need to be considered when selecting sample conditions for a non-competitive peak decay analysis.
3 Materials and methods
3.1 Reagents
The HSA (Cohn fraction V, approximately 99% pure, fatty acid free), racemic warfarin, and reagents for the bicinchoninic acid (BCA) protein assay were from Sigma (St. Louis, MO, USA). The Nucleosil Si-300 (5 or 7 µm particle size with 300 Å pores) was from P.J. Cobert (St. Louis, MO, USA). The R- and S-warfarin were donated by Dupont Pharmaceuticals (Wilmington, DE). All other chemicals and biochemicals were of the purest grades available. All solutions were prepared in water obtained from a Nanopure water system (Barnstead, Dubuque, IA, USA).
3.2 Apparatus
The chromatographic system consisted of one CM300 isocratic pump (Milton Roy, Riviera Beach, IL, USA) and one RF-535 fluorescence detector (Shimadzu, Kyoto, Japan). Samples were injected using a Rheodyne PR700-100 injection valve (Cotati, CA, USA) or an AS3000 autosampler from Thermoseparations (Schaumberg, IL, USA) with a 100 µl sample loop. The elution profiles were collected using Labview software from National Instruments (Austin, Texas, USA) and processed using spreadsheets written in Excel (Microsoft, Redmond, WA). The columns were packed using a CM3200 pump from LDC Analytical (Riviera Beach, FL, USA) and a modified Valco N60 six-port valve (Houston, TX, USA), as reported previously [27]. The column and mobile phase temperatures were controlled using an Isotemp 9100 circulating water bath (Fisher Scientific, Pittsburgh, PA).
3.3 Methods
Two types of HPLC-grade silica (Nucleosil Si-300 with 5 or 7 µm particle size) were used in this study. Diol-bonded silica was prepared from each of these starting supports according to a previous procedure [28]. The diol content was determined by an iodometric capillary electrophoresis assay [29] to be 212 (± 2) µmol/g for the 7 µm silica and 276 (± 2) µmol/g for the 5 µm silica, where the numbers in parentheses represent a range of ± 1 S.D. HSA was immobilized to these supports by the Schiff base method [26]. The protein content for the final supports was 730 (± 10) nmol HSA/g silica for the 7 µm silica and 930 (± 20) nmol HSA/g silica for the 5 µm silica, as determined in triplicate by a BCA assay [30] using HSA as the standard and diol-bonded silica as the blank. Both the HSA and control supports (containing no immobilized HSA) were packed at 3000 psi into 2.5 mm × 2.1 mm I.D. columns using pH 7.4, 0.067 M potassium phosphate buffer as the packing solution. These columns were stored in this pH 7.4 buffer at 4°C until use. From the known protein content of the HSA support and reported activity for HSA that has been immobilized by the Schiff base method [19,26], it was estimated that there were 1.50 nmol of warfarin binding sites in the HSA column.
All mobile phases were filtered through a 0.45 µm cellulose acetate filter and degassed under vacuum for 10 min prior to use. Warfarin was detected by using its fluorescence at an excitation wavelength of 320 nm and an emission wavelength of 380 nm. The non-competitive peak decay method was optimized and characterized using injections of racemic warfarin in the presence of pH 7.0, 0.1 M potassium phosphate buffer and at 25°C on columns packed with 5 µm or 7 µm silica particles. Later experiments examining the dissociation of R- and S-warfarin from HSA at various temperatures were performed on a column packed with 5 µm silica and using pH 7.4, 0.067 M potassium phosphate buffer as the mobile phase.
The concentrations of warfarin applied to the HSA and control columns ranged from 0.1–30 µM (note: it has been shown in previous reports that warfarin has little or no measurable non-specific binding to the types of supports that were used within these columns under such conditions) [9,19]. The flow rates used in this study ranged from 0.1 to 5 ml/min. The back pressure across each column was less than 2500 psi under these conditions. The chromatographic data were collected at a rate of 4 points/s. After collection, these results were used to prepare a plot of the natural logarithm of response versus time. The slope of this response was then used to obtain the dissociation rate constant for the analyte-ligand interaction, as shown earlier in Eq. (6).
4 Results and discussion
4.1 General peak decay results
Figure 1 shows typical decay curves and logarithmic decay profiles that were obtained for injections of racemic warfarin on a 2.5 mm × 2.1 mm I.D. HSA column and control column of identical size. In this example, a 100 µl sample of 10 µM warfarin was applied at 25°C and a flow rate of 4 ml/min. As the sample first entered these columns, some of the applied warfarin was bound by the HSA. The use of a relatively large amount of warfarin in the sample allowed the immobilized HSA to become partially saturated during this step. As the non-bound warfarin was washed from the column, some of the warfarin that had been bound to HSA began to slowly dissociate and was carried off the column to the detector.
Figure 1.
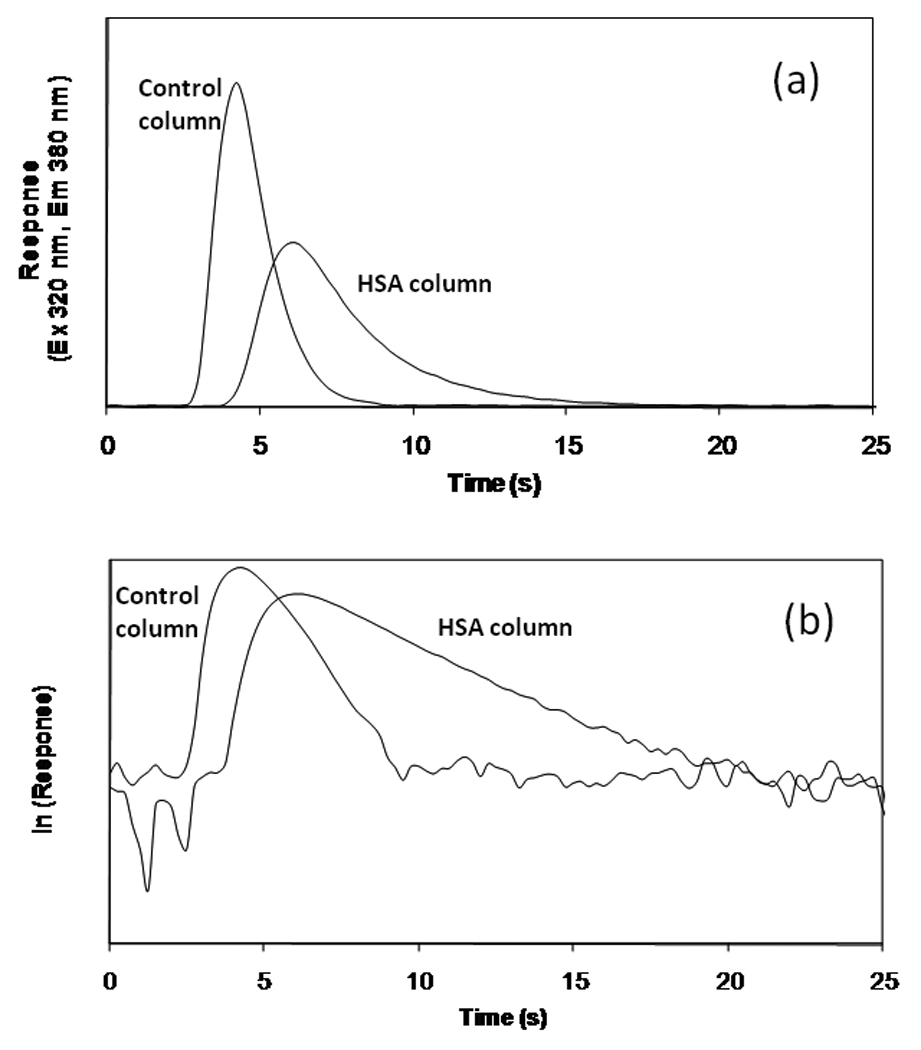
Comparison of the (a) response and (b) logarithmic response profile for a 100 µl injection of 10 µM racemic warfarin onto a 2.5 mm × 2.1 mm I.D. control column or HSA column that was prepared using Nucleosil 300-7 silica. These chromatograms were obtained at 25°C and 4 ml/min using pH 7.0, 0.10 M potassium phosphate buffer as the mobile phase.
According to Eq. (6), a plot of the natural logarithm for the detector response versus time should give a straight line for the dissociation-limited release of analyte from the immobilized ligand. After excess warfarin had been washed from the column, a linear change in the natural logarithm of the response was indeed observed, as shown in Figure 1(b). The control column also gave a relatively linear relationship. This latter response was used to help minimize the effects of analyte washing and mass transfer during the peak decay studies. It can be seen in Figure 1 that excess analyte was washed from the column in a relatively short period of time (i.e., less than 10 s in this specific example). However, the retained analyte was released over longer periods of time. To avoid overlap between the response for the excess analyte and dissociating analyte, all further measurements of the peak decay slopes were performed at times greater than those observed for the elution of excess analyte from the control column (e.g., times greater than 10 s in Figure 1).
4.2 Column size & plate height considerations
The peak decay method developed in this report generally requires the use of a small column to minimize reassociation of the analyte after it dissociates from the column. Ideally, the column should contain less than one theoretical plates for such work (i.e., less than one effective equilibration step between the analyte and immobilized protein used as the stationary phase). In earlier studies with an HSA support similar to those used in this report, it was estimated that the plate heights for R- and S-warfarin on a 4.5 cm × 4.1 mm I.D. column were in the range of 0.03–0.50 cm when working at 4–45°C and a linear velocity of 0.005–0.04 cm/s [8]. For the 2.5 mm × 2.1 mm I.D. HSA column employed in this current report, this would correspond to 0.5–8 theoretical plates at a flow rate of 0.01–0.08 ml/min. Much higher flow rates (i.e., up to 4 ml/min) were used with this small column in the peak decay measurements conducted in this current report. These conditions provided an even lower number of theoretical plates and helped to minimize analyte reassociation with HSA on the time scale of the experiment.
A second estimate of the number of theoretical plates that would be expected in a 2.5 mm × 2.1 mm I.D. HSA column was made by using chromatographic band-broadening theory. To do this, the total plate height for the column (Htot) was calculated by finding the sum of contributions due to mobile phase mass transfer (Hm), longitudinal diffusion (Hl), stagnant mobile phase mass transfer (Hsm), and stationary phase mass transfer (Hk), as described by the following relationships [4,31].
| (10) |
| (11) |
| (12) |
| (13) |
In Eqs. (10)–(13), u is the linear velocity, k’ is the analyte’s retention factor, Vp is the column pore volume, dp is the particle diameter of the support, γ is the obstruction or tortuosity factor, and Dm is the diffusion coefficient for the analyte in the mobile phase. All other terms are as defined previously. The plate height contribution due to extra-column band broadening (Hec) was also considered in these calculations by using equations given in Ref. [33].
To estimate the size of these plate height terms, the retention factor for warfarin was calculated from the binding capacity of the column (mL) and the association equilibrium constant for the analyte with the immobilized ligand (Ka) by using the relationship k’ = Ka mL/VM (note: a calculated value for k’ was used due to the low number of theoretical plates for the HSA column used in this study, which made direct measurements of the retention factor impractical). An average value for kd was obtained by using previous estimates of this parameter for warfarin with immobilized HSA (i.e., 0.14–0.40 s−1 at 25°C for R- and S-warfarin) [9] and the values for kd that were obtained later in this report (i.e., 0.34–0.37 s−1 at 25°C for racemic warfarin). The mass transfer constant k−1 was calculated for warfarin according to the following formula [4],
| (14) |
where Dm for warfarin was estimated to be 5 × 10−6 cm2/s [32], γ was assigned a value of 0.5 (a typical result for a small analyte), and dp was set equal to a particle diameter of 7 µm. This gave an estimated value for k−1 of 306 s−1.
Table 1 shows the results calculated for the various plate height terms under the conditions employed in this study to examine the dissociation rate of warfarin from HSA at 25°C using 7 µm silica (Note: values for HL are not shown since these were all less than 10−4 cm and were not significant compared to other plate height terms). As can be seen from these results, the total plate height estimated for this system would be expected to increase as the flow rate was increased, resulting in less than one theoretical plate at the upper end of the flow rate range considered in this study. This confirmed that such flow rates were adequate for peak decay experiments by minimizing warfarin reassociation after it had been released from a 2.5 mm × 2.1 mm I.D. HSA column. The same general result was obtained when these plate height calculations were made for warfarin and HSA at the other temperatures that were examined (i.e., 4 and 37°C, as based on data from this report and Refs. [9,19])
Table 1.
Predicted plate height terms for racemic warfarin applied to a 2.5 mm × 2.1 mm I.D. HSA column at 25°C and various flow ratesa
| Flow rate | Hsm | Hk | Hm | Hi | Hec | Htot | Hk/Htot | n |
|---|---|---|---|---|---|---|---|---|
| (ml/min) | (cm) | (cm) | (cm) | (cm) | (cm) | (cm) | ||
| 0.1 | 0.0006 | 0.0052 | 0.0035 | 0.0229 | 0.0004 | 0.0326 | 0.1605 | 7.6606 |
| 0.5 | 0.0031 | 0.0262 | 0.0035 | 0.0205 | 0.0004 | 0.0537 | 0.4878 | 4.6574 |
| 1 | 0.0062 | 0.0524 | 0.0035 | 0.0189 | 0.0005 | 0.0814 | 0.6431 | 3.0700 |
| 1.5 | 0.0092 | 0.0785 | 0.0035 | 0.0172 | 0.0006 | 0.1091 | 0.7201 | 2.2919 |
| 2 | 0.0123 | 0.1047 | 0.0035 | 0.0183 | 0.0007 | 0.1396 | 0.7503 | 1.7910 |
| 2.5 | 0.0154 | 0.1309 | 0.0035 | 0.0125 | 0.0006 | 0.1629 | 0.8038 | 1.5350 |
| 3 | 0.0185 | 0.1571 | 0.0035 | 0.0133 | 0.0007 | 0.1931 | 0.8135 | 1.2946 |
| 3.5 | 0.0215 | 0.1833 | 0.0035 | 0.0126 | 0.0007 | 0.2217 | 0.8266 | 1.1275 |
| 4 | 0.0246 | 0.2095 | 0.0035 | 0.0145 | 0.0009 | 0.2530 | 0.8279 | 0.9881 |
The equations and methods used to determine the individual plate terms in this table are summarized in the text. The number of theoretical plates (n) was calculated by using the relationship n = L/Htot, where L is a column length of 2.5 mm in this particular example. An average value for racemic warfarin of 0.35 s−1 was used for kd and a value of 3.0 × 105 M−1 was used for Ka in this particular calculation.
4.3 Effects of flow rate and analyte concentration
As shown in Table 1 for a 2.5 mm × 2.1 mm I.D. HSA column, the plate height contribution due to analyte-ligand dissociation (i.e., the stationary phase mass transfer term, Hk) would be expected to increase as the flow rate increases. Furthermore, as the flow rate increases to about 3.0 ml/min, this plate height term accounts for more than 80% of the total plate height. This indicated that work under such flow rate conditions would not only help prevent analyte reassociation but would also increase the relative importance of analyte dissociation versus mass transfer in determining the slope of the peak decay response. This effect is illustrated by the leveling that was found to occur in the absolute value of this slope for racemic warfarin as the flow rate is increased on a 2.5 mm × 2.1 mm I.D. HSA column, as shown in Figure 2.
Figure 2.
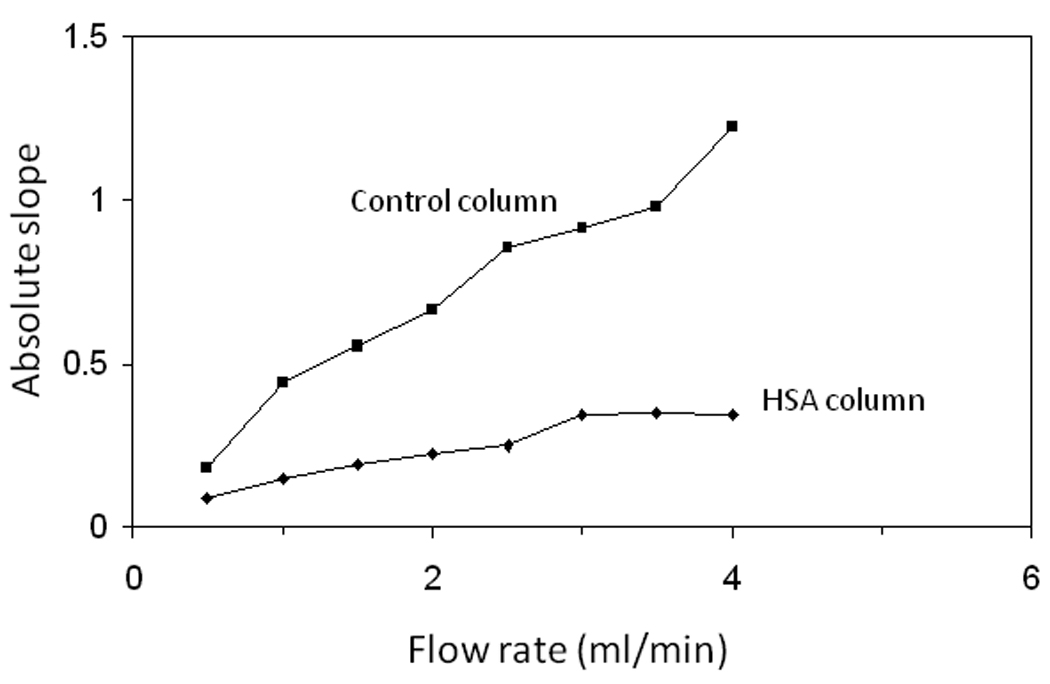
Absolute values of the slopes measured at various flow rates from the logarithmic decay profiles obtained on a 2.5 mm × 2.1 mm I.D. control column (■) or HSA column (◆) containing 7 µm silica particles. The injections consisted of 100 µl of 10 µM racemic warfarin made at 25°C and using pH 7.0, 0.10 M potassium phosphate buffer as the mobile phase.
The effect of changing the analyte concentration on the behavior of the peak decay curves was also examined. This was considered by using 100 µl samples of 1–10 µM racemic warfarin applied at various flow rates to a 2.5 mm × 2.1 mm I.D. HSA column and control column. A summary of the results that were obtained are given in Table 2. The peak retention times seen for the 1 µM sample of racemic warfarin were longer than those observed for the 10 µM warfarin sample at all flow rates. This was expected because under the given experimental conditions the relatively large sample concentration partially saturated the column, giving rise to non-linear elution conditions and weaker retention for the analyte. Another difference between the 1 and 10 µM warfarin results was in the dependence of their peak decay slopes on the flow rate. For the 1 µM warfarin sample, the slope measured for the HSA column continued to change as the flow rate increased from 0.1 to 4 ml/min; however, an essentially constant slope was obtained for the 10 µM sample at flow rates higher than 3 ml/min. This supported the conclusion made earlier that the use of faster flow rates help minimize the effects of mass transfer and reassociation on peak decay results [14]. As a result, the fact that the larger warfarin concentration gave a smaller flow rate effect was not surprising because the higher degree of column saturation with this sample made reassociation less likely to occur.
Table 2.
Elution time of peak maximum (tp) and slopes of peak decay curves for racemic warfarin on the HSA column and control columns at 25°C and various flow ratesa
| Flow rate (ml/min) |
1 µM Warfarin on HSA column |
10 µM Warfarin on HSA column |
10 µM Warfarin on control column |
|||
|---|---|---|---|---|---|---|
| tp (s) | Slope (s−1) | tp (s) | Slope (s−1) | tp (s) | Slope (s−1) | |
| 0.1 | 231.3 | −0.015 (± 0.001) | 139.6 | −0.020 (± 0.001) | 82.4 | −0.051 (± 0.001) |
| 0.5 | 48.6 | −0.061 (± 0.002) | 29.2 | −0.086 (± 0.005) | 17.1 | −0.182 (± 0.002) |
| 1.0 | 25.7 | −0.094 (± 0.006) | 16.3 | −0.147 (± 0.012) | 10.0 | −0.443 (± 0.012) |
| 1.5 | 17.8 | −0.150 (± 0.007) | 11.9 | −0.196 (± 0.002) | 7.5 | −0.551 (± 0.009) |
| 2.0 | 14.2 | −0.162 (± 0.007) | 9.4 | −0.229 (± 0.009) | 6.2 | −0.666 (± 0.007) |
| 2.5 | 12.0 | −0.190 (± 0.006) | 8.2 | −0.250 (± 0.006) | 5.1 | −0.855 (± 0.006) |
| 3.0 | 9.9 | −0.212 (± 0.014) | 7.3 | −0.344 (± 0.003) | 4.8 | −0.915 (± 0.013) |
| 3.5 | 9.1 | −0.236 (± 0.022) | 6.7 | −0.347 (± 0.007) | 4.5 | −0.981 (± 0.015) |
| 4.0 | 8.0 | −0.248 (± 0.019) | 6.0 | −0.344 (± 0.007) | 4.2 | −1.226 (± 0.013) |
The values in parentheses represent a range of ± 1 S.D. All experiments in this table were performed using a 100 µl sample volume.
The 100 µl sample volume used in this study was much larger than the void volume of the HSA and control columns, which had a value of approximately 8.7 µl. This allowed for the injected analyte to have more time to bind the immobilized ligand. This greater extent of initial binding helped to lower the term ka [L] during the peak decay analysis when the retained analyte later began to dissociate from the column (see Theory). From the known protein content and volume and estimated binding capacity of the HSA column (i.e., 1.5 nmol warfarin), the effective concentration of active ligand in this column was determined to be 172 µM. The total amount of analyte applied in 100 µl of the 1 and 10 µM warfarin samples was 0.1–1.0 nmol. This meant that the moles of analyte in the highest concentration sample represented approximately two-thirds of the estimated column binding capacity.
Figure 3 shows how the value of ka [L] (i.e., as related to the effective rate of analyte association) would vary with the mobile phase concentration of analyte [A] if the HSA column had reached a local equilibrium with the sample during injection; this plot also shows how the relative amount of analyte in solution versus analyte bound to the ligand (as given by the ratio [A]/[A−L]) would vary under these conditions. To obtain accurate rate constants measurements, it is desirable to have a large fraction of bound analyte (i.e., low [A]/[A−L]) while also minimizing analyte reassociation (i.e., low ka [L]). These conditions maximize the amount of analyte for which dissociation is measured and reduce multiple interactions of the analyte with the stationary phase. It can be seen from Figure 3 that low sample concentrations would be expected to result in a large amount of bound versus free analyte at equilibrium (i.e., a small ratio for [A]/[A−L]). However, these conditions also gave relatively large values for ka [L] (approximately 27 s−1 below 0.1 µM), which was undesirable since it would create more reassociation. Sample concentrations up to 30 µM should give a decrease in ka [L] (5.7 s−1 at 10 µM or 2.3 at 30 µM) without significantly decreasing the relative amount of free versus bound analyte (i.e., increasing [A]/[A−L] to only 0.06 at 10 µM or 0.15 at 30 µM). Higher sample concentrations would lead to a large increase in the relative amount of free warfarin and a higher background signal. These results agree with the general observation made throughout this report that 10–30 µM warfarin samples gave better decay curves than 1 µM samples under the stated experimental conditions and provided less background interference than higher concentration samples.
Figure 3.
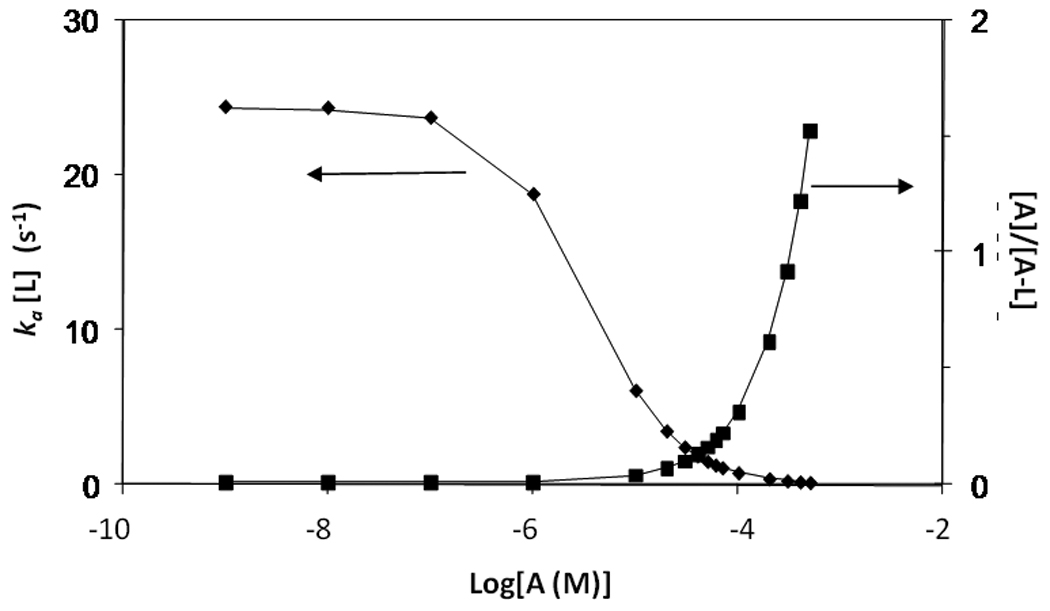
Theoretical plots showing the values expected for ka [L] (◆) and [A]/[A−L] (■) as a function of log[A] if a local equilibrium is established between a warfarin sample and immobilized HSA column. These results were calculated using Eqs. (8) and (9) along with an average association equilibrium constant for racemic warfarin with HSA of 3.0 × 105 M−1 at 25°C, an association rate constant of 1.0 × 105 M−1 s−1 and a total effective concentration of 172 µM for warfarin binding sites in the HSA column.
It was further possible to compare the expected values of ka[L]/k−1 for these two types of samples (i.e., 1 µM and 10 µM warfarin). This was accomplished by using previous estimates made for k−1 and [L] and an average association rate constant of 1.0 ×105 M−1s−1 for warfarin with HSA at 25°C [9]. This calculation gave values for ka[L]/k−1 of 0.03 and 0.08 (or 3% and 8%) for the 10 µM and 1 µM warfarin samples, respectively. These ratios provided some information concerning the validity of the assumption that analyte reassociation was not significant during the peak decay studies. The small value of ka[L] indicated that analyte-ligand association in this case should be slow relative to analyte diffusion out of the pores. The lower value of ka[L]/k−1 obtained for the 10 µM sample indicated that the assumption that analyte reassociation was not significant was slightly better for this sample than it was for the 1 µM sample.
4.4 Comparison of peak decay results for HSA columns with different size supports
The last item considered during the optimization of the peak decay method was the effect of varying the particle size and efficiency of the support within the column. This was of interest because an efficient column with fast mass transfer would allow dissociation rate constants to be more easily measured. However, efficient columns would also result in small plate heights, which would allow for greater reassociation of analyte during its release from the column. To study this further, two series of columns were prepared with identical lengths but different sized support particles (i.e., 300 Å porous supports with a mean diameter of 5 or 7 µm). Injections of 100 µl 10–30 µM warfarin were then made to each column at 0.5–5.0 ml/min. The larger concentrations of warfarin used in this experiment versus those employed in the earlier studies was due to the greater surface area of the supports in this particular experiment and the larger amount of immobilized HSA that was present within these columns.
Figure 4 shows some typical chromatograms that were obtained on the control and HSA columns containing 7 µm silica as the flow rate was varied. Similar results were obtained for columns containing 5 µm silica (data not shown). For the HSA column containing 7 µm silica , the slope approached a constant value in the logarithmic plots as the flow rate exceeded 3.0 ml/min (see Figure 2). For the HSA column containing 5 µm silica, the slope also approached a plateau as the flow rate increased but the leveling of this slope now occurred more gradually and the plateau was reached at slightly higher flow rates (i.e., 3.5–4.0 ml/min). These differences were expected due to the better efficiency of the columns containing 5 µm vs. 7 µm silica. However, both types of columns gave comparable slopes and values for kd when using data from their plateau regions (i.e., kd = 0.34–0.37 s−1). This result indicated that mass transfer effects were not a problem with either type of column when peak decay data was obtained at higher flow rates and in the plateau region of plots like those in Figure 2.
Figure 4.

(a) Original chromatograms and (b) logarithmic peak profiles for 100 µl injections of 10 µM racemic warfarin applied to a 2.5 mm × 2.1 mm I.D. HSA column or control column containing 7 µm silica particles. The flow rates used in these experiments (from left-to-right) were 4.0, 3.5, 3.0, 2.5, and 2.0 ml/min. The mobile phase was pH 7.0, 0.10 M potassium phosphate buffer and the temperature was 25°C.
4.5 Determination of dissociation rates for R- and S-warfarin from HSA
The final series of experiments used the non-competitive peak decay method to study the dissociation of warfarin from immobilized HSA at pH 7.4. These experiments were carried out in the presence of pH 7.4, 0.067 M potassium phosphate buffer using a 100 µL sample that contained 20 µM of R- or S-warfarin. A 2.5 mm × 2.1 mm I.D. HSA column containing 5 µm silica was used in this part of the study and the temperature of this column was held at either 4°C or 37°C. To avoid thermal mismatches during these experiments, the samples and mobile phase were kept at the same temperature as the column by means of a circulating water bath. In addition, all samples and mobile phase solutions were passed through a serpentine coil of tubing held at the same temperature as the column prior to contact with immobilized HSA. Measurements of the mobile phase and column temperatures with this system gave a difference of less than 0.2°C even when working at flow rates up to 5.0 ml/min. Identical studies were performed with the control columns. Some typical peak decay profiles that were obtained are shown in Figure 5.
Figure 5.
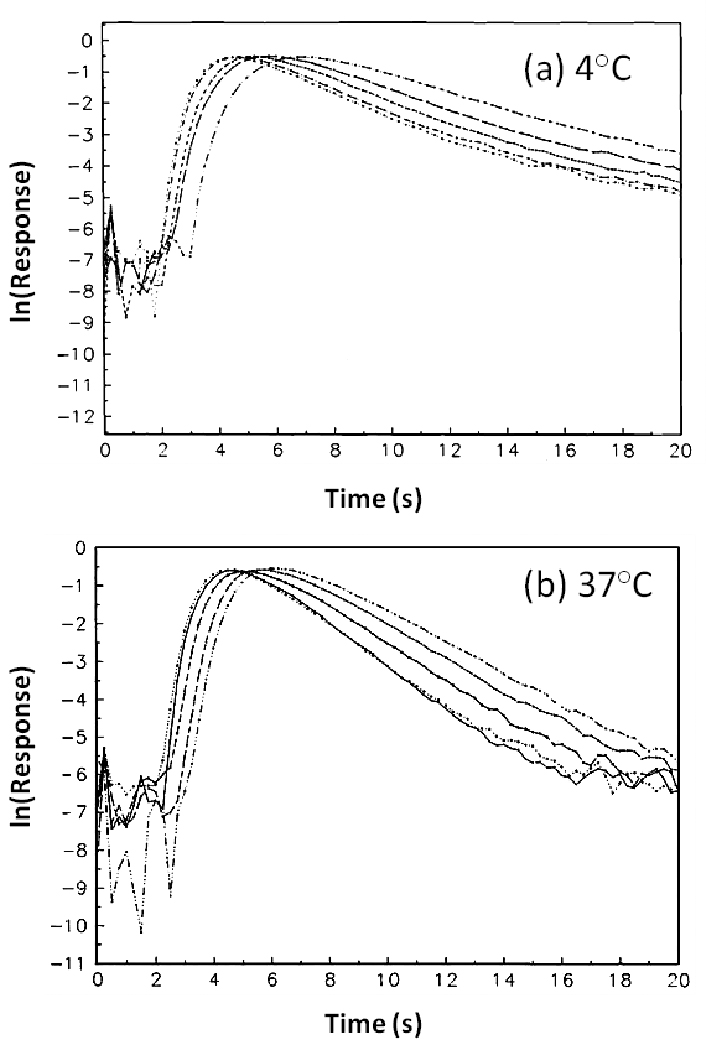
Representative decay profiles for R-warfarin at (a) 4°C and (b) 37°C. The chromatograms represent elution at flow rates of (left to right) 5.0, 4.5, 4, 3.5, and 3.0 mL/min and were obtained using a 100 µL sample containing 20 µM of R- or S-warfarin injected onto 2.5 mm × 2.1 mm I.D. columns packed with 5 µm silica.
At 4°C, the slopes obtained for peak decay plots generated at 4.0–5.0 ml/min were quite close for the two enantiomers of warfarin. The plateau region of these plots gave dissociation rate constants of 0.39 (± 0.01) and 0.44 (± 0.01) s−1 for R- and S-warfarin, respectively. At 37°C, the plateaus of the peak decay plots were less pronounced, as might be caused by faster mass transfer and reassociation, but the results obtained at the highest flow rates were still used to provide estimates of the dissociation rate constants for the warfarin-HSA system. Under these conditions, the dissociation rate constants were determined to have apparent value of 0.56 (± 0.01) and 0.66 (± 0.01) s−1 for R- and S-warfarin, respectively.
The rate constants measured in this work were close to the average value of 0.7 s−1 that has been determined for racemic warfarin with solution-phase HSA at 6°C by stopped flow analysis [20]. These results also agreed with previous dissociation rate constants that have been measured for immobilized HSA, where values of 0.1–2 s−1 at 4–37°C have been determined using surface plasmon resonance [34] and values of 0.06–0.56 s−1 have been reported at 4–37°C using chromatographic band-broadening studies [9]. Thus, there appeared to be good agreement between the results of this current work and previous values in the literature. This comparison indicated that the non-competitive peak decay method developed in this study could be used as an effective tool in determining the dissociation rate constants for the warfarin-HSA system.
5 Concluding remarks
In this study a modified non-competitive peak decay method was developed and optimized for the study of drug-protein dissociation in weak-to-moderate affinity systems. This approach was tested by used it to examine the dissociation of warfarin from HSA. Several parameters were considered in the development of this method, including the effects of changing the column size, analyte concentration, sample volume, flow rate, and particle size of the support material. Dissociation rate constants were obtained for R- and S-warfarin during their release from HSA at pH 7.4 and 4°C or 37°C, as well as the average dissociation rate constant for racemic warfarin from HSA at pH 7.0. These results are summarized in Table 3. The results obtained by this method were similar to those determined previously by other methods for both soluble and immobilized HSA [9,20,34]. The agreement of these results indicated that this approach could be used to successfully estimate drug-protein dissociation rates, especially in work with weak-to-moderate affinity proteins like HSA.
Table 3.
Summary of dissociation rate constants determined by the peak decay method for warfarin from HSA
| Dissociation rate constant, kd (s−1)a | |||
|---|---|---|---|
| Temperature | R-Warfarin | S-Warfarin | Racemic warfarin |
| 4°C | 0.39 (± 0.01) | 0.44 (± 0.01) | --- |
| 37°C | 0.56 (± 0.01) | 0.66 (± 0.01) | --- |
| 25°C | --- | --- | 0.35 (± 0.02)b |
The values for the individual enantiomers of warfarin were measured in pH 7.4, 0.067 M potassium phosphate buffer, while the value for the racemic mixture was measured in pH 7.0, 0.10 M potassium phosphate buffer. The values in parentheses represent a range of ± 1 S.D.
Individual estimates for kd ranged from 0.34 s−1 to 0.37 s−1 for the various columns and analysis conditions used in this study.
This non-competitive peak decay method has several possible advantages in the study of drug-protein kinetics and other systems with relatively fast association/dissociation kinetics. For instance, previous peak decay theory was revised in this work to consider analyte reassociation, thereby eliminating the need for a competing agent and its associated experimental complications [4,14]. In comparison to earlier studies using band-broadening measurements, this new approach does not require the estimation or measurement of plate heights, which can be a tedious process [4]. Because linear elution conditions are not required, this method can also use higher analyte concentrations than band-broadening measurements. In addition, this new technique does not require a change in flow rate or mobile phase between the sample application and elution steps, as is needed in previous peak decay work, which avoids changes in the background response due to flow rate and pressure changes [4,14]. These features should make this approach useful in studying the kinetics of other drugs with HSA or in the analysis of other solute-ligand systems with similar equilibrium and rate constants. In addition, the ability of this method to work with small columns and at high flow rates should make it appealing as a method for the high-throughput screening of drug candidates for their interactions with HSA and other proteins.
Acknowledgments
This work was supported by the National Institutes of Health under grant R01 GM044931. The authors thank Sanjay Mukherjee for providing the immobilized HSA support that was prepared using Nucleosil Si-300-7 silica and for determining the diol content and protein content of this material.
Glossary
Abbreviations
- HPAC
high-performance affinity chromatography
- HSA
human serum albumin
Nomenclature
- A
Analyte or solute applied to the column
- dp
Packing material particle diameter
- Dm
Diffusion coefficient of analyte in the mobile phase
- [A]
Analyte concentration in the mobile phase
- Ae
Analyte outside of the pores of the packing material
- Ap
Analyte inside the pores of the packing material
- A−L
Complex of analyte and immobilized ligand
- Hk
Plate height due to stationary phase mass transfer
- Hsm
Plate height due to stagnant mobile phase mass transfer
- Hm
Plate height due to mobile phase mass transfer
- Hl
Plate height due to longitudinal diffusion
- Hec
Plate height due to extracolumn band-broadening
- k’
Retention factor
- k1
Diffusion rate constant of analyte from outside of the pore to inside
- k−1
Diffusion rate constant of analyte from inside of the pore to outside
- ka
Association rate constant
- kd
Dissociation rate constant
- Ka
Association equilibrium constant
- L
Immobilized ligand
- mA0
Initial number of moles of adsorbed analyte
- mAe
Number of moles of analyte eluted at time t
- mL
Number of moles of active ligand in the column
- mL,app
Apparent number of moles of analyte required to saturate the column
- u
Linear velocity
- VM
Void volume
- Vp
Pore volume
- γ
Tortuosity factor
References
- 1.Rich RL, Myszka DG. J. Mol. Recogn. 2005;18:1–39. doi: 10.1002/jmr.726. [DOI] [PubMed] [Google Scholar]
- 2.Myszka DG. Anal. Biochem. 2004;329:316–323. doi: 10.1016/j.ab.2004.03.028. [DOI] [PubMed] [Google Scholar]
- 3.Ramakrishnan A, Sadana A. Methods for Affinity-Based Separations of Enzymes and Proteins. 2002:195. [Google Scholar]
- 4.Walters RR. Ch. 3. In: Chaiken IW, editor. Analytical Affinity Chromatography. Boca Raton, FL: CRC Press; 1987. [Google Scholar]
- 5.Hage DS, Austin J. J. Chromatogr. B. 2000;739:39–54. doi: 10.1016/s0378-4347(99)00445-4. [DOI] [PubMed] [Google Scholar]
- 6.Talbert AM, Tranter GE, Holmes E, Francis PL. Anal. Chem. 2002;74:446–452. doi: 10.1021/ac010643c. [DOI] [PubMed] [Google Scholar]
- 7.Anderson DJ, Walters RR. J. Chromatogr. 1986;376:69–85. [Google Scholar]
- 8.Chaiken IM. Anal. Biochem. 1979;97:1–10. doi: 10.1016/0003-2697(79)90319-1. [DOI] [PubMed] [Google Scholar]
- 9.Loun B, Hage DS. Anal. Chem. 1996;68:1218–1225. doi: 10.1021/ac950827p. [DOI] [PubMed] [Google Scholar]
- 10.Muller AJ, Carr PW. J. Chromatogr. 1984;284:33–51. [Google Scholar]
- 11.Yang J, Hage DS. J. Chromatogr. A. 1997;766:15–25. doi: 10.1016/s0021-9673(96)01040-0. [DOI] [PubMed] [Google Scholar]
- 12.Hage DS, Walters RR, Hethcote HW. Anal. Chem. 1986;58:274–279. doi: 10.1021/ac00293a003. [DOI] [PubMed] [Google Scholar]
- 13.Renard J, Vidal-Madjar C. J. Chromatogr. 1994;661:35–42. doi: 10.1016/0021-9673(94)85174-3. [DOI] [PubMed] [Google Scholar]
- 14.Moore RM, Walters RR. J. Chromatogr. 1987;384:91–103. [Google Scholar]
- 15.Sudlow G, Birkett DJ, Wade DN. Mol. Pharmacol. 1976;12:1052–1061. [PubMed] [Google Scholar]
- 16.He XM, Carter DC. Nature. 1992;358:209–215. doi: 10.1038/358209a0. [DOI] [PubMed] [Google Scholar]
- 17.Lagercrantz C, Larsson T, Denfors I. Comp. Biochem. Physiol. C. 1981;69:375–378. doi: 10.1016/0306-4492(81)90153-2. [DOI] [PubMed] [Google Scholar]
- 18.Miller JHM, Smail GA. J. Pharm. Pharmacol. 1977;29:33P. doi: 10.1111/j.2042-7158.1977.tb11501.x. [DOI] [PubMed] [Google Scholar]
- 19.Loun B, Hage DS. Anal. Chem. 1994;66:3814–3822. doi: 10.1021/ac00093a043. [DOI] [PubMed] [Google Scholar]
- 20.Rietbrock N, Lassmann A. Naunyn-Schmiedeberg's Arch. Pharmacol. 1980;313:269–274. doi: 10.1007/BF00505744. [DOI] [PubMed] [Google Scholar]
- 21.Wilting J, Kremer JMH, Ijzerman AP, Schulman SG. Biochim. Biophys. Acta. 1982;706:96–104. [Google Scholar]
- 22.Maes V, Engelborghs Y, Hoebeke J, Maras Y, Vercruysse A. Mol. Pharmacol. 1982;21:100–107. [PubMed] [Google Scholar]
- 23.Kremer JMH, Bakker G, Wilting J. Biochim. Biophys. Acta. 1982;708:239–242. doi: 10.1016/0167-4838(82)90227-8. [DOI] [PubMed] [Google Scholar]
- 24.Bos OJM, Fischer MJE, Wilting J, Janssen LHM. Biochem. Pharmacol. 1989;38:1979–1984. doi: 10.1016/0006-2952(89)90497-8. [DOI] [PubMed] [Google Scholar]
- 25.Twine SM, Gore MG, Morton P, Fish BC, Lee AG, East JM. Arch. Biochem. Biophys. 2003;414:83–90. doi: 10.1016/s0003-9861(03)00173-5. [DOI] [PubMed] [Google Scholar]
- 26.Loun B, Hage DS. J. Chromatogr. 1992;579:225–235. [PubMed] [Google Scholar]
- 27.Clarke W, Hage DS. Anal. Chem. 2001;73:1366–1373. doi: 10.1021/ac000870z. [DOI] [PubMed] [Google Scholar]
- 28.Ruhn PF, Garver S, Hage DS. J. Chromatogr. A. 1994;669:9–19. doi: 10.1016/0021-9673(94)80332-3. [DOI] [PubMed] [Google Scholar]
- 29.Chattopadhyay A, Hage DS. J. Chromatogr. A. 1997;758:255–261. doi: 10.1016/s0021-9673(96)00742-x. [DOI] [PubMed] [Google Scholar]
- 30.Smith PK, Krohn RI, Hermanson GT, Mallia AK, Gartner FH, Provenzano MD, Fujimoto EK, Goeke NM, Olson BJ, Klenk DC. Anal. Biochem. 1985;150:76–85. doi: 10.1016/0003-2697(85)90442-7. [DOI] [PubMed] [Google Scholar]
- 31.Giddings JC. United Separation Science. New York: Wiley; 1991. [Google Scholar]
- 32.Perry J. Chemical Engineers Handbook. New York: McGraw-Hill; 1963. [Google Scholar]
- 33.Neue UD. HPLC Columns: Theory, Technology and Practice. New York: Wiley-VCH; 1997. [Google Scholar]
- 34.Rich RL, Day YSN, Morton TA, Myszka DG. Anal. Biochem. 2001;296:197–207. doi: 10.1006/abio.2001.5314. [DOI] [PubMed] [Google Scholar]


