Shape transition during nest digging in ants

Abstract

Nest building in social insects is among the collective processes that show highly conservative features such as basic modules (chambers and galleries) or homeostatic properties. Although ant nests share common characteristics, they exhibit a high structural variability, of which morphogenesis and underlying mechanisms remain largely unknown. We conducted two-dimensional nest-digging experiments under homogeneous laboratory conditions to investigate the shape diversity that emerges only from digging dynamics and without the influence of any environmental heterogeneity. These experiments revealed that, during the excavation, a morphological transition occurs because the primary circular cavity evolves into a ramified structure through a branching process. Such a transition is observed, whatever the number of ants involved, but occurs more frequently for a larger number of workers. A stochastic model highlights the central role of density effects in shape transition. These results indicate that nest digging shares similar properties with various physical, chemical, and biological systems. Moreover, our model of morphogenesis provides an explanatory framework for shape transitions in decentralized growing structures in group-living animals.

The building of structures by animals is a widely spread phenomenon, from protozoa to primates (1). These structures can be considered an extension of the animal body: They have an adaptive value by improving the regulation of energetic exchanges with the outer environment (2), by ensuring the management of waste compounds (3), and by allowing food storage or protection against predation, but also by shaping the spatial distribution of social interactions (4). The nests of social insects take over all of these functions and show a robust relationship between nest volume and colony size (5 –9). In ants, every nest is made of the same basic building modules (9 –11) (i.e. chambers, tunnels), the sameness of which contrasts with the diversity of nest architecture (number and proportion of different modules, nest topology, and pattern regularity) that varies not only interspecifically but also intraspecifically according to the colony growth process (7, 9).

Although a dynamic study of nest building is essential to understand how the diversity of patterns is generated, there are few such studies (5, 6) addressing this issue. Most research describes final nest structures (7, 9, 12) or focuses on particular digging behaviors (13, 14) but provides few insights on the building process as a whole or on the mechanisms that generate a diversity of nest shapes.

The prevailing questions, therefore, are: Does the shape diversity find its origin in the complexity of the building behaviors of the insects, a specific behavior being associated to a specific shape or in quantitative changes in digging activity? Does it result from changes in the insect environment due to the building process itself? Or does the nest pattern emerge under strict control of the environment? Undoubtedly, all these parameters and behaviors should not be considered as alternatives: They interact constantly with one another and influence the building process at different levels.

In order to set apart the influence of environmental heterogeneities on the diversity of nest shapes, our experiments on Lasius niger ants were conducted by using a two-dimensional (2D)-homogeneous setup. Such a study is required to understand how, and to what extent, morphogenesis relies on the digging dynamics and the influence of the excavated structure on the building behavior. Furthermore, as the colony size is known to regulate the digging activity (5, 8), we compared two experimental conditions (groups of 50 and 300 workers) to assess the influence of group size on morphogenesis as well as on shape transition during the building process.

Results

Excavation Dynamics.

Our results show that the nest excavation begins with fast and amplified growth and reaches a saturation phase at which activity almost totally ceases (Fig. 1 A), as highlighted in previous works (5, 8). We fit this digging dynamics with the following equation:

where A (in cm²) is the excavated area (i.e. the nest area), t (in hours) is the time elapsed since the start of nest digging, A _M is the maximal area of the nest that is ultimately dug out, α stands for the cooperation level between ants (300 ants: α = 1.72 ± 0.33, n = 33; 50 ants: α = 1.38 ± 0.33, n = 20) and β is the time value when A = 0.5A _M (i.e. when half of the maximal nest area has been excavated; 300 ants: β = 8.84 ± 3.84 h, n = 33; 50 ants: β = 12.17 ± 5.37 h, n = 20) (fitting with Eq. 1 always returned coefficient of determination r ² ≥ 0.95). High α and low β values characterize a high and fast digging activity that is enhanced in large groups of ants. During the experiment, the digging rate (R), calculated as the derivative $\frac{dA}{dt}$ of the fitted area from Eq. 1, reaches a maximum and decreases until it ceases, or tends to be residual when A ≃ A _M.

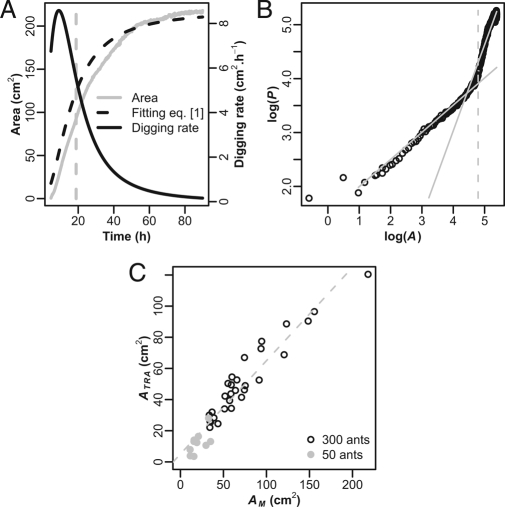
Fig. 1.

Quantitative characterization of morphological transition. (A and B) Example of experimental results (experiment 30). The gray dashed vertical line corresponds to the occurrence of the morphological transition, which separates the first and second growth stages. (A) Evolution of the nest area and digging rate (Eq. 1 fitting parameters: A_M = 218.10 cm²; α = 1.95; β = 16.3 h; r ² = 0.99). The gray line represents the area, the black dashed line corresponds to the Eq. 1 fitting curve, and the black curve represents the digging rate. The digging rate is calculated as the derivative $\frac{dA}{dt}$ of the fitted area from Eq. 1. (B) Logarithm of the perimeter (log(P)) versus logarithm of the area (log(A)) of the nest. Gray lines correspond to the linear fits for the first and second stages with slope ω (respectively ω = 0.50 and ω = 1.60). (C) The relation between nest areas at transition (A _Tra) and at the end of experiments (A _M) for both group size (black open circles: 300 ants, n = 29; gray open circles: 50 ants, n = 12) (A _Tra = 0.60 * A _M + 5.06, F _1,39 = 446, P < 0.0001, r ² = 0.92).

Morphological Growth.

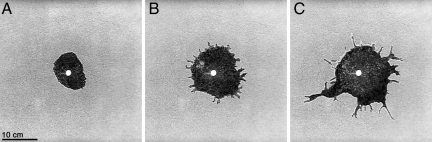
The most striking result of our experiments is the occurrence of a sharp morphological transition (Fig. 2; see also Movies S1 and S2 of the SI Appendix) that separates two distinct growth stages. The morphological transition occurs when the nest excavation goes from a first stage of circular and isotropic growth (Fig. 2 A) to a second one of ramified growth (Fig. 2 B – C). During this second stage, characterized by a branching pattern, small buds appear regularly along the wall of the nest, some of them growing into lateral galleries. We note that because the environment is identical throughout the experimental arena, this transition must be purely a result of the internal dynamics.

Fig. 2.

Morphological transition occurring during nest digging in ants. (A–C) Snapshots of the nest showing the two successive digging stages (experiment 30). (A) First stage of homogeneous and circular digging. (B and C) Second stage where buds appear over the nest wall, some of them growing into lateral galleries through a branching process.

The relationship between nest area (A) and nest perimeter (P) (P = μA ^ω) characterizes the nest morphology, and its variation through time allows us to identify the occurrence of such morphological transition (see Materials and Methods). During the first stage, where activity rate is the highest, the nest cavity can be roughly approximated by a growing disc with a smooth and regular wall. The value of ω during this stage (300 ants: ω₁ = 0.50 ± 0.03, n = 29; 50 ants: ω₁ = 0.56 ± 0.05, n = 12) (Fig. 1 B and Table 1) confirms that the nest is close to a regular disc (ω = 0.5). When the nest area A reaches a critical value (A _Tra), several buds appear along the nest wall and make the perimeter increase longer abruptly than the area, the nest shape being no longer like a disc. The relationship between A and P, therefore, changes sharply, as evidenced by the high values of ω (300 ants: ω₂ = 1.84 ± 0.83, n = 29; 50 ants: ω₂ = 1.55 ± 0.62, n = 12). In some cases, no transition occurred. These experiments are characterized during the whole digging process by a ω value close to 0.5 (300 ants: ω₁ = 0.49 ± 0.03, n = 4; 50 ants: ω₁ = 0.61 ± 0.10, n = 8), meaning that nests dug remained smooth and round.

Table 1.

Comparison between 300- and 50-ant experiments with a morphological transition

		Mean ±SD (number of replicates)		Mann–Whitney test
Feature	Parameter	300 ants	50 ants	U statistics	P value
Dynamic	α	1.71 ± 0.34 (29)	1.39 ± 0.33 (12)	72	0.003
	β	9.16 ± 4.00 (29)	12.61 ± 5.76 (12)	245	0.042
	AM	75.18 ± 42.76 (29)	20.18 ± 7.99 (12)
	AMNorm	0.251 ± 0.143 (29)	0.404±0.160 (12)	61	<0.001
Transition	ω1	0.50 ± 0.03 (29)	0.56 ± 0.05 (12)	291	<0.001
	ω2	1.84 ± 0.83 (29)	1.55 ± 0.62 (12)	132	0.238
	ATra	51.99 ± 24.41 (29)	12.60 ± 6.35 (12)
	ATraNorm	0.173 ± 0.081 (29)	0.252 ± 0.127 (12)	92	0.018
Density*	PTra	36.47 ± 11.98 (29)	21.85 ± 8.71 (12)
	ρM	0.535 ± 0.390 (29)	0.758 ± 0.908 (12)	148	0.470
	ρ75	0.291 ± 0.170 (29)	0.388 ± 0.448 (12)	155	0.601
	ρ50	0.066 ± 0.029 (29)	0.072 ± 0.050 (12)	187	0.724
	ρTra	0.038 ± 0.022 (29)	0.041 ± 0.045 (12)	202	0.436

Boldface font values have been normalized before statistical comparison (see Materials and Methods).

*Reference densities corresponding to specific values of digging rate are calculated chronologically: ρ_M when rate is maximum (R = R_M), ρ₇₅ when R = 0.75R_M, ρ₅₀ when R = 0.50R_M and ρ_Tra at the transition time.

The main difference between the two experimental conditions lies in the number of experiments showing no transition from a circular to a ramified nest: 40% for 50 ants (n = 20 experiments) against 12% for 300 ants (n = 33 experiments). Furthermore, values of the estimated area dug per ant (A _MNorm, Table 1) are lower for large group size, which supports a rule previously shown in several studies (5 –8), according to which the nest area increases sublinearly with the group size.

The larger the group size, the higher the transition (A _Tra) and ultimate (A _M) area values (Table 1). The transition occurs when the nest area has reached 60% of its final value A _M whatever the group size (Fig. 1 C and Table 1). Within the same group size (50 or 300 ants), A _Tra and A _M vary between experiments (Table 1). This variance is probably due to differences in the activity level of tested groups of ants that can also be increased by amplification processes (15, 16). The larger the group and the more active the ants, the more workers dig (A _M) and the later (greater A _Tra) the morphological transition occurs.

Experiments without transition are characterized by lower ultimate nest areas (A _M) that are similar to area values of transition (A _Tra) of ramified nests (experiments without transition = 300 ants: A _M = 53.81 ± 20.35 cm², n = 4; 50 ants: A _M = 11.95 ± 4.25 cm², n = 8), suggesting that a threshold of mean digging activity and/or of excavated area must be reached in order to observe a change in the nest shape.

Combining the global digging activity (approximated by the digging rate R) and the cavity area (A) at any time of the experiment, we define the density of activity (ρ),

which should not be confused with density of individuals. The density of activity decreases from the beginning of the experiment until its end (Table 1). Despite the high variability of densities of activity during the first stage, the morphological transition is characterized by a value of ρ(ρ_Tra) independent of group size (300 ants: ρ_Tra = 0.038 ± 0.022 h⁻¹, n = 29; 50 ants: ρ_Tra = 0.041 ± 0.045 h⁻¹, n = 12) (see Table 1).

Simulations.

Based on these results, we propose a scenario to explain the morphological transition in nest shape. We assume that the nest area is a limiting factor of the digging activity, because crowding close to the digging front and/or limitation of the worker traffic between the front and the unloading zone of excavated material may occur depending on nest size (see Fig. S1 of the SI Appendix). At the start of nest excavation, the digging behavior of ants is stimulated and amplified by different processes, such as pheromone release (17), interattraction between workers (18), and/or activity by-product (14, 19). Then the group of digging ants quickly reaches a maximal value of potentially active workers. As the number of digging ants stays large (relatively to nest area and perimeter), workers cannot perform localized digging because of the crowding of ants along the perimeter of the nest. However, as the nest area increases, the average density of activity (ρ) tends to decrease until it reaches a critical value where the transition may occur, and localized excavated buds may appear because of amplification processes.

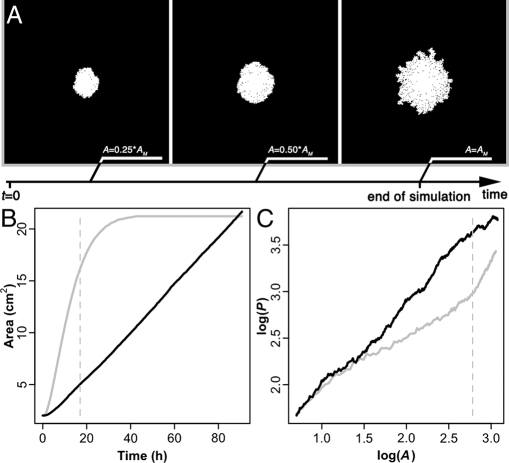
To test the validity of our scenario, we have used a multi-agent model (see Materials and Methods and Fig. S3 of the SI Appendix) based on crowding along the nest perimeter and amplification processes (previous digging increases the probability of digging at the same place). The results of our simulations demonstrate that with such digging rules, a morphological transition can occur during the nest growth (Fig. 3 A and C and Table 2). Simulation-generated patterns for both group sizes show a morphological transition in agreement with experimental values (simulation values: 300 ants: ω₁ = 0.53 ± 0.00, ω₂ = 3.17 ± 0.51, n = 30; 50 ants: ω₁ = 0.59 ± 0.01, ω₂ = 1.66 ± 0.41, n = 30) (Table 2). The fact that neither behavioral changes nor environmental heterogeneities are implemented in our model strongly suggests that the shape transition is due to interplay between the geometry of the nest and the global digging activity. Moreover, the model shows that, in the range of our experimental data, no morphological transition occurs in the case of a linear digging dynamics. The nest is weakly heterogeneously dug during the overall simulation (ω = 0.93 during the whole excavation) (Fig. 3 B and C). A nonlinear dynamic seems to be required to observe the morphological transition we describe here, as it may strongly reinforce the variation of ρ through time. As a first step, it may stabilize the isotropic growth during the first stage, as crowding is maintained by the accelerating dynamics. In a second step, it may drastically accelerate the decreasing of ρ: When the digging rate decreases, the nest becomes ramified.

Fig. 3.

Nest-digging simulations reproduce the morphological transition. (A – C) Results of the simulations with 50 ants (A _M50 = 20.18 cm², K = 50, ξ = 0.1 %, ν = 0.05), each condition being represented by a given color: nonlinear dynamics condition in gray (experimental digging dynamics: θ₅₀ = 0.38); linear dynamics condition in black (linear digging rate: σ = 0.0037). (A) Nest morphology at different times (A = 0.25A _M; A = 0.5A _M; A = A _M) for the nonlinear dynamics condition. Dug area is represented in white. (B and C) Morphological transition for nonlinear dynamics condition is represented in gray dashed lines. (B) Nest area (A) against time. (C) Logarithm of the perimeter (log(P)) versus logarithm of the area (log(A)) (nonlinear dynamics condition: ω₁ = 0.57, ω₂ = 1.73; linear dynamics condition: ω = 0.93).

Table 2.

Comparison between experimental and simulations results for both group sizes (300 and 50 ants)

Parameter	Mean ± SD (number of replicates)
	300 ants (exp.)	300 ants (sim.)	50 ants (exp.)	50 ants (sim.)
ω1	0.5 ± 0.03 (29)	0.53 ± 0.00 (30)	0.56 ± 0.05 (12)	0.59 ± 0.01 (30)
ω2	1.84 ± 0.83 (29)	3.17 ± 0.51 (30)	1.55 ± 0.62 (12)	1.66 ± 0.41 (30)
ATra	49.92 ± 23.11 (29)	69.10 ± 1.18 (30)	12.60 ± 6.35 (12)	16.14 ± 1.19 (30)
ρTra	0.038 ± 0.022 (29)	0.015 ± 0.002 (30)	0.041 ± 0.045 (12)	0.031 ± 0.010 (30)

Experimental results (exp.) are those of experiments with a morphological transition. Simulation results (sim.) are those of nonlinear dynamics condition (A_{M 300} = 75.18 cm², A_{M 50} = 20.18 cm², θ₃₀₀ = 1.08, θ₅₀ = 0.38, K = 50, ξ = 0.1 %, ν = 0.05).

Discussion

Nest digging in ants presents a morphological transition between two distinct growth stages, this phenomenon being controlled by the dynamics of digging ants' density. Our results show that different patterns may emerge even in a homogeneous environment and without behavioral changes, only as by-products of the digging process.

Our theoretical and experimental results explain the patterns of ants' nests observed under rocks, which are dug in almost 2D-conditions, and that share shapes similar to those described here. Moreover, several field studies on ants (9, 20, 21) and termites (22) have described flat, horizontal chambers that are rounded and may become lobed as they are enlarged.

Previous works (23) have shown that the relationship between colony size and nest volume could be explained without an explicit measure of the nest volume. By considering a heterogeneous distribution of ants in the nest (12), coupled to our algorithm based on nest-digging activity, one may reproduce the succession of chambers (high-activity period) and tunnels (residual activity before global shutdown). This framework may conciliate the regulation of nest volume and the diversity of nest structures, as suggested by the strong relationship between A _Tra and A _M.

In addition, our 2D model can be easily extended to a three-dimensional (3D) model, the perimeter and area of the 2D nest becoming surface and volume of the 3D nest respectively. From our model, one can expect the excavation of spherical chambers under high digging rates that may later become ramified. However, the scenario, developed in homogeneous conditions, has to be completed with several environmental parameters. For instance, one unavoidable parameter is gravity, to which ants are known to respond by digging more frequently towards the bottom of a vertical setup (24). It has been shown that the coupling between amplification mechanisms modulated by the group size and such environmental templates may lead to very different patterns or dynamics (10, 15, 23, 25). This template effect of gravity may account for the formation of ellipsoidal chambers or of vertical tunnels (7, 9, 12, 20).

To conclude, the morphological transition described here corresponds to a branching process in which instabilities along a growth interface (i.e., the nest perimeter) lead to the formation of branched patterns (i.e. lateral galleries). Our results show that the characteristics and the occurrence of transitions depend on the group size. In social insects, such transitions have been reported for trail foraging: Small ant colonies forage in a disorganized manner, with a transition to organized pheromone-based foraging in larger colonies (26 –28). Other examples are reported for gregarious insects where the density of individuals controls the emergence of aggregation patterns (29 –31) or for fish, where the number of individuals affects collective decision making (32). Such morphological transitions between two stages of growth have already been described in several chemical [electrochemical deposition (33), combustion (34)], physical [viscous fingering in Hele–Shaw cells (35)], and biological [coral (36) or bacteria community (37) growth, wound healing (38), or collective migration (39)] systems.

Concerning social animals, different examples reported in the literature strongly suggest that shape transitions are not restricted to the digging of social insects. Army ants start their foraging raids by forming a swarm that sweeps the neighborhood of their bivouac. This pattern later shifts towards a small number of well-marked chemical trails (40). Gregarious larvae of bark beetles (Dendroctonus sp) feed side by side on the inner bark, digging a 2D feeding chamber that becomes ramified (41, 42). We postulate that such shape transition could be observed in many other group-living species. Based on our model assumption, these transitions are independent of the species and its specificities. Indeed, shape transitions can occur in any species that exhibits group activities that are based on mimetic behavior and that lead to spatial competition and exhaustion of the resources. Our scenario, based on digging ants' density, provides a new explanatory framework to account for the shift in growth stages and for the emergence of branched patterns that are widely spread in biological systems and in animal societies.

Materials and Methods

Ant Biology.

L. niger is a common monogynous and monomorphic Palaearctic ant species whose colony size may vary from thousands to tens of thousands of individuals. Workers are characterized by age polyethism (43), in which younger ants are brood tenders and may become foragers as they grow older. L. niger is an opportunistic species that can feed on living or dead insects (44), but its main food consists of aphids, honeydew (45), and, occasionally, extrafloral nectaries (46). Some nests may be found under plate rocks, but most of them are dug in the soil and can be easily located by the soil crater(s) or mound(s) surrounding their entrance(s). The nest structure consists mainly of two fundamental building blocks), (i.e. chambers and tunnels), whereas the volume of the nest is correlated to the colony size (8). Colonies of L. niger species were reared into laboratory conditions at a temperature of 20 °C. Colonies were fed with water–sugar solution (1M) and freshly killed mealworms (Tenebrio molitor). Groups of 50 or 300 workers (no brood, no queen) were randomly selected from 11 mother colonies. These groups were not fed during the whole experiment to prevent the ants from being engaged in tasks other than digging.

Digging Setup.

The setup was a dark box containing a horizontal digging area: two glass plates (42 × 42 cm), between which was placed a 2-mm high layer of wet Brusselean sand (15% of water). Groups of 300 (n = 33) or 50 (n = 20) ants were placed in a Petri dish, which was connected with the top center of the digging area by a tunnel with a radius r = 5.5 mm. This setup is considered 2D-effective, as ants dig the sand layer over its entire thickness and move only into horizontal directions. Such experimental digging conditions allow dynamical observations of the nest (13, 14). Two-dimensional nest patterns also exist in the field, especially under plate rocks, because of the strong thigmotactism shown by ants (25). All the experiments were carried out between November 2005 and April 2007, with each experiment ending after 90 h.

Experimental Measures.

Snapshots of the digging area were taken from below every 10 minutes under red light (47). Pictures have been automatically segmented to measure both the area and perimeter of the nest. All the statistical analyses were made by using R software (version 2.8.0) (48).

Analysis of Nest Shape and Morphological Transition.

The relationship between area (A) and perimeter (P) of the nest has been used to characterize changes of the nest pattern and the occurrence of the morphological transition. This relationship describes the roughness of the nest cavity with the equation P = μA ^ω, the parameters' values being, in the case of a circle, $\mu =2\sqrt{\pi }$ and ω = 0.5. The experimental value of ω is estimated by calculating the slope of the regression line of log(P) = ωlog(A). When ω is close to this lowest theoretical value, the nest border is as smooth as that of a disc. This parameter value will increase over time as soon as “buds” appear along the nest wall and make the nest cavity rough after the first transition. The transition point is characterized by a steep increase in the aforementioned relationship.

Statistical Characterization of the Transition Point.

The transition point has been characterized for each experiment by using a linear regression method (49) that splits a global set of values (of size N) into two subsets (of sizes n ₁ and n ₂ = N − n ₁), calculates their linear regression parameters, and computes a global standard deviation. This method is based on the following equation:

where a ₀ and b ₀ are the linear regression line parameters of the first subset (before transition) and a ₀ + a ₁ = a ₂ and b ₀ + b ₁ = b ₂ are those of the second subset (after transition). Stage is a binary variable whose value is 0 and 1 for points of the first and second subsets respectively. The first standard deviation value is calculated with n ₁ = 1. For each subsequent calculation step (as long as n ₁ < N − 1), the size of n ₁ is increased by adding the next point (in chronological order), this value being removed from the n ₂ subset. The transition point is the point at which the global standard deviation is the lowest. The relevance of the transition point is tested with an F -test that compares the r squared of the first subset with that of the global set of values.

Comparison Between 50- and 300-Ant Experiments.

All measured parameters (α, β, ω, ρ) from each set of experimental conditions have been compared by using Mann–Whitney rank sum test. Area (A) has been normalized before comparison. A _Norm is the area dug per ant $A_{\text{NORM}}=\frac{A_{300}}{300}=\frac{A_{50}}{50}$.

Simulations.

Simulations have been made by using lattices of square cells (600 × 600) standing for the digging setup. The correspondence between physical and theoretical values has been determined by using experimental measures (see SI Appendix). We determine that a nest cell has an area of A _cell = 0.07 mm² and that an ant is four cells wide (L. niger head's width is ≈1 mm). The duration of a time step is 1 minute, and a simulation lasts 5,400 time steps (which corresponds to the 90-h duration of the experiments). Each simulation starts with an initial circular area A ₀ (radius = 20 cells, which corresponds to the access hole of the experimental setup); (see Fig. S3 of the SI Appendix).

The experimental nonlinear digging dynamic is a by-product of the competition between positive feedback loops amplifying digging and negative loops consisting of aggregation. The calculation of the digging rate takes into account a saturation process (A _M) and an excavation process limited by the crowding close to the digging zone. This crowding zone is approximated by the perimeter P of a circle of surface A as P ≃ A ^0.5 (see SI Text and Fig. S1 of the SI Appendix). The area excavated per time step is therefore

where A _M is the nest final area and θ is a characteristic parameter of the digging rate. The resulting digging dynamics are well fitted by Eq. 1 (Fig. S2 of the SI Appendix). The mean values of θ were then estimated with experimental dynamics: θ₅₀ = 0.38 ± 0.43 (n = 12); θ₃₀₀ = 1.08 ± 0.39 (n = 29). The number of sand pellets that are excavated at each time step (N _pel) is calculated as

We also studied how the level of nonlinearity of the excavation process may act upon the nest morphogenesis by making simulations with a linear digging dynamic defined as

with $\sigma =\frac{A_M}{totalnumberoftimesteps}$, which gives σ₃₀₀ = 0.0139 and σ₅₀ = 0.0037.

To be dug, a cell must have at least one of its eight nearest neighboring cells already dug, and a cell must be reachable by an ant (taking an ant head's width into account). At each time step, the list of reachable cells (of length N _reach) is updated, and the number of excavated pellets at this time step (N _pel) is calculated (Eq. 4 or 6, depending on the chosen digging dynamics).

Then, for each of N _pel pellet excavations, the probability of each cell i to be dug is computed as follows:

where x is the total quantity of pheromone already present in the eight nearest neighboring cells, K is the number of pheromone units needed to get a response of 50%, and ξ is the intrinsic probability of the cell to be dug (i.e., when x = 0). One of these cells is randomly chosen and dug according to its value of p _dig and then is filled with 100 units of pheromones. At the end of the time step, a given fraction of pheromone (ν) has evaporated while nest area and perimeter are computed. Then the simulation enters the following time step.