Long-lived states to sustain hyperpolarized magnetization

Abstract

Major breakthroughs have recently been reported that can help overcome two inherent drawbacks of NMR: the lack of sensitivity and the limited memory of longitudinal magnetization. Dynamic nuclear polarization (DNP) couples nuclear spins to the large reservoir of electrons, thus making it possible to detect dilute endogenous substances in magnetic resonance spectroscopy (MRS) and magnetic resonance imaging (MRI). We have designed a method to preserve enhanced (“hyperpolarized”) magnetization by conversion into long-lived states (LLS). It is shown that these enhanced long-lived states can be generated for proton spins, which afford sensitive detection. Even in complex molecules such as peptides, long-lived proton states can be sustained effectively over time intervals on the order of tens of seconds, thus allowing hyperpolarized substrates to reach target areas and affording access to slow metabolic pathways. The natural abundance carbon-13 polarization has been enhanced ex situ by almost four orders of magnitude in the dipeptide Ala-Gly. The sample was transferred by the dissolution process to a high-resolution magnet where the carbon-13 polarization was converted into a long-lived state associated with a pair of protons. In Ala-Gly, the lifetime T_LLS associated with the two nonequivalent H^α glycine protons, sustained by suitable radio-frequency irradiation, was found to be seven times longer than their spin-lattice relaxation time constant (T_LLS/T₁ = 7). At desired intervals, small fractions of the populations of long-lived states were converted into observable magnetization. This opens the way to observing slow chemical reactions and slow transport phenomena such as diffusion by enhanced magnetic resonance.

One of the many advantages of magnetic resonance (MR) compared with computed tomography (CT) and imaging methods based on radioactive tracers, such as positron emission tomography (PET) or single photon emission computed tomography (SPECT), lies in the ability of MR to determine both the spatial distribution of the substrates and their transformation through metabolic processes. Unfortunately, most applications of magnetic resonance imaging (MRI) techniques are limited to the detection of water, because other substances are not sufficiently abundant. Even with infusion of labeled substrates, chemical shift imaging (CSI) suffers from poor sensitivity. Thus, the potential to differentiate between molecules is often left unused. The sensitivity of magnetic resonance spectroscopy (MRS) and imaging (MRI) may be considerably improved by coupling the nuclear spins to electron spins via dynamic nuclear polarization (DNP) (1). By enhancing the nuclear polarization of selected endogenous substances, one cannot only image their spatial distribution without background signals, but also visualize their metabolic reaction products (2). The use of hyperpolarized substrates to follow metabolic pathways should become widespread, provided nuclear magnetization can be sustained for sufficiently long times. The short T₁ lifetimes of longitudinal proton magnetization constitute a serious obstacle in the way of applications of hyperpolarization to protons, so that DNP tends to be confined to the realm of nuclei with low gyromagnetic ratios. We demonstrate that significant gains in lifetimes may be obtained for protons. Increasing the lifetimes of polarized molecules leads to better spatial and temporal resolution in MRI (3).

A first type of experiments that can enhance nuclear polarization, known as in situ DNP, relies on irradiation of electron spin ESR transitions in the same magnet where NMR signal detection is performed. These experiments yield polarization enhancements via DNP using gyrotrons (4) or via the Overhauser effect (5–7). An important characteristic of these experiments is that they can be repeated within short time intervals, allowing one to improve the signal-to-noise ratio by signal averaging or to record multidimensional spectra. Another class of experiments, which have come to be known as dissolution DNP (8), relies on ex situ irradiation of the ESR transitions at a temperature of ≈1.2 K to enhance the nuclear polarization. The sample is then heated up rapidly, before its transfer from the polarizing magnet to a high-resolution magnet for NMR detection. This approach can yield enhancements of more than four orders of magnitude, but the number of observations (“scans”) is limited, and it takes several hours to build up the enhanced nuclear polarization, so that one can typically perform only one or two experiments per day. The intrinsically short lifetimes of the hyperpolarized magnetization, limited by the longitudinal relaxation time constant T₁ at the temperature of the NMR detection, compel one to make use of this slowly built polarization within a time interval t < 5T₁. The short lifetime of the polarization of sensitive spins is the most serious constraint on dissolution DNP experiments to this date, according to the inventors of the method (3). In this work, we show that enhanced proton polarization may be stored in so-called long-lived states (LLS) (9, 10), with lifetimes T_LLS that are much longer than the proton T₁, so as to relax the constraints on the interval between low-temperature prepolarization and room-temperature NMR detection.

Potential applications of dissolution DNP using long lifetimes of magnetization include mapping the slow spread of endogenous substances through organisms by angiography (3), real-time metabolic imaging (11), monitoring the flux of substrates through enzymatic processes on long time scales (12), and following slow diffusion in porous materials (13). For imaging of metabolic processes, the excitation of spin states with long lifetimes in hyperpolarized substances leads to a better contrast against the background (14). The lifetimes T_LLS are more sensitive to the environment than the T₁ and T₂ relaxation time constants, and may thus constitute a probe for localized variations of the environment.

In this work, LLS are sustained by radio-frequency irradiation in high static magnetic fields, but a similar effect can be achieved in a vanishing magnetic field. This has potential applications for prepolarized MRI (15).

In the dynamic nuclear polarization (DNP) experiment introduced by Ardenkjaer-Larsen et al. (8), which has come to be known as ex situ or dissolution DNP, the polarization from the unpaired electrons of admixed free radicals like TEMPO or trityl is transferred to nuclear spins such as those of carbon-13, yielding nuclear polarization on the order of P = (P_α − P_β)/(P_α + P_β) ∼ 20%. This corresponds to sensitivity enhancements of >10,000 compared with the signal obtained at room temperature in a static field B₀ = 7 T. This dramatic increase in polarization makes dissolution-DNP attractive for pharmaceutical and functional studies in liquids (16). However, the time required to build up the enhanced nuclear polarization at low temperatures can be as long as several hours, and the liquid helium required to cool the samples makes the technique expensive. It is noteworthy that the enhanced nuclear spin polarization may be used for several consecutive observations, provided small flip-angle pulses (typically β = 10°) are used to convert only small fractions of the longitudinal magnetization into detectable transverse magnetization. However, the enhanced polarization must be used before it is destroyed by spin-lattice relaxation. This limits applications to studies of dynamic phenomena such as slow diffusion, flow and metabolic conversion. The remarkable sensitivity afforded by DNP may be combined with so-called “ultrafast” or “single-shot” two-dimensional spectra (17–19), and with high-resolution spectroscopy in inhomogeneous magnetic fields (20).

Long-lived states, introduced by M. H. Levitt and collaborators (9, 21), are nuclear spin configurations delocalized on two or more coupled spins that have unusually long relaxation times T_LLS, which can be up to 36 times longer (22) than the spin-lattice relaxation time constant T₁ of the same nuclei. The relaxation properties of LLS are favorable because these states are not affected by dipolar interactions between the spins involved. In some systems, the LLS can be boosted by magnetization transferred from para-hydrogen (23, 24). In selected molecules featuring chemically equivalent nuclei, spin states with relatively long lifetimes are believed to exist that may be converted into detectable magnetization through a hydration reaction (25).

We demonstrate here that in systems with J-coupled spins the enhanced polarization generated via dissolution DNP can be converted into LLS for safekeeping during time intervals 5T_LLS of significant length, before their conversion into detectable magnetization. So far, most dissolution DNP experiments have been performed for unprotonated (e.g., carboxyl) carbon-13 nuclei in fairly small molecules. The technique is bound to evolve toward the use of molecules of increasing mass and complexity including peptides, which regulate many physiological processes, and act as endo- and paracrine signals, neurotransmitters and growth factors (26). So far, only secondary hyperpolarization (27) of peptides was achieved. It is shown here that the polarization of natural-abundance carbon-13 spins in a dipeptide can be enhanced directly by a factor close to 10,000, using dissolution DNP, and converted into long-lived states associated with protons, yielding a lifetime T_LLS that is seven times longer than the longitudinal relaxation time constant T₁ of the same protons. These long-lived states may be sustained using moderate radio-frequency (rf) irradiation or by removing the sample from the magnetic field, as demonstrated by the Levitt group (28), who determined lifetimes of several minutes for LLS involving a pair of nitrogen-15 nuclei in ¹⁵N₂O. The ability to extract controlled amounts of the magnetization stored in long-lived states after arbitrarily chosen time intervals makes this an attractive tool to study slow metabolic reactions.

Results and Discussion

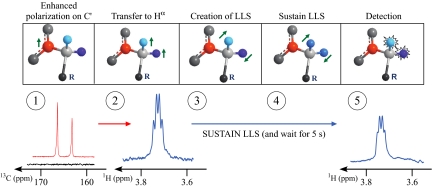
The new experiment comprises five steps (Fig. 1): (i) hyperpolarization, consisting of the creation of enhanced carbon-13 magnetization in an intermediate magnetic field (in our case, B₀ = 3.35 T and T = 1.2 K) followed by rapid heating, dissolution and transfer of the polarized sample in a high-resolution magnet (in our case, B₀ = 7.05 T and T = 300 K); (ii) transfer of the enhanced magnetization from carbon-13 to protons to improve the sensitivity of the subsequent detection; (iii) transformation of the enhanced proton polarization into long-lived states; (iv) sustaining these LLS; and (v) “reading out” by (partial) conversion into observable proton magnetization. The transfer of the sample between the two magnets typically lasts a few seconds, so it is advantageous to keep the magnetization on slowly relaxing “transporter spins” with low gyromagnetic ratios (such as ¹³C). Because of the large enhancements, isotopic enrichment is not necessary and isotopes such as nitrogen-15 or carbon-13 may be used in natural abundance, as in the present study.

Fig. 1.

The DNP-LLS experiment. (i) Signal of hyperpolarized carbonyl ¹³C spins (highlighted in red) of Ala-Gly detected using a single 10° pulse (red trace) compared with a room-temperature spectrum (black trace) obtained by averaging 128 scans using 90° pulses. (ii) Proton signals of the two Gly-H^α spins in Ala-Gly (in light and dark blue). (iii) Conversion into an LLS involving two inequivalent spins. (iv) These proton spins (in blue) are temporarily rendered equivalent by WALTZ irradiation (see Methods) to sustain the LLS. (v) The same proton signals, following an interval τ_m = 5 s where LLS are sustained.

The dipeptide Ala-Gly was chosen to demonstrate the experiment described above. Natural-abundance ¹³C nuclei (Fig. 1) were hyperpolarized as described in ref. 29 (see Methods). The long spin-lattice relaxation time constant of ¹³CO carbons in Gly, T₁(¹³C) = 25.9 ± 0.2 s at 7 T and 300 K, made it possible to heat the sample from 1.2 K to ≈300 K and to transfer it from the polarizing to the high-resolution magnet in 6 s without significant loss of polarization. We estimate the signal enhancement of the polarized sample with respect to the room-temperature equilibrium signal measured in the high-resolution magnet to be at least 7,600, corresponding to a polarization P = (P_α − P_β)/(P_α + P_β) = 4.6% or better. (This lower-limit estimate is rough due to the poor signal-to-noise of the room-temperature reference spectrum.) The enhanced ¹³CO polarization is converted by a reverse INEPT (30) experiment into proton magnetization, and then into an LLS involving the two nonequivalent protons H^α1 and H^α2 of the Gly residue, sustained over a period that can be as long as T = 5T_LLS, and finally transformed into detectable proton magnetization (10, 22). The two H^α protons of glycine in Ala-Gly have a difference in chemical shifts Δν_IS = 0.15 ppm = 45 Hz at 7.05 T. Only two doublets are detected, centered at the chemical shifts of the H^α1 and H^α2 protons, with a coupling constant J(H^α1, H^α2) = −17.3 Hz (Fig. 1). The lifetime of this LLS in Ala-Gly in degassed water (without radicals) is T_LLS = 42.2 ± 0.1 s at 298 K and 11.4 T, i.e., much longer than the spin-lattice relaxation time T₁ of the same protons. In samples stemming from the dissolution-DNP procedure this lifetime is shortened by dipolar interactions with radicals and paramagnetic oxygen. In our experiments (see Methods), we have measured T_LLS(¹H) = 16 ± 0.6 s and T₁(¹H) = 2.3 ± 0.2 s at 298 K and 7.05 T. Degassing has little effect, because the contribution of oxygen to R₁ is <0.5 s⁻¹.

Depending on the system, the T₁ of the “transporter nucleus” may be either shorter or longer than the lifetime of the proton LLS. In the present case, the ratios are T_LLS(¹H)/T₁(¹³C) = 0.63 and T_LLS(¹H)/T₁(¹H) = 7. Transferring the magnetization to protons obviously results in more sensitive detection. The method described in Fig. 2 allows one to convert only a fraction of proton LLS to transverse proton magnetization for detection, whereas the remaining LLS can be sustained for later observation. This would be difficult to achieve had magnetization been stored on the transporter nuclei. In molecules such as amino acids containing at least three aliphatic protons, the proton with the longest T₁ may be used as transporter before creating an LLS involving all three spins. In these molecules, the T₁ of the transporter is shorter than the LLS lifetime by a factor of ∼2 (31).

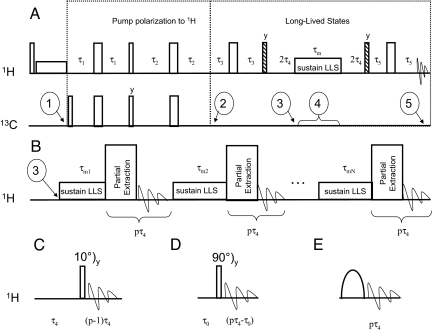
Fig. 2.

Conversion of enhanced polarization into long-lived states (LLS). (A) Pulse sequences for the DNP-LLS experiment, used to transfer hyperpolarized natural- abundance ¹³C magnetization (1) to the CH^α₂ protons of Gly (2), excite (3), and sustain (4) a LLS on these spins, and transform this into detectable magnetization (5). Hatched, narrow and wide rectangles represent (π/4), (π/2), and π pulses, respectively. The first two proton pulses may be removed for routine applications. The phases are given only when they differ from x. The delays were τ₁ = 1/(8J₁) = 24 ms, τ₂ = 1/(4J₁) = 48 ms, τ₃ = 5/(4J₂) − τ₂ = 24.3 ms, τ₄ = 1/(4Δν_IS) = 6.7 ms, and τ₅ = 1/(4J₂) = 14.5 ms, where J₁ = J(C^′,H^α1,2) = 5.2 Hz, J₂ = |J(H^α1,H^α2)| = 17.3 Hz, and Δν_IS = 0.12 ppm = 37.2 Hz at 7 T is the chemical shift difference between the two protons. The interval τ_m where LLS are sustained ranged from 4 to 25 s. (B) Variant of the (4)–(5) segment of the pulse sequence in A, designed to transform only fractions of LLS into detectable terms, sustaining the remaining part again as LLS. The number p must be a multiple of 4, i.e., pτ₄ equals an integer number of precession periods of the zero-quantum coherence. The process may be repeated N times. (C) Method for partial extraction of detectable magnetization from LLC using an interval τ₄ = 1/(4Δν_IS) followed by a 10° pulse and detection. (D) Partial extraction of detectable magnetization from LLC using a brief interval τ₀ = arcsin(π/18)/(2πΔν_IS) ≈ 2 ms, followed by a 90° pulse and detection. (E) Same as C and D, using a selective pulse affecting one of the components of either doublet of the two coupled spins.

The pulse sequence used to transfer polarization from carbon-13 to proton spins, excite and sustain LLS is shown in Fig. 2. Once magnetization is stored as LLS, it is possible either to convert it entirely into detectable single-quantum terms (Fig. 2A) or to transfer only a fraction for detection, after which the remaining part is again sustained, to be detected at a later stage (Fig. 2 B–E). The first proton pulses in Fig. 2A saturate the “native” proton magnetization, notably in molecules that do not contain any carbon-13 isotopes. These pulses may be removed for routine applications, although they improve the accuracy of the exponential fits of T_LLS decays. The refocused inverse-INEPT sequence is followed by a spin-echo τ₃ − π − τ₃ to continue the evolution under J(H^α1, H^α2), which started during the previous τ₂ − π − τ₂ interval, to generate LLS (32, 33), which are then sustained by a suitable rf irradiation (see Methods), before their conversion into detectable in-phase terms. The enhanced polarization can be converted in part from LLS to detectable terms using the sequence in Fig. 2B. The idea is to interrupt the rf irradiation during a delay pτ₄ that must be a multiple of the precession period of the zero-quantum coherences, pτ₄ = n/Δν_IS. After this delay, the LLS, which is comprised of a sum of zero-quantum terms (which have undergone n complete rotations), and longitudinal two-spin order terms (which do not precess) is restored, ready to be sustained again by rf irradiation. The part that has been converted into single-quantum terms cannot be recovered, and relaxation of zero-quantum coherences and two-spin order will take their toll during the delay pτ₄. The interval during which detection is performed has a lower limit τ_min = 1/J, imposed by the minimum resolution required. The “partial extraction” method may be carried out in at least three ways. A first method (Fig. 2C) relies on the insertion of a small flip angle β pulse during the precession interval, at the point where the conversion from ZQ_x to ZQ_y coherence is complete (32, 34). In Fig. 2D, however, depending on the delay τ₀, only a fraction of ZQ_x is transformed into ZQ_y, which is then entirely converted into observable terms. The choice of τ₀ = arcsin(π/18)/(2πΔν_IS) leads to M^extracted/M^total = sin(π/18) with the method in Fig. 2D. This is the same fraction as obtained with β = π/18 = 10° in Fig. 2C. Finally (Fig. 2E), it is possible to apply a selective pulse to one of the four proton transitions to transform a fraction of the LLS into detectable terms, as shown in ref. 22. An error of ± 10% in the estimated value of either J_IS or Δν_IS leads to a 1.5% loss in sensitivity.

Beyond our earlier work on the excitation of LLS (10, 32, 33, 35), the idea of converting small fractions of LLS into observable magnetization should open new possibilities for the study of slow diffusion and slow exchange by NMR spectroscopy. The present experiments are also designed to cope with heteronuclear J-couplings between the protons involved in the LLS and transporter nuclei such as carbon-13 or nitrogen-15.

No special hardware or software is required to implement these experiments, so that routine NMR equipment suffices. For in vivo studies, the preparation step (1–3) can be performed in the separator/infusion pump described in ref. 29, which can host an NMR coil, whereas the sustain (4) and detection (5) steps have to be performed using the imaging coil.

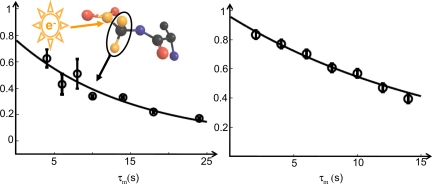
Each dissolution DNP experiment yielded 2 to 5 mL of hyperpolarized solution. Rather than using the entire amount for one NMR experiment, several experiments requiring only 1 mL each were carried out, whereas the remainder of the hyperpolarized solution was stored in a container located immediately above the high-resolution NMR probe. In each experiment, a different τ_m interval (Fig. 2) was used. Because the polarization level is not identical from one experiment to the next, inter alea because of the dilution of the freshly injected solution in the sample that was already present in the tube, the final proton signal intensities were normalized dividing them by the intensity of the enhanced ¹³C signal, measured by direct ¹³C detection after a 10° pulse. The ratio between proton signals derived from LLS and the ¹³C signal obtained in this manner was fitted to an exponential decay with three parameters (Fig. 3). The resulting lifetime was in agreement with the T_LLS measured for a similar sample without DNP enhancement and without degassing, but with the same radical concentration. Once the proton LLS is generated, it can be sampled at any desired point. The sustaining sequence may be composed of a series of shaped rf pulses (32) interleaved with delays. Some sustaining sequences can keep the dissipated power to a minimum, in view of possible in vivo applications. We have also used the sequence in Fig. 2B to convert small fractions of LLS into detectable magnetization with n = 5 successive time intervals, each with τ_m = 4 s, and observed the signals during 5 acquisition intervals of ≈50 ms each. These intervals do not lead to any significant signal losses, because they are much shorter than the long periods (up to 25 s) where the LLS is sustained.

Fig. 3.

Fits of the exponential decay of a DNP-enhanced long-lived state of the two H^α Gly protons in Ala-Gly (insert) with T_LLS = 15 ± 2 s (Left), and LLS decay in a similar sample obtained without DNP enhancement, yielding T_LLS = 16 ± 0.6 s (Right).

Concerning the size-limit for DNP-LLS targets, we know that LLS can be excited and sustained in molecules containing more than two spins (31, 36, 37), such as taurine and amino acids like Gly, Asp, Asn, and Cys, and in mobile parts of proteins. Thus, a significant ratio T_LLS(¹H)/T₁(¹H) = 6 has been observed for glycine residues in the C-terminus of Ubiquitin (38). However, no hyperpolarization using dissolution DNP has been reported so far for molecules larger than ≈600 Da (39).

In conclusion, we present a method to alleviate one of the main drawbacks of the dissolution-DNP experiment, i.e., the need to use the enhanced nuclear polarization within a short time interval on the order of 5T₁. The new DNP-LLS experiment may find applications for the study of (bio)chemical reactions both in MRI and high-resolution NMR. We demonstrated that dissolution DNP can achieve direct “hyperpolarization” in peptides. Our experiments create long-lived magnetization that should be useful for obtaining maps of the biodistribution of complex tracers and their metabolites (3, 11). The metabolic rates may be followed using detection of controlled amounts of magnetization at desired time intervals.

Methods

The experiments were performed using 0.6 M l-Ala-Gly mixed with 50 mM tetramethylpiperidine-oxyl (TEMPO) and dissolved in 35%/65% vol/vol glycerol-d₈/D₂O. The frozen beads were placed in a home-built prepolarizer (29), and irradiated at 94 GHz with 30 mW microwave power for 5 h at 1.2 K and 3.35 T. The sample was quickly dissolved in 5 mL of D₂O (preheated to 190 °C at 12 bar) to a final concentration of 40 mM. The hyperpolarized solution was transferred to 10-mm tubes maintained at a temperature of 25 °C in an inverse broadband probe in a high-resolution B₀ = 7.05 T magnet (Bruker 300 WB). The transfer time was 6 s. The room-temperature experiments using nuclear polarization at Boltzmann equilibrium were carried out at 300 MHz and 298 K using ≈20 mM Ala-Gly solutions in deuterated water. Eight transients were acquired for the reference LLS experiments using a delay of 30 s between consecutive experiments. Experimental relaxation time constants T₁ and T_LLS were determined by fitting normalized spectral intensities to mono-exponentially decaying functions, and the reported standard deviations are derived from 50 fits of the data, with random noise added to the experimental signal intensities based on the observed noise in the spectra. A WALTZ (40) sequence with an rf amplitude ν₁ = 1.5 kHz was used to sustain the LLS.