Senescence of the temporal impulse response to a luminous pulse

Abstract

An impulse response function (IRF) to a luminous pulse was derived for 70 normal observers ranging in age from 16 to 86 years. Thresholds were measured for two pulses separated by interstimulus intervals from 6.7 to 180 ms. The pulses had a spatial Gaussian shape (±1 SD = 2.3° diam) and were presented as increments on a 10 cd/m² background, having the same chromaticity as the pulse. A spatial 4-alternative forced-choice method was combined with a staircase procedure. Retinal illuminance was equated individually by heterochromatic flicker photometry and control of pupil area. Each IRF was measured four times, in separate sessions, for each observer. IRFs calculated from the threshold data revealed significant age-related changes in the response amplitude of both excitatory and inhibitory phases. In general, there were no significant changes in the time to the first peak or in the first zero crossing. For 12 of 20 observers over 60 years of age, however, the amplitude of the second (inhibitory) phase was reduced relative to the excitatory phase so their IRFs were quite slow and long. Control conditions with three pseudophakic observers and two normal observers with induced blur demonstrated that age-related changes in the IRF under these conditions cannot be ascribed to optical factors. The data suggest that the human visual system generally maintains a stable speed of response to a flash until at least about 80 years of age, even while there are senescent reductions in response signal amplitude.

1. Introduction

Senescent losses in temporal sensitivity of the human visual system have been demonstrated extensively through early studies of critical flicker frequency, the lowest frequency of temporal modulation that is indiscriminable from a steady light (Coppinger, 1955; see reviews by Kline & Scheiber, 1982; Weale, 1982). Part of this loss in temporal vision is due to retinal illuminance differences between younger and older observers. For example, Wright and Drasdo (1985) (see also Kuyk & Wesson, 1991) reported losses in contrast sensitivity to sinusoidal flicker (3.3–30 Hz) that were greatest at higher frequencies and they ascribed most of this change to age-related decreases in pupillary area. This interpretation is supported by a shift in the temporal contrast sensitivity function (tCSF) downward (lower sensitivity) and to the left (lower temporal resolution, longer time constants) with reduced retinal illuminance (DeLange, 1958; Kelly, 1961) or equivalently, reductions in pupillary area (Mayer, Kim, Svingos, & Glucs, 1988).

Age-related reductions in retinal illuminance due to increases in ocular media density could also contribute to senescent losses in temporal contrast sensitivity, especially for stimuli that include short- and middle-wave light (Werner, 1982; Weale, 1988). The effects of ocular media senescence can be minimized by long-wave stimuli. Thus, Tyler (1989) used an LED with dominant wavelength of 660 nm and found an age-related loss after ~16 years at high (20–30 Hz) but not low (5 Hz) temporal frequencies. He interpreted these results in the time domain as due to an impulse response with a change in timing parameters (time to peak and duration of excitatory response or zero crossing), but not amplitude. With the same apparatus, but incorporating a forced-choice psychophysical procedure, Kim and Mayer (1994) measured the tCSF of 89 observers (18–77 years). They found changes after ~44 years for intermediate through high temporal frequencies (>7–50 Hz). Calculated impulse response functions showed significant age-related reductions in response amplitude but not in time to the peak or in the zero crossing. There is thus an inconsistency between these studies in the nature of age-related changes in the IRF for luminance modulation. It may be added that the latter two studies used a relatively high luminance, long-wavelength test stimulus which may have produced frequency-dependent adaptation at a post-receptoral site (Swanson, 1993). A subsequent study with a test stimulus of lower retinal illuminance reported tCSFs consistent with those of Mayer and Kim (Swanson, Fiedelman, & Fish, 1995).

The tCSF is commonly used for inferring the IRF, however, it only provides information about amplitude and does not preserve phase (Victor, 1989). A complementary basis for obtaining the IRF is to measure thresholds for two consecutive pulses as a function of the time between them, or inter-stimulus interval (ISI). The shape of the IRF can be derived more accurately using this double-pulse method because an auto-correlation function of the IRF can be obtained (Ikeda, 1965; Rashbass, 1970; Watson & Nachmias, 1977; Uchikawa & Yoshizawa, 1993) whereas measurement of tCSFs provides only the maximum contrast in the convolution between the impulse response and flicker threshold. The two-pulse method was used to measure senescent changes in the IRF in this study. We used the model of Burr and Morrone (1993) to calculate the IRF from the two-pulse detection data from a large group of observers, covering a broad age range, with controls for variation in retinal illuminance and psychophysical criterion. We found significant age-related changes in IRF amplitude and a complex relation between aging and temporal parameters, with no change for most observers, but an increase for some older observers due to the loss of inhibitory phase.

2. Methods

2.1. Subjects

Seventy phakic (natural lenses) observers (32 males and 38 females) ranging in age from 16 to 86 years participated in this experiment. They were approximately evenly distributed across age (~10 each decade) and ethnically diverse. In addition, three pseudophakes (subjects with an intraocular lens implant following removal of a cataractous lens), 67–76 years, served as controls for effects of retinal illuminance.

None of the subjects reported systemic, ocular or neurological conditions known to disrupt vision. All subjects received a complete optometric/ophthalmologic examination in the Department of Ophthalmology at the UC-Davis Medical Center. The presence of retinal disease and abnormal ocular media in the tested eye were ruled out by ocular examination including visual acuity, slit lamp examination, and direct and indirect ophthalmoscopy. Color stereo fundus photographs of the macula and optic disc (ETDRS Fields 1 and 2) were evaluated by a retinal specialist using a stereo viewer. The retinae of all subjects were found to have no more than five small (≤63 µm) drusen and no vascular, retinal, choroidal or optic nerve findings known to disrupt visual function. Intraocular pressure was ≤22 mmHg. All subjects demonstrated a corrected Snellen acuity of ≥20/30 in the tested eye, as well as normal color vision when tested with the Neitz anomaloscope, the HRR pseudoisochromatic plates and the Farnsworth F-2 plate. Subjects with refractive errors greater than +4.00 or −6.50 D were excluded.

Written informed consent was obtained following the Tenets of Helsinki, and with approval of the Office of Human Research Protection of the University of California, Davis, School of Medicine.

2.2. Apparatus and stimuli

Thresholds for contrast detection were measured by presenting test stimuli as luminance increments on a 10 cd/m² (1.69 log Td.) background of the same chromaticity (CIE x, y = 0.33, 0.33). Two pulses (~1.2 ms each with interstimulus intervals ranging from 6.7 to 180 ms) were presented in one of four quadrants defined by a central fixation cross. The four positions of the test stimuli were located 1.70° to one side or the other and 1.70° above or below the center of the fixation cross. A Gaussian patch with a 2.26° diameter at 1 SD was chosen for a test spatial profile to eliminate artifacts caused by spatial transients. These stimuli were presented on a CRT display (Sony GDM-200 PS) operating at a 150 Hz frame rate that was controlled by a video board with 15-bit resolution (Cambridge Research Systems, VSG 2/4) using a Dell Pentium computer. A second CRT monitor displayed the stimuli for the experimenter.

An astronomical telescope was focused so that the subject viewed the CRT at optical infinity with a 2.16 × magnification. A 5.0 mm aperture stop was positioned in front of the telescope objective such that the 2.5 mm image of the stop formed the exit pupil of the optical system in the plane of the subject’s anatomical pupil. Trial lenses were mounted in a holder positioned in front of the eye to correct individual refractive error. An adjustable chair and a dental-impression bite-bar assembly, with movement in three orthogonal directions, were used to maintain the subject’s position. A pellicle was placed in the optical path so that light from the subject’s eye was directed into an auxiliary optical system. Using a reticule aligned with the optic axis of the telescope, this auxiliary system permitted precise alignment of the subject’s pupil. The display monitor, optical system and subject were enclosed within a light-tight viewing lane.

2.3. Calibrations

A spectroradiometer/photometer (Photo Research, Model PR703-A) and a chromameter (Minolta, CS-100) were used to measure the luminance and chromaticity coordinates of the CRT phosphors. A gamma correction to linearize the relation between phosphor radiance and voltage was based on lookup tables using a photodiode and calibration software in the VSG software (Cambridge Research Systems, OptiCal).

Rise and fall times of the CRT phosphors were measured with a p–i–n 10 silicon photodiode (United Detector technology, Optometer 81, 10 mm diameter) connected to a digital oscilloscope. Intensity increments and decrements were ~1.2 ms for all phosphors. Because the diameter of the Gaussian patch at 1 SD was 106 pixels on a 640 × 480 pixel display, the decay of the test stimulus at the vertical scan frequency was less than 1.5 ms from the maximum. Peak-to-peak timing error of the ISI was <3%.

2.4. Procedure

In the first session, 18 Hz heterochromatic flicker photometry was used to equate the intensity of the blue and green phosphors to the red phosphor. The stimulus was a 0.64°–2.77°. annulus surrounding a central fixation cross, and coincided with the four positions of IRF test stimuli. Practice was provided in free view before formal testing using the bite-bar. Because ocular media transmission of the red phosphor is affected negligibly by lenticular senescence, and because the optical system produced an image of the stimulus in the plane of the pupil that was smaller (2.5 mm diameter) than that expected for observers spanning our age range (Loewenfeld, 1979), it follows that retinal illuminance was equated across observers.

Following 5 min dark adaptation and 10 min adaptation to the background, subjects were presented with test stimuli preceded by a high pitch tone and followed by a low pitch tone. The subject’s task was to press one of four buttons to indicate the quadrant in which the stimulus was detected. This 4-alternative forced-choice (4AFC) method was combined with a two-down, one-up staircase in which the luminance of both pulses was changed simultaneously to obtain a contrast threshold. Thresholds were based on the last four of six reversals, corresponding to a probability of 70.7% detection. During each session the 14 ISI settings were tested with 14 different staircases interwoven in random order. Each subject participated in at least four test sessions.

3. Results

3.1. Derivation of the impulse response

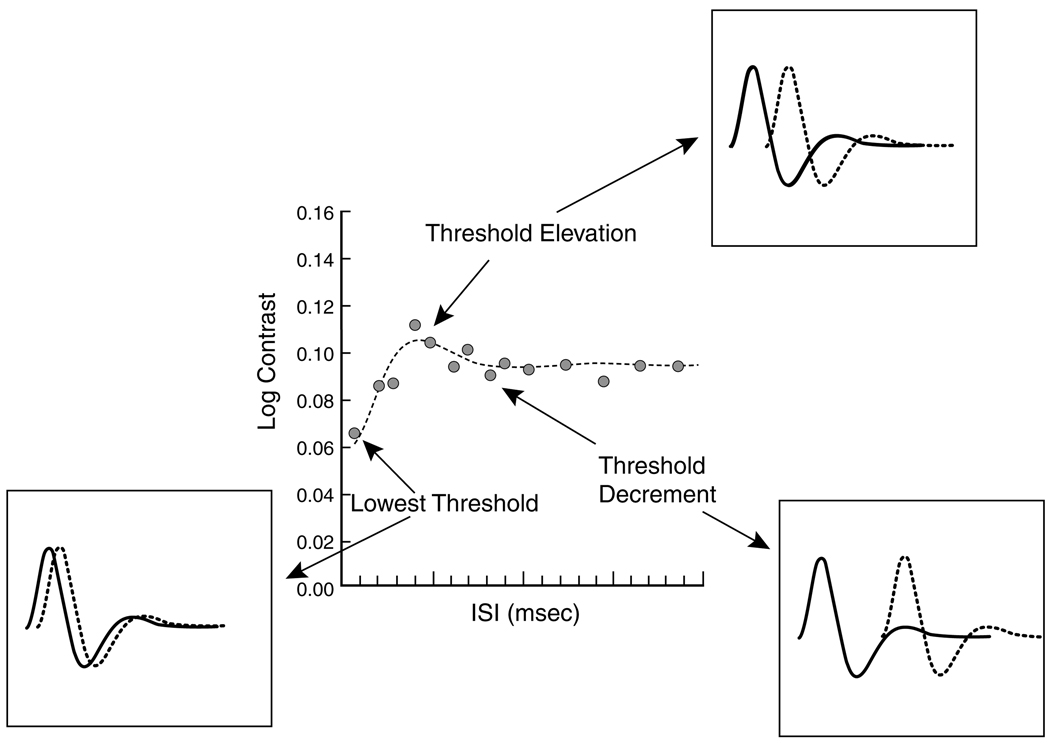
Fig. 1 shows log contrast plotted as a function of ISI for a young observer (18.8 years). Insets illustrate the theoretical relations between thresholds and the impulse response. It is assumed that each stimulus pulse elicits a response that may be approximated by an exponentially-damped oscillation. The temporal separation between the stimuli will influence threshold. For example, at the shortest ISI, the two responses will be nearly in phase and summation will result in low contrast threshold. At higher temporal separation, when the responses are out of phase, there is interference between excitatory and inhibitory phases of the two responses so threshold will be elevated. With further separation between pulses, interference will be reduced so threshold will fall, albeit not to the extent of the first case because summation of responses is incomplete.

Fig. 1.

Central panel shows log contrast threshold as a function of ISI. Insets show the theoretical manner in which threshold varies due to the phase relations of the responses generated by each pulse pair.

Following Burr and Morrone (1993), we calculated IRFs from the threshold data using the following equation for an exponentially damped frequency-modulated sine wave:

$$I(t)=a_{0}H(t)t\text{sin}\{2\pi [a_{1}t{(t+1)}^{-a_2}]\}\text{exp}(-a_{3}t),$$ (1)

where I(t) is the impulse response as a function of time (t), parameters a_0–3 are positive with a₀ defining the overall gain, a₁ the fundamental frequency of oscillation, a₂ the modulation frequency over time, and a₃ the steepness of the decay. H(t) is the Heaviside function to assure that I(t) begins with a value of 0 when t < 0. Thus,

$$\begin{array}{cc}H(t)=0,& t<0,\\ H(t)=1,& t\ge 0.\end{array}$$

The model was fitted to the data by varying four parameters, a_0–3, using a least-squares criterion. We chose this model because it has fewer free parameters than other models of the impulse response and does not require the unproven assumption that the impulse response derives from a minimum-phase filter (Watson, 1982; Swanson, Ueno, Smith, & Pokorny, 1987; Uchikawa & Yoshizawa, 1993). That assumption can be included, however, by using a₂ = 0, but we found that this had little effect on the derived IRF in most cases. For 19 of 70 observers, the value of a₂ was more than 35% of minimum values of a₀, a₁, and a₃. But in 15 of these subjects, the difference in fits between a₂ = 0 vs. a₂ ≠ 0 was negligible. Monophasic, biphasic and triphasic IRFs can be described with changing values of a_0–3, and without a priori assumptions about the number of lobes in the IRF.

The fitted functions are based on a model of probability summation of visual response (Watson, 1979), R(t, τ):

$$R(t,\tau )=K[I(t)+H(t-\tau )I(t-\tau )],$$ (2)

where τ is the SOA (ISI is (τ-[pulse duration])) and H(t) is the Heaviside function. K is the luminance of each pulse over the background luminance and p, proportion correct, is:

$$p=1-(1-r)\text{exp}\left(-\left[{\displaystyle {\int }_0^T{\left|R(t,\tau )\right|}^{\beta }\mathrm{d}t}\right]\right),$$ (3)

parameter r is the probability due to chance (0.25 in this experiment) and parameter β, which determines the steepness of the psychometric function, was set to 4. T is the time to take the integral and must be long enough so that all response will be zero within ISIs. We set T as 3.18 s. P₀, the proportion correct at threshold, was (√2)/2, which is determined by the two-down one-up procedure in the 4AFC method we employed. From Eqs. (2) and (3), we obtained Eqs. (4) and (5) as:

$$\begin{array}{l}K=[\raisebox{1ex}{$C$}\!\left/ \!\raisebox{-1ex}{$\{\left({\displaystyle \sum _{n=0}^{2385}|I(n\mathrm{\Delta }t)+H(n\mathrm{\Delta }t-\mathrm{\tau })I(n\mathrm{\Delta }t-\mathrm{\tau }){|}^{\beta }}\right)$}\right.\\ {\times \mathrm{\Delta }t\}]}^{1/\beta },\end{array}$$ (4)

$$(\text{Log contrast at threshold})={\text{log}}_{10}((10+K)/10),$$ (5)

where C is − ln [(p₀ − 1)/(r − 1)] (= − ln((4 − 2221A2)=3)) and Δt was set to 1.333 ms. n was changed from 0 to 2385 (3.18 s). In the model fit, parameters of the IRF (a₀–a₃) were changed to obtain the best fit to threshold data points for each ISI using a least-squares method.

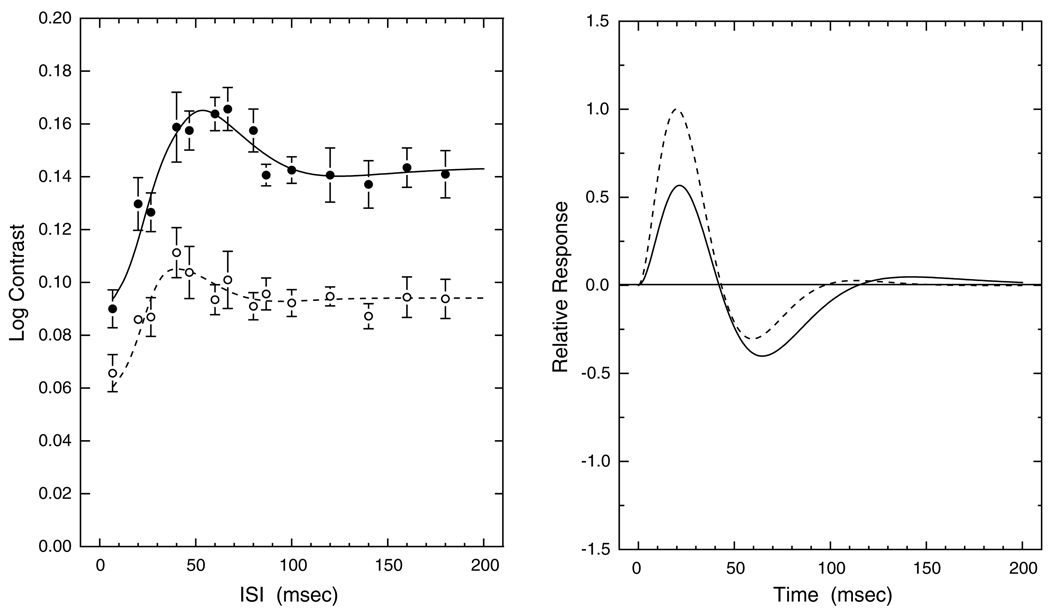
The left panel of Fig. 2 shows log contrast threshold plotted as a function of ISI for typical younger (18.8 years) and older (60.2 years) observers. As expected, thresholds are higher for the older observer. This was confirmed for the entire sample by linear regression analyses. Two-pulse contrast thresholds increased significantly with age for each of the 13ISIs (p < 0.001). The IRFs computed from the data of these two observers are presented in the right panel of Fig. 2. The first and second phases of the IRF are interpreted as excitatory and inhibitory phases, respectively. The younger observer in this figure has a higher first-phase amplitude, but does not differ from the older observer in response timing for this phase. The younger observer also has a faster second (inhibitory) phase. Overall, excitatory amplitude and timing parameters were not correlated across observers, except for certain elderly observers as defined in Section 3.3.

Fig. 2.

Left panel shows contrast thresholds and model fits plotted as a function of ISI for two observers: open symbols and dashed curve, age 18.8 years; closed symbols and solid curve, age 60.2 years. Error bars denote ±1 SEM. Right panel shows IRFs calculated from Eq. (1) for the same two observers with dashed and solid curves as in the left panel.

Because phase is lost in the double-pulse method, it was occasionally found that two very different IRFs could be fitted about equally well. In those cases, we selected the IRF that was closest to the mean because the shape of the other IRF always looked unrealistic (e.g., low amplitude of excitation with high amplitude of inhibition) relative to physiological measures.

3.2. Individual differences: trimodal impulse response functions

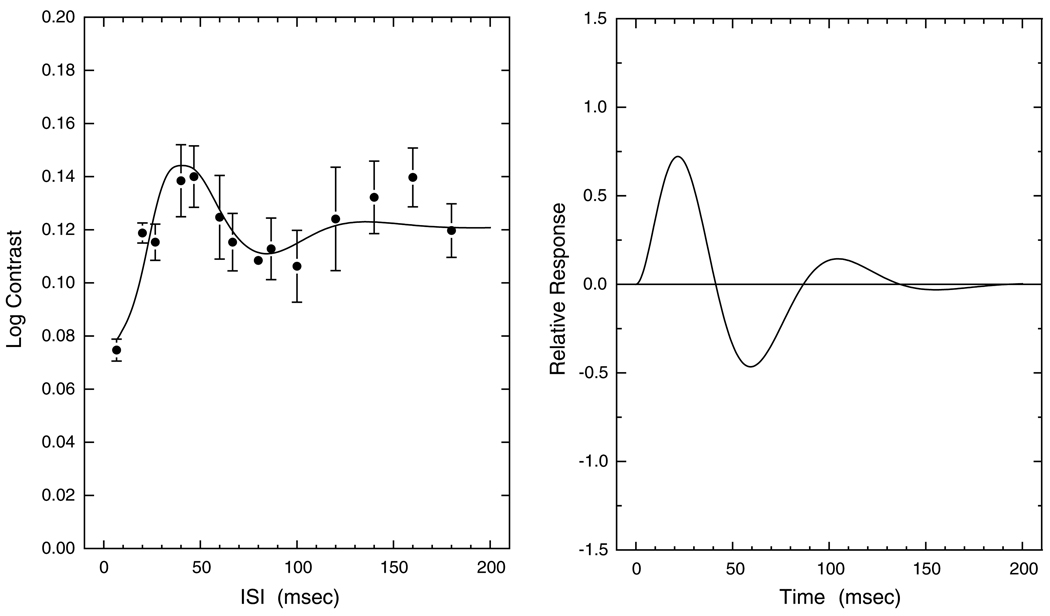
The IRF was characterized by initial excitatory and inhibitory phases, but for some observers the IRF was trimodal due to a second excitatory phase. Fig. 3 shows a trimodal IRF from a 37-year-old observer. In this example, there is even a fourth phase (second inhibitory phase) with low amplitude. Overall, IRFs with at least three phases were obtained for 32 of the 70 observers. There tended to be fewer trimodal functions among the older observers, although this may have been secondary to a generalized loss of inhibition as described in the next section.

Fig. 3.

Left panel shows contrast thresholds and model fits plotted as a function of ISI for a 37.0-year-old observer. Error bars denote ±1 SEM. Right panel shows the corresponding IRF calculated from Eq. (1).

3.3. Individual differences: inhibitory phase

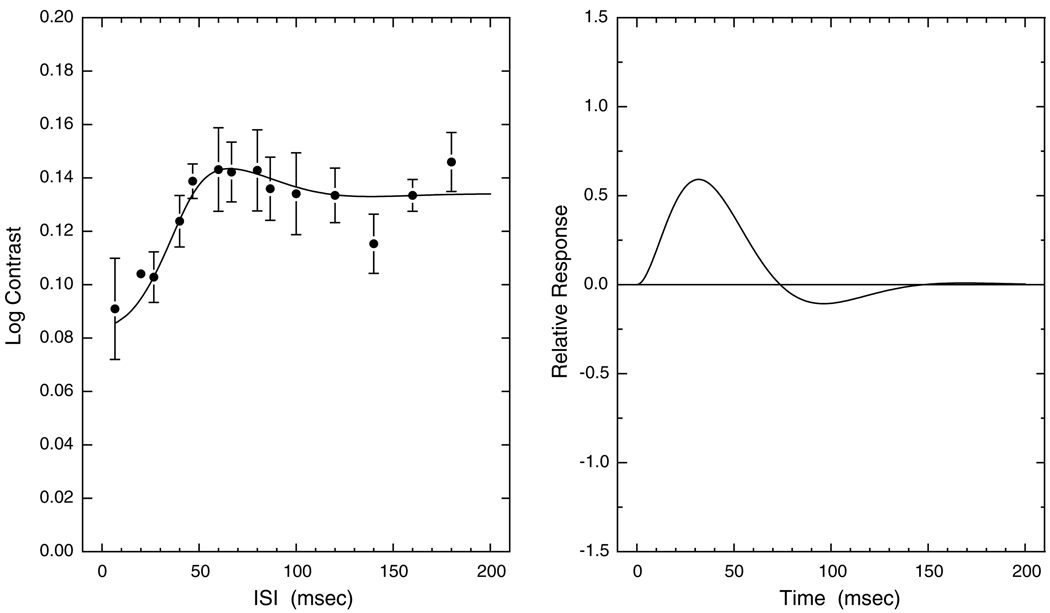
Fig. 4 shows data and model fits for a 71.6-year-old observer. Note that the amplitude of the inhibitory phase of the IRF is low. The excitatory phase is thus slow and long. A reduced inhibitory phase (to <20% of the absolute value of the excitatory phase) was found in 17 observers. Subjects with reduced inhibitory phase could be observed from age 26 years, after which their proportion was stable until about 60, but the proportion rapidly increased with age after about 60 years. Additionally, six other observers demonstrated near-zero inhibitory phase. The near absence of inhibitory phase was found only for observers above the age of 70 years. In observers over 70, who have little or no inhibitory phase, six were male and seven were female. Overall, there was no significant difference in the proportion of males and females with reduced or near-absent IRF inhibition.

Fig. 4.

Left panel shows contrast thresholds and model fits plotted as a function of ISI for a 71.6-year-old observer. Error bars denote ±1 SEM. Right panel shows corresponding IRF calculated from Eq. (1).

3.4. Control for optical factors

The contrast thresholds from the three pseudophakic observers were in agreement with that of their age-matched cohorts as will be shown in subsequent figures and as might be expected with our procedures that essentially equate retinal illuminance across observers.

Subjects were refracted for the test distance and our conditions were chosen to be insensitive to blur and small fixation inaccuracies, as the stimuli were large and spatially tapered by a Gaussian envelope. In addition, the effective pupil diameter of 2.5 mm helps to maintain contrast sensitivity across spatial frequencies that would otherwise decline with the introduction of optical aberrations and optical defocus (Green & Campbell, 1965; Charman, 1979). As a control, however, we tested two observers (ages 29 and 38 years) with and without 1.0–1.5 D of positive defocus. Contrast thresholds were measured for all ISIs over several sessions for each observer. The results of the induced blur condition differed negligibly from that obtained under our standard conditions. Individual and age-related changes in the IRF under these conditions, therefore, are not attributable to optical factors.

3.5. Senescent changes in the impulse response

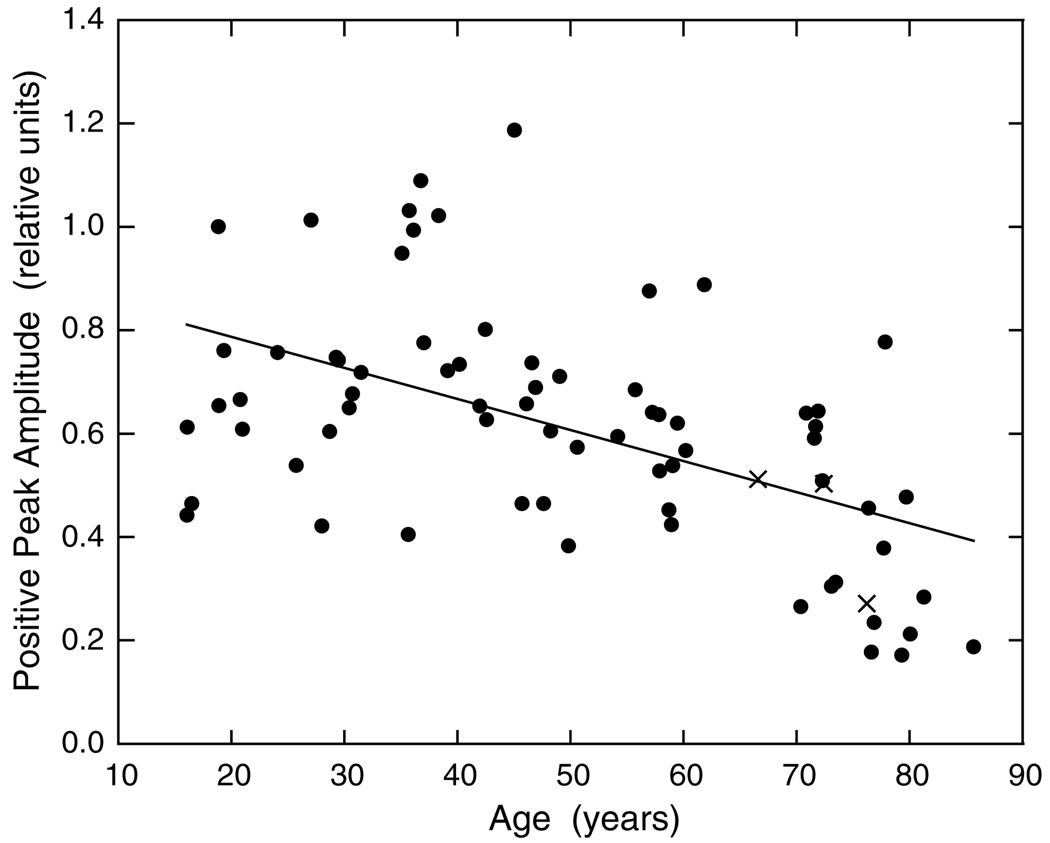
Individual differences in the IRF are substantial so a large group of observers is required to evaluate changes in relation to age. Fig. 5 shows the peak amplitude of the first phase of the IRF for 70 phakic and three pseudophakic observers (X’s) plotted as a function of age. A regression analysis based on all phakic observers showed that there is a significant reduction in first-phase amplitude with age (r = −0.53; F_1,68 = 24.600, p < 0.001).

Fig. 5.

Amplitude of the first (positive, excitatory) phase of the IRF is plotted as a function of age. The regression line was fitted to the data of all (phakic) observers denoted by filled symbols. X’s denote pseudophakic observers.

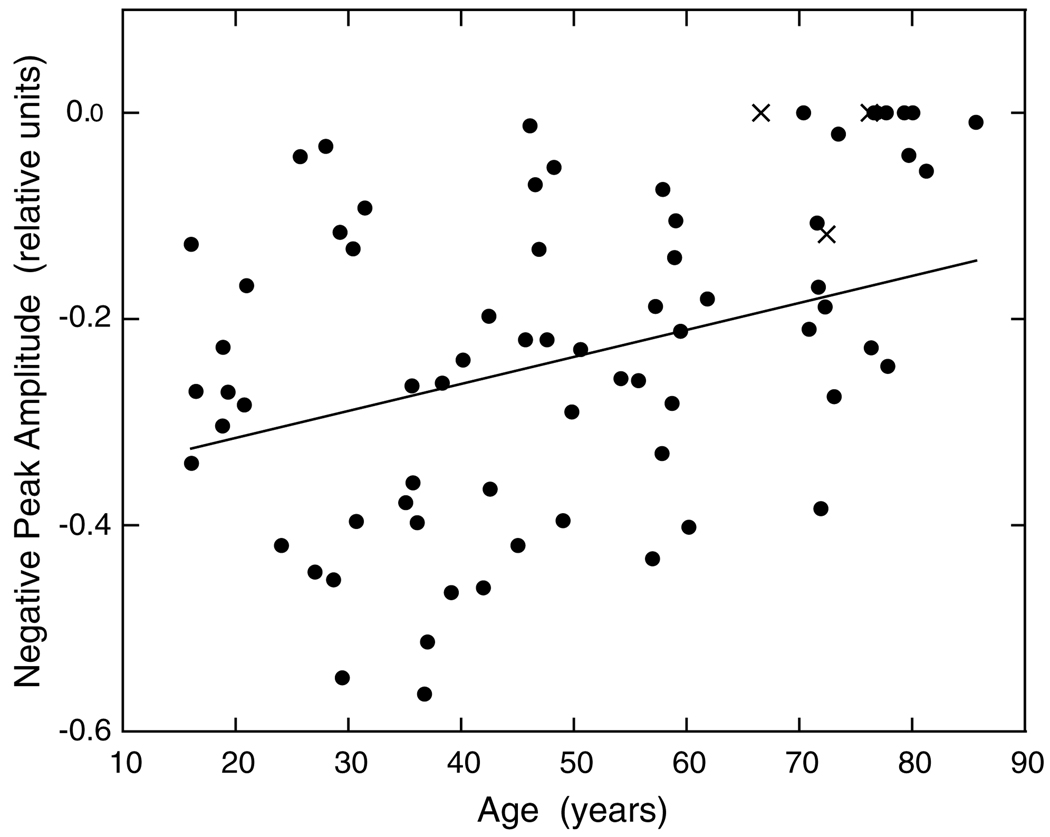
Fig. 6 shows the change in inhibitory amplitude of the IRF plotted as a function of age. The regression line indicates a significant reduction in inhibitory amplitude with increasing age (r = 0.46; F_1,69 = 7.951, p < 0.01). A number of the older observers had a complete loss of inhibitory phase as is evident from examination of the figure and this causes a ceiling effect that reduces the strength of the correlation. Overall, it is clear that the two primary phases of the IRF undergo a significant loss in amplitude with increasing age, and that some elderly observers exhibit a complete loss of IRF inhibition.

Fig. 6.

Amplitude of the second (negative, inhibitory) phase of the IRF is plotted as a function of age. Regression line was fitted to the data of all observers denoted by filled symbols. X’s denote pseudophakic observers.

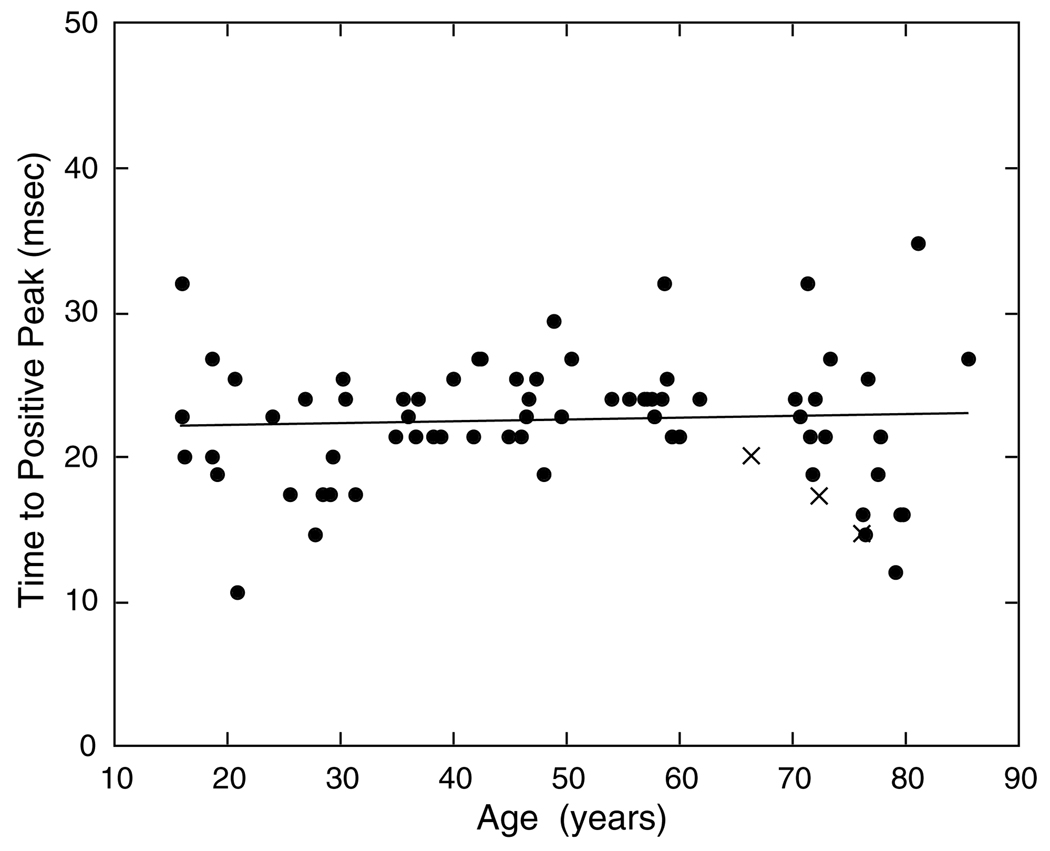
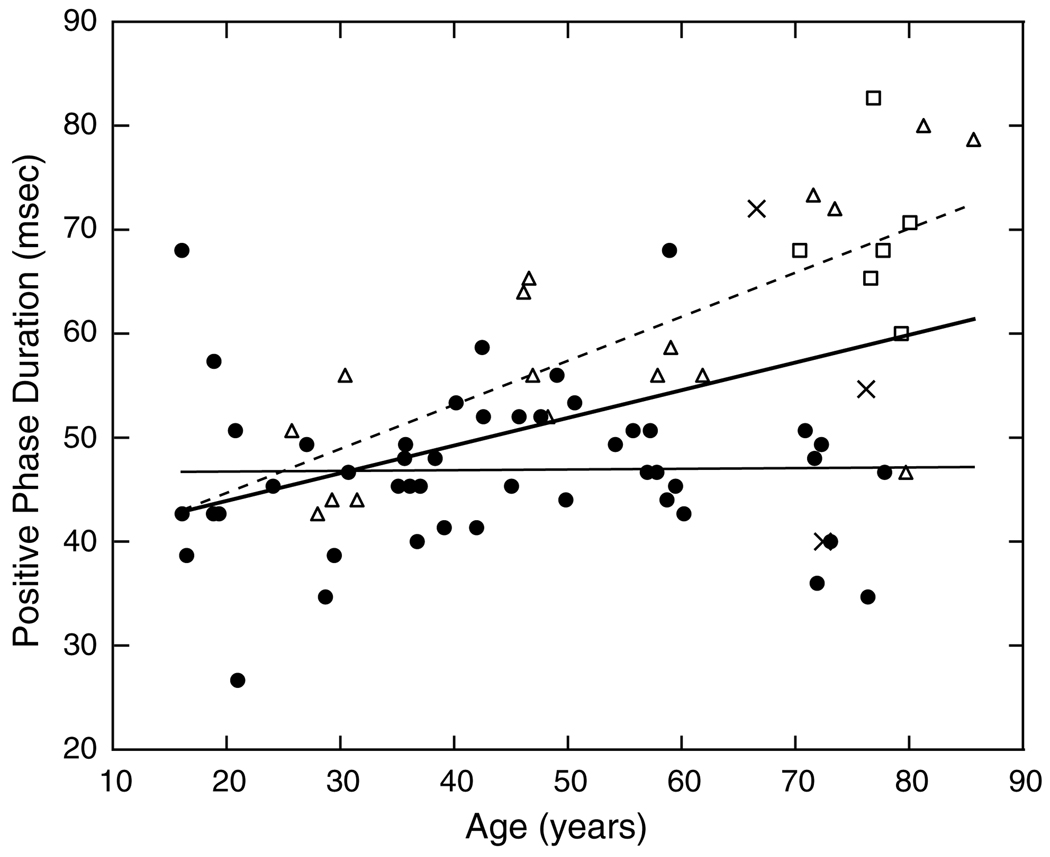
In contrast to amplitude, response timing of the excitatory phase is stable across the age range of our observers. This is shown in Fig. 7. The slope of the regression line is not statistically significant. The analysis of the duration of the first excitatory phase is more complicated due to observers with little or no inhibitory phase. For those observers with a loss of inhibition (Section 3.3), the duration of excitation necessarily increases. To provide a clearer evaluation of possible age-related changes, least-squares linear regression lines in Fig. 8 are presented for the overall group and after removing observers with little inhibitory amplitude (<20% of the absolute value of the excitatory phase) or no inhibitory phase, denoted by triangles and squares, respectively. For the latter observers, the duration of the excitatory phase steadily increased with age and the slope of the regression line is significant (F_1,21 = 23.921, p < 0.0001). This is shown in Fig. 8 by the dashed line. These observers are responsible for a significant increase in the duration of the positive phase of the IRF for the overall group (F_1,68 = 18.988, p < 0.0001), shown by the bold solid line. When observers with little or no inhibition are excluded, as shown by the thin solid regression line, there is no significant change with age. For this group, the duration of the first excitatory phase of the IRF was 40–60 ms, regardless of age (intercept of the regression line = 46.6 ms). Thus, for the majority of observers, the excitatory phase has stable temporal characteristics with age, while for some observers there is a change secondary to the loss of inhibitory amplitude.

Fig. 7.

Time to peak of the first (positive, excitatory) phase of the IRF is plotted as a function of age. The regression line was fitted to the data of all observers denoted by filled symbols. X’s denote pseudophakic observers.

Fig. 8.

Duration of the first (positive, excitatory) phase of the IRF is plotted as a function of age. Bold regression line was fitted to all phakic observers. X’s denote pseudophakic observers. Filled circles and thin solid regression line represents phakic observers except for those with little (Δ) or no (□) inhibitory amplitude. The dashed regression line was fitted based on the latter observers.

Fig. 9 shows the peak time for the inhibitory phase of the IRF plotted as a function of age using the same plotting conventions as in Fig. 8. The thin solid line fitted to phakic observers, except for those with little inhibitory amplitude, is not statistically significant, indicating that the time to the peak of the inhibitory IRF was essentially constant (intercept = 65.89 ms). For observers with little inhibitory amplitude, a separate regression shows that there is a significant increase in the time to the peak inhibitory phase (F_1,15 = 12.988, p < 0.01) as can be seen from the dashed line. This subset of observers is responsible for a modest but significant increase among the overall group of phakic subjects indicated by the bold regression line in Fig. 9 (F_1,62 = 7.314, p < 0.01).

Fig. 9.

Time to peak of the second (negative, inhibitory) phase of the IRF is plotted as a function of age. Symbols and regression lines as in Fig. 8.

4. Discussion

The results of this research demonstrate that there are significant reductions in the amplitude of both the excitatory and inhibitory phases of the IRF. For some observers, there is a dramatic loss of inhibitory phase (<20% of the excitatory phase). Those observers with no inhibitory phase are only found among the elderly (>70 years). When those observers are excluded from analyses of the timing of the IRF, there is no significant change in relation to age for either the positive or negative phases of the IRF.

In our previous work, we have shown that much of the senescent sensitivity loss in cone pathways is due to early changes in the stream of processing, mathematically equivalent to reduced quantal efficiency or elevations in neural noise (Schefrin, Werner, Plach, & Utlaut, 1992; Schefrin, Shinomori, & Werner, 1995). Senescent changes in additive neural noise have not been found for an M-/L-cone pathway (Werner, Schelble, & Bieber, 2001), but a change in the IRF amplitude might result, at least in part, from the sensitivity losses in cone pathways that occur with age.

In a parallel study in our laboratory (Gerth, Sutter, & Werner, 2002), a retinal IRF was extracted from the multifocal electroretinogram (mfERG) obtained from 71 observers ranging in age from 9 to 80 years. The kernel series was used to synthesize a single-flash response (Sutter, 2000). The mfERG results are remarkably similar to the psychophysical results presented in this paper. The retinal IRF demonstrated significant reductions in amplitude (response density), but not speed (implicit time) with age. These findings support the interpretation that some of the loss in psychophysical IRF may be due to changes in the outer retina. None of the IRFs obtained with the mfERG were triphasic, however. This component of the psychophysical IRF may be derived from processes beyond the retina.

4.1. Trimodal IRFs and possible sites of senescent changes

Nearly half (46%) of our observers demonstrated triphasic IRFs. Trimodal impulse response functions have been reported for some observers by Kim and Mayer (1994) who derived their IRFs from tCSFs. Triphasic IRFs have also been inferred under supra-threshold conditions with pairs of intense brief (5 ms) flashes (Bowen, 1989) and for luminance modulated patterns during saccades (Burr & Morrone, 1996). The importance of the number of phases in the IRF was examined by Stork and Falk (1987) through modeling of Kelly’s (1961) tCSFs obtained with large fields (60°). They show that the more narrow the bandpass of a tCSF, the more oscillations inherent in the corresponding IRFs. When the triphasic function is reduced to a biphasic function in modeling, it results in a calculated tCSF that is in error by as much as 50% at low temporal frequencies implying that multiple oscillations of the IRF are not an artifact of modeling. Stork and Falk found that multiple oscillations of the IRF were most evident in Kelly’s data measured at 77 Trolands, which is similar to the retinal illuminance of this study (49 Td.).

Trimodal IRFs can also be seen in the membrane current response of some primate cones, although they are more typically diphasic (Schnapf, Nunn, Meister, & Baylor, 1990). A trimodal response is not typically reported for P-cells, but is seen for M-cells at higher contrasts (Lee, Pokorny, Smith, & Kremers, 1994). Benardete (1994) reported trimodal IRFs in M ON cells, in response to achromatic, low spatial frequency stimuli, but not with high spatial frequency patterns. Our achromatic increments presented on an achromatic background are consistent with the conditions in which Benardete found trimodal impulse response functions from primate M-cells. It seems likely that M-cells are responsible for detection of the stimuli in this experiment because of their larger receptive fields and higher contrast sensitivity compared to P-cells (Kaplan & Shapley, 1986). In this context, it is worth noting that age-related changes in an M-cell pathway have been inferred from senescent changes in scotopic contrast sensitivity under conditions in which only M-cells are likely to be sensitive (Schefrin, Tregear, Harvey, & Werner, 1999). It is possible that the changes in the IRF demonstrated here are due, in part, to changes in an M-cell pathway.

4.2. Slower IRFs with reduced or near-zero inhibitory phase

As described in Section 3.5, the time to the peak of the IRF is nearly constant for all observers, but the duration of the positive phase of the IRF is necessarily longer for observers with reduced inhibitory phase. This is inherent in the antagonistic relation between excitation and inhibition; reduced inhibition causes the crossover to shift toward higher first-phase duration. The loss of IRF inhibition in some elderly observers could be due to (1) an overall reduction in signal strength and/or (2) a specific loss of inhibition.

Stork and Falk’s analyses demonstrate that with reduced retinal illumination, there is a reduction in inhibitory phase and a loss of higher-order oscillations in the IRF. The stimuli used in this study were essentially equated for retinal illuminance, but they may never-theless have been less effective for older observers due to reduced sensitivity of cone pathways. The inhibitory amplitude of the IRFs derived in this study may have been more stable across age if the stimuli were initially equated with respect to increment threshold.

The site of inhibitory loss in some older observers could occur in an M-cell pathway as already mentioned, but it could also involve a change in low-pass filtering mechanisms in the cortex (Lee, Pokorny, Smith, Martin, & Valberg, 1990). This suggestion is buttressed by simultaneous recordings of pattern electroretinograms (pERG) and visually evoked potentials (VEPs) in young and elderly observers by Porciatti, Burr, Morrone, and Fiorentini (1992). They concluded that at least some of the loss in temporal response with age is due to changes at post-retinal sites.

Senescent loss of inhibition in the spatial domain has been demonstrated through single-unit recordings in primary visual cortex of elderly rhesus macaque monkeys (Schmolesky, Wang, Pu, & Leventhal, 2000). Specifically, elderly animals had decreased orientation and direction selectivity and these changes appear not to be secondary to changes at precortical sites (Spear, Moore, Kim, Xue, & Tumosa, 1994). Thus, while the senescent reduction in the overall amplitude of the IRF may occur at a retinal stage, the specific loss in the inhibitory phase could be mediated at more central sites of temporal processing.

4.3. Implications for temporal contrast sensitivity

For a linear system, the impulse response is directly related to the tCSF by the inverse Fourier transform. Burr and Morrone (1993) calculated tCSFs from their two-pulse data using Eq. (1) and found that they predicted the shape of empirically-determined tCSFs measured with counterphase sinusoidal gratings. Several previous studies of age-related change in temporal vision have derived a theoretical IRF based on measured tCSFs for younger and older observers (Tyler, 1989; Kim & Mayer, 1994), but not the other way around.

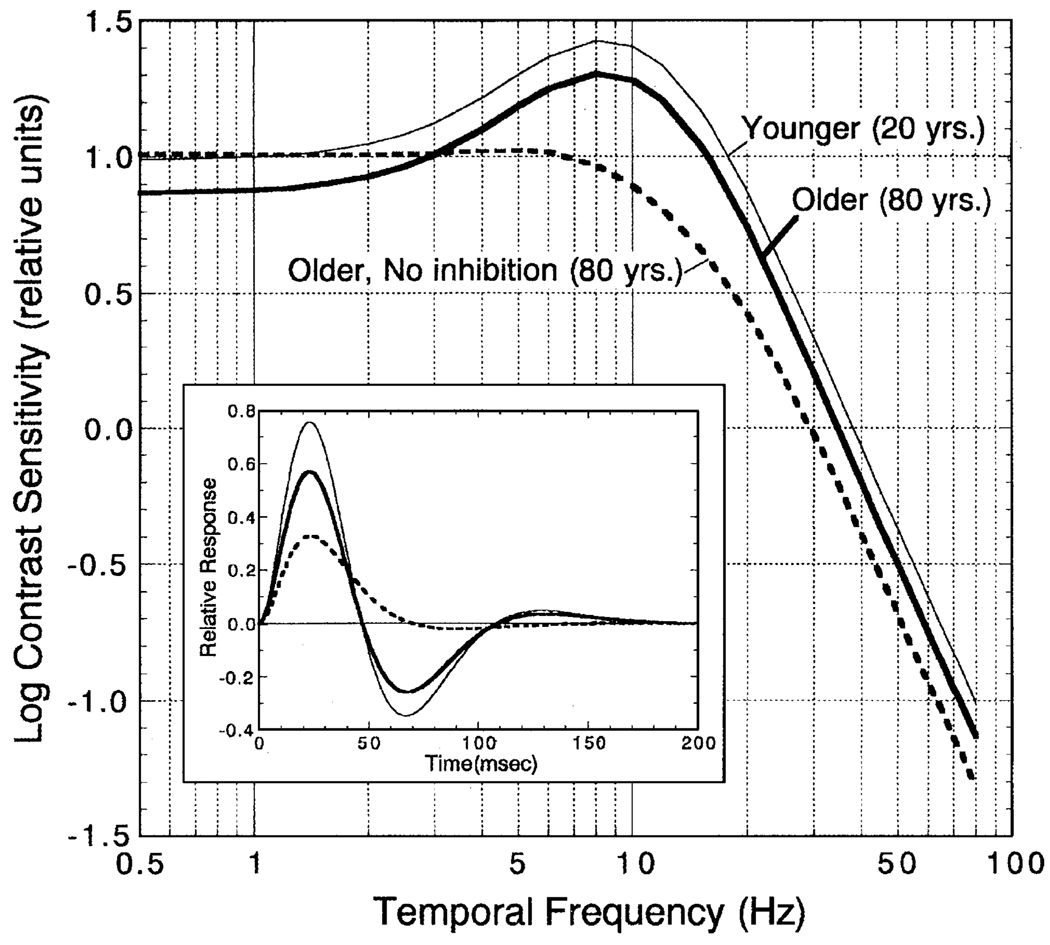
Theoretical tCSFs were calculated for younger (20 years) and older (80 years) observers of this study. The latter were generated for older observers with normal age-related losses in inhibition or a complete loss of inhibitory IRF amplitude. These tCSFs were generated from theoretical IRFs calculated using six parameters from the regression lines fitted to the data: (1) positive peak amplitude (Fig. 5), (2) negative peak amplitude (Fig. 6), (3) time to positive peak (Fig. 7), (4) duration of the positive phase (Fig. 8), (5) time to negative peak (Fig. 9), and (6) second zero crossing time (i.e., combined duration of the first positive and negative phases; not shown in figures). From Eq. (1) a set of a₀–a₃ parameters was calculated such that the theoretical IRFs agreed with the six empirical constraints based on least-squares criteria. The resultant theoretical IRFs are shown by the inset in Fig. 10.

Fig. 10.

Temporal contrast sensitivity functions (tCSFs) for theoretical 20-year-old (thin smooth curve) and 80-year-old observers with normal or no second phase (inhibitory) amplitude. Log contrast sensitivity in relative units is plotted as a function of temporal frequency. Inset: The theoretical IRFs used to generate these tCSFs calculated from Eq. (1). Curves are plotted as in the main figure.

A fast Fourier transform of the theoretical IRFs was calculated to obtain theoretical tCSFs (MATLAB v. 6.1, The MathWorks, Inc., Natick, MA). To minimize the assumptions inherent in this computation (Dagnelie, 1992), we also calculated a discrete convolution of the IRF and sinusoidal stimulus modulation in 13.3–1.11 ms steps (0.5–80 Hz in the frequency domain). Temporal contrast sensitivity was defined by the output-signal contrast at the stable portion of the convolution (i.e., when the amplitude of the IRF was less than 1% of the maximum or minimum to avoid phase-dependent stimulus transients). Error associated with this approximation is ~±3%. The resultant tCSFs are shown in Fig. 10 for each type of observer. As expected from the shape of the IRFs, the theoretical tCSF of the older observer with IRF inhibition has the same shape as the younger observer, but overall sensitivity is lower. These functions are consistent with previously reported data (Kim & Mayer, 1994; Tyler, 1989). The theoretical tCSF of the older observer lacking IRF inhibition is quite different. It has a low-pass shape with reduced sensitivity at middle- and higher temporal frequencies; at frequencies below ~3Hz, the predicted sensitivity of the older observer with no inhibitory amplitude is higher than for the older cohort and is similar to that of a younger observer. The reduction of inhibitory phase of this older theoretical observer is consistent with longer integration of cone signals and reduced temporal resolution. Older observers with low-pass tCSFs have not been reported, presumably because previous studies have not used stimuli below 1.5 Hz and the luminance levels used in previous studies were substantially higher than in the present study. Overall, the IRFs and theoretical tCSFs of this study are consistent with the conclusion of Kim and Mayer (1994) that senescent changes in temporal processing primarily involve sensitivity, not resolution. This follows from the relatively stable temporal characteristics of the IRF for most observers, but a senescent reduction in IRF amplitude.